Reinforcement Learning with Quantitative Veriﬁcation for Assured

Multi-Agent Policies

Joshua Riley

1 a

, Radu Calinescu

, Colin Paterson

, Daniel Kudenko

and Alec Banks

Department of Computer Science, University of York, York, U.K.

L3S Research Centre, Leibniz University, Hanover, Germany

Defence Science and Technology Laboratory, U.K.

Keywords:

Reinforcement Learning, Multi-Agent System, Quantitative Veriﬁcation, Assurance, Multi-Agent

Reinforcement Learning.

Abstract:

In multi-agent reinforcement learning, several agents converge together towards optimal policies that solve

complex decision-making problems. This convergence process is inherently stochastic, meaning that its use in

safety-critical domains can be problematic. To address this issue, we introduce a new approach that combines

multi-agent reinforcement learning with a formal veriﬁcation technique termed quantitative veriﬁcation. Our

assured multi-agent reinforcement learning approach constrains agent behaviours in ways that ensure the

satisfaction of requirements associated with the safety, reliability, and other non-functional aspects of the

decision-making problem being solved. The approach comprises three stages. First, it models the problem

as an abstract Markov decision process, allowing quantitative veriﬁcation to be applied. Next, this abstract

model is used to synthesise a policy which satisﬁes safety, reliability, and performance constraints. Finally, the

synthesised policy is used to constrain agent behaviour within the low-level problem with a greatly lowered risk

of constraint violations. We demonstrate our approach using a safety-critical multi-agent patrolling problem.

1 INTRODUCTION

Multi-agent systems (MAS) have the potential for use

in a range of different industrial, agricultural, and de-

fence domains (Fan et al., 2011). These systems,

which allow multiple robots to share responsibilities

and work together to achieve goals, can be used in ap-

plications where it would not be practical or safe to in-

volve humans. Multiple robotic agents ﬁtted with spe-

cialised tools and domain-speciﬁc functionality can

work together to achieve complex goals which would

otherwise require human agents to place themselves

at risk. MAS could be particularly beneﬁcial within

hazardous work environments, such as search and res-

cue operations (Gregory et al., 2016), or where tasks

need to be completed in irradiated places. Indeed this

has been seen previously with the Fukushima nuclear

power plant disaster, where multiple robots were used

to complete jobs (Schwager et al., 2017).

Many of these complex and hazardous environ-

ments require the agents to operate independently of

direct human control, and it is these environments

which are the focus of our study.

Reinforcement learning (RL) is one promising

https://orcid.org/0000-0002-9403-3705

technique which enables agents to learn how to

achieve system objectives efﬁciently (Patel et al.,

2011). MAS with RL has been proposed for work

within many scenarios and has become a signiﬁcant

research area, including the use of MAS for nuclear

power plant inspections (Bogue, 2011).

However, successful deployment of these systems

within safety-critical scenarios must consider hazards

within the environment, which if not accounted for,

can lead to unwanted outcomes and potentially result

in damage to the system, resources, or personnel.

Such safety considerations and guarantees are

missing from traditional RL, which aims to learn

a policy which maximises a reward function with-

out consideration of safety constraints (Garcia and

Fern

andez, 2012). An RL policy deﬁnes which action

an agent should take when it ﬁnds itself in a particular

state within the problem space.

Our approach extends previous work on safe

single-agent RL (Mason et al., 2017; Mason et al.,

2018) by integrating formal veriﬁcation with multi-

agent reinforcement learning (MARL) algorithms to

provide policies for use in safety-critical domains.

In this work, we present a 3-stage approach for

safe multi-agent reinforcement learning. First, we

encode the problem as an abstract Markov decision

Riley, J., Calinescu, R., Paterson, C., Kudenko, D. and Banks, A.

Reinforcement Learning with Quantitative Veriﬁcation for Assured Multi-Agent Policies.

DOI: 10.5220/0010258102370245

In Proceedings of the 13th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2021) - Volume 2, pages 237-245

ISBN: 978-989-758-484-8

237

process (AMDP). Abstracting the problem is a com-

mon technique used within safety engineering for re-

ducing complexity (Cizelj et al., 2011). The AMDP

must contain all relevant information needed to de-

scribe the problem space, including all of the features

necessary to capture the mandated safety constraints.

Next, we synthesise policies for the abstract model us-

ing quantitative veriﬁcation (QV), a mathematically

based technique for the veriﬁcation (Kwiatkowska,

2007; Calinescu et al., 2012) and synthesis (Calinescu

et al., 2017; Gerasimou et al., 2018; Calinescu et al.,

2018) of probabilistic models whose properties and

safety constraints are expressed formally using proba-

bilistic computation tree logic (PCTL) (Ciesinski and

oßer, 2004). Using QV for this stage allows for for-

mal guarantees that properties will be met such that

the policy generated is safe with respect to the de-

ﬁned constraints. Finally, these policies deemed as

safe by the veriﬁcation stage are used to constrain

a multi-agent reinforcement learning problem where

the agents learn a policy within a ROS simulator

which more closely resembles the real-world environ-

ment.

In order to demonstrate our approach, we intro-

duce a MARL safety domain based on a MAS pa-

trolling problem. In this domain, two robots share the

responsibility of performing tasks within the rooms

of a nuclear power plant. They must work together

to ensure these rooms are visited three times in order

to complete their tasks successfully. However, one

of these rooms has very high amounts of radiation—

enough to damage the robots unless the three visits of

this room are partitioned between the robots in a sen-

sible way. Another requirement from these robots is

to ensure their battery does not drop below a certain

level, and ideally to ﬁnish the objective with spare bat-

tery above the minimum requirement.

Our research contributes to the areas of safe

MARL and safe RL, speciﬁcally to constrained

RL (Garcia and Fern

andez, 2012). To our knowl-

edge, this is the ﬁrst piece of work to apply safe RL

methods to MAS in this fashion. Our approach al-

lows for the use of MARL while having guarantees

on meeting all safety requirements without the need

to restrict the environment as strictly as previous ap-

proaches (Moldovan, 2012).

The remainder of this paper is structured as fol-

lows. Section 2 provides an introduction to the rel-

evant tools and techniques used throughout the pa-

per. Section 3 introduces a domain example which

we use to demonstrate our approach. Section 4 pro-

vides an overview of each stage in our approach. Sec-

tion 5 evaluates the effectiveness of our approach.

Section 6 reﬂects on related research, and ﬁnally, Sec-

tion 7 gives a summary of the results and future work.

2 BACKGROUND

2.1 Single-agent Reinforcement

Learning

Reinforcement learning (RL) is a technique that en-

ables an agent to learn the best action to take depend-

ing upon the current state of the system. This learning

makes use of past experiences to inﬂuence an agent’s

future behaviour. In this way, rewards are associated

with each possible action as the agent explores the

problem space.

The problem space is typically represented as a

Markov Decision Process (MDP) with an agent able

to select from a set of actions in each state. As

the agent moves through the environment, it may

choose between using an action known to be beneﬁ-

cial (exploitation) and those actions about which little

is known (exploration).

When the action is taken a reward (or penalty)

is obtained and the agent updates the reward asso-

ciated with the state action pair Q : (s, a) → R. Q-

learning (Patel et al., 2011) is commonly used to ﬁnd

an optimal value for this mapping.

Once the mapping of state, action pairs to rewards

is complete, we can extract a policy by selecting the

action which returns the maximum reward for the

state we are currently in.

A policy can be seen as a mapping of which ac-

tions should be taken in each state. An optimal policy

is the most efﬁcient collection of state action pairings

possible to reach the desired goal. Standard RL is

concerned with ﬁnding an optimal policy; however,

it does not allow for safety constraints to be deﬁned

as part of the learning process, which means that an

optimal policy may be unsafe.

2.2 Multi-Agent Reinforcement

Learning (MARL)

MARL is an extension of single-agent RL in which

multiple agents learn how to navigate and work to-

gether towards the desired outcome (Boutilier, 1996).

There is a great deal of literature exploring the ben-

eﬁts and challenges of MARL discussed at length

in (Bus¸oniu et al., 2010). Beneﬁts include efﬁciency,

and robustness through the division of labour while

challenges include ensuring reliable communications

and increased complexity. A number of algorithms

have been created explicitly for learning in MAS;

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

238

these algorithms are commonly classiﬁed as inde-

pendent learners, joint action learners, and gradient-

descent algorithms (Bus¸oniu et al., 2010; Bloember-

gen et al., 2015).

Independent learners employ techniques in which

agents learn within a MARL environment but ignore

joint actions for reduced complexity. Independent

learners are the primary type of algorithm on which

this paper focuses. This is largely due to the lack

of assumptions that these algorithms need to make

about observations made between different learning

agents. This means that they are widely applicable to

a range of contexts, including those where environ-

mental variables can diminish the reliability of com-

munication. Independent learners typically learn how

to react to the presence of other robots because of how

other robots alter the environment. However, we note

that while this paper focuses on individual learners,

our approach is not limited to solely these algorithms.

The speciﬁc individual learner algorithm we look

at within the context of this paper is Q-learning.

While the Q-learning algorithm was developed for

single-agent RL, it has been shown to also provide

promising results when used in a MARL setting. This

learning approach was therefore selected for use in

our work due to its simplicity and popularity (Bus¸oniu

et al., 2010; Zhu et al., 2019).

2.3 Quantitative Veriﬁcation (QV)

When a system is described as a state transition

model, QV allows us to determine if quantitative

properties of the model hold. QV relies on efﬁcient

algorithms which examine the entire state-space of a

given model. Probabilistic model checkers such as

PRISM (Parker and Norman, 2014) and Storm (Dehn-

ert et al., 2017) allow for such analysis.

The veriﬁcation process takes as input the model

and a set of properties to be checked against that

model. For an MDP, these properties are ex-

pressed using probabilistic computation tree logic

(PCTL) (Ciesinski and Gr

oßer, 2004). PCTL, as the

name suggests, is a temporal logic and can be used

to express functional and safety speciﬁcations which

need to be met. PCTL is used to work with tempo-

ral properties in the form of sequences, and forms a

common basis for describing property speciﬁcation in

model checkers.

We may also associate a reward with states and

transitions in the model. In this way, we can check

bounds on reachability (of fail states, for example) as

well as the cumulative reward associated with actions

taken within the problem space (e.g. battery usage).

3 DOMAIN EXAMPLE

In order to demonstrate our approach, we have con-

structed a domain example that takes the form of a

patrolling robot system within a nuclear power plant.

There have been many situations in which robots have

been used within this setting, and new technologies

continue to emerge (Bogue, 2011).

The domain is based on the premise of a two robot

system which has the shared responsibility of nav-

igating the rooms and hallways of the plant, shown

in Figure 1. The system must fulﬁl the following re-

quirements:

• C1: Visit each room a minimum of three times

• C2: Complete all tasks without exhausting their

batteries

Constraint C1 may be considered a functional require-

ment whilst C2 is a safety requirement since exhaust-

ing the battery would lead to a need for robot extrac-

tion putting human life at risk. We may also add a

functional requirement with respect to C2 to max-

imise the amount of remaining battery. For our ex-

ample, we assume that the battery life for a robot is

assumed to decrease with every action undertaken in

the problem space.

In addition, we note that Room 4 has a signif-

icantly high level of radiation and whilst this room

must be visited a minimum of three times the amount

of time a single robot spends in the area should be

limited. An additional safety constraint is therefore

added as:

• C3: The amount of time spent in room 4 should

be minimised

Radiation can cause serious damage to robots, as well

as humans. Therefore, using radiation and avoiding

overexposure is a natural safety constraint for us to

use within our example domain.

Figure 1 is a screenshot from the ROS simulator

and illustrates the environment within the 3D simula-

tor from a birds-eye view, and the red lines show the

movement options between each room for the robots.

Let us consider a robot in room 3. From this state,

the robot has 6 possible actions and may move to:

Room 0, Room 1 (travelling west), Room 1 via Hall-

way A, Room 4 via Hallway A, Room 4 via Hallway

B or Room 5. Each route will take a different amount

of time, and hence a different amount of battery usage

will be associated with each transition.

For Room 4, we associate a risk value which is depen-

dent on the route taken through the room and hence

the amount of time expected to be spent in the room

on average. This is shown in Table 1 and was used as

a reward structure for the risk within our model.

Reinforcement Learning with Quantitative Veriﬁcation for Assured Multi-Agent Policies

239

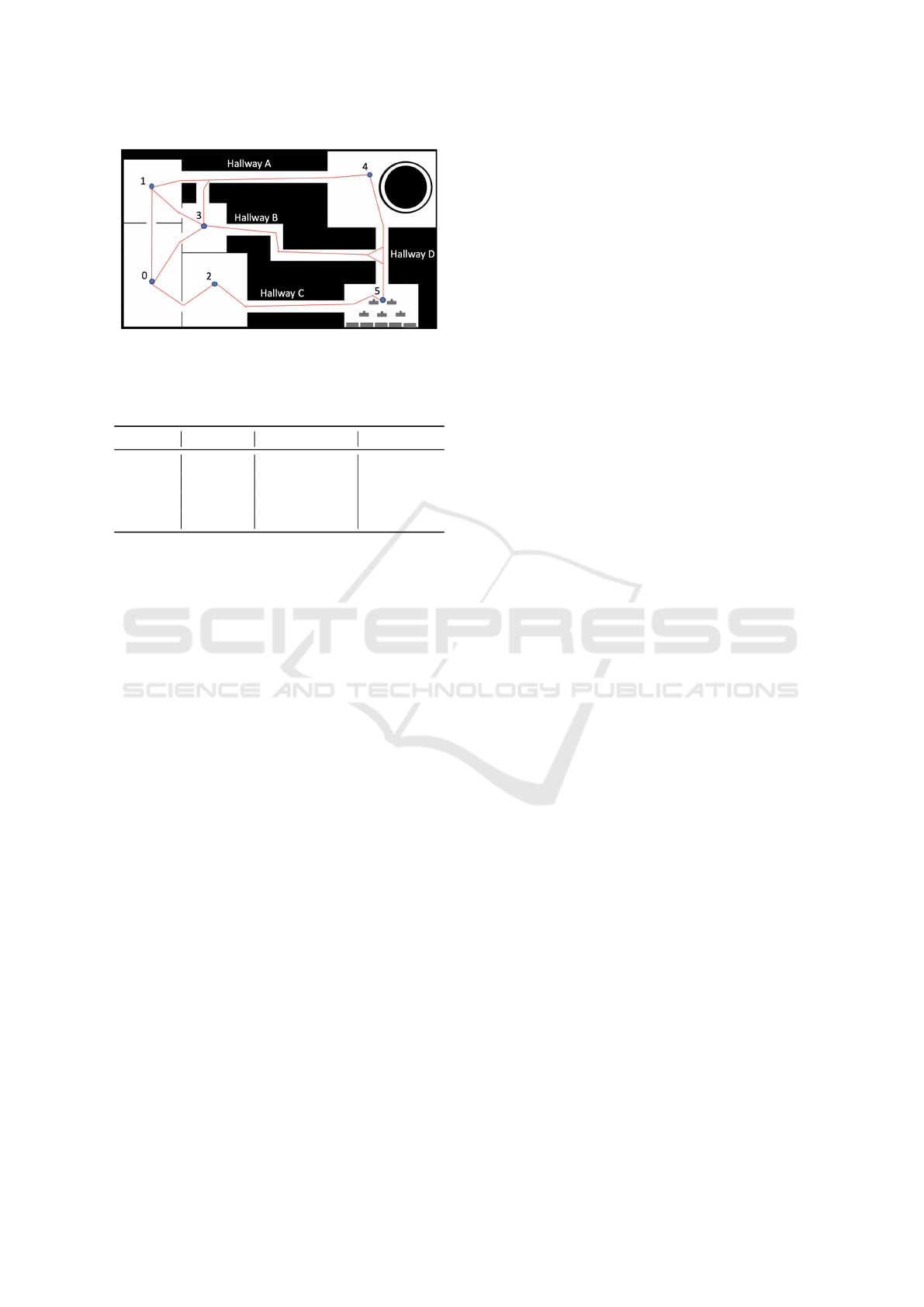
Figure 1: Nuclear reactor map within the simulator, overlaid

with states and possible routes.

Table 1: Options for entering and leaving room 4 and the

corresponding risk of damage.

Entrance Exit Exposure Time Risk

Hallway A Hallway A 30 (seconds) 0.03

Hallway A Hallway D 34 (seconds) 0.04

Hallway D Hallway D 46 (seconds) 0.07

Hallway D Hallway A 34 (seconds) 0.04

4 APPROACH

The approach which we put forward within this

paper comprises three main stages, the abstraction

of the problem, the synthesising of abstracted safe

MARL policies through QV techniques, and ﬁnally,

the MARL learning within the QV restricted envi-

ronment. Our approach can be seen visualised in

Figure 2, as shown, the domain expert must supply

knowledge about the domain, and also supply the de-

sired constraints to allow the problem to be abstracted

for easier use within a QV tool. The ﬁrst two stages of

our approach are aimed at obtaining a deﬁnition of ac-

ceptable safety within the problem domain. The ﬁnal

stage applies MARL techniques in the knowledge that

all policies produced will fulﬁl the safety constraints.

4.1 Stage 1: Constructing an AMDP

In the ﬁrst stage, it is required that all required in-

formation is gathered about the MARL domain. Any

information which is not relevant to the constraints

that govern the domain problem is abstracted away,

with a distinct focus on properties which inform on

the safety of the robots. The remaining information

should allow for the deﬁnition of states, actions or

events, rewards, or costs. Our aim in abstracting out

all unneeded information is to obtain a model which is

small enough for effective and efﬁcient QV whilst re-

taining sufﬁcient knowledge for meaningful policies

to be produced.

For our example, the rooms, as seen in Figure 1,

become states in the AMDP. The actions which a

robot may undertake in each state are then derived

through a consideration of the options available to

transition to another room, e.g. 6 possible actions in

room 3.

Since constraint C1 requires us to know the num-

ber of times a room was visited this leads to each

room state being ‘expanded’ into 4 possible states, i.e.

never visited, visited once, twice, three or more times.

With this, the policy associated with being in room x

is now also a function of how many times the room

has been visited.

One way in which the information is abstracted in

our domain example concerns the time which it takes

for the robots to traverse between locations and the

exact routes which an individual robot may follow.

However, we take a pessimistic approach to battery

usage based on the worst-case distance between the

two locations. In the abstracted model, it is assumed

that the robots move between locations without com-

plex travel and movement within rooms. Abstracting

time from this model dramatically reduces the com-

plexity. Indeed this abstraction is necessary in order

for the model to be analysed using QV since large

complex models are not able to be analysed using tra-

ditional computing resources.

4.2 Stage 2: Synthesising Abstract

Policies

In this stage, the AMDP previously generated is anal-

ysed using quantitative veriﬁcation (QV). A QV tool

such as Prism allows us to describe the AMDP in a

state-based language. Below we show a fragment of

the model for our domain example.

// In room Zero and making a movement choice

[visit0_1_1] !done & r1=0 & visits1<N ->

1:(r1’=1)&(visits1’=visits1+1); // robot 1

visits room 1

[visit0_1_2] !done & r2=0 & visits1<N ->

1:(r2’=1)&(visits1’=visits1+1); // robot 2

visits room 1

In this fragment, we examine the option of moving

from room 0 to room 1 for robots 1 and 2. Here we

see a done variable which is used to indicate the task

of complete and a counter visits1 which indicates the

number of times room 1 has been visited. r1 and r2 in-

dicate the location of robots 1 and 2 respectively. Here

we see that if the action is taken to move to room 1 for

robot 1, then the robot locations are updated, and the

counter associated with room visits is incremented.

rewards "energy"

[visit0_1_1] true : 3;

[visit0_2_1] true : 1.5;

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

240

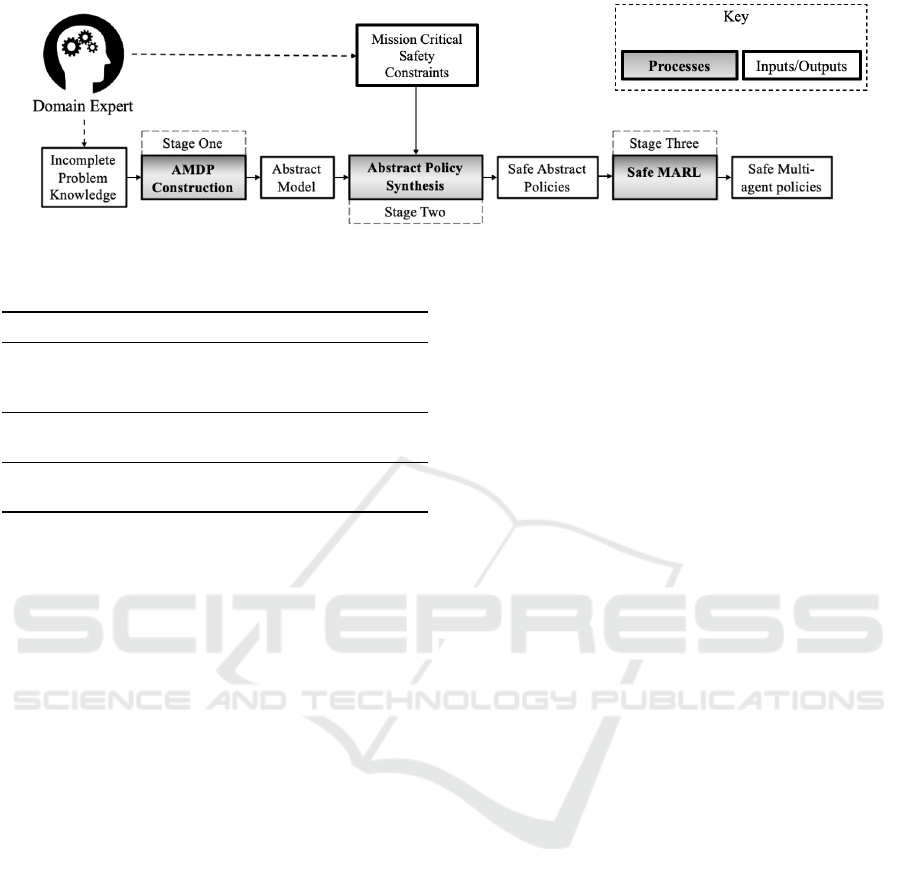
Figure 2: The three stages of our assured MARL approach.

Table 2: Constraints of the domain example.

Constraints PCTL

C1: The probability of all rooms

being visited three times must

be at least 0.8

≥0.80

[F ﬁnished]

C2: The battery of the robots

must not drop below 0.35

≥0.35

[F ﬁnished]

C3: The risk of damage must

not exceed 0.20

≤0.20

[F ﬁnished]

[visit0_3_1] true : 2;

Within this next fragment, shown above, we show

how battery expenditure is represented within the

ADMP as a reward structure. The code within the

square brackets relates to the option names shown

within the ﬁrst fragment and assigns a numerical re-

ward if the corresponding action is taken. This numer-

ical reward will be larger or smaller, depending on the

battery consumption related to the action choice.

Having deﬁned the states, actions and rewards as-

sociated with the AMDP, we must now encode the

functional properties and safety constraints as PCTL

for it to be used in the QV tool in the next stage. First,

we need to add bounds to constraints such that they

may be analysed. The results PCTL with accompany-

ing bounding values are shown in Table 2.

Finally, the QV tool is presented with the model

and the constraints and asked to derive a policy which

minimises the battery usage, and the amount of cumu-

lative risk. This is achieved using an RMIN command

to direct the QV tool and as shown in the code frag-

ment, framing these properties as reward functions.

QV can return multiple policies which are all

guaranteed to fulﬁl the safety requirements. Where

multiple policies are generated, the user may select a

policy by comparing the rewards associated with each

policy. For example, policy 1 may use less battery, but

policy 2 may have a lower risk of damage.

Where a policy can not be found, it may be nec-

essary to revisit stage 1 and modify the safety con-

straints.

The formal guarantees which we reference

throughout the paper relate to the quantitative analy-

sis which we perform. We describe the domain within

PRISM, as mentioned previously, in the form of an

AMDP. This description we create within PRISM in-

cludes the six rooms, the relative actions to move be-

tween these rooms and two agents which can work

through this AMDP. We include reward structures

which allow us to monitor the battery usage and also

counters to determine how much a room as been vis-

ited. In this way, we create a simpliﬁed representation

of our domain problem, including all the information

relevant to the safety constraints. By using QV on

this simpliﬁed representation, we can determine how

likely it is for our safety constraints to be met by any

given policy.

We note that the formal guarantees produced re-

late to the model which is analysed by the QV and that

where the AMDP is insufﬁcient to capture the prob-

lem domain, these guarantees may not hold. It is vital,

therefore that the problem is abstracted appropriately.

This ability to derive policies for which guarantees

are possible is signiﬁcantly different to other forms

of RL, and also most other forms of safe RL, minus

(Mason et al., 2017), which this paper is largely inﬂu-

enced by.

The policy synthesised from the tool maps states

to actions for each agent, and an example of how the

synthesised policy may look like can be seen below.

In this example, each line is a tuple (r

, r

, id) such

that The ﬁrst number is representing the room the

robot is currently in, the second number is represent-

ing the room which the robot will move into, and the

ﬁnal number is acting as an ID to show which robot is

taking action.

2_0_2

3_1_1

1_3_1

3_1_1

1_3_1

...

Reinforcement Learning with Quantitative Veriﬁcation for Assured Multi-Agent Policies

241

4.3 Stage 3: Safe Multi-Agent

Reinforcement Learning

The third and ﬁnal part of our approach involves

learning policies within the non-abstracted domain

but within the constraints learnt in the second stage.

This entails the partitioning and constraint of tasks

and the domain space based on the synthesised pol-

icy. These constraints allow the robots to explore and

learn about the problem domain without violating the

constraints encoded in the veriﬁed policy.

This kind of restriction allows the robots to learn

within their partitioned tasks, without being able to

unnecessarily enter unsafe situations which will con-

ﬂict with the mission objectives. While under these

restrictions, an action may be taken which holds a

quantiﬁed level of risk, but with the use of QV, we can

guarantee that the cumulative risk, and the probability

of risky events happening, is bounded. This approach

does not aim for optimality, as the most optimal ap-

proach may be disallowed during the QV process; it

does, however, guarantee a level of safety and quality

while increasing the speed of the learning process.

5 EVALUATION

5.1 Experimental Setup

We demonstrated our approach using an openly avail-

able ROS simulator (Portugal et al., 2019). The sim-

ulator makes use of simulated lasers for localisation

and can be used to control physical robots as well

as the simulated robots used in our work. Within

the simulation, agents must navigate ‘patrol points’

which are single geographical coordinates within the

domain; these patrol points are connected through ac-

tion choices.

A model of the nuclear reactor was created in the

simulator, as shown in Figure 1, and an AMDP was

constructed in the PRISM language to represent the

rooms and available transitions and rewards we as-

signed. The constraints we require to be met were

encoded as properties in PCTL, as seen in Table 2.

The AMDP was then analysed using PRISM.

PRISM allowed a policy to be produced which met

the constraints while minimising risk and battery us-

age. This policy was then used to constrain the state

action pairings of each robot. After this was com-

pleted, MARL was allowed to run episodically using

the constrained state action pairings in the ROS sim-

ulator.

To demonstrate the value of our approach, we con-

ducted two sets of experiments, one which makes use

of standard MARL and one which utilises our ap-

proach. Within our experiments, we make use of

the Q-learning algorithm; within this algorithm, we

use the discount factor γ = 0.7 and a learning rate of

α = 0.3. Within both experiments, we make use of an

exploration of ε = 0.5., this simply being the proba-

bility that the agents will choose to explore their envi-

ronment rather than exploit. These values were found

experimentally after multiple interactions of testing

based on the non-constrained and constrained learn-

ing runs, inﬂuenced by the nature of the domain and

the number of episodes in a learning run.

For our RL implementation, a reward structure

was used, which complements this type of patrolling

problem. A numerical reward is given every time a

room is reached, based on how long it has been left

unattended; this is a common reward structure used

within patrolling (Portugal and Rocha, 2016). We

tailored this reward structure with additional rewards

based on how little battery was expected to be used

by making an action. This ensured that eventually,

the robots would locate a suitable policy while not

frivolously using the battery. We tailored this stan-

dard reward function for the example domain’s re-

quirements; we also end an episode when a failure

event occurs.

5.2 Results

For our experiments, 200 learning episodes were run,

with a single episode being completed when all rooms

had been patrolled three times. While this is not a

large number of learning episodes, it was sufﬁcient

for a domain of this simplicity. The results of these

experiments are shown in Figure 3 and 4.

The ﬁrst experiment which was completed was the

unsafe baseline experiment with no assured MARL

constraints.

It took over 150 learning runs for this to consis-

tently produce an intelligent policy which satisﬁed

the overall mission objective to visit all rooms three

times. An intelligent policy is a policy which com-

pletes all tasks within the environment without com-

plete loss of battery power. Learning episodes that

produce policies that also satisfy constraint C1 from

Table 2 are annotated with a triangle.

As can be seen in Figure 3, the battery usage for the

unconstrained robots is considerably higher with the

battery of robot one often depleted before the end of

the episode.

Figure 4 also shows us that the unconstrained

robots did violate the amount of permitted time spent

in the reactor room. Joint risk, as we refer to it in this

paper, is the risk related to time spent exposed to ra-

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

242

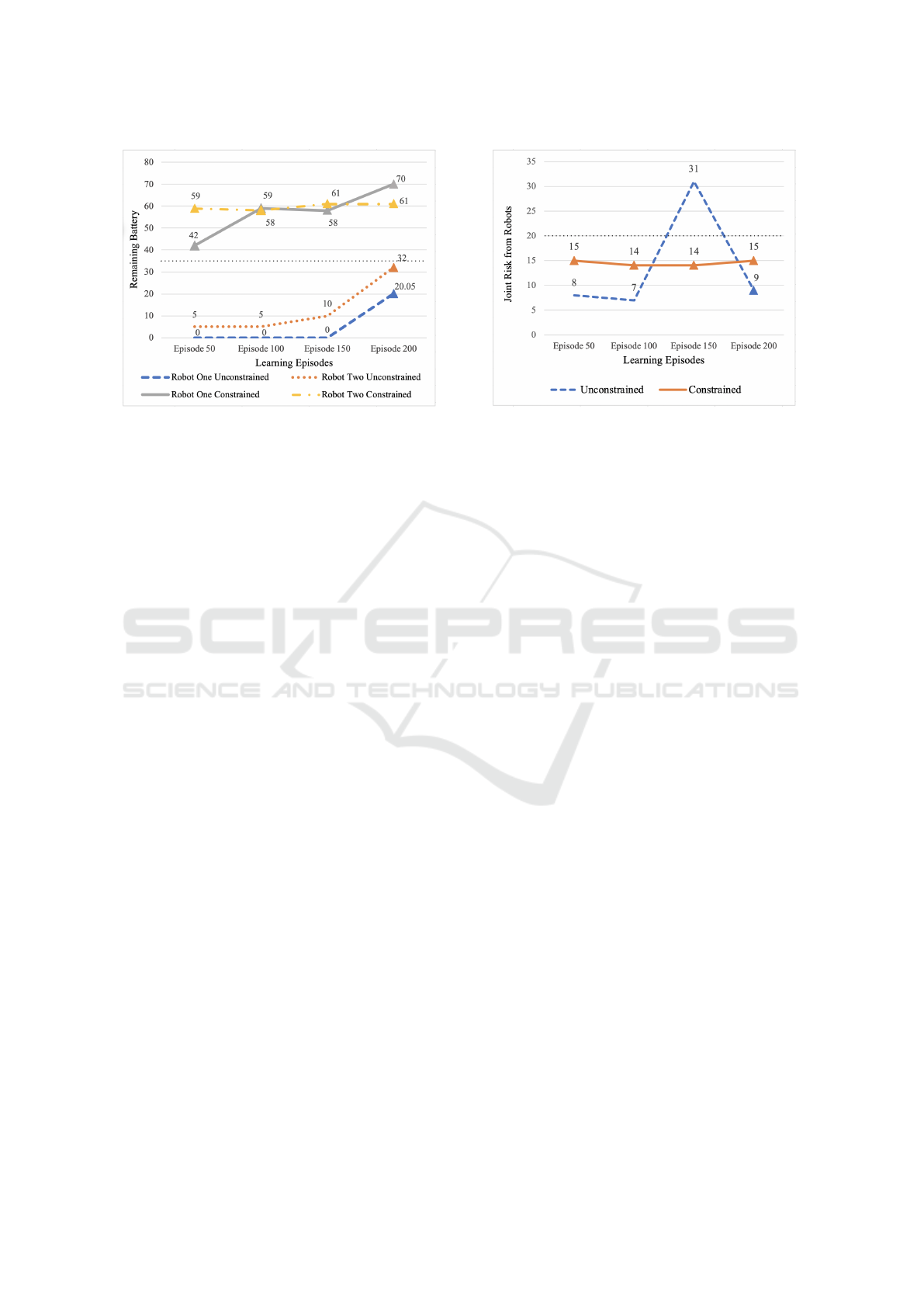
Figure 3: Battery conservation results.

diation for both of the robots. This drastic increase in

joint risk comes from policies which do not complete

the mission objective, so continue following their pol-

icy until a fail condition is reached, just as with learn-

ing episodes 50 and 100, which only visited room 4

twice. However, the ﬁnal learned policy of the uncon-

strained robots did produce a policy which completed

the mission objective (C1), and to the least amount of

possible risk (C3), as seen by unconstrained reaching

a risk level of 9, it did this, however, at the cost of

failing the battery safety constraint (C2). These ex-

periments show that standard learning, while able to

produce intelligent policies, is not guaranteed to meet

the safety requirements constraints.

A second experiment was run using a policy con-

strained by our approach. These constraints saw

the responsibilities within the domain partitioned for

each agent, resulting in each agent having two rooms

which they were solely responsible for and two rooms

in which they shared responsibility. This limits the

agents’ ability to frivolously use their battery, as seen

from the constrained values in Figure 3, from very

early on, the remaining battery was higher than the

safety constraint. This approach, while not removing

the most risk of damage, produced a very consistent

amount of risk throughout the entire learning run, as

seen in Figure 3, never dropping below the safety con-

straint, this is a function of our approach which con-

strains the actions to ensure this. It also drastically

reduced the search space for both agents and limited

the number of learning episodes needed compared to

the unconstrained learning run.

The results of the constrained and unconstrained

experiments, which are shown in Figure 3 and Fig-

ure 4 show that the agents which are constrained us-

ing our approach not only learn to complete the patrol

quicker but also never exceed the accepted level of

risk and quickly learn to conserve its battery to the

Figure 4: Accumulated risk results.

accepted amount.

6 RELATED WORK

Our approach to safe MARL draws signiﬁcantly from

work within safe RL (Garcia and Fern

andez, 2015).

The majority of these approaches are focused on a

single-agent perspective but are directly related to our

research. Our approach extends safe MARL past the

tailoring of reward functions and the restriction or

manipulation in some form on the rewards received;

there are many which attempt this in several ways

(Serrano-Cuevas et al., 2019; Kroening et al., 2020).

There are other techniques for safe RL which com-

plemented the creation of our approach; these in-

clude constraints being placed on which behaviours

can be followed and which ones cannot, such as in

(Moldovan, 2012) which avoids irreversible actions,

amongst others (Moldovan, 2012; Biyik et al., 2019).

Our approach to safe MARL uses strict constraints,

but unlike other approaches mentioned, does not en-

tirely remove actions which contain risk, and justi-

ﬁes allowing such risk by using guarantees obtained

through quantitative analysis. The risk which our ap-

proach allows is a calculated risk, which allows mis-

sions to be still completed, this differs from these pre-

vious approaches,

Assured RL (Mason et al., 2017) made the novel

step to incorporate a QV stage into the RL processes,

in which it produced very promising results. Our ap-

proach applies this directly to our MARL research.

Our approach differs from the majority of recent ad-

vancements in safe MARL, as it is a multi-step ap-

proach that aims to be used in a broad scope of ap-

plications, not focusing on one speciﬁc problem or

domain. As well as this, our approach is not reliant

Reinforcement Learning with Quantitative Veriﬁcation for Assured Multi-Agent Policies

243

on a speciﬁc algorithm, reward structure, or tool, and

aims to be ﬂexible to the requirements of the prob-

lem. When looking at recent advancements, includ-

ing research into anti-collision (Zhang et al., 2019;

Cheng et al., 2020), learning for automated vehicles

(Shalev-Shwartz et al., 2016), limited broad scope ap-

proaches to safety have been introduced so far, and

others typically follow the trends of single-agent RL.

A recent study which works within safe RL makes use

of constrained MDPs and proposes a novel policy op-

timisation algorithm by using convex quadratic func-

tions obtained from policy gradient estimators (Yu

et al., 2019). Our approach also makes use of a con-

strained approach, but through the formal proofs sup-

plied through QV in an abstracted way.

7 CONCLUSION

We introduced a novel approach to Safe MARL,

building from a recent advancement in safe RL, util-

ising QV with a MARL algorithm. Through the use

of a domain example, we demonstrated that our three-

stage approach allows for MARL policies to be learnt

with safety constraints.

Our approach improves upon standard MARL by

allowing complex safety, performance, and reliabil-

ity constraints to be implemented into the learning

process of multiple agents. Deﬁning these strict con-

straints is not possible using reward functions, but we

demonstrate how these may be speciﬁed using PCTL.

Our approach makes use of an abstracted ver-

sion of the targeted domain; this means that complete

knowledge of the problem does not need to be known

to work with the problem. Indeed only limited infor-

mation is required, including the nature of the perfor-

mance and safety constraints which are necessary for

formal encoding in PCTL. This abstraction also aids

the scalability of our approach, which is always a con-

cern when dealing with MAS (Xiao and Tan, 2008).

This approach does not aim for optimality in terms

of maximum rewards received from the environment.

It aims to produce reliable policies which satisfy all

safety constraints.

While our example domain is small in size as it

is a ﬁrst example case. Our aims can be seen being

achieved in our example domain, showcasing some

of the potentials of this approach.

Future work includes two main points, the ﬁrst be-

ing the examination of how well our approach can

be adjusted to work with larger team sizes, and the

second how our approach can be used in larger more

complex domains and dynamic environment, e.g. (Liu

et al., 2020; Gerasimou et al., 2017). Despite the al-

gorithms and tools we used within our example, our

approach is largely independent of the learning algo-

rithm chosen, and the tools used. We plan to investi-

gate the generality of our approach by utilising more

specialised MARL algorithms within its framework,

including MARL algorithms that incorporate deep

learning techniques. Lastly, it could be extremely

beneﬁcial to apply non-in-dependant learners to our

approach, given the plug-in nature of our approach to

different tools and algorithms.

ACKNOWLEDGEMENTS

This paper presents research sponsored by the UK

MOD. The information contained in it should not be

interpreted as representing the views of the UK MOD,

nor should it be assumed it reﬂects any current or fu-

ture UK MOD policy.

REFERENCES

Biyik, E., Margoliash, J., Alimo, S. R., and Sadigh, D.

(2019). Efﬁcient and safe exploration in determinis-

tic markov decision processes with unknown transi-

tion models. In American Control Conference, pages

1792–1799.

Bloembergen, D., Tuyls, K., Hennes, D., and Kaisers, M.

(2015). Evolutionary dynamics of multi-agent learn-

ing: A survey. Journal of Artiﬁcial Intelligence Re-

search, 53:659–697.

Bogue, R. (2011). Robots in the nuclear industry: a review

of technologies and applications. Industrial Robot: An

International Journal.

Boutilier, C. (1996). Planning, learning and coordination

in multiagent decision processes. In 18th Theoretical

aspects of rationality and knowledge, pages 195–210.

Bus¸oniu, L., Babu

ska, R., and De Schutter, B. (2010).

Multi-agent reinforcement learning: An overview. In

Innovations in multi-agent systems and applications-

1, pages 183–221.

Calinescu, R., Autili, M., C

amara, J., Di Marco, A., Gerasi-

mou, S., Inverardi, P., Perucci, A., Jansen, N., Katoen,

J.-P., Kwiatkowska, M., Mengshoel, O. J., Spalazzese,

R., and Tivoli, M. (2017). Synthesis and Veriﬁca-

tion of Self-aware Computing Systems, pages 337–

373. Springer International Publishing, Cham.

Calinescu, R.,

ska, M., Gerasimou, S., Kwiatkowska, M.,

and Paoletti, N. (2018). Efﬁcient synthesis of robust

models for stochastic systems. Journal of Systems and

Software, 143:140–158.

Calinescu, R., Ghezzi, C., Kwiatkowska, M., and Miran-

dola, R. (2012). Self-adaptive software needs quanti-

tative veriﬁcation at runtime. Communications of the

ACM, 55(9):69–77.

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

244

Cheng, R., Khojasteh, M. J., Ames, A. D., and Burdick,

J. W. (2020). Safe multi-agent interaction through ro-

bust control barrier functions with learned uncertain-

ties. arXiv preprint arXiv:2004.05273.

Ciesinski, F. and Gr

oßer, M. (2004). On probabilistic com-

putation tree logic. In Validation of Stochastic Sys-

tems, pages 147–188.

Cizelj, I., Ding, X. C. D., Lahijanian, M., Pinto, A., and

Belta, C. (2011). Probabilistically safe vehicle control

in a hostile environment. IFAC Proceedings Volumes,

44(1):11803–11808.

Dehnert, C., Junges, S., Katoen, J.-P., and Volk, M. (2017).

A storm is coming: A modern probabilistic model

checker. In International Conference on Computer

Aided Veriﬁcation, pages 592–600. Springer.

Fan, Y., Feng, G., Wang, Y., and Qiu, J. (2011). A novel

approach to coordination of multiple robots with com-

munication failures via proximity graph. Automatica,

47(8):1800–1805.

Garcia, J. and Fern

andez, F. (2012). Safe exploration

of state and action spaces in reinforcement learning.

Journal of Artiﬁcial Intelligence Research, 45:515–

564.

Garcia, J. and Fern

andez, F. (2015). A comprehensive sur-

vey on safe reinforcement learning. Journal of Ma-

chine Learning Research, 16(1):1437–1480.

Gerasimou, S., Calinescu, R., Shevtsov, S., and Weyns,

D. (2017). Undersea: an exemplar for engineering

self-adaptive unmanned underwater vehicles. In 2017

IEEE/ACM 12th International Symposium on Soft-

ware Engineering for Adaptive and Self-Managing

Systems (SEAMS), pages 83–89. IEEE.

Gerasimou, S., Calinescu, R., and Tamburrelli, G. (2018).

Synthesis of probabilistic models for quality-of-

service software engineering. Automated Software

Engineering, 25(4):785–831.

Gregory, J., Fink, J., Stump, E., Twigg, J., Rogers, J.,

Baran, D., Fung, N., and Young, S. (2016). Appli-

cation of multi-robot systems to disaster-relief scenar-

ios with limited communication. In Field and Service

Robotics, pages 639–653. Springer.

Kroening, D., Abate, A., and Hasanbeig, M. (2020). To-

wards veriﬁable and safe model-free reinforcement

learning. CEUR Workshop Proceedings.

Kwiatkowska, M. (2007). Quantitative veriﬁcation: models

techniques and tools. In 6th Joint meeting of the Eu-

ropean software engineering conference and the ACM

SIGSOFT symposium on The foundations of software

engineering, pages 449–458.

Liu, Z., Chen, B., Zhou, H., Koushik, G., Hebert, M.,

and Zhao, D. (2020). Mapper: Multi-agent path

planning with evolutionary reinforcement learning

in mixed dynamic environments. arXiv preprint

arXiv:2007.15724.

Mason, G., Calinescu, R., Kudenko, D., and Banks, A.

(2018). Assurance in reinforcement learning using

quantitative veriﬁcation. In Advances in Hybridiza-

tion of Intelligent Methods, pages 71–96. Springer.

Mason, G. R., Calinescu, R. C., Kudenko, D., and Banks, A.

(2017). Assured reinforcement learning with formally

veriﬁed abstract policies. In 9th International Confer-

ence on Agents and Artiﬁcial Intelligence (ICAART).

York.

Moldovan, T. M. (2012). Safe exploration in markov deci-

sion processes. arXiv preprint arXiv:1205.4810.

Parker, D. and Norman, G. (2014). Quantitative veriﬁca-

tion: Formal guarantees for timeliness reliability and

performance. a Knowledge Transfer Report from the

London Mathematical Society and Smith Institute for

Industrial Mathematics and System Engineering.

Patel, P. G., Carver, N., and Rahimi, S. (2011). Tuning

computer gaming agents using q-learning. In 2011

Federated Conference on Computer Science and In-

formation Systems (FedCSIS), pages 581–588.

Portugal, D., Iocchi, L., and Farinelli, A. (2019). A ros-

based framework for simulation and benchmarking of

multi-robot patrolling algorithms. In Robot Operating

System (ROS), pages 3–28.

Portugal, D. and Rocha, R. P. (2016). Cooperative multi-

robot patrol with bayesian learning. Autonomous

Robots, 40(5):929–953.

Schwager, M., Dames, P., Rus, D., and Kumar, V. (2017).

A multi-robot control policy for information gather-

ing in the presence of unknown hazards. In Robotics

research, pages 455–472. Springer.

Serrano-Cuevas, J., Morales, E. F., and Hern

andez-Leal, P.

(2019). Safe reinforcement learning using risk map-

ping by similarity.

Shalev-Shwartz, S., Shammah, S., and Shashua, A. (2016).

Safe, multi-agent, reinforcement learning for au-

tonomous driving. arXiv preprint arXiv:1610.03295.

Xiao, D. and Tan, A.-H. (2008). Scaling up multi-agent

reinforcement learning in complex domains. In Int.

Conf. Web Intelligence and Intelligent Agent Technol-

ogy, volume 2, pages 326–329.

Yu, M., Yang, Z., Kolar, M., and Wang, Z. (2019). Conver-

gent policy optimization for safe reinforcement learn-

ing. In Advances in Neural Information Processing

Systems, pages 3127–3139.

Zhang, W., Bastani, O., and Kumar, V. (2019).

Mamps: Safe multi-agent reinforcement learning

via model predictive shielding. arXiv preprint

arXiv:1910.12639.

Zhu, C. et al. (2019). A q-values sharing framework for

multiple independent q-learners. In 18th Conf. Au-

tonomous Agents and MultiAgent Systems, volume 1,

pages 2324–2326.

Reinforcement Learning with Quantitative Veriﬁcation for Assured Multi-Agent Policies

245