Integrating Kahn Process Networks as a Model of Computation in an

Extendable Model-based Design Framework

Omair Raﬁque and Klaus Schneider

Department of Computer Science, University of Kaiserslautern, Kaiserslautern, Germany

Keywords:

Model-based Synthesis, Kahn Process Networks, Runtime System.

Abstract:

This work builds upon an extendable model-based design framework called SHeD that enables the automatic

software synthesis of different classes of dataﬂow process networks (DPNs) which represent different kinds

of models of computation (MoCs). SHeD proposes a general DPN model that can be restricted by constraints

to special classes of DPNs. It provides a tool chain including different specialized code generators for speciﬁc

MoCs and a runtime system that ﬁnally maps models using a combination of different MoCs on cross-vendor

target hardware. In this paper, we further extend the framework by integrating Kahn process networks (KPNs)

in addition to the so-far existing support of dynamic and static/synchronous DPNs. The tool chain is extended

for automatically synthesizing the modeled systems for the target hardware. In particular, a specialized code

generator is developed and the runtime system is extended to implement models based on the underlying

semantics of the KPN MoC. We modeled and automatically synthesized a set of benchmarks for different

target hardware based on all supported MoCs of the framework, including the newly integrated KPN MoC. The

results are evaluated to analyze and compare the code size and the end-to-end performance of the generated

implementations of all MoCs.

1 INTRODUCTION

1.1 Motivation and Problem Setting

A model of computation (MoC) precisely determines

why, when and which atomic component of a sys-

tem is executed. Dataﬂow process networks (DPNs)

(Karp and Miller, 1966; Dennis, 1974) can be used

to deﬁne such MoCs. In general, a DPN is a sys-

tem of autonomous processes that communicate with

each other via dedicated point-to-point channels hav-

ing First-In-First-Out (FIFO) buffers. Each process

performs a computation by ﬁring where it consumes

data tokens from its input buffers and produces data

tokens for its output buffers. The ﬁring of a pro-

cess is generally triggered by the availability of in-

put data. While the general model of computation

does not impose further restrictions, many different

classes of DPNs (Kahn and MacQueen, 1977; En-

gels et al., 1995; Buck, 1993; Lee and Messerschmitt,

1987; Lee and Parks, 1995) have been introduced

over time. These classes mainly differ in the kinds

of behaviors of the processes which affects on the

one hand the expressiveness of the DPN class as well

as the methods for their analysis (predictability) and

synthesis (efﬁciency). These behaviors are precisely

described based on the underlying semantics of how

each atomic process is triggered for an execution, and

how each execution of a process consumes/produces

data, in particular, whether a statically or dynami-

cally determined amount of data is consumed and pro-

duced.

Design tools for modeling like Ptolemy (Brooks

et al., 2010) and FERAL (Kuhn et al., 2013) sup-

port the modeling and simulation of behaviors based

on different MoCs, including particular classes of

DPNs. These frameworks are used to model and to

design parallel embedded systems using well-deﬁned

and precise MoCs. In (Golomb, 1971), Golomb dis-

cussed models and their relationship to the real world,

and famously stated that ”you will never strike oil by

drilling through the map”. Of course, this does not

reduce the importance and great value of a map. We

therefore appreciate the convenient use of these well-

established frameworks to study and analyze differ-

ent MoCs at the design level. However, we also en-

counter a lack of emphasis on automatically synthe-

sizing models to real implementations, to analyze and

evaluate the artifacts exhibited by particular MoCs in

the real world.

Raﬁque, O. and Schneider, K.

Integrating Kahn Process Networks as a Model of Computation in an Extendable Model-based Design Framework.

DOI: 10.5220/0010260500870099

In Proceedings of the 9th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2021), pages 87-99

ISBN: 978-989-758-487-9

12 March 20202

Modeling

Synthesis

OpenCL Abstraction

Code-Generators

Centralized-Host

Runtime

Manager

𝒑

𝟏

𝒑

𝟏

(Core0)

𝒑

𝟏

(Core0)

Dispatcher

𝒑

𝟐

𝒑

𝟑

_𝒑

𝟏

Process-Queue

Device-Queue

Core 0

Core 1

CU 0

𝒑

𝟐

(Core1)

𝒑

𝟐

(Core1)

Kernels

𝒑

𝟑

(

𝒑

𝟑

(CU 0)

_𝒑

𝟐

_𝒑

𝟑

𝒑

𝟏

𝒑

𝟐

𝒑

𝟑

𝒑

𝟒

𝒑

𝒏

Dataflow Process Network

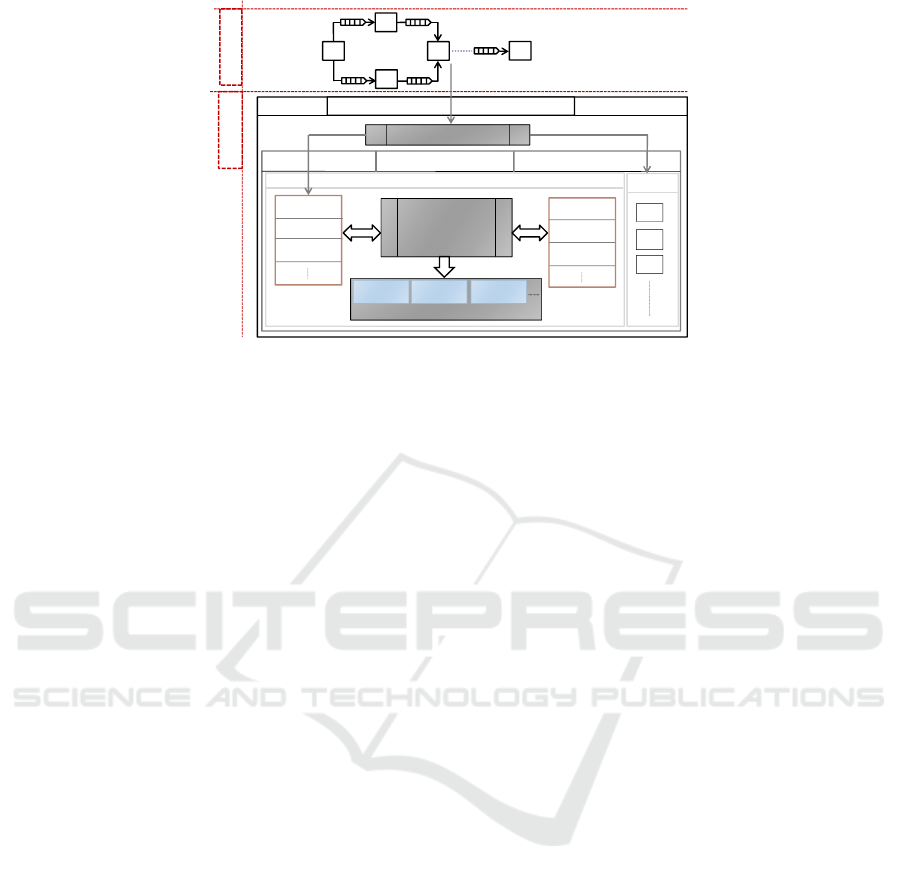
Figure 1: The basic building block diagram of the framework.

The existing design tools for synthesis are usually

limited to speciﬁc classes of DPNs, i.e., each tool is

dedicated to a particular DPN class. These frame-

works provide specialized tool chains, in particular,

a specialized code generator for a speciﬁc MoC. Each

framework therefore allows one to model and to im-

plement systems based on a speciﬁc MoC, i.e., the

underlying DPN class. For instance, a design tool

that only supports a synchronous (static) DPN class

can be used for the modeling and synthesis of syn-

chronous behaviors. Similarly, a design tool based on

a dynamic DPN class can be employed for dynamic

and asynchronous behaviors.

The overall motivation is therefore to enable the

modeling as well as the automatic software synthesis

of systems using different well-deﬁned and precise

MoCs (classes of DPNs) under the supervision of a

common extendable model-based design framework.

1.2 Previous Work and Challenges

In (Raﬁque and Schneider, 2020b), we presented

an extendable model-based design framework called

SHeD which essentially enables the modeling as well

as the automatic software synthesis of systems based

on different classes of DPNs. The overall design ﬂow

is systematically organized in two phases of modeling

and synthesis as shown in Fig. 1. First, the modeling

phase proposes a common general DPN model that

relies on an abstract notion of a process. A process is

composed of a ﬁnite set of actions where each action

can perform a computation by consuming tokens from

input buffers and producing tokens to output buffers.

This general model is used with speciﬁc constraints

and deﬁnitions to specify the precise classes of DPNs.

The underlying modeling language of the proposed

DPN model is the CAL actor language (Eker and

Janneck, 2003). The framework currently supports

two different classes of DPNs, namely the dynamic

dataﬂow (DDF) MoC and the synchronous (static)

dataﬂow (SDF) MoC. The DDF MoC allows pro-

cesses whose actions consume different numbers of

inputs and produce different numbers of outputs while

the actions of processes in the SDF MoC all con-

sume the same number of input tokens and produce

the same number of output tokens.

Second, the synthesis part provides a tool chain

that consists of various essential tools including dif-

ferent specialized code generators and runtime sys-

tems for different MoCs. Using the open computing

language (OpenCL) (Stone et al., 2010), it incorpo-

rates a standard hardware abstraction for cross-vendor

heterogeneous hardware architectures. OpenCL of-

fers a programming model consisting of a host and

several kernels where the host is a centralized en-

tity that is connected to one or more computing de-

vices and is responsible for the execution of kernels

(Raﬁque and Schneider, 2020a). Each kernel is a C

function that actually implements one instance of the

behavior of a system or part of a system. The frame-

work adopts this idea of host and kernels for the syn-

thesis as shown in Fig 1. The synthesis phase uses a

combination of different code generators which gen-

erates an OpenCL kernel for each process in the net-

work based on the underlying class of that process.

The runtime system, in particular, is organized in a

centralized host and kernels architecture, built under

the OpenCL abstraction. The host accommodates dif-

ferent essential components along with the Runtime-

Manager. The Runtime-Manager exploits other com-

ponents of the host and provides different low-level

implementations to ﬁnally execute the modeled DPNs

(kernels) on the target hardware.

MODELSWARD 2021 - 9th International Conference on Model-Driven Engineering and Software Development

As presented in (Raﬁque and Schneider, 2020b),

the SDF MoC proved to be the most effective one

in terms of the generated code size, the build time,

and the end-to-end performance. This is mainly be-

cause the SDF MoC only supports statically schedu-

lable systems and therefore generates very succinct

code for static processes. In contrast, the implemen-

tations based on the DDF semantics accommodate ad-

ditional code for enabling the dynamic evaluation of

actions at runtime. The DDF MoC offers semantics to

model static as well as dynamic behaviors, but at the

cost of the additional runtime overhead. Therefore,

it exhibits a trade-off between ﬂexibility and overall

performance. The main challenge is therefore to in-

tegrate a MoC in the framework that is able to cap-

ture dynamic behaviors and that allows one to gener-

ate succinct code.

1.3 Idea and Contributions

Kahn process networks (KPNs) (Kahn and Mac-

Queen, 1977) are dynamic DPNs that exhibit latency-

insensitive deterministic behaviors that do not depend

on the timing or the execution order of the processes.

The KPN MoC is typically speciﬁed with the follow-

ing restrictions and properties: (1) Processes are not

allowed to test input buffers for the existence of to-

kens. (2) Reading from input buffers is blocking, and

writing to output buffers is non-blocking. (3) Pro-

cesses must implement deterministic sequential func-

tions. (4) Processes do not need all of their inputs

to get triggered for execution. Based on these re-

strictions/properties, it can be implied that in con-

trast to the DDF MoC, the KPN MoC only triggers

a process for execution if the exact information on in-

puts required to produce the output is available. This

avoids the generation of additional code for processes

to dynamically evaluate actions at runtime, and hence,

avoids the runtime overhead associated with the DDF

MoC. In contrast to the SDF MoC, the KPN MoC

can capture both static as well as dynamic behaviors.

Altogether, the integration of the KPN MoC in the

framework will potentially provide more efﬁcient sys-

tem implementations by combining the ﬂexibility to

support dynamic processes and the ability to produce

succinct kernel code for processes.

In this paper, we therefore integrate the KPN MoC

based on the proposed general model of DPN and

the runtime system of the framework. Since chan-

nels/buffers with unbounded capacity cannot be re-

alized in real implementations, the proposed DPN

model only supports blocking write. However, a

KPN semantics-preserving implementation can use

bounded buffers using blocking read and write (Parks,

1995). In summary, we make the following contribu-

tions in this paper:

• We integrate the KPN MoC in an extendable

model-based design framework, mainly with the

aim to produce more efﬁcient system implemen-

tations in terms of end-to-end performance com-

pared to the already supported MoCs (DDF and

SDF) of the framework.

• We formally describe the integrated KPN MoC

and its corresponding code generator based on the

proposed general model of DPN through struc-

tural operational semantics (SOS).

• We present the extended runtime system for ﬁ-

nally implementing KPN models on the target

hardware.

• We designed a set of simple benchmarks involv-

ing static as well as dynamic behaviors. Each

benchmark is modeled and automatically synthe-

sized three times (when possible): First, based

on the DDF MoC, second using the SDF MoC,

and ﬁnally using the newly integrated KPN MoC.

Each generated implementation is evaluated on

two different target hardware platforms. The re-

sults are presented to analyze and to compare the

code size and the end-to-end performance of all

generated implementations.

2 RELATED WORK

Design tools for modeling like Ptolemy (Brooks et al.,

2010) and FERAL (Kuhn et al., 2013) support vari-

ous MoCs including different classes of DPNs. These

frameworks use software components called directors

that control the semantics of the execution of pro-

cesses as well as the communication between them.

However, Ptolemy provides also a preliminary code

generation facility

. It requires the supporting helper

code for each process to generate a general C pro-

gram. This helper code is required to be provided

manually using a fairly complex procedure for each

process. Currently, only speciﬁc processes have sup-

porting helper code.

Another well known design tool called System-

CoDesigner (Haubelt et al., 2008) supports different

classes of DPNs. It incorporates an actor-oriented be-

havior built on top of SystemC. System-CoDesigner

currently supports only hardware synthesis based on

a commercial tool named Forte’s Cynthesizer.

Design tools for synthesis are moreover limited to

particular MoCs where each framework usually only

http://ptolemy.berkeley.edu/ptolemyII/ptII10.0/ptII10.

0.1/ptolemy/cg/

Integrating Kahn Process Networks as a Model of Computation in an Extendable Model-based Design Framework

supports a speciﬁc DPN class. We present a few ex-

amples of dataﬂow-oriented synthesis frameworks:

• The framework presented in (Schor et al., 2013)

introduces a design ﬂow for executing applica-

tions speciﬁed as SDF graphs on heterogeneous

systems using OpenCL. The main focus of this

work is to develop features to better utilize the

parallelism in heterogeneous architectures.

• The DAL framework (Schor et al., 2012) presents

a scenario-based design ﬂow for mapping stream-

ing applications onto heterogeneous systems. Be-

haviors are modeled based on Kahn process net-

works (KPNs) (Kahn and MacQueen, 1977) and a

ﬁnite state machine.

• The work presented in (Lund et al., 2015) trans-

lates DPN models to programs using OpenCL.

The methodology incorporates static analysis and

transformations and conﬁned to the synthesis of

SDF models. Similarly, another dataﬂow ori-

ented framework (Boutellier et al., 2018) proposes

a MoC as a symmetric-rate dataﬂow, a restriced

form of SDF where the token production rate and

the token consumption rate per FIFO channel is

symmetric.

Thus, the existing frameworks based on DPNs gen-

erally support the modeling and synthesis of systems

based on a particular MoC, i.e., a speciﬁc DPN class.

In contrast, our approach enables the modeling as well

as the automatic software synthesis of systems using

different classes of DPNs, including their heteroge-

neous combinations under the supervision of a com-

mon extendable framework.

3 THE GENERAL MODEL OF

DPN

A general dataﬂow process network is a triple ℵ =

(D,F,P ), consisting of a data type D, FIFO buffers F

and processes P . The data type D always includes

a special symbol ⊥ ∈ D to indicate the absence of

a value. The semantics of FIFO buffers is a pair

of {i, o} × N where i and o denotes input and out-

put buffers, respectively. Each FIFO buffer f ∈ F

provides a channel to a sequence of tokens over D,

termed as a stream, denoted by X

. Following that,

is the set of all ﬁnite sequences of tokens over

D. For convenience, we simply denote the contents of

buffers by X

∗

. P is the ﬁnite set of processes. Each

process p = (F

out

,Act) ∈ P consists of a list of

input buffers F

, a list of output buffers F

out

, and an

associated set of actions Act. The input and output

buffers of a process are always mutually exclusive,

i.e., F

∩ F

out

= {}. We further organize each process

in a set of what we call actions Act.

3.1 The Basic Structure of Actions

Each action act = (F

act

) ∈ Act con-

sists of a list of input buffers F

act

⊆ F

, a list of out-

put buffers F

act

⊆ F

out

, a list of sequences of input

token variables

act

of F

act

, and a list of sequences

of output token variables

act

of F

act

. All sequences

∈

act

= (

act

) contain a list of local variables

for temporary storage of data and are exclusive to a

single action. Each sequence ∈

act

contains a list

of local variables, denoting a ﬁnite sequence of in-

put tokens that will be consumed per execution of an

action from its respective input buffer ∈ F

act

. Sim-

ilarly, each sequence ∈

act

contains a list of local

variables, denoting a sequence of output tokens that

will be produced per execution of an action in its re-

spective output buffer ∈ F

act

. For an action with ’t’

inputs F

act

= {F

, F

..., F

} providing input streams

act

= {X

, X

..., X

}, the corresponding se-

quences of local input variables are deﬁned by

act

,...,V

act

}. Each sequence V

act

∈

act

consists of a ﬁnite number of input token variables.

For instance, if F

has a sequence of ’q’ tokens per

action execution, the corresponding list of local vari-

ables is deﬁned by V

act

= {v

act

j 1

act

j 2

,...,v

act

j q

}. The

number of token variables in each sequence, denoted

by L(V

act

), determines the token consumption rate

per execution of the corresponding input buffer.

Similarly, an action with ’l’ outputs F

act

, F

..., F

} is deﬁned with the correspond-

ing sequences of local output variables

act

,...,V

act

}. Each sequence V

act

∈

act

consists of a ﬁnite number of output token variables.

The number of token variables in each sequence, de-

noted by L(V

act

), determines the token production

rate per execution of the corresponding output buffer.

This structure of inputs and outputs of actions is illus-

trated in Listing 1 and Listing 2 (Lines 1 and 6). The

declaration of inputs and outputs is separated by the

identiﬁer ’==>’.

For an action that requires input tokens to have

particular values, an additional condition can be spec-

iﬁed using a guard (Lines 2 and 7, in Listing 1 and

Listing 2). The inputs used for guards (guarded in-

puts) and their corresponding token variables are de-

noted by F

act

⊆ F

act

and

act

⊆

act

, respectively.

In particular, a guard is composed of a list of Boolean

MODELSWARD 2021 - 9th International Conference on Model-Driven Engineering and Software Development

Listing 1: Dynamic split using the proposed model.

1 act

: action F

:[v

act

1 1

] ,F

:[v

act

2 1

] = = > F

:[v

act

1 1

]

2 guard v

act

1 1

= 1

3 do

4 v

act

1 1

:= v

act

2 1

;

5 end

6 act

: action F

:[v

act

1 1

] ,F

:[v

act

2 1

act

2 2

] = = > F

:[v

act

1 1

] ,F

act

2 1

]

7 guard v

act

1 1

= 2

8 do

9 v

act

1 1

:= v

act

2 1

; v

act

2 1

:= v

act

2 2

;

10 end

expressions E

act

= {E

act

,...,E

act

}, where n ∈

N. Each expression ∈ E

act

can be applied on an in-

dividual input token variable. A guard consisting of

a list of Boolean expressions E

act

is therefore ap-

plied on a list of individual token variables denoted

by V

act

⊆

act

3.2 Basic Deﬁnitions for Actions

For any action act in a deﬁned behavior of a process to

be ﬁred, there exists two necessary conditions and the

additional condition of a guard (if used): First, there

must be enough input tokens available as speciﬁed by

the sequences of input token variables

act

in F

act

Second, there must be enough space available as spec-

iﬁed by the sequences of output token variables

act

in F

act

. Finally, the required values on the guarded

inputs must be available, i.e., the guard must be true.

These conditions can be described with the following

deﬁnitions:

Deﬁnition 1 (Input Constraint (δ

)). For an action

act ∈ Act to be ﬁred, each sequence of token variables

∈

act

must be a preﬁx of the sequence of tokens

available on the corresponding input buffer (where

v s

means that s

is a preﬁx of s

): ∀V

act

∈

act

v X

Deﬁnition 2 (Output Constraint (δ

)). For an action

act ∈ Act to be ﬁred, each output ∈ F

act

must contain

space for the corresponding sequence of output token

variables ∈

act

. Overall, this yields:

∀F

∈ F

act

, (size(F

) − count(X

)) ≥ L (V

act

)

where

• size( f ) returns the total size ∈ Z of the buffer f ,

and

• count(X

) returns the current count ∈ Z, i.e., the

available number of tokens in the buffer f .

Listing 2: Dynamic merge using the proposed model.

1 act

: action F

:[v

act

1 1

] ,F

:[v

act

2 1

] = = > F

:[v

act

1 1

]

2 guard v

act

1 1

= 1

3 do

4 v

act

1 1

:= v

act

2 1

;

5 end

6 act

: action F

:[v

act

1 1

] ,F

:[v

act

2 1

] ,F

:[v

act

3 1

] = = > F

:[v

act

1 1

act

1 2

]

7 guard v

act

1 1

= 2

8 do

9 v

act

1 1

:= v

act

2 1

; v

act

1 2

:= v

act

3 1

;

10 end

Deﬁnition 3 (Guard Constraint (δ

)). For an action

act ∈ Act to be ﬁred, the combined evaluation of all

Boolean expressions must evaluate to 1 (true). With

B = {0, 1}, this yields:

∀act ∈ Act, (E

act

) → B )

= 1

Upon ﬁring, each action performs the desired compu-

tation deﬁned within do/end construct, as illustrated

in Listing 1 and Listing 2 (Lines 3-5, Lines 8-10).

4 KPN FORMULATION AND

OPERATIONAL SEMANTICS

In this section, we formulate the KPN MoC and de-

ﬁne its operational semantics based on the proposed

general model of DPN, as presented in Section 3.

We introduce a state transition system of a DPN by

Σ = hAct, M

i. The behavior of a process is de-

scribed by a set of actions Act = {act

,act

,...,act

}

where n ∈ N. Each act ∈ Act is of the form l:

act

→

act

that upon ﬁring consumes to-

kens as speciﬁed by

act

from the corresponding

streams of F

act

and produces tokens as speciﬁed by

act

to the corresponding streams of F

act

. The la-

bels l of actions are mutually exclusive. For all FIFO

buffers, the function M

: F → X

∗

maps each buffer

f to a sequence of data values (tokens) of data type

D. Similarly, for all sequences of local token vari-

ables, the function M

V → D maps each local to-

ken variable to a data value of type D. The KPN MoC

formulation and operational semantics are elaborated

formally based on the state transition system Σ.

4.1 Organization of Actions

Each process p ∈ P can be composed of a set of

actions ∈ Act with guards. The inputs and out-

puts and their associated number of token variables

Integrating Kahn Process Networks as a Model of Computation in an Extendable Model-based Design Framework

(i.e., token consumption and production rates) can

be different across different actions with the excep-

tion of guarded inputs. In particular, the inputs used

for guards (guarded inputs) across all actions in a

process have at least one common input. This im-

plies that for any pair of guarded actions in a process

act

∩ F

act

6= {}. The consumption rates of guarded

inputs are always same across actions in a process,

i.e., L(

act

) = L (

act

). For convenience we sim-

ply denote all guarded inputs in a process and their

token variables by F

and

, respectively. Second,

the Boolean expressions E

of guards are always ap-

plied on the same tokens in inputs F

act

provided by

different token variables across actions. However, the

Boolean expressions E

of guards are always exclu-

sive, e.g., E

act

∩ E

act

= {}. These restrictions facil-

itate the imposition of sequential function implemen-

tations in processes. In particular, they ensure that

for each execution of a process, the actions will never

compete for an execution for any set of tokens. They

enable the execution of processes with dynamic data

rates and dynamic data paths, mainly dependent on

which guards are enabled on each execution.

Examples. Two different dynamic processes,

namely the dynamic split (d-split) and the dynamic

merge (d-merge) are illustrated in Listing 1 and List-

ing 2, respectively. The d-split process consists of two

actions (act

and act

) that depending on the value of

token at input F

split the tokens from input F

outputs F

and F

. Both actions use the same input

for the guard, declared with the same consumption

rate (Lines 1 and 6). The guard is composed of dif-

ferent exclusive Boolean expressions (Lines 2 and 7).

Both actions declare the input F

with different con-

sumption rates i.e., L (V

act

) 6= L (V

act

) (Lines 1 and

6). The action act

has an additional output F

. On

the contrary, the d-merge process depending on the

value of token at input F

merges the tokens from in-

puts F

and F

to output F

. Both actions in d-merge

declare the guarded input F

with the same consump-

tion rate (Lines 1 and 6), which is used with differ-

ent exclusive guard expressions (Lines 2 and 7). The

action act

has an additional input F

. Both actions

declare output F

with different production rates i.e.,

L(V

act

) 6= L (V

act

) (Lines 1 and 6).

4.2 Evaluation and Execution of Actions

As discussed, the KPN MoC does not allow processes

to test input buffers for the existence of tokens. A

process is only triggered for execution if the exact in-

formation on inputs required to execute an action is

available. Therefore, each time a process p ∈ P is

triggered for an execution, a particular action is exe-

cuted, mainly dependent on which guard is enabled.

The guards of actions ∈ Act are always evaluated se-

quentially in the same order of their actions deﬁni-

tions. This execution of actions is formally described

using the state transition system Σ with two speciﬁc

rules. Deﬁnitions 4-7 (i.e., Rules 1-4) have already

been proposed for the existing DDF and SDF MoCs

of the framework in (Raﬁque and Schneider, 2020b).

Deﬁnition 8 (Rule 5, PREPARE (ρ

)). This rule is

ﬁred to read the speciﬁed ﬁxed number of tokens

without consuming them from all inputs F

used for

guards in a process p ∈ P . It is formally described as:

∅

hAct, M

i → hAct, M

with, M

= M

[

Therefore, a ﬁnite number of tokens designated by

are read (not consumed) from streams

pro-

vided by the guarded inputs F

Deﬁnition 9 (Rule 6, PROCEED (ρ

)). An action

act

∈ Act ﬁres for an execution if the required val-

ues on the guarded inputs are available, i.e., the guard

is true. It is formally described as:

(act

∈ Act, δ

)

hAct, M

i → hAct, M

with M

= M

act

],M

= M

[

act

Therefore, a ﬁnite number of tokens

act

are con-

sumed from streams

act

provided by the inputs

act

, the deﬁned computation is performed, and a ﬁ-

nite number of tokens

act

are produced to streams

act

4.3 Triggering Processes for Execution

The KPN MoC only triggers a process for execution

if the exact information on inputs required to produce

the output is available. Therefore, each process p ∈ P

is triggered for an execution if there exists at least

one action act ∈ Act having: enough tokens as speci-

ﬁed by

act

in inputs F

act

, enough space as speciﬁed

act

in outputs F

act

, and required values on the

guarded inputs F

act

. This can be formally deﬁned as:

∀p ∈ P ∃act ∈ Act. (δ

,δ

) = true

When a process is triggered for an execution, the ac-

tions are executed based on the proposed rules ρ

and

MODELSWARD 2021 - 9th International Conference on Model-Driven Engineering and Software Development

5 KPN SYNTHESIS

The synthesis phase of the framework, as shown in

Fig. 1, provides a tool chain including code genera-

tors for speciﬁc MoCs and the runtime system. These

tools work together and ﬁnally implement the mod-

eled systems on the target hardware based on the un-

derlying semantics of the used MoCs (i.e., classes of

DPNs). In particular, a code generator is designed

and developed based on the underlying semantics of

each used DPN class. Each code generator generates

an OpenCL kernel for each process based on the un-

derlying DPN class. Second, the runtime system is

organized in a centralized host and kernels program

model, built under the OpenCL abstraction. The host

features different components including the Runtime-

Manager that schedule and execute processes (gener-

ated kernels) on the target hardware.

The complete synthesis phase and the associ-

ated tool chain is presented in detail in (Raﬁque and

Schneider, 2020b). In this section, we mainly present

the tools extended to support the synthesis of KPN

models. This includes the specialized code genera-

tor designed for generating kernels based on the KPN

MoC, and the extended Runtime-Manager for ﬁnally

implementing KPN models on the target hardware.

Algorithm 1: Code generation of the KPN MoC.

1 foreach process p ∈ P in Network ℵ do

2 PREPARE(ρ

){

3 peek(for all guarded inputs of this process)}

4 foreach action act ∈ Act in a process p do

5 evaluate all guard expressions E

act

6 if δ

then

7 PROCEED(ρ

){

8 read(for all inputs of this action)}

9 perform modeled computations()

10 write(for outputs of this action)}

11 end

12 end

13 end

5.1 KPN Code Generation

Prior to presenting the KPN code generation, we ﬁrst

introduce some additional execution primitives using

the state transition system Σ:

The read(F

act

,L(V

act

)) method consumes a

number of tokens as speciﬁed by L (V

act

) from the in-

put buffer F

, and stores them in the temporary input

token variables V

act

read(F

act

,L(V

act

))

hAct, M

i → hAct, M

with M

= M

], M

= M

act

The peek(F

act

,L(V

act

)) method reads a

number of tokens (without consuming them) as spec-

iﬁed by L (V

act

) from the input buffer F

, by simply

copying them into the temporary input token variables

act

peek(F

act

,L(V

act

))

hAct, M

i → hAct, M

with M

= M

act

The write(F

act

,L(V

act

)) method writes a

number of tokens as speciﬁed by L(V

act

) from the

output token variables V

act

into the output buffer F

write(F

act

,L(V

act

))

hAct, M

i → hAct, M

with M

= M

The code generation based on the underlying se-

mantics of the KPN MoC is shown in Algorithm 1.

The fundamental principle of the KPN code gener-

ation is based on the dynamic execution of actions

using the proposed rules (ρ

and ρ

) of the underly-

ing KPN semantics. For each process p ∈ P in the

network ℵ, the proposed algorithm works as as de-

scribed in the followning.

First, the code is generated to ﬁre the rule ρ

(PREPARE) (Lines 2-3). To this end, the peek

method is inserted for all guarded inputs of a pro-

cess (Line 3). The algorithm then iterates through the

set of modeled actions in the order of their deﬁnitions

(Line 4), where for each action ∈ Act, it proceeds as

follows: First, the code is generated to evaluate all

the guarded Boolean expressions E

act

(Line 5). Next,

the code is generated to evaluate and ﬁre the rule ρ

(PROCEED) (Lines 6-11). For ρ

, ﬁrst, the code is

generated to read (consume) all the inputs of an action

(Line 8). For this purpose, the read method is inserted

for each input of an action. Second, the generated

code for the modeled computations is inserted, prior

to generating code for writing the computed results

on the outputs (Lines 9-10). For writing, the write

method is inserted for outputs based on the modeled

computations of an action.

The generated kernel for d-split as illustrated in

Listing 1 is listed in Listing 3. The code generator

generates generic kernel code to enable the central-

ized host to dispatch multiple execution (instances) of

kernels on the device at a time. However, for brevity,

we only list and focus on the kernel code generated

based on the KPN semantics. For better correspon-

dence, we use the same conventions for inputs/out-

Integrating Kahn Process Networks as a Model of Computation in an Extendable Model-based Design Framework

Listing 3: Generated kernel for d-split.

1 _ k er n el v oi d d- s p l it ( __ gl o ba l f i fo _t * F

, __g l ob a l

fi f o _ t * F

, __g l ob a l f if o_ t * F

, __g l ob a l f if o_ t

* F

) {

2 __ pr i va t e u i n t V

[L(V

act

)];

3 __ pr i va t e u i n t V

[L(V

act

)];

4 __ pr i va t e u i n t V

[L(V

act

)];

5 __ pr i va t e u i n t V

[L(V

act

)];

6 uin t * v

act

1 1

= &V

[0 ]; u in t * v

act

1 1

= &V

[0 ];

7 uin t * v

act

2 1

= &V

[0 ]; u in t * v

act

2 1

= &V

[0 ];

8 uin t * v

act

2 2

= &V

[1 ]; u in t * v

act

1 1

= &V

[0 ];

9 uin t * v

act

1 1

= &V

[0 ]; u in t * v

act

2 1

= &V

[0 ];

10 /

PREPARE(ρ

)

11 pee k (F

, V

, 1 ) ;

12 /

PROCEED(ρ

): act1

13 if (*v

act

1 1

== 1) {

14 re ad (F

, V

, 1 ) ;

15 re ad (F

, V

, 1 ) ;

16 *v

act

1 1

= *v

act

2 1

;

17 by te s = wri te (F

, V

, 1 ) ; }

18 /

PROCEED(ρ

): act2

19 els e if ( * v

act

1 1

== 2) {

20 re ad (F

, V

, 1 ) ;

21 re ad (F

, V

, 2 ) ;

22 *v

act

1 1

= *v

act

2 1

; *v

act

2 1

= *v

act

2 2

;

23 by te s = wri te (F

, V

, 1 ) ;

24 by te s = wri te (F

, V

, 1 ) ; }

25 }

puts as were used throughout the paper. The gener-

ated code can be explained as described in the follow-

ing.

First, the arrays are declared for the sequences of

input/output token variables (Lines 2-5). In each ex-

ecution of a KPN process, only a particular action

is executed, which depends on the enabled guards.

To avoid unnecessary duplication, an array is de-

clared for each input/output with the highest con-

sumption/production rate of all actions. For instance,

an array is declared for the input F

with the high-

est consumption rate L(V

act

) of both actions (Line

3). Second, the individual input/output token vari-

ables are declared and pointed to their respective se-

quences i.e., arrays (Lines 6-9). Next, the rule ρ

(PREPARE) is followed to peek the tokens from the

inputs used for guards (Line 10-11). Finally, the rule

(PROCEED) is invoked to execute a particular ac-

tion (i.e., either act

or act

) based on the activation

of guard. To this end, if the guard is true for act

, a

single token is consumed from F

and written to the

output F

(Lines 13-17). On the other hand, if the

guard is true for act

, two tokens are consumed from

, where the ﬁrst token is written to F

, and the

other to F

(Lines 19-24).

5.2 KPN Runtime-Manager

General Workﬂow. The Runtime-Manager is a

part of the host that uses the Process-Queue and

the Device-Queue as shown in Fig. 1 and provides

the schedulers for triggering processes for execution

based on the used MoCs, a dispatcher for mapping

processes executions to devices, and a communica-

tion and synchronization mechanism between the host

and kernels. The Process-Queue provides the de-

sired information about each process to the Runtime-

Manager such as the associated FIFO buffers, the pro-

cess’s status (idle, running or blocked), the associ-

ated kernel, etc. The Device-Queue lists all the avail-

able devices of the target hardware using the OpenCL

speciﬁcation. Each element of this queue provides

a command queue of a device where the processes

can be dispatched for execution. While a scheduler

fetches a ready process from the Process-Queue based

on the underlying MoC, the dispatcher ﬁnds the de-

vice from the Device-Queue with the least load and

maps the fetched process on that device. The gener-

ated kernel of the dispatched process is then executed

based on the used MoC. The data communication be-

tween the host (FIFO buffers) and the OpenCL de-

vice is carried out using OpenCL buffers. For each

bounded FIFO buffer, an OpenCL buffer is created

with the same design and size of the FIFO buffer.

When all the dispatched instances of the kernel are

executed, the Runtime-Manager is then automatically

notiﬁed to update the components using a synchro-

nization mechanism. During synchronization, a set of

general tasks are performed including retrieving data

from OpenCL buffers, updating all the FIFO buffers

of the process, updating the Process-Queue as well as

device’s load and so on.

KPN Extension. The communication and syn-

chronization mechanism is common to all DPN

classes of the framework including the newly inte-

grated KPN MoC. Second, as the main aim of this

work is to analyze and evaluate the artifacts exhib-

ited by the underlying semantics of particular MoCs

in real world. The same dispatcher is used for map-

ping execution on devices for the KPN MoC as used

for existing MoCs in (Raﬁque and Schneider, 2020b).

Schedulers are designed for triggering processes

for execution based on the underlying MoCs, and are

therefore MoC dependent. To trigger processes for

execution based on the KPN semantics, as described

in Section 4.3, the Runtime-Manager is extended with

a specialized KPN scheduler. The KPN MoC only

triggers a process for execution if the exact infor-

mation on inputs/outputs required to ﬁre an action is

available. Since the host and generated kernels are in-

MODELSWARD 2021 - 9th International Conference on Model-Driven Engineering and Software Development

dependent components, this information is required

to be extracted from modeled processes at compile

time. The extracted information can be used by the

KPN scheduler at runtime to trigger processes for ex-

ecution. To this end, we propose a systematic way of

extracting the information by introducing the input-

output tree wrapper (IOT-wrapper).

5.2.1 Introducing IOT-wrapper

The IOT-wrapper wraps the exact information of in-

puts/outputs required to trigger a process in a standard

tree structure, while taking into account the underly-

ing semantics of the KPN MoC. For each process in a

network, a wrapper is generated at compile time from

the modeled behavior. The IOT-wrapper generation

based on the underlying KPN semantics is shown in

Algorithm 2. For each process p ∈ P in the network

ℵ, the proposed algorithm works as follows:

The IOT-wrapper is initialized, ﬁrst, by adding the

root node, and second, by generating and assigning

a function StepFunction to the root node (Lines 2-

5). The StepFunction of the root node is generated

with the code speciﬁcally related to the guards (Line

5) and hence also termed as guard node. In partic-

ular, the code is generated for each action in the or-

der in which actions were deﬁned to ﬁrst check if

each input used for guard (F

∈ F

act

) has enough to-

kens (V

act

v X

), and second to evaluate the guard

act

) → B). For each action, if the guard is

true, the StepFunction returns a different number num

∈ Z that corresponds to a speciﬁc branch in the tree

originating from the root node. The algorithm then

iterates through the modeled set of actions Act in

the order of there deﬁnitions (Line 7). For each ac-

tion act ∈ Act, the algorithm adds nodes for all non-

guarded inputs (F

act

) and all outputs (F

act

). For

each non-guarded input and each output in act, the

algorithm proceeds as follows: First, if the current

node is the root node, a new node is added at a spe-

ciﬁc branch of the root node provided by the variable

num (Line 11), which is incremented by 1 for each

action (Line 15). On the contrary, if the current node

is not the root node, a new node is always added at the

branch 0 (leftest) of the current node (Line 19). Sec-

ond, for a non-guarded input node, the StepFunction

is generated with the code to check if that input (F

)

has enough tokens (V

act

v X

) (Line 13). For an

output node, the StepFunction is generated with the

code to check if that output (F

) has enough space

(size(F

) − count(X

) ≥ L (V

act

) (Line 14).

The IOT-wrapper generated for d-split, as illus-

trated in Listing 1, is shown in Figure 2. The root

node only involves the input F

as it is the only input

used for guard by d-split. The StepFunction gener-

ated and assigned to each node is shown mathemati-

cally in dashed boxes. The set of branches originat-

ing from the root node and extending up to the leaf

node represents a particular action. For instance, act

is represented by branches originating from the root

node (F

) and extending up to the leaf node (F

Algorithm 2: IOT-wrapper generation.

1 foreach process p ∈ P in Network ℵ do

2 Initialize IOT-wrapper{

3 add root (guard) node

4 for root node, generate StepFunction{

5 ∀act ∈ Act, [∀V

act

∈

act

, V

act

v X

∧

act

) → B] }}

6 Initialize num to 0

7 foreach act ∈ Act do

8 current node = root node

9 foreach ( (F

∈ F

act

\ F

act

) ∧ (F

∈ F

act

) ) do

10 if current node == root node then

11 new node = add child node to current node

at branch num

12 for new node, generate StepFunction{

13 V

act

(∈

act

) v X

∨

14 size(F

) − count(X

) ≥ L (V

act

) }

15 increment num by 1

16 current node = new node

17 end

18 else

19 new node = add child node to current node

at branch 0

20 for new node, generate StepFunction{

same as Lines 13-14 }

21 current node = new node

22 end

23 end

24 end

25 end

5.2.2 KPN Scheduler based on IOT-wrapper

The KPN scheduler is provided with the generated

IOT-wrappers of all processes in the used network.

It uses a variant of depth-ﬁrst search (DFS) method

(Tarjan, 1972) that starts at the root of the tree, selects

a branch, and traverses through that branch as deep

as possible until the leaf node is reached. In gen-

eral, for each node, the scheduler calls the assigned

StepFunction, and only moves to the next node if the

function returns true. In particular, the StepFunction

of the root node returns a number num ∈ Z mainly

dependent on which guard is true. This number is

Integrating Kahn Process Networks as a Model of Computation in an Extendable Model-based Design Framework

KPN MoC:‘dynamic split’ IOT-Wrapper

𝒂𝒄𝒕𝟏

𝒂𝒄𝒕𝟐

1. act1: action 𝐹





: [𝑣



_





], 𝐹





: [𝑣



_





] ==> 𝐹





: [𝑣



_





]

2. guard 𝑣



_





= 1

3. do

𝑣



_





:= 𝑣



_





;

5. end

6. act2: action 𝐹





: [𝑣



_





], 𝐹





: [𝑣



_





, 𝑣



_





] ==> 𝐹





: [𝑣



_





], 𝐹





: [𝑣



_





]

7. guard 𝑣



_





= 2

8. do

9. 𝑣



_





:= 𝑣



_





;

10. 𝑣



_





:= 𝑣



_





;

11. end

𝑭

𝒊

𝟏

𝑭

𝒊

𝟐

𝑭

𝒊

𝟐

𝓥

𝒊

𝟏

𝒂𝒄𝒕

𝟏

⊑ 𝑿

𝑫

𝑭

𝒊

𝟏

&& 𝒗

𝒊

𝟏_𝟏

𝒂𝒄𝒕

𝟏

= 1

𝓥

𝒊

𝟏

𝒂𝒄𝒕

𝟐

⊑ 𝑿

𝑫

𝑭

𝒊

𝟏

&& 𝒗

𝒊

𝟏_𝟏

𝒂𝒄𝒕

𝟐

= 2

𝓥

𝒊

𝟐

𝒂𝒄𝒕

𝟏

⊑ 𝑿

𝑫

𝑭

𝒊

𝟐

𝓥

𝐢

𝟐

𝐚𝐜𝐭

𝟐

⊑ 𝐗

𝐃

𝐅

𝐢

𝟐

(size(𝑭

𝒐

𝟏

) – count(𝑿

𝑫

𝑭

𝒐

𝟏

)) ≥ 𝓛(𝓥

𝒐

𝟏

𝒂𝒄𝒕

𝟏

)

(size(𝐅

𝐨

𝟐

) – count(𝐗

𝐃

𝐅

𝐨

𝟐

)) ≥ 𝓛(𝓥

𝐨

𝟐

𝐚𝐜𝐭

𝟐

)

(size(𝐅

𝐨

𝟏

) – count(𝐗

𝐃

𝐅

𝐨

𝟏

)) ≥ 𝓛(𝓥

𝐨

𝟏

𝐚𝐜𝐭

𝟐

)

𝑭

𝒐

𝟏

𝑭

𝒐

𝟐

𝑭

𝒐

𝟏

Figure 2: IOT-wrapper for d-split.

used to select a speciﬁc branch originating from the

root node that directs to a speciﬁc action for which

the guard is true. In case if the leaf node is reached

and its StepFunction returns true, the scheduler trig-

gers the process for execution. On the contrary, if the

StepFunction of one of the nodes returns false, the

process gets blocked until that node returns true.

6 EXPERIMENTAL EVALUATION

6.1 Benchmarks

We designed a set of simple benchmarks involving

static as well dynamic behaviors. These benchmarks

are typically designed to offer a variety of processes

that enable the evaluation and comparison of imple-

mentations based on all three different MoCs of the

framework. Each benchmark is organized in a net-

work of three processes which are connected in a

producer-worker-consumer setting. While the pro-

ducer process produces the source data, the consumer

process displays the results of the benchmark. The

worker process performs the main operation, e.g., the

d-split process illustrated in Listing 1. The list of

benchmarks is shown in Table 1.

The SWITCH benchmark is designed to switch

one of several input channels through to a single com-

mon output channel by the application of a control

input. In contrast, the DWORKER benchmark per-

forms the opposite operation by taking one single in-

put channel and switching it to any one of a number of

individual output channels, one at a time. The DITE

benchmark is a dynamic version of the if-then-else

operation that sequentially consumes data from input

channels based on the value of data on a control input.

In contrast, the SITE benchmark, a static version of

the if-then-else operation, always consumes data from

all input channels in parallel. The DMERGE bench-

mark is based on the d-merge process, as illustrated in

Listing 2. It is designed to merge several input chan-

nels to a single common output channel by the ap-

plication of a control input. In contrast, the DSPLIT

benchmark, based on the d-split process as illustrated

in Listing 1, splits a single input channel to a num-

ber of individual output channels. Apart from SITE,

which only offers a static behavior, all other bench-

marks provide dynamic behaviors.

Each benchmark is modeled and automatically

synthesized (when possible) based on all three sup-

ported MoCs of the framework. Thereby, generat-

ing three different implementations, namely the DDF

MoC version, the SDF MoC version and the KPN

MoC version. The end-to-end performance, i.e., the

total execution time of the network to process the

complete input data set including initialization and

termination of the program is considered as the com-

parison metric. The data set used has a maximum of

10,000 samples per input and the average of 50 repe-

titions is taken for each version.

6.2 Experimental Setup

We executed the generated versions of benchmarks on

the following hardware:

• Intel i5-4460 @ 3.20GHz CPU

• AMD Radeon HD 5450 GPU

• 8GB RAM

The software environment used for execution is:

• AMD Radeon HD 5450 Driver Version

15.201.1151.1008

• Intel OpenCL SDK Version 6.3.0.1904

• Windows 10 Pro Version 1903 Build 18362.720

6.3 Evaluation

The generated implementations for each benchmark

based on all three MoCs are evaluated based on their

code size and the end-to-end performance.

MODELSWARD 2021 - 9th International Conference on Model-Driven Engineering and Software Development

Results: comparison - CPU

1K 2K 5K 8K 10K

DDF: 'DMERGE' KPN: 'DMERGE'

DDF: 'DSPLIT' KPN: 'DSPLIT'

DDF: 'DWORKER' KPN: 'DWORKER'

DDF: 'SWITCH' KPN: 'SWITCH'

SDF: 'SITE' DDF: 'SITE'

KPN: 'SITE' DDF: 'DITE'

KPN: 'DITE'

Average Execution Time (secs)

Number of Samples

Figure 3: Performance comparison of all classes on CPU.

6.3.1 Generated Code Size

The generated code size of each benchmark for the

complete network based on all three MoCs is depicted

in Table 1. The code size for each generated ver-

sion (implementation) of benchmark is measured as

the sum of lines of code of all generated kernels for

that version. Since the SDF MoC only supports static

behaviors, it can only model and synthesize the SITE

benchmark.

Discussion. The SDF MoC only supports static

behaviors and therefore triggers a process when the

data/space is available for all inputs/outputs. Hence,

it generates very succinct kernel code for static pro-

cesses as observed in the case of SITE. The KPN

MoC also supports dynamic behaviors, however, only

triggers a process for execution when the exact in-

formation on inputs/outputs required to ﬁre an ac-

tion is available. In contrast, the DDF MoC dynam-

ically evaluates actions including their inputs/outputs

when the process is triggered for execution. There-

fore, it accommodates additional code for enabling

the dynamic evaluation of actions within kernels at

runtime. This overhead can therefore be observed

from the number of lines of the generated code for

each benchmark. In particular, the generated code

based on the DDF MoC for SITE is 147% and 136%

greater than the SDF and KPN versions, respectively.

The same trend has been observed for dynamic bench-

marks. The biggest difference is recorded in DITE

where the generated code based on the DDF MoC is

122% greater than the KPN version.

6.3.2 End-to-End Performance

Each generated version of a benchmark is either ex-

ecuted on the CPU or the GPU at a time to evaluate

and compare the end-to-end performance of all used

Results: comparison GPU

0.5

1.5

2.5

3.5

4.5

1K 2K 5K 8K 10K

DDF: 'DMERGE' KPN: 'DMERGE'

DDF: 'DSPLIT' KPN: 'DSPLIT'

DDF: 'DWORKER' KPN: 'DWORKER'

DDF: 'SWITCH' KPN: 'SWITCH'

SDF: 'SITE' DDF: 'SITE'

KPN: 'SITE' DDF: 'DITE'

KPN: 'DITE'

Average Execution Time (secs)

Number of Samples

Figure 4: Performance comparison of all classes on GPU.

Table 1: Generated code size of each process.

Benchmarks

Lines of Code

SDF DDF KPN

SWITCH - 148 74

DWORKER - 124 56

DITE - 140 63

SITE 63 156 66

DMERGE - 142 66

DSPLIT - 152 78

MoCs. On each target hardware, i.e., the CPU and

the GPU, the average execution time of each gener-

ated version of a benchmark is measured against the

number of data samples as shown in Fig. 3 and Fig. 4,

respectively.

Discussion. Regardless of which target hardware

is used, the average execution time of each benchmark

version increases with the increase in the number of

data samples. On the CPU, in general, the KPN MoC

performed substantially better than the DDF MoC as

shown in Fig. 3. In particular, for the only static

benchmark, i.e., SITE, the KPN MoC version is about

36% faster than the DDF MoC version. For SITE,

the SDF MoC performed only slightly faster than the

KPN MoC for smaller number of samples. However,

with the increase in the number of samples, the KPN

MoC performed slightly better than the SDF MoC.

For the highest number of data samples used, the KPN

MoC version performed about 4% faster than the SDF

MoC version. This is mainly because the SDF MoC

checks for the availability of data/space for all input-

s/outputs in a process and therefore induces a schedul-

ing overhead. For all dynamic benchmarks, the KPN

MoC performed at least 27% faster than the DDF

MoC. The biggest difference has been recorded in the

case of DITE where the KPN MoC version is about

55% faster than the DDF MoC version.

Integrating Kahn Process Networks as a Model of Computation in an Extendable Model-based Design Framework

In comparison to the CPU, the average execution

time of each benchmark version is highly reduced

on the GPU. On average, the generated versions on

the GPU executed 15x faster than on the CPU. This

is mainly because the used GPU provided superior

processing power over the used CPU. Similar to the

CPU, the KPN MoC provided signiﬁcantly improved

performance for majority of the benchmarks on the

GPU. In particular, for SITE, the KPN MoC version

is 24% and 5% faster than the DDF MoC and SDF

MoC versions, respectively. For all dynamic bench-

marks, the KPN MoC performed at least 19% faster

than the DDF MoC. The biggest difference has been

recorded in the case of DITE where the KPN MoC

version is about 51% faster than the DDF MoC ver-

sion.

7 CONCLUSIONS AND FUTURE

WORK

We extended a model-based design framework us-

ing different classes of dataﬂow process networks

(DPNs) as different models of computation (MoCs)

by Kahn process networks. We modeled and auto-

matically synthesized a set of benchmarks for differ-

ent target hardware architectures based on all sup-

ported MoCs of the framework, including the newly

integrated KPN MoC. We evaluated all generated ver-

sions of benchmarks for their code sizes and the end-

to-end performance.

Based on our evaluations, we observed that the

SDF MoC generated the most succinct kernel code

for static processes. The KPN MoC also supports dy-

namic behaviors and generated more compact kernel

code than the DDF MoC. The DDF MoC used addi-

tional lines of code for dynamically evaluating actions

at runtime within kernels. Furthermore, the KPN

MoC provided more efﬁcient implementations for all

benchmarks in terms of end-to-end performance on

all target architectures. The KPN MoC effectively

performed up to 1.55x and 1.51x faster than the DDF

MoC on the CPU and the GPU, respectively.

Future work aims at exploring the schemes for ef-

ﬁciently mapping the models on heterogeneous archi-

tectures for performance acceleration.

REFERENCES

Boutellier, J., Wu, J., Huttunen, H., and Bhattacharyya, S.

(2018). PRUNE: Dynamic and decidable dataﬂow for

signal processing on heterogeneous platforms. IEEE

Transactions on Signal Processing, 66(3):654–665.

Brooks, C., Lee, E., and Tripakis, S. (2010). Exploring

models of computation with ptolemy II. In Givargis,

T. and Donlin, A., editors, International Conference

on Hardware/Software Codesign and System Synthe-

sis (CODES+ISSS), pages 331–332, Arizona, USA.

ACM.

Buck, J. (1993). Scheduling Dynamic Dataﬂow Graphs with

Bounded Memory Using the Token Flow Model. PhD

thesis, University of California, USA. PhD.

Dennis, J. (1974). First version of a data-ﬂow procedure

language. In Robinet, B., editor, Programming Sym-

posium, volume 19 of LNCS, pages 362–376, France.

Springer.

Eker, J. and Janneck, J. (2003). CAL language report. ERL

Technical Memo UCB/ERL M03/48, EECS Depart-

ment, University of California at Berkeley, Berkeley,

California, USA.

Engels, M., Bilsen, G., Lauwereins, R., and Peperstraete, J.

(1995). Cyclo-static dataﬂow. In International Con-

ference on Acoustics, Speech and Signal Processing,

pages 3255–3258, USA. IEEE Computer Society.

Golomb, S. (1971). Mathematical models: Uses and limita-

tions. IEEE Transactions on Reliability, R-20(3):130–

131.

Haubelt, C., Schlichter, T., Keinert, J., and Meredith, M.

(2008). SystemCoDesigner: automatic design space

exploration and rapid prototyping from behavioral

models. In Fix, L., editor, Design Automation Con-

ference (DAC), pages 580–585, Anaheim, California,

USA. ACM.

Kahn, G. and MacQueen, D. (1977). Coroutines and net-

works of parallel processes. In Gilchrist, B., edi-

tor, Information Processing, pages 993–998. North-

Holland.

Karp, R. and Miller, R. (1966). Properties of a model

for parallel computations: Determinacy, termination,

queueing. SIAM Journal on Applied Mathematics

(SIAP), 14(6):1390–1411.

Kuhn, T., Forster, T., Braun, T., and Gotzhein, R. (2013).

FERAL - framework for simulator coupling on re-

quirements and architecture level. In Formal Methods

and Models for Codesign, pages 11–22, USA. IEEE

Computer Society.

Lee, E. and Messerschmitt, D. (1987). Synchronous data

ﬂow. Proceedings of the IEEE, 75(9):1235–1245.

Lee, E. and Parks, T. (1995). Dataﬂow process networks.

Proceedings of the IEEE, 83(5):773–801.

Lund, W., Kanur, S., Ersfolk, J., Tsiopoulos, L., Lilius, J.,

Haldin, J., and Falk, U. (2015). Execution of dataﬂow

process networks on OpenCL platforms. In Euromi-

cro International Conference on Parallel, Distributed,

and Network-Based Processing, pages 618–625, Fin-

land. IEEE Computer Society.

Parks, T. (1995). Bounded Scheduling of Process Networks.

PhD thesis, Department of Electrical Engineering and

Computer Sciences, University of California. PhD.

Raﬁque, O. and Schneider, K. (2020a). Employing OpenCL

as a standard hardware abstraction in a distributed

embedded system: A case study. In Conference

on Cyber-Physical Systems and Internet-of-Things,

Budva, Montenegro. IEEE Computer Society.

MODELSWARD 2021 - 9th International Conference on Model-Driven Engineering and Software Development

Raﬁque, O. and Schneider, K. (2020b). SHeD: A frame-

work for automatic software synthesis of heteroge-

neous dataﬂow process networks. In Euromicro Con-

ference on Digital System Design (DSD) and Software

Engineering and Advanced Applications (SEAA), Por-

toroz, Slovenia. IEEE Computer Society.

Schor, L., Bacivarov, I., Rai, D., Yang, H., Kang, S.-H.,

and Thiele, L. (2012). Scenario-based design ﬂow for

mapping streaming applications onto on-chip many-

core systems. In Compilers, Architecture, and Syn-

thesis for Embedded Systems, pages 71–80, Finland.

ACM.

Schor, L., Tretter, A., Scherer, T., and Thiele, L. (2013).

Exploiting the parallelism of heterogeneous systems

using dataﬂow graphs on top of OpenCL. In IEEE

Symposium on Embedded Systems for Real-time Mul-

timedia, pages 41–50. IEEE Computer Society.

Stone, J., Gohara, D., and Shi, G. (2010). OpenCL: A paral-

lel programming standard for heterogeneous comput-

ing systems. Computing in Science and Engineering,

12(3):66–73.

Tarjan, R. E. (1972). Depth-ﬁrst search and linear graph

algorithms. SIAM J. Comput., 1:146–160.

Integrating Kahn Process Networks as a Model of Computation in an Extendable Model-based Design Framework