
Hydra: Practical Metadata Security for Contact Discovery, Messaging,
and Dialing
David Schatz, Michael Rossberg and Guenter Schaefer
Telematics and Computer Networks Research Group, Technische Universit
¨
at Ilmenau, Germany
Keywords:
Strong Anonymity, Onion Encryption, Circuits, Messaging.
Abstract:
Communication metadata may leak sensitive information even when content is encrypted, e.g. when contacting
medical services. Unfortunately, protecting metadata is challenging. Existing approaches for anonymous
communications either are vulnerable in a strong (but feasible) threat model or have practicability issues like
intense usage of asymmetric cryptography. We propose Hydra, a mix network that is able to provide multiple
anonymous services in a uniform way. In contrast to previous messaging systems with strong anonymity,
we deliberately use padded onion-encrypted circuits. This allows to support connectionless applications like
contact discovery with authenticated key exchange, messaging, and dialing (signalling for connection-oriented
communications) with strong anonymity and relatively low latency. Our cryptography benchmarks show that
Hydra is able to process messages an order of magnitude faster than state of the art messaging systems with
strong anonymity. At the same time, bandwidth overhead is comparable to previous systems. We further
develop an analytical model to predict the end-to-end latency of Hydra and validate it in a testbed.
1 INTRODUCTION
IP-based human-to-human communications like
email, instant messaging and Voice over IP (VoIP)
are ubiquitous in the private and professional sector.
Consequently, it is crucial to protect the privacy of
users. While confidentiality of content is achieved by
cryptographic mechanisms, communication metadata
is more challenging to protect. Unfortunately, meta-
data leakage may also be a serious privacy invasion
for users. E.g., the mere fact that someone contacted
a specific counseling or medical service may allow
to infer sensitive information (Mayer et al., 2016).
One challenge for realizing metadata confidentiality
(anonymity) is that various characteristics of IP pack-
ets (like size, encrypted content) may be correlated at
different positions in the network.
Using communication mixes (Chaum, 1981) is
a promising approach to overcome the challenges:
Routing uniformly sized messages across multiple re-
lays and utilizing layered encryption defeats many
attacks, even if some relays act maliciously. Mes-
sages are further mixed in batches to prevent tim-
ing analyses. A more severe challenge for protect-
ing anonymity in the presence of global observers
are long-term intersection/disclosure attacks exploit-
ing user churn (Pham et al., 2011; Oya et al., 2014).
To mitigate disclosure attacks, users should appear
to be online as long as possible, even when they are
not participating in a communication. For this, recent
anonymous messaging systems rely on synchronized
rounds, requesting every user to send a message ev-
ery round (Lazar et al., 2018; Gelernter et al., 2016;
Kwon et al., 2017). They further require asymmetric
cryptography for layered encryption, restricting their
scalability: Supporting millions of users with low
end-to-end latency requires many powerful mixes.
In contrast, scalability for connection-oriented ap-
plications is achieved by onion routing, with Tor be-
ing the most prominent implementation today (Din-
gledine et al., 2004): Users create circuits before-
hand by exchanging session keys with each relay on
selected paths. For onion encryption of application
data, only symmetric ciphers are required. How-
ever, onion routing as implemented by Tor is sus-
ceptible to attacks based on traffic and timing anal-
yses. First, timing of circuit setup at different re-
lays may be correlated by malicious mixes. Sec-
ond, attackers may correlate relative timing between
data packets of the same connection at sender and
receiver. This is especially effective when attackers
introduce artificial patterns, i.e. network flow water-
marking (Wang et al., 2007). Recent circuit-based
systems like TARANET (Chen et al., 2018) and Yo-
Schatz, D., Rossberg, M. and Schaefer, G.
Hydra: Practical Metadata Security for Contact Discovery, Messaging, and Dialing.
DOI: 10.5220/0010262201910203
In Proceedings of the 7th International Conference on Information Systems Security and Privacy (ICISSP 2021), pages 191-203
ISBN: 978-989-758-491-6
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
191

del (Lazar et al., 2019) tackle both problems: Cir-
cuit setup packets are batched and mixed before for-
warding. Furthermore, the packet flow of each cir-
cuit is shaped to a constant rate at each hop by for-
warding packets at deterministic times and injecting
dummy packets if necessary (padded circuit). Un-
fortunately, both systems share the drawback that re-
ceivers directly attach to circuit endpoints: First, this
implies that the same circuit may not be used to con-
tact two different users. Otherwise, observers could
infer that these two users have a common contact and
thus are likely to also know each other. Second, loca-
tion anonymity is weak: Malicious users may easily
disclose the IP address of their communication part-
ners, e.g. by selecting a cooperating endpoint.
In this article we present Hydra, a system that pro-
vides strong anonymity for connectionless services.
Similar to Yodel, users are synchronized to periodi-
cally create onion encrypted circuits that are used for
multiple messages. During such an epoch, only sym-
metric cryptography is required, significantly improv-
ing scalability. Circuit padding provides unlinkabil-
ity of circuit endpoints to users, even when users dis-
connect or active attacks are performed. To support
common services like contact discovery with authen-
ticated key exchange, messaging, and dialing with
low latency, a padding rate like 3 pkt/min is sufficient.
Consequently, Hydra is suited for mobile devices, en-
abling widespread deployment and large anonymity
sets. Messages are forwarded across circuit endpoints
by a rendezvous mechanism that overcomes the weak-
nesses of similar systems: Hydra provides strong lo-
cation anonymity and a circuit may be used for differ-
ent contacts, the latter inspiring the name Hydra.
The rest of this article is structured as follows:
Sec. 2 defines our objectives and threat model. Re-
lated work is discussed in Sec. 3. Design details of
Hydra are presented in Sec. 4. We evaluate Hydra in
Sec. 5 and conclude in Sec. 6.
2 SYSTEM OBJECTIVES AND
THREAT MODEL
First of all, users must be able to discover new con-
tacts. This should be possible based on the knowledge
of long-term user pseudonyms. After contact discov-
ery, users must be able to send arbitrary messages to
their contacts, with end-to-end confidentiality and au-
thenticity protected by session keys. When recipients
are offline, messages must be stored for later delivery.
Non-functional objectives are categorized as follows:
Anonymity. Two forms of anonymity need to be
focused on: Communication relationships (includ-
ing metadata like frequency and duration) shall be
hidden from third parties (relationship anonymity).
To avoid geographical tracking (Mayer et al., 2016),
location anonymity is required, i.e. the mapping of
pseudonyms to IP addresses must be hidden from
third parties and contacts if they are not trusted. For
both forms of anonymity, graceful degradation is re-
quired: Small fractions of malicious or compromised
system entities shall not be able to break anonymity
to a disproportional extend. Moreover, forward se-
crecy is desirable, i.e. leaked long-term secrets shall
not compromise anonymity of past communications.
Quality of Service (QoS). End-to-end latency of
messages shall be low. Acceptable latencies depend
on the kind of application: Contact discovery is ex-
pected to be used infrequently (once per contact), per-
haps accepting latencies up to minutes or hours. Other
messages should be delivered in the order of seconds.
Efficiency and Scalability. For fixed system re-
sources, the system shall support many active com-
munications with good QoS. Power consumption for
users shall be low to allow usage on mobile devices.
Moreover, horizontal scalability is required: The sys-
tem shall be able to support more users by adding
more system entities.
Threat Model. We assume powerful attackers: A
global external attacker may observe, manipulate,
delay, drop, replay, or forge packets. However, he
cannot bypass cryptographic protections (Dolev-Yao
model). In addition, malicious system entities may
share their internal state, e.g. key material. In coop-
eration with external attackers, their goal is to break
relationship anonymity of users. Naturally, the frac-
tion of malicious entities is assumed to be limited.
Malicious users may share their view on end-to-end
messages with attackers to break location anonymity
of their contacts.
3 RELATED WORK
We focus on anonymity systems that use communi-
cation mixes (Chaum, 1981) as a building block. To
recap, the main idea of a mix is to collect fixed-sized
messages in a batch, discard duplicates, transform bit
patterns in a cryptographically secure way and for-
ward messages in randomized order. Using a chain of
mixes and layered encryption defeats a limited num-
ber of malicious mixes. For completeness, we note
ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy
192

that there are other primitives to anonymous com-
munication, namely Dining Cryptographer networks
(DC-nets) (Chaum, 1988) and private information re-
trieval (PIR). However, these techniques suffer from
inherent scalability issues due to broadcast mecha-
nisms or computational expensive operations. Con-
sequently, they are only suited for small user popu-
lations. Riposte (Corrigan-Gibbs et al., 2015) uses
ideas from both DC-nets and PIR, but introduces la-
tencies of several hours for one million users.
Mix Networks. Many mix networks have been pro-
posed to provide anonymity for connectionless appli-
cations. Recent proposals share a core concept (Van
Den Hooff et al., 2015; Tyagi et al., 2017; Lazar
et al., 2018; Gelernter et al., 2016; Kwon et al., 2020):
Users send and receive onion-encrypted packets to ex-
change messages via some form of mailboxes. Mail-
box identifiers are used to match messages of contacts
even though their location is hidden behind a path of
mixes. To defeat long-term disclosure attacks, peri-
odic and synchronized rounds are enforced. In each
round, every user is expected to participate. This im-
plies creating dummy messages if no real messages
have to be sent. Atom (Kwon et al., 2017) shares sim-
ilar ideas, but does not expect users to participate ev-
ery round, facilitating disclosure attacks.
Systems mentioned so far mainly differ in path
selection, mailbox management, and defense against
active attacks. Unfortunately, they all share draw-
backs that limit their practicability: First, onion en-
cryption uses asymmetric cryptography every round,
limiting scalability. Supporting more users either de-
grades latency or requires significantly more mix re-
sources. Second, mailbox identifiers (or shared se-
crets in general) rely on out-of-band exchange, in-
troducing another attack vector. Moreover, mailbox
identifiers are valid for exactly one round in some de-
signs (Van Den Hooff et al., 2015; Tyagi et al., 2017;
Lazar et al., 2018). As a result, contacts may only
exchange messages when both participate in the same
round (no offline storage). This also degrades location
anonymity over time because rounds in which senders
definitively were online are leaked to receivers.
Riffle (Kwon et al., 2016) allows users to anony-
mously upload messages to a set of servers efficiently:
After a setup phase, messages are onion-encrypted
with a symmetric cipher for multiple rounds. Unfor-
tunately, anonymous download by receivers is not as
efficient because it relies on PIR or broadcast.
Loopix (Piotrowska et al., 2017) introduces Pois-
son mixing: Instead of mixing in explicit batches or
synchronized rounds, users select a random waiting
time at each mix, exponentially distributed. More-
over, users send real messages and dummy messages
following a Poisson process. Its arrival rate controls
the trade-off between latency and overhead on a per-
user basis. Unfortunately, sending less messages in
an asynchronous systems leads to smaller anonymity
sets on average, accelerating disclosure attacks, de-
spite attackers’ uncertainty due to mixing and cover
traffic (Oya et al., 2014). Location anonymity relies
on honest “providers” that act as offline-storage.
cMix (Chaum et al., 2017) avoids asymmetric
cryptography at users for sending messages. Asym-
metric cryptography by mixes is pre-computed, not
degrading message latency. However, the protocol
only works for a fixed mix cascade. Thus, cMix ei-
ther does not scale horizontally, or anonymity sets are
partitioned by using independent cascades in parallel.
Alpenhorn (Lazar and Zeldovich, 2016) uses
identity-based encryption (IBE) to exchange a secret
between contacts, and implements a dialing protocol:
The secret is used to initialize a hash chain provid-
ing session keys and dial tokens. Using a synchro-
nized mix network, the initiator sends the current dial
token to a public mailbox server. To protect loca-
tion anonymity of responders, dial tokens are stored
in a Bloom filter that is fetched by every user. Sub-
sequently, users check the existence of all possible
tokens they know. To keep Bloom filters efficient,
mailboxes may be split to multiple filters based on
the hash of users’ pseudonyms. However, this par-
titions responder anonymity sets because queries are
not protected by mixes. Due to Bloom filter encoding,
Alpenhorn is not able to support arbitrary messages.
Circuit-based Systems. To reduce the number of
asymmetric cryptographic operations, many systems
use pre-built circuits, Tor (Dingledine et al., 2004)
being the most prominent example. During circuit
setup, users and relays negotiate keys for subsequent
onion encryption with symmetric ciphers. If respon-
der anonymity is desired, users may setup hidden ser-
vices. For this, service identifiers are publicly mapped
to introduction points to which responders connect
via circuits. While Tor defeats weak attackers with
low overhead, it deliberately does not provide strong
anonymity: Aiming at minimal circuit setup time and
end-to-end latency allows various timing correlation
attacks like watermarking (Wang et al., 2007).
Herd (Le Blond et al., 2015) and Aqua (Le Blond
et al., 2013) are designed for anonymous VoIP and file
sharing, respectively. They use onion routing similar
to Tor, but hide activity patterns of users and circuit
setup from observers by link padding. However, there
is no protection from malicious mixes trying to corre-
late circuit setup at different positions in the network.
Hydra: Practical Metadata Security for Contact Discovery, Messaging, and Dialing
193
Yodel (Lazar et al., 2019) provides VoIP calls with
strong anonymity. To defeat disclosure attacks, users
are synchronized to build two padded circuits every
round, even when they are not in an active call. Un-
fortunately, location anonymity regarding a malicious
contact a is weak: If there is a malicious mix v, a may
simply select v as his circuit endpoint, forcing his con-
tact to attach to v without protection. Similar, circuits
cannot be used to contact multiple users. Otherwise,
observers could correlate different contacts of a user,
which are likely to also know each other.
TARANET (Chen et al., 2018) provides relation-
ship anonymity at network layer. An application’s
data flow is split across different circuits, each padded
to a static rate. While circuit setup packets are batched
at each hop, users do not setup any circuits if they
are inactive, accelerating disclosure attacks. Further-
more, TARANET deliberately does not provide loca-
tion anonymity (senders have to know the network lo-
cation of receivers beforehand).
Conclusion. Defeating disclosure attacks by global
observers is challenging. In theory, it requires users
to constantly send messages or dummies, preferably
in a synchronized way. Besides bandwidth overhead,
scalability of recent connectionless systems is mainly
limited by using asymmetric cryptography for layered
encryption of every message. The opposite approach,
padded circuits, is far more promising when padding
rates are adjusted to suit common connectionless ser-
vices. Unfortunately, existing implementations have
severe drawbacks as discussed above.
4 SYSTEM DESIGN
Hydra uses padded circuits to achieve strong
anonymity in a scalable way. In contrast to similar
proposals, circuits are combined with a novel ren-
dezvous mechanism to overcome the deficiencies dis-
cussed in Sec. 3. We now define our assumptions,
give an overview of Hydra, and present design de-
tails: Path selection, circuit design, user registration,
contact discovery, and messaging. Finally, we discuss
some considerations for users on mobile devices.
4.1 Assumptions and Overview
We assume time synchronization with an accuracy
of ≈ 10ms between all system entities, e.g. via NTP
and GPS. It is used to synchronize start and end times
of epochs and multiple rounds during one epoch. Loss
of synchronization results in increased packet loss as
described in Sec. 4.3, but does not affect anonymity.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
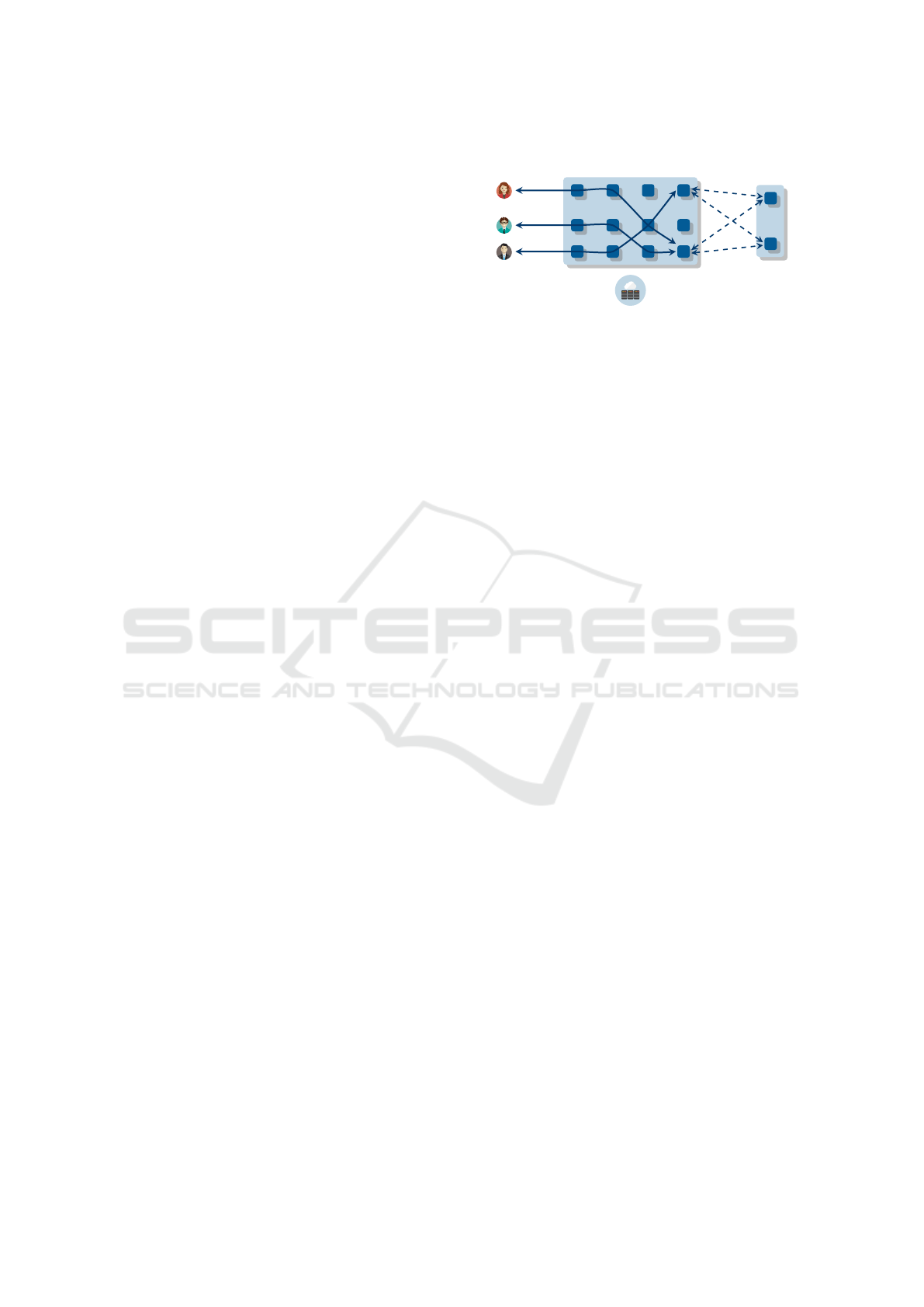
Mixes
Rendezvous
nodes
Padded circuits
setup by users
Publish/subscribe
to hydra tokens
Infrastructure (directory
and contact service)
Figure 1: Overview of Hydra’s design.
We further assume that users participate in as many
epochs as possible to maximize anonymity set sizes
and mitigate disclosure attacks.
Fig. 1 gives an overview of Hydra, including com-
munication via circuits and the rendezvous mecha-
nism. The following entities are involved:
• A user set U. Each user u ∈ U has a pseudonym
nym
u
and a long-term key pair (k
+
u
,k
−
u
). E.g., u
may reuse an existing PGP key pair.
• A set of mixes V . We assume all honest mixes to
be independently deployed. For key exchange with
forward secrecy, each v ∈ V generates ephemeral
key pairs (g
x
e,v
,x
e,v
) for each epoch e and securely
deletes old ones. For brevity, we use the classical
Diffie-Hellman (DH) notation throughout the sec-
tion, but elliptic curve DH and post-quantum secure
key exchange protocols are also supported.
• Mixes further implement a distributed rendezvous
service. For clarity, we denote mixes as the set of
rendezvous nodes R when acting in this role.
• A contact service cs, which is only trusted to pro-
vide availability of contact discovery. If desired by
user u, cs stores the mapping (nym
u
,k
+
u
).
• A directory service managing available mixes with
network addresses and public keys. As the service
is trusted to provide unbiased information for path
selection, we assume de-centralized deployment,
e.g. like Tor’s directory servers (Dingledine et al.,
2004). The registration process is out of scope, but
could be a voluntary-based system like Tor.
• Direct communication between any pair of system
entities is assumed to be reliable, e.g. using TCP.
The functionality of Hydra may be summarized as
follows: Each epoch consists of two phases, namely
setup and communication. During setup, users es-
tablish padded circuits that tunnel various types of
messages in synchronized rounds. For end-to-end de-
livery, a publish/subscribe protocol based on hydra
tokens is used to forward messages between circuit
endpoints via rendezvous nodes R. Tokens are gen-
erated by cryptographic secure hash functions with
ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy
194

64 bit output. If collisions occur, messages are copied
so that all users subscribed to the same token receive
them. Confidentiality is still protected by end-to-end
encryption of all messages. For each token, the re-
sponsible r ∈ R is determined deterministically, e.g.
the directory service could sort R by key fingerprints.
Then, the modulo operation on tokens may be used to
determine the list index. Two types of tokens exist:
• The contact token ct
u
of a user u is a hash of k
+
u
.
Using ct
u
, other users may initiate an authenticated
key exchange. Alternatively, users may agree on
a secret out-of-band. The shared secret is used
to synchronize a hash chain that generates session
keys with forward secrecy for every epoch.
• Using the session keys, contacts further derive ren-
dezvous tokens. Each rendezvous token rt
e,a,b
is
valid for one epoch e and one pair of users (a,b).
4.2 Path Selection and Dummy Circuits
For each epoch e a user wants to participate in, he in-
dependently selects a path p
e
∈ V
l
of mixes for his
circuit. We denote the l possible positions on a path
as layers and the endpoints of a path as entry and
exit mixes/layers. Users select one mix for each layer
in
{
1,...,l
}
uniformly at random, avoiding duplicates
(sampling without replacement). As an exception, the
entry mix is selected independently, allowing it to be
on the path in one additional layer. Otherwise, attack-
ers could rule out possible entry mixes by knowing
parts of the path, e.g. the exit mix. Further optimiza-
tions of path selection are left for future work, e.g.
restricting used links between layers, considering net-
work latency and heterogeneous mix capacities.
Using a fixed path length l enables horizontal scal-
ability, but has two important consequences: First, if
the number of malicious mixes is ≥ l, there is a non-
zero probability of selecting malicious mixes only,
breaking location anonymity for one epoch. This
probability may be reduced by increasing l, at the
cost of increased latency and overhead. To find suit-
able values for l, our analytical model developed in
Sec. 5.2 may be used. Second, if p
e
does not intersect
with any other circuits, global observers may iden-
tify p
e
. We counter this with dummy circuits created
by mixes. To be more precise, mixes ensure that adja-
cent layers are fully connected, i.e. there is at least
one circuit using each possible link in V
2
between
layer i and i+1. Mixes use the same path selection as
users, but with shorter paths depending on the layer i.
While this results in up to (l − 1) ×
|
V
|
2
dummy cir-
cuits at exit layer when no one uses Hydra, our eval-
uation in Sec. 5 shows that horizontal scalability for
Rendezvous
nodes
v
1
v
2
v
3
Mixing packets
Mixing cells
Setup packet
Subscribe
Circuit cell
Send/receive
based on tokens
Dropped cell
Dummy cell
Start of
epoch
Setup
phase
One
round
∆t
w
∆t
c
Figure 2: Synchronization during one epoch, l = 3.
large user populations is not affected. To defeat flood-
ing attacks, e.g. attackers manage to block all but two
users and create a matching number of circuits them-
selves, v creates at least one dummy circuit at each
layer. Dummy circuits are also used by mixes to send
messages to themselves, covering observed traffic at
rendezvous nodes and the contact service.
4.3 Circuit Design
After selecting a path p
e
= (v
1
,...,v
l
), users initi-
ate the creation of circuits during the setup phase of
epoch e. Circuits are subsequently used to transport
fixed-sized cells. The objective of circuits is to unlink
users from messages sent during one epoch. Defeat-
ing long-term disclosure attacks requires further cau-
tion as discussed later. The main threat for anonymity
during one epoch are malicious mixes and attackers
that control communication links of paths. Especially,
attackers might try to link a user to his exit mix by ma-
nipulating packet timing (network flow watermark-
ing) or packet content (tagging attacks) in a way that
is observable even after packets pass honest mixes.
To avoid leaking information based on timing of
circuit setup packets or circuit cells, forwarding be-
tween layers is synchronized by time (see Fig. 2). The
communication phase is further divided into multiple
rounds. Each round consists of one upstream and a
subsequent downstream phase, each transporting ex-
actly one cell per circuit. Before forwarding setup
packets or circuit cells, mixes check for duplicates
and apply a cryptographically secure transformation
and a random permutation. During communication
rounds, mixes additionally create dummy cells if they
did not receive a cell on a circuit in time (both up-
and downstream). The duration of one epoch is fur-
ther specified by three parameters:
Hydra: Practical Metadata Security for Contact Discovery, Messaging, and Dialing
195

tokens
v
3
g
y
3
n
3
τ
3
v
2
g
y
2
n
2
τ
2
g
y
1
n
1
τ
1
AEnc
(s
3
,n
3
)
AEnc
(s
2
,n
2
)
AEnc
(s
1
,n
1
)
Figure 3: Example for authenticated onion encryption of a
circuit setup packet for path p
e
= (v
1
,v
2
,v
3
), i.e. l = 3.
• The interval ∆t
c
between synchronized forwarding
of cells on adjacent layers. It has to be large enough
to allow each mix to receive and process (onion
decryption, random permutation) all cells from the
previous layer in time. On the other side, ∆t
c
should
not be too high, because the (minimum) end-to-end
latency is ≈ 2(l + 1)∆t
c
. Consequently, ∆t
c
should
dynamically be set based on the expected number
of circuits. E.g., mixes may send statistics of past
epochs to the directory service, which in turn deter-
mines a suitable value for upcoming epochs.
• The interval ∆t
w
between communication rounds,
tuning a trade-off between bandwidth overhead and
latency. To compensate for potentially long setup
(asymmetric cryptography), this time is used to
process setup packets for the next epoch.
• The number k of rounds, tuning a trade-off between
efficiency and robustness to mix churn: Long
epochs are efficient as they avoid asymmetric cryp-
tography for a long time. But if mixes fail, affected
circuits break till the start of the next epoch.
To allow a seamless transition between subsequent
epochs, the total idle time k × ∆t
w
has to be long
enough to run the next setup phase. Finding suitable
values for ∆t
c
, ∆t
w
and k is part of our quantitative
evaluation in Sec. 5.2. The following paragraphs fur-
ther detail setup and communication.
Setup Phase. During circuit setup, every user u ex-
changes session keys s
i
with each mix v
i
,1 ≤ i ≤ l
on his selected path and subscribes to a set of to-
kens. For this, u sends a single onion-encrypted setup
packet (see Fig. 3) to his entry mix v
1
. To create the
setup packet, u generates fresh key pairs (g
y
i
,y
i
). In
combination with the ephemeral public key g
x
e,x
i
of
mix v
i
, session keys s
i
are derived from g
x
e,x
i
y
i
. Fur-
thermore, u generates nonces n
i
(96 bit each) and ap-
plies an authenticated encryption scheme in layers.
Naturally, the innermost layer is destined for the exit
mix v
l
, containing the tokens that u wants to subscribe
to. We suggest to use 256 tokens (adding dummy to-
kens if necessary) for now, allowing enough contacts
for normal usage. Users with more contacts may also
circId
rndNo
cmd
args
token
payload
Onion-encrypted
8 B 4 B 7 B 1 B 8 B 240 B
Figure 4: Packet format of circuit cells.
subscribe to tokens by using special cells during com-
munication phase as detailed later. However, tokens
of frequent contacts should be placed in setup packets
to allow receiving matching cells in all communica-
tion rounds. Token order is randomized to avoid to-
kens of the same contact to be linkable across epochs.
After encryption of one layer, n
i
and g
y
i
are added
in plaintext so that mixes may decrypt their layer and
check the authentication tag τ
i
(128 bit). Address in-
formation (up to 144 bit for IPv6 address and port)
of mix v
i
is prepended before applying the next layer
of encryption. After successful decryption, mix v
i
strips g
y
i
, n
i
, τ
i
, and the decrypted address informa-
tion v
i+1
before mixing and forwarding the packet.
Note that packet sizes decrease deterministically and
uniformly at each layer, not leaking information. Fi-
nally, the exit mix forwards the tokens to the respon-
sible rendezvous nodes. A random circuit identifier
circId is added to the setup packet and re-randomized
at every hop. For later usage, mixes map ingress
circIds to egress circId, s
i
, previous hop and next hop.
Moreover, setup packets include the epoch number e.
Due to layered encryption, mixes only learn pre-
vious and next hop. Honest mixes drop setup packets
if authentication fails or duplicates are detected, de-
feating tagging and replay attacks. Dropped packets
are compensated by creating dummy circuits. Replay
protection may be based on τ
i
: If attackers manipulate
the tag to hide a replay, authentication fails. Similar,
replays from past epochs result in failed authentica-
tion because of fresh DH values of honest mixes. Par-
tially created circuits still participate in the communi-
cation phase up to the layer the setup was successful.
Static DH exchange allows users to prepare and
send setup packets in advance without having to wait
for a response. As a result, users may participate in an
epoch e even when they miss the start of e due to loss
of connectivity. This is beneficial not only for usabil-
ity but also for anonymity: Attackers cannot exclude
users from anonymity sets based on the fact whether
they were online at epoch start.
Communication Phase. During communication
phase, circuits transport fixed-sized cells, see Fig. 4.
Apart from the circId, which is re-written at every hop,
a cell contains the following data:
• The round number rndNo within an epoch, used for
detection of duplicates and missing cells. More-
ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy
196

over, it acts as the tweak for a tweakable block ci-
pher that is used for onion encryption as motivated
later. A tweak is an additional, non-secret input to
the block cipher.
• (cmd, args) may be used to send commands to
an arbitrary mix on the circuit, inspired by Tor’s
“leaky pipe” design. Whenever a mix finds the cmd
value to be a valid command code after onion de-
cryption, he performs the specified action with op-
tional arguments args. One command may be used
to signal the exit mix that the cell contains more
tokens to subscribe to at rendezvous nodes as de-
scribed above. We define two more commands in
the corresponding sections about contact discovery
and messaging. If a user has no command to send,
he randomizes both data fields, resulting in a suffi-
cient small probability of the field being misinter-
preted as one of the three valid commands.
• The token, used by exit mixes to forward the cell
to the responsible rendezvous node. To not leak
tokens to observers, they are encrypted for this step.
If a subscription is found, the cell is forwarded to
the corresponding exit mix, which in turn injects
the data into the downstream circuit. If multiple
cells are received for one circuit in the same round,
they are queued for subsequent rounds. At epoch
end, queued cells have to be dropped. Therefore,
applications should implement an error correction
protocol on top of Hydra.
• An end-to-end encrypted payload. Its size of 240 B
is a reasonable trade-off between usability and
bandwidth overhead caused by dummy cells. It
should be large enough for most compressed text
messages and larger messages may of course be
split to multiple cells.
Onion encryption of cells works as usual: In up-
stream direction, users encrypt the cell l times using
the exchanged session keys s
i
, starting with s
l
. Subse-
quently, each mix decrypts one layer. In downstream
direction, mixes add one layer of encryption each, all
decrypted by the user. We do not apply any authen-
tication to cells. This is crucial to allow any mix to
inject dummy cells that are not distinguishable from
real cells by randomizing all bytes: Whenever a mix
does not receive a cell for a round in time, he gener-
ates, mixes and sends a dummy cell instead. When
users do not have real data to send and are online,
they also generate dummy cells. Similar, exit mixes
generate dummy cells in downstream direction if they
do not receive any data from a rendezvous node for a
circuit. Dummy cells are discarded by users (down-
stream) and rendezvous nodes (upstream) because the
cell’s token is not known (with high probability).
As encryption scheme, we propose to use a tweak-
able block cipher with a block size of 256 B, i.e.
onion encryption works on a single block. Ciphers
with a smaller block size may be “extended” to larger
blocks (Patarin et al., 2012). Using a tweakable block
cipher on a single block has two advantages:
• Decryption of the complete block depends on the
tweak, i.e. the rndNo. Consequently, replaying old
cells with an increased rndNo to avoid replay de-
tection still leaks no information. That is because
the bit pattern of the complete cell changes in an
unpredictable way at the next honest hop. Similar,
replayed cells from past epochs are transformed in
an unpredictable way due to fresh session keys.
• Not using authentication potentially allows tagging
attacks on data fields that are predictable. For Hy-
dra, these fields are (cmd, args) and token if it is a
contact token or rendezvous tokens are used more
than once during an epoch. E.g., using AES in
counter mode results in the plaintext being xored
with a key stream. Consequently, attackers could
tag messages by using xor with few 1 bits and
checking for a low hamming distance to a valid
command/known token at other hops. Contrary,
the complete cell changes in an unpredictable way
at the next honest hop when using a single block.
This also destroys the token and consequently de-
feats tagging attacks in the presence of malicious
contacts because the cell is not delivered correctly.
4.4 User Registration
Note that users may participate in epochs any time.
Registration is only required if a user u wants to pub-
lish his pseudonym nym
u
and public key k
+
u
with
his location anonymity protected. Alternatively, users
may use out-of-band mechanisms for contact discov-
ery, e.g. by publishing on their own website or by
meeting in person. If registration is desired, u gen-
erates (or requests) a cryptographic binding bind
u
for k
+
u
to defeat impersonation. If this requires com-
munication, circuits may be used to protect user lo-
cations. We do not enforce a specific implementa-
tion, but assume that u’s contacts may verify bind
u
.
A fingerprint of k
+
u
could be used and verified out-
of-band, e.g. by meeting in person. Existing (veri-
fied) public keys may also be reused, e.g. from PGP.
To register, u uses the payload of (multiple) cells to
send (nym
u
,k
+
u
,bind
u
) to the contact service, using
a reserved token. However, u should participate in a
random number of epochs before registration. Other-
wise, users who setup a circuit for the first time are
linkable to new requests to the contact service.
Hydra: Practical Metadata Security for Contact Discovery, Messaging, and Dialing
197

4.5 Contact Discovery
The objective of contact discovery is an authenticated
key exchange. A pre-condition for contacting a user b
for the first time is to know its pseudonym nym
b
or
public key k
+
b
. Furthermore, b has to subscribe to
his contact token ct
b
on a regular, but random ba-
sis. Subscribing to ct
b
every epoch is risky for lo-
cation anonymity: If attackers block all packets of b
(and only his), a malicious contact service may ob-
serve the missing subscription and link b’s IP address
to nym
b
. To resist longer blocking, a distribution with
a large average (hours) should be used to draw wait-
ing times between subscriptions. To further mitigate
the attack, mixes use cells of their dummy circuits to
randomly subscribe to publicly known contact tokens.
However, b should also use cells for his subscriptions
(instead of setup packets) to not be distinguishable.
He may further send contact requests to himself to
cover how many real requests he gets.
If only nym
b
is known, a user a may re-
quest (k
+
b
,bind
b
) from the contact service by using
his circuit. Then, a initializes a temporary hash chain
with a random seed s, starting at the current epoch e
a
.
Using the hash chain, temporary session keys and ren-
dezvous tokens may be derived for epochs e ≥ e
a
.
Using circuit cells, a initiates the contact discovery
by sending s addressed to contact token ct
b
and en-
crypted using k
+
b
. As b’s subscription is not per-
formed every epoch, the cells are likely dropped by
the responsible rendezvous node if no further action is
taken. Therefore, we use a special command in these
cells to signal that its purpose is contact discovery.
Then, the cell is forwarded to the contact service for
later delivery instead of being dropped. Missed cells
may be polled by b whenever he subscribes to his con-
tact token. We expect this delay in contact discovery
to be acceptable because it has to be performed only
once per contact. Starting with epoch e
a
+ 1, a sub-
scribes to the temporary rendezvous tokens to receive
the response from b. Similar, b subscribes to the tem-
porary tokens as soon as he sends the response, start-
ing at epoch e
b
> e
a
. Then, a and b may tunnel an
arbitrary key exchange protocol by using circuit cells
addressed to the temporary tokens, protected by us-
ing the temporary session keys. Note that a must not
initiate discovery for multiple contacts on the same
circuit: This would allow to link the contact tokens.
As soon as a and b share a secret, they use
it to synchronize a long-term hash chain to derive
future session keys and rendezvous tokens as de-
scribed in Sec. 4.1. Only then a may reveal his iden-
tity (nym
a
,k
+
a
,bind
a
) to b. While this implies that b
cannot reject a request before key exchange is done,
it is inevitable to protect anonymity with forward se-
crecy: If k
−
b
was compromised, attackers could de-
crypt anything based on the temporary hash chain.
4.6 Messaging
To receive messages from contact a in epoch e, user b
subscribes to the shared rendezvous token rt
e,a,b
.
Then, a can send arbitrary messages using the payload
of one or multiple cells during the communication
phase of e. Note that using the same rendezvous token
for a complete epoch leaks the number of exchanged
cells to exit mixes, but they cannot link rt
e,a,b
to a
or b. The payload of each cell is secured end-to-end
by using authenticated encryption with a session key
derived from the hash chain. In contrast to onion en-
cryption, we do not impose restrictions on the used
scheme. In case of temporary disconnected users, en-
try mixes may act as offline storage. Alternatively,
a non-trusted storage service may be used, mapping
circuit ids to cells. Using reliable communication for
all direct communication channels, the message loss
probability is expected to be negligible in absence of
active attacks. Nevertheless, the messaging applica-
tion may still run an error correction protocol on top.
End-to-end latency is minimized when every cell
is delivered to b the same round i as a sends it.
However, this leaks that a was online in round i to
malicious contacts. Cooperating with a global ob-
server, b could then perform an intersection attack
to disclose a’s location over time due to inevitable
user churn. Pre-sending cells for future rounds does
not help either if a’s entry mix is malicious. Conse-
quently, if a does not trust b, he proceeds as follows:
For every cell he sends to b, he uses (cmd, args) of the
preceding cell to instruct a random mix v on the cir-
cuit to delay forwarding by args rounds. If v is neither
the entry nor the exit mix, the sending round is un-
linked from the receiving round. That is because even
if v is malicious, he does not know both circuit end-
points if l > 3. Note that a has to consider the “shift”
in the rndNo at v to derive the correct tweaks for onion
encryption. If v fails to delay the cell correctly, onion
decryption fails and the cell is turned into a dummy.
Our protocol is best suited for text-based messag-
ing. When aiming at a low bandwidth overhead dur-
ing communication, sending rates are low. Conse-
quently, sending application data that requires many
cells to be encapsulated is possible, but introduces
large end-to-end latencies. Still, Hydra can be used to
dial a contact and agree on a switch to an anonymous
protocol that supports higher bandwidth. E.g., an
anonymous VoIP service could be used to also trans-
port pictures. Unfortunately, user populations are ex-
ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy
198

pected to be smaller for these applications, possibly
degrading anonymity. Further note that users send-
ing/receiving many messages in a short time-frame
might experience increased end-to-end latency due to
queuing delay. That is because messages have to be
multiplexed over one circuit with low sending rates. If
users do not mind leaking the fact that they (plan to)
send/receive with high rates, they may create multiple
circuits per epoch to increase throughput.
4.7 Notes on Mobile Devices
While the timing shown in Fig. 2 achieves the lowest
end-to-end latency, it requires users to be active twice
per communication round (send and receive at differ-
ent times). To optimize battery life on mobile devices
at the cost of an increased latency of ≈ ∆t
w
, users may
instead fetch the downstream cell of round r while
sending the upstream cell of round r + 1.
While developing a prototype client application
for Android, we further noticed that new versions of
Android enter “doze mode” very quickly after turn-
ing off the screen. During doze, an application cannot
schedule an accurate wake timer (it may be delayed
up to some minutes). Even explicitly asking the user
for permissions cannot completely circumvent these
restrictions. A workaround is to use Google’s fire-
base service to periodically send an “external wake
timer” to mobile users, using a high priority message.
These are guaranteed to not be delayed as long as the
application is frequently used (“working set bucket”).
Our first prototype confirms that ≈ 90% of “timers”
arrive within 1 s. Nevertheless, native support for ac-
curate timers during doze mode is desirable in future.
5 EVALUATION
We start with a qualitatively discussion if and to what
extend our objectives (Sec. 2) are met. Many aspects
were also discussed in Sec. 4 to guide our design, but
are summarized here. Subsequently, a quantitative
evaluation shows the practicability of Hydra using an
analytical model, validated by a prototype.
5.1 Qualitative Discussion
Hydra supports contact discovery, messaging, and di-
aling with key exchange and offline storage. The fol-
lowing paragraphs discuss non-functional properties.
QoS, Efficiency, and Scalability. Using circuits for
many rounds enables an efficient deployment. Over-
lapping epochs allow compensation of potentially
long circuit setup times (asymmetric cryptography).
However, epochs should not be too long with regard
to robustness: A failing mix disrupts communication
for many circuits for up to two epochs because the
setup phase of the subsequent epoch may also be af-
fected. The minimum epoch length to compensate for
the setup phase is part of our quantitative evaluation.
The interval ∆t
w
between subsequent rounds tunes a
trade-off between end-to-end latency and overhead.
The overhead is limited to efficient symmetric cryp-
tography and small dummy cells. We further evalu-
ate this trade-off in our quantitative evaluation as it
also affects setup time. Preparing setup packets be-
forehand and using padded circuits enable users to
skip some rounds or complete epochs without degrad-
ing anonymity. This is especially useful for usage
on mobile devices (power saving, temporary loss of
connectivity). Increased latency for receiving mes-
sages often is acceptable, e.g. when a user does not
want to be disturbed anyway. Horizontal scalability is
part of our quantitative evaluation: On the one hand,
adding more mixes decreases the number of user cir-
cuits one mix has to handle at each layer. On the other
hand, adding more mixes potentially increases the to-
tal number of circuits due to more dummy circuits.
Anonymity. We start by discussing possible attack
vectors by weak attackers and (cumulatively) move
on to more powerful attackers. The weakest attack-
ers we assume are global observers. They observe
when users join Hydra and in which epochs they par-
ticipate. However, they cannot track paths of circuits
due to onion encryption and synchronization for both
setup and communication phase. This is true even
when only few users participate (e.g. bootstrapping
Hydra) because mixes also create dummy circuits to
ensure that every possible link carries a circuit. If only
two users are online, observers cannot decide whether
they are communicating or not: They observe traffic
to/from both users, and to/from rendezvous nodes and
the contact service in any case because mixes also
send subscriptions, contact requests and end-to-end
messages on dummy circuits. Furthermore, observers
cannot read any tokens due to encryption between exit
mixes and rendezvous nodes/contact service.
Active external attackers may further drop, delay,
replay, manipulate, or forge packets. Dropping setup
packets does not leak information as it is similar to a
scenario where only few users participate. Especially,
missing subscriptions to contact tokens are covered
by mixes randomly subscribing to user tokens. Drop-
ping or delaying circuit cells has no observable ef-
fect on circuit endpoints due to synchronization and
padding: Because authentication of cells is avoided,
Hydra: Practical Metadata Security for Contact Discovery, Messaging, and Dialing
199

dummies are not distinguishable from real cells. In-
cidentally dropping a cell, with content (cmd/contact
tokens) that is predictable for attackers, has no ob-
servable effect either, because attackers do not know
when those are sent. Replay protection is employed
for both phases. Tagging attacks are defeated by lay-
ered authentication for setup packets and by using a
tweakable block cipher with a large block size for
cells. Forging setup packets is detectable due to au-
thentication. Forging a cell for round i is possible
and potentially has the same effect as dropping the
cell with rndNo = i because mixes only forward one
cell per round. Nevertheless, the bit pattern of forged
cells changes at the next mix in an unpredictable way,
leaking no information. In summary, anonymity sets
include all active users. Disclosure attacks based on
user churn are still possible in theory and will always
be in any anonymity system. Nevertheless, by sup-
porting large users populations and minimizing ob-
servable churn by pre-sending setup packets, disclo-
sure attacks are mitigated as good as possible.
If at least one mix v on a path is honest, malicious
mixes positioned before and after v cannot infer that
they are part of the same circuit: Any manipulation
of packets before they reach v has no observable ef-
fects after passing v. If the honest mix v further is
not the entry mix, dummy circuits ensure that attack-
ers cannot further track possible path prefixes/suffixes
as there is at least one circuit between v and all other
mixes in both adjacent layers. If only the entry mix
of a circuit is honest, attackers can narrow down the
location anonymity set to all users that use this en-
try mix. At worst, all mixes are malicious and lo-
cation anonymity is broken. Relationship anonymity
is preserved unless the circuits of both contacts are
completely malicious. Malicious exit mixes further
observe the number of exchanged real messages for a
rendezvous token, but cannot link them to users.
Malicious directory servers may try to manipu-
late path selection by not announcing honest mixes
or replacing address information and public keys.
This is defeated by a distributed consent of multiple
servers. Nevertheless, the number of malicious direc-
tory servers has to be limited to guarantee security. A
malicious contact service may observe the number of
contact requests to a given contact token. However,
this information is fuzzy because users also contact
themselves. Apart from the contact token, packets re-
layed by the contact service only contain an encrypted
random seed. The contact service cannot manipulate
the user database because of cryptographic bindings.
Malicious users may attack location anonymity by
intersection if they can infer in which round their con-
tacts were definitively sending cells. To defeat such
attacks, we allow users to delay forwarding of cells
within their circuit. There is a theoretical attack on
location anonymity of user a in epoch e by a mali-
cious user b, an external attacker (or entry mix) and
a malicious rendezvous node r responsible for rt
e,a,b
:
If the setup packet of a is dropped (and only his) r
observes the missing subscription to rt
e,a,b
. However,
attackers have to guess which setup packet to drop. If
they drop the wrong one, they can only exclude a sin-
gle user from the anonymity set. And even if attack-
ers guess correctly, a is still indistinguishable from all
users that do not participate in epoch e, e.g. because
they are temporarily offline. Further note that a simi-
lar attack on location anonymity exists in any system:
If one user is permanently blocked and the malicious
contact does not receive new messages afterwards, at-
tackers may assume that the guess was correct.
If attackers manage to forge cryptographic bind-
ings of public keys to users, they may impersonate
users at the contact service. Subsequently, they may
wait for contact requests to disclose communication
relationships. Consequently, secure handling of pub-
lic keys is crucial, but outside the scope of this article.
5.2 Quantitative Evaluation
We aim to answer the following research questions:
• Given fixed capacities (number of mixes, their pro-
cessing power and bandwidth), how many users
may be supported with good end-to-end latency?
• How does Hydra’s performance compare to other
approaches that provide strong anonymity? To the
best of our knowledge, Karaoke (Lazar et al., 2018)
is one of the most efficient candidates to date and
is therefore used for our comparison.
• Can Hydra support more users by adding more
mixes, despite increased overhead due to dummy
circuits (horizontal scalability)?
• How many rounds must circuits be used to allow
the next setup phase to complete in time?
We answer the questions using an analytical model.
Furthermore, performance results are validated using
a prototype of Hydra deployed on a small testbed.
Model. Let n = |U| be the number of users
and m = |V | the number of mixes. We assume each
mix to have identical performance characteristics, i.e.
using the minimum. The available bandwidth is de-
noted by β (full duplex). To model bandwidth over-
head caused by a reliable transport protocol, the ef-
fective bandwidth is η
t
× β, with η
t
< 1. Each mix
may process setup packets on a single core with a rate
ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy
200

Table 1: Default parameters.
Parameter Default Comments
m 100
t 18 AWS c4.8xlarge
f 0.2
l 14 Pr(
˜
C) ≤ 1.7×10
–10
σ
s
l×102B+2064B ECDH, Curve448
σ
c
268B
δ 100 ms
ω 10 ms
β 10 Gbit s
−1
η
t
, η
c
0.25
∆t
w
30 s
of µ
s
, and circuit cells with a ratio of µ
c
, both given
in pkt/s. To model the total processing power, µ
s
and µ
c
are further multiplied by the number t of cores
and a factor η
c
< 1 that models additional overhead,
like key lookups and thread synchronization. We fur-
ther denote the maximum propagation delay between
any pair of mixes by δ and the maximum clock off-
set (time synchronization) by ω. The size of setup
packets (at clients) is denoted by σ
s
, cell size by σ
c
.
For our model, a constant fraction f < 1 of mixes is
malicious, i.e. a total of ˜m = b f × mc. If l ≤ ˜m, the
probability Pr(
˜
C) of a circuit to consist of malicious
mixes only (the entry mix may be duplicated) is:
Pr(
˜
C) =
˜m
m
×
˜m
m
×
˜m − 1
m − 1
× ··· ×
˜m − l + 2
m − l + 2
≤
˜m
m
l
(1)
If not stated otherwise, we use the parameters shown
in Table 1. For fair comparison with Karaoke, the
values are inspired by their setup using 100 Ama-
zon AWS c4.8xlarge instances as mixes (Lazar
et al., 2018). Note that they use very long
paths, l = 14, which should be reconsidered in prac-
tical deployments. Our default cryptographic algo-
rithms are ECDH on Curve448 for key exchange and
AES-256-GCM for authenticated encryption during
setup. Onion encryption of cells uses the Three-
fish cipher with 128 B block size and 12 rounds of a
Feistel network to double the block size as described
in (Patarin et al., 2012). To find reasonable values
for µ
s
and µ
c
, we benchmarked single core perfor-
mance for one minute, using openssl speed (asym-
metric cryptography) and our prototype code (Three-
fish). To approximate single core performance of an
AWS c4.8xlarge instance, we benchmarked an In-
tel Core i7-7500U. Mixes in our testbed use an AMD
GX-412TC at 1 GHz. The results are shown in Ta-
ble 2 and already indicate the significant advantage of
Threefish for onion encryption of cells.
Dummy Circuits. As the processing time at each
layer highly depends on the total number of circuits,
we first approximate the expected number E(F) of
Table 2: Cryptography benchmark, single core.
Algorithm i7-7500U GX-412TC
Curve448 1745 pkts
−1
128 pkts
−1
Curve25519 29705 pkt s
−1
1550 pkts
−1
Threefish 336604 pkt s
−1
39245 pkt s
−1
dummy circuits. For this, we approximate our path
selection strategy by allowing duplicates at any layer.
Then, there are m
2
possible links between each pair of
adjacent layers, i.e. up to m
2
new dummy circuits at
each layer. Furthermore, every mix creates at least
one dummy circuit per layer. Given the expected
number n
i
of “regular” circuits (users and dummy cir-
cuits created in previous layers) arriving at layer i, the
expected number of new dummy circuits E(F
i
) is:
E(F
i
) = m + m
2
× (1 −
1
/m
2
)
n
i
(2)
Summing all E(F
i
),1 ≤ i ≤ l − 1 yields the total ex-
pected number of dummy circuits E(F).
End-To-End Latency. The duration of both setup
phase and one round of communication depends on
the number c
i,v
of circuits a mix v has to handle at
layer i. A reasonable (with high probability) up-
per bound for all c
i,v
may be determined as fol-
lows: First, the exit layer l has the highest load due
to E(F) additional dummy circuits. Second, c
l,v
may
be modelled by a Binomial distribution because all
mixes have the same probability of being used as exit
mix: c
l,v
∼ B(n + E(F),
1
/m) = B
l,v
. Consequently,
reasonable upper bounds for all c
i,v
,1 ≤ i ≤ l, v ∈ V
are given by the quantiles ˜c
q
of B
l,v
. We use q = 0.99
for the remaining evaluation.
To process the cells of all circuits in time without
packet loss, the lower bound for ∆t
c
(interval between
synchronized forwarding on adjacent layers during
communication phase) is as follows:
∆t
c
≥ ω + δ + max
˜c
q
× σ
c
η
t
× β
,
˜c
q
η
c
×t × µ
c
(3)
It is dictated by the (assumed) accuracy of time syn-
chronization (receiver clock may be ahead of sender
clock by ω), the maximum propagation delay δ be-
tween any pair of mixes and the forwarding bot-
tleneck (either communication bandwidth or crypto-
graphic performance). The lower bound for the dura-
tion of one communication round and thus the end-to-
end latency of a message is given by d
c
= 2(l + 1)∆t
c
.
Additionally, the end-to-end latency is increased
by
(d
c
+∆t
w
)
/2 on average because users first have to
wait for the start of the next round. The resulting av-
erage end-to-end latency is depicted in Fig. 5. For
comparison, we included the empirical results from
Hydra: Practical Metadata Security for Contact Discovery, Messaging, and Dialing
201
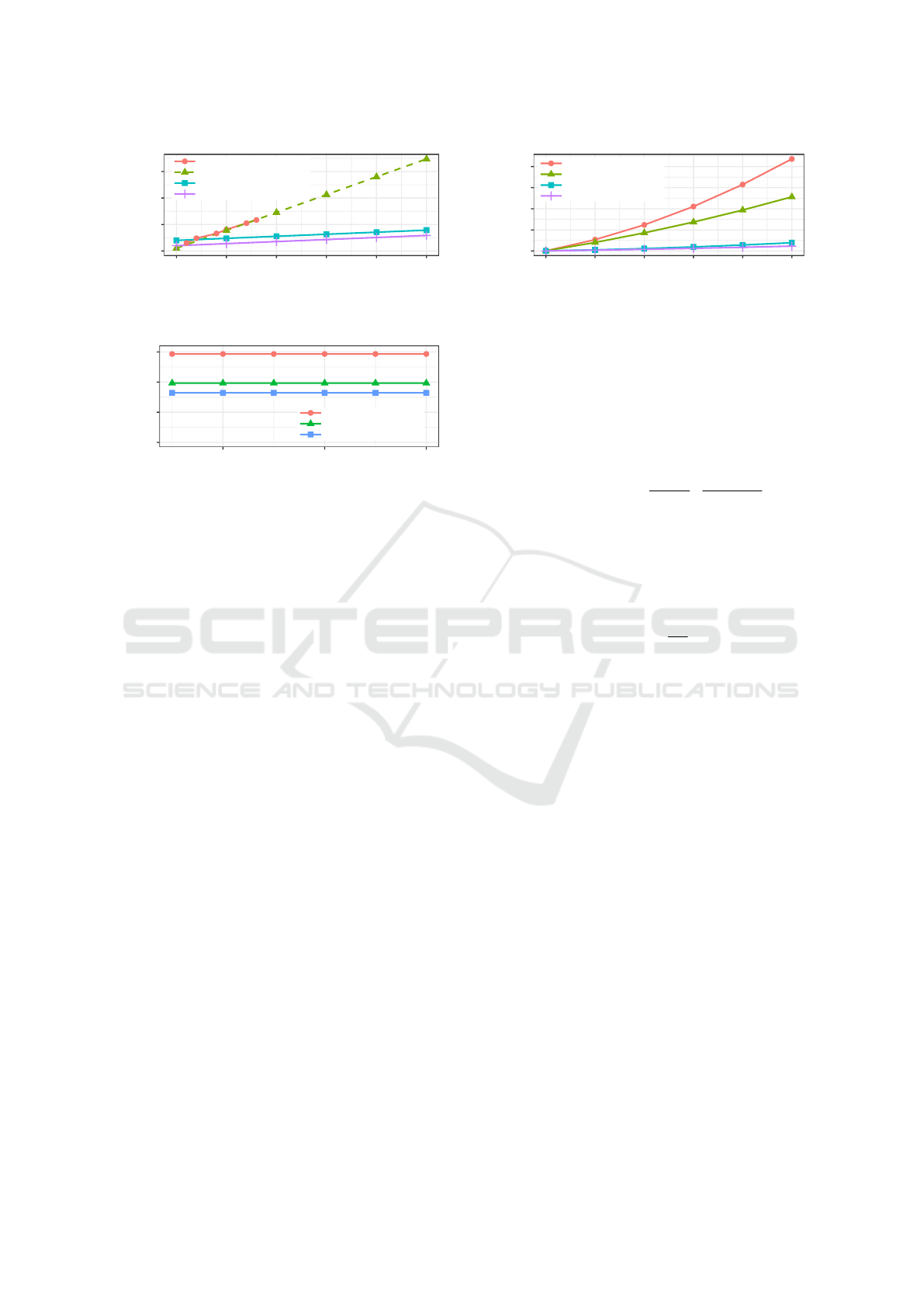
0
50
100
150
0 M 10 M 20 M 30 M 40 M 50 M
Number of users
n
(in millions)
End-to-end latency [s]
(average)
Karaoke, c4.8xlarge
Model, Curve25519 for cells
Hydra, Δt_w = 30s
Hydra, Δt_w = 10s
Figure 5: Average end-to-end latency for Karaoke, Hydra,
and an instantiation of our model with Curve25519 for cells.
0
20
40
60
100 M 200 M 300 M
Number of users
n
(in millions)
End-to-end latency [s]
(average)
1 mix per million users
2 mixes per million users
3 mixes per million users
Figure 6: Average end-to-end latency of Hydra for vary-
ing m and n, with fixed ratios
m
/n.
Karaoke (Lazar et al., 2018), scenario with 100 AWS
c4.x8large instances (up to 16 million users). Note
that we multiplied their results by 1.5 to compensate
for the average waiting time till the next round starts
(while ∆t
w
= 0 in Karaoke, rounds cannot overlap).
Furthermore, we also instantiated our model by using
Curve25519 for onion encryption of cells instead of
Threefish. This basically models a generic anonymity
system that works similar to Karaoke and uses asym-
metric cryptography for every message. Note that
this instantiation (with η
t
= η
c
= 0.25, ∆t
w
= 0) pre-
dicts the performance of Karaoke quite accurately and
thus can be used as an extrapolation for more users.
Further note that optimized implementations of both
Karaoke and Hydra potentially yield higher values
for η
t
and η
c
, i.e. lower end-to-end latency.
As expected, our results show that using a sym-
metric cipher for cells drastically improves the scala-
bility. Nevertheless, the end-to-end latency may be
comparatively high for very small user populations
due to the inevitable waiting time between rounds.
Scalability. Fig. 6 shows the average end-to-end
latency of Hydra for varying number of users and
mixes, with fixed ratios
m
/n of mixes per users. The
results show that Hydra is able to scale horizontally:
More users can be supported without degrading la-
tency by proportionally adding more mixes. Note that
for fixed n, deploying more mixes has limited advan-
tages: Many mixes per user may increase the over-
head due to additional dummy circuits and waiting
times between rounds still impose a lower bound on
average end-to-end latency (15 s for ∆t
w
= 30 s).
0
1000
2000
3000
4000
0 M 10 M 20 M 30 M 40 M 50 M
Number of users
n
(in millions)
Minimum
epoch duration [s]
Curve448, Δt_w = 10s
Curve448, Δt_w = 30s
Curve25519, Δt_w = 10s
Curve25519, Δt_w = 30s
Figure 7: Minimum epoch duration in Hydra.
Epoch Duration. As shown above, ∆t
w
should not
be too high. However, smaller values for ∆t
w
decrease
energy efficiency for mobile devices. Furthermore,
an epoch needs more communication rounds k to al-
low the setup to finish in time when ∆t
w
is small, po-
tentially degrading robustness. Consequently, a good
trade-off has to be found. Similar to our calculations
above, the total setup time d
s
is:
d
s
= (l − 1)
ω + δ + max
˜c
q
× σ
s
η
t
× β
,
˜c
q
η
c
×t × µ
s
(4)
To allow the setup to finish in time, d
s
further has to be
less or equal to the total idle time during one epoch:
d
s
≤ k × ∆t
w
(5)
Then, the epoch duration d
e
, which is the twice the
communication duration, is bounded as follows:
d
e
≥ 2k(d
c
+ ∆t
w
) ≥ 2
d
s
∆t
w
(d
c
+ ∆t
w
) (6)
The lower bound increases quadratically with the
number of users, because both d
s
and d
c
increase.
This can also be seen in Fig. 7. Consequently, using a
“weaker” curve (Curve25519 still has a security level
of ≈ 128 bit) may be a reasonable trade-off to avoid
very long epochs when user population grows.
Testbed. We implemented a prototype of the
core Hydra mix functionality (synchronized for-
warding and rendezvous) in Rust, using gRPC as
user API and plain TCP for relaying cells be-
tween mixes. We deployed m = 9 mixes us-
ing PC Engines APU3c4 SoCs (system on a
chip, β = 1Gbits
−1
, t = 4 cores at 1 GHz). As all
mixes are directly attached to one switch, ω + δ
should be negligible. Remaining parameters for the
testbed are l = 4, ∆t
c
= 0.5 s, ∆t
w
= 25 s and k = 20.
Circuit setup uses Curve25519. We further imple-
mented a load generator that mimics many users, us-
ing their circuits to send one message to themselves
every round and measuring packet loss. Our experi-
ments, each running 3 consecutive epochs, show that
the small deployment can support up to 260 thou-
sand users with packet loss below 1 %. The bottle-
neck is the comparatively weak CPU. Compared to
our model, the results indicate a value of η
c
≈ 0.37.
ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy
202

Summary. Compared to previous messaging sys-
tems with strong anonymity, our model shows that
Hydra is able to support significantly more users with
acceptable latency by not using asymmetric cryptog-
raphy for every message. Even more users are sup-
ported by deploying more mixes. Our findings are
supported by benchmarks and a prototype of Hydra.
6 CONCLUSION
Using padded circuits for multiple rounds allows Hy-
dra to support millions of users with strong anonymity
and relatively low latency. Further, our rendezvous
mechanism avoids shortcomings of previous circuit-
based systems with strong anonymity: A circuit may
be used to communicate with multiple contacts and
location anonymity is significantly improved.
In future, we want to combine Hydra with an
anonymity system that is able to support applications
with higher bandwidth and stricter latency require-
ments, like VoIP. For this, a similar protocol may be
used, but with tuned parameters and path selection.
Moreover, we evaluate post-quantum secure key ex-
change protocols for circuit setup. Our prototypes are
published at https://github.com/hydra-acn.
REFERENCES
Chaum, D. (1981). Untraceable electronic mail, return ad-
dresses, and digital pseudonyms. Communications of
the ACM, 24(2):84–90.
Chaum, D. (1988). The dining cryptographers prob-
lem: Unconditional sender and recipient untraceabil-
ity. Journal of Cryptology, 1(1):65–75.
Chaum, D., Das, D., Javani, F., Kate, A., Krasnova, A.,
De Ruiter, J., and Sherman, A. T. (2017). cMix: Mix-
ing with minimal real-time asymmetric cryptographic
operations. In International Conference on Applied
Cryptography and Network Security, pages 557–578.
Chen, C., Asoni, D. E., Perrig, A., Barrera, D., Danezis, G.,
and Troncoso, C. (2018). TARANET: Traffic-analysis
resistant anonymity at the network layer. In IEEE Eu-
roS&P, pages 137–152.
Corrigan-Gibbs, H., Boneh, D., and Mazi
`
eres, D. (2015).
Riposte: An anonymous messaging system handling
millions of users. In IEEE Symposium on Security and
Privacy, pages 321–338.
Dingledine, R., Mathewson, N., and Syverson, P. (2004).
Tor: The second-generation onion router. In 13th
USENIX Security.
Gelernter, N., Herzberg, A., and Leibowitz, H. (2016). Two
cents for strong anonymity: The anonymous post-
office protocol. PETS, 2016(2):1–20.
Kwon, A., Corrigan-Gibbs, H., Devadas, S., and Ford, B.
(2017). Atom: Horizontally scaling strong anonymity.
In 26th ACM SOSP, pages 406–422.
Kwon, A., Lazar, D., Devadas, S., and Ford, B. (2016). Rif-
fle: An efficient communication system with strong
anonymity. PETS, 2016(2):115–134.
Kwon, A., Lu, D., and Devadas, S. (2020). XRD: Scalable
messaging system with cryptographic privacy. In 17th
USENIX NSDI, pages 759–776.
Lazar, D., Gilad, Y., and Zeldovich, N. (2018). Karaoke:
Distributed private messaging immune to passive traf-
fic analysis. In 13th USENIX OSDI, pages 711–725.
Lazar, D., Gilad, Y., and Zeldovich, N. (2019). Yodel:
Strong metadata security for voice calls. In 27th ACM
SOSP, pages 211–224.
Lazar, D. and Zeldovich, N. (2016). Alpenhorn: Bootstrap-
ping secure communication without leaking metadata.
In 12th USENIX OSDI, pages 571–586.
Le Blond, S., Choffnes, D., Caldwell, W., Druschel, P., and
Merritt, N. (2015). Herd: A scalable, traffic analysis
resistant anonymity network for VoIP systems. ACM
SIGCOMM, 45(4):639–652.
Le Blond, S., Choffnes, D., Zhou, W., Druschel, P., Bal-
lani, H., and Francis, P. (2013). Towards efficient
traffic-analysis resistant anonymity networks. ACM
SIGCOMM, 43(4):303–314.
Mayer, J., Mutchler, P., and Mitchell, J. C. (2016). Eval-
uating the privacy properties of telephone metadata.
Proceedings of the National Academy of Sciences,
113(20):5536–5541.
Oya, S., Troncoso, C., and P
´
erez-Gonz
´
alez, F. (2014). Do
dummies pay off? Limits of dummy traffic protection
in anonymous communications. In International Sym-
posium on Privacy Enhancing Technologies, pages
204–223. Springer.
Patarin, J., Gittins, B., and Treger, J. (2012). Increasing
block sizes using feistel networks: The example of the
aes. In Cryptography and Security: From Theory to
Applications, pages 67–82. Springer.
Pham, D. V., Wright, J., and Kesdogan, D. (2011). A prac-
tical complexity-theoretic analysis of mix systems. In
European Symposium on Research in Computer Secu-
rity, pages 508–527. Springer.
Piotrowska, A. M., Hayes, J., Elahi, T., Meiser, S., and
Danezis, G. (2017). The loopix anonymity system.
In 26th USENIX Security, pages 1199–1216.
Tyagi, N., Gilad, Y., Leung, D., Zaharia, M., and Zeldovich,
N. (2017). Stadium: A distributed metadata-private
messaging system. In 26th ACM SOSP, pages 423–
440.
Van Den Hooff, J., Lazar, D., Zaharia, M., and Zeldovich,
N. (2015). Vuvuzela: Scalable private messaging re-
sistant to traffic analysis. In 25th ACM SOSP, pages
137–152.
Wang, X., Chen, S., and Jajodia, S. (2007). Network flow
watermarking attack on low-latency anonymous com-
munication systems. In IEEE Symposium on Security
and Privacy, pages 116–130.
Hydra: Practical Metadata Security for Contact Discovery, Messaging, and Dialing
203
