
Pairwise Cosine Similarity of Emission Probability Matrix as an
Indicator of Prediction Accuracy of the Viterbi Algorithm
Guantao Zhao
a
, Ziqiu Zhu
∗ b
, Yinan Sun
∗ c
and Amrinder Arora
d
The George Washington University, Washington, DC 20052, U.S.A.
∗
These authors contributed equally to this work
Keywords:
HMM, Viterbi, Markov Model, Speech Recognition, NLP.
Abstract:
The Viterbi Algorithm is the main algorithm for the Most Likely Explanation (MLE) used in the HMM.
We study the hypothesis that the prediction accuracy of the Viterbi algorithm can be estimated a priori by
computing the arithmetic mean of the cosines of the emission probabilities. Our analysis and experimental
results suggest a close relationship between these two quantities.
1 INTRODUCTION
Hidden Markov Model (HMM) is a statistical model
based on the joint probability of sequence events and
has complete applications in multiple fields of artifi-
cial intelligence, such as speech recognition (Gales,
1998), computational linguistics (Blunsom and Cohn,
2011), bioinformatics (K
¨
all et al., 2005), and human
activity recognition (Sung-Hyun et al., 2018). Apply-
ing the Hidden Markov Model, the problem generally
satisfies two conditions:
1. It is a discrete-time stochastic process.
2. The states are hidden, only indirectly inferred or
estimated from the observations.
For example, a sequence-based series can be a time-
series or a state-series, and its states could be observed
or non-observed (hidden). The Viterbi algorithm (a
dynamic programming algorithm) is the most com-
monly used algorithm to find the sequence of most
likely hidden states in the HMM model.
It is easy to observe that the Viterbi algorithm per-
forms better when the differences between the emis-
sion probabilities are higher. Based on this observa-
tion, we propose the hypothesis that the accuracy of
the Viterbi algorithm can be approximated by a math-
ematical formula involving the cosine similarity mea-
sures. We conduct empirical analysis and find a close
a
https://orcid.org/0000-0002-0286-8757
b
https://orcid.org/0000-0002-5969-3839
c
https://orcid.org/0000-0002-7299-0432
d
https://orcid.org/0000-0003-0239-1810
relationship between the accuracy of the Viterbi algo-
rithm and the cosine similarity of the emission prob-
abilities. To the best of our knowledge, applying co-
sine similarity to estimate the accuracy of the Viterbi
algorithm is a novel way. Further, it is a simple com-
putation, and understanding the theoretical basis of
the accuracy may lead to newer and improved algo-
rithms to solve the most likely explanation problem
itself.
1.1 Related Work
In this section, we present a summary of the back-
ground research in this field. The basics of HMM was
found in a standard text such as (Russell and Norvig,
2009). A more conceptual understanding was pro-
posed in (Stamp, 2004). The Viterbi Algorithm has
been widely used to produce the maximum likelihood
estimation of the continuing states from the output se-
quence. Andrew Viterbi proposed the Viterbi algo-
rithm in 1967 (Viterbi, 1967), and numerous appli-
cations of the Viterbi algorithm have been discussed
over the past several decades.
1.2 Structure of This Paper
This paper is structured as follows. In Section 2, we
introduce the system model and the problem state-
ment, and made our hypothesis with the mathemati-
cal formula in Section 3; also present the empirical
results for this proposed algorithm in Section 4. Even-
tually, our discussion and conclusions wrap up the pa-
per in Section 5.
Zhao, G., Zhu, Z., Sun, Y. and Arora, A.
Pairwise Cosine Similarity of Emission Probability Matrix as an Indicator of Prediction Accuracy of the Viterbi Algorithm.
DOI: 10.5220/0010266509410946
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 2, pages 941-946
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
941

2 SYSTEM MODEL AND
PROBLEM STATEMENT
2.1 System Context
For estimating the most likely explanation of a given
observation sequence for a given HMM, the Viterbi
algorithm is the main algorithm. It is a dynamic pro-
gramming algorithm that runs in polynomial time that
was written as O(t n
2
), where t is the length of the ob-
servation sequence is and n is the number of states in
the HMM.
For a given HMM, the accuracy of the Viterbi al-
gorithm can be computed by conducting numerical
experiments as follows:
1. Generate an observation sequence
2. Present it to the Viterbi algorithm
3. Compare the hidden state sequence results from
the predicted hidden state sequence
We believe that this accuracy can be expressed as a
closed-form expression of the model (the underlying
HMM) itself, specifically the transition and the emis-
sion probability matrices. This paper assumes a fixed
transition probability matrix and focuses on the emis-
sion probability component of the HMM.
2.2 Problem Statement
The objective is to find a closed-form mathematical
formulation for the accuracy of the Viterbi algorithm
in terms of the underlying Hidden Markov Model.
Even more specifically, given the problem scope, we
can restate the objective as assuming a constant tran-
sition matrix, estimate the accuracy in terms of the
n × n emission probability matrix.
3 PROPOSED MATHEMATICAL
MODEL
3.1 Main Hypothesis
We assume a uniform transition matrix then estimate
the accuracy of the Viterbi algorithm by calculating
the cosine similarity of emission probabilities. The
mathematical model can be stated as follows:
Pa =
1 −
∑
k
i=1
{
X
k
}
k
×
n − 1
n
+
1
n
(1)
where
Pa : The accuracy of the prediction
k : The number of pairs of cosine similarity = C(n,2)
n : The number of states
K
∑
i=1
X
i
: Sum of the pairwise cosine similarity
3.2 Analysis and Discussion of the Main
Hypothesis
In HMM, the characteristic of the emission matrix
plays a key role. For the prediction results obtained
from the Viterbi Algorithm, the accuracy of predic-
tion increases as the emission vectors become more
different from each other. The larger differences cre-
ated by the states will produce a more accurate result
of the prediction. This is the main motivation to use
cosine similarity to calculate the differences between
each pair of emission probability of states.
After calculating the arithmetic mean, we add the
“normalization” step as can be seen in the last two cal-
culations in Formula 1. The terms
n−1
n
and
1
n
corre-
spond to this normalization step, to account for agree-
ment occurring by chance. Such a term can also be
witnessed in other measures, such as Cohen’s Kappa
statistic, originally proposed in (Galton, 1892). A
simple way to “derive” this formula can be to map
the overall probability to 1 when the cosine similarity
is 0 and to map the overall probability to
1
n
when the
cosine similarities are 1. We observe that the
1
n
is the
expected accuracy even if the emission matrix is the
same for all emissions and there is no basis to infer
which hidden state led to any given emission.
We can apply the following common-sense vali-
dation to the proposed formula, by way of observing
it in the context of two boundary conditions:
• Emissions Uniquely Identify the State: In this
case, the cosine measures are 0, and the for-
mula returns 1. Therefore, emissions can uniquely
identify the hidden states.
• Emission Probabilities Are Equal for All
States: When the emission probabilities of each
pair are the same, the cosine similarity of each
pair is 1. In this case, the formula returns 1/n,
which matches our intuitive result of a correct pre-
diction “by chance”.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
942

4 EMPIRICAL RESULTS
This section focuses on building simulation scenar-
ios and representing the empirical results. Our overall
simulation follows the next outline and more specific
details can be found in Section 4.1.
i We firstly generate an HMM, keeping a uniform
transition matrix
ii For that HMM, we generate the hidden sequence
of states and the observation sequence of emis-
sions.
iii We apply the Viterbi algorithm on the emissions
and retrieve the predicted set of states.
iv We compare the explanation retrieved from
Viterbi against the actual set of states generated
in step (ii) to calculate its accuracy.
v The experiment is repeated several times to pro-
duce the mean of accuracy.
The results of 3 × 3 matrix, 4 × 4 matrix are pre-
sented separately in section 4.2 and we analyzed the
possible contributors to the accuracy of the Viterbi al-
gorithm as well.
4.1 Simulation Scenarios
In this section, we illustrate the simulation scenarios
in more detail.
4.1.1 The State Sequence
We generated a state sequence as a reference. These
states are recorded to track the accuracy later on. The
initial state is set randomly, and the state sequence is
generated randomly based on the probability of the
transition.
4.1.2 Initial Probability
The initial probability is specified as
1
n
; it is equally
likely to be chosen as the initial state.
4.1.3 Transition Probability
As discussed in the scope of this paper, the transition
probability is set to equal between all states. That is,
from any state, it is equally likely to transition to any
of the other states (including itself).
4.1.4 Emission Probability
As the main study area of this paper, we consider dif-
ferent scenarios on emission probability and divide
them into three categories.
1. Emission probability for every emission is the
same from every state, as the Scenarios 3(10) in
Table 5.
2. Emission probability uniquely defines a state;
they’re either a 0 or a 1. In other words, each
emission comes from only a single state. The ma-
trix, in this case, looks like a permutation of the
identity matrix, as the Scenarios 3(1) in Table 5.
3. Emission probabilities are random; they are nei-
ther the same nor uniquely defined.
4.2 Numerical Results
In this section, we outline the results of the 1000 ex-
periments within 15-length of the state sequence on
the scenario described in section 4.1. We tested two
different data sets for this, 3×3 and 4×4 respectively,
and the results are included in Table 1 and Table 2.
For the data matrix of 3 × 3, We set all transition
probability to be
1
3
first. Then, we need to obtain three
cosine similarity, respectively. As shown in Table 1,
cos1 is the cosine similarity of E1 and E2, cos2 is the
cosine similarity of E2 and E3, and cos 3 is the cosine
similarity of E1 and E3. Meanwhile, we also compare
the prediction accuracy (PA) proposed by formula 1
with the Viterbi algorithm’s accuracy (AA), and the
difference between the two variables, is called an Er-
ror.
For the data matrix of 4 × 4, we have to change
the transition probability to
1
4
, and another difference
with 3 × 3 is that the 4 × 4 data matrix requires six
cosine similarities. cos1 is the Cosine similarity be-
tween E1 and E2, cos 2 is the Cosine similarity be-
tween E1 and E3, cos 3 is the Cosine similarity be-
tween E1 and E4, cos 4 is the Cosine similarity be-
tween E2 and E3, cos 5 is the Cosine similarity be-
tween E2 and E4, and cos 6 is the Cosine similarity
between E3 and E4.
4.3 Discussion
In the experiments, we attempted to establish a dif-
ferent matrix of transition probability under the cir-
cumstance of using the same emission probability;
we found that different entries of transition probabil-
ity will have an impact on the accuracy of the Viterbi
algorithm. Therefore, to keep the consistency of ex-
perimental results, we divided every variable in the
transition matrix Table 3 and Table 4 into equal parts
to reduce the effect of the transition probability on the
result.
In Table 1, the emission probability has size 3× 3;
we calculate the cosine similarity for the three pairs
Pairwise Cosine Similarity of Emission Probability Matrix as an Indicator of Prediction Accuracy of the Viterbi Algorithm
943
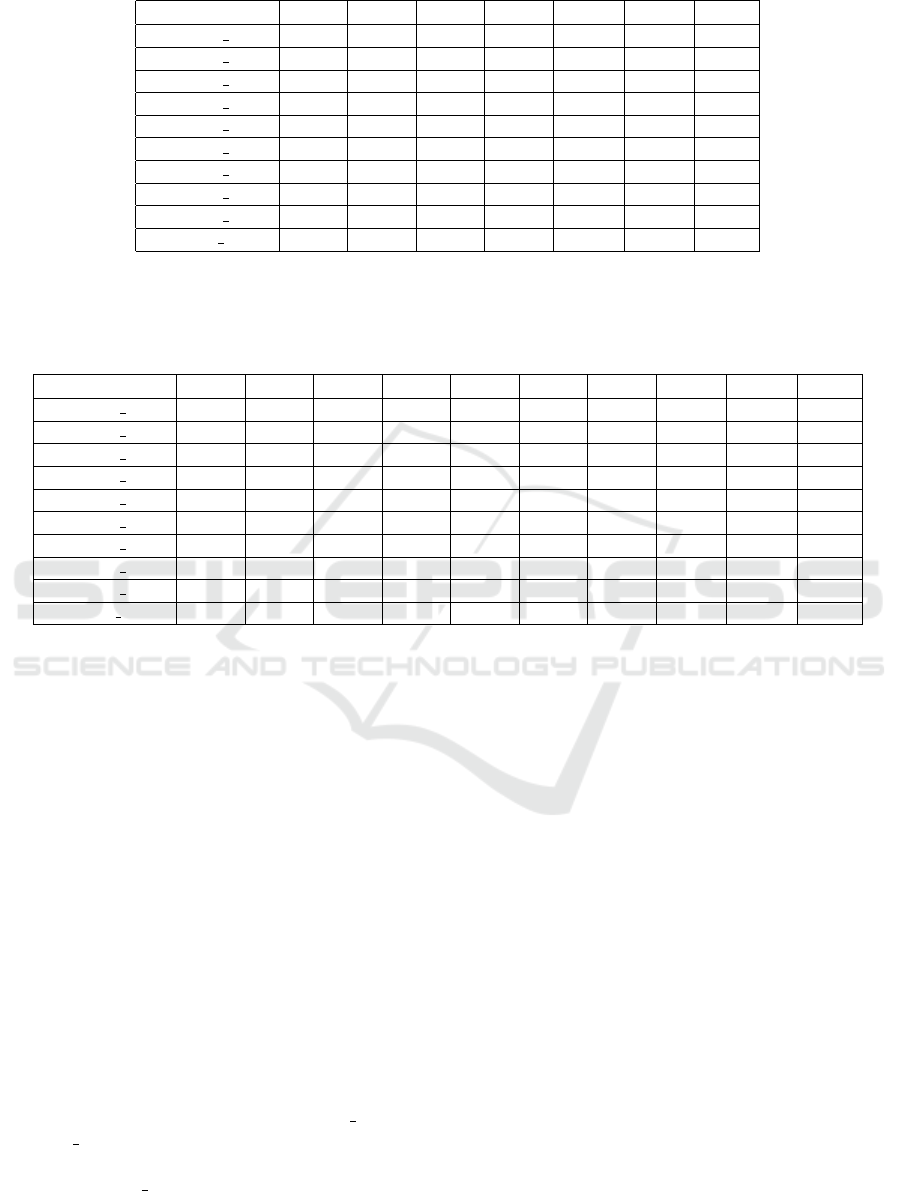
Table 1: Predicted Accuracy and Actual Accuracy of Viterbi Algorithm for a 3 × 3 HMM.
Scenario cos1 cos2 cos3 Mean
1
PA
2
AA
3
Error
Scenario 3(1) 0 0 0 0 100% 100% 0%
Scenario 3(2) 0.133 0.521 0.127 0.261 83% 80% 3%
Scenario 3(3) 0.258 0.258 0.258 0.258 83% 80% 3%
Scenario 3(4) 0.388 0.276 0.266 0.31 79% 76% 3%
Scenario 3(5) 0.313 0.477 0.632 0.474 68% 64% 4%
Scenario 3(6) 0.398 0.405 0.969 0.591 61% 58% 3%
Scenario 3(7) 0.784 0.491 0.849 0.708 52% 52% 0%
Scenario 3(8) 0.956 0.676 0.467 0.699 53% 50% 3%
Scenario 3(9) 0.895 0.830 0.987 0.904 40% 43% 3%
Scenario 3(10) 1 1 1 1 33% 33% 0%
1
The arithmetic mean of cos1, cos 2, and cos3
2
The predicted accuracy, given by the formula 1
3
The actual accuracy of the Viterbi algorithm
Table 2: Predicted and Actual Accuracy Values for the Viterbi Algorithm for a 4 × 4 HMM.
Scenario cos1 cos2 cos3 cos4 cos5 cos6 Mean
1
PA
2
AA
3
Error
Scenario 4(1) 0 0 0 0 0 0 0 100% 100% 0%
Scenario 4(2) 0.043 0.043 0.127 0.127 0.127 0.127 0.099 93% 94% 1%
Scenario 4(3) 0.308 0.308 0.308 0.308 0.308 0.308 0.308 77% 70% 7%
Scenario 4(4) 0.371 0.333 0.254 0.340 0.312 0.446 0.343 74% 68% 6%
Scenario 4(5) 0.449 0.342 0.266 0.528 0.483 0.479 0.424 68% 63% 5%
Scenario 4(6) 0.449 0.582 0.265 0.961 0.446 0.583 0.548 59% 54% 5%
Scenario 4(7) 0.452 0.582 0.268 0.986 0.542 0.580 0.569 57% 54% 3%
Scenario 4(8) 0.427 0.465 0.301 0.873 0.671 0.694 0.572 57% 51% 6%
Scenario 4(9) 0.427 0.526 0.311 0.832 0.768 0.867 0.622 53% 48% 5%
Scenario 4(10) 1 1 1 1 1 1 1 25% 25% 0%
1
The arithmetic mean of cos1∼cos 6
2
The predicted accuracy, given by the formula 1
3
The actual accuracy of the Viterbi algorithm
of emission probabilities. Based on the formula 1 dis-
cussed in Section 3.1, the predicted accuracy is calcu-
lated, then we can get the error between the predicted
accuracy and the actual accuracy.
Similarly, in Table 2 the emission probability has
size 4 × 4, we calculate the cosine similarity for the
six pairs of emission probabilities. Based on the for-
mula 1 discussed in section 3.1, the predicted accu-
racy is calculated, then we can get the error between
predicted accuracy and actual accuracy.
As a quick observation, the cosine similarity of
emission probability dramatically affects the accuracy
of the Viterbi algorithm. When the overall cosine sim-
ilarity is high, the accuracy of the Viterbi algorithm
decreases. On the contrary, the accuracy of the Viterbi
algorithm is higher when the arithmetic mean of co-
sine similarity is smaller.
Consider the two scenarios: Scenario 3(2) and
Scenario 3(3) in Table 1. There is a certain differ-
ence in the cosine similarity of the emission proba-
bility of Scenario 3(2), but their arithmetic means are
the same, and therefore, the predicted accuracy is also
the same.
4.3.1 Error Rate
Combining the results in Table 1 and Table 2, the
range of error is between 0% and 7%. Moreover, we
found the overall error in Table 1 is smaller, which is
about 2%.
5 CONCLUSIONS AND FUTURE
WORK
In this paper, we have attempted to predict the accu-
racy of the well known and well studied the Viterbi
algorithm in simple terms, specifically in terms of the
cosine similarity of the emission matrix. The experi-
mental results show that the proposed formula for pre-
dicted accuracy matches the observed accuracy very
well.
In this work, we assumed a random transition ma-
trix, but clearly, it can have a significant impact on
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
944

the accuracy as well. Just as a quick example, if some
part of the HMM network can never be “reached” due
to the transition probabilities, that part of the HMM
network should have no role in the prediction of the
hidden states. However, this analysis is not covered
in the current paper, and future work can consist of
studying the relationship between transition probabil-
ity and the accuracy of the Viterbi algorithm.
REFERENCES
Blunsom, P. and Cohn, T. (2011). A hierarchical pitman-
yor process hmm for unsupervised part of speech in-
duction. In Proceedings of the 49th Annual Meeting
of the Association for Computational Linguistics: Hu-
man Language Technologies, pages 865–874.
Gales, M. J. (1998). Maximum likelihood linear transfor-
mations for hmm-based speech recognition. Com-
puter speech & language, 12(2):75–98.
Galton, F. (1892). Finger Prints. Macmillan and Company.
K
¨
all, L., Krogh, A., and Sonnhammer, E. L. (2005). An
hmm posterior decoder for sequence feature predic-
tion that includes homology information. Bioinfor-
matics, 21(suppl 1):i251–i257.
Russell, S. and Norvig, P. (2009). Artificial Intelligence:
A Modern Approach. Prentice Hall Press, USA, 3rd
edition.
Stamp, M. (2004). A revealing introduction to hidden
markov models. Department of Computer Science San
Jose State University, pages 26–56.
Sung-Hyun, Y., Thapa, K., Kabir, M. H., and Hee-Chan,
L. (2018). Log-viterbi algorithm applied on second-
order hidden markov model for human activity recog-
nition. International Journal of Distributed Sensor
Networks, 14(4):1550147718772541.
Viterbi, A. (1967). Error bounds for convolutional
codes and an asymptotically optimum decoding al-
gorithm. IEEE Transactions on Information Theory,
13(2):260–269.
APPENDIX
In appendix, Table 3 represents the transition matrix
of 3×3, Table 4 represents the transition matrix of 4×
4. Table 5 and Table 6 are the corresponding emission
matrices.
Table 3: Transition Matrix 3 × 3.
Scenario 3(1∼10) T1 T2 T3
S1 1/3 1/3 1/3
S2 1/3 1/3 1/3
S3 1/3 1/3 1/3
Table 4: Transition Matrix 4 × 4.
Scenario 4(1∼10) T1 T2 T3 T4
S1 1/4 1/4 1/4 1/4
S2 1/4 1/4 1/4 1/4
S3 1/4 1/4 1/4 1/4
S4 1/4 1/4 1/4 1/4
Table 5: Emission Matrix 3 × 3.
Scenario 3(1) E1 E2 E3
S1 1 0 0
S2 0 1 0
S3 0 0 1
Scenario 3(2) E1 E2 E3
S1 0.99 0.005 0.005
S2 0.1 0.25 0.65
S3 0.1 0.75 0.15
Scenario 3(3) E1 E2 E3
S1 0.8 0.1 0.1
S2 0.1 0.1 0.8
S3 0.1 0.8 0.1
Scenario 3(4) E1 E2 E3
S1 0.8 0.1 0.1
S2 0.1 0.1 0.8
S3 0.2 0.7 0.1
Scenario 3(5) E1 E2 E3
S1 0.8 0 0.2
S2 0.24 0.25 0.51
S3 0.2 0.7 0.1
Scenario 3(6) E1 E2 E3
S1 0.5 0.2 0.3
S2 0.1 0.8 0.1
S3 0.45 0.1 0.45
Scenario 3(7) E1 E2 E3
S1 0.6 0.2 0.2
S2 0.4 0.5 0.1
S3 0.45 0.1 0.45
Scenario 3(8) E1 E2 E3
S1 0.1 0.4 0.5
S2 0.25 0.4 0.35
S3 0.4 0.6 0
Scenario 3(9) E1 E2 E3
S1 0.4 0.2 0.4
S2 0.3 0.4 0.3
S3 0.3 0.5 0.2
Scenario 3(10) E1 E2 E3
S1 0.333 0.333 0.333
S2 0.333 0.333 0.333
S3 0.333 0.333 0.333
Pairwise Cosine Similarity of Emission Probability Matrix as an Indicator of Prediction Accuracy of the Viterbi Algorithm
945

Table 6: Emission Matrix 4 × 4.
Scenario 4(1) E1 E2 E3 E4
S1 1 0 0 0
S2 0 1 0 0
S3 0 0 1 0
S4 0 0 0 1
Scenario 4(2) E1 E2 E3 E4
S1 0.94 0.02 0.02 0.02
S2 0.02 0.94 0.02 0.02
S3 0.02 0.02 0.94 0.02
S4 0.02 0.02 0.02 0.94
Scenario 4(3) E1 E2 E3 E4
S1 0.7 0.1 0.1 0.1
S2 0.1 0.7 0.1 0.1
S3 0.1 0.1 0.7 0.1
S4 0.1 0.1 0.1 0.7
Scenario 4(4) E1 E2 E3 E4
S1 0.7 0.15 0.1 0.05
S2 0.1 0.7 0.1 0.1
S3 0.1 0.1 0.6 0.2
S4 0.1 0.1 0.1 0.7
Scenario 4(5) E1 E2 E3 E4
S1 0.7 0.15 0.1 0.05
S2 0.1 0.5 0.2 0.2
S3 0.1 0.1 0.6 0.2
S4 0.1 0.1 0.1 0.7
Scenario 4(6) E1 E2 E3 E4
S1 0.7 0.15 0.1 0.05
S2 0.1 0.5 0.2 0.2
S3 0.1 0.1 0.05 0.75
S4 0.1 0.1 0.1 0.7
Scenario 4(7) E1 E2 E3 E4
S1 0.7 0.15 0.1 0.05
S2 0.1 0.5 0.2 0.2
S3 0.1 0.1 0.05 0.75
S4 0.1 0.2 0.1 0.6
Scenario 4(8) E1 E2 E3 E4
S1 0.7 0.15 0.1 0.05
S2 0.1 0.5 0.3 0.1
S3 0.1 0.1 0.2 0.4
S4 0.1 0.4 0.1 0.4
Scenario 4(9) E1 E2 E3 E4
S1 0.7 0.15 0.1 0.05
S2 0.1 0.5 0.2 0.2
S3 0.1 0.1 0.2 0.4
S4 0.1 0.4 0.1 0.4
Scenario 4(10) E1 E2 E3 E4
S1 0.25 0.25 0.25 0.25
S2 0.25 0.25 0.25 0.25
S3 0.25 0.25 0.25 0.25
S4 0.25 0.25 0.25 0.25
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
946
