
Dimensionality Reduction and Bandwidth Selection for Spatial Kernel
Discriminant Analysis
Soumia Boumeddane
1 a
, Leila Hamdad
1 b
, Hamid Haddadou
1 c
and Sophie Dabo-Niang
2 d
1
Laboratoire de la Communication dans les Syst
`
emes Informatiques, Ecole Nationale Sup
´
erieure d’Informatique,
BP 68M, 16309, Oued-Smar, Algiers, Algeria
2
Univ. Lille, CNRS, UMR 8524, Laboratoire Paul Painlev
´
e, F-59000 Lille, France
Keywords:
Spatial Kernel Discriminant Analysis, Feature Extraction, Principle Component Analysis, Particle Swarm
Optimization, Hyperspectral Image Classification.
Abstract:
Spatial Kernel Discriminant Analysis is a powerful tool for the classification of spatially dependent data. It
allows taking into consideration the spatial autocorrelation of data based on a spatial kernel density estimator.
The performance of SKDA is highly influenced by the choice of the smoothing parameters, also known as
bandwidths. Moreover, computing a kernel density estimate is computationally intensive for high-dimensional
datasets. In this paper, we consider the bandwidth selection as an optimization problem, that we resolve using
Particle Swarm Optimization algorithm. In addition, we investigate the use of Principle Component Analysis
as a feature extraction technique to reduce computational complexity and overcome curse of dimensionality
drawback. We examined the performance of our model on Hyperspectral image classification. Experiments
have given promising results on a commonly used dataset.
1 INTRODUCTION
Probability density estimation is a key concept for
many machine learning tasks and real-world applica-
tions, such as hotspot detection (of pandemics, crimes
and accidents), wind speed prediction, cluster analy-
sis, images analysis ... etc. Kernel density estima-
tion is a popular non-parametric density estimation
method with a well-known application in Kernel Dis-
criminant Analysis (KDA). In this work, we focus on
Spatial Kernel Discriminant Analysis (SKDA), pro-
posed by (Boumeddane et al., 2019) and (Boumed-
dane et al., 2020). SKDA is a supervised classifica-
tion algorithm accounting spatial dependency of data.
This algorithm is built using Spatial Kernel Density
Estimation (SKDE) (Dabo-Niang et al., 2014) which
includes two kernels: one controls the observed val-
ues while the other controls the spatial locations of
observations. Since SKDA is based of a kernel den-
sity estimation technique, its performance is highly
influenced, in one hand, by the choice of the smooth-
a
https://orcid.org/0000-0002-5595-3306
b
https://orcid.org/0000-0003-4515-5519
c
https://orcid.org/0000-0003-0824-0124
d
https://orcid.org/0000-0002-4000-6752
ing parameters, also known as bandwidths. Band-
width selection consists of finding the optimal values
that minimize the error between the estimated and the
real density, most proposed methods are costly since
they involve brute-force or exhaustive search strate-
gies (Zaman et al., 2016). Moreover, these methods
may note be suitable for classification purpose (Ghosh
and Chaudhuri, 2004). In (Dabo-Niang et al., 2014),
cross-validation was used to determine the best band-
widths for SKDE from a list of proposed values, for
a clustering application. Moreover, in (Boumeddane
et al., 2020), the bandwidths were determined experi-
mentally using a grid-search like approach.
In addition to bandwidth selection problem in ker-
nel density estimation, the choice of the most relevant
features is also crucial. In fact, the rise of high per-
formance technologies has resulted in an exponential
increase in collected data, in terms of both size and di-
mensionality. Nonetheless, these data usually contain
a high level of noise with irrelevant or redundant fea-
tures which can lead to lower classification accuracy
and an unnecessary increase in computational costs
and storage.
An optimal choice of features can improve the es-
timation perfomances and the learning speed, which
affects the classification performance of a kernel
278
Boumeddane, S., Hamdad, L., Haddadou, H. and Dabo-Niang, S.
Dimensionality Reduction and Bandwidth Selection for Spatial Kernel Discriminant Analysis.
DOI: 10.5220/0010269002780285
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 2, pages 278-285
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

density estimator based classifier (Sheikhpour et al.,
2016). Moreover, Kernel density estimation is com-
putationally intensive for high dimensional data, due
to the design of this estimator. Dimensionality reduc-
tion has been proven to be efficient to preprocess high
dimensional data and to remove noisy (i.e. irrelevant)
and redundant features. It aims to reduce the com-
plexity of a model and build a more comprehensible,
simpler and understandable data (Li et al., 2018).
In this study, we address the problem of band-
width selection for Spatial Kernel Discriminant Anal-
ysis in a context of high-dimensional feature space.
We propose a new hybrid approach to resolve both
dimensionality reduction and bandwidth selection for
Spatial Kernel Discriminant Analysis. Using Prin-
cipal Component Analysis (PCA) as a feature ex-
traction technique which consist of projecting data
to a new feature subspace with lower dimensional-
ity. Moreover, we consider the bandwidth selection as
an optimisation problem, that we resolve using Par-
ticle Swarm Optimization, a powerful and efficient
population-based optimization technique which has
been successfully applied in many complex optimi-
sation problems (Wang et al., 2018).
We validate our approach on hyperspectral image
(HSI) classification. These images provide rich in-
formation despite other remote sensing technologies.
However, this technique offers a large spectral vec-
tors with hundreds of wavelengths including possible
irrelevant or redundant data. This increases signifi-
cantly the computation time and model complexity of
classification algorithms.
This paper is organized as follows: In Section 2,
we present kernel density estimation and highlight the
effect of the bandwidth selection. In section 3, we
give a brief overview of Spatial Kernel Discriminant
Analysis (SKDA). Section 4 is dedicated to related
work. In section 5, we present Principle component
Analysis and Particle Swarm Optimisation. Then, we
explain in section 6 our proposed approach for dimen-
sionality reduction and the selection of SKDA band-
widths. Finally, we present the experimental results
of our approach for HSI classification.
2 KERNEL DENSITY
ESTIMATION
Suppose we have a random variable X with a proba-
bility density function f . Typically, the precise form
of the density function f is not known and needs to
be estimated. Kernel density estimation (KDE), also
known as Parzen Window method (Silverman, 1986)
is a common approach to compute a non-parametric
estimates of the probability density functions f . This
non-parametric nature makes KDE a flexible and at-
tractive method, since it can estimate the density di-
rectly from data samples without any assumptions
about the form of the distribution (Gramacki, 2018).
Let X be a random variable with an un-
known probability density function f . Given n d-
dimensional, independent and identically distributed
samples X
1
, X
2
, ..., X
n
of X, the kernel estimate of the
density function f denoted
ˆ
f is given by:
ˆ
f (x) =
1
nh
d
n
∑
i=1
K
x − X
i
h
, x ∈ R
d
(1)
Where: h is a hyperparameter named the bandwidth
which controls the amount of smoothing, and K is a
smoothing function called the kernel function, that as-
sign a weight according to the distance between X
i
and x.
Fig. 1 illustrates a set of data points (black vertical
lines on the x-axis) and their individual kernels (red
lines) computed using Gaussian kernel. The overall
density (blue curve) is computed by summing these
individual functions according to Equation 1.
Figure 1: Kernel density estimate (KDE).
The bandwidth h plays the role of a smoothing scale,
and determines how much emphasis is put on the clos-
est points. It is well recognized that the choice of the
bandwidth is a crucial problem for KDE (Gramacki,
2018). This problem is often known as bandwidth se-
lection.
To illustrate the effect of this hyperparameter , Fig.
2 shows the kernel density estimate of a random sam-
ple of 1000 samples from a Gaussian distribution us-
ing different bandwidth values. As we can see, the
most appropriate estimation has been obtained when
h = 0.22. However, when h is too small, (h = 0.03)
the density is undersmoothed. On the contrast, for a
large value of the bandwidth (h = 1.5), the density is
oversmoothed (Chen, 2017).
Dimensionality Reduction and Bandwidth Selection for Spatial Kernel Discriminant Analysis
279

Figure 2: Kernel density estimate (KDE) with different
bandwidths.
One of the well-known application of Kernel Den-
sity Estimation is its use to build a supervised clas-
sifier upon Bayes’ theorem, called Kernel Discrim-
inant Analysis (KDA). In fact, for a training set
of n d-dimensional samples grouped into m classes,
Bayes discriminant rule consists of assigning a d-
dimensional observation x to the class k
0
with highest
posterior probability, formulated as:
k
0
= argmax
k∈{1,2,...,m}
(π
k
f
k
(x)) (2)
Where f
k
is the probability density function of x in
the class k and π
k
is the a priori probability that an ob-
servation belongs to the class k(k = 1, ..., m). Kernel
Discriminant Analysis rule consists of using Kernel
Density Estimation (Equation 1) to estimate the the
density functions f
k
.
3 SPATIAL KERNEL
DISCRIMINANT ANALYSIS
Like most classification algorithms, Kernel Discrim-
inant Analysis assumes that data samples are inde-
pendent and identically distributed (i.i.d). However,
this assumption is often violated in many real-life
problems, for example, in georeferenced data con-
taining a spatial dimension and characterized by spa-
tial autocorrelation phenomena. This characteristic
comes from the fact that more the objects are close
to each other, the higher is the correlation between
them (Miller, 2004).
In (Boumeddane et al., 2019) and (Boumeddane
et al., 2020), the authors proposed an extension of
Kernel Discriminant Analysis (KDA) for spatially de-
pendent data, based on a Spatial Kernel Density Esti-
mator (SKDE) proposed by (Dabo-Niang et al., 2014)
which takes into account the spatial positions of data.
We consider a spatial process {Z
s
= (X
s
, Y
s
) ∈
R
d
× [1, m], s ∈ Z
2
, d ∈ N
∗
, m ∈ N
∗
}, representing a
set of d-dimensional observations x
s
measured each at
a site (geographic position) s ∈ Z
2
and y
s
is the class
label (1...m) to which x
s
belongs.
Suppose that x
(k)
1
, x
(k)
2
, ..., x
(k)
m
k
are d-dimensional
observations from the k-th class (k = 1, 2, ..., m) of the
training set (of a total size n), measured at the sites
s
1
, s
2
, ..., s
m
k
respectively.
An observation x
j
∈ R
d
located at a site s
j
, will
be assigned to the class k
0
, where:
k
0
= argmax
k∈{1,2,...,m}
(
ˆ
π
k
ˆ
f
k
(x)) (3)
The class density function f
k
of the k-th class is
estimated using the spatial kernel density estimator
(SKDE) of (Dabo-Niang et al., 2014), defined as:
ˆ
f
k
(x
j
) =
1
m
k
h
d
v
h
2
s
m
k
∑
i=1
K
v
x
j
− x
(k)
i
h
v
!
K
s
ks
j
− s
i
k
h
s
,
(4)
where:
• h
v
and h
s
are two bandwidths controlling, respec-
tively, features and spatial neighbourhood,
• K
v
and K
s
are two kernels respectively defined in
R
d
and R, where K
v
manages observations’ values
while K
s
deals with the spatial dimension of data,
• k s
j
− s
k
i
k is the Euclidean distance between the
sites s
j
and s
i
,
4 RELATED WORK
In literature, a set of data-based bandwidth selec-
tors have been proposed for kernel density estima-
tion. The core idea behind these methods is to find
the optimal bandwidth which minimises the Mean In-
tegrated Squared Error (MISE) between the estimated
and actual probability density function (Chen, 2017),
formulated as:
MISE(h) = E[
Z
(
ˆ
f (x) − f (x))
2
dx] (5)
These methods include: (1) Rules-of-thumb : such as,
Silverman’s rule of thumb and Scott’s rule of thumb.
These rules rely upon some assumption on the den-
sity, like the assumption of a normal density in Silver-
man’s rule, which makes these methods not totality
data-driven (Zhou et al., 2018) , (2) Cross-validation
based approaches: including least square cross val-
idation, biased cross validation and smoothed cross
validation, (3) Plug-in approaches and (4) Bootstrap
approaches (Chen, 2017).
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
280

These bandwidth selection techniques that aim to
minimise the MISE may note be suitable for classifi-
cation purpose, in other words the optimal bandwidth
that minimise the MISE may not be optimal to min-
imise the misclassification rate (Ghosh and Chaud-
huri, 2004). In addition, SKDA depends on two band-
widths related to featutes on one hand, and spatial
neighbourhood on the other hand. These bandwidth
selection methods do not consider the spatial dimen-
sion of data.
Few works has addressed dimensionality reduc-
tion and bandwidth selection for Kernel Discrimi-
nant Analysis. In (Sheikhpour et al., 2016), the au-
thors proposed a hybrid model of Particle Swarm Op-
timization (PSO) and Kernel Discriminant Analysis
using PSO metaheuristic for both features and op-
timal bandwith selection. This model was applied
for breast cancer diagnosis. Moreover, (Baek et al.,
2016) proposed an approach which integrates Ker-
nel Discriminant analysis and the information theo-
retic measure of complexity (ICOMP) with genetic
algorithm (GA), used simultaneously for features and
bandwidth selection. Recently, (Sheikhpour et al.,
2017) proposed a kernelized non-parametric classifier
based on feature ranking in anisotropic Gaussian ker-
nel (KNR-AGK). This approach uses features’ ranks
for both feature selection and parameters learning
of the anisotropic Gaussian kernel, considering these
ranks as the kernel bandwidths of different dimen-
sions.
5 BACKGROUND
In this section we present an overview of the two con-
cepts that we will use in our hybrid method : Principle
Component Analysis and Particle Swarm Optimisa-
tion.
5.1 Principle Component Analysis
Principal component analysis (PCA) is a dimension-
ality reduction technique, which projects a data set
of a high-dimensional space into a lower-dimensional
sub-space, with the goal of preserving most of the
variation. It is a mathematical algorithm, which con-
sists of finding a linear combination converting the
original variables into a new set of uncorrelated vari-
ables (the principle components) which capture max-
imal variance. PCA can be performed via an eigen
decomposition of the covariance matrix C (d × d) (Pu
et al., 2014), given by:
C = W ΛW
−1
(6)
where:
• W is a (d × d) matrix of eigenvectors, which rep-
resents the principle components,
• and Λ is a diagonal matrix of d eigenvalues.
Principle components are ordered such that first
ones has maximum variance. For a dimensionality re-
duction purpose, features with small eigenvalues may
be dismissed and the data points will be projected
onto the first k Principle Components (van der Walt
and Barnard, 2017).
5.2 Particle Swarm Optimisation
Particle Swarm Optimisation (PSO) is a nature-
inspired metaheuristic originally proposed by
Kennedy and Elberhart in 1995, that simulates the so-
cial behaviour of some animals such as insects, herds,
schools of fish or flocks of birds which cooperate to
find food. PSO is a population based stochastic opti-
mization technique, which uses a population called
swarm composed of N particles that moves over the
research space, iteration to iteration. Each particle
has a position vector X
i
(x
i1
, x
i2
, ...., x
id
) and a velocity
vector v
i
(v
i1
, v
i2
..., v
id
), where i ∈ {1, 2, ..., N} and
d is the number of dimensions in the vector. Each
particle represents a potential solution to the problem
in the d-dimensional research space (Wang et al.,
2018).
The optimization process starts with a randomly
initialized population of solutions. During the re-
search process of the optimal solution, each parti-
cle adjust its search direction toward a promising
search region according to its own optimal experi-
ence (pbest
i
) and the optimal experience of the swarm
(called the global best: gbest). The performance of
each particle is measured using a fitness function re-
lated to the problem definition.
The velocity and position of each particle are up-
dated using the following equations (Wang et al.,
2018):
v
d
i,t+1
= wv
d
i,t
+ c
1
r
1
(p
d
i,t
− x
d
i,t
) +c
2
r
2
(p
d
g,t
− x
d
i,t
) (7)
x
d
i,t+1
= x
d
i,t
+ v
d
i,t+1
(8)
Where: w is the inertia weight, c
1
and c
2
are acceler-
ation constants, and r
1
and r
2
are uniformly random
values between 0 and 1.
This process is repeated until a stop criteria is sat-
isfied, such as a maximum number of iterations.
Dimensionality Reduction and Bandwidth Selection for Spatial Kernel Discriminant Analysis
281

6 PROPOSED APPROACH
We summarize in Fig. 3 the steps of our proposed
approach that we called PSO-SKDA.
Figure 3: PSO-SKDA approach.
Step 1: PCA for Features Extraction. We pro-
pose to apply PCA as a preprocessing step prior to
SKDA. PCA will serves as a dimensionality reduc-
tion technique and also as bandwidth regularizer. As
previously explained, only the first principle compo-
nents with highest eigenvalues will be kept. More-
over, we performed PCA on non-spatial dimensions
only, while preserving spatial information. In addi-
tion, we performed PCA on the training set samples,
than apply the same linear transformation on the test
set before the classification. The number of selected
principal components will be denoted d
0
.
Step 2 : PSO for Bandwidths Selection. In this
step we use PSO technique to carry out the selec-
tion of the optimal values of the bandwidths h
s
and h
v
which maximise the classification accuracy of SKDA.
That is to say that, we defined the fitness function as
the classification overall accuracy of SKDA and band-
width selection consists of finding the optimal band-
widths which maximise the classification accuracy.
Moreover, we encode the solutions as a (d
0
+ 1) di-
mensional vector H = [hv
1
, hv
2
, ..., hv
d
0
, h
s
] where d
0
is the number of the retained principal components
and hv
i
is the bandwidth of the i-th feature.
In each iteration of PSO, the objective function is
calculated for all particles using SKDA, based on a
k-fold cross validation on the training set. Figure 4 il-
lustrates the concept of k-fold cross validation, which
consists of splitting the training set into k subsets of
same size and using k −1 folds to train the model and
the remaining fold for validation. The output of the
model is the average of the values computed in the
loop.
Figure 4: k-fold cross validation.
Also, the position of particles are updated using
Equations 7 and 8, and global and per-particle best
solutions are updated.
Step 3: Classification with the Optimal Deter-
mined Kernel Bandwidths. The final step consists
of the classification of the transformed testing data us-
ing SKDA classifier based on the determined optimal
kernel bandwidths.
7 EXPERIMENTS
7.1 Experimental Setup
We applied our approach for Hyperspectral image
classification which consists of assigning a label (ex:
water, forest ...) to a pixel. A hyperspectral image
(HSI) is a set of simultaneous images collected for
the same area on the surface of the earth with hun-
dreds of spectral bands at different wavelength chan-
nels and with high resolution. Each pixel of a HSI
at a position s
i
(representing the spatial dimension) is
characterized by a d-dimensional spectral vector (rep-
resenting the spectral dimension).
These images are characterised by the high num-
ber of spectral bands. Also, from a spectral point
of view, pixels of the same materials have similar
spectral signature (Benediktsson and Ghamisi, 2015).
Moreover, a strong correlation exists between neigh-
bouring bands of a hyperspectral image. This fact
motivates the use of feature selection and feature ex-
traction techniques to reduce the dimensionality of the
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
282

Figure 5: Indian Pines dataset: (a) false color image,
(b) training samples, and (c) test samples (Ghamisi et al.,
2014).
hyperspectral cube.
Moreover, from the spatial perspective, the spec-
tral signatures are spatially correlated, which mean
that neighbouring pixels usually belongs to the same
material especially for high-resolution images. This
characteristic known as spatial autocorrelation should
be taken into account for an effective analysis.
We conducted our experiments on a 200-
dimensional dataset named Indian Pines dataset,
which consists of a 145 × 145 pixels image over
the Indian Pines site in Northwestern Indiana. The
ground truth is classified into 16 classes, containing
agriculture, forest and natural vegetation. We used
standard training and test sets (Mou et al., 2018),
widely used by the HSI classification community.
This makes our results entirely comparable to state-
of-the-art methods. Fig. 5 visualizes this image and
the training and test samples that we used. Table 1
displays the size of each class of this dataset’s train-
ing and testing sets.
To evaluate the performance of our algorithm,
we use the following measures: 1) Average Accu-
racy (AA) : representing the average value of the
class classification accuracy (CA). 2) Overall accu-
racy (OA) : which represents the ratio of correctly
classified samples, i.e. calculated as the number of
correctly classified pixels, divided by the number of
test samples. 3) Kappa Coefficient (κ) : that pro-
vides information regarding the amount of agreement
corrected by the level of agreement that could be ex-
pected due to chance alone.
7.2 Experimental Results
To decide how much principle components to keep,
while retaining as much of the information as pos-
sible, we use the Cumulative Proportion of Variance
Explained graph (Figure 6). We only keep the trans-
formed features with highest eigenvalues such that the
cumulative proportion of variance explained is about
98%. For the Indian Pines dataset with an original
feature space of 200 variables, only 25 principle com-
ponents are selected.
Table 1: Class labels and the number of training and testing
samples for Indian pines dataset.
Name Train Test Total
1 Corn-no till 50 1384 1434
2 Corn-min till 50 784 834
3 Corn 50 184 234
4 Grass-pasture 50 447 497
5 Grass-trees 50 697 747
6 Hay-windrowed 50 439 489
7 Soybean-no till 50 918 968
8 Soybean-min till 50 2418 2468
9 Soybean-clean 50 564 614
10 Wheat 50 162 212
11 Woods 50 1244 1294
12 Bldg-grass-tree-
drives
50 330 380
13 Stone-Steel-
Towers
50 45 95
14 Alfalfa 15 39 54
15 Grass-pasture-
mowed
15 11 26
16 Oats 15 5 20
Total 695 9671 10366
Figure 6: Cumulative Proportion of Variance Explained
graph for IP dataset.
Moreover, we executed the PSO process to select
the optimal bandwidth with 20 iterations where each
swarm contains 20 particles. Using a 5-fold cross-
validation and an Epanechnikov kernel for K
v
and K
s
.
The parameters of PSO are initialized as follows:
c
1
= c
2
= 1.93 , w = 0.72. Also, the solution space is
reduced to the values between 1 and 10.
Using our approach, the best solutions found are:
h
v
= 6 and h
s
= 3.5, here we used same h
v
for all
feature dimensions.
We compared PSO-SKDA results to state-of-the-
art techniques related to Hyperspectral images classi-
Dimensionality Reduction and Bandwidth Selection for Spatial Kernel Discriminant Analysis
283
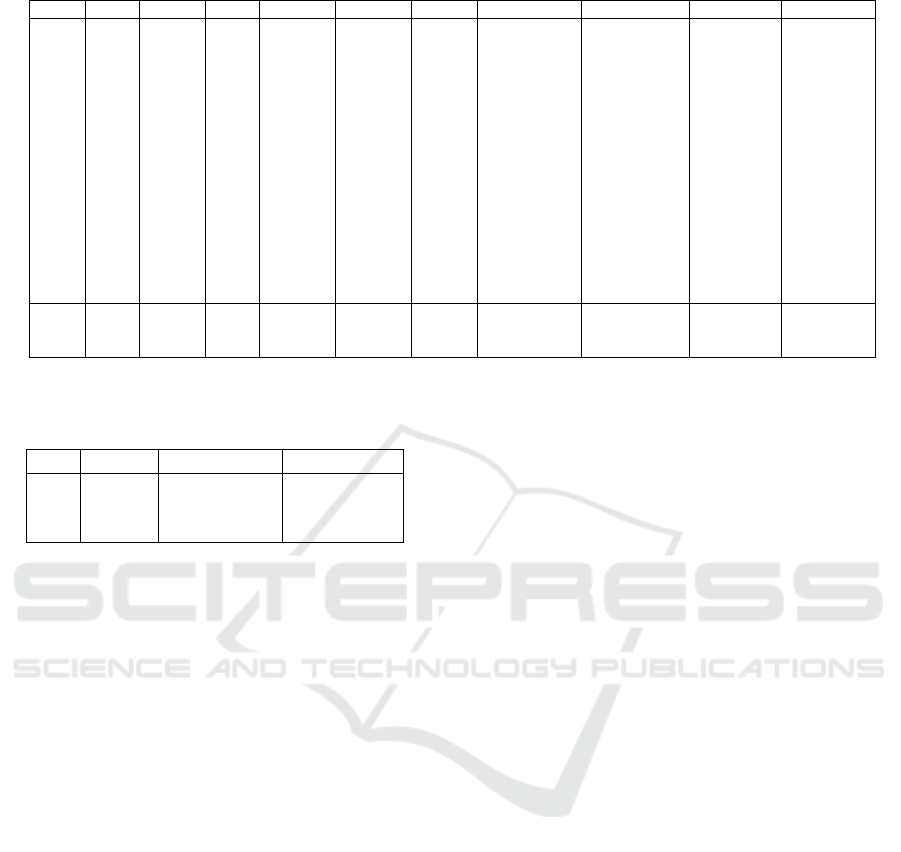
Table 2: Classification results (%) for Indian Pines dataset using standard training and test sets.
SVM RF-200 RNN 1D-CNN 2D-CNN SICNN Res. C-D Net RNN-GRU-Pr SSCasRNN PSO-SKDA
CA1 64.31 54.84 64.74 61.34 82.51 79.84 74.86 70.59 86.99 89.74
CA2 70.92 58.42 61.35 60.33 88.14 92.47 95.28 70.82 98.72 97.07
CA3 84.78 82.61 74.46 80.43 100.0 99.46 100.0 81.52 100.0 100.0
CA4 91.05 85.91 83.45 89.04 94.85 93.29 95.08 90.16 94.41 88.14
CA5 85.94 80.49 77.04 90.53 85.80 92.68 96.56 91.97 97.42 95.84
CA6 93.62 94.76 87.70 96.13 99.77 96.58 99.09 96.13 100.0 99.77
CA7 69.17 77.34 76.03 72.11 82.35 86.82 84.42 84.75 87.15 90.63
CA8 52.90 59.43 60.79 54.47 73.86 69.52 74.57 59.64 85.98 85.98
CA9 76.60 63.48 61.17 75.71 86.00 83.69 80.14 86.17 87.23 88.30
CA10 97.53 96.06 93.21 99.83 100.0 100.0 100.0 99.38 100.0 99.38
CA11 77.49 88.26 81.67 80.87 94.53 96.70 95.74 84.97 97.51 98.07
CA12 73.33 54.85 55.45 78.48 97.27 96.97 96.06 77.58 99.70 99.09
CA13 100.0 97.78 86.67 91.11 100.0 100.0 100.0 95.56 100.0 100.0
CA14 87.18 58.97 69.23 94.87 97.44 94.87 84.62 84.62 100.0 100.0
CA15 90.91 81.82 90.91 90.91 100.0 100.0 100.0 90.91 100.0 100.0
CA16 100.0 100.0 80.00 100.0 100.0 100.0 100.0 100.0 100.0 100.0
OA 70.55 69.79 69.82 70.79 85.43 85.13 85.76 88.63 91.79 92.07
AA 82.23 77.13 75.24 82.23 92.66 92.68 92.28 85.63 95.79 95.75
κ 66.90 65.89 65.87 67.07 83.49 83.13 83.85 73.66 90.62 90.94
Table 3: Comparaison between SKDA, PCA-SKDA and
PSO-SKDA for Indian Pines dataset.
SKDA PCA-SKDA PSO-SKDA
OA 93.89 92.71 92.07
AA 96.67 96.13 95.75
κ 93.01 98.18 90.94
fication, including: SVM, RF-200 which consists of
a Random forest with 200 trees, RNN, 1D CNN, 2D
CNN, SICNN, Res. Conv-Deconv Net (Mou et al.,
2018), RNN-GRU-PRetanh (Mou et al., 2017) and
SSCasRNN (Hang et al., 2019).
Since we use same sets of training and test, we
reported the results of SVM, RNN, 1D-CNN and 2D-
CNN from (Hang et al., 2019). In addition, the re-
sults of RF-200 and RNN-GRU-PRetanh are reported
from (Mou et al., 2017). Finally, those of SICNN and
Res. Conv-Deconv Net are reported from (Mou et al.,
2018).
Table 2 shows classification results of Indian pines
dataset. As we might notice, PSO-SKDA gives com-
petitive classification accuracies comparing to state-
of-the art methods with highest overall accuracy and
kappa coefficient. PSO-SKDA gives best or equiva-
lent results for 10 classes from 16, with a 100% accu-
racy for 5 classes. This experiment shows the effec-
tiveness of the proposed method, and that dimension-
ality reduction using PCA didn’t affected the accuracy
of our classifier. In addition, even with limited num-
ber of training set, the hypermatametrs tuning from
the training set gave good results on the new values of
the test set.
In Table 3, we compare the results of PSO-SKDA
to SKDA (Boumeddane et al., 2020) and PCA-SKDA
where the bandwidths where tuned experimentally us-
ing a grid search like approach based on test set.
This results shows that our new approach PSO-
SKDA is more accurate then SKDA and PCA-SKDA.
In fact, the results of these two approaches are over-
estimated since the test set was used for the hyperpa-
rameters tuning, this introduces a bias in the results.
8 CONCLUSION
In this paper, we introduced a new hybrid approach,
which integrates Spatial Kernel Discriminant Anal-
ysis, Principle Components Analysis and Particle
Swarm Optimisation. This model aims to automate
the choice of the optimal values of the bandwidths
h
v
an d h
s
and reduce the computational complex-
ity due to the high dimensionality of data. Exper-
iments on Hyperspectral Image classification have
shown promising results of PSO-SKDA on Indian
Pines dataset compared to latest state-of-the-art algo-
rithms for HSI classification. As a future work, we
aim to validate our approach on other datasets and to
enhance the execution time which remains problem-
atic for kernel density estimation based algorithms es-
pecially for huge datasets. This issue needs more in-
vestigation to improve the computational complexity.
REFERENCES
Baek, S. H., Park, D. H., and Bozdogan, H. (2016). Hy-
brid kernel density estimation for discriminant anal-
ysis with information complexity and genetic algo-
rithm. Knowl.-Based Syst., 99:79–91.
Benediktsson, J. A. and Ghamisi, P. (2015). Spectral-spatial
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
284

classification of hyperspectral remote sensing images.
Artech House.
Boumeddane, S., Hamdad, L., Dabo-Niang, S., and Had-
dadou, H. (2019). Spatial kernel discriminant anal-
ysis: Applied for hyperspectral image classification.
In Proceedings of the 11th International Conference
on Agents and Artificial Intelligence, ICAART 2019,
Volume 2, Prague, Czech Republic, February 19-21,
2019., pages 184–191.
Boumeddane, S., Hamdad, L., Haddadou, H., and Dabo-
Niang, S. (2020). A kernel discriminant analysis for
spatially dependent data. Distributed and Parallel
Databases, pages 1–24.
Chen, Y.-C. (2017). A tutorial on kernel density estimation
and recent advances. Biostatistics & Epidemiology,
1(1):161–187.
Dabo-Niang, S., Hamdad, L., Ternynck, C., and Yao, A.-
F. (2014). A kernel spatial density estimation allow-
ing for the analysis of spatial clustering. application
to monsoon asia drought atlas data. Stochastic envi-
ronmental research and risk assessment, 28(8):2075–
2099.
Ghamisi, P., Benediktsson, J. A., Cavallaro, G., and Plaza,
A. (2014). Automatic framework for spectral-spatial
classification based on supervised feature extraction
and morphological attribute profiles. IEEE J. Sel. Top.
Appl. Earth Obs. Remote. Sens., 7(6):2147–2160.
Ghosh, A. K. and Chaudhuri, P. (2004). Optimal smooth-
ing in kernel discriminant analysis. Statistica Sinica,
pages 457–483.
Gramacki, A. (2018). Nonparametric kernel density esti-
mation and its computational aspects. Springer.
Hang, R., Liu, Q., Hong, D., and Ghamisi, P. (2019). Cas-
caded recurrent neural networks for hyperspectral im-
age classification. IEEE Trans. Geoscience and Re-
mote Sensing, 57(8):5384–5394.
Li, J., Cheng, K., Wang, S., Morstatter, F., Trevino, R. P.,
Tang, J., and Liu, H. (2018). Feature selection: A data
perspective. ACM Comput. Surv., 50(6):94:1–94:45.
Miller, H. J. (2004). Tobler’s first law and spatial analysis.
Annals of the Association of American Geographers,
94(2):284–289.
Mou, L., Ghamisi, P., and Zhu, X. X. (2017). Deep recur-
rent neural networks for hyperspectral image classifi-
cation. IEEE Trans. Geoscience and Remote Sensing,
55(7):3639–3655.
Mou, L., Ghamisi, P., and Zhu, X. X. (2018). Un-
supervised spectral-spatial feature learning via deep
residual conv-deconv network for hyperspectral image
classification. IEEE Trans. Geoscience and Remote
Sensing, 56(1):391–406.
Pu, H., Chen, Z., Wang, B., and Jiang, G.-M. (2014). A
novel spatial–spectral similarity measure for dimen-
sionality reduction and classification of hyperspectral
imagery. IEEE Transactions on Geoscience and Re-
mote Sensing, 52(11):7008–7022.
Sheikhpour, R., Sarram, M. A., Chahooki, M. A. Z., and
Sheikhpour, R. (2017). A kernelized non-parametric
classifier based on feature ranking in anisotropic gaus-
sian kernel. Neurocomputing, 267:545–555.
Sheikhpour, R., Sarram, M. A., and Sheikhpour, R. (2016).
Particle swarm optimization for bandwidth determina-
tion and feature selection of kernel density estimation
based classifiers in diagnosis of breast cancer. Appl.
Soft Comput., 40:113–131.
Silverman, B. W. (1986). Density estimation for statistics
and data analysis, volume 26. CRC press.
van der Walt, C. M. and Barnard, E. (2017). Variable
kernel density estimation in high-dimensional feature
spaces. In Proceedings of the Thirty-First AAAI Con-
ference on Artificial Intelligence, February 4-9, 2017,
San Francisco, California, USA., pages 2674–2680.
Wang, D., Tan, D., and Liu, L. (2018). Particle swarm op-
timization algorithm: an overview. Soft Computing,
22(2):387–408.
Zaman, F., Wong, Y., and Ng, B. (2016). Density-based
denoising of point cloud. CoRR, abs/1602.05312.
Zhou, Z., Si, G., Zhang, Y., and Zheng, K. (2018). Robust
clustering by identifying the veins of clusters based on
kernel density estimation. Knowledge-Based Systems,
159:309–320.
Dimensionality Reduction and Bandwidth Selection for Spatial Kernel Discriminant Analysis
285
