
Analysing the Risk Propagation in the Project Portfolio Network
using the SIRF Model
Xingqi Zou
a
, Qing Yang
b
and Qinru Wang
c
School of Economics and Management, University of Science and Technology Beijing, 30 Xueyuan Road, Beijing, China
Keywords: Portfolio Risk, SIRF (Susceptible-Infected-Recovered-Failed) Model, Risk Propagation, K-shell, Centrality
of Eigenvectors, Link Entropy.
Abstract: Due to the existence of dependencies among the projects, the risk in one project will cause risks in other
projects, which will lead to the risk propagation in the portfolio network. To measure the criticality of projects
in the portfolio considering risk propagation, the paper builds the risk analysis model using the complex
network and SIRF model. Firstly, we build the network of the project portfolio based on the analysis of the
independency among projects, then we propose the integrated project criticality measurement (IPCM)
algorithm based on the complex network theory. The IPCM algorithm integrates the K-shell, eigenvector
centrality and the neighbour nodes in the complex network to analyse the project criticality. Furthermore, the
link entropy is used to calculate the influence of the project in the network. On this basis, combined with the
practice of R&D project management, the SIRF (susceptible-infected-recovered-failed) model is proposed to
analyse the dynamic propagation process of the risk in the project portfolio network. Then the priority ranking
of the project portfolio is realized under the dynamic risk propagation. Finally, a representative example is
provided to illustrate the validity of proposed models.
1 INTRODUCTION
4
Project portfolio is a collection of projects, project
sets, sub-project portfolios, and operations that are
managed together to achieve strategic goals (Project
Management Institute, 2018). Due to the existence of
dependencies between projects, the occurrence of
risks in a certain project will make other projects
risky, which will lead to the "domino effect" in the
portfolio, and ultimately lead to the failure of the
entire project portfolio (Neumeier et al., 2018).
Aiming at the shortcomings of the traditional project
portfolio
critic
ality analysis that ignore the dynamic
spread of risk in the project portfolio, the paper uses
SIR (susceptible-infected-recovered) model to
analyse the project portfolio risk. The SIR is often
used to describe the spread of diseases, viruses and
rumours in social network (Wen et al., 2012). Similar
to the spread of infectious diseases in the population,
the propagation of risk in the portfolio also conforms
to the dynamics of complex networks. Therefore,
a
https://orcid.org/0000-0001-5679-8152
b
https://orcid.org/0000-0002-7529-9065
c
https://orcid.org/0000-0002-3267-7804
depending on the analysis of the portfolio, the paper
extends the traditional SIR model to the SIRF
(susceptible-infected-recovered-failed) to analyse the
dynamic propagation process of the risk, and then
measure the criticality of projects in the portfolio.
The paper measures the criticality of projects
using the complex network theory. The node
centrality is widely used to identify influential nodes
in the network (Liu et al., 2015). Among them, the K-
shell measures the importance based on the location
attribute. The Kitsak et al. (2010) pointed out that the
most influential node in the network is not the node
with the largest degree value, but the node at the core
position of the network obtained through K-shell
decomposition. It means that the position of a node in
the network determines its criticality, that is, the
higher the Ks value of the node in the network, the
stronger its criticality and the greater its influence.
Another measure of node importance is eigenvector
centrality. The eigenvector centrality calculates that
the influence of the node in network not only depends
226
Zou, X., Yang, Q. and Wang, Q.
Analysing the Risk Propagation in the Project Portfolio Network using the SIRF Model.
DOI: 10.5220/0010288102260232
In Proceedings of the 10th International Conference on Operations Research and Enterprise Systems (ICORES 2021), pages 226-232
ISBN: 978-989-758-485-5
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
on the number of its neighbour nodes (the number of
nodes that the node can affect, that is, the out-degree),
but also depends on the influence of neighbour nodes
(Liu et al., 2015). The eigenvector centrality is
proportional to the influence of neighbour nodes.
Therefore, the paper proposes the integrated
project criticality measure (IPCM) algorithm, which
integrates the location attribute (K-shell), the local
attribute (neighbour node analysis) and the global
attribute (eigenvector centrality) of the node in the
project portfolio network. The IPCM algorithm can
measure the comprehensive criticality. Furthermore,
to analyse the dynamic propagation process of risk in
the project portfolio network, the link entropy is
defined to measure the propagation influence of the
projects in network. And the link entropy is used to
measure the propagation influence of project’s
spreading in the network (Pan et al., 2006).
In terms of project criticality in the portfolio,
Ghapanchi et al(2012) proposed a method of portfolio
selection based on the Date Envelopment Analysis
(DEA), considering the uncertainty and dependency
relationship; Killen (2017) used the network mapping
to analyse the impact of inter-project dependencies on
project portfolio selection results; Jafarzadeh et
al.(2018) proposed an integrated project portfolio
selection model to achieve project priority ranking by
analysing the priority criteria, uncertainty and inter-
project dependencies; Ghasemi et al. (2018)defined
the project risks from the level of the project, project
portfolio and inter-project dependencies, and used
Bayesian network to realize the project portfolio risk
analysis; Neumeie et al. (2018) used the Bayesian to
achieve project portfolio prioritization based on the
inter-project dependencies and project risks.
However, these studies ignore the dynamic
propagation of risk in the portfolio network. In the
portfolio network, the risk of a project will cause the
risk of other projects which are dependent on it, and
then the risk source of the project will spread to other
projects in the network, which will affect the success
of the whole project portfolio.
Overall,we contribute to research in the project
criticality using IPCM algorithm, link entropy and
SIRF model. Attempts are also made to build the
project portfolio network and measure the
propagation influence using IPCM algorithm and link
entropy. Furthermore, the paper uses the SIRF to
analyse the criticality of projects in the portfolio
considering the risk propagation. The contributions of
this paper are summarized as follows:1)From the
perspective of risk propagation, the criticality the
project portfolio of projects in the portfolio network
is analysed; 2)According to the practice of complex
R&D projects, the traditional infectious disease
model (SIR) is extended, and the SIRF model is
proposed to analyse the propagation process of risks
in the portfolio network;3)The IPCM algorithm
proposed in the paper integrates the local, global and
location attributes of nodes in the network, and is
used to analyse the criticality the project portfolio of
a project on other projects in the portfolio network.
2 MEASURING THE
PROPAGATION CRITICALITY
THE PROJECT PORTFOLIO
OF PROJECTS
2.1 The Project Portfolio Network and
Its Comprehensive Criticality
p
1
p
2
p
3
p
4
p
5
p
6
p
7
p
8
0.7
0.3
0.9
0.6
0.2
0.6
0.2
0.5
0.6
0.2
0.6
0.6
0.1
0.5
0.3
0.3
0.1
0.7
0.8
0.3
0.2
0.4
0.7
0.1
0.3
0.3
0.4
0.4
0.4
0.4
0.2
Figure 1: The project portfolio network.
p
1
p
2
p
3
p
4
p
5
p
6
p
7
p
8
p
1
p
2
p
3
p
4
p
5
p
6
p
7
p
8
p
1
.4 .4 .1 .7
.7 p
2
.3 .7 .1 .2
.3 p
3
.8 .3
.6 .6 p
4
.3 .4
.2 .9 p
5
.3 .3
.6 .5 p
6
.4 .2 .2 .2 p
7
.2 .5 .6 .1 .4 .6 p
8
Figure 2: The DSM description of network.
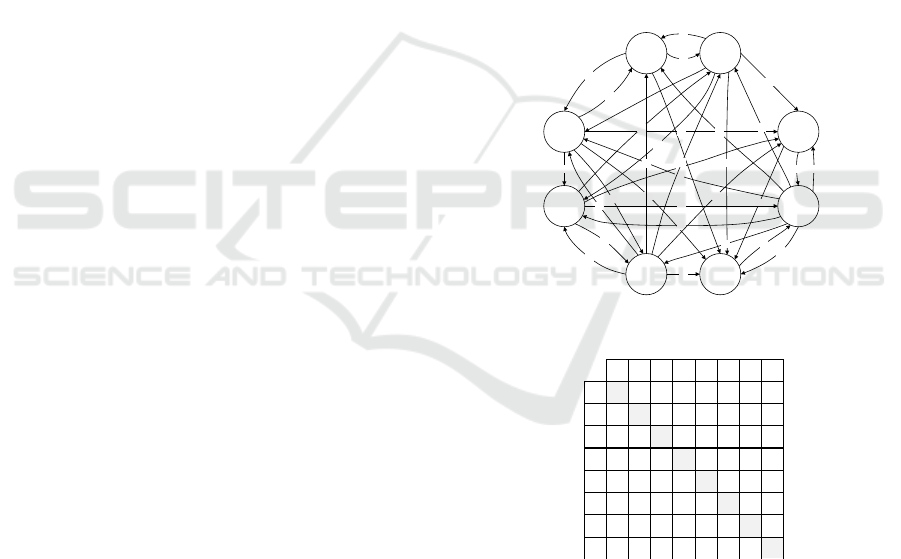
As shown in Figure 1, the project portfolio network is
constructed by taking the project as “node” and the
dependency relationship between projects as “edge”.
The network reflects the direction and strength of the
dependency relationship among projects in the
portfolio. Further, the project portfolio network can
be defined as the design structure matrix (DSM)
(Browning, 2016). In the portfolio DSM, the column
indicates the dependency of the project on other
Analysing the Risk Propagation in the Project Portfolio Network using the SIRF Model
227
projects, the row indicates that the project is
dependent on other projects, and the non-diagonal
number indicates the dependency strength of a project
on other projects, as shown in Figure 2.
Further, we use the IPCM algorithm to measure
the comprehensive criticality of projects in the
portfolio. The proposed algorithm in the paper
integrates the location (K-shell), local (neighbour
node analysis) and the global (eigenvector centrality)
attributes of nodes in the network and analyses the
degree of influence of a project on other projects in
portfolio network. The specific process is as follows:
1) Measuring the importance of projects (Ks value) in
the network based on the K-shell decomposition
method. The Ks value reflects the importance of the
project’s position in the network; 2) Further, based on
the calculation of Ks value, the influence is defined
according to the “neighbour nodes” in the complex
network. It analyses the project criticality of projects
from the location and local attributes; 3) Using
eigenvector centrality to measure the influence of the
project in the network from the global attribute; 4)
Integrating the analysis results of step 2 and 3, we
define an integrated influence measurement model
and analyse the comprehensive influence in the
portfolio network.
(1) Measuring the criticality based on the K-shell
and neighbouring nodes
It can be seen from Figure 1 that the project
portfolio network in the paper is a weighted directed
graph, so the K-shell decomposition method for
undirected weighted network proposed by Garas et al.
is extended to directed weighted K-shell (Garas,
2012). The Ks(p
i
) is the project criticality using the
K-shell decomposition:
(1)
where OD (p
i
) is the out-degree of project p
i
, which is
the number of project nodes adjacent to the p
i
in the
network; PI_DSM (p
k
, p
i
) is the dependency strength
between project p
i
and p
k
. The values of and are
1 in the paper.
The strength of the dependency relationship
between projects in the portfolio network is a decimal
between 0 and 1. Therefore, the Ks(p
i
) calculated by
formula (1) is no longer an integer number. Before
using the K-shell algorithm to decompose, the paper
performs the following processing on the dependency
strength PI_DSM, 1) Normalize all the elements in
PI_DSM based on their average value; 2) Divide the
normalized result by its minimum value, and the
minimum value in PI_DSM is 1;3) The value in
PI_DSM is processed by rounding down strategy, as
shown in Figure3, that is , all the values in PI_DSM
are rounded down.
Figure 3: Rounded down graph.
Furthermore, on the basis of calculating the Ks
value of all projects in the project portfolio network,
we measure the criticality using K-shell, as shown in
Figure 4. The specific process is:1) Remove all nodes
in the network that the degree is 1, as p
1
and p
2
in the
Figure 4 (b). After removing the 1-degree nodes,
there may be some nodes in the network with only
one link, shown as the p
7
in Figure 4 (c). We
iteratively remove these nodes until there are nodes
with degree 1 in the network, as shown in Figure 4
(d). The removed nodes with Ks=1 are considered to
be in the first layer of the network; 2) In a similar way,
nodes with a degree value≤2 are removed; 3) We
continue the process until all the nodes with higher Ks
values are removed; 4) In the iterative decomposition
process, if there are isolated nodes in the network,
then we assign 0 to their Ks values; 5) Finally, each
node in the network is assigned with a Ks value. And
the network can be seen as a hierarchical structure
from the core to edge layer, as shown in Figure 4(a).
P
1
P
2
P
3
P
4
P
5
P
6
P
7
P
8
P
9
P
3
P
4
P
5
P
6
P
7
P
8
P
9
P
3
P
4
P
5
P
6
P
8
P
9
(a)
(b)
(c) (d)
Figure 4: K-shell decomposition process.
Then, define the influence based on the location
attributes as shown in formula (2), which is obtained
based on the calculation of the Ks value.
()
()
ii
iv
LI p Ks p
()=
(2)
where the
()v
is the out-degree neighbour nodes of
p
i.
()
()
i
iv
Ks p
is the sum of Ks values of all the out-
degree neighbour nodes.
Ks( p
i
) OD p
i
PI _ DSM p
k
, p
i
1
1234
1
2
3
4
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
228

(2) Measuring the project criticality based on
eigenvector centrality
We use the eigenvector centrality to measure the
influence of the project in portfolio network.
Eigenvector centrality holds that the influence of a
node in the network depends on not only on the
number of its neighbours, but also on the influence of
the neighbour nodes it affects (Joyce et al., 2010). The
centrality of eigenvector is directly proportional to the
influence of the neighbour nodes. Therefore, the
higher the influence of a project node in the network,
the higher the influence of the project node. The
specific calculation is shown in formula (3). The
paper defines the influence of the projects using
eigenvector as EI (p
i
),
1
()
n
ii ijj
j
E
Ip x c ax
(3)
where c is a constant.
12
(, , , )
T
n
x
xx x
,
when
the steady state is reached after iterations, it can be
written in the following matrix form.
*
RAR
(4)
where A is the dependency matrix between projects
and
*
R
is the eigenvector for the largest eigenvalue of
(i.e., principal Eigenvector). The eigenvector
*
R
is
finally normalized by dividing each element in R by
the sum over all the elements in
*
R
. The normalized
value in R* determines the project influence in the
project portfolio network.
(3)
Measuring the comprehensive influence of the
project based on the IPCM
We measure the comprehensive criticality by
integrating the results of LI(P
i
) and EI(P
i
):
11
iii
CI p LI p EI p
()=1- () ()
(5)
where the LI (p
i
) is calculated by formular (2) and EI
(p
i
) is calculated by formular (3).
2.2 Measuring the Propagation
Influence using the Link Entropy
The link entropy is used to measure the propagation
influence of the project in portfolio network, that is,
the degree of influence of a certain project on other
project in the network after the occurrence of risk is
shown in formula (6). The greater the influence of the
project in the network, the more likely the risk will
affect other projects in the network.
,
11
1(,) (,)
() ()
(,) (,)
ij i i
NN
qq
D
SM k i DSM k i
LE CI p ln
ln
CI p
D
SM q i DSM i
L
q
(6)
where CI (p
i
) is calculated by formular (5),
1
(,)/ (,)
N
q
D
SM k i DSM q i
is the ratio of the
dependency strength of p
i
to p
k
to the dependency
strength of p
i
on all other projects.
3 ANALYZING THE RISK
PROPAGATION IN THE
PROJECT PORTFOLIO
NETWORK BASED ON SIRF
MODEL
In the project portfolio network, after a project has a
risk, it will make the dependent projects risky, which
may cause risk propagation. Based on the SIRF
model, the paper analyses the propagation process of
risk factors in the project portfolio network, and then
realizes the project prioritization considering
dynamic risk propagation.
3.1 Building the SIRF Model
In the traditional SIR model, the project has three
states: S(susceptible) state, which means that the
project is vulnerable to the spread of the project risk
associated with it in the portfolio network; I(infected)
state, which means that the risk of the project has
occurred; R(recovered) state, which means the
probability of the risk is within the tolerance ability
or the risk is resolved. According to the practice of
project portfolio management, the traditional SIR
model is extended to the SIRF model. The project has
a F(failure) state in the SIRF model, which means the
project failed. Then, the project and its dependency
relationship are removed from the portfolio network.
The project portfolio network in the initial state is
described as
G= (V, E), where V is the set of projects,
and E is the set of inter-project dependency
relationship (directed edges between projects). When
the project in the F state is removed from the portfolio
network, the network is described as G
’
={V
’
, E
’
},
where V
’
⊆ V,E
’
⊆ E。When there are no projects
removed from the portfolio network, then V
’
= V,E
’
=E.
Furthermore, the risk of project p
i
in the project
portfolio network will lead to the risk of other projects
Analysing the Risk Propagation in the Project Portfolio Network using the SIRF Model
229
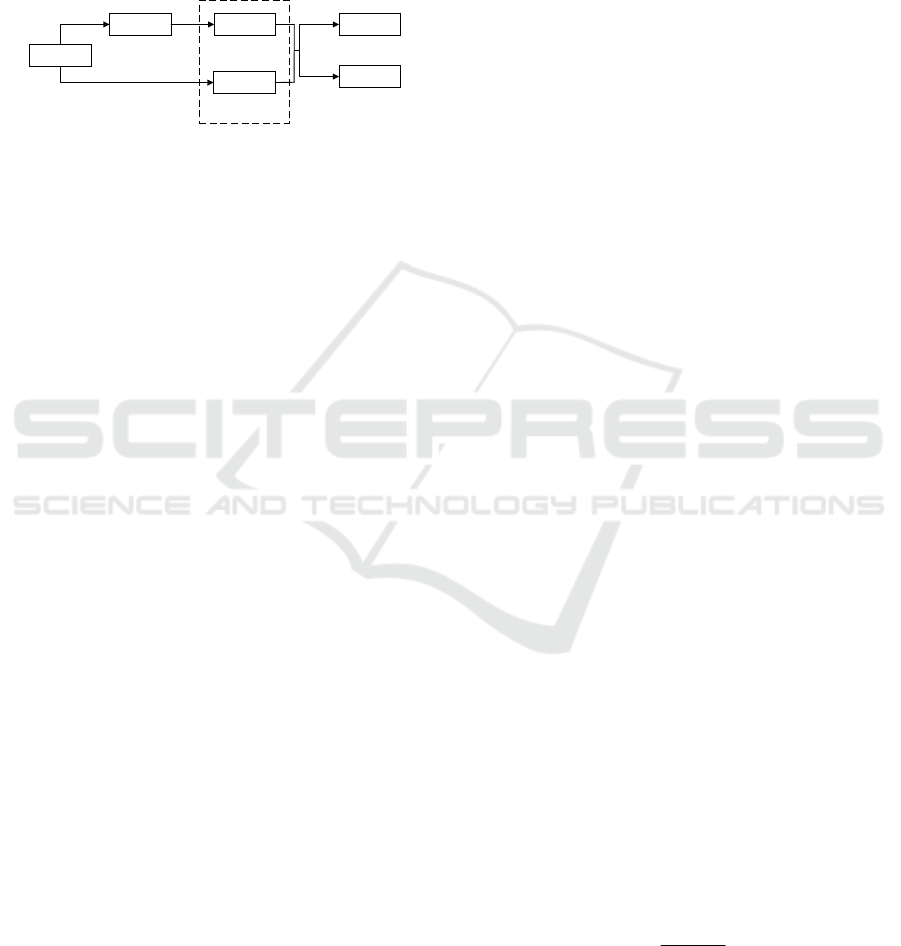
which are dependent on it, and then lead to the
“domino effect” of risk in the portfolio network. For
example, the risk of project p
i
will change the state of
p
j
that is dependent on it. The state of project p
j
will
change from the S to I state. At the same time, the
project node in the I state will be converted to the R
or F state. The flow relationship of the process is
shown in Figure 5.
S(t)
I(0) I
1
(t)
I
2
(t)
I(t)
R(t)
F(t)
γ
1
γ
2
μ
1-
μ
Figure 5: Project state transition due to risk propagation.
3.2 Analysing the Risk Propagation
using the SIRF
Projects in the R or F state in the portfolio network
will no longer be infected again. The probability that
the project in the S state will change to the I state
under the influence of the dependent project is
, and
the value of
is determined by the link entropy
(equation 6). The project in the I state will change to
the R state with the probability of μ, and to the F state
with the probability of 1-μ. The value of μ is
determined by the project’s risk tolerance. The
specific calculation process is as follows, if the
probability of project p
j
in I state at the initial moment
is P
j
I
(0), then the probability of project p
i
changing
from S to I state is:
,
1
() 1 1 (0)0
II
iji
j
j
N
P
PLE
(7)
where the LE
i,j
is the link entropy from p
j
to p
i
.
Similarly, it is supposed that the probability of the
project p
i
in the R state at the initial moment is P
i
R
(0)
, and the probability of the F state is P
i
F
(0).
Therefore, as shown in Figure 5, the transition
relationship between S, I, R and F states of the project
p
i
is:
P
i
R
(0)
P
i
I
(0)
(8)
P
i
F
(0) (1
)P
i
I
(0)
(9)
Suppose P
i
S
(t),P
i
I
(t),P
i
R
(t) and P
i
F
(t) are the
probabilities that the project p
i
is in the state of S, I, R
and F respectively at time t, and ,P
i
S
(t+1),P
i
I
(t+1),
P
i
R
(t+1) and P
i
F
(t+1) are the probability at the time
t+1. Therefore, it can be seen from Figure 5 that the
iterative process of risk propagation in the portfolio
network can be expressed as:
,
1
11 1 )() (
N
IS
ijij
j
Pt Pt LE
(10)
P
i
R
(t 1)
P
i
I
(t)
(11)
P
i
F
(t 1) (1
)P
i
I
(t)
(12)
We can get the probability that the projects in the
portfolio network will be in S, I, R and F at any time
form formular (10)-(12). When the number of
iterations in infinite, the probability matrix P will tend
to be stable, so a stable probability value can be
obtained. Also, the sum of probabilities of the project
in S, I, R and F is 1.
((((
() () () () 1
SIRF
iiii
PtPtPtPt
)) ) )
(13)
3.3 Using SIRF for Ranking the
Projects in the Portfolio
To quantitatively analyse the propagation process of
risk in the portfolio network, we define the indicator
of spreading influence strength (SIS). The SIS refers
to the final infection scale of the project p
i
have a risk
in the network. It is the sum of the probability of all
project risks that can eventually be infected by project
p
i
, that is, it includes the neighbour nodes directly
infected by project p
i
, and the nodes that can be
transmitted form the project infected by project p
i
as
the intermediary. In the project portfolio network, the
probability P
i
in the risk state is determined by the
sum of the stable probabilities of the project in the I
and F state. Therefore, the spreading influence
strength (SIS) of p
i
can be calculated as:
() ()
IF
ij
AjA
j
j
j
SIS P P P
(14)
where the set A is all the projects infected by the
project p
i
.
Totally, the criticality of projects in the portfolio
network considering the risk propagation can be
defined as the proportion of the spreading influence
strength (SIS) of p
i
to the sum of the spreading
influence strength (SIS) of all projects in the project
portfolio network.
i
j
i
P
j
P
SIS
PC
SIS
(15)
where PP is the set of all projects in the portfolio.
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
230

4 AN ILLUSTRATIVE EXAMPLE
Taking the project portfolio of an aviation equipment
of R&D enterprise as an example, the paper
conducted a laboratory experiment to priority the
project in the portfolio considering the dynamic
propagation of risks. The company’s R&D project
portfolio contains 10 projects, and the dependency
relationship between these projects is described based
on DSM as shown in Figure 6, and the link entropy
between projects measured using equation 6 is as
shown in Figure 7.
p
1
p
2
p
3
p
4
p
5
p
6
p
7
p
1
p
1
.3
.1
.4
p
2
.6
p
2
p
3
.4
.1
p
3
.3
.1
.6
p
4
.2
.5
p
4
.3
.2
.1
p
5
.5
.5
.1
p
5
.1
.3
p
6
.1
.7
.2
p
6
.6
p
8
.2
.3 .5 .2 p
8
p
9
.6 .4
p
10
.5 .4 .3 .7
p
7
.4
.5
.8
.1
.2
p
7
p
8
.7
.1
.2
.3 .3
.1
p
9
.4
.2
.3
.1
.1
.8
.4
p
10
.6
.3
.6
.5
.1
p
9
.3
.5 p
10
.3
Figure 6: the dependency relationship between projects.
p
1
p
2
p
3
p
4
p
5
p
6
p
7
p
1
p
1
.47
.23
p
2
.31
p
2
p
3
.25
.09
p
3
.2
.09
.33
p
4
.22
.4
p
4
.29
.22
.13
p
5
.06
.11
.22
.15
p
5
.32
.15
p
6
.25
.21
.23
.21
.23
p
6
.18
p
8
.37
.19 .29 .11 .25 .31 p
8
p
9
.33 .25
p
10
.27 .25 .29 .27 .25
p
7
.28
.07
.12
.07
.17
p
7
p
8
.49
.13
.21
.17 .28
21 .13
p
9
.2
.12
.16
.35
.2
.32
.2
p
10
.27
.16
.27
.24
.35
p
9
.33
.23 p
10
.16
Figure 7: the link entropy between projects.
The probability that the project in the S, I, R and
F in a stable state obtained by the analysis of SIRF
model is shown in Figure 8(a). Furthermore, the
scores of importance are shown in Figure 8(b) by
using equations (14) and (15). Therefore, the priority
ranking that project manager should pay attention to
is P
1
-P
6
-P
10
-P
8
-P
3
-P
9
-P
4
-P
2
-P
5
-P
7,
when the project
manager is considering the risk dynamic propagation.
PS PI PR PF
p
1
p
2
p
3
p
4
p
5
p
6
p
7
p
8
p
9
p
10
.3 .41 .09 .21
.36 .27 .11 .26
.34 .31 .1 .24
.36 .28 .1 .25
.38 .23 .11 27
.3 .4 .09 .21
.43 .14 .13 .3
.32 .35 .09 .23
.36 .28 .11 .25
.31 .39 .09 .21
PC
p
1
p
2
p
3
p
4
p
5
p
6
p
7
p
8
p
9
p
10
.703
.636
.657
.640
.617
.701
.571
.675
.64
.694
(a) The output of SIRF (b) The scores of importance
Figure 8: The results of portfolio risk analysis.
(16)
where the n is the number of projects in the portfolio,
d
i
is the difference of criticality ranking of each
project in the portfolio under different measurement
conditions.
Furthermore, the Spearman correlation coefficient
is calculated to measure the consistency between
criticality ranking and actual ranking results, as
shown in Table 1. It can be seen from the table 1 that
the project criticality ranking results obtained in the
paper based on the integrated project criticality
measure (IPCM) algorithm and SIRF model have the
highest consistency with the actual results.
Furthermore, the eigenvector centrality is second, and
eigenvector centrality measures the relative
importance of projects based on neighbour nodes.
The results can also reflect the relative importance of
projects better with the position of the project in the
network ignored. However, the ranking results based
only the location attribute without considering the
propagation attribute have a large deviation from the
actual situation. In conclusion, the IPCM algorithm
proposed in this paper can analyse the relative
importance of the project’s location, local and global
attributes in the portfolio network. At the same time,
the project criticality ranking results obtained based
on the SIRF model considering the dynamic
propagation of risks are in the highest agreement with
reality. Therefore, the project’s location, local and
global attributes should be integrated when analysing
the criticality of projects in the portfolio. The absence
of any analysis element will cause project criticality
deviating from the actual situation.
p
s
1
6 d
i
2
i1
n
n(n
2
1)
Analysing the Risk Propagation in the Project Portfolio Network using the SIRF Model
231

Table 1: The consistency results of using Spearman
correlation coefficient.
K-shell
Eigenvector
centrality
IPCM
IPCM
&
SIRF
Spearman
correlation
coefficient
-0.309 0.939 0.867 0.952
Therefore, we propose the integrated project
criticality measure (IPCM) to measure the
comprehensive influence of the projects in the
portfolio network. It has the highest consistency with
the actual situation.
4 CONCLUSIONS
To analyse the criticality of projects in the portfolio
considering dynamic risk propagation, the paper
proposes the integrated project criticality
measurement (IPCM), and the algorithm is divided
into 4 steps, 1) Using the K-shell to analyse the
criticality based on the location attributes; 2)
Analysing the project’s impact based on the
neighbour nodes in the complex network; 3)
Measuring the project’s impact using the eigenvector
centrality; 4) Integrating the calculation results of the
above to construct a measurement model of the
project’s comprehensive influence. Furthermore, link
entropy is used to measure the propagation influence
of project’s spreading in the network. Furthermore,
combined with the practice of R&D project
management, the traditional SIR model is extended to
the SIRF model. The paper considers that there is a
F(failure) state in the project portfolio network,
which means that the project has failed. Finally, the
SIRF model is used to analyse the dynamic
propagation process of risks in the project portfolio
network, and the priority ranking is realized under the
risk dynamic propagation.
ACKNOWLEDGEMENTS
This study was supported by the National Natural
Science Foundation of China (No. 71929101 and
71872011).
REFERENCES
Browning T. R.,2016. Design Structure Matrix Extensions
and Innovations: A Survey and New Opportunities [J].
IEEE Transactions on Engineering Management,
63(1):27-52.
Garas A, Schweitzer F, Havlin S., 2012.A k-shell
decomposition method for weighted networks[J]. New
Journal of Physics, 4(8): 083030.
Ghapanchi A H, Tavana M, Khakbaz M H, Low, G.,2012.
A methodology for selecting portfolios of projects with
interactions and under uncertainty[J]. International
Journal of Project Management, 30(7): 791-803.
Ghasemi F, Sari M H M, Yousefi V., 2018. Project
Portfolio Risk Identification and Analysis, Considering
Project Risk Interactions and Using Bayesian
Networks[J]. Sustainability, 10(5): 1609.
Killen C P.,2017. Managing portfolio interdependencies:
The effects of visual data representations on project
portfolio decision making[J]. International Journal of
Managing Projects in Business, 10(4): 856-879.
Jafarzadeh H, Akbari P, Abedin B. ,2018. A methodology
for project portfolio selection under criteria
prioritization, uncertainty and projects
interdependency–combination of fuzzy QFD and
DEA[J]. Expert Systems with Applications,110:237-
249.
Joyce K E, Laurienti P J, Burdette J H, Hayasaka, S.,2010.
A new measure of centrality for brain networks[J].
PLoS One, 5(8): e12200.
Kitsak M, Gallos L K, Havlin S.,2010. Identification of
influential spreaders in complex networks[J]. Nature
physics, 6(11): 888.
Liu Y, Tang M, Zhou T, Do, Y., 2015. Improving the
accuracy of the k-shell method by removing redundant
links: From a perspective of spreading dynamics[J].
Scientific reports, 5: 13172.
Neumeier A, Radszuwill S, Garizy T Z., 2018.Modeling
project criticality in IT project portfolios. International
Journal of Project Management, 36(6): 833-844.
Pan-xiang R, Hong-zhang J, Qi W.,2006. Brittleness
research on complex system based on brittle link
entropy[J]. Journal of Marine Science and Application,
5(2): 51-54.
Project Management Institute, 2018. A Guide to the Project
Management Body of Knowledge (PMBOK Guide),
Sixth Edition. Project Management Institute. Newtown
Square (PA).
Wen S, Zhou W, Zhang J., 2012. Modelling propagation
dynamics of social network worms[J]. IEEE
Transactions on Parallel and Distributed Systems,
24(8): 1633-1643.
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
232
