
2D and 3D Measurement Algorithms for Real Front and Back
Curved Surfaces of Contact Lenses
Kentaro Saeki
1,2 a
, Decai Huyan
2
, Akira Nakamura
1
, Shin Kubota
1
, Kenji Uno
1,3
,
Kazuhiko Ohnuma
1,3
and Tatsuo Shiina
2b
1
SEED CO., LTD, 2-40-2 Hongo, Bunkyo-ku, Tokyo, Japan
2
Graduate School of Science and Engineering, Chiba University 1-33 Yayoi-cho, Inage-ku, Chiba-shi, Chiba, Japan
3
Laboratorio de Lente Verde, 98-1 Nozomino, Sodegaura, Chiba, 299-0251, Japan
Keywords: OCT, Vertical Incidence, Shape Measurement, Transparent Sample, Contact Lens.
Abstract: The 2D and 3D measurement algorithms for real front and back curved surfaces of contact lenses (CL) were
developed. The purpose of 2D algorithm is to evaluate spherical lenses. We adopted the algorithm to be
incident the probe light vertically along the curved surfaces of CLs under the condition that the difference of
curvature radii between the front and back surfaces is small enough within numerical aperture (N.A.) of the
optical probe. The vertical incidence against the curved surface is judged by using the intensity balance
between OCT interference signals from both front and back surfaces of CL. As a result, the lens shape matched
with the design value and RMSE of the thickness was 5.33 μm. Also, regarding the curvature radii,
compatibility between this OCT device and the conventional device was indicated. In the 3D algorithm, we
conducted a basic experiment using some special lenses in order to develop non-cylindrical lens measurement.
By moving a 2-axis (vertical and horizontal) Micro Electro Mechanical System (MEMS) mirror with phase
difference of 90°, it was designed to conduct circular scanning while maintaining vertical incidence of probe
beam on the front surface of CL. The shape and the curvature radius was evaluated with simulation data under
the same conditions. As a result, although it has an error against the design value, the result and the simulation
result matched well.
1 INTRODUCTION
In contact lens (CL) manufacturing processes, it is
essential to evaluate the shape of the transparent
object (B. J. Coldrick 2016,
D, Luo 2019
). When
measuring the refractive power of CL, non-contact
measurement is critical and it is necessary to evaluate
the following three elements that determine the
refractive power: 1. Lens center thickness, 2.
Curvature radius of the front and back surfaces and 3.
Refractive index. In addition, at present, CL
peripheral shape is emerging as an important issue for
new design such as lenses for myopia control.
Shape measurement using a tool such as a contact
gauge is limited because it is a single-sided shape
measurement at the light incidence position. Also,
with this contact gauge, only data of the central part
is collected, the device provides no information
a
https://orcid.org/0000-0002-4902-3110
b
https://orcid.org/0000-0001-9292-4523
regarding the shape from lens center to the peripheral
part. Similarly, regarding the thickness of a CL, since
the peripheral thickness is manually measured at only
several points with a thickness gauge, it is difficult to
know a thickness distribution of CL over a wide
range. And regarding the conventional 3D measuring
device, it needs to be measured by using a special
antireflection so that the reflection from inside
doesn’t interfere with the measurement (
F. Drouet
2014)
. In addition, even with a measuring device
using a confocal method, when measuring the front
surface of a thin CL, the back surface is sometime
focused and it may affect the result (Saeki 2020).
These are disadvantages of single-sided shape
measurement. Their problems can be solved if
simultaneous front and back measurement can be
achieved. In addition, it is important for optical lens
Saeki, K., Huyan, D., Nakamura, A., Kubota, S., Uno, K., Ohnuma, K. and Shiina, T.
2D and 3D Measurement Algorithms for Real Front and Back Curved Surfaces of Contact Lenses.
DOI: 10.5220/0010291800730080
In Proceedings of the 9th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2021), pages 73-80
ISBN: 978-989-758-492-3
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
73
evaluation because it can evaluate the misalignment
of the both surfaces.
Optical Coherence Tomography (OCT) is a non-
invasive and non-contact technology that has the
advantages of high speed and high accuracy (Tanno
1990). It has been attracting a lot of attention from the
ophthalmology industry in the medical field (
P.
Massatsch 2005)
. On the other hand, in the industrial
field, although it is mainly used for thickness
inspections (Hibino 2004, H. C. Cheng 2010), there are
few reports about the application for measurement of
shape. The reason for this is that the measurement
sample is usually placed in the epi-illumination
position. Therefore, since the back shape is greatly
affected by the refractive index, it has not been used
for shape measurement.
This study proposes two algorithms for accurately
measurement of the real CL shape of the front and
back surfaces with 2 dimensional and 3 dimensional
methods. In 2D algorithm, spherical lenses were
evaluated. We adopted the algorithm to be incident
light vertically along the curved surfaces of CL under
the condition that the difference of curvature radii
between the front and back surfaces is small enough
within numerical aperture (N.A.) of the optical probe.
The vertical incidence against the curved surface is
judged by using the intensity balance between OCT
interference signals from both front and back surfaces
of CL. On the other hand, in 3D algorithm, we
conducted a basic experiment using some special
lenses in order to develop non-cylindrical lens
measurement. By controlling a 2-axis (vertical and
horizontal) Micro Electro Mechanical System
(MEMS) mirror with phase difference of 90 °, it
conducted circular scanning while maintaining
vertical incidence of probe beam on the front surface
of CL. In this design, as the drive angle can be
changed by adjusting the voltage applied to the
MEMS mirror, the measurement range can be
changed. In this report, the shape, thickness, and
curvature radius of the front and back surfaces of the
transparent CL were evaluated using two algorithm.
2 EXPERIMENTAL SET-UP
2.1 TD-OCT Systems
In this study, Time-Domain (TD) OCT was adopted.
It allows its optical probe design to have long working
distance and wide measurement range (Shiina, 2003).
The measurement probe can be designed
independently from other parameters such as
resolution, scanning speed and measurement range in
its specification. Furthermore, since the interference
signal is magnified linearly, the linearity of the
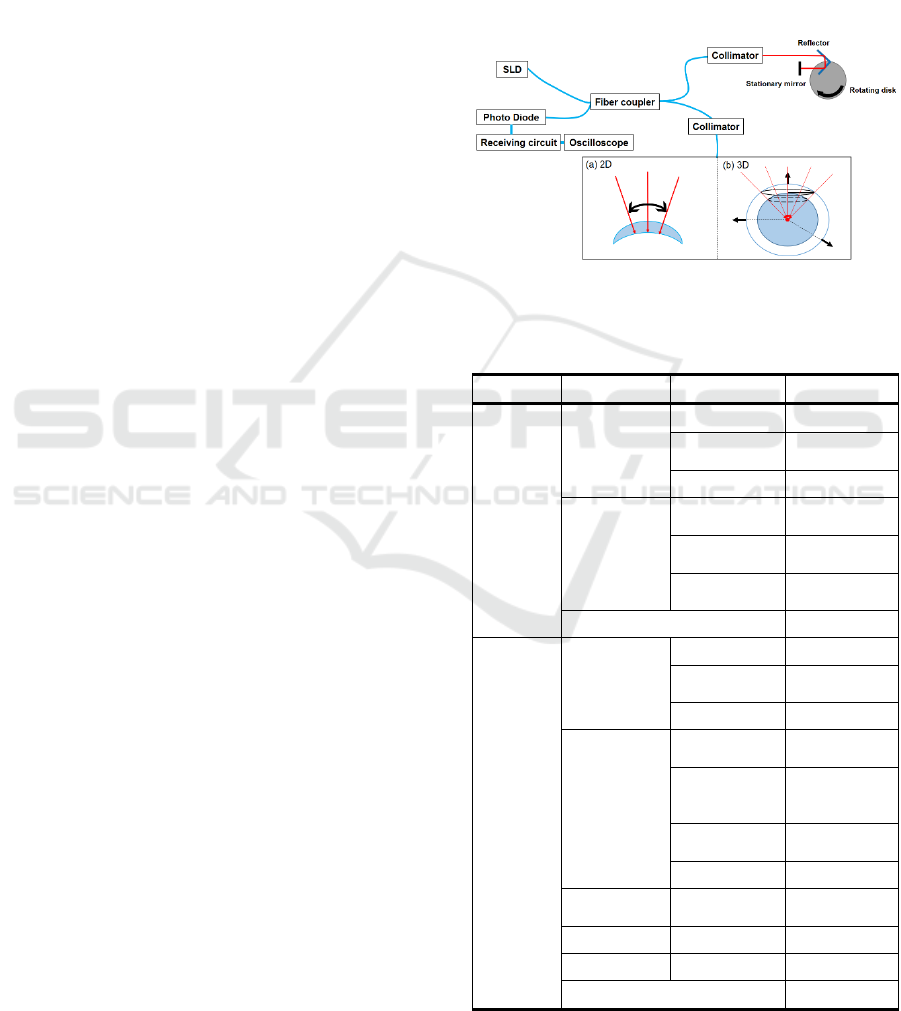
measured signal is high. Figure 1 shows a schematic
diagram of this system. In addition, Table 1 shows the
specifications of 2D and 3D system, respectively. The
2D’s super luminescent diode (SLD) light is 1310nm.
This is to measure the lens itself. In contrast, for 3D,
SLD light 856nm was selected in consideration of the
development of eyeball model for axial length
measurement.
Figure 1: A schematic diagram for TD-OCT system. (a) is
2D and (b) is 3D.
Table 1: Specifications of TD-OCT measurement system.
Algorithm Parts Item Specifications
2D
SLD
Wavelength
1310 nm
Spectral
Width
55 nm
Resolution
13.8 μm
Measurement
stage
Position
Accuracy
1 μm
Rotation 15 scan/s
(900rpm)
Rotation
Radius
15 mm
N.A.
0.14
3D
SLD
Wavelength
856nm
Spectral
Width
32.1nm
Resolution
10.1μm
MEMS
Angular
resolution
< 5 μrad
Maximum
scanning
angle
±10 deg
Drive
frequency
< 450 Hz
Drive voltage
-5 ~ 5 V
Cylindrical
Lens
Focal length 200 mm
Lens1
Focal length
100 mm
Lens2
Focal length
40 mm
N.A
0.015
PHOTOPTICS 2021 - 9th International Conference on Photonics, Optics and Laser Technology
74
2.2 2D Shape Measurement Algorithm
In this study, we propose a measurement algorithm
which makes the incidence light always hits
perpendicularly to front and back surfaces of a
spherical CL to measure its real shapes. Figure 2
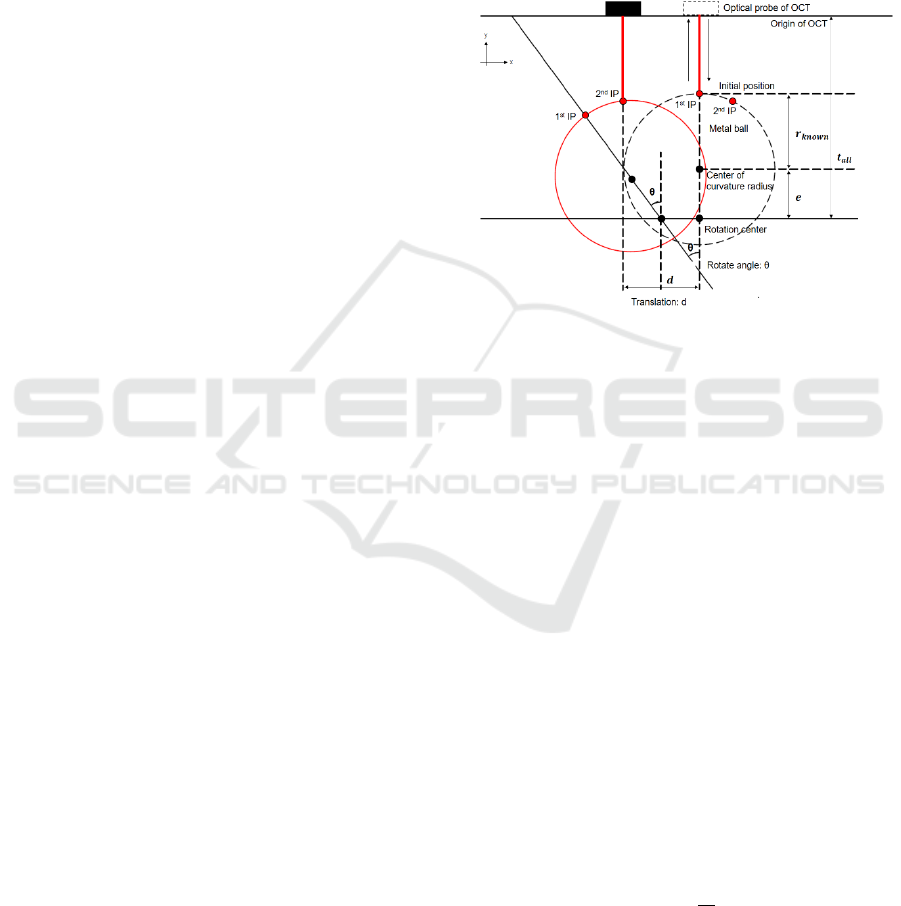
shows the measurement algorithm using the metal
ball. The sample stage mechanism was designed so
that its translation movement and vertical rotation can
be changed in order to measure both front and back
surfaces’ interference echoes, which assume sign of
the vertical incidence. In the Fig. 2, the dash line
shows the initial position of the metal ball and the
solid line shows the position where it is rotated on the
vertical rotation angle and translated to get the
vertically incidence position. The position of 2
nd
interference point (IP) is calculated by using the
vertical rotation angle and translation.
The measurement data includes the translation
distance d, the vertical rotation angle θ and the optical
path positions of the front surface interference time
𝑡
, and the back surface interference time 𝑡
. The
OCT interference times are converted into the
distance using the reflector rotation speed. Then the
distance is converted into the coordinates with the
equation (1) - (4) using the vertical rotation angle and
translation distance on this algorithm. In the case of
CLs, two interference signals occur. The interval
between them indicates the thickness. Since light
passes through the substance, the group refractive
index was taken into consideration for calculating the
back surface coordinates. Equation (1) and (2) were
used to calculate the front curvature coordinate, and
(3) and (4) were used to calculate the back curvature
coordinate.
𝑥
=dcosθ− a
(
t
−t
)
sinθ (1)
𝑦
=dsinθ+a
(
t
−t
)
cosθ − e (2)
𝑥
= dcosθ − a{t
−[t
+(t
−t
)/n]}sinθ (3)
𝑦
=dsinθ+a{t
−[t
+(t
−t
)/n]}cosθ − e
(4)
a is a time-distance conversion coefficient which
is calculated from the change of the optical path
length depending on the rotation speed of the
reflector. 𝑡
is the optical path length (time unit)
from the OCT measurement range origin to the center
of CL rotation. n is the group refractive index of the
CL. e is the difference in length between the center of
the curvature radius and the center of the CL rotation.
It was calculated by using a curvature radius of a
known spherical metal ball. Then, the curvature
radius was estimated from the (x,y) coordinates by a
circle approximation using the least-squares method.
For comparison with a conventional measurement
device, a confocal laser microscope (Sensofar: Plu
Apex) was adopted. Since it is single-sided shape
measurement device, the CL was turned over to
measure the shape of the back surface after measuring
the front surface. The curvature radius was compared
with the OCT result.
Figure 2: 2D measurement algorithm using the metal ball.
2.3 3D Shape Measurement Algorithm
In 3D algorithm, we conducted a basic experiment
using some special lenses in order to develop a non-
cylindrical lens measurement. In order to realize this
algorithm, it was designed to conduct circular
scanning by driving two MEMS mirror (Hamamatsu
Photonics: 2D-OSE201) on the vertical and
horizontal axes with a phase difference of 90 ° .
Moreover, since this MEMS mirrors don’t have a
resonance frequency, the drive frequency can be
changed, and the measurement angle can also be
changed by the drive voltage. By using two MEMS
mirrors, a cylindrical lens was used to correct the
misalignment for each axis. The number of
measurement points in this OCT system depends on
the difference between the reflector rotation
frequency 𝑓
of the variable optical path mechanism
and the drive frequency 𝑓
of MEMS mirrors.
Assuming that the minimum measurement point is 2n
(n=1, 2, 3,⋯), 𝑓
is calculated from equation (5)
using 𝑓
.
𝑓
=
1+
𝑓
(5)
In this measurement, firstly, the time difference
𝑡
between the trigger signal at focal position of the
measurement probe and the OCT interference
position was measured. And in the circular sannning,
2D and 3D Measurement Algorithms for Real Front and Back Curved Surfaces of Contact Lenses
75
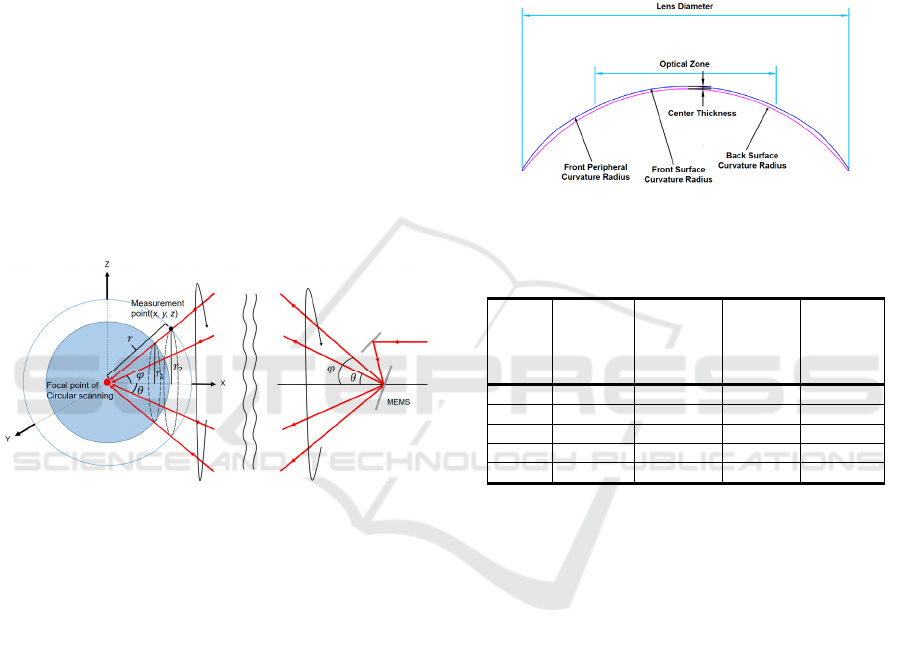
the time difference 𝑡
is measured. Using these time
differences, the distance r from the focal point of the
measurement probe to each measurement point is
estimated. In addition, in the MEMS mirrors, the time
difference 𝑡
and 𝑡
between the driving singnals of
MEMS mirror in the horizontal/vertical direction and
the interference positions are defined, respectively.
The incident angle θ and the vertical incident angle φ
are calculated using 𝑡
and 𝑡
. Three-dimensional
coordinates (x, y, z) are caluculated from r, θ and φ
using equation (6) – (8).
x = rcos𝜃 cos𝜑 (6)
y = rcos𝜃sin𝜑 (7)
z=rsin𝜃 (8)
After the coordinate conversion, the position (x, y,
z) of each OCT inteference point were fitted by the
least squares method of the sphere. Then, after
applying the correction, the curvature radius and
center coordinates were evaluated.
Figure 3: 3D measurement algorithm.
2.4 Measurement Sample
Rigid CLs were adopted as transparent samples. They
were practically designed and specially manufactured
for the purpose of this study. The refractive index of
the material is 1.455
± 0.02, which was measured with
Abbe’s refractometer (Atago: NAR-1T SOLID). The
curvature radii of both front and back surfaces were
manually measured with a contact gauge (NEITZ:
CGX-3). A typical CL structure including names of
each part is shown in Fig 4.
In 2D experiment, the optical lens power of 21
lenses are from -10D and 10D in 1D steps, which
were named A through U. They have the same
diameter and curvature radius of the back surface, but
the curvature radius of the front surface depends on
the lens power. Also, the curvature radius of the lens
periphery of the front surface, the diameter of the
optical zone, which is the area displaying the required
correction lens power, and the center thickness are
different depending on lens. Therefore, the
measurement range is calculated from the optical
zone diameter and the curvature radius of the front
surface.
In 3D experiment, we adopted 5 lenses which
have the specialized characteristics. It is whether the
centers of curvature radius on the front and back
surface are same or not. Accordingly, the thicknesses
are adjusted. The specifications of the sample lenses
are shown in Table 2.
Figure 4: Structure of a typical contact lens.
Table 2: Specifications of the sample lenses for 3D
measurement.
Sample
lens
Front
Surface
Curvature
Radius
Back
Surface
Curvature
Radius
Lens
Diameter
Center
Thickness
[mm] [mm] [mm] [mm]
A 7.92 7.82 10.0 0.10
B 7.97 7.82 10.0 0.15
C 7.92 6.67 10.0 1.25
D 6.77 6.67 10.0 0.10
E 7.92 6.67 10.0 0.054
3 EXPERIMENTAL RESULTS
3.1 2D Shape Measurement
In 2D measurement study, shape, curvature radius
and thickness of sphere lenses were evaluated. Figure
5 shows (a) design drawing of the lens as a
representative sample and (b) its measurement
results. In Fig. 5 (a), within 5.77 mm of the optical
zone, the curvature radius was 6.68 mm (Designed
FS1) whereas in the peripheral part, it was 7.20 mm
(Designed FS2). The curvature radius of the back
surface had a constant 6.67 mm (Designed BS). In
Fig. 5 (b), 3 trial measurements were conducted in the
vertical rotation angle, ranging from -35° to 35° in 5°
steps. Compared with the design value in Fig. 5 (a),
the same transition of the curvature radii was
observed in the OCT measurement results in Fig. 5
(b). That is, Designed FS1 and FS2 well matched with
the result (FS) 1-3 on optical zone and peripheral part,
PHOTOPTICS 2021 - 9th International Conference on Photonics, Optics and Laser Technology
76
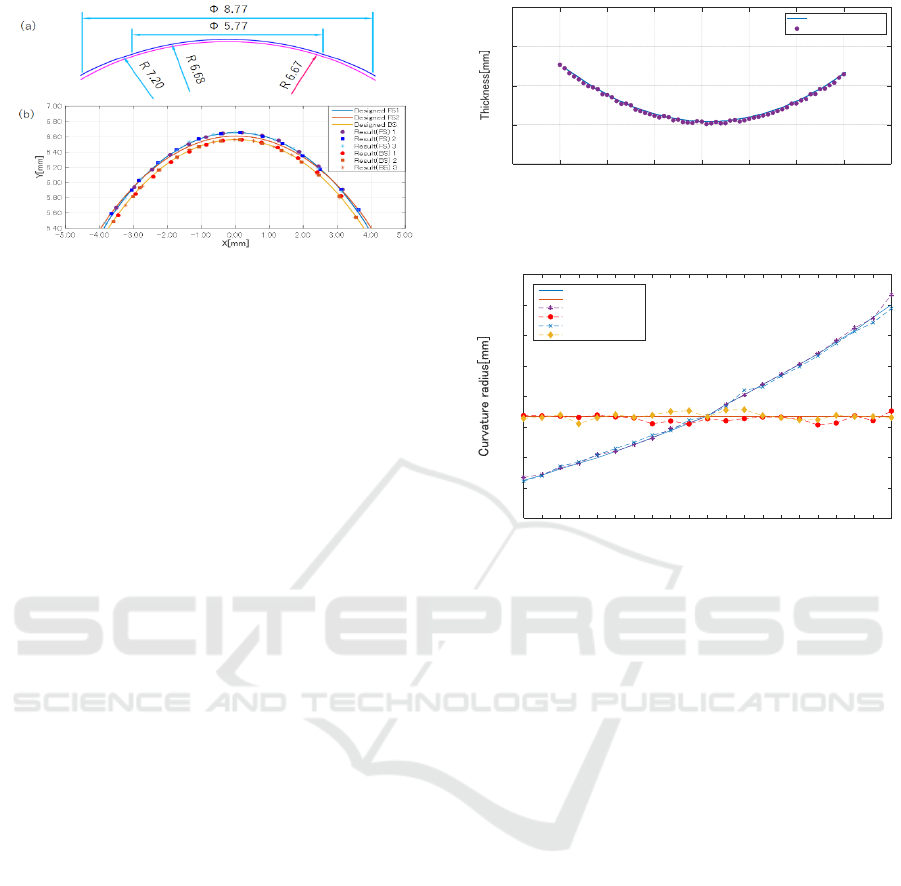
Figure 5: (a) Drawing for lens design and (b) measurement
results of the front and back surfaces with OCT of sample
lens K (Power 0.00D).
respectively. When the curvature radius was
estimated by the circle approximation of the OCT
results, the curvature radii of the back surface was
6.71 mm, and for the optical zone and peripheral part
of the front surface, they were 6.70 mm and 7.21 mm,
respectively.
Figure 6 shows the result of the thickness
distribution compared with the designed values. The
thickness is shown at each vertical rotation angle,
which ranges from -30° to 30° in 1° steps. The root
mean square error (RMSE) was 5.33 μm against the
distribution of the designed thickness. The ISO
standard is only applicable to the central part and the
tolerance limit for the design value is within ±
0.02mm. Even though the experimental error of 5.33
μm takes into account the thickness of the peripheral
part, it was remarkably small compared with the
criteria value.
The curvature radius estimated by our OCT was
evaluated in comparison with Plu Apex. Figure 7
shows the measured curvature radius results of 21
sample lenses. Compared with the designed values,
with respect to the front surface, the errors from the
designed values tend to increase as the curvature radii
become large in both of our OCT and Plu Apex
results.
In our OCT results, the error is large in the sample
lens U, which has the largest difference in the
curvature radii between the front and back surfaces.
That is, since there is a big difference of incident
angles on both surfaces, the intensity of the vertically
reflected light measured within N.A. is weaker than
that of a lens with smaller difference in curvature
radius. Thus, this algorithm affects the measurement
results of the curvature radius because it determines
the measurement point based on the interference
intensity ratio between the front and back surfaces.
On the back surface, both devices caused large errors
on the same lens and their tendencies were opposite.
Figure 6: Thickness distribution of sample lens N (Power -
3.00D).
Figure 7: Estimation of curvature radii from our OCT and
Plu Apex for sample lenses.
easuring the back surface shape, the lens was turned
over to measure the front surface shape. On the other
hand, our OCT can simultaneously measure front and
back surfaces.
Here, analysis of results of Plu Apex and our OCT
was performed by using Bland-Altman analysis.
Regarding the front surface, the 95% limits of
agreement (LoA) was from -0.77% to -2.09% and the
correlation coefficient was 0.57, indicating a
proportional bias. And Plu Apex and the developed
OCT were compatible with each other on the front
surface results. On the other hand, regarding the back
surface, the error was large in the sample H to J, L
and M, but there was no systematic bias (LoA was
from -2.22% to -4.37%). Since there was no
systematic bias, the Minimal Detectable Change
(MDC) was 0.178 mm with 95% confidence interval
(CI) due to the random error. Therefore, if the error is
within 0.178 mm, the result is a measurement error. It
is large for inspection of contact lens. This mainly
came in the sample H to J, L and M results. Since CLs
are manufactured with contact gauge check, if the
measurement position is compatible with the
designed values, the measured lens is considered as a
good product. That is, there is an error factor outside
the measurement range of contact gauge. Since the
standard deviation (SD) is calculated by using the
-40 -30 -20 -10 0 10 20 30 40
Vertical rotation an
g
le[de
g]
0
0.05
0.1
0.15
0.2
Designed thickness
Measured thickness
ABCDE FGH I JKLMNOPQRS TU
Sample lens
5.000
5.500
6.000
6.500
7.000
7.500
8.000
8.500
9.000
Designed FS
Designed BS
Measured OCT FS
Measured OCT BS
Measured PluApex FS
Measured PluApex BS
2D and 3D Measurement Algorithms for Real Front and Back Curved Surfaces of Contact Lenses
77

difference of the measured results from both devices,
SD became large and the MDC calculated using SD
accordingly became large. This shows that it is
possible to measure a wider range than contact gauge,
and measure the part that could not be measured by
the current method.
3.2 3D Shape Measurement
In 3D experiment, the front and back shape of CL
were simultaneously measured. The measurement
range was set to 1.53°, 3.60°, 5.66°, and 7.72° in
consideration of the optical zone where the correction
power is designed. The curvature radius and thickness
were evaluated. Table 3 shows the curvature radius of
each lens, and Table 4 shows the center coordinates,
respectively.
Regarding the front curvature radius of lens A and
lens B, lens A was 7.68 mm (error rate: 3.0%) and
lens B was 7.71 mm (error rate: 3.2%). On the other
hand, the back surface is 7.49 mm for lens A (error
rate: 4.2%) and 7.51 mm for lens B (error rate: 4.0%).
An error of about 0.3 mm was observed on the both
surfaces compared with the design values. Here, in
order to discuss the error, the simulation using known
curvature radius was performed under the same
conditions as this measurement. In other words, the
measurement environment was reproduced and the
results were evaluated. As a result, the error rate
equivalent to the measurement result by OCT was
obtained when 0.7% noise was added to the ideal
value of the sphere. And then, the error rate was
11.0% as a result of applying the correction to the
simulation data. In other words, a maximum error rate
of 11.0% can occur in this measurement environment.
Since the measurement range is narrow against the
entire sphere, the error was occurred by applying the
sphere fitting. Compared with the results, both A and
B lenses had good results in this measurement
environment. Regarding the lens C, the curvature
radius of the front surface was 8.01 mm (error rate:
1.1%), and the radius of curvature of the back surface
was 6.96 mm (error rate: 4.3%). Compared with lens
A and lens C, it had a smaller difference from the
design value on the both surfaces. Also, as the feature,
the error of the lens A is on the minus side, but the
error of the lens C is on the plus side. This was
affected by the displacement (fixing method,
humidity, etc.) due to the measurement environment.
Since the lens C has a large thickness, it is not easily
attached by deformation. Regarding the lens D, the
curvature radius of the front surface was 6.84 mm
(error rate: 1.0%), and the back surface was 6.93 mm
(error rate: 3.9%). Compared with lens A, the result
of lens D was better. Since the lens D has a smaller
curvature radius than the lens A, it is possible to
measure data in a deeper direction to the center,
which was led to good results when fitting the sphere.
Finally, the lens E had a curvature radius on the front
surface of 6.77 mm (error rate: 14.5%) and the back
surface is 6.74 mm (error rate: 1.0%). The error rate
on the lens surface was the largest. Compared with
lens C, Table 4 shows that the center coordinates of
the lens surface were shifted in the optical axis
direction, and the tendency was that they are
vertically incident on the back surface. Therefore, it
is considered that the lens E had a larger error rate on
the lens surface than the lens C, but the lens back
surface was smaller. This result suggests to
distinguish that the centers of the front and back are
same or not.
Regarding the thickness, Figure 8 shows the
thickness distribution of lens D. Since the center
coordinates of the both surfaces are the same, the
thickness is uniform. As shown in Figure 8, the
uniform thickness were obtained. Compared with the
design value, the difference was 6 μm. Also, Table 5
shows the average thickness and standard deviation
of each lens. As shown in this Table 5, accurate
measurement was possible. Regarding the lens C,
which has the largest error and standard deviation
from the design value, an error of 53 μm was occurred
because the lens thickness was set to be so thicker lens
that is not used for normal vision correction in order
to match the center coordinates of the both surfaces.
Since this lens is thick, the internal reflections
affected to the result. The thickness result verified
highly accurate measurement even when compared
with the resolution of 10.1 μm of this OCT.
Table 3: The results of each curvature radius.
Front surface[mm] Back surface[mm]
A 7.68 7.49
B 7.71 7.51
C 8.01 6.96
D 6.84 6.93
E 6.77 6.74
Table 4: The results of the center coordinates.
Front surface [mm] Back surface [mm]
x y z x y z
A 0.00 0.01 0.28 0.16 0.06 0.03
B 0.00 0.02 0.01 0.05 0.00 0.05
C 0.25 0.00 0.00 0.01 0.01 0.02
D 0.50 0.00 0.01 0.09 0.00 0.00
E 0.13 -0.01 0.01 0.08 0.00 0.00
PHOTOPTICS 2021 - 9th International Conference on Photonics, Optics and Laser Technology
78
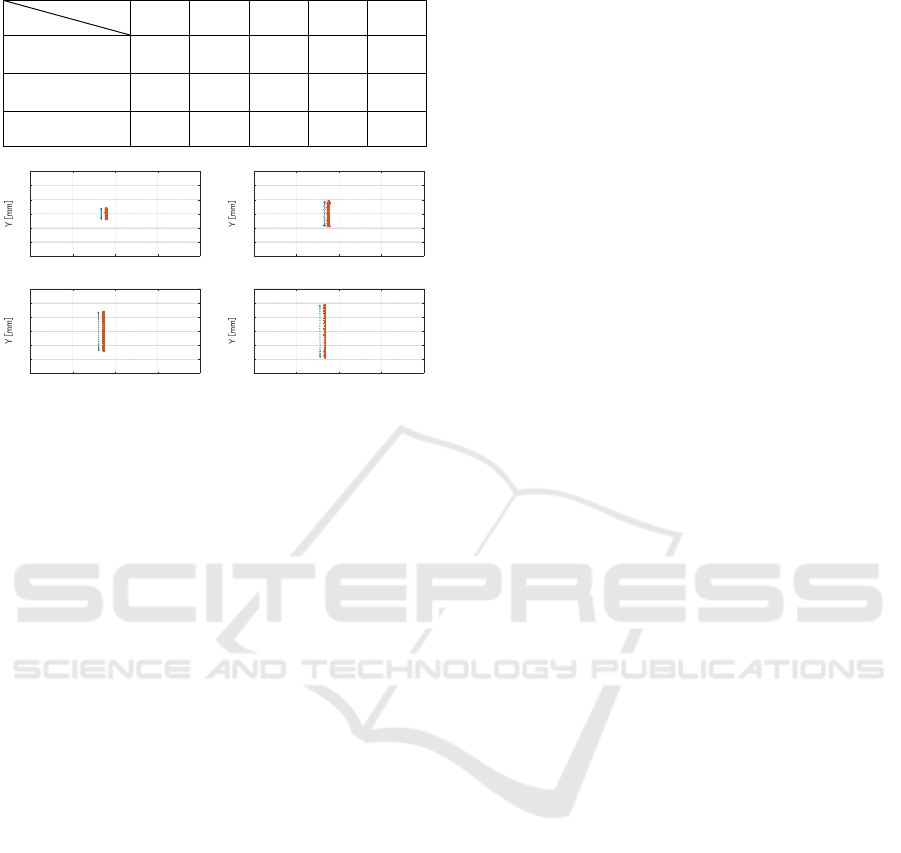
Table 5: The results of the thickness.
A B C D E
Design value
[mm]
0.10 0.15 1.25 0.10 0.054
Average value
[mm]
0.088 0.143 1.197 0.094 0.055
Std [mm] 0.013 0.008 0.020 0.003 0.008
Figure 8: Lens D’s thickness distribution for each
measurement range. ‘*’ is the front surface. And ‘.’ is the
back surface.
4 CONCLUSIONS
In this paper, we proposed the 2D and 3D
measurement algorithms for the real front and back
curved surfaces of CL. Since 2D uses the interference
intensity ration of the front and back surfaces, it takes
time to measure, and although 3D has a limited
measurement range, two measurement algorithms
that can measure both shapes of transparent objects
have great advantage.
Regarding 2D measurement algorithm, changes in
curvature radius and a wide range of thickness
distributions can be measured. In recent years,
peripheral shape of CL is an important issue for the
design of new lenses, such as CL for myopia control.
The fact that OCT provides quantitative measurement
is advantageous as a CL shape measuring device.
Also, since the front and back surfaces can be
measured simultaneously, it is possible to analyze the
misalignment between the both surfaces. This is
important for small optical lenses such as CLs. For
lens curvature radius, circle approximation results
from the obtained shape coordinates were equivalent
to those of Plu Apex. Nevertheless, our OCT device
is more superior because it can measure lens front and
back surfaces simultaneously.
Regarding 3D measurement, the simulation was
performed under the same conditions and compared
with the error rate of experimental results. Compared
with the simulation data, it was confirmed that the
error rate became smaller and the accuracy was
satisfied in this measurement environment. In
addition, the thickness was sufficiently accurate
compared with the resolution of this OCT. The next
step is to evaluate toric-shaped contact lens.
From these results, 2D and 3D algorithm were
able to solve the problem of the shape measurement
device, which is the measurement of transparent
object, by measuring the front and back surfaces at
the same time. Therefore, this algorithm can be
applied to the medical field such as the
ophthalmology field. For example, it is an eyeball
shape measurement. By using this method,
information such as the corneal shape of the front and
back surfaces, thickness and the center coordinates of
the curvature radius can be obtained. Also, it can
measure non-cylindrical shapes such as keratoconus
for eye diseases in which the cornea protrudes (
D.
Fadel 2018)
. In addition, it can be applied not only in
the medical field but also in the industrial field.
Nowadays, small lenses such as mobile phone camera
lenses is frequently used. It is also possible to
evaluate the misalignment of the front and back
surfaces, which is applicable to the inspection of such
lenses. This is an advantage of simultaneous front and
back measurement. Simultaneous measurement of the
shapes of front and back curved surfaces of
transparent bodies such as CL provides a new
measurement possibility for the industry.
REFERENCES
B. J. Coldrick, C. Richards, K. Sugden, J. S. Wolffsohn, and
T. E. Drew, “Developments in contact lens
measurement: A comparative study of industry
standard geometric inspection and optical coherence
tomography,” Contact Lens Anterior Eye, 270-276
(2016).
D. Luo, L. Qian, L. Dong, P. Shao, Z. Yue, J. Wang, B. Shi,
S. Wu, and Y. Qin, “Simultaneous measurement of
liquid surface tension and contact angle by light
reflection,” Opt. Express, Vol. 27, No. 12, 16703-
16712 (2019).
F. Drouet, C. Stolz, O. Laligant, and O. Aubreton, “3D
reconstruction of external and internal surfaces of
transparent objects from polarization state of
highlights,” Opt. Lett., 39 (10):2955-8 May (2014).
K. Saeki, D. Huyan, M. Sawada, Y. Sun, A. Nakamura, M.
Kimura, S. Kubota, K. Uno, K. Ohnuma and T. Shiina,
“Measurement algorithm for real front and back curved
surfaces of contact lenses,” Appl. Opt. 59, No. 29
(2020).
N. Tanno, S. Kishi : “Optical Coherence Tomographic
Imaging and Clinical Diagnosis,” Medical Imaging
Technology, Volume 17: 3-10 (1990).
66.577.58
X [mm]
-1.5
-1
-0.5
0
0.5
1
1.5
1.53°
6 6.5 7 7.5 8
X [mm]
-1.5
-1
-0.5
0
0.5
1
1.5
3.60°
66.577.58
X [mm]
-1.5
-1
-0.5
0
0.5
1
1.5
5.66°
6 6.5 7 7.5 8
X [mm]
-1.5
-1
-0.5
0
0.5
1
1.5
7.72°
2D and 3D Measurement Algorithms for Real Front and Back Curved Surfaces of Contact Lenses
79

P. Massatsch, F. Charriere, E. Cuche, P. Marquet and C. D.
Depeursinge, “Time-domain optical coherence
tomography with digital holographic
microscopy,”Appl.Opt. 44, 1806-1812 (2005).
K. Hibino, Bozenko F. Oreb, Philip S. Fairman, and Jan
Burke, "Simultaneous measurement of surface shape
and variation in optical thickness of a transparent
parallel plate in wavelength-scanning Fizeau
interferometer," Appl. Opt. 43, 1241-1249 (2004).
H. C. Cheng and Y. C. Lin, “Simultaneous measurement of
group refractive index and thickness of optical samples
using optical coherence tomography,”Appl.Opt. 49,
790-797 (2010).
T. Shiina, Y. Moritani, M. Ito and Y. Okamura, “Long-
optical-path scanning mechanism for optical coherence
tomography,”Appl. Opt. 42, 3795-3799 (2003).
D. Fadel, “The influence of limbal and scleral shape on
scleral lens design,” Contact Lens and Anterior Eye.,
41, 321-328 (2018).
PHOTOPTICS 2021 - 9th International Conference on Photonics, Optics and Laser Technology
80
