
Modeling the Cabin Capacity Allocation Problem in the Cruise Industry:
An Italian Case Study
Giusy Macrina
1 a
, Francesca Guerriero
1 b
and Luigi Di Puglia Pugliese
2 c
1
Dipartimento di Ingegneria Meccanica, Energetica e Gestionale, Universit
´
a della Calabria, 87036, Rende, Italy
2
Istituto di Calcolo e Reti ad Alte Prestazioni, Consiglio Nazionale delle Ricerche, 87036, Rende, Italy
Keywords:
Revenue Management, Cruise Sector, Allocation Problem.
Abstract:
In this paper we present several optimization models for cruise cabin capacity allocation. In particular, we
address the problem of managing the booking requests for a set of cabins with different type and price in
a cruise ship. We formulate three models, considering several features of the problem such as: the limited
number of bookable places on the ship, different planning and operation horizon, the possibility to postpone
a departure or to apply special offers. Then, we present an Italian case study and we analyze the impact of
different strategies on the revenues achievable by the company.
1 INTRODUCTION
Since 1980, the cruise industry has grown rapidly
worldwide, with an impressive annual rate of 8.4%.
Between 2009 and 2019, the number of cruise passen-
gers increased from 17.8 millions in 2009 to 30 mil-
lions in 2019. In 2017 the cruise sector contributed
114 billion euros to the global economy, counting
28.5 millions of passengers (www.cruising.org). The
cruise sector is expected to grow more, in fact, the
occupancy rate of cabins is very high compared to
other tourism sectors, such as the hotels. It is impor-
tant to note that this parameter plays a crucial role.
In fact, if in other sectors, such as the hotels or the
airlines, having an occupancy rate equals to 70% in-
dicates a success, in a cruise ship this rate must be
around 95% or more. Thus, a cruise company al-
ways tries to complete the booking for a ship, apply-
ing discounts or promotions, avoiding empty cabins
during the trips. The main reason is that the rev-
enues of a cruise are not only related to the tickets,
but also to several services offered on-board, such as
excursions, photo books and other entertainment ac-
tivities. Hence, choosing a strategy for maximizing
the overall revenues is a very challenging task. This
makes the cruise sector an interesting and profitable
area for applying revenue management techniques.
a
https://orcid.org/0000-0001-6762-3622
b
https://orcid.org/0000-0002-3887-1317
c
https://orcid.org/0000-0002-6895-1457
Revenue management methods are useful tools for
helping companies in finding profitable policies to al-
locate their limited resources to different customer
segments, in a given planning horizon (Klein et al.,
2020). Originating in the airline industry in the 1970s,
these techniques have been extended to many indus-
tries, we cite for example restaurants (Saito et al.,
2019), (Guerriero et al., 2014), railway (Meissner
and Strauss, 2010), car rental (Guerriero and Olivito,
2014), (Oliveira et al., 2017). However, the scien-
tific production related to the application of revenue
management techniques in the cruise industry is not
very extensive (Sturm D., 2018). Only few contri-
butions, addressing real-case applications of revenue
management methods in this sector, have been pub-
lished. The paper of (Ladany and Arbel, 1992) repre-
sents one of the first work addressing pricing strate-
gies for passenger cabins on cruise-liners. (Biehn,
2006) emphasized that the cruise ships are not float-
ing hotels, and explained why common hotel rev-
enue management methods cannot be applied to the
cruise sector. He focused on several critical factors
such as: pricing, multiple capacity limitations, book-
ing periods, the huge number of cabin categories and
the trips extensions (i.e., additional services offered
to customers for extending the base itinerary). (Mad-
dah et al., 2010) proposed a dynamic model to han-
dle multi-dimensional cabin category and lifeboat ca-
pacity constraints, and to consider the uncertainty of
demand by assuming that customers arrive according
to a discrete-time stochastic process. (Li et al., 2014)
Macrina, G., Guerriero, F. and Pugliese, L.
Modeling the Cabin Capacity Allocation Problem in the Cruise Industry: An Italian Case Study.
DOI: 10.5220/0010299402330240
In Proceedings of the 10th International Conference on Operations Research and Enterprise Systems (ICORES 2021), pages 233-240
ISBN: 978-989-758-485-5
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
233

modeled a problem which considers pricing and room
assignment as well as the potential on-board expenses
of customers. (Sturm and Fischer, 2019) extended the
work of (Li et al., 2014) taking into account addi-
tional issues, such as the interdependence of booking
request components, i.e., inseparable group arrivals,
and exploiting the possibility to use connected cab-
ins. (Li, 2014) considered the risk of cancellation
and focused on the possibility to accept overbook-
ing requests. Hence, he applied a real options ap-
proach to formulate a risk decision model for cruise
line dynamic overbooking. (Ayvaz-Cavdaroglu et al.,
2019) developed a pricing approach focusing on the
customer habits and three main features of cruise in-
dustry: the long booking period, the restriction on the
price variations from week to week, and the effect of
promotion expense decisions on the total revenues of
the company.
Contribution and Organization of the Work. In
this work we present three mathematical formula-
tions, of incremental complexity, for the cabin capac-
ity allocation problem in the cruise industry. The first
model is a basic problem, in which booking requests
are accepted until a maximum capacity is reached,
then, they are rejected. In the second and third models
we consider the possibility to offer customers a post-
poned departure time at the same price, in case all the
cabins of the requested type are all booked for the se-
lected data. The main difference between these last
two models is that in the second one, we suppose that
all the customers accept the postponement, while in
the third one we consider also the possibility of rejec-
tion. This specific feature (i.e., postponement of the
departure date) has not been considered in the scien-
tific contributions published on the same topic so far.
It is worth observing that the proposed models can be
used to evaluate booking limits and thus the obtained
solutions can support the decision maker in accepting
or denying arriving booking requests, when booking
limit revenue management policies are implemented.
The behaviour of the proposed models are evalu-
ated empirically on realistic data related to the Italian
cruise line: Costa Crociere. In particular, we investi-
gate how different price strategies may influence the
achievable revenues. The rest of the paper is orga-
nized as follows: in Section 2 we describe the pro-
posed models. In Section 3 we describe the real case
study and we discuss on the results obtained by testing
the proposed models, on realistic data and considering
different pricing schemes. In Section 4 we summarize
the conclusions of our work.
2 MATHEMATICAL
PROGRAMMING MODELS
In this section we present the proposed models, aimed
at allocating the cruise cabin capacity, in such a way
to maximize the revenue. In particular, we present
three mathematical formulations, we describe the ob-
jective functions and constraints of each model and
we highlight their most important features and limits.
2.1 First Mathematical Model
Let k = 1. . .
¯
K indicate the cabins type available for
the booking. In each time period t = 1 . . . T of the
booking horizon, a customer may book a cabin of type
k. Let
¯
t = 1 . . .
¯
T be the operational horizon, i.e. the
period of time where the ships embark the passengers.
It is worth noting that the boarding/landing operations
are not scheduled each day of the operation horizon,
hence, let Ω ⊆
¯
T be the subset of days in which a ship
embarks the passengers (i.e., boarding/landing opera-
tions are allowed). In other words, we may introduce
a binary vector H of size
¯
T which refers to the ports
where the ships stop and passengers may get on/off.
The generic element h
¯
t
belonging to the vector H is
equal to one if during the day
¯
t the boarding/landings
operations are allowed, zero otherwise. Hence, we
may set Ω = {
¯
t : h
¯
t
= 1}.
The booking horizon is defined such that the last
possible day of booking is the day before the starting
of the operational horizon, i.e., the day before the start
date of the cruise.
On the other hand, each cabin can be reserved up
to F days before departure. Thus, a customer, who
wants to depart at time
¯
t, can book a cabin at any in-
stant of time t belonging the set L(
¯
t) = {t|
¯
t − F ≤ t ≤
¯
t − 1}.
Each cruise trip has a duration of α days. Let p
¯
t
kt
be the price at time t for booking a cabin of type k for
the departure time
¯
t, while d
¯
t
kt
be the requests received
at time t for booking a cabin of type k for the departure
time
¯
t. A ship has a limited number of cabins of type
k, indicated as C
k
.
Let x
¯
t
kt
be an integer decision variable that rep-
resents the number of accepted booking requests for
cabins of type k arrived at time t, for the period
¯
t,
∀
¯
t ∈ Ω;k ∈
¯
K, t ∈ L(
¯
t).
Using the notation introduced above, the first for-
mulation takes the following form.
Max
¯
K
∑
k=1
∑
¯
t∈Ω
∑
t∈L(
¯
t)
p
¯
t
kt
x
¯
t
kt
(1)
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
234

x
¯
t
kt
≤ d
¯
t
kt
¯
t ∈ Ω, k = 1...
¯
K, t ∈ L(
¯
t)
¯
t+α−1
∑
τ=
¯
t−α+1
t−1
∑
s=1
x
τ
ks
+
¯
t+α−1
∑
τ=
¯
t−α+1
x
τ
kt
≤ C
k
¯
t ∈ Ω, k = 1...
¯
K, t ∈ L(
¯
t)
x
¯
t
kt
≥ 0, integer
¯
t ∈ Ω, k = 1...
¯
K, t ∈ L(
¯
t)
(2)
(3)
(4)
The objective function (1) maximizes the total
revenue. Constraints (2) guarantee that the number
of accepted booking requests does not exceed the de-
mand. Ships capacity constraints are modeled by
equations (3), finally; constraints (4) define the vari-
ables domain.
It is worth noting that this model can be easily de-
composed in
¯
K smaller sub-problems, simpler to be
solved. In fact, since the requests arrive for single
type of cabins and they are not related each others, the
total number of cabins of each type k may be consid-
ered as a single ship. Hence, for modelling the sub-
problem, we may modify the quantities defined for
the previous model as follows: let d
¯
t
t
the booking re-
quests of cabins received at time t for the time depar-
ture
¯
t, and p
¯
t
t
be the price for booking a cabin at time
t for the time departure
¯
t. C is the maximum capacity
of the ship. Let x
¯
t
t
be an integer decision variable that
represents the number of accepted booking requests
for cabins arrived at time t, starting from the period
¯
t,
∀
¯
t ∈ Ω;k ∈
¯
K, t ∈ L(
¯
t). We named this requests regu-
lar” requests. A sub-problem for a ship composed of
cabins of type k, which maintains the same objective
and constraints of the previous one, can be modelled
as follows:
Max
∑
¯
t∈Ω
∑
t∈L(
¯
t)
p
¯
t
t
x
¯
t
t
(5)
x
¯
t
t
≤ d
¯
t
t
¯
t ∈ Ω, t ∈ L (
¯
t)
¯
t+α−1
∑
τ=
¯
t−α+1
t−1
∑
s=1
x
τ
s
+
¯
t+α−1
∑
τ=
¯
t−α+1
x
τ
t
≤ C
¯
t ∈ Ω, t ∈ L (
¯
t)
x
¯
t
t
≥ 0, integer
¯
t ∈ Ω, t ∈ L (
¯
t)
(6)
(7)
(8)
2.2 Second Mathematical Model
The model proposed in Section 2.1 is a basic version
in which the booking requests for cabins of type k are
accepted until the maximum number of available cab-
ins in the ship, for the departure time
¯
t, is reached.
The other requests are rejected. However, adopting
this strategy could be not profitable, since the pos-
sibility to offer alternative travel options to the cus-
tomer is not taken into account. Sometime, some cus-
tomers could be interested in booking a cruise, but
their requests cannot be accepted due to the unavail-
ability of cabins at departure time
¯
t. Hence, an inter-
esting strategy is to propose to customers who try to
book a cabin of type k for the departure time
¯
t, another
cabin of the same type k but in another departure time
indicated as α, in the same port, maintaining the same
price proposed at time t. In fact, since α is the dura-
tion of the trip, the same tour of a cruise ship starts
each α days, in the same port.
To model this possibility, we need to introduce
a new set of variables y
¯
t
kt
,
¯
t ∈ Ω, k = 1. . .
¯
K, t =
1. . . L(
¯
t), that represent the number of accepted re-
quests of cabins of type k for the departure time
(
¯
t − α) that will be scheduled at departure time
¯
t. We
referred to this type of requests as promo” requests.
The related problem can be represented mathemati-
cally as follows.
Max
¯
K
∑
k=1
∑
¯
t∈Ω
∑
t∈L(
¯
t)
p
¯
t
kt
(x
¯
t
kt
+ y
¯
t+α
kt
)
(9)
x
¯
t
kt
≤ d
¯
t
kt
¯
t ∈ Ω, k = 1...
¯
K, t ∈ L(
¯
t)
¯
t+α−1
∑
τ=
¯
t−α+1
t−1
∑
s=1
(x
τ
ks
+ y
τ
ks
) +
¯
t+α−1
∑
τ=
¯
t−α+1
(x
τ
kt
+ y
τ
kt
) ≤ C
k
¯
t ∈ Ω, k = 1...
¯
K, t ∈ L(
¯
t)
y
¯
t
kt
≤ d
¯
t−α
kt
− x
¯
t−α
kt
¯
t ∈ Ω, k = 1...
¯
K, t ∈ L(
¯
t)
x
¯
t
kt
≥ 0, integer
¯
t ∈ Ω, k = 1...
¯
K, t ∈ L(
¯
t)
y
¯
t
kt
≥ 0, integer
¯
t ∈ Ω, k = 1...
¯
K, t ∈ L(
¯
t)
(10)
(11)
(12)
(13)
(14)
The objective function (9) maximizes the total
revenue, obtained by accepting the regular and the
promo requests. Constraints (10) are the same as
the conditions (2). Equations (11) model the capac-
ity constraints, taking into account both the regular
requests and the promo ones. Constraints (12) guar-
antee that the number of accepted promo requests for
the departure time
¯
t and the cabin type k, does not
exceed the demand, considering also the regular re-
quests. Constraints (13) and (14) define the domain
of variables.
As for the model (1)– (4) presented in Section 2.1,
we can decompose this model in
¯
K sub-problems, one
for each type of cabin k. With this purpose, we mod-
ify the parameters and the variables by removing the
index related to the type of cabin k, maintaining the
same objective function and constraints. Hence, for
each type of cabin, we model and solve the follow-
ing optimization problem, which is easier to be solved
than the mathematical formulation (9) – (14).
Max
∑
¯
t∈Ω
∑
t∈L(
¯
t)
p
¯
t
t
(x
¯
t
t
+ y
¯
t+α
t
) (15)
x
¯
t
t
≤ d
¯
t
t
¯
t ∈ Ω, t ∈ L(
¯
t) (16)
¯
t+α−1
∑
τ=
¯
t−α+1
t−1
∑
s=1
(x
τ
s
+ y
τ
s
)+
Modeling the Cabin Capacity Allocation Problem in the Cruise Industry: An Italian Case Study
235

¯
t+α−1
∑
τ=
¯
t−α+1
(x
τ
t
+ y
¯
t
t
) ≤ C
¯
t ∈ Ω, t ∈ L (
¯
t)
y
¯
t
t
≤ d
¯
t−α
t
− x
¯
t−α
t
¯
t ∈ Ω, t ∈ L (
¯
t)
x
¯
t
t
≥ 0, integer
¯
t ∈ Ω, t ∈ L (
¯
t)
y
¯
t
t
≥ 0, integer
¯
t ∈ Ω, t ∈ L (
¯
t)
(17)
(18)
(19)
(20)
2.3 Third Mathematical Model
The main limit of the model proposed in Section 2.2
is that it assumes a customer will accept to book a
cabin even if the departure will be postponed of α
days. Actually, a customer could not accept the de-
parture postponement, hence, taking into account the
possibility of rejection is a critical issue. To model
this possibility, we introduce the customer’s probabil-
ity of acceptance. Let a
¯
t
kt
be a binary parameter that
will be equal to one if the probability of acceptance
is larger than P, zero otherwise for each k = 1, . . .
¯
K,
t = 1. . . L(
¯
t),
¯
t ∈ Ω.
Hence, we formulate the problem as follows:
Max
¯
K
∑
k=1
∑
¯
t∈Ω
∑
t∈L(
¯
t)
p
¯
t
kt
(x
¯
t
kt
+ a
¯
t
kt
y
¯
t+α
kt
) (21)
x
¯
t
kt
≤ d
¯
t
kt
¯
t ∈ Ω, k = 1...
¯
K, t ∈ L(
¯
t)
¯
t+α−1
∑
τ=
¯
t−α+1
t−1
∑
s=1
(x
τ
ks
+ a
τ
ks
y
τ
ks
)+
¯
t+α−1
∑
τ=
¯
t−α+1
(x
τ
kt
+ a
τ
kt
y
τ
kt
) ≤ C
k
¯
t ∈ Ω, k = 1, ...,
¯
K, t ∈ L(
¯
t)
a
¯
t
kt
y
¯
t
kt
≤ d
¯
t−α
kt
− x
¯
t−α
kt
¯
t ∈ Ω, k = 1, ...,
¯
K, t ∈ L(
¯
t)
x
¯
t
kt
≥ 0, integer
¯
t ∈ Ω, k = 1, ...,
¯
K, t ∈ L(
¯
t)
y
¯
t
kt
≥ 0, integer
¯
t ∈ Ω, k = 1, ...,
¯
K, t ∈ L(
¯
t)
(22)
(23)
(24)
(25)
(26)
The objective function (21) maximizes the rev-
enue, while constraints (22) – (26) are similar to (10)
– (14). This model, as the previous ones, can be de-
composed in easier sub-problems. However, the main
limit of this model is that the demand is considered
an aggregate data. Hence, it supposes that all the cus-
tomers behave similarly.
3 COMPUTATIONAL RESULTS
In this section we describe our computational study
and analyze the obtained results. In particular, we
firstly describe the case study features. Then, we dis-
cuss on the experimental results obtained by applying
the different models presented in Section 2, by high-
lighting the impact of the use of these models in terms
of achievable revenue.
3.1 The Italian Case Study
In this section, we present the main features of
the realistic case study used in the computational
phase. We have considered the Italian cruise line:
Costa Crociere. Thus the cabin capacities, the
cabin types and the the tariff segments are de-
rived from the web-site of the considered cruise line
(https://www.costacruises.com/), whereas the cabin
rates are obtained from the data published by the on-
line travel agency Logitravel (www.logitravel.it).
Some of the available data have been slightly
modified in order to fit with the models assumptions.
In particular, we consider only three categories of cab-
ins, i.e., low that includes the intern cabins, medium
that contains both ocean and balcony, and high that
refers to the suite. Thus, capacities and prices have
been appropriately defined (see Tables 1–3).
We have chosen the itinerary Marseille -
Barcelone - Palma de Maiorca - Cagliari - Civitavec-
chia (Rome)” depicted in Figure 1. It is worth observ-
ing, that not all the cities are embarkation ports. In
fact, it is possible to start the cruise only from Savona,
Cagliari and Rome.
Figure 1: Cruise itinerary.
The ship which performs this trip, named Costa
Diadema” (see Figure 2), is one of the largest in the
fleet of Costa Crociere. In fact, it can host 4947 pas-
sengers and 1253 crew members, and also has an out-
side promenade extending over 500 m. There are sev-
eral on-board activities in Costa Diadema: 4D cine-
mas, lively bars, gourmet restaurants and the spa area.
Figure 2: Costa Diadema (www.costacruises.com).
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
236

Costa Diadema has 1862 cabins of three types: In-
side (i.e., the most economic), Balcony and Ocean
view, Suite and Samsara. We will refer to these
classes as: low, medium and high, respectively. Ta-
ble 1 summarizes the capacities, i.e., the number of
available places, of each type of cabin.
Table 1: Capacity of the cabins classified by type.
Type Low Medium High
Capacity 701 1086 75
The cruise starts its journey in June and repeats its
tour until the end of September. It is 7-days long and
it visits the same port each week in the same day. The
first city, visited on Monday, is Savona, then Marseille
in Tuesday and so on. We have considered data refer-
ring to 2018, thus the first possible departure was on
June the 2
nd
. For our study, we have considered two
weeks of service, thus 14 days when it is possible to
embark on the cruise and 21 days of service.
Prices. The cabins rates vary depending on the de-
parture date and the type of cabins, Table 2 reports the
prices related to the period 02/06 – 30/06 of the year
2018.
Table 2: Prices of the cabins for the year 2018
(www.logitravel.it).
Type 02/06 09/06 16/06 23/06 30/06
Intern e669 e669 e669 e749 e749
Ocean e839 e869 e869 e919 e929
Balcony e949 e949 e949 e998 e1,018
Suite e1,194 e1,194 e1,194 e1,243 e1,263
In our experimental study, we assume that the
price is influenced by the time of booking, the depar-
ture date and the availability of the cabins in the ship.
Hence, for representing the variation of price, we fol-
low the idea considered by (Joshi, 2004). At first, we
evaluated a maximum and a minimum price for each
cabin type, denoted as p
max
and p
min
, respectively and
summarized in Table 3.
Table 3: Maximum and minimum prices for each type of
cabin.
Type Low Medium High
p
min
e669 e839 e1,194
p
max
e749 e1,018 e1,263
Then, the first strategy we consider for incentiviz-
ing customers to buy, is related to the time remaining
before the departure. Hence, we apply the lowest fare
if the requests arrive very early, i.e., when the ship
is almost empty. On the contrary, the fares will be
increased if the booking requests arrive close to the
departure time, i.e., when only few cabins are avail-
able and the customers are willing to pay the most
extensive price for booking a cabin. To calculate the
corresponding fare p
ask
(i.e., the price offered to the
customers), we use the next linear equation (27) pro-
posed by (Joshi, 2004):
p
a
ask
= p
max
−t
r
j (27)
where t
r
is the remaining time that is the time left for
the cruise to start and j is a normalizing constant de-
fined in such way that p
a
ask
will be p
min
, when t
r
is
equal to the maximum number of days before the de-
parture in which the booking is possible.
The second strategy is related to the number of
available cabins. Hence, we calculate the price as fol-
lows:
p
b
ask
= p
max
− c
r
k (28)
where c
r
is the number of remaining cabins and k is a
normalizing constant such that p
b
ask
will be p
min
, when
c
r
is equal to the maximum number of available cab-
ins.
The last strategy is a hybrid approach, which takes
into account both time of booking and the available
cabins. The p
c
ask
is calculated as follows:
p
c
ask
= p
max
− (t
r
j) − (c
r
k) (29)
where j and k are normalizing constants such that p
c
ask
is p
max
, when t
r
is equal to the booking period and c
r
is close to zero.
Demands. To calculate the demand, we consider a
linear demand function (Cohen et al., 2015) denoted
by:
Q(p) = A − Bp (30)
We use the price elasticity of demand to calcu-
late the parameters A and B. The demand curve is
high elastic for luxury goods and we can state that
the higher the price the higher the elasticity. We use
a linear regression and calculate the curve demand
through Microsoft Excel. The equations are depicted
in Tab 4, where y represents Q(p) and x is p.
Table 4: Demands equations for each type of cabin.
Type elasticity equation
low 7 y=-0.2857x+221.43
medium 15 y=-0.7778x+ 765.22
high 20 y=-0.3347x+420
3.2 Results
We now describe the results obtained by solving the
three mathematical models proposed in Section 2. We
Modeling the Cabin Capacity Allocation Problem in the Cruise Industry: An Italian Case Study
237

use the Excel solver to find the solutions and we anal-
yse the results discussing the obtained revenues as
well as the occupancy of the cabins, considering the
21 days of service.
First Mathematical Model. We firstly analyse the
results obtained for the basic mathematical model rep-
resented by equations (1) – (4). We use the decom-
posed formulation (5)– (8), hence, we solve three sub-
problems, one for each type of cabin. We consider
four scenarios, by varying the prices p: 1) p = fixed
price, 2) p = p
a
ask
, 3) p = p
b
ask
and 4) p = p
c
ask
.
The first scenario is the most improbable, how-
ever, we want to analyse the case in which the price is
fixed, equal for each day of the time horizon.
Looking at results in Table 5, which summarizes
the revenues for each type of cabin as well as the total
revenue for the 21 days of service, it is evident that
the medium” cabins are the most profitable.
Table 5: Cruise revenue solving the first mathematical
model with fixed price.
type low medium high total
revenue (e) 892,386.00 1,880,706.00 20,980.00 2,976,072.00
This result, considering this setting, is obvious be-
cause of the higher number of available medium cab-
ins. Looking at Figure 3 we can observe that overall,
the highest numbers of reservations is concentrated in
the central departure dates.
Figure 3: Occupancy of cabins, using the first mathematical
model and a fixed price.
Then, we analyse the results obtained by varying
the prices. Table 6 reports the parameters used in the
computational experiments
Table 6: Parameters setting.
Type Low Medium High
p
min
(e) 669 839 1,194
p
max
(e) 749 1,018 1,263
capacity 701 1086 75
j 2.150 3.210 3.500
k 0.002 0.020 0.320
We summarize the results in Table 7 which de-
picts the obtained revenues, for each price strategy
and each type of cabins. Overall, the total revenues
are less than that obtained with the fixed price, this
numbers confirm that making a sales forecast using
a fixed price leads to erroneous results, since using a
fixed price is an impracticable strategy. Looking at
Table 7 we may observe that the most profitable strat-
egy is obtained by using p
c
ask
. Hence, considering the
price as a function of both booking time and available
cabins is the most profitable approach.
Table 7: Cruise revenue solving the first model varying
price strategy.
type low medium high total
revenue p
a
ask
603,730.00 993,900.00 182,460.00 1,780,063.00
(e) p
b
ask
566,647.00 1,008,569.00 182,138.00 1,757,354.00
p
c
ask
600,678.00 1,071,410.00 130,649.00 1,802,737.00
Figure 4 depicts the comparison of the cabins oc-
cupancy, for each departure date, varying p
ask
. It is
evident that p
c
ask
is not only the price that allows to
reach higher values of revenues, but also higher value
of occupancy.
Figure 4: Occupancy of cabins, using the first mathematical
model and varying p
ask
.
Second and Third Mathematical Models. As for
the first mathematical model, we fix the price and
solve also the second mathematical model presented
in Section 2 (i.e., (9) – (14)), that considers the possi-
bility to postpone the departure time of one week. In
this setting, we suppose that all the customers accept
the postponement. We recall that the third mathemat-
ical model is an extension of the second one, in which
the probability of acceptance is considered. Hence,
we need to take into account the possibility that a
customer accepts or not this postponement. For our
computational study, we suppose that the probability
of acceptance is about 70%. Table 8 summarizes the
results for both the models considering a fixed price.
From Table 8, it is evident that both the models pro-
vide the same revenue and the most profitable type
cabins is once again the medium one.
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
238
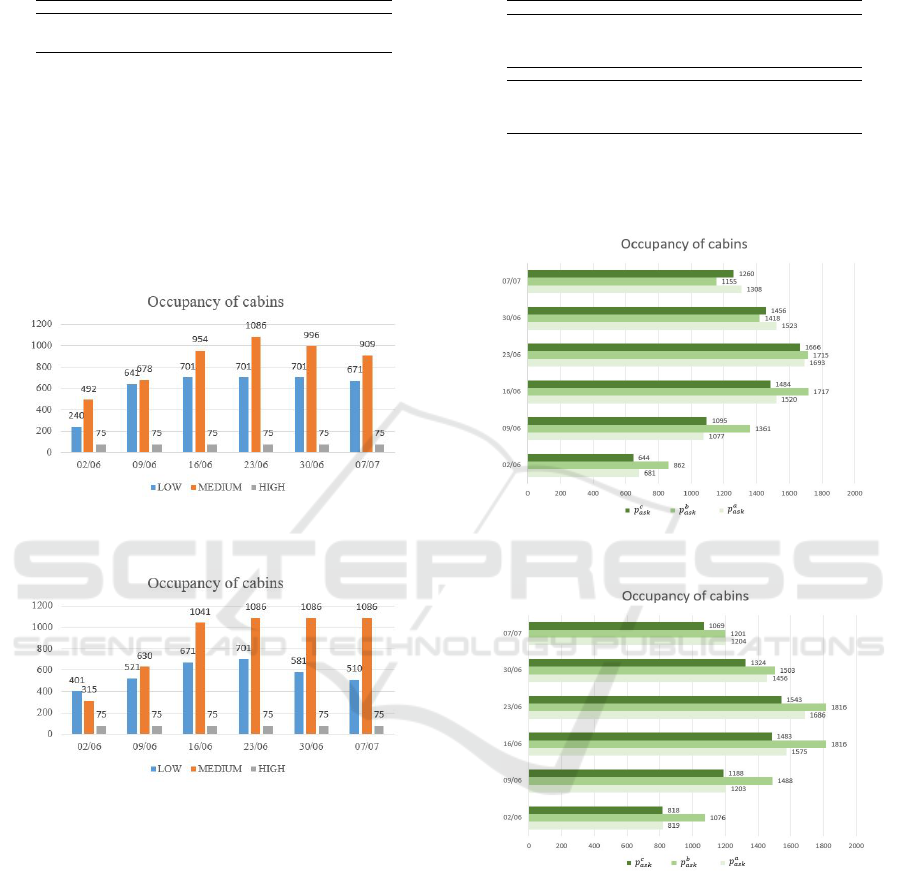
Table 8: Cruise revenue solving the second and third math-
ematical models with fixed price.
type low medium high total
model
revenue II 610,370.00 1,297,326.00 179,100.00 2,086,796.00
(e) III 610,370.00 1,297,326.00 179,100.00 2,086,796.00
Figures 5 and 6 show the occupancy of cabins
for the solutions obtained using the second and third
models, respectively. Even if we obtain the same rev-
enues, looking at Figures 5 and 6 we may see some
differences in the configurations. In particular, focus-
ing on the first departure date, using the second model
the number of medium type cabins is higher than that
used by solving the third model. On the contrary, the
number of low cabins is lower.
Figure 5: Occupancy of cabins, using the second mathemat-
ical model and a fixed price.
Figure 6: Occupancy of cabins, using the third model and a
fixed price.
As for the first model, we analyse the results ob-
tained by varying the prices. Table 9 reports the re-
sults obtained for the second and third mathematical
model, respectively. Looking at Table 9 and focusing
on low type cabin, the third model finds more effec-
tive solutions. As a matter of fact, overall the revenues
are higher than those obtained with the second model.
The revenues achieved for the medium and high types
of cabins are similar, with the only exception of the
medium type when considering p
b
ask
, in that case, the
third model finds more profitable solutions than the
second one.
Figures 7 and 8 depict the overall occupancy of the
cabins for the second and third mathematical model,
respectively, by varying p
ask
. Comparing these fig-
Table 9: Cruise revenue solving the second and third math-
ematical models varying price strategy.
second
type low medium high total
revenue p
a
ask
579,735.00 943,484.00 183,237.00 1,706,456.00
(e) p
b
ask
546,678.00 998,892.00 182,220.00 1,727,790.00
p
c
ask
559,054.00 882,467.00 182,974.00 1,624,495.00
third
type low medium high total
revenue p
a
ask
603,854.00 943,484.00 182,460.00 1,729,798.00
(e) p
b
ask
603,727.00 1,166,082.00 182,163.00 1,951,972.00
p
c
ask
608,690.00 800,025.00 182,203.00 1,590,918.00
ures, it is easy to see that using p
b
ask
, the third model
finds more balanced solutions also in terms of occu-
pancy of the cabins.
Figure 7: Occupancy of cabins, using the second mathemat-
ical model and varying p
ask
.
Figure 8: Occupancy of cabins, using the third mathemati-
cal model and varying p
ask
.
4 CONCLUSIONS
In this work we presented three optimization mod-
els for the cabin allocation problem in the cruise in-
dustry. We assess the performance of the proposed
models by considering realistic data, derived from an
Italian cruise line (i.e., Costa Crociere). In the com-
putational experiments we investigate the impact of
different pricing schemes on the total revenues the
Modeling the Cabin Capacity Allocation Problem in the Cruise Industry: An Italian Case Study
239

company can achieve. Some extensions to our work
are possible. It could be interesting to develop so-
phisticated revenue management strategies to support
cruises business, by optimizing the cabins allocation
and boosting revenues growth. In particular, it could
be interesting to define policies with upgrading, that
allow to sell superior-type cabins to a lower price if
some booking requests for cabins of a certain lower
type cannot be accepted, because of the capacity con-
straints. In this case, the main decision is to accept the
risk of selling a superior cabin at lower price, given
that unknown but, probably, more profitable demand
will arrive in the future. The development of buy-
up policies represents another important topic for fu-
ture investigation. It is important to note that, the
implementation of revenue management policies re-
quires the efficient solution of the cabin capacity allo-
cation problem, studied in this paper. Thus it could be
also interesting to deeply investigate the mathematical
structure of the models proposed and to exploit the re-
lated features to improve the solution approaches.
ACKNOWLEDGEMENTS
The authors are grateful to Dr. Roberto Tenuta, for his
assistance in the experiments and to the three anony-
mous reviewers for their insightful suggestions and
careful reading of the manuscript.
REFERENCES
Ayvaz-Cavdaroglu, N., Gauri, D., and Webster, S. (2019).
Empirical evidence of revenue management in the
cruise line industry. Journal of Travel Research,
58(1):104120.
Biehn, N. (2006). A cruise ship is not a floating ho-
tel. Journal of Revenue and Pricing Management,
5(2):135142.
Cohen, M., Perakis, G., and Pindyck, R. (2015). A simple
rule for pricing with limited knowledge of deman. ,
MIT Sloan, Research Paper No. 5145-15.
Guerriero, F., Miglionico, G., and Olivito, F. (2014). Strate-
gic and operational decisions in restaurant revenue
management. European Journal of Operational Re-
search, 237:1119–1132.
Guerriero, F. and Olivito, F. (2014). Revenue models and
policies for the car rental industry. Journal of Mathe-
matical Modelling and Algorithms in Operations Re-
search, 13:247282.
Joshi, K. (2004). Modeling alternate strategies for airline
revenue management. Graduate theses and disserta-
tions, University of South Florida.
Klein, R., Koch, S., Steinhardt, C., and Strauss, A. (2020).
A review of revenue management: Recent generaliza-
tions and advances in industry applications. European
Journal of Operational Research, 284(2):397 – 412.
Ladany, S. and Arbel, A. (1992). Optimal cruise-liner pas-
senger cabin pricing policy. European Journal of Op-
erational Research, 55(2):136147.
Li, B. (2014). A cruise line dynamic overbooking model
with multiple cabin types from the view of real op-
tions. Cornell Hospitality Quarterly, 55(2):197209.
Li, Y., Miao, Q., and Wang, B. (2014). Modeling a cruise
line revenue management problem. Journal of Rev-
enue and Pricing Management, 13(3):247260.
Maddah, B., L., M.-H., El-Taha, M., and Rida, H. (2010).
Dynamic cruise ship revenue management. European
Journal of Operational Research, 207(1):445455.
Meissner, J. and Strauss, A. (2010). Railway revenue man-
agement: overview and models. Working paper (avail-
able at http://www.meiss.com), Lancaster University
Management School.
Oliveira, B., Carravilla, M., and Oliveira, J. (2017). Fleet
and revenue management in car rental companies: A
literature review and an integrated conceptual frame-
work. Omega, 71:11 – 26.
Saito, T., Takahashi, A., Koide, N., and bIchifuji, Y. (2019).
Application of online booking data to hotel revenue
management. International Journal of Information
Management, 46:37 – 53.
Sturm, D. and Fischer, K. (2019). A cabin capacity alloca-
tion model for revenue management in the cruise in-
dustry. Journal of Revenue and Pricing Management,
18:441450.
Sturm D., F. K. (2018). Cruise line revenue management:
Overview and research opportunities. In Fink A.,
Fgenschuh A., G. M., editor, Operations Research
Proceedings 2016. Operations Research Proceedings
(GOR (Gesellschaft fr Operations Research e.V.)),
pages 441–447. Springer, Cham.
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
240
