Dynamic Lot Sizing in a Self-organizing Production

Martin Krockert, Marvin Matthes and Torsten Munkelt

Faculty of Computer Science, Dresden University of Applied Sciences, Friedrich-List-Platz 1, Dresden, Germany

Keywords:

Self-organization, Lot Sizing, Group Technology, Job Shop, Setup Time Reduction, Multi-Agent-Systems.

Abstract:

Companies more and more offer individual products to satisfy their customers and stand out from other com-

petitors. Those individual products differ in their production process and thus require many different tool-

resource combinations, so called setups. In order to reduce the number of setups, shortening the overall setup

time, reducing throughput time, while increasing the adherence to delivery dates, we propose a dynamic lot

sizing approach that combines separate operations into so-called buckets. In this paper, we present the im-

plementation of the dynamic lot sizing approach in our multi-agent based self-organizing production, using

two different production models, which demonstrate the efﬁciency of our solution in comprehension to an

exhaustive rule to create buckets as a results of an empirical study.

1 INTRODUCTION

Today, the increasing needs for companies to offer in-

dividualized products to their customers to stand out

from other competitors, poses new challenges for man

and machine, especially in the area of piece goods

production, where a high degree of product diversiﬁ-

cation leads to the development of ever new tools and

thus to ever new machine tool combinations, so called

setups. The process to equip a tool on a machine takes

time and is referenced as setup time in production

context. Production facilities usually group products

that require the same setup to be produced together as

lots. Under the assumption of producing individual

goods for every customer it is not viable to create lots

based on products, because every product will require

different setups. This will lead to high frequent setup

changes on machines. Irrespective of all measures

to shorten setup times technologically, setup times of

considerable length still occur(Kim and Bobrowski,

1994; M. M. Orta-Lozano and B. Villarreal, 2015).

However, it is still necessary to create lots in order

to reduce frequent setup changes on machines. It is

well known that long setup times extend throughput

times and reduce effective capacity utilization(Spence

and Porteus, 1987). In order to reduce the number

of setups, thereby shortening the overall setup time,

reducing their negative effects, while maintaining a

high adherence to delivery dates as our main goal, we

present a dynamic lot sizing approach, which groups

together operations with the same setup requirements

in so-called buckets. These buckets are only created

temporarily. The operations assigned to the buckets

are processed sequentially by the machine. After a

machine processed an operation the material can be

routed onwards and is not bound to the bucket. In

this way, our dynamic lot sizing approach differs from

conventional lot sizing, which usually keeps lots to-

gether during the processing of their production or-

ders.

The paper is organized as follows: The next sec-

tion classiﬁes the problem and provides a review of

related work. Section III declares the approach in-

cluding components and procedure for dynamically

lot sizing. Subsequently, Sections IV describes our

empirical study. Finally, Section V concludes and

gives an outlook on feature work.

2 PROBLEM DESCRIPTION

2.1 Classiﬁcation

Customers want more and more individual products.

But no company today can afford to not take these

individual wishes into account. This results in many

different products which can not be produced together

and thus even smaller lots in production. Planing for

individual products makes it very difﬁcult to achieve

a good central production plan. Creating an optimal

schedule for job shop productions is even regarded as

NP-complete (Garey et al., 1976; Domschke et al.,

Krockert, M., Matthes, M. and Munkelt, T.

Dynamic Lot Sizing in a Self-organizing Production.

DOI: 10.5220/0010300803610367

In Proceedings of the 13th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2021) - Volume 1, pages 361-367

ISBN: 978-989-758-484-8

361

1997; Herrmann, 2011). The problem still remain

NP-complete by integrating setup times (Ng et al.,

2005). In addition, deviations of processing times

and machine failures occur, which invalidate plans

and lead to inefﬁcient production. To counteract these

negative occurrences, we present a method to dynam-

ically create lots in the form of buckets.

Figure 1: Lots;(A) production orders based; (B) operation

based.

According to (Z

apfel, 1982), a lot is deﬁned as

the quantity of a product that passes through the

production process as one item as shown in Fig-

ure 1A. However, this is impossible due to the na-

ture of individual products, where the product struc-

ture and their operations differs, and therefore can

not be combined to lots. The only remaining pos-

sibility is to build lots based on operations of prod-

ucts which require the same machine setups - so

called Group Technologies.(Kusiak, 1987; Gombin-

ski, 1967) Those Group Technologies share the same

technology requirements, but can be assigned to dif-

ferent products(Ham et al., 1985; Brennan, 1995).

Consequently, the operations combined to one

group can be seen as a horizontal cross-linked ag-

gregation of different products over the same Group

Technology (see Figure 1B). By grouping operations

requiring the same technology, the schedule becomes

more efﬁcient, because operations of the same group

can be processed without intermediate machine se-

tups. This directly eliminates additional setup times

compared to pure priority heuristics.

Because of the uncertainty about the product

structures, required machines and required setups of

the newly created product which should satisfy the

customer individual needs, it is not possible to deter-

mine an optimal bucket size for the production objec-

tives. In current manufacturing environments, suffer-

ing from high uncertainty, group heuristic dispatching

rules have become the most common solution (Klaus-

nitzer et al., 2017). Dispatching rules are generally

applied to queues to prioritize the operation to be pro-

cessed next. Those rules mostly aim to reduce setup

times and increase processing efﬁciency in production

(Frazier, 1996; Ruben et al., 1993; Grabot and Gen-

este, 1994; van der Zee et al., 2011). Several stud-

ies with focus on ﬂow cell manufacturing and group

heuristics already exist (Klausnitzer et al., 2017; Fra-

zier, 1996; Egilmez et al., 2016). There are also pos-

sibilities to solve the scheduling problem using mixed

integer linear programming (MILP) but as it requires

complete and accurate knowledge about all operations

and has high computational cost, even for small prob-

lem sizes, we do not consider MILP.

Group scheduling heuristics can be divided

into two categories - exhaustive and non-

exhaustive(Frazier, 1996). While exhaustive rules

process all operations of the same Group Technology

existing in one queue together, non-exhaustive rules

allow splitting of grouped operations and therefore

switching of setups even though there are still

operations remaining requiring the current setup.

In previous research from Frazier, exhaustive rules

prove to be superior to non-exhaustive rules in ﬂow

shop production (Frazier, 1996). As our research

focuses on high ﬂexibility and robustness in a job

shop production, we developed a non-exhaustive

approach and compare it with an exhaustive heuristic.

Our problem is a job shop scheduling problem

including setup times, which differs from the ﬂow

shop problem analyzed by Frazier. But like Frazier,

we cover uncertainty: Production orders arrive after

exponentially distributed inter-arrival times, and

processing times of operations are log-normally

distributed.

2.2 Disadvantages of Exhaustive Group

Heuristics

To validate that exhaustive heuristics lead to good per-

formance in a highly dynamic production, we created

different test scenarios. Therefore we created two

production models and three setup models, which we

combined to six different scenarios as shown in Table

1. The production is organized as decentralized man-

ufacturing grid, where products can be routed freely

between all machines. Our production model con-

sists of three different machine groups. Machines

can be equipped with different tools. It is possible

to equip multiple machines with a tool of the same

kind at the same time. Working with the same tool

on many machines offers ﬂexibility in production, es-

pecially when the proportion of setups differs and a

single setup potentially dominates.

The size of the production model determines the

amount of machines created for each machine group.

The size of the setup model determines the number

of tools each machine of a machine group can be

equipped with. The product has a three level deep

bill of materials, which consists of 14 materials and

each material requires up to three operations to be

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

362

Table 1: Production scenarios.

Production with

number of machines

Setup Model with number of

tools equipable to machines

Scenario

Model

Saw Drill Assembly Size Saw Drill Assembly

1 Small 2 2 2

2 A 2 1 2 Medium 4 4 7

3 Large 8 8 14

4 Small 2 2 2

5 B 4 2 4 Medium 4 4 7

6 Large 8 8 14

produced. Each operation is connected to a previously

deﬁned machine group. During the model creation,

the setups are assigned in a round robin procedure to

each operation, where the assignment is restricted by

the machine group of the operation. For example, an

operation for sawing a wooden panel is assigned to

the machine group ”saws”. While creating the model,

the operation will be assigned to a speciﬁc setup i.e.,

”small saw blade”. The setup model size is deter-

mined, based on the number of operations assigned

to setups of a machine group. The lower bound, rep-

resented by the small setup model, uses the minimum

of two setups to ensure at least one setup change. The

large setup model, which represents the upper bound,

uses as many setups as there are operations. That

means all operations’ setups differ from each other.

As medium setup model, we calculated the number

of setups by dividing the numbers of the large setup

model by two. We tested an exhaustive heuristic with

the model combinations from Table 1. The tests show

that using an exhaustive heuristic leads to high setup

times. The tests with large setup models demonstrate,

that in extreme cases, the heuristic leads to a lower

timeliness caused by limitations of production capac-

ities through high setup times, as shown in Table 2.

3 THE DYNAMIC LOT SIZING

APPROACH

3.1 Components of the Approach

The dynamic lot sizing approach is based on three

components: a set of operations, a set of machines,

and a ”bucket manager” for organizing the operations

in buckets.

The ﬁrst component contains operations from pro-

duction orders. We assume that each production order

consists of a ﬁxed sequence of operations to be pro-

cessed in that sequence. Consequentially, we do not

consider alternative or parallel operations. Each op-

eration contains the following information: estimated

processing duration, due time of the production order,

Table 2: Exhaustive Heuristic KPI.

Production

Model

Setup

Model

Timeliness

Throughput

time in min

Setup

time

Model A

Small 100.0% 274 26.8%

Medium 76.8% 746 31.6%

Large 22.2% 1274 35.6%

Model B

Small 100.0% 277 29.0%

Medium 100.0% 475 39.2%

Large 69.6% 901 44.1%

average duration of the transition between two con-

secutive operations, required setup, and earliest start

as well as latest start obtained by forward and back-

ward scheduling. The second component contains the

machines. Each machine provides a certain capabil-

ity, i.e. drilling capability, and can be equipped with

similar tools, i.e. drills. In order to process oper-

ations, the machine must be equipped with the re-

quired tool, while each tool has a sequence indepen-

dent setup time. Each machine and tool combination

is referenced as setup and is capable to fulﬁll a certain

capability, i.e. drill a hole with a diameter of one cen-

timeter. However, a machine can only be equipped

with one tool at a time.

The third component is the ”bucket manager”. It

is a persistent instance that organizes buckets and

schedules those buckets on machines. It assigns open

operations requiring the same Group Technology to

buckets linked to the same setup. If there is no suit-

able bucket for an operation, the bucket manager will

create a new bucket and assign the operation to this

bucket. After creating a bucket, the allocation of the

bucket to the machine starts. A separate scheduling

procedure allocates the bucket to the machine. The

procedure can be any scheduling algorithm, while the

bucket manager organizes the buckets, which are cre-

ated upon or ﬁlled with incoming operations. To en-

able multiply machines to process buckets requiring

the same setup, multiple buckets can be created. This

way we maintain ﬂexibility by splitting or merging

buckets. Nevertheless, each bucket must contain at

least one operation. This is the operation the bucket

manager originally created the bucket for. After the

creation of the bucket, further operations can be added

depending on the time scope of the bucket. To de-

termine the time scope, we schedule the production

order forwards and backwards when it enters the pro-

duction. In order to guarantee a robust production,

we limit the bucket not only based on the time scope.

We also introduce a method to dynamically limit the

bucket size depending on existing machines and se-

tups for a certain capability. Thus, we ensure that the

production stays ﬂexible and achieves its objectives.

After processing the last operation of the bucket, the

operation is removed from the bucket and the bucket

Dynamic Lot Sizing in a Self-organizing Production

363

dissolves.

3.2 Determine the Bucket Limits

Finding a suitable bucket size is crucial for the dy-

namic lot sizing: Buckets that are too small lead to

more frequent setups, while buckets that are too large

block the machine for too long with one setup, and

thus the production will lose ﬂexibility. The bucket

size determines the operations that ﬁt in a bucket and

will be later on processed sequentially on a machine.

To ﬁnd a suitable bucket size, we use two mecha-

nisms. Based on the symbol deﬁnition in Table 3,

we ﬁrstly create a dynamic time scope for the bucket,

limited by subtracting the earliest and latest start time,

obtained from forward and backward scheduling of

the ﬁrst operation assigned the to bucket (see 1). The

release time of the production order strongly inﬂu-

ences the dynamic time scope, because production or-

ders with a late release lead to small time scopes and

production orders with an early release lead to large

time scopes. Hence, the dynamic time scopes devi-

ate considerably. To avoid too large time scopes, we

implemented a second limitation.

Table 3: Symbol deﬁnition.

Symbol Deﬁnition

c capability with c ∈ C

s setup s ∈ S

d processing duration d > 0

sbt start time from backward scheduling

s f t start time from forward scheduling with (sbt > s ft)

o is a column vector

with (c, s, d, sbt, s f t)

O is a set {o

, ··· , o

} of operations

includes all setups assigned

to a capability

includes all machines assigned

to a capability

f bucket factor with f > 0

workload with

∑

o∈O

∑

o∈O

l limit with l ≥ 0

The second limitation takes the current number of

machines and their possible setups as well as a bucket

factor into account. The bucket factor is predeﬁned

upon the underlying production and can be experi-

mentally determined. The initial value of the bucket

factor can be based on the length of working shifts,

such as 8, 4 or 2 hours. To verify if an operation ﬁts

into a bucket, we calculate a setup limit by taking the

number of machines and setups of the capability as

well as the current workload of the setup into account

(see 2). This consideration is necessary due to the im-

pact of numbers of machines and numbers of setups

to the bucket size. This means, more possible setups

should lead to larger buckets, while more machines

should lead to smaller buckets. As deﬁned in equa-

tion 3 we determine the bucket minimum by taking

the smaller number from scope limit and setup limit.

scope

= sbt

− s ft

(1)

setup

= f ·

· w

(2)

bucket

= min(l

scope

setup

) (3)

3.3 Procedure to Create, Modify or

Dissolve Buckets

As mentioned before, buckets are virtual elements.

The bucket manager creates, modiﬁes or dissolves

buckets event-based when new operations occur and

have to be assigned to a bucket. At the beginning, all

operations of the production orders are added to the

list of unassigned operations. The procedure (shown

in Figure 2) repeats itself as long as unassigned oper-

ations exits.

Figure 2: Procedure to assign operations to buckets.

Firstly, the procedure selects the operation with

the highest priority from the list of unassigned op-

erations. If any unassigned operation exits, the pro-

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

364

cedure selects all buckets from the list of buckets re-

quiring the same setup as the operation. After select-

ing the buckets, the procedure loops through the these

buckets prioritized by the earliest start and calculates

whether the operation ﬁts inside the current bucket or

not. The operation will ﬁt inside this bucket if the

sum of the duration of all the bucket’s operations in-

cluding the new operation is lower or equal than the

dynamically calculated limit of the bucket (see 4).

bucket

≤



∑

o∈O

d(o)

+ d

unassigned operation



(4)

If this is the case, the operation will be added to

the bucket. If no suitable bucket can be found or

the bucket size of all found buckets is exceeded, the

bucket manager creates a new bucket, assigns the op-

eration to the bucket and schedules the bucket at any

of the capable machines. After creating a new bucket,

all other buckets with the same setup and an earliest

start later than the earliest start of the newly created

bucket dissolve into their operations. These opera-

tions are rescheduled during the next loop of the pro-

cedure.

3.4 The Bucket Life-cycle

The scheduling mechanism schedules the bucket as

soon as it is created. After assigning a bucket to a

machine, the bucket remains in the planning queue

in front of the machine. The machine picks the next

bucket from the planning queue using the least slack

time (LST) rule. From all due date based rules, LST

is the rule best known for achieving high timeliness

and high throughput (Kannan and Lyman, 1994). Of

course LST can be replaced by any other priority rule,

but this contribution does not consider other rules.

Our approach includes the setup time in the calcula-

tion of the LST. All operations are queued regardless

of whether their preconditions have been met or not.

It is likely that a bucket contains operations that are

not ready to be processed as their materials are not

yet in stock or preceding operations of the same pro-

duction order are not yet completed. Until the bucket

is ﬁxed, new operations can be added and removed

or the bucket can be dissolved. But at some point a

bucket has to be ﬁxed, so that no operation can be

added or removed anymore. In our scenario we ﬁx

the bucket when it is considered to be the next bucket

to be processed. We achieve this by giving the bucket

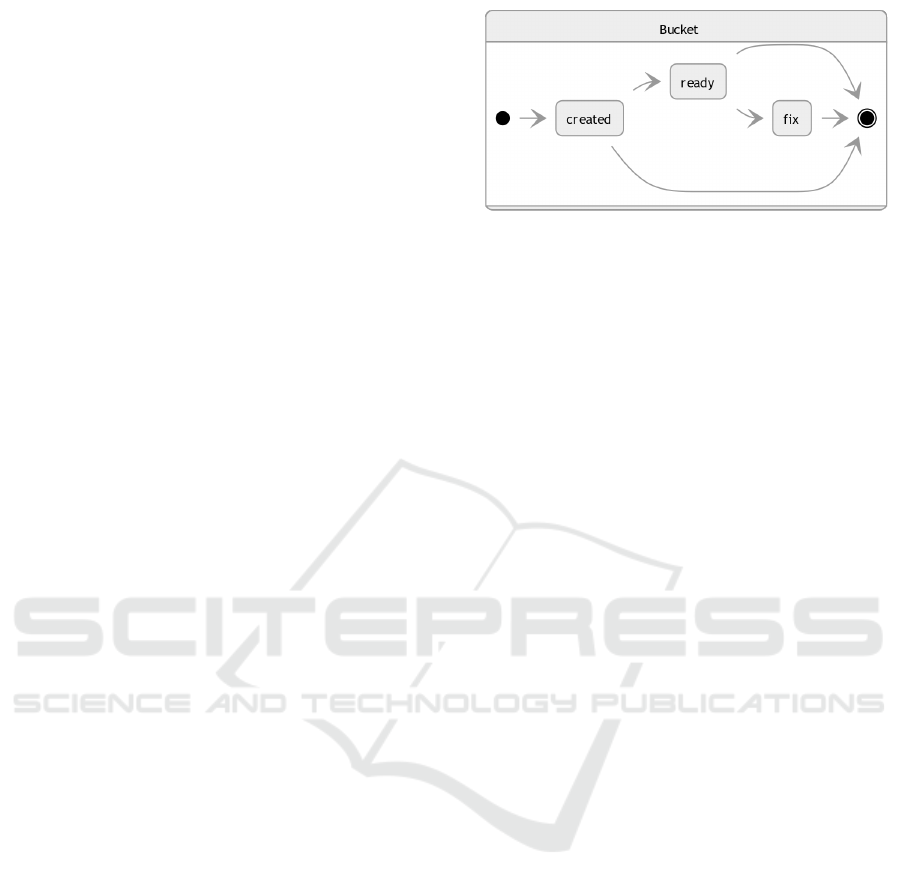
three states. Figure 3 shows all three states of the

bucket and the transitions between them.

If at least one operation of the bucket receives ma-

terial and the preceding operation is completed, we

set the state of the operation and the bucket to ready.

Once setting the bucket ready, we enable the machine

Figure 3: The state transition of a bucket.

to select the bucket from the planning queue in front

of the machine. At this time, new operations can still

be inserted into the bucket. The bucket reaches the

state ﬁx when the machine selects the bucket as the

next bucket to be processed. At that moment, all op-

erations of the bucket without satisﬁed preconditions

are sent back to the bucket manager and trigger the

procedure in Figure 2 to ﬁnd or create a new bucket. It

is not possible to insert new operations into the bucket

in state ﬁx. Anyway, it is possible that the bucket will

be dissolved if the bucket is not yet set to ﬁx.

After the machine chooses the bucket and sets its

state to ﬁx, the machine organizes the processing of

the operations of the bucket. In general the operations

in the bucket are unsorted. However, the operations

can be processed according to any priority rule. For

our empirical study we apply the LST.

4 EXPERIMENTAL RESULTS

4.1 General Assumptions

We implemented the dynamic lot sizing approach into

our agent-based simulation of a self-organized pro-

duction (described in detail at (Munkelt and Krockert,

2018)) and compared it with an exhaustive heuristic

based on LST. The exhaustive heuristic processes all

operations of the machine queue sequentially, which

are matching the currently equipped setup and having

all preconditions satisﬁed. Only after all operations

for the matching setup were processed, the machine

decides for which operation to set-up next, prioritized

by the LST.

For our simulation model, we assume the follow-

ing simulation parameters. In order to test our dy-

namical lot sizing approach, our production runs for

two weeks, 24 hours a day. During this time, we gen-

erate new sales orders for different products with a

product structure list with a maximum depth of three

levels and at least 2 operations per material. During

the simulation of the production, new sales orders ar-

Dynamic Lot Sizing in a Self-organizing Production

365

Table 4: Test scenario for bucket.

Exhaustive Heuristic Dynamic Lot Sizing Differences

Production

Model

Setup

Model

Timeliness

Throughput

time in min

Setup

time

Timeliness

Throughput

time in min

Setup

time

∆ Timeliness

∆ Throughput

time

∆ Setup

time

Model A

Small 100.0% 274 26.8% 95.4% 259 20.8% -4.8% -5.8% -28.8%

Medium 76.8% 746 31.6% 76.8% 610 28.0% ± 0.0% -22.1% -12.9%

Large 22.2% 1274 35.6% 58.9% 772 30.6% +62.4% -61.7% -16.3%

Model B

Small 100.0% 277 29.0% 100.0% 259 19.3% ± 0.0% -6.8% -50.3%

Medium 100.0% 475 39.2% 99.7% 454 28.4% -0.3% -4.6% -38.0%

Large 69.6% 901 44.1% 91,5% 803 29.9% +23.9% -12.2% -47.5%

rive continuously at the production. The inter-arrival

time of customer orders is exponentially distributed as

apfel and Braune, 2005) and (Ko

sturiak and Gre-

gor, 1995) suggest. We choose an inter-arrival time

based on the available capacity to simulate a well uti-

lized production and not cause an overload. There-

fore, new orders arrive approximately every 40 min-

utes at the production model ”A” and every 25 min-

utes at the production model ”B”. To enable one order

overtake another order, the delivery date is evenly dis-

tributed in an interval of 12 hours with an average of

36 hours. To simulate disturbances in the production

process and examine the ﬂexibility of our approach,

we vary the processing times of the operations. The

processing times are distributed log-normally. Trans-

portation times are not considered yet, but can be rep-

resented by an additional operation assigned to the

material. Starting with an empty production, the pro-

duction reaches its steady state after approximately 24

hours in all simulated models. In addition we add an-

other 24 hours before we start the measurement of the

KPIs. For the constant bucket factor we determined

a value of 960 by experiments for all our production

models. Table 5 summarizes the simulation parame-

ters.

4.2 Simulation Results

The simulation results are shown in Table 4 and

demonstrate the superiority of the dynamical lot siz-

ing over the exhaustive heuristic for the empirically

tested production models. The dynamic lot sizing out-

performs the exhaustive heuristic especially when the

production model becomes more complex by consid-

ering more machines and more setups. The timeliness

of the small to medium sized setup models decreases

slightly for the ﬁrst tested production model, at the

same time the model combination reduces the setup

time by 30%. The setup times in general were re-

duced by 30-50% for all simulated models. The rea-

son is, that the exhaustive heuristic schedules oper-

ations to all machines equally and therefore the ma-

chines permanently switch between various setups. In

contrast, the dynamic lot sizing groups similar oper-

ations and enforces buckets to be processed on one

machine with a suitable setup. Due to the lower setup

time, the machine has more capacity to process opera-

tions. This leads to an increased adherence to delivery

dates indicated by a higher timeliness, while the re-

duced throughput times indicates a more ﬂexible and

robust scheduling.

Table 5: Simulation parameters.

Value Unit Description

14(3) days simulation end time (with settling time)

32 hours release time for production orders

36 hours average time from order placement to delivery

25 minutes average inter-arrival time of new products (Model A)

40 minutes average inter-arrival time of new products (Model B)

20 % deviation of operation’s expected processing time

960 minutes bucket factor to estimate maximum bucket size

5 CONCLUSION

The target of our research was to decrease setup time

in a highly diverse production characterized by un-

certainty. For this purpose, we developed a concept to

non-exhaustively group operations requiring the same

setup. We developed an algorithm for dynamic lot siz-

ing and applied the algorithm to our agent based sim-

ulation using two different production models. Then,

we simulated a two week production cycle and were

able to prove the viability of our approach. In our

simulation model, we were able to reduce throughput

times, the timeliness of sales orders and the average

setup times, while completing the same amount of or-

ders. The results also show that our approach per-

forms excellent with both production models while

we are able to maintain the ﬂexibility and robustness,

although the processing times of the operations devi-

ate. The only trade off is currently, that we have to

experimentally determine the ”bucket factor”. In the

future, we want to investigate further possibilities to

dynamically adapt this factor by taking environmen-

tal conditions into account, i. e. the current workload

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

366

of our machines, the average duration of the transi-

tion time for operations of one setup and the times of

releasing buckets into the production. To gain more

general results, we want to investigate further sim-

ulation parameters like different setup distributions,

more divers variants of our production model and dy-

namic generated product structures. We are also look-

ing forward to apply our approach to real world sce-

narios of the companies we are cooperating with.

ACKNOWLEDGEMENTS

The authors acknowledge the ﬁnancial support by

the German Federal Ministry of Education and Re-

search within the funding program ”Forschung an

Fachhochschulen” (contract number: 13FH133PX8).

REFERENCES

Brennan, R. W. (1995). Modeling and analysis of manufac-

turing systems. isbn 0-417-51418-7 [pp.461]. Inter-

national Journal of Computer Integrated Manufactur-

ing, 8(2):155–156.

Domschke, W., Scholl, A., and Voß, S. (1997). Produc-

tion planning: aspects of industrial engineering (Pro-

duktionsplanung: Ablauforganisatorische Aspekte).

Springer-Lehrbuch. Springer, Berlin, 2.,

uberarb. und

erw. auﬂ. edition.

Egilmez, G., Mese, E. M., Erenay, B., and S

uer, G. A.

(2016). Group scheduling in a cellular manufactur-

ing shop to minimise total tardiness and nt: a compar-

ative genetic algorithm and mathematical modelling

approach. International Journal of Services and Op-

erations Management, 24(1):125.

Frazier, G. V. (1996). An evaluation of group scheduling

heuristics in a ﬂow-line manufacturing cell. Inter-

national Journal of Production Research, 34(4):959–

976.

Garey, M. R., Johnson, D. S., and Sethi, R. (1976).

The complexity of ﬂowshop and jobshop scheduling.

Mathematics of Operations Research, 1(2):117–129.

Gombinski, J. (1967). Group technology - an introduction.

Production Engineer, 46(9):557–564.

Grabot, B. and Geneste, L. (1994). Dispatching rules in

scheduling: a fuzzy approach. International Journal

of Production Research, 32(4):903–915.

Ham, I., Hitomi, K., and Yoshida, T. (1985). Group technol-

ogy: Applications to production management. Inter-

national series in management science/operations re-

search. Kluwer-Nijhoff, Boston.

Herrmann, F. (2011). Operational planning in IT systems

for production planning and control: (Operative Pla-

nung in IT-Systemen f

ur die Produktionsplanung und

-steuerung). Vieweg+Teubner, Wiesbaden.

Kannan, V. R. and Lyman, S. B. (1994). Impact of family-

based scheduling on transfer batches in a job shop

manufacturing cell. International Journal of Produc-

tion Research, 32(12):2777–2794.

Kim, S. C. and Bobrowski, P. M. (1994). Impact of

sequence-dependent setup time on job shop schedul-

ing performance. International Journal of Production

Research, 32(7):1503–1520.

Klausnitzer, A., Neufeld, J. S., and Buscher, U. (2017).

Scheduling dynamic job shop manufacturing cells

with family setup times: a simulation study. U. Lo-

gist. Res.

sturiak, J. and Gregor, M., editors (1995). Simulation of

production systems (Simulation von Produktionssyste-

men). Springer Vienna, Vienna.

Kusiak, A. (1987). The generalized group technology con-

cept. International Journal of Production Research,

25(4):561–569.

M. M. Orta-Lozano and B. Villarreal (2015). Achieving

competitiveness through setup time reduction. In 2015

International Conference on Industrial Engineering

and Operations Management (IEOM), pages 1–7.

Munkelt, T. and Krockert, M. (2018). Agent-based self-

organization versus central production planning. In

2018 Winter Simulation Conference (WSC), pages

3241–3251, [Piscataway, NJ]. IEEE.

Ng, C. T., Cheng, T. C. E., Janiak, A., and Kovalyov, M. Y.

(2005). Group scheduling with controllable setup and

processing times: Minimizing total weighted comple-

tion time. Annals of Operations Research, 133(1-

4):163–174.

Ruben, R. A., Mosier, C. T., and Mahmoodi, F. (1993). A

comprehensive analysis of group scheduling heuris-

tics in a job shop cell. International Journal of Pro-

duction Research, 31(6):1343–1369.

Spence, A. M. and Porteus, E. L. (1987). Setup reduction

and increased effective capacity. Management Sci-

ence, 33(10):1291–1301.

van der Zee, D.-J., Gaalman, G. J., and Nomden, G.

(2011). Family based dispatching in manufacturing

networks. International Journal of Production Re-

search, 49(23):7059–7084.

apfel, G. (1982). Production management (Produk-

tionswirtschaft). De-Gruyter-Lehrbuch. de Gruyter,

Berlin.

apfel, G. and Braune, R. (2005). Modern heuristics of pro-

duction planning: (Moderne Heuristiken der Produk-

tionsplanung). WiSo-Kurzlehrb

ucher Reihe Betrieb-

swirtschaft. Vahlen, Munich.

Dynamic Lot Sizing in a Self-organizing Production

367