A Novel Approach for Experimental Earthquake Engineering

Utilizing Mirror Reflections of Point Clouds Collected by Laser

Scanner

Shakhzod Takhirov

, Mukhady Israilov

and Sultan Kudratov

Department of Civil and Environmental Engineering, University of California, Berkeley, U.S.A.

Joint Research Institute of Russian Academy of Sciences (KNII-RAN), Grozny, Russian Federation

Department of Information Technologies, Tashkent University of Information Technologies, Tashkent, Uzbekistan

Keywords: Laser Scanning, Point Cloud, Experimental Earthquake Engineering, Mirror Reflection, 4D Surface Tracking,

Surface Deformation.

Abstract: A laser scanner is an optical instrument that emits laser beams toward objects surrounding the scanner and

measures the location of the objects’ points in space. As a result, it collects the so-called point clouds. In

experimental earthquake engineering, the laser scanners have been used in many applications. In quasi-static

testing, they used for four-dimensional tracking of the test specimen's condition in three spatial coordinates

and time. When a single scanner is used, the object's rear surface is in shadow zone and as such, the points of

the rear surface are not collected. To acquire the point cloud of the object's rear side two commonly used

options are utilized. In Option 1, several scanners working in parallel can be deployed. In Option 2, the same

scanner can be moved to other positions to cover the shadow zones. Option 1 represents an expensive option

that requires an investment in two or more scanners, finding a way of triggering them simultaneously, and

time required for registration of the point clouds collected by several scanners. The main shortcoming of

Option 2 is that is does not allow simultaneous scans from both sides and registration of the laser scans from

many different points can be time consuming. To overcome shortcomings of these two options, this paper

introduces a novel approach (Option 3) of using several mirrors strategically placed in respect to a single

scanner to cover the shadow zones with a single scanner and from the same position. To ensure cost-

effectiveness of the approach, this research was focused on the utilization of affordable and commonly used

rear-reflective mirrors. This paper investigates the point clouds obtained from the mirror reflections and

quantifies the quality of these data by estimating accuracy and reliability of the reflected point cloud data.

The theoretical estimates were verified by laser scanning of sample test specimens.

1 INTRODUCTION

A laser scanner is an optical instrument that emits

laser beams toward objects surrounding the scanner

and measures the duration of the time-of-flight (TOF)

of the laser beams that are reflected back. The

distance to the object is computed by multiplying this

duration by the speed of light in the air. Obviously,

only the points of the object’s surface visible from the

location of the scanner will be collected. The object’s

rear side is not visible, and this will result in a shadow

zone in the point cloud where the points cannot be

collected from this particular location of the laser

https://orcid.org/0000-0002-4396-7946

https://orcid.org/0000-0001-9650-4331

scanner. Situations where a reflective surface of any

kind is present in close proximity to the laser scanner

are quite common as presented in Figure 1. In this

case, the laser acquires the points representing a rear

portion of the object that would not be detected by a

laser scanner otherwise. This paper investigates the

point clouds obtained from the mirror reflections and

quantifies the quality of these data by estimating

accuracy and reliability of the reflected point cloud

data.

Takhirov, S., Israilov, M. and Kudratov, S.

A Novel Approach for Experimental Earthquake Engineering Utilizing Mirror Reﬂections of Point Clouds Collected by Laser Scanner.

DOI: 10.5220/0010301500810087

In Proceedings of the 9th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2021), pages 81-87

ISBN: 978-989-758-492-3

Figure 1: Laser scanning next to a mirror at a department

store (point cloud).

2 MOTIVATION

In experimental earthquake engineering the laser

scanners have been used in many applications (see

Takhirov, 2010; Mosalam, Takhirov, and Hashemi,

2009; Mosalam, Takhirov, and Park, 2014, as

representative examples). It is used for four-

dimensional tracking of the test specimen's condition

in three spatial coordinates and time. When a single

scanner is used, the object's rear surface is in shadow

zone and the points of the rear surface are not

collected. To acquire the point cloud of the object's

rear side two options can be used. In Option 1, several

scanners working in parallel can be deployed. In

Option 2, the same scanner can be moved to other

positions to cover the shadow zones. Option 1 is

expensive as it requires an investment in two or more

scanners, finding a way of triggering them

simultaneously, and a registration of the point clouds

collected by several scanners. The main shortcoming

of Option 2 is that it does not allow simultaneous

scans from both sides, and a registration of the laser

scans from many different points can be time

consuming. This paper introduces a novel approach

of using several mirrors strategically placed in respect

to a single scanner to cover the shadow zones with a

single scanner and from the same position.

3 GENERAL COMMENTS

ABOUT THE LIGHT

REFLECTION PROBLEM

For simplicity, let us assume that the coordinate

system is selected in such a way that the mirror is

located in the horizontal plane. We will assume that

the imperfections of the mirror are negligible and as

such, the incident and the reflected rays remain in the

same plane as presented in Figure 2.

Figure 2: Trajectories of incident beam and beam reflected

from horizontal surface remain in the same plane.

One of the main principles in optics is that the

incident and reflected angles will be the same in

respect to the normal of the plane from which the

reflection occurs (Lekner, 1987). Therefore, all

trajectories of the incident and reflected laser beams

will be in a plane that contains the focal center of the

scanner (emitting point) and the location of the point

measured by the laser scanner. As discussed above

this plane is orthogonal to the plane of the mirror.

4 EXPERIMENTAL SETUP AND

SUBSETS OF COLLECTED

POINT CLOUD

The quality of the reflected point cloud was

investigated in the following experimental setup.

Several tinted glass globes, two prismatic shapes (one

wooden block and one cardboard box) and several

high-definition laser targets (HDLT) were

strategically placed inside an experimental room. The

laser scanner was installed in such a way that all

objects were visible from the scanner’s location and

were visible in the mirror’s reflection. To minimize

the effect of the reflectivity of the shiny glass surface,

the globes were spray painted with a flat grey paint.

The mirror’s location in space was identified by using

three HDLTs that are commonly used for stitching the

laser scans. In addition, three HDLTs were placed on

the walls of the room. Twelve targets were placed on

a large piece of thick plywood. Special plywood with

a high flatness tolerance was selected for this purpose.

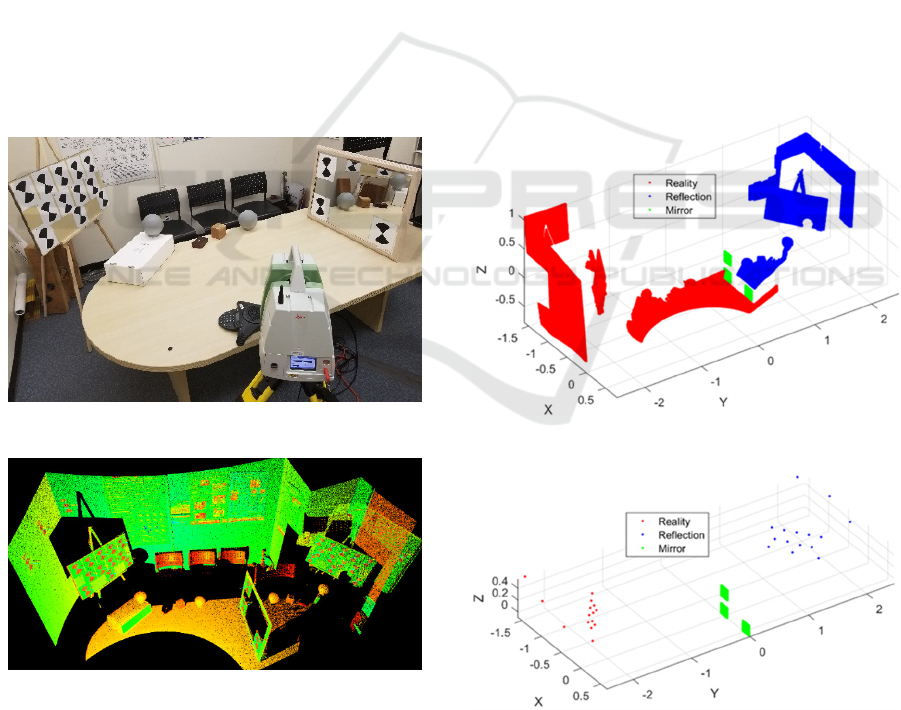
A photo of the experimental setup is presented in

Figure 3. The corresponding point cloud is presented

in Figure 4. The scans were performed with Scan

PHOTOPTICS 2021 - 9th International Conference on Photonics, Optics and Laser Technology

Station C10 (Leica Geosystems AG, 2011), Scan

Station P40 (Leica Geosystems AG 2019), both from

Leica Geosystems, Focus S-350 from FARO

Technologies Inc (FARO Technologies Inc., 2020)

and TX6 scanner form Trimble (Trimble, 2016). For

the purpose of this paper, the results for one of the

scanners (namely, Scan Station C10) are discussed in

more detail.

It is worth noting that usage of the HDLTs was

crucial for achieving the objectives of the paper.

Earlier it was observed that the mid-range (up to 200

m) laser scanners from Leica Geosystems produce a

noisier point cloud than a close-range high-accuracy

laser scanner (Takhirov, 2010). Nevertheless,

averaging the point cloud brings it much closer to the

actual surface. In addition, it was shown that while

the nominal accuracy of individual point cloud

acquisition is ±6 mm at 50 m range (Leica

Geosystems AG, 2011 and 2019) the accuracy of

HDLT’s acquisition is less than 1 mm (Takhirov,

2008). The high accuracy of the flat black and white

geometric patterns similar to the HDLTs used in this

paper was reported earlier by many other authors (see

Janßen et al, 2019 as a representative example).

Figure 3: Photo of experimental setup.

Figure 4: Corresponding point cloud.

The initial data manipulation was conducted in

Cyclone (Leica Geosystems AG, 2018). The acquired

point cloud was separated in three subsets. First, the

subset consisting of the point cloud excluding the

mirror reflection was separated. It was called

‘Reality’. Second, the subset consisting of the point

cloud behind the mirror surface was separated. It was

called ‘Reflection’. Third, the subset of the point

cloud corresponding to the HDLTs on the mirror’s

front surface was separated. It was called ‘Mirror’. To

simplify the data manipulation, the coordinate system

of the point cloud was changed in Cyclone [10] to

have all the vertices of the mirror’s targets in the plane

Y=0. After all these preparations, the subsets were

exported as ASCII files to be manipulated in the

Matlab [MathWorks, 2016] environment. All subsets

are presented in Figure 5. It was expected that a

geometric transformation corresponding to the mirror

reflection would result in consistent point clouds of

the objects with actual surfaces completed by

reflected point clouds. To improve the accuracy of

mirror transformation vertices of the high-definition

targets were used. The targets and their locations in

respect to the mirror are presented in Figure 6.

In Figure 5 and Figure 6, the points related to

Reality, Reflection and Mirror are presented in red,

blue and green colors, respectively.

Figure 5: Point clouds.

Figure 6: Vertices of targets.

A Novel Approach for Experimental Earthquake Engineering Utilizing Mirror Reﬂections of Point Clouds Collected by Laser Scanner

5 GEOMETRIC

TRANSFORMATION USED

FOR THE REGISTRATION OF

REAL AND REFLECTED

CLOUDS

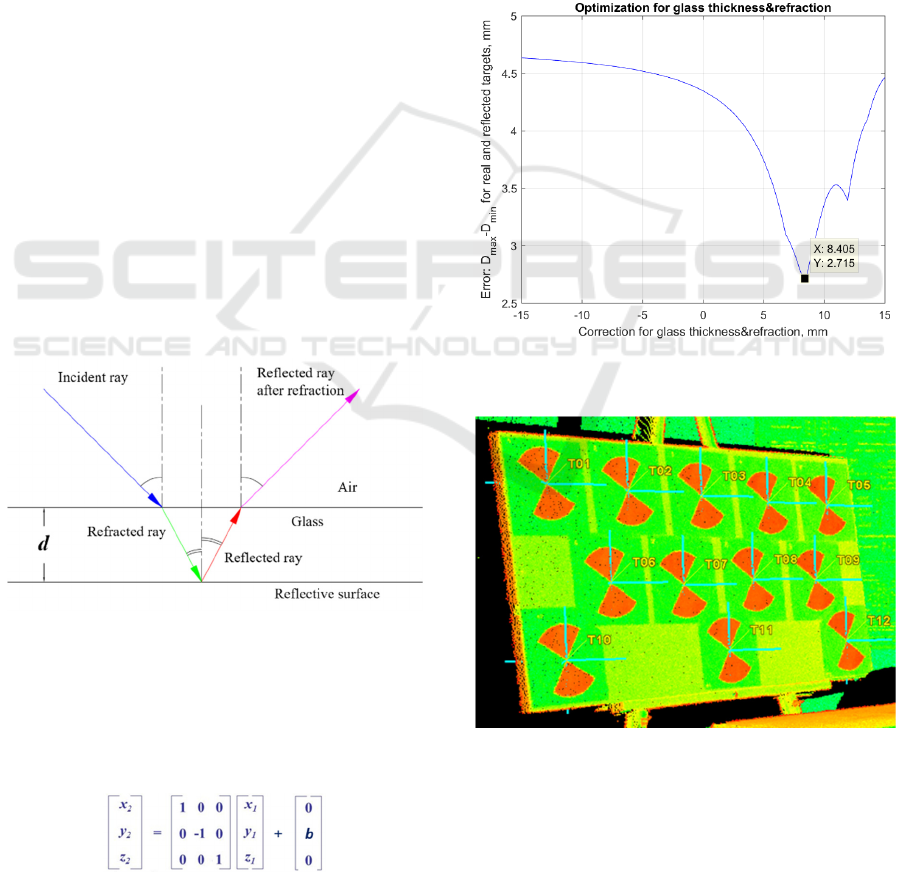
The mirror transformation of the point clouds based

on the location of the front surface of the mirror

resulted in a large error between the real and reflected

targets. The error related to the assumption that the

reflective surface is located on the front side of the

mirror. In reality, consumer grade mirrors are

manufactured as a large piece of glass with the

reflective surface on its rear side as presented in

Figure 7. When the laser beam comes into contact

with the front side of the glass it refracts and changes

its direction and velocity of propagation.

Subsequently, the refracted laser beam reflects from

the reflective surface and it refracts again while

exiting the glass layer. Therefore, an offset needs to

be introduced into the geometric transformation that

will account for the thickness of the glass layer, d, and

the refraction of the laser beams in the glass layer. It

is obvious that the offset, b, will depend on the

incidence angle of the incident laser beam. For the

purpose of the paper, this offset was estimated by

minimizing the distance between real and reflected

targets. To this extent, an effective thickness of the

glass that includes the refraction effect was obtained.

Figure 7: Mirror with a glass layer (consumer grade mirror).

The following procedure was used. To obtain a

transformed point cloud of Reflection, (x

, y

, z

), a

mirror geometric transformation was applied to

Reflection point clouds (x

, y

, z

) with an offset

vector of (0, b, 0):

The glass thickness and refraction correction factor,

b, was varied from 15 mm to -15 mm. For each value

of b, the distances between the real and reflected

targets were computed. The maximum variation of

these distances was estimated by subtracting the

minimum value from the maximum value. The result

presented in Figure 8 shows that the smallest error

occurs when b = 8.405 mm. The procedure was used

for the targets in close proximity to the mirror as

shown in Figure 9. This offset value was used in

combination with the mirror transformation to

compare reality and reflection point clouds. The

resultant registration is presented in Figure 10. All

targets in 3D space are shown in Figure 6a and errors

in the target locations are presented in Figure 11.

Figure 8: Minimization of error between real and reflected

targets.

Figure 9: Only HDLTs in close proximity to the mirror were

used for the optimization.

PHOTOPTICS 2021 - 9th International Conference on Photonics, Optics and Laser Technology

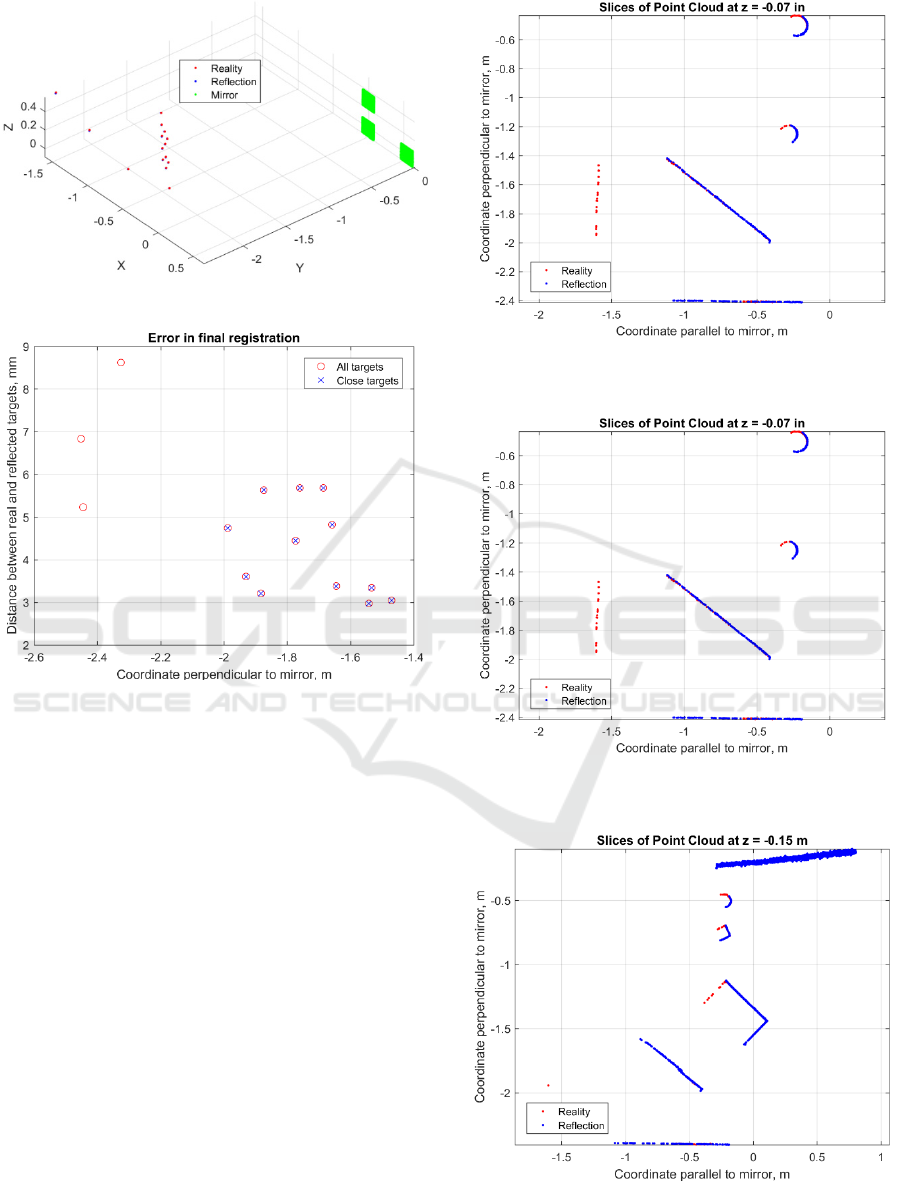
Figure 10: All targets in 3D space.

Figure 11: Distance between real and reflected targets:

close targets have smaller distance.

The final registration resulted in a reflected point

cloud with a reasonably good quality that

complemented the point cloud collected by the

scanner without the mirror. The overall view of the

real and reflected point clouds combined in the final

registration is presented in Figure 12. A horizontal

section of the same registration showing a close

matching of the two globes is presented in Figure 13.

Figure 14 presents another horizontal section of the

registration that shows closely matched point clouds

for both prismatic shapes and a globe. A good

correlation between point clouds of Reality and

Reflection relative to the walls of the room is

presented in Figure 15.

Figure 12: Registration of Reality and Reflection in 3D

space.

Figure 13: Horizontal slice of the registration at Z = -0.07m:

two globes, surface with targets, two walls.

Figure 14: Horizontal slice of the registration at Z = -0.15m:

a globe, two prismatic shapes, surface with targets, a wall.

A Novel Approach for Experimental Earthquake Engineering Utilizing Mirror Reﬂections of Point Clouds Collected by Laser Scanner

Figure 15: Horizontal section at Z = 0.62 m (two walls and

a plywood with targets).

The same approach was used for registering real point

clouds with the ones obtained from the reflection in

the laser scans obtained by the TX6 scanner (Trimble,

2016). A typical experimental setup with the TX6

scanner is presented in Figure 16. Figure 17 presents

the experimental setup with the P40 scanner, which

was also used in this study.

Figure 16: Experimental setup with TX6 scanner.

Figure 17: Experimental setup with P40 scanner.

This approach was also used for registering the real

point clouds with those reflected by the mirror in the

case of the Focus S-350 scanner too. A typical result

showing real and reflected point clouds stitched

together based on this approach are presented in

Figure 18.

Figure 18: Registration of real and reflected point clouds for

globes (Focus S-350 scanner).

This approach allows the registration of reflected

point clouds with the real ones for more complex and

irregular shapes as presented in Figure 19.

Figure 19: Laser scanning of complex shapes by utilizing

the mirror approach.

In addition to a regular scanning of the objects,

this approach can be used for 4D surface tracking of

test specimens during their deformation under a test.

If the position of the scanner is fixed for the duration

of the test, the registration between the reflected and

real point clouds needs to be done only once. The

latter makes the approach quite valuable and cost

effective for this kind of application and does not

require having several scanners to capture the shadow

zones.

The process of registration can be established

and/or mathematically verified by an analytical

formula based on geometry and the physics of

reflection and refraction of laser beams. This portion

of the research is ongoing and will be included in

future publications.

PHOTOPTICS 2021 - 9th International Conference on Photonics, Optics and Laser Technology

6 CONCLUSIONS

This paper investigates the point clouds obtained

from mirror reflections and quantifies the quality of

these data by estimating accuracy and reliability of

the reflected point cloud data. It is shown that the

accuracy of the reflected point cloud will depend on

the thickness of the front glass layer that is usually

present in consumer grade mirrors. In addition,

accuracy depends on the refraction effects and the

angle of incident beams. In the particular case where

the variation of the incident angles is limited, a

simplified correction factor can be introduced that

significantly improves the quality of the final

registration. The correction factor is obtained by

minimizing the error between the high-definition

targets visible with and without the mirror during

optimization of the registration process. In this case,

it is shown that the overall error of the registration is

less than 4 mm, which is acceptable for many

applications. When the deformed shape of a test

specimen is tracked in 3D over time (4D tracking),

the scanner’s position does not change and such, the

registration discussed above needs to be done only

once, let’s say for the very first scan of the specimen’s

undeformed shape.

ACKNOWLEDGEMENTS

Special thanks are due to the Pacific Earthquake

Engineering Research Center (PEER), UC Berkeley

for providing access to Scan Station C10. Also,

special thanks are due to Leica Geosystems for

providing access to Scan Station P40 which was

crucial for achieving the objectives of the paper. The

authors would like to thank FARO Technologies Inc

for providing access to Focus S-350. Special thanks

are due to Sensor Fusion and Monitoring

Technologies, LLC, for providing access to TX6

scanner from Trimble. The active participation of

Dr. Gregory Walsh of Leica Geosystems in

discussion of the project’s objectives is greatly

appreciated. Special thanks are due to Holly Halligan

of UC Berkeley for editing the paper.

REFERENCES

FARO Technologies Inc. (2020). https://www.faro.com/

products/construction-bim/faro-focus/.

Janßen, J., Medic, T., Kuhlmann H., and Holst, C. (2019).

Decreasing the Uncertainty of the Target Center

Estimation at Terrestrial Laser Scanning by Choosing

the Best Algorithm and by Improving the Target

Design. Remote Sensing. 11, 845; doi:10.3390/

rs11070845.

Leica Geosystems AG (2011). Leica ScanStation C10.

https://w3.leica-geosystems.com/downloads123/hds/

hds/ScanStation%20C10/brochures-datasheet/ Leica_

ScanStation_C10_DS_en.pdf.

Leica Geosystems (2018). Cyclone Version 9.2.1.

Leica Geosystems AG (2019). Leica ScanStation P40/P30

- High-Definition 3D Laser Scanning Solution.

https://leica-geosystems.com/en-us/products/laser-

scanners/scanners/leica-scanstation-p40--p30.

Lekner, John (1987). Theory of Reflection, of

Electromagnetic and Particle Waves. Springer. ISBN

9789024734184.

MathWorks (2016). Matlab Version R2016b.

Mosalam, K.M., Takhirov, S.M., and Hashemi, A., 2009.

Seismic Evaluation of 1940s Asymmetric Wood-Frame

Building Using Conventional Measurements and High-

Definition Laser Scanning, Earthquake Engineering

and Structural Dynamics, 38(10), 1175–1197.

Mosalam, K.M., Takhirov, S.M., and Park, S. (2014).

Applications of Laser Scanning to Structures in

Laboratory Tests and Field Surveys. Journal of

Structural Control and Health Monitoring, Volume 21,

Issue 1, pages 115–134, January 2014.

Takhirov, S.M. (2008). Applications of High-Definition

Laser Scanning Technology in Experimental

Earthquake Engineering. Presentation at HDS Leica

User’s Conference.

Takhirov, S.M. (2010). Laser Scanners in Structural

Assessment and FE modeling, 2010 Structures

Congress, Orlando, Florida, May 12-15, 2010.

Trimble (2016). https://geospatial.trimble.com/sites/

geospatial.trimble.com/files/2019-03/Datasheet%20-%

20Trimble%20TX6%20Laser%20Scanner%20-%20

English%20USL%20-%20Screen.pdf.

A Novel Approach for Experimental Earthquake Engineering Utilizing Mirror Reﬂections of Point Clouds Collected by Laser Scanner