Evaluation of Thermal Resistance of Surface-emitting Quantum

Cascade Laser using Structural Function and 3D Thermal Flow

Simulation

Shigeyuki Takagi

, Hirotaka Tanimura

, Tsutomu Kakuno

, Rei Hashimoto

, Kei Kaneko

and Shinji Saito

Department of Electrical and Electronics Engineering, School of Engineering, Tokyo University of Technology,

1404-1 Katakura-cho, Hachioji, Tokyo, Japan

Corporate Manufacturing Engineering Center, Toshiba Corporation, 8 Shinisogo-cho, Isogo,

Yokohama, Kanagawa, Japan

Keywords: Quantum Cascade Lasers, QCLs, Surface-emitting QCL, Photonic Crystal, PhC, Static Method, Structure

Function, Thermal Resistance, Three-dimensional Simulation.

Abstract: We analysed the thermal characteristics of a surface-emitting quantum cascade laser (QCL), which is expected

to increase output and improve beam quality, on the basis of structural functions and 3D thermal flow

simulation. The surface-emitting QCL has a device size of 3 mm x 3 mm and has a photonic crystal for

extracting laser light vertically from the QCL. The structural function indicating the heat capacity and thermal

resistance of the surface-emitting QCL was measured by the static method, and the total thermal resistance

including the mount was about 4.7 K/W. On the other hand, the thermal resistance calculated from the 3D

thermal flow simulation of the surface-emitting QCL was 4.55 K/W, showing the results of the two methods

to be in good agreement. It was shown that the structural function and the 3D simulation are effective for the

thermal analysis of surface-emitting QCLs.

1 INTRODUCTION

Quantum cascade lasers (QCLs) are n-type

semiconductor lasers that can emit laser light in the

infrared region (Faist et al., 1994). Since the

oscillation wavelength of the QCL is in the infrared

region called the fingerprint region of molecules,

many gases can be measured with high sensitivity. In

particular, QCLs are applicable to trace substance

detection and distant gas detection. With such trace

substance detection and distant gas detection, higher

sensitivity is expected upon increasing the output.

Since the amount of laser absorption is measured in

the detection of trace substances, it is necessary to

propagate a large optical path length. Also, in far-

field gas detection, a high-power laser is required

since the weakly reflected light during laser light

propagation is detected.

Regarding high-power lasers, watt-class laser

oscillation has been reported by Evans et al. (Evans et

https://orcid.org/0000-0002-7653-4602

al., 2007). This laser is an end-face emitting-type

laser in which the directions of the laser excitation

and the laser emission coincide with each other. In an

end-face light-emitting laser, the laser beam is excited

by concentrating the current along a narrow current

path called a ridge, and heat dissipation is low.

Moreover, the laser beam is emitted from the narrow

ridge into a wide space, and the rapid expansion of

the beam area causes the deterioration of the beam

quality.

On the other hand, a surface-emitting QCL that

emits laser light in the vertical direction of the device

using a photonic crystal (PhC) has been proposed. By

increasing the area of the excited part called a mesa,

improvements of the beam quality and the heat

dissipation can be expected. In the surface emitting

QCL using PhC, laser oscillation was reported by

Colombelli et al. (Colombelli et al., 2003), and laser

oscillation of 5 W was reported by Wang et al. (Wang

et al., 2019).

Takagi, S., Tanimura, H., Kakuno, T., Hashimoto, R., Kaneko, K. and Saito, S.

Evaluation of Thermal Resistance of Surface-emitting Quantum Cascade Laser using Structural Function and 3D Thermal Flow Simulation.

DOI: 10.5220/0010302700880093

In Proceedings of the 9th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2021), pages 88-93

ISBN: 978-989-758-492-3

It has been reported that the gain of QCLs

improves with decreasing temperature (Gresch et al.,

2009). Therefore, it is important to improve the

cooling of the device, that is, the heat dissipation of

the device in order to increase the laser power. Since

thermal resistance is the ratio of temperature rise to

power input, in this paper we use thermal resistance

as an index of heat dissipation. By reducing the

thermal resistance, high heat dissipation can be

achieved and the laser output power can be improved.

We have reported on the relationship between the

ridge structure and the heat-dissipating structure

using structural functions and simulations in an end-

face light-emitting QCL (Takagi et al., 2019). Laser

oscillations of the surface-emission type QCLs have

been reported, but there are few reports on their

thermal analysis.

So far, we have reported the results of applying the

structural functions and the thermal simulations to the

thermal analysis of end-face emission QCLs. The

structural function was measured by applying the

static method to the surface-emitting QCL, and the

thermal resistance of the device was extracted to be

about 4.7 K/W. On the other hand, thermal analysis

was performed using a 3D simulation model for the

surface emitting QCL, and a thermal resistance of

4.55 K/W was obtained. The thermal resistance

values obtained by the two methods were in good

agreement. It has been shown that both methods are

effective for the thermal analysis of surface-emitting

QCLs.

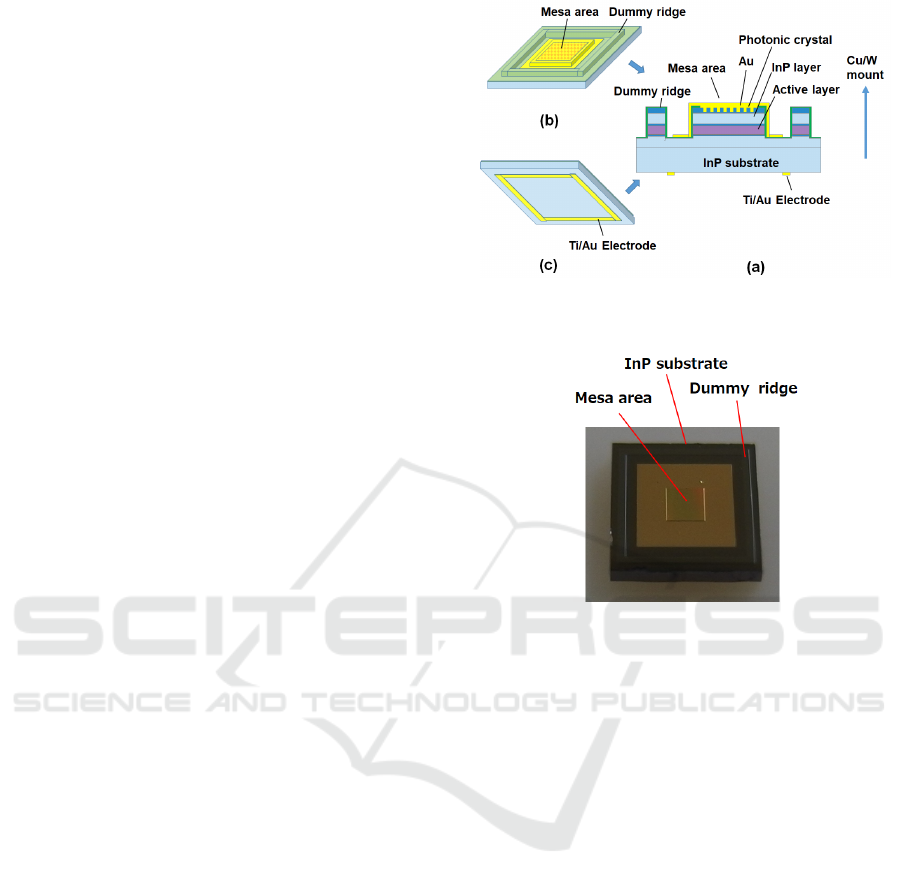
2 SURFACE-EMITTING QCL

The structure of the surface-emitting QCL is shown

in Fig. 1, where (a) is a cross-sectional view, (b) is a

top view, and (c) is a bottom view. A mesa area that

emits laser light and a dummy ridge are formed on an

InP substrate of 600 µm thickness. In the mesa area,

InP layer is formed on the active layer that excites the

laser, a photonic crystal made of InGaAs is formed on

the InP layer, and the photonic crystal is embedded

with AuSn. An Au electrode for current supply is

formed on the opposite side of the InP substrate. The

surface-emitting device has an epi-side-down

structure in which the mesa and dummy ridge sides

are mounted on a Cu/W mount with AuSn solder.

Figure 2 shows a photograph of the surface-

emitting QCL used for the measurement, in which the

mesa and dummy ridge are observed to be formed on

the InP substrate.

Figure 1: Surface emitting QCL. (a) Cross-sectional view,

(b) top view, and (c) bottom view.

Figure 2: Photograph of surface-emitting QCL.

3 MEASUREMENT OF

STRUCTURE FUNCTION

3.1 K-factor Measurement

Dynamic and static methods are used to measure the

thermal resistance of semiconductor devices. The

static method is a method of measuring the thermal

resistance from the voltage/current characteristics at

the time of cooling after heating the device. The

measurement time is short and the reproducibility is

excellent (Székely, 1997).

We have reported a method for measuring the

thermal resistance of an end-face emitting QCL by

the static method. In this study, we applied a static

method to the thermal resistance measurement of the

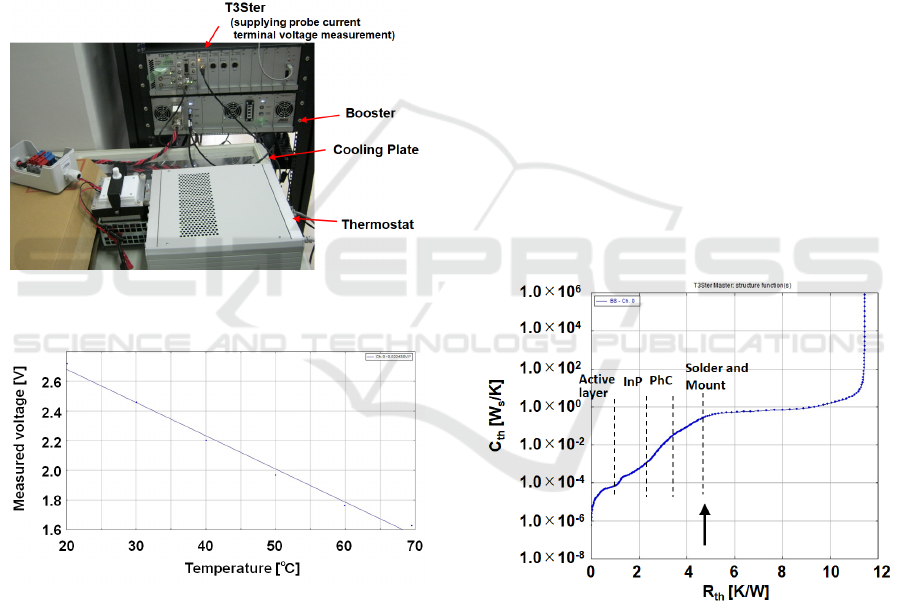
surface-emitting QCL. The T3Ster (Siemens AG)

shown in Fig. 3 was used for the measurement. Since

the total thermal resistance of a semiconductor device

changes with temperature, the temperature change is

proportional to the voltage change at the end of the

device when a constant current is flowing. In the

static method, the voltage change of ΔTSP [mV] is

Evaluation of Thermal Resistance of Surface-emitting Quantum Cascade Laser using Structural Function and 3D Thermal Flow Simulation

measured, and the device temperature change of ΔTj

[K] is calculated using

∆𝑇



=𝐾∙∆𝑇𝑆𝑃 ,

(1)

where K is a coefficient called the K-factor.

The K-factor is required to measure the

temperature of a surface-emitting QCL by the static

method. The surface-emitting QCL was installed in

the thermostat shown in Fig. 3. The thermostat

temperature was changed from 20 °C to 70 °C, and

the K-factor was measured. Figure 4 shows the

measurement result of the K-factor of the surface-

emission QCL. As a result, the K-factor of –0.02243

V/° was obtained.

Figure 3: Measuring Equipment of K-factor and structure

function.

Figure 4: Measurement result of K-factor.

3.2 Measurement of Structure

Function

T3Ster was also used to measure the structural

function by the static method. The QCL mount was

set on the cooling plate of T3Ster. The QCL mount

was cooled to 20 °C, and the QCL device was heated

by supplying about 200 mA of electric current. After

stopping the heating power supply, the QCL

temperature during cooling was measured and the

cooling curve was obtained. Denoting the thermal

resistance as R

and the thermal capacity as C

in the

elements constituting the QCL, the time constant τ

during cooling is expressed by

𝜏=𝐶



∙𝑅



(2)

The time constant τ was extracted from the

inflection point of the cooling curve, and C

and R

were obtained from τ using Eq. (2). In structural

functions graphs, R

is plotted on the horizontal axis

and C

is plotted on the vertical axis (Székely, 1997).

Figure. 5 shows the structural function of the

surface-emitting QCL. As shown in Fig. 1, the

surface-emitting QCL is divided into the mount,

AuSn solder, PhC, InP layer, and the active layer.

From the thermal conductivity and component size, it

is estimated that the structural function divided by

inflection points corresponds to the four QCL

components. In addition, the flat region with a

thermal resistance of 5 K/W or more changes

depending on whether the QCL is attached to a

cooling plate and is considered to be the thermal

resistance between the surface-emitting QCL and the

T3Ster cooling plate. The total thermal resistance of

the surface emitting QCL is estimated to be about 4.7

K/W.

Figure 5: Measurement results of structure function.

4 THERMAL SIMULATION OF

SURFACE-EMITTING QCL

4.1 3D Thermal Flow Simulation

Model

As another method for analysing the thermal

characteristics of the surface-emitting QCL, thermal

PHOTOPTICS 2021 - 9th International Conference on Photonics, Optics and Laser Technology

flow simulation using a 3D model was performed.

The 3D configuration and physical property data of

the surface-emitting QCL were input to the

simulation model. The thermal flow simulation

software FloTHERM (Siemens Product Lifecycle

Management Software Inc.) was used for the

simulator. The simulation is performed using a

natural convection model in which the active is

overheated and natural convection is generated (Ho et

al., 2008). The equation for gas flow is expressed by

𝜕𝜌

𝜕𝑡

∂



𝜌𝑣

𝑥



∂

∂𝜌𝑣

𝑦



∂



𝜌𝑣

𝑧



∂

=0,

(3)

where ρ is density, t is time, and 𝑣

𝑥

, 𝑣

𝑦

, and 𝑣

𝑧

are

velocities in the x, y, and z directions, respectively.

The heat equation is determined as

𝜕𝑢

𝜕𝑡

𝐾

𝜎𝜌



𝜕

𝑢

𝜕𝑥

𝜕

𝑢

𝜕𝑦

𝜕

𝑢

𝜕𝑧



𝜎

𝐹



𝑥, 𝑦,𝑧, 𝑡



(4)

where u is the temperature and is a function of the

position and time. σ is the specific heat, and Κ is the

thermal conductivity. F is the external heating value

per time, and is a function of position and time.

Figure 6 (a) shows the three-dimensional model

of the surface-emitting QCL. The InP substrate with

the mesa area on the lower side is placed on the Cu/W

mount, and the mount is fixed on the Peltier element.

Figure 6 (b) shows the top view of the 3D model as

shown in Fig. 2. The outlines of the InP substrate,

AuSn solder, mesa, dummy ridge, and the Au

electrode on the opposite side of the InP substrate to

the mesa are observed.

Figure 5: 3D thermal flow model (a) and its top view.

In the 3D model, the temperature distributions in

the QCL components were simulated using the

isotropic thermal conductivities as follows. The

thermal conductivity of the Cu/W mount, AuSn

solder, InP, SiO

, Ti, Au, and Cu are 157 W/mK, 59

W/ mK, 68 W/mK, 1.38 W/mK, 21 W/mK, 296

W/mK, and 403 W/mK, respectively. For the PhC in

which Au was embedded, the thermal conductivity

was calculated using the volume ratio of PhC and Au.

In the active layer, thin films of Al

0.638

0.362

As and

0.331

0.669

As were alternately laminated. The

thermal conductivity of the active layer was

calculated by multiplying the film thickness ratio with

InAlAs of 10.0 W/mK (Kim et al., 2002) and InGaAs

of 5.6 W/mK (Adachi, 1985), and was estimated to be

7.5 W/ mK.

The temperature boundary condition is fixed at 0

°C on the mount with a cooling Peltier device, and the

ambient temperature of the surface-emitting QCL is

set at 30 °C. Assuming that the power from the power

supply is input to the active layer, the temperature rise

was calculated by changing the power supplied to the

active layer.

4.2 Simulation Results

The temperature distribution of the surface-emitting

QCL was calculated by changing the input power to

the active layer to 2 and 10 W. Figures 7 (a) and 7 (b)

show the temperature distribution of the surface-

emitting QCL in the central cross section. The Cu/W

mount has high thermal conductivity, and the

temperature in the mount is approximately 0 °C. The

temperature is high in the active layer where power is

applied and in the mesas around it. The maximum

temperature of air is 21.3 °C because the calculation

region is set to the region where the temperature of air

is affected by the temperature of the surface-emission

QCL.

When the input power was increased from 2 to 6

W, as shown in Figs. 7 (a) and (b), the temperature of

the mesa area increased from 8.6 to 45.5 °C. Then, the

input power to the active layer was increased from 0

W to 16 W, and the relationship between the input

power to the active layer and the maximum

temperature of the surface-emission QCL was

calculated. The simulation results are shown in Fig.

8. The maximum temperature of the surface emitting

QCL increases in proportionally to the power input to

the active layer. Figure 8 shows that the maximum

temperature rise at 10 W is 45.5 °C (K), and the

thermal resistance is estimated to be 4.55 K/W.

Evaluation of Thermal Resistance of Surface-emitting Quantum Cascade Laser using Structural Function and 3D Thermal Flow Simulation

Figure 6: Simulation results of thermal flow analysis. (a)

Input power: 2 W, (b) Input power: 10 W.

Figure 7: Relationship between input power and maximum

temperature of the mesa section.

5 DISCUSSION AND

CONCLUSIONS

In the surface-emitting QCL, the Cu/W mount with

the size of 6 x 4 x 2 (t) mm has the maximum heat

capacity of the device. The heat capacity is calculated

to be 0.123 J/K from the density of 17.2 g/cm

and the

specific heat of 0.15 kJ/(kg/K). This is almost the

same as the thermal resistance of the threshold value

at which the heat capacity becomes flat in the

structural function. Therefore, it is reasonable to

estimate the thermal resistance of the structural

function to be about 4.7 K/W.

On the other hand, the thermal resistance is

calculated to be 4.55 K/W from the 3D simulation,

and the thermal resistances obtained by 3D simulation

are in good agreement with that obtained from the

structure function. Therefore, the thermal analyses

using the structural function and 3D simulation are

effective for calculating the thermal characteristics of

the surface-emitting QCL. In addition, thermal

resistance measurement using the structural function

is effective for evaluating the validity of the

calculation model of 3D simulation.

ACKNOWLEDGMENTS

This work was supported by Innovative Science and

Technology Initiative for Security (Grant Number

JPJ004596), ATLA, Japan.

REFERENCES

Faist, J., Capasso, F., Sivco, D. L., Sirtori, C., Hutchinson,

A., & Cho, A. Y. (1994). Quantum cascade laser.

Science, 264, 553-556.

Evans, A., Darvish, S. R., Slivken, S., Nguyen, J., Bai, Y.,

& Razeghi, M. (2007). Buried heterostructure quantum

cascade lasers with high continuous-wave wall plug

efficiency. Appl. Phys. Lett., 91, 071101-1-3.

Colombelli, R., Srinivasan, K., Troccoli, M., Painter, O.,

Gmachl, C. F., Tennant, D. F., Sergent, A. M., Sivco,

D. L., Cho, A. Y., & Capasso, F. (2003). Quantum

cascade surface-emitting photonic crystal laser.

Science, 302, 1374–1377.

Wang, Z., Liang., Y., Meng, B., Sun., Y-T., Omanakttan,

G., Gini, E., Beck, M., Ilia, S., Lourdudoss, S., Faist, J.,

Scalari, G. (2019). Large area photonic crystal quantum

cascade laser with 5 W surface-emitting power. Opt.

Express, 27, 22708–22716.

Gresch, T., Faist, J., & Giovannini, M. (2009). Gain

measurements in strain-compensated quantum cascade

laser. Appl. Phys. Lett., 94, 161114-1-3.

Takagi, S., Tanimura, H., Kakuno, T., Hashimoto, R., Saito,

S. (2019). Thermal analysis and heat dissipation

improvement for quantum cascade lasers through

experiments, simulations, and structure function. Jpn.

J. Appl. Phys., 58, 091008-1–6.

Székely, V. (1997). A new evaluation method of thermal

transient measurement results. Microelectron. J., 28,

277–292.

Ho, C. J., Chen, M. W., Li, Z. W. (2008). Numerical

simulation of natural convection of nanofluid in a

square enclosure: Effects due to uncertainties of

viscosity and thermal conductivity. Int. J. Heat Mass

Transfer, 51, 4506–4515.

PHOTOPTICS 2021 - 9th International Conference on Photonics, Optics and Laser Technology

Kim, Y. M., Rodwell, M. J. W., Gossard, A. C. (2002).

Thermal characteristics of InP, InAlAs, and AlGaAsSb

metamorphic buffer layers used in

In0.52Al0.48/In0.53Ga0.47As heterojunction bipolar

transistors grown on GaAs substrates. J. Electron.

Mater., 31, 196–199.

Adachi, S. (1985). GaAs, AlAs, and AlxGa1−xAs: Material

parameters for use in research and device applications.

J. Appl. Phys., 58, R1–R29.

Evaluation of Thermal Resistance of Surface-emitting Quantum Cascade Laser using Structural Function and 3D Thermal Flow Simulation