
On the Relevance of Extracting Macro-operators with Non-adjacent
Actions: Does It Matter?
Sandra Castellanos-Paez
a
, Romain Rombourg and Philippe Lalanda
Univ. Grenoble Alpes, CNRS, Grenoble INP, France
Keywords:
Automated Planning, Macro-operators, Learning, Data Mining.
Abstract:
Understanding the role that plays the extraction phase on identifying potential macro candidates to augment a
domain is critical. In this paper, we present a method to analyse the link between extracting macro-operators
from non-adjacent actions and the correctness of (1) the frequency and (2) the number of occurrences per plan.
We carried out experiments using our method on five benchmark domains and three different planners. We
found that extracting macro-operators with only adjacent actions leads to important errors in macro-operator
frequency and occurrences per plan.
1 INTRODUCTION
In AI planning, macros can model system routines. A
macro consists of a sequence of actions that occurs
frequently in solution plans. Once learned, macros
can be re-injected directly into the planning domain.
Thus, the domain benefits from the knowledge ex-
tracted from previous problem solving. The planning
system applies a macro in the same way as a primi-
tive action. However, macros allow jumping into the
search space by building deep and promising states
to reach a goal state. Learning macros from previ-
ously acquired knowledge has proven to be beneficial
for improving a planner’s performance (Botea et al.,
2005b; Coles and Smith, 2007; Chrpa et al., 2014).
Macros have been widely studied to speed-up
planning processes (Newton and Levine, 2010; Dulac
et al., 2013). These approaches consist of two main
phases: extraction and selection. Extraction consists
in identifying, either by using previous knowledge
or by ad-hoc construction, sequences of actions that
could be potential candidates to augment the domain.
The selection phase must find a trade-off between the
benefit expected by adding macros and the additional
cost induced by the branching factor increase.
Literature about macros presents various tech-
niques to deal with the extraction phase, ranging from
simple combination of primitive actions and the use
of chunks of plans to the use of genetic learning algo-
rithms or statistical analyses based on n-grams.
a
https://orcid.org/0000-0002-6241-7974
Understanding the impact of the extraction phase
on the identification of potential macro candidates to
augment a domain is critical. Indeed, through this
phase, the infinite set of possible candidates to be-
come macros passes through a first “filter”. The aim
is to make the set finite while keeping, among that
set, the best possible macros to add to the domain
in order for them to be identified and selected in the
next phase. We are aware that the selection is the
main concern when dealing with macro-operator re-
search. However, lots of selection methods use in-
formation that can be acquired during the extraction
phase (Botea et al., 2005a; Hofmann et al., 2017;
Castellanos-Paez, 2019). For example, in (Botea
et al., 2005a), they present the CA-ED method which
ranks a given macro based on the number of plans
where it occurs (hereafter called support) and the to-
tal number of times it occurs in each plan (hereafter
called number of occurrences). It seems then crucial
to assess the correctness of such information to obtain
better results.
When extracting macro-operators from non-
adjacent actions, the number of actions possibly ig-
nored between two considered actions is called the
gap. In this paper, we investigate if a finite gap
could ensure in most cases that all macro occurrences
are found. More precisely, we analyse the link be-
tween the use of a finite gap when extracting macro-
operators and the correctness of (1) the support and
(2) the number of occurrences per plan. By correct-
ness we mean how close are the computed macro-
operator characteristics (i.e. support and number of
Castellanos-Paez, S., Rombourg, R. and Lalanda, P.
On the Relevance of Extracting Macro-operators with Non-adjacent Actions: Does It Matter?.
DOI: 10.5220/0010305110211029
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 2, pages 1021-1029
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
1021

occurrences) to the ones computed when all macro-
operator occurrences are found. Besides, we anal-
yse the effect of the gap with plans obtained through
three different planners by comparing extraction re-
sults with an infinite gap and a range of finite gaps.
The paper is structured as follows. First, we in-
troduce the concepts of classical planning, macro-
operators and some concepts borrowed from sequen-
tial pattern mining. Then, we present our method to
evaluate the impact of a finite gap on the extraction of
macro-operators. After, we present our results on five
benchmark domains. Finally, we provide a discussion
of the results and a conclusion.
2 BACKGROUND THEORY
We are interested in plan synthesis, a particular form
of planning which takes a description of the world
state, all its known actions and a goal (Ghallab et al.,
2004). As a result, we get an organised set of actions
whose execution makes it possible to solve the plan-
ning task. In this work, we address sequential plan-
ning in the STRIPS framework (Fikes and Nilsson,
1971).
A state is defined as a set of predicates. A planning
task is composed of a planning domain and a planning
problem and the purpose of this task is to find a plan to
solve this problem. A planning domain describes the
world through a set of predicates and a set of planning
operators. A planning problem describes the initial
state of the world and the goal state to be attained.
A planning operator is a triple o = (name(o), pre(o),
effects(o)) where its elements are defined as follows:
• name(o) is in the form name(x
1
, ...,x
n
) where
x
1
, ..., x
n
are the object variable symbols that ap-
pear in o.
• pre(o) is the set of predicates involving the vari-
ables of o and that must be satisfied when o is in-
stantiated.
• effects(o) is the set of literals (i.e. atoms and nega-
tion of atoms) involving the variables of o to be
applied to a state when o is instantiated.
A grounded operator is an instance of a planning op-
erator (i.e. a lifted operator for which variables are
instantiated). A ground operator a is applicable in a
state s if and only if all predicates in the precondi-
tions of a belong to s. A state s
0
is reached from s if
a grounded operator can be applied. Finally, a (solu-
tion) plan π is an ordered sequence of grounded oper-
ators to reach a goal state s
g
from an initial state s
i
.
Macros are based on the idea of composing a se-
quence of primitive operators and viewing the se-
quence as a single operator. For our purposes, we
distinguish two related but different terms: grounded
macros and lifted macros. A grounded macro is re-
lated to a lifted macro as a ground operator is related
to a lifted operator. We use these terms according to
literature common terminology.
In the following, we define a set of concepts
(borrowed from Sequential Pattern Mining (Fournier-
Viger et al., 2017; Han et al., 2011)) necessary for the
understanding of this work.
A sequence database C is a set of pairs < sid, s >,
where sid is a sequence identifier and s is a sequence.
A sequence S
A
= X
1
, X
2
, . . . , X
k
, where X
1
, . . . , X
k
are ground operators, is a sub-sequence of another
sequence S
B
= Y
1
,Y
2
, . . . ,Y
m
, where Y
1
, . . . ,Y
m
are
ground operators, if and only if there exists integers
1 ≤ e
1
< e
2
·· · < ek ≤ m such that X
1
= Y
e
1
, X
2
=
Y
e
2
, . . . , X
k
= Y
e
k
.
The absolute support of a sequence S is the num-
ber of sequences S
i
, in the sequence database C,
where S is a sub-sequence of S
i
. The relative support
of a sequence S is the absolute support of S divided
by the total number of sequences in C. A frequent se-
quence is a sequence whose relative support satisfies
a given relative support threshold. Thereafter, we will
call this threshold minsup.
Besides, notice that a frequent sequence can oc-
cur in several other sequences but not necessarily in a
contiguous fashion, as the definition of sub-sequence
implies. So, we define a gap as the number of op-
erators allowed between two consecutive operators of
a sequence and it can take values in [0, ∞]. A sub-
sequence S = Y
e
1
,Y
e
2
, . . . ,Y
e
k
satisfies a gap constraint
g if ∀i ∈ [2, k], e
i
− e
i−1
≤ g + 1.
3 EVALUATING THE IMPACT OF
A FINITE GAP
In planning, each plan is composed of an ordered se-
quence of grounded operators which in turn are com-
posed of parameters (objects). In Figure 1, we give
an example of plan from the depots
1
domain, denoted
π
1
.
Mining lifted macro-operators (in the following,
macro-operators) from a set of plans requires an ap-
proach that ensures to find the frequent sequences of
operators without a loss of information about their
characteristics. The often expected characteristics for
1
Domain description: https://www.cs.cmu.edu/afs/cs/
project/jair/pub/volume20/long03a-html/node38.html
Domain PDDL definition: https://www.cs.colostate.edu/
meps/aips02data/depots/Strips/Depots.pddl
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
1022

Figure 1: Example plan for depots domain.
each macro-operator m are : the support, i.e. the num-
ber of plans containing at least one occurrence of m,
and the number of occurrences of m in each plan. The
former represents a general view of the frequency of
m. The latter represents a more detailed view of the
use of m through each plan.
In (Castellanos-Paez et al., 2020), we highlighted
the capital role of the gap in the extraction of macro-
operators. In this paper, we analyse the loss of in-
formation when a finite gap is used to extract macro-
operators. More precisely, we analyse the impact on
the correctness of the characteristics computed for
these macros (support, number of occurrences). Also,
we investigate if there is a different impact on correct-
ness when extracting macro-operators from optimal
or sub-optimal plans.
By correctness we mean how close are the com-
puted macro-operator characteristics (i.e. support and
number of occurrences) to the ones computed when
all macro-operator occurrences are found.
3.1 Overview of the Analysis Procedure
Our analysis focused on evaluating the impact of
a finite gap on the correctness of the support and
the number of occurrences. First, we extracted a
reference set of frequent macro-operators, M
re f
and
their characteristics. This reference set is guaran-
teed to be correct since we used the ERA algorithm
(Castellanos-Paez et al., 2020) with a minsup of 0.85,
an infinite maximum length and an infinite gap. By
correct, we mean that all possible occurrences were
found, thus, the computed support and number of oc-
currences are exact. Indeed, the ERA algorithm pro-
duces exhaustive results with the aforementioned gap
and length parameters.
Then, we extracted different sets of macro-
operators by varying the gap parameter. Intuitively,
using a finite gap implies that some occurrences may
be missed by the algorithm. Therefore, a minsup of
0 was used to avoid losing information on the charac-
teristics of macro-operators in the reference set.
Finally, we compared the results of the reference
set (infinite gap) with the results of the sets obtained
by varying the gap parameter. The comparisons were
made by using three different metrics.
Details on the extraction algorithm and the metrics
definition are given in the following sections.
3.2 Extraction Algorithm: ERA
The ERA algorithm mines all macro-operators (re-
gardless of their length or up to a maximum length)
satisfying a frequency threshold and under a gap con-
straint from a set of solution plans. Additionally, for
each macro-operator m, this algorithm yields the fol-
lowing characteristics:
• support [integer]: the number of plans contain-
ing at least one occurrence of m.
• sequence ids [list]: the plan identifiers where m
appears.
• number of occurrences [list]: the number of oc-
currences of m in each plan.
The ERA algorithm checks, for each plan, every sub-
sequence satisfying the gap constraint. If an infinite
gap is used, the algorithm is then guaranteed to find all
macro-operators, satisfying the frequency threshold,
and all their occurrences. Also, macro-operator oc-
currences (even non-adjacent occurrences) registered
by ERA are valid. Indeed, to be registered, an occur-
rence must be composed of grounded operators that
can be moved contiguously in the analysed plan with-
out impacting its final state or impeding its execution.
Finally, if the macro-operator occurrences satisfy the
frequency threshold, a macro-operator is built as a
contiguous sequence of lifted operators.
To illustrate how ERA registers occurrences,
let us consider the plan π
1
in Figure 1 and
a gap parameter of 1. The set of all sub-
sequences of π
1
satisfying the gap constraint of 1
is {(a
1
, a
2
), (a
2
, a
3
), (a
3
, a
4
), (a
1
, a
3
), (a
2
, a
4
)}. If we
focus on the sub-sequence (a
1
, a
3
), ERA will reg-
ister it as a valid occurrence of the macro-operator
lift-load
2
. Indeed, the grounded operators com-
posing that sub-sequence can be moved contigu-
ously in the plan π
1
yielding the modified plan π
0
1
=
ha
1
, a
3
, a
2
, a
4
i, where π
0
1
is executable and leads to the
same final state as π
1
. Notice that gaps are only con-
sidered during the generation of sub-sequences to be
analysed but not when building the macro-operator.
For more details about the mining and the build-
ing of macro-operators in the ERA algorithm, see
(Castellanos-Paez et al., 2020).
2
A hoist lifting a crate and loading it into a truck.
On the Relevance of Extracting Macro-operators with Non-adjacent Actions: Does It Matter?
1023

3.3 Metrics Definition
To compare the results of the reference set (infinite
gap) with the results of the sets obtained by varying
the gap parameter, we defined the following metrics:
The mean support error, Err
supp
, defined in (1):
Err
sup
(g) =
1
|M
re f
|
∑
m∈M
re f
(s(m;∞) − s(m; g)) (1)
represents the mean difference across each macro-
operator m in the reference set M
re f
between the terms
s(m;∞) and s(m;g). The former represents the sup-
port obtained with an infinite gap for a macro m. The
latter represents the supports obtained with a finite
gap g for a macro m. The term |M
re f
| is the number
of macros in the set M
re f
.
The mean relative occurrence error, Err
occ
, de-
fined in (2):
Err
occ
(g) =
1
|M
re f
|
∑
m∈M
re f
o(m;∞) − o(m; g)
o(m;∞)
(2)
represents the mean relative difference across each
macro-operator m in the reference set M
re f
. In (2),
o(m;∞) represents the total number of occurrences
obtained with an infinite gap, and o(m;g) represents
the total number of occurrences obtained with an fi-
nite gap g.
Finally, the total relative occurrence error, Err
tot
defined in (3):
Err
tot
(g) =
∑
m∈M
re f
(o(m;∞) − o(m; g))
∑
m∈M
re f
o(m;∞)
(3)
represents the fraction of occurrences missed when
using a finite gap g.
4 RESULTS
In the following, we show the impact of a finite gap on
the characteristics of the extracted macro-operators.
For this purpose, we used five benchmarks domains,
two sub-optimal planners and one optimal planner.
Keep in mind that this study does not address planner
performance or macro quality. The planner choices
were then solely based on the optimality or sub-
optimality of the plans produced.
4.1 Experimental Setup
To the best of our knowledge, no open plan database is
available. Thus, for each benchmark domain, we gen-
erated a set of 35 distinct problem instances using the
generators
3
from the International Planning Competi-
tion. Then, we solved the problems by using each of
the three planners (Helmert, 2006; Richter and West-
phal, 2014; Helmert and Domshlak, 2011). As a re-
sult, we obtained a total of fifteen sets of solution
plans (each with 35 plans) divided as follows: ten sets
of sub-optimal plans (5 domains times 2 planners) and
five sets of optimal plans (5 domains times one plan-
ner). Indeed, we also investigated the behaviour of the
loss of information when extracting macro-operators
from optimal or sub-optimal plans.
The analysis procedure was carried out on each
one of the fifteen sets of solution plans and the impact
of a finite gap was evaluated for gap values ranging
from 0 to 15. The average plan length was about 30
for the sets of sub-optimal plans and was about 25
for the sets of optimal plans. Experiments were per-
formed on dedicated machine with an Intel Core i7-
4710MQ quad-core CPU clocked at 2.5GHz and with
8GB of RAM. Table 1 presents the different parame-
ters tested.
Table 1: Parameters of the gap evaluation experiment.
Parameter Values tested
Gap 0 - 15
Planner
FastDownward (A* and FF heuristic)
LAMA
LM-Cut
Domain
Barman, Blockworld,
Depots, Rover, Satellite
4.2 Results of the Impact of a Finite
Gap
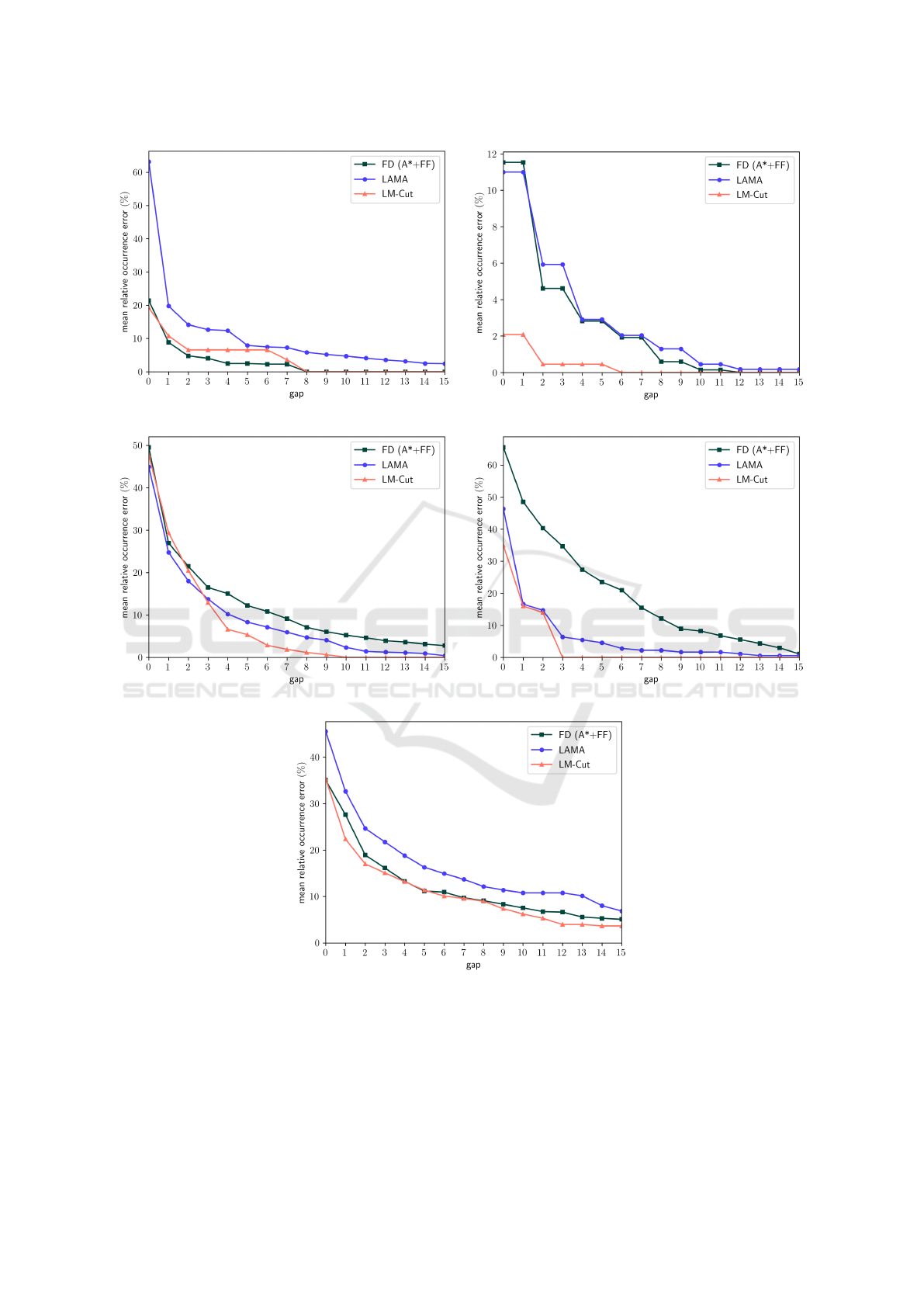
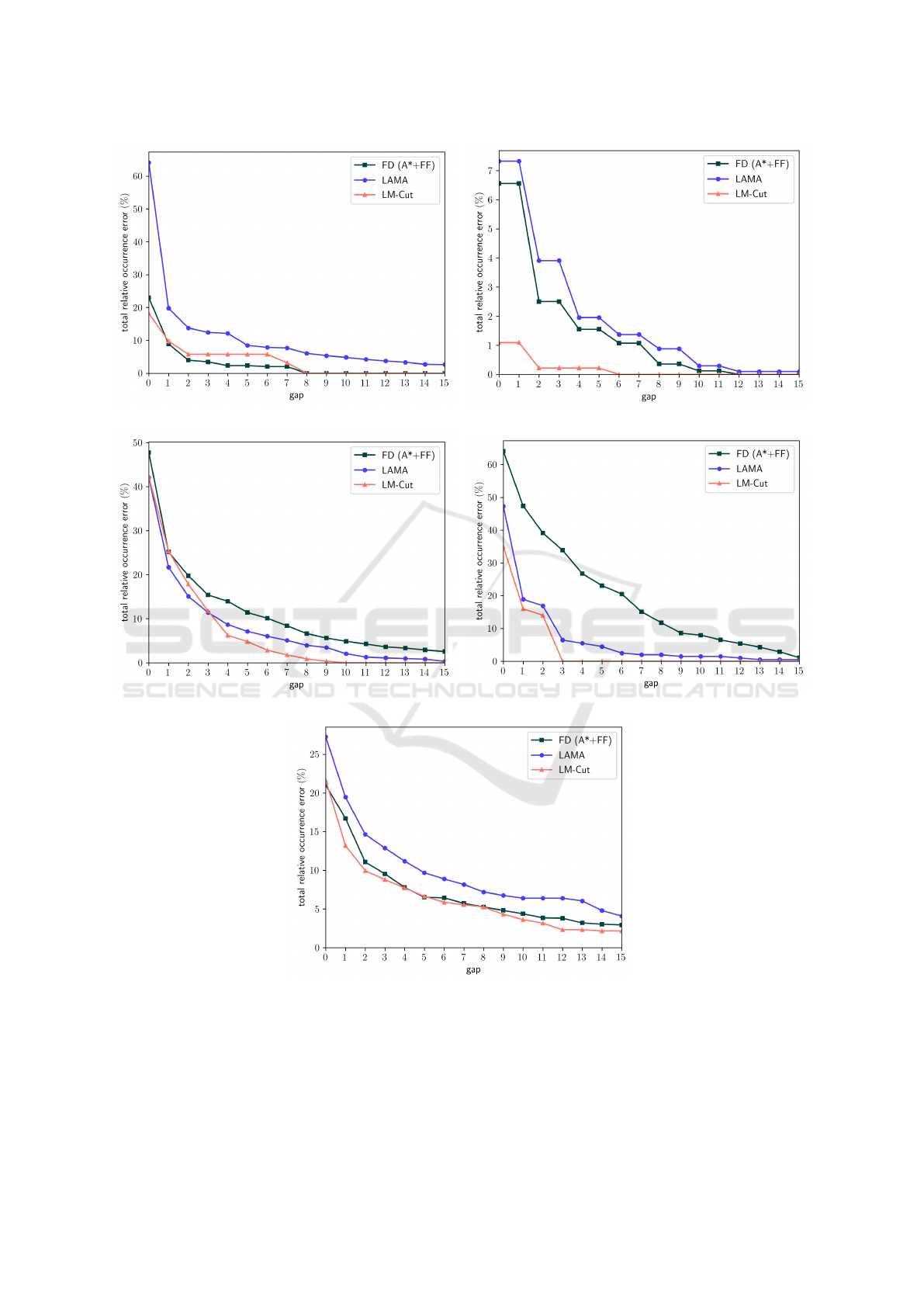
In Figures 2, 3 and 4, for each domain and for each
planner, we present respectively: Err
sup
, Err
occ
and
Err
tot
, as a function of the gap. As expected, we ob-
served that these errors decreased consistently with
the gap for all domains and planners.
We observed across almost all domains that the
errors were less important when using plans ob-
tained with the LM-Cut planner. However, between
FD(A*+FF) and LAMA, there was not a planner that
presented consistently higher errors. Compared to
the other domains, blocksworld showed significantly
lower errors.
Additionally, we present in Table 2, for each do-
main and planner, the errors obtained with a gap value
of 0. And, in Table 3 we show the minimal gap value
required, for all domains and errors, to have an error
value below 5% for all planners.
3
https://bitbucket.org/planning-tools/pddl-generators
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
1024

(a) Barman
(b) Blocksworld
(c) Depots (d) Rover
(e) Satellite
Figure 2: Mean support error. Errors are given in percentage of the plan set.
On the Relevance of Extracting Macro-operators with Non-adjacent Actions: Does It Matter?
1025
(a) Barman
(b) Blocksworld
(c) Depots (d) Rover
(e) Satellite
Figure 3: Mean relative occurrence error.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
1026
(a) Barman
(b) Blocksworld
(c) Depots
(d) Rover
(e) Satellite
Figure 4: Total relative occurrence error.
On the Relevance of Extracting Macro-operators with Non-adjacent Actions: Does It Matter?
1027
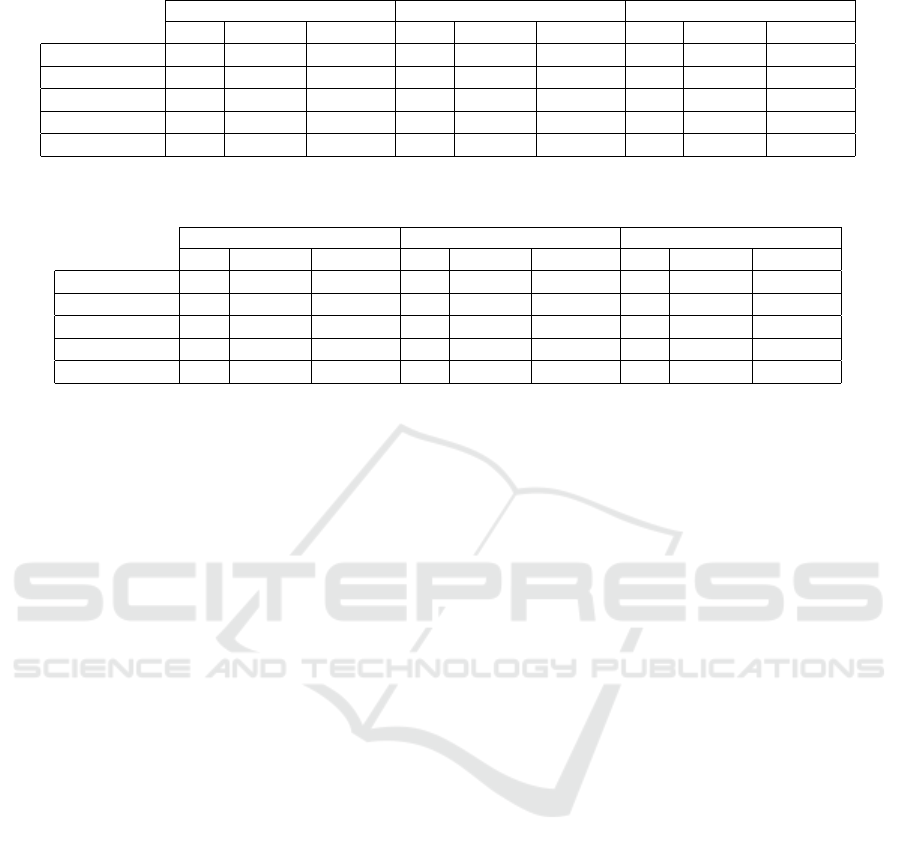
Table 2: Errors for each domain and planner when using a gap value of 0 (extraction made only from contiguous actions).
Err
sup
(%) Err
occ
(%) Err
tot
(%)
FD LAMA LM-Cut FD LAMA LM-Cut FD LAMA LM-Cut
Barman 7.9 56.2 17.8 21.4 63.2 19.3 22.9 64.1 18.2
Blocksworld 5 3.8 1.1 11.5 11 2.1 6.5 7.3 1.1
Depots 25.4 21.5 26.9 49.5 44.9 47.7 47.7 42 42.2
Rover 43.4 21.9 5.7 65.5 46.4 35 64.1 47.3 35
Satellite 27.1 38.9 27.8 35 45.6 35.4 21 27.3 21.7
Table 3: Minimal gap value required to have an error value below 5% for all planners. ’-’ indicates that the error was still
above 5% for a gap of 15.
Err
sup
Err
occ
Err
tot
FD LAMA LM-Cut FD LAMA LM-Cut FD LAMA LM-Cut
Barman 1 5 7 2 10 7 2 10 7
Blocksworld 0 0 0 2 4 0 2 2 0
Depots 4 4 3 11 8 6 10 8 5
Rover 8 1 1 13 6 3 13 5 3
Satellite 4 5 11 - - 12 9 14 9
5 DISCUSSION AND RELATED
WORKS
Our results clearly show that extracting macro-
operators by only considering adjacent groups of ac-
tions (zero gap) leads to high errors (often above
50%!) in terms of support and occurrences for every
domain and planner. Besides, errors are similar for
optimal and sub-optimal plans. Intuitively, one could
think that high gap values would not impact signifi-
cantly the extraction results since two distant opera-
tors should be less related than two close operators.
Indeed, that would be true if the planning system was
focused on accomplishing sequentially disconnected
groups of sub-goals, e.g. preparing and serving a spe-
cific cocktail in barman. However, every plan (even
optimal) can be reordered in hundreds or even thou-
sands of different ways from which only a few corre-
spond to a configuration where all disconnected goals
are accomplished sequentially.
An infinite gap is required to guarantee correct-
ness of the support and the number of occurrences.
However, we showed that a finite and relatively small
gap value (compared to the plan length) yields accept-
able results. We also observed higher gap require-
ments for the satellite and depots domains. It
could be explained by the fact that problems from
these domains often consist in several disconnected
sub-goals e.g. take a specific picture with any satel-
lite or bring a given crate to a given truck.
One could point out that using non-adjacent ac-
tions to generate macro-operators leads to the extrac-
tion of more macros therefore possibly making the se-
lection problem more difficult. However, should we
consider that with gap, more useless macros are ex-
tracted? Or, should we rather consider that without
gap, the most useful macros could be missed? We be-
lieve in the second proposition, the extraction should
never take the risk to rule out possible useful macros.
There are a number of works handling non-
adjacent operators to build macros. Botea et al.
(Botea et al., 2005b) extract macros from solution
graphs of training problems. They enumerate and se-
lect sub-graphs from the solution graphs and build one
macro for each selected sub-graph. They introduce a
k parameter as the maximal number of operators that
can be skipped between the first and the last element
of the sub-graph (we can roughly see a sub-graph as
a sub-sequence). Their handling of the gap does not
allow an exhaustive search and can then miss many
macro-operator occurrences. Also, they set a hard
limit on the upper bound of the maximal length of the
extracted macro-operators. Chrpa et al. (Chrpa et al.,
2014) extract macros by iteratively combining opera-
tors (even non-adjacent) in plans that share some pa-
rameters while keeping the plan valid. However, their
technique is not guaranteed to find all macro-operator
occurrences. In Castellanos-Paez et al. (Castellanos-
Paez et al., 2020), we present a pattern mining in-
spired algorithm to mine lifted macro-operators di-
rectly from a set of plans. Besides, this algorithm can
detect the occurrence of a macro-operator even if the
actions composing it are not adjacent.
To the best of our knowledge, our work is the only one
evaluating the impact of extracting macro-operators
from a set of plans by considering non-adjacent oper-
ators.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
1028

6 CONCLUSIONS
Macro-operators for automated planning are of great
importance to improve performance by using past ex-
periences. Understanding the role that plays the ex-
traction phase on identifying potential macro candi-
dates to augment a domain is critical. In this paper, we
did not address planner performance or macro qual-
ity, however, we answered the question: ”Does con-
sidering non-adjacent actions when extracting macro-
operators matter?”. The answer is yes, and a rela-
tively small gap of 5 to 10 actions can go a long way
in reducing the error in support and number of occur-
rences below five percent. The reader can clearly take
away from this study that when dealing with macro-
operators, we should not only look at adjacent oper-
ators. For future work, we believe that the consid-
eration of these results could be advantageous when
designing new macro-learning methods.
REFERENCES
Botea, A., Enzenberger, M., M
¨
uller, M., and Schaeffer, J.
(2005a). Macro-FF: Improving AI planning with au-
tomatically learned macro-operators. Journal of Arti-
ficial Intelligence Research, 24:581–621.
Botea, A., M
¨
uller, M., and Schaeffer, J. (2005b). Learn-
ing partial-order macros from solutions. In Proceed-
ings of the Fifteenth International Conference on In-
ternational Conference on Automated Planning and
Scheduling, pages 231–240. AAAI Press.
Castellanos-Paez, S. (2019). Learning routines for sequen-
tial decision-making. PhD thesis, Universit
´
e Grenoble
Alpes.
Castellanos-Paez, S., Rombourg, R., and Lalanda, P.
(2020). ERA: extracting planning macro-operators
from adjacent and non-adjacent sequences. In Pacific
Rim Knowledge Acquisition Workshop, PKAW 2020.
Springer.
Chrpa, L., Vallati, M., and McCluskey, T. L. (2014). MUM:
A technique for maximising the utility of macro-
operators by constrained generation and use. In Pro-
ceedings of the Twenty-Fourth International Confer-
ence on Automated Planning and Scheduling.
Coles, A. and Smith, A. (2007). Marvin: A heuristic search
planner with online macro-action learning. Journal of
Artificial Intelligence Research, 28:119–156.
Dulac, A., Pellier, D., Fiorino, H., and Janiszek, D. (2013).
Learning useful macro-actions for planning with n-
grams. In 2013 IEEE 25th International Conference
on Tools with Artificial Intelligence, pages 803–810.
Fikes, R. and Nilsson, N. (1971). STRIPS: A new approach
to the application of theorem proving to problem solv-
ing. Artificial Intelligence, 3-4(2):189–208.
Fournier-Viger, P., Lin, J. C.-W., Kiran, R. U., Koh, Y. S.,
and Thomas, R. (2017). A survey of sequential pat-
tern mining. Data Science and Pattern Recognition,
1(1):54–77.
Ghallab, M., Nau, D., and Traverso, P. (2004). Automated
planning: theory and practice.
Han, J., Pei, J., and Kamber, M. (2011). Data mining: con-
cepts and techniques. Elsevier.
Helmert, M. (2006). The fast downward planning system.
Journal of Artificial Intelligence Research, 26:191–
246.
Helmert, M. and Domshlak, C. (2011). Lm-cut: Optimal
planning with the landmark-cut heuristic. Seventh in-
ternational planning competition (IPC 2011), deter-
ministic part, pages 103–105.
Hofmann, T., Niemueller, T., and Lakemeyer, G. (2017).
Initial results on generating macro actions from a plan
database for planning on autonomous mobile robots.
In Twenty-Seventh International Conference on Auto-
mated Planning and Scheduling.
Newton, M. A. H. and Levine, J. (2010). Implicit learning
of macro-actions for planning. In Proceedings of the
19th European Conference on Artificial Intelligence
(ECAI 2010).
Richter, S. and Westphal, M. (2014). The LAMA planner:
Guiding cost-based anytime planning with landmarks.
CoRR, abs/1401.3839.
On the Relevance of Extracting Macro-operators with Non-adjacent Actions: Does It Matter?
1029
