
Towards Distributed Local Search Through Neighborhood Combinators
Gustavo Ospina and Renaud De Landtsheer
CETIC Research Centre, Charleroi, Belgium
Keywords:
Parallelization, Multi-core, Akka, Local Search, Combinatorial Optimization, OscaR.cbls.
Abstract:
This paper presents an approach for making local search algorithms distributed, to get speed improvements
thanks to the growth both in multi-core hardware and the massive availability of distributed computing power,
notably in the cloud. Local search algorithms rely on the exploration of neighborhoods on a given solution
space model. Our distribution approach relies on the exploration of multiple neighborhoods in parallel, per-
formed by different workers located on different CPU cores (locally or distributed). This approach relies on
neighborhood combinators, which are composite neighborhoods built out of basic neighborhoods. Combina-
tors allows us to introduce metaheuristics (restart, tabu search, simulated annealing), neighborhood selection
(hill-climbing, round-robin) and handle search strategies. We propose some parallel search combinators that
can be instantiated to build search strategies encompassing parallel neighborhood exploration. An implemen-
tation is proposed in the OscaR.cbls framework, using the Actor model of computation.
1 INTRODUCTION
Nowadays, processing power available in a single
CPU Core is somewhat reaching a plateau, while the
number of available cores per CPU is regularly in-
creasing. To be able to exploit such computing power,
optimization algorithms should be redesigned to sup-
port multiple core computing.
There are a few challenges to solve in order to ex-
ploit distributed computation power and ensure that
the resulting distributed algorithm is faster than the
non-distributed one. These challenges include:
• keeping technical overhead to an acceptable level.
This includes synchronization and message pass-
ing.
• finding a proper way to split up the algorithm, so
that the different parts can be usefully executed in
parallel.
• ensuring a fair load balancing among cores, so
that there is as little idle time as possible. This
is more complex when cores have different com-
puting power.
This paper proposes a generic way to make use
of distributed computation in local search engine
by proposing a standard worker-supervisor approach,
and a presentation of the latter in the form of neigh-
borhood combinators, as part of a search procedure.
Essentially, a local search algorithm is nothing
else but a set of nested loops:
• higher-level loops compose the search procedure:
the highest one is the global loop that repeatedly
triggers solution exploration and moves.
• a series of intermediary loops are related to meta-
heuristics, such as restarts and search strategies.
• in lower-level loops, neighborhoods explore the
different neighboring solutions for the current so-
lution and evaluates the best solution.
• below the search procedure, there is another loop
that updates the model in response to the changes
in decision variables: the propagation process
(Van Hentenryck and Michel, 2009).
• each constraint and invariant can also execute
some loops during its propagation, although they
are expected to have very good complexity. An
O(1) time complexity is rather common for con-
straints.
This paper focuses on making distributed search at
the high level of loops, not distributed model evalua-
tion at lower levels. Although promising, distributed
model evaluation requires much more synchroniza-
tion, and the overhead may be quite high.
Neighborhood combinators is an approach pro-
posed in (De Landtsheer et al., 2016) to assemble a
full-fledged local search procedure out of base neigh-
borhoods, and of combinators that incorporate various
248
Ospina, G. and De Landtsheer, R.
Towards Distributed Local Search Through Neighborhood Combinators.
DOI: 10.5220/0010308602480255
In Proceedings of the 10th International Conference on Operations Research and Enterprise Systems (ICORES 2021), pages 248-255
ISBN: 978-989-758-485-5
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

aspects such as metaheuristics, neighborhood selec-
tion, stop criteria, utility functions, among others.
We are currently developing this worker-
supervisor approach into the OscaR.cbls engine using
the Actor model implemented in the Akka framework
(OscaR Team, 2012; Hewitt, 2017; Lightbend Inc.,
2020). This position paper presents the first results of
our work.
The paper is structured as follows: Section 2 re-
calls the concept of combinator and illustrates it on
an example of simple warehouse location problem.
Section 3 presents a worker-supervisor architecture to
enable the distribution of neighborhood exploration.
Section 4 presents the notion of distributed combina-
tors and illustrates that concept on the same problem
example. Section 5 shows the results of some bench-
marks over the number of threads while solving sev-
eral instances of the problem example. Section 6 con-
cludes and introduces future work.
2 BACKGROUND
This section presents the notions of local search, the
basics of neighborhood combinators and the existing
approaches for parallelization of local search.
2.1 Constraint-based Local Search
Local search (Aarts and Lenstra, 1997; Van Henten-
ryck and Michel, 2009) is an approach for tackling
large combinatorial optimization problems in a rea-
sonable amount of time. Usually a local search algo-
rithm is built on top of two main components: a model
and a search procedure. The model is a representation
of the optimization problem, composed of decision
variables and constraints on these variables, including
the objective function as a special constraint. A solu-
tion of the problem is a set of values for each variable
that fulfills the constraints. The search procedure is
an algorithm that aims at finding an optimal solution,
minimizing the value of the objective function. The
search procedure is basically a loop through the space
of solutions, where the exploration is made within
neighborhoods, representing sets of “close” solutions
that can be reached from a given solution in one it-
eration (move), in order to find a better solution with
respect to the objective function.
The main loop is enriched with several compo-
nents. Besides neighborhoods, the search procedure
may include strategies to escape from local minima,
also called metaheuristics, as well as solution man-
agers that handles the best solution found so far and
restore it when needed, and stop criteria to be met
when the current best solution is good enough to fin-
ish the search.
A good design of search procedures in local search
is critical since it influences the efficiency of the al-
gorithm and the quality of the solution. Most lo-
cal search algorithms are built from scratch with
problem-specific neighborhoods and procedural pro-
gramming languages. One of the aims of OscaR.cbls
is to facilitate the development of local search al-
gorithms through standard bricks encapsulating the
needed features for the model and the search proce-
dure.
2.2 Neighborhood Combinators
In OscaR.cbls, a neighborhood is a data structure
bound to a local search model, that manipulates the
decision variables, and can be queried for a move,
given a current solution, an acceptance criterion, and
the objective function. The query triggers the actual
neighborhood exploration. If an acceptable move is
found, it returns a description of the move and the
value of the objective function after the move if the
move is committed. When the found move is com-
mitted, a propagation process is triggered to update all
the variables and constraints according to the reached
solution. Propagation is performed in a way that
a variable is updated at most once and only when
needed.
Oscar.cbls provides a library of standard domain-
independent neighborhoods as well as specific neigh-
borhoods for routing and scheduling problems.
Neighborhoods can include features such as symme-
try elimination, mechanisms to perform intensifica-
tion or tabu search, move selection, and hot restart-
ing, which allows the possibility of restart the neigh-
borhood exploration from a last explored point of the
previous query instead of the initial position at each
query.
Neighborhood combinators were introduced in
(De Landtsheer et al., 2016) as a declarative frame-
work to elaborate richer search procedures with sev-
eral neighborhoods, including operational aspects as
metaheuristics, move selection, stop criteria, search
restarting, and solution handling.
We illustrate the principles of neighborhood com-
binators with an example for solving the uncapac-
itated Warehouse Location Problem. The problem
takes as input a set of warehouses W and a set of de-
livery points D. Opening a warehouse has a fixed cost
f
w
and the transportation cost from warehouse w to
a delivery point s is c
ws
. The solution is a subset of
warehouses to open that minimizes the sum of fixed
costs for open warehouses and transportation costs for
Towards Distributed Local Search Through Neighborhood Combinators
249

each delivery point to its nearest open warehouse.
Figure 1 presents a WLP solver in OscaR.cbls.
The model is composed of an array of Boolean vari-
ables indicating which warehouses are open. The as-
sociated constraints are the open warehouses and the
distances between points and their nearest open ware-
house. The objective function is the total cost.
The search procedure is declared as fol-
lows: the base neighborhoods used are: assign-
Neighborhood, where the value of one ware-
house is changed; swapsNeighborhood, where
the values of two warehouses are swapped; and
randomSwapNeighborhood, where the values of a
random number of warehouses are swapped. In this
problem, we use two neighborhood combinators:
bestSlopeFirst evaluates a set of neighborhoods
and select the move that decreases the most the
objective function; onExhaustRestartA f ter evaluates
a neighborhood (here, the bestSlopeFirst) and select
its moves until no more moves are found, then
it performs a restart of the search using a second
neighborhood to find a new starting point. The stop
criteria is a given number of consecutive restarts
without improving the objective function.
2.3 Parallelization of Local Search
Since the beginnings of Operational Research, the
first algorithms and their improvements followed the
sequential nature of the computers where those algo-
rithms ran. With the arrival of parallel computing, the
first approaches to parallelization were based on sim-
ple changes on the original sequential algorithm, for
instance, replacing a loop with a parallel loop. This
is not a trivial task, since some algorithms use se-
quential mechanisms that are lost when the algorithm
is parallelized. An example of this loss is given in
(Isoart and R
´
egin, 2020) in a parallel constraint solver
for the Travelling Salesman Problem. As a result, at
some scale, parallel algorithms may be slower than an
optimal sequential algorithm.
Since the first theoretical works about local search
were developed (Aarts and Lenstra, 1997), several ap-
proaches were considered for parallelizing different
aspects of local search algorithms. A first work is
presented at (Verhoeven and Aarts, 1995), where a
general approach independent of the problem is de-
scribed. In that general approach we can distinguish
between single-walk algorithms, where the solution
space is explored only once, and multiple-walk algo-
rithms, where several explorations are triggered con-
currently and may or may not communicate with each
other. In both kinds of algorithms, parallelism arises
in other aspects like neighborhood exploration and
move committing. The latest can be made in a single-
step way, it means that only one move is commit-
ted at a time after a parallel exploration of neigh-
borhoods, or in a multiple-step way, where several
moves are committed in parallel. Most interesting ap-
plications use multi-walk based algorithms. For in-
stance, in (Handa et al., 2004), a distributed algorithm
with a worker-supervisor architecture is presented.
The local search algorithm consists on splitting the
solution space and trigger several workers that per-
forms the search and specially the neighborhood ex-
ploration. Each worker can use a different neighbor-
hood. The supervisor waits for the solutions found by
each worker and performs the actual move commit-
ting. A recent work in (Codognet et al., 2018) pro-
poses an extension of multiple-walk algorithms with
a cooperation layer between the different explorers.
The resulting framework is called Cooperative Pa-
rallel Local Search (Munera et al., 2014), and is im-
plemented in the X10 parallel programming language.
After their design of Comet programming lan-
guage, (Michel et al., 2009) propose parallel con-
structs to extend Comet. The proposed constructs
are quite similar to the ones used in Java: moni-
tors for synchronized blocks, threads, processes, and
shared objects, as well as parallel loop statements.
Those language constructors support the development
of both single-walk and multi-walk algorithms.
The framework we propose in this paper is a
multi-walk approach, based on the Actor model,
where workers perform single neighborhood explo-
rations of a part of the search space, as it is explained
in next section.
3 A WORKER-SUPERVISOR
ARCHITECTURE
Before this work, local search solvers in OscaR.cbls
run as monolithic applications in a mono-thread en-
vironment. In this section, we present the architec-
tural extensions which support the distribution of lo-
cal search in a multi-threading environment.
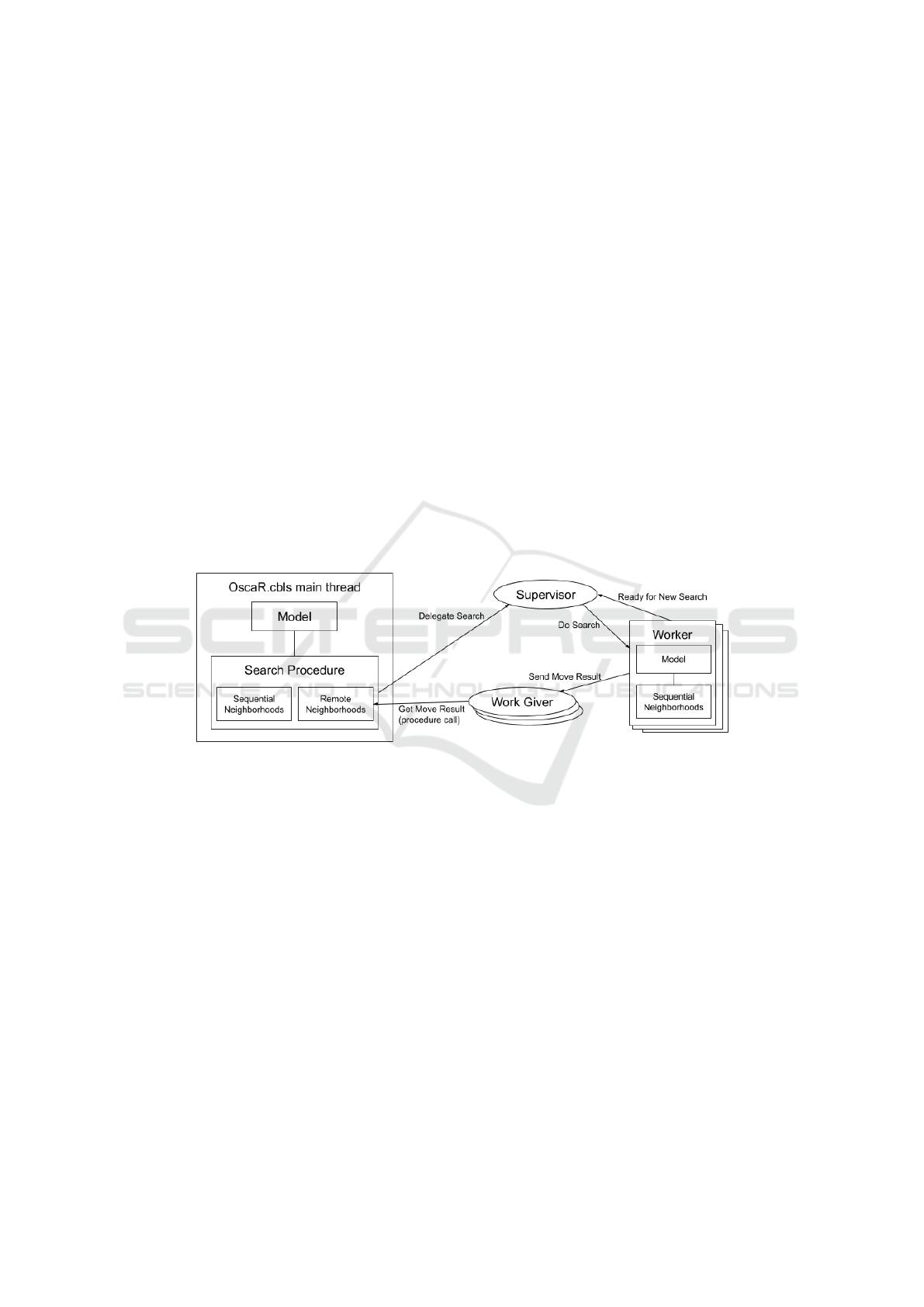
The architecture shown in Figure 2 is based on
the Akka actor model (Lightbend Inc., 2020). Akka
makes easier the implementation of complex soft-
ware communication protocols, and is also able to
support network communication in a seamless way.
Our architecture follows a Supervisor-Worker pattern,
where a supervisor actor dispatches search requests to
worker actors, who synchronize their search results to
work giver actors. Work givers are associated to spe-
cific “remote” neighborhoods.
In the context of a multi-threaded local search
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
250
val W:Int = ... //the number of warehouses
val D:Int = ... //the number of delivery points
val defaultCostForNoOpenW = ... //default cost if no warehouse is open
val costForOpeningWarehouse = ... //the costs for keeping open each warehouse
val distanceCost = ... //the cost between a warehouse and a delivery point
//problem model
val m = Store()
val warehouseOpenArray = Array.tabulate(W)(w => CBLSIntVar(m, 0, 0 to 1, s"w_$w"))
val openWarehouses = filter(warehouseOpenArray, _==1)
val distanceToClosestOpenWarehouse = Array.tabulate(D)(d =>
min(distanceCost(d), openWarehouses, defaultCostForNoOpenW))
val obj = objective(sum(distanceToClosestOpenWarehouse)
+ sum(costForOpeningWarehouse, openWarehouses))
m.close()
//define the search procedure
val neighborhood = (
bestSlopeFirst(
assignNeighborhood(warehouseOpenArray, "SwitchWarehouse"),
swapsNeighborhood(warehouseOpenArray, "SwapWarehouses"))
onExhaustRestartAfter(
randomSwapNeighborhood(warehouseOpenArray, W/10),
maxRestartWithoutImprovement = 2, obj))
//run the search
neighborhood.doAllMoves(obj)
Figure 1: A simple script solving the uncapacitated warehouse location problem.
Figure 2: Distribution of search in OscaR.cbls using actors.
with OscaR.cbls, the main thread executes the search
procedure. When the search procedure executes
a neighborhood combinator requiring some remote
neighborhood exploration, appropriate requests are
sent to the supervisor, which include the current val-
ues stored in the model and the set of neighborhoods
to explore. The main thread can be stopped by syn-
chronization in the combinator, on one or more results
of the remote searches. Remote searches can also
be cancelled by the combinator that requested these
searches, notably when an acceptable move has been
found by some worker.
The supervisor has an internal queue of searches
waiting to start, and manages the set of available
workers with their current status. Those status are ei-
ther “idle” or “busy”. The supervisor assign searches
to idle workers.
When a search request is processed by the super-
visor, it creates a work giver actor and dispatches the
search to an idle worker, with the reference of the
work giver. Workers notify the search results to their
work givers, who passes those results to the main
thread, while workers notify the supervisor on their
state change for eventually processing another search
request.
The main thread and each worker have their own
instances of the same search procedure and model,
which includes variables, constraints, and the objec-
tive function. Each variable and base neighborhood
in workers have a unique identifier, which is created
in the same deterministic way for all workers. Dupli-
cating the neighborhood data through workers is re-
quired since instantiating the model is time consum-
ing, and we want to avoid creating and destroying
workers too often, because those operations induces
overhead in the solver.
Towards Distributed Local Search Through Neighborhood Combinators
251

4 DISTRIBUTING SEARCH WITH
COMBINATORS
This section presents the extension of the neighbor-
hood combinator framework for covering the distri-
bution of search through several workers.
We defined three distributed combinators which
take a set of base neighborhoods that will be explored
remotely. Distributed combinators have a reference to
the supervisor actor and sends messages representing
search requests for each base neighborhood to that su-
pervisor. The supervisor puts the requests in its search
queue and creates the corresponding work givers. Re-
quests in the queue will be eventually dispatched to
workers, who perform the search for a move and send
the results about the found move to the corresponding
work givers.
The three distributed combinators deal with the re-
sults of parallel neighborhood explorations in a spe-
cific way:
The Remote combinator just takes a base neigh-
borhood and performs its exploration remotely.
The DistributedFirst combinator dispatches all
searches on base neighborhoods and selects the first
move received as the next move. This implies to send
cancel search messages to the other workers when the
first move is found.
The DistributedBest combinator dispatches all
searches on base neighborhoods and selects the move
that best improves the objective function..
In Figure 3 is presented a solver of the uncapac-
itated warehouse location problem using OscaR.cbls
with distributed search. The main difference with the
sequential version is the configuration of the super-
visor and workers. The Actor system is started by
the main thread with the Supervisor actor and the
main components of solver (model, neighborhoods,
and objective function). Then, the local workers can
be created with their own instances of both model and
neighborhoods. We have also split the swapsNeigh-
borhood into four parts with a module rule on their
domain, so that they can be explored in parallel.
5 BENCHMARKING
In this section, we evaluate the efficiency of using dis-
tributed combinators through a set of benchmarks on
the uncapacitated warehouse location problem. The
benchmarks were performed in a laptop with Intel i7-
7700HQ processor at 2.80 Ghz, with 4 cores and 8
logical processors, 16 Gb of RAM, and a SSD disk.
These benchmarks used the algorithm in Figure 3,
which uses the DistributedFirst combinator, with two
dimensional parameters: the problem size, expressed
in the number of warehouses and delivery points, and
the number of local search workers. Four different
problem sizes were used, respecting a ratio 2:1 bet-
ween warehouses and delivery points. The number of
workers varies between 1 and 16. For each problem
size, a random warehouse location problem was ge-
nerated. The same problem is then solved by search
procedures which are parameterized with the number
of workers. Within a given number of workers, se-
veral iterations of the same search procedure are done,
and their run times are averaged. Since there are a
non-determinism on workers, the objective value may
be different on iterations of the same problem. The
comparison between the different problem sizes are
done with respect to the best (minimal) value found
in all the iterations.
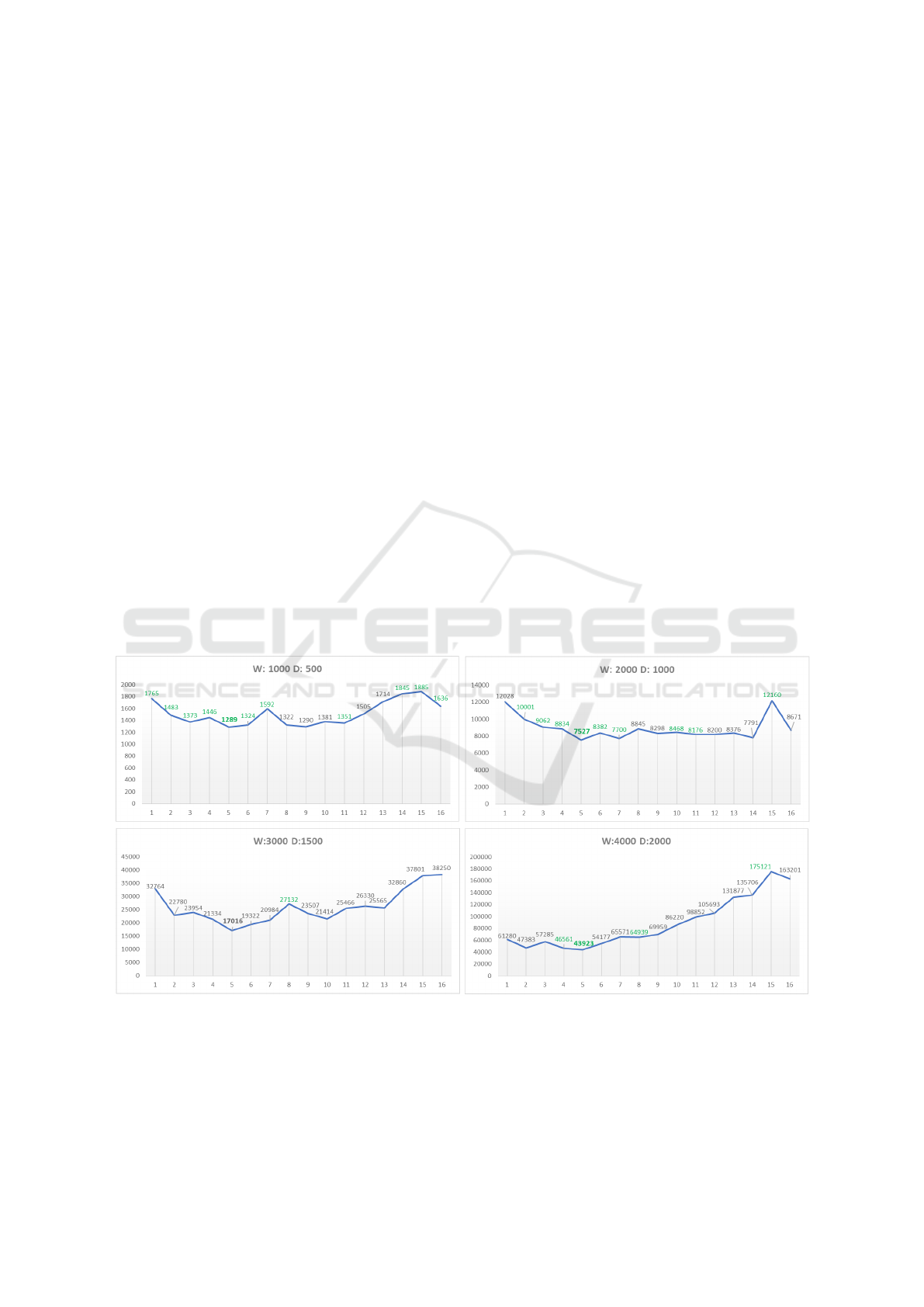
The results are presented in Figure 4. The X axis
represents the number of workers, The Y axis is the
average solving time in milliseconds. The best run
time is shown in bold, whereas the green values rep-
resent the instances having the best value of the ob-
jective function.
For smaller problem sizes with short run times
(W=1000, W=2000), there is no significant differ-
ences in the run times when the number of work-
ers are between 3 and 12. In bigger problem sizes
(W=3000, W=4000), the performance significantly
decreases within 10 or more workers. This is prob-
ably due to the saturation of the CPU cores, CPU
cache and the bus to the RAM, which is shared by all
cores. In addition, since every worker has a copy of
model variables and neighborhoods, RAM could also
be saturated and computation relies on slower swap-
ping memory.
These limitations might actually disappear by us-
ing cores from different CPUs, as they would have
their own memory space, to the cost of creating higher
communication overhead.
Considering that the supervisor and workers con-
stitutes the principal threads in the solver, it is recom-
mended to set the number of workers in a range bet-
ween the number of processor cores and the number
of logical processors.
6 CONCLUSION AND FUTURE
WORK
We presented an extension of a local search frame-
work to handle distributed computation in a multi-
threading environment. Our current work covers the
distribution of neighborhood exploration by extend-
ing the neighborhood combinators library with dis-
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
252
// loading instance data into constants (same as the non-parallelized case)
...
def createSearchProcedure():(Store,Neighborhood,Objective) = {
//instantiate model (same as the non-parallelized case)
val m = Store()
...
val obj = ...
m.close()
//instantiate search procedure
val neighborhood =
distributedFirst(
assignNeighborhood(wOpen, "SwitchW"),
swapsNeighborhood(wOpen,searchZone1=(0 until W/4).map(_*4 ), "SwapW0"),
swapsNeighborhood(wOpen,searchZone1=(0 until W/4).map(_*4+1), "SwapW1"),
swapsNeighborhood(wOpen,searchZone1=(0 until W/4).map(_*4+2), "SwapW2"),
swapsNeighborhood(wOpen,searchZone1=(0 until W/4).map(_*4+3), "SwapW3")),
onExhaustRestartAfter(randomSwapNeighborhood(wOpen,W/10), 2, obj)
//result
(m,neighborhood,obj)
}
//supervisor side
val (store,search,obj) = createSearchProcedure()
val supervisor = Supervisor.startSupervisorAndActorSystem(store,search)
//creating 5 workers in the same JVM as the supervisor
for(_ <- 1 to 5) {
val (store2, search2, _) = createSearchProcedure()
supervisor.createLocalWorker(store2,search2)
}
//run the search on the supervisor side, which delegates that to the workers
search.doAllMoves(obj)
Figure 3: A script solving the uncapacitated warehouse location problem with a distributed neighborhood.
Figure 4: Benchmarks for distributed solvers of warehouse location problems.
tributed combinators on an underlying supervisor-
worker architecture implemented in the Akka Actor
model.
The proposed extensions are functional and the
first benchmarks show that a good efficiency of the
solver is obtained with a limited number of worker
actors running in separated threads. Besides, the in-
tegration with existing sequential neighborhoods is
Towards Distributed Local Search Through Neighborhood Combinators
253

seamless.
However, the benchmarks also revealed some
drawbacks. We could not see a direct relation between
the solver speed and the number of CPU cores, event
though it was evident that the efficiency decreases
with a high number of workers. Another drawback
is the need to make explicit the copy of the model
and neighborhoods at the creation of the actor model,
which implies an extra work to the developer.
Building a parallel version of an algorithm inher-
ently hinders the use of some mechanisms that rely on
sequential exploration. In the case of constraint-based
local search solvers, we can find several mechanisms,
implemented in OscaR.cbls. These will be carefully
examined to check if they can cope with multi-core
computation:
• some metaheuristics that select neighborhood or
define a stop criterion rely on time measurement.
These are affected because the main thread does
not know when and where computation takes
place anymore.
• some neighborhoods are stateful because state
provides speed improvements. Our approach will
instantiate neighborhoods on different machines,
and their internal state is not shared, so these
mechanisms cannot be enabled.
• constraints tend to work based on incremental
model updates. So far, in our framework, when
a remote neighborhood exploration is started, the
start value of the model is loaded in a non-
incremental way, thus disabling these mecha-
nisms.
These mechanisms must somehow be adapted to
work within distributed search because their ben-
efits generally surpass the ones achieved by the
parallelization. Similar issues where encountered
with distributed constraint programming, where a
learning-based search heuristics is disabled because
distribution forces a breadth-first search instead of se-
quential depth-first search (Isoart and R
´
egin, 2020).
Our library of distributed combinators can be ex-
tended to make existing neighborhood distributed as
well, such as:
• restart metaheuristics, that could explore different
restarts in a distributed way. Notice that this can
be mimicked using the DistributedBest combina-
tor.
• making an implementation of Very Large Scale
Neighborhood that uses multi-core processing
(Mouthuy et al., 2012).
So far our local search framework is only working
in a single machine with an unique thread. Akka ac-
tors make it reasonably easy to work in a distributed
fashion, this was a rationale behind our choice of
Akka to implement the distributed extensions. An al-
ternative is the use of remote procedure calls mech-
anisms like Protocol Buffers (Google, 2020) for se-
rializing data through remote workers, but the block-
ing nature of remote calls will not give a real speedup
without using multi-threading.
Further work will include reducing the technical
overhead in the distribution layer, with the aim of im-
proving the efficiency of the solvers as well as the ex-
pressiveness of the new programming idioms induced
by the distribution of computation.
Computational power available in multi-core or
distributed systems might be exploited to speed up lo-
cal search engines in other ways:
• the evaluation of the objective function can be per-
formed in a parallel way. In some problems, this
evaluation can be time consuming and it is worth
to parallelize. To this end, the propagation algo-
rithm that drives the whole CBLS engine could
be made multi-core (Van Hentenryck and Michel,
2009).
• some constraints already available in our frame-
work exhibit poor complexities and a multi-
threaded version of these might be proposed.
ACKNOWLEDGEMENTS
This research was supported by the European project
TrackOpt (grant number 753592).
REFERENCES
Aarts, E. and Lenstra, J. K., editors (1997). Local Search
in Combinatorial Optimization. John Wiley & Sons,
Inc., New York, NY, USA, 1st edition.
Codognet, P., Munera, D., Diaz, D., and Abreu, S. (2018).
Parallel local search. In Hamadi, Y. and Sais, L.,
editors, Handbook of Parallel Constraint Reasoning,
pages 381–417. Springer.
De Landtsheer, R., Guyot, Y., Ospina, G., and Ponsard,
C. (2016). Recent developments of metaheuristics,
chapter Combining Neighborhoods into Local Search
Strategies. Springer.
Google (2020). Protocol Buffers. Available from
https://bit.ly/2FZRG2h.
Handa, Y., Ono, H., Sadakane, K., and Yamashita, M.
(2004). Neighborhood composition: A parallelization
of local search algorithms. In Kranzlm
¨
uller, D., Kac-
suk, P., and Dongarra, J. J., editors, Recent Advances
in Parallel Virtual Machine and Message Passing In-
terface, volume 3241 of Lecture Notes in Computer
Science, pages 155–163. Springer.
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
254

Hewitt, C. (2017). Actor Model of Computation for Scal-
able Robust Information Systems. In Symposium on
Logic and Collaboration for Intelligent Applications,,
Stanford, USA.
Isoart, N. and R
´
egin, J. (2020). Parallelization of TSP solv-
ing in CP. In Simonis, H., editor, Principles and Prac-
tice of Constraint Programming (CP 2020), volume
12333 of Lecture Notes in Computer Science, pages
410–426. Springer.
Lightbend Inc. (2020). Akka. Available from
https://akka.io/.
Michel, L., See, A., and Van Hentenryck, P. (2009). Parallel
and distributed local search in comet. Computers &
OR, 36:235–7–2375.
Mouthuy, S., Van Hentenryck, P., and Deville, Y. (2012).
Constraint-based Very Large-Scale Neighborhood
search. Constraints, 17(2):87–122.
Munera, D., Diaz, D., Abreu, S., and Codognet, P. (2014).
A parametric framework for cooperative parallel local
search. In Blum, C. and Ochoa, G., editors, Evolu-
tionary Computation in Combinatorial Optimisation
(EvoCOP 2014), volume 8600 of Lecture Notes in
Computer Science, pages 13–24. Springer.
OscaR Team (2012). OscaR: Operational research in
Scala. Available under the LGPL licence from
https://bitbucket.org/oscarlib/oscar.
Van Hentenryck, P. and Michel, L. (2009). Constraint-
based Local Search. MIT Press.
Verhoeven, M. and Aarts, E. (1995). Parallel local search.
Journal of Heuristics, 1:43–65.
Towards Distributed Local Search Through Neighborhood Combinators
255
