
Distributed Service Area Control for Ride Sharing by using Multi-Agent
Deep Reinforcement Learning
Naoki Yoshida
1
, Itsuki Noda
2 a
and Toshiharu Sugawara
1 b
1
Computer Science and Engineering, Waseda University, Tokyo 1698555, Japan
2
National Institute of Advanced Industrial Science and Technology, Ibaraki 3058560, Japan
Keywords:
Multi-Agent Learning, Transportation and Logistics, Ride Sharing, Deep Reinforcement Learning.
Abstract:
We propose a decentralized system to determine where ride-sharing vehicle agents should wait for passengers
using multi-agent deep reinforcement learning. Although numerous drivers have begun participating in ride-
sharing services as the demand for these services has increased, much of their time is idle. The result is
not only inefficiency but also wasted energy and increased traffic congestion in metropolitan area, while also
causing a shortage of ride-sharing vehicles in the surrounding areas. We therefore developed the distributed
service area adaptation method for ride sharing (dSAAMS) to decide the areas where each agent should
wait for passengers through deep reinforcement learning based on the networks of individual agents and the
demand prediction data provided by an external system. We evaluated the performance and characteristics
of our proposed method in a simulated environment with varied demand occurrence patterns and by using
actual data obtained in the Manhattan area. We compare the performance of our method to that of other
conventional methods and the centralized version of the dSAAMS. Our experiments indicate that by using the
dSAAMS, agents individually wait and move more effectively around their service territory, provide better
quality service, and exhibit better performance in dynamically changing environments than when using the
comparison methods.
1 INTRODUCTION
With advances in computer and communication tech-
nologies and the expanded use of smartphones with
the global positioning system (GPS), on-demand ride-
sharing services have become widespread and have
begun to attract many users. Because ride sharing al-
lows passengers who do not know one another to ride
in a single taxi/car, it increases their access to low-
priced transportation. Moreover, ride-sharing ser-
vices are expected to reduce both the number of cars
in a city area and the operational cost of services.
Ride sharing therefore provides advantages on both
the customer side and the provider side, and as a
result, ride sharing has been adopted by numerous
users (Yaraghi and Ravi, 2017) while the number of
participating companies, such as Uber and Lyft
1
, has
also increased.
Nevertheless, congestion is likely in urban and
a
https://orcid.org/0000-0003-1987-5336
b
https://orcid.org/0000-0002-9271-4507
1
https://www.uber.com/ and https://www.lyft.com/
busy areas due to the excessive number of taxis and
ride-sharing vehicles thanks to the rapid growth of
ride-sharing services (Erhardt et al., 2019). For exam-
ple, to increase their earnings, drivers tend to gather
around shopping areas, train stations, and airports,
where they can most easily find passengers. This does
not cause a problem if the number of drivers is appro-
priate to the demands of the area. However, it is dif-
ficult to maintain an appropriate number of drivers in
a given area and coordinate with each other to avoid
congestion. As a result, a supply bias may occur:
there may be both an oversupply of drivers in urban
areas, causing congestion, and a shortage of drivers
in suburban or residential areas, causing opportunity
loss.
In the recent years, there have been many studies
on taxi demand forecasting that analyze information
obtained from smart phones with GPS about where
people get in and out of taxis (Ke et al., 2017; Ma
et al., 2019). If a service provider can predict pas-
senger boarding and alighting points in advance using
forecasting information, the supply bias can be par-
tially solved by controlling the location of individual
Yoshida, N., Noda, I. and Sugawara, T.
Distributed Service Area Control for Ride Sharing by using Multi-Agent Deep Reinforcement Learning.
DOI: 10.5220/0010310901010112
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 1, pages 101-112
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
101

cars. For example, Miao et al. (Miao et al., 2015) and
Iglesias et al. (Iglesias et al., 2017) proposed methods
to reduce the difference between the number of de-
mands and the number of taxis in an area by using de-
mand forecast information. However, taxi allocation
that strictly follows the demand forecast is vulnera-
ble because such the forecasting data usually contain
errors, actual demand is always fluctuating, and taxi
demands may occur unexpectedly in inactive areas.
To improve the robustness of allocation methods
to data errors and dispersion, we have already pro-
posed the service area adaptation method for ride
sharing (SAAMS) as a control method for determin-
ing service areas, which are the areas where idle (so
empty) agents are to wait for future passengers, using
deep reinforcement learning (DRL) (Yoshida et al.,
2020), where agents driving control programs by as-
suming future self-driving vehicles. The neural net-
work in the SAAMS provides information about the
waiting areas for all independent agents based on the
demand forecast data. Although the SAAMS out-
performs conventional methods, it was designed as
a centralized system to be operated by a ride-sharing
company that would distribute the information to their
agents. When considering the actual usage and opera-
tion of ride-sharing services, it seems better for agents
to be able to independently choose their waiting area
to maximize their individual earnings, which are usu-
ally determined by the number of passengers to whom
they give rides. Furthermore, because a centralized
network requires the input information to be sent from
all agents and must then output the joint action of all
agents, its structure must be modified if the number of
agents changes, requiring a new learning process.
We therefore propose the distributed SAAMS
(dSAAMS) for each agent to improve the applica-
bility to actual operations and to improve the overall
profits. Whereas the complexity of a centralized net-
work grows in accordance with the number of agents,
the independent network treats other agents as part of
the environment. Thus, the network structure does
not need to be changed when the number of agents
changes and that it is less complex. Nevertheless, it is
possible for the method to not converge due to its non-
stationarity and instability. Thus, in this paper, we ex-
perimentally show that it can converge and that coor-
dination and cooperation emerge even without giving
additional rewards to promote cooperation. We also
show that the dSAAMS can adapt to complex sim-
ulated environments in which demand is generated
in static and dynamic manners. Finally, we examine
its performance on a benchmark dataset obtained in
Manhattan, New York City (NYC).
2 RELATED WORK
Several different ride-sharing systems have been pro-
posed and studied. Before the 2010s, dial-a-ride on-
demand bus systems attracted attention, and many
methods were proposed to find (near) optimal solu-
tions for arranging buses to minimize the travel and
waiting times (Cordeau and Laporte, 2003; Berbeglia
et al., 2012). Then, with the proliferation of mobile
devices, research has shifted to the problem of taxi
placement to anticipate passengers in ride-sharing ser-
vices (Nakashima et al., 2013; Alonso-Mora et al.,
2017). For example, Nakashima et al. (Nakashima
et al., 2013) proposed a ride-sharing service system
that seeks a reasonable arrangement of vehicles by (1)
sending a passenger’s demand to all cars, (2) calcu-
lating the expected trip time, including waiting time
and travel time, for each car, and (3) assigning the
demand to the vehicle with the shortest expected trip
time. They demonstrated that their allocation method
worked well experimentally for an actual ride-sharing
system in Hakodate City, Japan. Alonso-Mora et
al. (Alonso-Mora et al., 2017) proposed a method to
formulate taxi allocation in ride-sharing services in
the framework of integer programming in order to ob-
tain a semi-optimal solution. They showed that their
solution can reduce the number of taxis needed to
cover demand in NYC by 70%.
Meanwhile, there have been many studies on de-
mand forecasting for ride-sharing services (Ke et al.,
2017; Ma et al., 2019), and forecasting data have been
used in ride-sharing systems in recent years. Because
an imbalance between driver supply and passenger
demand leads to reduced efficiency and unnecessary
traffic congestion, Miao et al. (Miao et al., 2015) pro-
posed the receding horizon control approach (RHC),
which is a position control method that uses the linear
programming framework to minimize the difference
between demand and supply using forecast data. They
have showed that their method can achieve efficiency
by dispatching empty taxis to expected busy areas.
However, by closely following the demand forecast,
this dispatch solution is not robust to errors contained
in the forecast.
Thanks to recent progress in research on DRL, es-
pecially deep Q-networks (DQNs) (Mnih et al., 2015),
It has been widely used to, for example, learn the
control of autonomous game playing and robot move-
ments even in complicated environments (Silver et al.,
2018; Akkaya et al., 2019). The use of the DQNs has
also been proposed in a number of studies on ride-
sharing systems (Lin et al., 2018; Oda and Joe-Wong,
2018; Wen et al., 2017), in which the proposed meth-
ods achieved similar or better allocation efficiency
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
102

△△
△
△
△
△
△
Passenger
△
Car
Figure 1: Environment of the ride-sharing problem.
than conventional methods that did not use the DQNs.
The systems proposed by Lin et al. (Lin et al., 2018)
and Oda et al. (Oda and Joe-Wong, 2018) have cen-
tralized deep networks, like the SAAMS (Yoshida
et al., 2020), that needed to learn micro-movements
in their environments (such as a sequence of mov-
ing up, down, left, and right) to generate the opti-
mal routes for traveling to destinations. As a result,
the learning was inefficient because the appropriate
route selection was not easy to learn due to the dy-
namic and complicated road conditions. Wen, Zhao,
and Jaillet (Wen et al., 2017) proposed the rebalancing
shared mobility-on-demand (RSM) system in which
agents have their own DQNs by combining the de-
mand forecast data and dynamically control indepen-
dently when empty, to reduce the difference between
supply and demand. Moreover, the networks provide
the micro-movements to control themselves. How-
ever, these studies did not investigate the mechanism
behind the improvements in performance.
In contrast, the dSAAMS that we propose here
does not provide micro-movements and eliminates
route selection by assuming these activities are
learned in other components. Instead, it focuses on
the learning how to decide the service area of each
agent. This approach makes the learning efficient and
enables the driver agents to follow the dynamics of
the environment.
3 PROBLEM AND MODEL
3.1 Problem Formulation and Issues in
SAAMS
We formulate the car dispatch problem for ride shar-
ing. We denote the set of agents by D = {1,...,n} and
introduce a discrete time t ≥ 0, for which one unit
of time, called a step, corresponds to approximately
2 to 3 min in our study. The environment is repre-
sented by an L × L grid (L ≥ 0 is an integer). Each
cell in the grid represents a K
x
×K
y
region (K
x
and K
y
are assumed to be approximately 500 m in the experi-
ments below). Fig. 1 shows an example environment,
in which the red circles represent agents and the tri-
angles represent passengers waiting for taxis. At each
time step, agent i can move up, down, left, or right by
one cell or can stay in their current cell. The goal of
this problem is for agents to pick up passengers from
their waiting places and deliver them to their desti-
nations in order to maximize their earnings. Agent
i ∈ D has a vehicle capacity Z
i
≥ 0 and cannot trans-
port more than Z
i
passengers. Let S be the set of states
of the environment. We denote the state at time t by
s
t
∈ S which includes all agents; the known passen-
gers in the environment; the current service areas of
all agents, which are be defined below; and the most
updated demand prediction data, provided every 30
steps by a forecasting system outside the SAAMS.
Conceptual diagrams of the ride-sharing systems
with the SAAMS is shown in Fig. 2. At time t, the
ride-sharing company operates the SAAMS to con-
trol all agents that belong to it. The SAAMS has the
centralized DQN whose input consists of states of all
agents, their received rewards and the forecast data.
It then assigns agent i (for ∀i ∈ D) to its service area
C
i,t+1
for next time, which are a subset of the envi-
ronment. When a passenger requests a taxi in a given
location, the operator in the company assigns the most
appropriate (i.e., the closest) agent whose service area
includes the passenger’s current location.
Agent i then attempts to move to the service area
(preferably, to its center) if its vehicle is empty. When
the vehicle of agent i is not empty (i.e., they are trans-
porting passengers or have been assigned passengers),
they continue their current service (i.e., they continue
driving to the passengers’ destination or waiting area).
After dropping off all passengers, agent i returns to
the center of C
i,t
. That is, the SAAMS indirectly nav-
igates the agents by flexibly changing the service area
locations. The SAAMS adjusts the position and size
of C
i,t
to improve the quality of the service and to in-
crease the total benefits. Meanwhile, the agents do
not independently change their service area and in-
stead wait for updates from the SAAMS.
3.2 Dispatch Management using
Distributed SAAMS
The SAAMS is a centralized controller for a ride-
sharing company. It may be able to coordinate be-
havior to some degree, i.e., a few agents may be al-
located to unbusy areas to provide better service for
rare demands even though these agents are likely to
remain idle. However, if the agents’ income is based
on commission in the ride-sharing service, it is more
appropriate for agents to autonomously choose their
service areas, even if they belong to the same com-
Distributed Service Area Control for Ride Sharing by using Multi-Agent Deep Reinforcement Learning
103
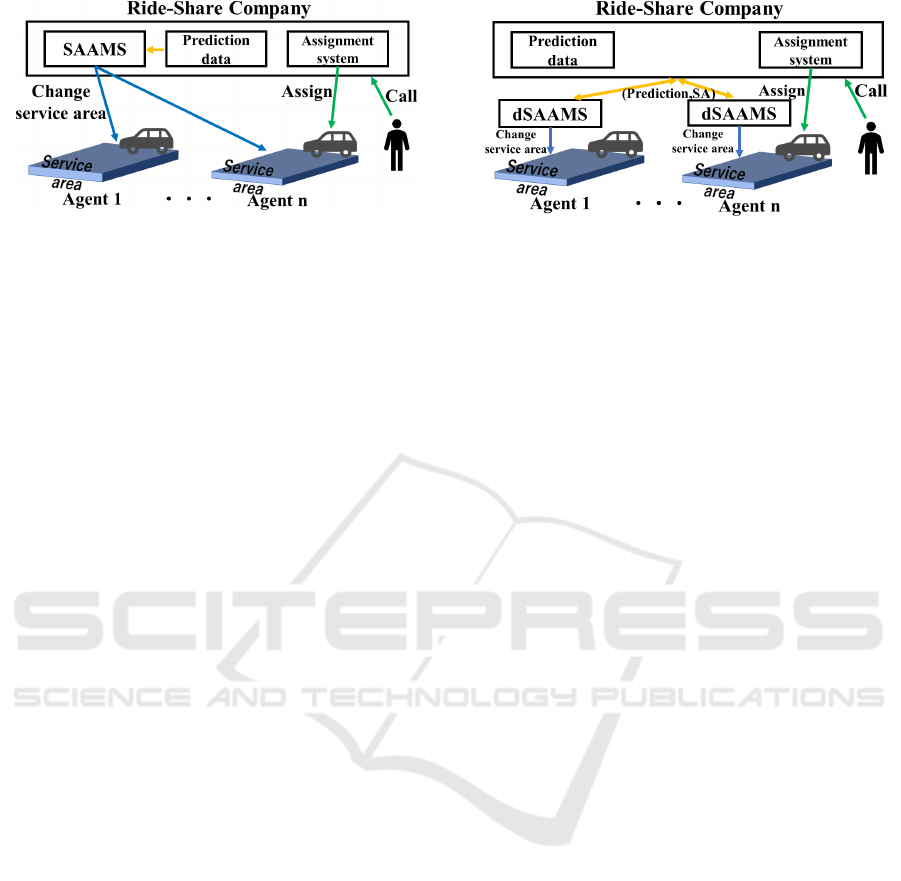
Figure 2: The SAAMS taxi dispatch system.
pany. Another drawback of SAAMS is that the struc-
ture of input has to change in accordance with the
increase of agents; this often occurs in a real-world
ride-sharing service company where more than a few
hundred agents are involved and the number of agents
is likely to change. Therefore, the network must be
reconfigured and need to be trained again. For this
reason, the central control of the SAAMS seems un-
suitable for real-world operations.
We thus introduced the dSAAMS, as shown in
Fig. 3. Agents in the dSAAMS may work for the
same company but they individually learn using their
own network to appropriately select their service ar-
eas by themselves. This system architecture makes
this method more flexible and widely applicable be-
cause the network structure is not affected by the
number of agents that belong to a company. How
to assign a request from passengers to the appropri-
ate agents is identical to that by the company us-
ing the SAAMS. The main concerns are whether the
dSAAMS can learn excellent (or at least acceptable)
strategies for determining service areas and the con-
vergence and stability of these strategies. A perfor-
mance comparison between the dSAAMS and a con-
ventional method (Wen et al., 2017) is also of inter-
est because the distributed setting of the conventional
method is quite similar to the method used in our
method.
When a ride-sharing company receives a request
from a group of passengers at time t, it immediately
attempts to assign the request to an agent i ∈ D who
meets the following conditions:
(a) Agent i is a vacant agent; that is, its vehicle is
empty or has enough empty seats for the new pas-
sengers (the capacity limit Z
i
cannot be violated);
(b) The service area C
i,t
of i includes the place where
the passengers are waiting; and
(c) The current location of i is closest to the place
where the passengers are waiting.
Because it may take extra time to pick up passengers
for carpooling, it is assumed that the time required
for carpooling passengers to board is twice as long as
Figure 3: The dSAAMS taxi dispatch system.
for a non-carpooling ride. This assignment process
requires that the ride-sharing company receive infor-
mation about the service areas of all agents, whereas
a ride-sharing company using the SAAMS determines
the service areas in a centralized way and distributes
them.
To avoid extreme detours that could be caused by
ride sharing with other passengers, we introduce the
additional condition of the expected maximum travel
time (EMTT). The EMTT is specified by the upper-
limit factor T
TT
(≥ 1). The EMTT condition is
The expected travel time for carpooling must not
exceed T
TT
times the expected travel time for a
non-carpooling ride.
T
TT
is set by the ride-sharing company to maintain
its service quality. The company only assigns agents
such that the EMTT condition is not violated. If more
than one agent meets the conditions, the dispatch sys-
tem randomly selects one of them. When there is no
assignable agent, the passengers are immediately de-
clined, and service is not provided. When multiple
demands arrive, they are processed sequentially by
the ride-sharing company. When agent i is assigned
passengers, they move to the waiting area, pick up the
passengers, drive to the destination, and drop off the
passengers. After that, agent i returns to their service
area.
In this study, the agents try to maximize the earn-
ings of the ride-sharing company, which is the sum
of the profits of the individual agents. On their own,
the agents would likely congregate in areas with high
demand to increase their personal earnings. How-
ever, this concentration can result in excessive com-
petition and many agents remaining idle. Moreover,
it also causes a lack of service in those areas where
demands occur infrequently. To avoid this, in our
system, agents learn coordinated behavior using their
own networks.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
104

Table 1: List of adjustments to a service area.
Name Manipulation to adjust C
i
Enlarge C
i
, of size T
i
x
× T
i
y
, is enlarged to size
(T
i
x
+ 2) × (T
i
y
+ 2).
Shrink C
i
, of size T
i
x
× T
i
y
, is shrunk to size
(T
i
x
− 2) × (T
i
y
− 2).
Up, down,
left, right
C
i
is moved up, down, left, or right
(without a change in size).
Stay The size and location of C
i
are main-
tained.
up
Car
Service Area
(a) up adjustment of C
i
.
(b) enlarge adjustment of C
i
.
Figure 4: Examples of manipulations for service areas.
3.3 Service Area and Its Adjustment
Agents using the dSAAMS adjust their service area
to increase earnings as well as to provide quality ser-
vice. Let A be the set of the manipulations to adjust
service area C
i,t
for agent i ∈ D. The service area C
i,t
is a rectangular area of cells (a square in the experi-
ments below) with a maximum size of T
x
× T
y
, where
L ≥ T
x
,T
y
≥ 1 are integers, and the minimum area
is 1 × 1. An adjustment a
i
t
∈ A at time t is one of
A = {enlarge,shrink,up,down,left,right,stay}; the
details of these adjustments are listed in Table 1. Ex-
amples of the adjustments up and enlarge are shown
in Fig. 4. Note that since agents are directed to move
to the center of their service area, after an up manip-
ulation of the service area as in Fig. 4a, the agent will
try to move up in next step if possible. If an adjust-
ment of C
i,t
would result in a violation of the size con-
straints, the selected adjustment is stay. Agents’ cur-
rent locations and the manipulations on their service
areas may be independent because if they are on their
way to drop off passengers, they may be far from their
service areas.
4 PROPOSED METHOD
4.1 Learning in dSAAMS
The DQN of the dSAAMS of agent i learns manipula-
tions to adjust C
i,t
to maximize the estimated rewards.
In this study, to balance the earnings and service qual-
Figure 5: Structure of the Dueling Neural Network in
dSAAMS.
3
3
5
1
(a) Prediction
data
1
1
1
1
1
1
1
1
1
(b) Individual ser-
vice area
1
1 1
1
1
1
1
1
1
3
3
3 3
3
3
3 3
3
3 3 3
3
3 3 3
4
4 4 4
4
4 4 4
4
4
4
4
4
4
4
4
3
5 5 5
3
5 5 5
3
5 5 5
3
3
3
3
(c) Collective ser-
vice area
Figure 6: Input to DQN.
ity, we introduce weighted rewards to agent i:
r
t
i
=
∑
p∈P
i
t
w
b
f
p
b
+ w
d
f
p
d
+ w
t
f
p
t
(1)
r
0i
t
= −w
g
f
g
, (2)
where w
b
, w
d
, w
t
, and w
g
are non-negative weights,
and P
i
t
is the set of passengers assigned to agent i at
time t. Parameter f
b
≥ 0 is the dispatch fee for passen-
ger p ∈ P
i
t
, parameter f
d
≥ 0 is the expected travel dis-
tance, and parameter f
t
≥ 0 is the service travel time
for passenger p. Since we assume that the routes are
determined using another mechanism, the travel dis-
tance and time are based on the shortest route between
two locations, and carpooling detours are not consid-
ered. Parameter f
g
≥ 0 is the cost of an empty agent
moving to a neighboring cell. We assume that r
i
t
(≥ 0)
is the reward (fare) obtained from passenger p. Agent
i receives r
i
t
only when they are assigned p, whereas
a negative reward (fuel expense) r
0i
t
arises whenever
agent i moves to a neighboring cell. All agents inde-
pendently learn how to adjust their own service areas
to increase the total rewards of
∑
r
i
t
+ r
0i
t
. Note that
since r
0i
t
is negative, agents attempt to transport pas-
sengers for as long as possible. All parameters used
in Formulae (1) and (2) should be defined by the ride-
sharing company.
4.2 Structure of Deep Q-Network
Because the proposed dSAAMS is a decentralized
control, where each agent learns behaviors indepen-
dently on the basis of locally earned rewards and ex-
pense, we have to verify if the decentralized control
by the dSAAMS converge.
Distributed Service Area Control for Ride Sharing by using Multi-Agent Deep Reinforcement Learning
105

The proposed DQN for the dSAAMS of each
agent is a dueling network (Wang et al., 2016), as
shown in Fig. 5, whose output is the combination of
the estimated values V(s) of state ∀s ∈ A and the ad-
vantages A(s, a) of a ∈ A in s. This network con-
sists of three convolutional layers (no pooling layers)
whose inputs to the first layer are matrices represent-
ing the environment in an abstract way, and four fully
connected network (FCN) layers for the estimated
values and the advantages. The activation function is
the rectified linear unit (ReLU). When the service area
of agent i is modified, agent i sends that information
to the ride-sharing company for proper assignment.
Three types of L × L matrices form the input to
the network of agent ∀i ∈ D (example matrices are
shown in Fig. 6, where a blank cell in the matrices
except that of prediction data indicates zero). The
first matrix includes the recent demand forecast data
from the demand forecast component. Its elements
are the demand forecast rates, which are non-negative
real numbers that indicate the expected number of de-
mands across 30 time steps at each cell. The blank
cells in Fig. 6a indicate uniform, low demand rates
(such as 0.1 and 0.025). The second matrix (Fig. 6b)
expresses the service area of agent i itself. The third
matrix (Fig. 6c) indicates the number of agents (in-
cluding that of agent i) whose service areas include
the corresponding cells. For example, a 5 indicates
that five agents include that cell in their service areas.
To generate the third matrix, we assume that the ride-
sharing company shares and distributes the service ar-
eas of all agents. This information is also needed for
the company to properly assign passenger demands to
appropriate agents.
5 EXPERIMENTAL EVALUATION
5.1 Experimental Setting
We experimentally evaluated the proposed method,
dSAAMS, in a simulation environment by compar-
ing it with other methods. Our experiments were
conducted in a 10 × 10 grid environment (L = 10,
see Fig. 7) using simulated scenarios and well-known
benchmark data obtained in Manhattan, NYC (NYC,
2020). We used a grid environment since it is sim-
ple and easy to understand to compare the features
of the methods used in our experiments. In addition,
the evaluation using the public benchmark dataset of
taxi trips in the Manhattan area allows us to evaluate
the performance of the methods in a real application.
The parameters of agent dSAAMS networks are listed
in Table 2. There were 2000 episodes in the train-
ing phase, and we used the ε-greedy learning strategy,
with a gradually decaying value of ε. The value of ε
in the N-th episode was 1.0 − 0.9N/2000, so ε was
gradually decreased to 0.1. ε = 0 in the testing phase.
We adopted the RHC (Miao et al., 2015), the
method used by Wen et al. in their RSM sys-
tem (referred to as the RSM hereafter) (Wen et al.,
2017), and SAAMS, which is the centralized version
of dSAAMS (Yoshida et al., 2020), as comparative
methods. The RHC tries to move unassigned cars
to areas with shortages by giving instructions based
on prediction data. It uses the linear programming
framework and has been often used for comparative
evaluation. We omitted the comparison with other
methods (Lin et al., 2018; Oda and Joe-Wong, 2018),
because they include the route selection, making a di-
rect performance comparison difficult.
The RSM learns to control agents with their own
DQNs. Each DQN takes as input the demand fore-
cast matrices, the positions of nearby agents, and the
estimated total supply of cars. It then outputs the Q-
value for each movement. One difference between the
RSM and the dSAAMS is that the dSAAMS takes the
entire environment as its input (because it is a natu-
ral assumption that agents have maps of the service
territory). In contrast, the agents in the RSM only
get information about the local 5 × 5 grid centered
on their location (probably assuming local commu-
nication). The rewards in the RSM might increase if
the agents could quickly move to areas where passen-
gers are waiting after dropping off their current pas-
sengers.
We adopted three evaluation measures in the test-
ing phase: the operating profits (OP), which are the
rewards from the passengers,
∑
L
e
t=1
∑
i∈D
r
i
t
, where L
e
is the episode length; the ratio of the waiting time
(RWT), i.e., the ratio of the required time in steps
to pick passengers up to the total travel time to their
destination; and the average travel distance per agent
(ATD) per episode, where the distance is defined as
the number of cells, making this value identical to
r
0i
t
= w
g
by setting f
g
= 1. The OP seems to be the
most important indicator for the ride-sharing com-
pany because it reflects the income of the company.
The reward weights for calculating r
i
t
and r
0i
t
in the
dSAAMS training phase were set to w
b
= 3, w
d
= 0.2,
w
t
= 0.2, and w
g
= 0.05 by referring to actual ride-
sharing operations. The value of RWT represents the
ratio of the waiting time which is one aspect of service
quality, so a smaller value is better. A smaller value
of ATD is also better because it represents the average
fuel consumption per episode of individual agents.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
106

Table 2: Network parameters.
Parameter Value
Replay buffer size, d 20,000
Learning rate, α 0.0001
Update interval of target network 20,000
Discount factor, γ
q
0.99
Mini batch size, U 64
Table 3: Setup parameters.
Parameter Value
Number of agents, |D| = n 20
Episode length, L
e
150
Vehicle capacity, Z = Z
i
for ∀i ∈ D 4
Max. size of service area, T
x
,T
y
5
Cost of moving to a neighboring cell, f
g
1
Upper-limit factor for EMTT, T
TT
2
5.2 Simulated Grid Environments
We conducted the first experiment (Exp. 1) in the sim-
ulated environment shown in Fig. 7, in which blue and
green cells correspond to busy areas/places such as
stations, halls, museums, shopping malls, and hospi-
tals. We prepared four scenarios with different pat-
terns in the demand occurrence rate in the grid envi-
ronment. The demand occurrence rate λ (> 0) in a cell
is defined as the demands from passengers, which are
generated according to the Poisson distribution P
o
(λ)
every 30 steps (i.e., P
o
(λ/30) per step). Note that the
expected value of P
o
(λ) is λ. The passenger destina-
tions are assigned randomly unless stated otherwise.
Figure 7: Experimental environment.
In Scenario 1, the pattern is static: the demand oc-
currence rate is 4 (λ = 4) in each green cell and
is λ = 0.025 for the other cells. Therefore, 18.4
(0.025 × 96 + 4 × 4) demands are generated on av-
erage every 30 steps in the whole environment. Sce-
nario 2 is uniform: λ = 0.25 for all cells. In Scenario
3, the pattern is dynamic and biased: the blue cell
is a train station, and the four green cells correspond
to other busy places. There are many demands for
rides between the station and one of the busy cells.
Therefore, the blue cell or one of the green cells is
randomly selected every 30 steps, and its demand oc-
currence rate is set to λ = 12, while for the other cells
λ = 0.025. Any demand occurring at the blue cell has
its destination as one of green cells with a probability
of 0.98 (otherwise, the destination is random with a
probability of 0.02). Similarly, a demand occurring at
one of the green cells has the station (blue cell) as its
destination with a probability of 0.98, with the des-
tination being randomly selected otherwise. Finally,
the pattern in Scenario 4 is more dynamic, and its de-
mand occurrence rate varies every 30 steps as listed
in Table 4.
We assume that the demand forecast matrix is cor-
rect in the sense that its elements are identical to their
demand occurrence rate λ for the corresponding cells.
However, since the demands are generated randomly
according to P
o
(λ), the number of demands gener-
ated in a cell may not be equal to λ. Moreover, since
the updated demand forecast data are given every 30
steps, the same demand forecast matrix is provided to
the individual agent networks until the next update ar-
rives, whereas it may almost be obsoleted in the last
part of the interval. The other setup parameters for
Exp. 1 are listed in Table 3.
5.3 Performance Comparison
The results of all scenarios of Exp. 1 are listed in
Table 5. Table 5a indicates that agents using the
dSAAMS earned the highest OP. We can thus say
that the dSAAMS outperformed the other methods in
all scenarios. Another observation is that the decen-
tralized control systems, i.e., the dSAAMS and RSM
earned more OP than the centralized control systems.
The difference between the OP obtained using the
dSAAMS and that using the RSM was the largest
in Scenario 3. Because most of the passenger flow
was unidirectional in this scenario, the movement of
agents using the dSAAMS, which returns agents to
their service areas after passengers are dropped off,
matched the flow well. The difference between the
dSAAMS and RSM was second largest in Scenario 4.
In this scenario, the flow of passengers was also dy-
namic, and its direction of movement was also some-
what biased. We believe that actual flow is likely to be
biased, as in Scenarios 3 and 4, making the dSAAMS
better for real ride-sharing applications.
The ratio of the waiting time (RWT) and the av-
erage travel distance (ATD) are listed in Tables 5b
and 5c. The RSM produced the shortest values for
the RWT, with the SAAMS and dSAAMS produc-
ing relatively longer values. Because the environ-
ment of Scenario 2 is uniform and has no busy areas
Distributed Service Area Control for Ride Sharing by using Multi-Agent Deep Reinforcement Learning
107

Table 4: Demand occurrence rates in Scenario 4 (per 30 steps).
Cell (t =)0 to 29 30 to 59 60 to 89 90 to 119 120 to 149
Green 4 2.5 0.025 2.5 4
Blue 0.025 8 18 8 0.025
Others 0.025 0.025 0.025 0.025 0.025
Table 5: Performance Comparison.
(a) Received operating profit (OP).
Scenario 1 Scenario 2 Scenario 3 Scenario 4
dSAAMS 682.7 801.3 510.3 728.7
SAAMS 594.0 690.3 406.5 591.4
RSM 660.4 771.9 440.9 680.6
RHC 631.9 766.1 464.9 619.4
(b) Ratio of the waiting time (RWT, %).
Scenario 1 Scenario 2 Scenario 3 Scenario 4
dSAAMS 5.3 18.9 13.0 9.3
SAAMS 10.1 10.5 13.3 10.2
RSM 4.6 10.5 11.2 5.2
RHC 11.0 17.1 11.3 11.0
(c) Average travel distance per agent (ATD).
Scenario 1 Scenario 2 Scenario 3 Scenario 4
dSAAMS 76.0 90.9 55.4 80.4
SAAMS 78.7 97.9 63.7 69.7
RSM 116.8 138.5 118.1 114.5
RHC 116.3 143.2 104.5 115.7
and because the (d)SAAMS includes the concept of
service areas, agents are occasionally far from their
service areas when dropping off passengers, meaning
that the passengers may have to wait longer. Never-
theless, the dSAAMS still earned the highest OP even
in Scenario 2 (Table 5a) and a uniform environment
is unrealistic. Table 5c shows that the agents using
the dSAAMS have the smallest ATD because agents
using the dSAAMS were likely to wait in their ser-
vice area, thereby avoiding unnecessary moves. The
dSAAMS is thus the most cost- and energy-effective
control system.
5.4 The Waiting Place Strategy
To investigate the waiting points of the agents, we
generated heatmaps that indicate the numbers of vis-
its to each cell in the grid by each agent in Sce-
nario 1 (since it is the simplest scenario, facilitat-
ing the understanding of the agent behavior). The
heatmaps for four agents are shown in Fig.8. We
selected four agents that they were likely to pick
up passengers from different busy cells. Since the
demand occurrence rates were high on four corner
cells, these agents, especially the agents using the
dSAAMS, were likely to visit and stay at one cor-
ner (Fig. 8a). The agents using the SAAMS exhib-
ited a similar tendency but wandered a little; their ser-
vice areas were probably strongly affected by the po-
sitions of other agents (Fig. 8b). The agents using the
RSM seemed to identify the busy corners (Fig. 8c),
but since they were not using the concept of service
areas, they were likely to wait for new passengers
at the destination of their previous passengers or in
crowded cells near those destinations. This type of
movement can be successful when all areas are busy,
in which case agents will soon be able to find new
passengers. However, in some cases, agents using the
RSM had to wait in quiet areas or even in busy places;
that is, their waiting places could be biased. Under
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
108

Agent 0 Agent 1 Agent 2 Agent 3
(a) dSAAMS
Agent 0 Agent 1 Agent 2 Agent 3
(b) SAAMS
Agent 0 Agent 1 Agent 2 Agent 3
(c) RSM
Agent 0 Agent 1 Agent 2 Agent 3
(d) RHC.
Figure 8: Heatmap of agent locations in an episode of the testing phase.
the control of the RHC approach, the waiting loca-
tions changed more frequently (Fig. 8d) because for
example, when agents with passengers moved to their
destinations, other empty agents near the destination
would move away to maintain the strict balance be-
tween the number of agents in busy cells.
To investigate the strategies of the agents with the
dSAAMS more thoroughly, we generated a snapshot
of the service areas of all the agents at a certain time
step. A snapshot of the 30th time step is shown in
Fig. 9. We can see that the agents attempted to set
their service areas to cover the whole environment.
The service areas of almost all agents include one of
the busy cells, while two agents (5 and 9) covered less
busy cells with relatively wider service areas (the size
of the service areas was limited by T
x
and T
y
, which
Distributed Service Area Control for Ride Sharing by using Multi-Agent Deep Reinforcement Learning
109

Agent 0
Agent 1 Agent 2 Agent 3 Agent 4
Agent 5
Agent 6
Agent 7 Agent 8 Agent 9
Agent 10 Agent 11 Agent 12 Agent 13 Agent 14
Agent 15 Agent 16 Agent 17 Agent 18 Agent 19
Figure 9: Snapshot of agent service areas with the dSAAMS.
were set to 5). Note that the location and size of the
service areas varied over time, and the agents were
thus able to accept almost all passenger demands.
5.5 Using Manhattan data
We also evaluated dSAAMS using real-world data
from Manhattan, with the RSM and RHC tested for
comparison in Exp. 2. The Manhattan area was di-
vided into regions of size 22×11, and it was assumed
to be a grid environment for our experiment. We used
data obtained from Feb. 1 to 14, 2018 for training and
data from Feb. 15 to 21, 2018 for testing. We set
the number of agents |D| to 100 due to the limited
computational resources. This is much smaller than
the number of yellow cabs in NYC, which is usu-
ally limited to around thirteen or fourteen thousand
(excluding ride-sharing vehicles, such as Uber and
Lyft). Although we could not determine the appro-
priate number of taxis and although some taxis might
not be operating at a given time, we randomly reduced
the data by selecting data points with a probability of
|D|/8000 = 0.0125 (8,000 is about 60% of 13,000, by
assuming about 60% of all taxis are in operation). We
assumed that one time step was one minute and that
the length of one episode was 1440 steps (L
e
= 1440),
which corresponds to one day. The update interval of
target network was thus also set to 1440. The num-
ber of episodes in the training phase was 100. Since
the training data cover only two weeks, the same data
were used multiple times. This training length may
seem short, but the learning almost converged. The
value of ε was decreased linearly from 1.0 to 0.1. The
other experimental parameters were identical to those
in Tables 2 and 3.
For Exp. 2, the demand forecast data were, as in
other studies (Oda and Joe-Wong, 2018), generated
by a neural network whose inputs are two matrices
that represent the distribution of passengers during the
previous two steps. The output is the demand forecast
data for next step. The first layer consisted of thirty-
two 3 ×3 filters with a leaky rectified linear activation
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
110

Table 6: Results for the Manhattan data.
Parameter OP RWT ATD
dSAAMS 16347.1 6.9 557.1
RSM 16072.8 10.6 1100.2
RHC 16055.3 15.7 1227.7
unit (leaky ReLU). The next layer consisted of sixty-
four 2 × 2 filters with a leaky ReLU. The last layer
was a 1 × 1 filter with the same activation function.
The forecast data were updated every 30 steps to es-
timate the demand occurrence rates for the next 30
steps.
The results are summarized in Table 6. This table
indicates that the dSAAMS exhibited the best perfor-
mance in these experiments. There are several rea-
sons for its relatively good performance. First, the
agents using the dSAAMS were able to accept and
meet almost all the passenger demands, whereas the
other methods were occasionally unable to accept a
few demands. This enabled agents using dSAAMS
to earn greater OP. Second, the RWT and ATD of the
dSAAMS were much smaller than for the other meth-
ods. The agents using the RSM were again likely to
wait for new passengers near the destination of their
previous passengers, but these places were not neces-
sarily busy. As a result, passengers were more likely
to have to wait longer.
The strategy learned with the RSM seems be ef-
fective when all areas are busy because agents can
pick up their next passengers where they drop off their
previous passengers. The full results are not provided
here, but if we change the probability of reduction of
data from 0.0125 to 0.05 (making the area four times
busier), the agents using the RSM generate slightly
more OP than the agents using the dSAAMS. This oc-
curs even though in an incredibly busy environment in
which many demands were rejected even when using
the RSM. We believe that such situations are not real-
istic and that the number of passengers per agent will
instead be relatively small due to the entry of other
ride-sharing companies into the business, increasing
the competition rate between agents in a ride-sharing
market of constant size.
5.6 Remark
Comparing the centralized and decentralized
SAAMSs, it seems that the dSAAMS can dispatch
agents more appropriately in static situations (such
as Scenarios 1 and 2) and can adapt more flexibly to
changes in the environment (Scenarios 3 and 4) than
the SAAMS. The RSM, which is also decentralized,
also exhibited better performance than the SAAMS.
Although there were concerns about instability and
non-convergence due to the decisions being fully
decentralized, the networks converged for good
results. Fig. 8 shows that the dSAAMS prompted
fewer unnecessary movements than the SAAMS and
that it earned higher OP. Since the number of taxis in
operation always varies, we believe that the dSAAMS
can be efficient for actual ride-sharing control.
6 CONCLUSION
To improve the applicability to actual operations and
the overall benefits and efficiency of ride-sharing con-
trol, we propose the dSAAMS, in which each agent
uses their own deep Q-network to determine the ser-
vice area where they should wait for passengers. The
dSAAMS is a decentralized and extended version of
the SAAMS (Yoshida et al., 2020). Using dSAAMS,
we can easily increase the number of agents in a ride-
sharing company. In contrast, the centralized network
of the SAAMS controls all agents, and the structure
of the network must therefore be modified and re-
trained when a new agent is added. We conducted
experiments in simple simulated environments and in
a more complicated environment based on real data
acquired in Manhattan, New York. By learning the
service areas, the dSAAMS was able to reduce supply
shortages and biases, resulting in higher rewards and
reduced travel distances compared to existing meth-
ods.
One drawback of the dSAAMS is that it requires
a relatively long training time to obtain stable learn-
ing results when the number of agents is large, but we
believe that these calculations can be performed on a
large number of PCs in the cloud. We may also need
to use incremental learning, in which the number of
agents is gradually increased by adding new agents
that have no prior learned knowledge. Another pos-
sible approach is transfer learning, in which a small
number of agents learn in advance, and the number of
agents is then increased by transferring their knowl-
edge to new agents. These are the topics of our future
work.
ACKNOWLEDGEMENTS
This work was partly supported by JSPS KAKENHI
(17KT0044) and JST-Mirai Program Grant Number
JPMJMI19B5, Japan.
Distributed Service Area Control for Ride Sharing by using Multi-Agent Deep Reinforcement Learning
111

REFERENCES
Akkaya, I., Andrychowicz, M., Chociej, M., Litwin, M.,
McGrew, B., Petron, A., Paino, A., Plappert, M., Pow-
ell, G., Ribas, R., et al. (2019). Solving rubik’s cube
with a robot hand. arXiv preprint arXiv:1910.07113.
Alonso-Mora, J., Samaranayake, S., Wallar, A., Fraz-
zoli, E., and Rus, D. (2017). On-demand high-
capacity ride-sharing via dynamic trip-vehicle assign-
ment. Proc. of the National Academy of Sciences,
114(3):462–467.
Berbeglia, G., Cordeau, J.-F., and Laporte, G. (2012). A
hybrid tabu search and constraint programming algo-
rithm for the dynamic dial-a-ride problem. INFORMS
Journal on Computing, 24:343–355.
Cordeau, J.-F. and Laporte, G. (2003). A tabu search
heuristic for the static multi-vehicle dial-a-ride prob-
lem. Transportation Research Part B: Methodologi-
cal, 37(6):579 – 594.
Erhardt, G. D., Roy, S., Cooper, D., Sana, B., Chen, M.,
and Castiglione, J. (2019). Do transportation network
companies decrease or increase congestion? Science
Advances, 5(5).
Iglesias, R., Rossi, F., Wang, K., Hallac, D., Leskovec, J.,
and Pavone, M. (2017). Data-driven model predictive
control of autonomous mobility-on-demand systems.
2018 IEEE Int. Conf. on Robotics and Automation,
pages 1–7.
Ke, J., Zheng, H., Yang, H., and Chen, X. M. (2017).
Short-term forecasting of passenger demand under
on-demand ride services: A spatio-temporal deep
learning approach. Transportation Research Part C:
Emerging Technologies, 85:591 – 608.
Lin, K., Zhao, R., Xu, Z., and Zhou, J. (2018). Ef-
ficient large-scale fleet management via multi-agent
deep reinforcement learning. In Proc. of the 24th ACM
SIGKDD Int. Conf. on Knowledge Discovery & Data
Mining, KDD ’18, pages 1774–1783, New York, NY,
USA. ACM.
Ma, W., Pi, X., and Qian, S. (2019). Estimat-
ing multi-class dynamic origin-destination demand
through a forward-backward algorithm on computa-
tional graphs.
Miao, F., Lin, S., Munir, S., A Stankovic, J., Huang, H.,
Zhang, D., He, T., and Pappas, G. (2015). Taxi dis-
patch with real-time sensing data in metropolitan ar-
eas — a receding horizon control approach *. IEEE
Trans. on Automation Science and Engineering, 13.
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Ve-
ness, J., Bellemare, M. G., Graves, A., Riedmiller,
M., Fidjeland, A. K., Ostrovski, G., Petersen, S.,
Beattie, C., Sadik, A., Antonoglou, I., King, H., Ku-
maran, D., Wierstra, D., Legg, S., and Hassabis, D.
(2015). Human-level control through deep reinforce-
ment learning. Nature, 518(7540):529–533.
Nakashima, H., Matsubara, H., Hirata, K., Shiraishi, Y.,
Sano, S., Kanamori, R., Noda, I., Yamashita, T., and
Koshiba, H. (2013). Design of the smart access vehi-
cle system with large scale ma simulation. In Proc. of
1st Int. Workshop on Multiagent-Based Societal Sys-
tems.
NYC (2020). Nyc taxi limousine commission-trip record
data-nyc.gov. http://www.nyc.gov.
Oda, T. and Joe-Wong, C. (2018). MOVI: A Model-Free
Approach to Dynamic Fleet Management. In IEEE
INFOCOM 2018 - IEEE Conf. on Computer Commu-
nications, pages 2708–2716.
Silver, D., Hubert, T., Schrittwieser, J., Antonoglou, I., Lai,
M., Guez, A., Lanctot, M., Sifre, L., Kumaran, D.,
Graepel, T., Lillicrap, T., Simonyan, K., and Hass-
abis, D. (2018). A general reinforcement learning
algorithm that masters chess, shogi, and go through
self-play. Science, 362(6419):1140–1144.
Wang, Z., Schaul, T., Hessel, M., Hasselt, H., Lanctot, M.,
and Freitas, N. (2016). Dueling network architectures
for deep reinforcement learning. In Int. Conf. on Ma-
chine Learning, pages 1995–2003.
Wen, J., Zhao, J., and Jaillet, P. (2017). Rebalancing shared
mobility-on-demand systems: A reinforcement learn-
ing approach. In 2017 IEEE 20th Int. Conf. on Intelli-
gent Transportation Systems (ITSC), pages 220–225.
Yaraghi, N. and Ravi, S. (2017). The Current and Future
State of the Sharing Economy. SSRN Electronic Jour-
nal.
Yoshida, N., Noda, I., and Sugawara, T. (2020). Multi-agent
service area adaptation for ride-sharing using deep re-
inforcement learning. In Advances in Practical Ap-
plications of Agents, Multi-Agent Systems, and Trust-
worthiness. The PAAMS Collection, pages 363–375,
Cham. Springer.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
112
