
Improved HTM Spatial Pooler with Homeostatic Plasticity Control
Damir Dobric
1
, Andreas Pech
2
, Bogdan Ghita
1
and Thomas Wennekers
1
1
University of Plymouth, Faculty of Sciences and Engineering, U.K.
2
Department of Computer Science and Engineering, Frankfurt University of Applied Sciences, Germany
Keywords: Hierarchical Temporal Memory, Corticallearning Algorithm, Spatial Pooler, Homeostatic Plasticity.
Abstract: Hierarchical Temporal Memory (HTM) - Spatial Pooler (SP) is a Learning Algorithm for learning of spatial
patterns inspired by the neo-cortex. It is designed to learn the pattern in a few iteration steps and to generate
the Sparse Distributed Representation (SDR) of the input. It encodes spatially similar inputs into the same or
similar SDRs memorized as a population of active neurons organized in groups called micro-columns.
Findings in this research show that produced SDRs can be forgotten during the training progress, which causes
the SP to learn the same pattern again and converts into the new SDR. This work shows that instable learning
behaviour of the SP is caused by the internal boosting algorithm inspired by the homeostatic plasticity
mechanism. Previous findings in neurosciences show that this mechanism is only active during the
development of new-born mammals and later deactivated or shifted from cortical layer L4, where the SP is
supposed to be active. The same mechanism was used in this work. The SP algorithm was extended with the
new homeostatic plasticity component that controls the boosting and deactivates it after entering the stable
state. Results show that learned SDRs remain stable during the lifetime of the Spatial Pooler.
1 INTRODUCTION
The Hierarchical Temporal Memory Cortical
Learning Algorithm (HTM CLA) is an algorithm
inspired by the biological functioning of the
neocortex, which combines spatial pattern
recognition and temporal sequence learning
(Hawkins, Subutai and Cui, 2017).
It organizes neurons in layers of column-like units
built from many neurons, such that the units are
connected into structures called areas. Areas,
columns and mini-columns are hierarchically
organized (Mountcastle, 1997) and can further be
connected in more complex networks, which
implement higher cognitive functions like invariant
representations, pattern- and sequence-recognition
etc. HTM CLA in general consists of two major
algorithms: Spatial Pooler and Temporal Memory.
The Spatial Pooler operates on mini-columns
connected to sensory inputs (Yuwei, Subutai and
Hawkins, 2017) . It is responsible to learn spatial
patterns by encoding the pattern into the sparse
distributed representation (SDR). The created SDR,
which represents the encoded spatial pattern is further
used as the input for the Temporal Memory (TM)
algorithm.
The TM is responsible for learning of sequences
from SDR. Experiments in this work show that the
current version of the Spatial Pooler is instable.
During the learning process, learned patterns will be
forgotten and learned again. Results show that the
Spatial Pooler oscillates between stable and unstable
stable. Moreover, experiments show the instability is
related to the single pattern and not to the set of
patterns.
For example, The Spatial Pooler can keep the
stable SDR1 for pattern p1 while SDR2 for pattern p2
becomes unstable and so on. Having stable Spatial
Pooler is essential for all applications that rely on
spatial pattern recognition. Because SDRs produced
by the Spatial Pooler are also used as an input for the
Temporal Memory algorithm, an unstable Spatial
Pooler will also cause the Temporal Memory
algorithm to forget learned sequences.
In this work, the instability of the SP was
investigated an extension (modification) of the
Spatial Pooler is proposed, which ensures the better
stability of the algorithm.
2 METHODS
To analyse the stability of the Spatial Pooler, an
instance of the SP with the set of common parameters
was created (see table 1).
98
Dobric, D., Pech, A., Ghita, B. and Wennekers, T.
Improved HTM Spatial Pooler with Homeostatic Plasticity Control.
DOI: 10.5220/0010314200980106
In Proceedings of the 10th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2021), pages 98-106
ISBN: 978-989-758-486-2
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Table 1: Spatial Pooler parameters. Set of parameters
shown in the table are commonly used when working with
the Spatial Pooler.
Parameters Value
INPUT BITS 200
COLUMNS 2048
GLOBAL_INHIBITION true
NUM_ACTIVE_COLUMNS_PER_
INH_AREA
2% (40)
STIMULUS_THRESHOLD 0.5
SYN_PERM_INACTIVE_DEC 0.01
SYN_PERM_ACTIVE_INC 0.01
SYN_PERM_CONNECTED 0.1
MIN_PCT_OVERLAP_DUTY_CYCLES 0.001
MIN_PCT_ACTIVE_DUTY_CYCLES 0.001
POTENTIAL_RADIUS 1024
DUTY_CYCLE_PERIOD 100
MAX_BOOST 10
Most experiments were done with 2048 columns. In
this specific case, the scalar encoder was used to
encode input scalar values that are presented to the
Spatial Pooler during the learning process. As an
input, values between 0 and 100 were used. Before
presenting an input to the Spatial Pooler, every input
value was encoded with 200 bits, each value is
encoded with 15 non-zero bits. Figure 1 shows a few
examples of encoded scalar values.
For more detailed information about the meaning
of all parameters please see (Dobric, 2018).
The first row in Figure 1 represents the value ‘0’
and second-row the value ‘1’. The input value is on
right and the corresponding SDR is on left. Yellow
colour in the figure represents zero-bits and the grey
colour represents the non-zero bits. Grey dots on left
represent set of active columns after encoding of the
given input.
The Spatial Pooler algorithm implements a
boosting of columns inspired by homeostatic
plasticity mechanism (Turrigiano and Nelson, 2004),
(Davis and Graeme, 2006). This mechanism
influences excitation and inhibition balance of neural
cells and is likely important for maintaining the stable
cortical state. The functional stability of neural
circuits is achieved by homeostatic plasticity. It keeps
in balance the network excitation and inhibition and
coordinates changes in circuit connectivity (Tien and
Kerschensteiner, 2018).
Excitation mechanism in HTM is implemented
explicitly by algorithms Spatial Pooler and Temporal
Memory by setting cells inactive or predictive state.
Moreover, Spatial Pooler provides two inhibition
algorithms: Global Inhibition and Local Inhibition.
Inhibition algorithms control which cells around the
currently processing cell must be activated or
inhibited.
The boosting in the Spatial Pooler tracks the
column activity and makes sure that all columns are
uniformly used across all seen patterns. Because this
mechanism is continuously active, it can perform the
boosting of columns that already build learned SDRs.
Once that happens the Spatial Pooler will briefly
“forget” some learned patterns. If the forgotten
pattern is presented again to the SP, it will start
learning it again.
To analyse the learning behaviour of the Spatial
Pooler, a set of input patterns was presented to the SP
instance in many iteration steps.
Figure 1: Examples of two input values encoded by the
scalar encoder (right) and their corresponding Sparse
Distributed Representation (left) encoded by the Spatial
Pooler.
Every input pattern is encoded by Spatial Pooler into
SDR represented as a set of indices of active columns
𝐴
of the given pattern in the iteration k.
In every learning step of the same pattern, the
similarity between SDR in step k and the step k+1 is
calculated as shown in equation 1.
𝑠
|
𝐴
∩
𝐴
|
max |
𝐴
|, |
𝐴
|
(1)
The similarity 𝑠 is defined as a ratio between the
number of elements (cardinality) of the same active
columns in SDRs generated in steps k and k+1 and a
maximum number of active columns in two
comparing steps.
The Spatial Pooler is by definition stable if SDRs
of the same pattern does not change for the entire life
Improved HTM Spatial Pooler with Homeostatic Plasticity Control
99
cycle of the Spatial Pooler. In this case, the similarity
𝑠 between all SDRs of the same pattern is 100%.
Figure 2 shows the single input pattern presented
to SP in more than 25000 iterations.
Typically, Spatial Pooler learns patterns very fast.
It requires usually no more than two to three iterations
to learn the presented pattern. This behaviour is very
useful for real-life application because it does not
require a long training process.
Figure 2: Unstable Spatial Pooler. SP learns the pattern and
keeps the SDR unchanged for some iterations. When
boosting gets active SP forgets the SDR (similarity drops)
and starts learning again.
The y-axis shows the similarity s of SDRs in the
current iteration step and the previous step. The x-axis
shows the iteration step. The similarity of 100%
means the learned SDR does not change over time.
After an unspecified number of iterations, the SP
forgets the learned SDR and starts learning again.
Every time the SDR changes, it means the learned
SDR for that pattern is changed. Because the new
SDR for the pattern is created, the previously learned
one is forgotten. In that case, the similarity drops from
100% to zero or some other value. In contrast,
keeping the similarity on 100% means that learned
SDR for the same input is the same for the entire
iteration interval. If the similarity is less than 100%,
generated SDRs of the same input are different. This
indicates an unstable Spatial Pooler. As shown in
Figure 2 the learned state oscillates between stable
and unstable state during entire learning time, which
is not a useful behaviour for real-life applications.
This experiment clearly shows the instability of
the Spatial Pooler, but it does not show any details
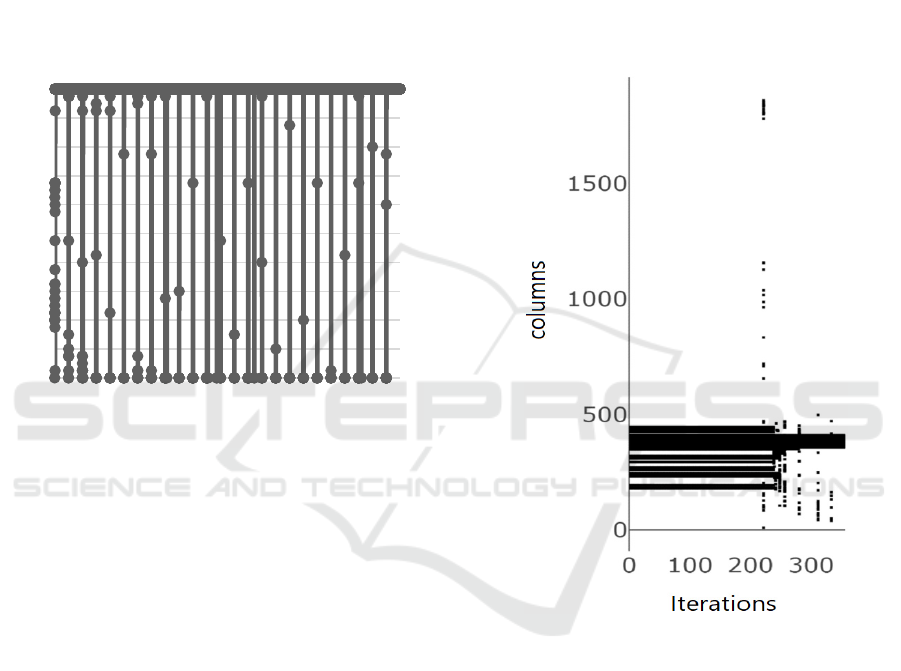
about the encoding of the SDR. Figure 3 shows the
same behaviour from a different point of view. It
shows how the SDR of the same pattern is encoded in
the first 300 iterations (cycles) on the example of a
single input value. The Spatial Pooler generates a
stable SDR right on the beginning of the learning
process and keeps it stable (unchanged) for approx.
200 iterations. After that SDR will change until the
Spatial Pooler enters the stable state again (not shown
in the figure) etc.
Figure 3: SDR shows active columns (SDR) of the learned
input in the first 300 iterations (cycles). The learned SDR is
unchanged (stable) in approx. first 200 iterations. After that,
it gets unstable.
In the next experiment, the boosting was disabled by
setting DUTY_CYCLE_PERIOD and
MAX_BOOST to zero value. These two values
disable boosting algorithm in the Spatial Pooler.
Results show that the SP with these parameters
produces stable SDRs as shown in Figure 4. The
figure shows an example of a stable encoding of the
single pattern with disable boosting algorithm. The
SP learns the pattern and encodes it to SDR in few
iterations (typically 2-3) and keeps it unchanged
(stable) during the entire life cycle of the SP instance.
By following this result, the stable SP can be
achieved by disabling of the boosting algorithm.
0
10
20
30
40
50
60
70
80
90
100
0
1667
3334
5001
6668
8335
10002
11669
13336
15003
16670
18337
20004
21671
23338
SDRsimilarityindependenceonthe
iterationstep
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
100
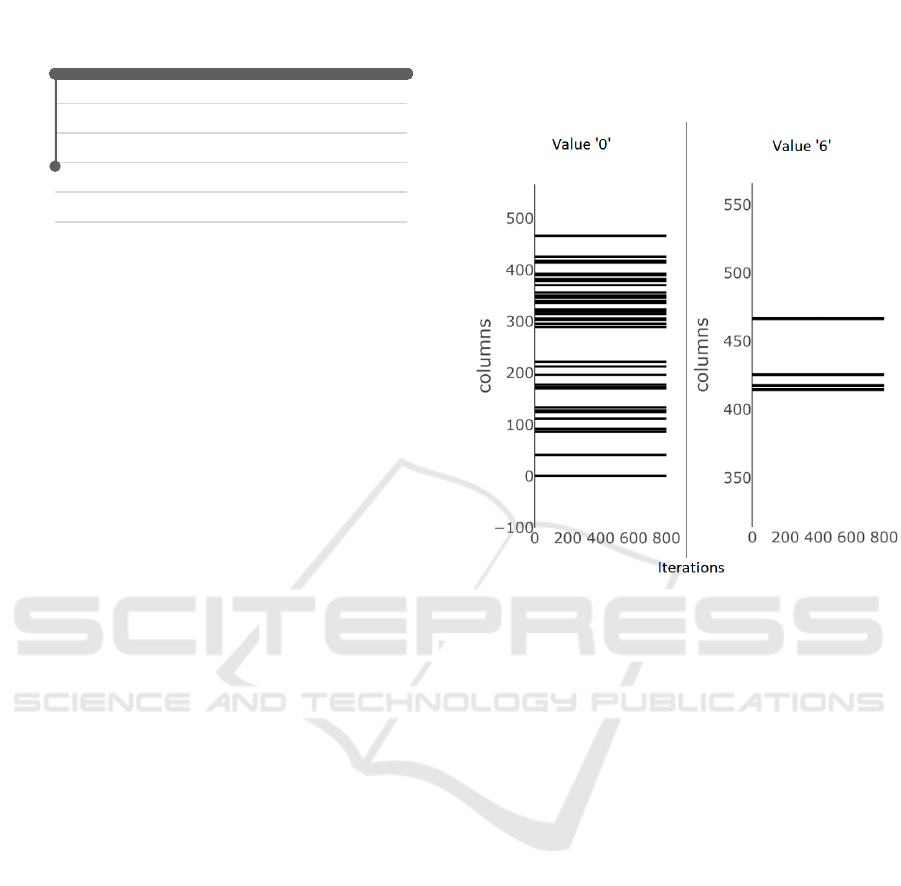
Figure 4: Spatial Pooler generates stable SDR after the
boosting is disabled.
Unfortunately, without the boosting mechanism, the
SP generates SDR-s with unpredictive number of
active mini-columns.
Figure 5 shows two input values ‘0’ and ‘6’. The
x-axis represents indexes of active mini-columns,
which participates in the encoding of the input value.
The y-axis represents the learning iteration. The SP is
stable if the SDR code does not change over time. As
already mentioned, disabling of boosting will cause
the SP to enter the stable state as shown in Figure 5.
The value ‘0’ is encoded with approx. 40 active
mini-columns and the value ‘6’ is encoded with 4
active mini-columns. This is a significant unwanted
difference. Experiments showed that some values can
even be encoded without any active mini-column if
boosting is disabled.
If the number of active mini-columns in an SDR
for different inputs is significantly different, the
further processing of memorized SDR-s will be
negatively influenced. Most operations in the
Hierarchical Temporal Memory rely on the
calculation of the overlap between neural cells,
synapses or mini-columns (Subutai, Hawkins, 2016).
In that case, SDR-s with the much higher number of
active columns will statistically produce higher
overlaps, which is not in balance with other SDR-s
with less active cells.
The parameter NUM_ACTIVE_COLUMNS_PER_
INH_AREA defines the percentage of columns in the
inhibition area, which will be activated by the
encoding of every single input pattern. Inspired by the
neocortex, this value is typically set on 2% (Hawkins,
Subtei, 2016). By using the global inhibition in these
experiments by the entire column set of 2048 columns
the SP will generate SDRs with approx. 40 active
columns. The boosting mechanism inspired by
homeostatic plasticity in neo-cortex solves this
problem by consequent boosting of passive mini-
columns and inhibiting too active mini-columns. As
long the learning is occurring, the SP will
continuously boost mini-columns. Every time the
boosting takes a place, some learned patterns (SDRs)
might be forgotten, and learning will continue when
the same pattern appears the next time.
Figure 5: Two SDRs with the different number of active
mini-columns produced by Spatial Pooler with disable
boosting.
It can be concluded that the stability of the SP can
be influenced by the boosting mechanism. The SP can
enter the stable state, but it will produce SDRs with a
significantly different number of active mini-
columns. In contrast, if boosting is enabled, the SP
will uniformly activate mini-columns, but the
learning will be unstable.
Previous findings in neural sciences (Maffei,
Nelson, Turrigiano, 2004) show that homeostatic
plasticity boosting is only active during development
of a newborn animal and then deactivated or shifted
from cortical layer L4, where Spatial Pooler is
supposed to be active. The Spatial Pooler operate on
sensory inputs, which are commonly connected to the
cortical layer L4 (Hawkins, Subutai and Cui, 2017).
By following this finding, this work extends the
Spatial Pooler algorithm and introduces the newborn
stage of the Hierarchical Temporal Memory and
Spatial Pooler.
2.1 The Spatial Pooler with the
New-born Stage
Deactivation of the boosting in homeostatic plasticity
in the cortical layer L4 can also be applied to Spatial
0
20
40
60
80
100
0
1563
3126
4689
6252
7815
9378
10941
12504
14067
15630
17193
18756
20319
21882
23445
SPkeepsstableSDR
Improved HTM Spatial Pooler with Homeostatic Plasticity Control
101

Pooler. It is still not clear exactly how this mechanism
exactly works. However, by following findings in this
area the same or similar mechanism inside of the SP
can be adopted. Currently, in the HTM, this
mechanism consists of boosting and inhibition
algorithms, which operate on the mini-column level
and not on the cell level inside of the mini-column.
The reason for this is that SP operates explicitly on
the population of neural cells in mini-columns and
does not makes usage of individual cells (Yuwei,
Subutai and Hawkins, 2017). Individual cells rather
play an important role in the Temporal Memory
algorithm (Hawkins, Subtei, 2016).
The main idea in this work, with the aim to
stabilize the SP and keep using the plasticity, is to add
an additional algorithm to SP, which does not
influence the existing SP algorithm. The extended
Spatial Pooler is based on the algorithm implemented
in the new component called Homeostatic Plasticity
Controller. The controller is “attached” to the existing
implementation of the Spatial Pooler. After the
compute in each iteration, the input pattern and
corresponding SDR are passed from the SP to the
controller. The controller keeps the boosting active
until the SP enters the stable state, measured over the
given number of iterations. During this time the SP is
operating in the so-called new-born stage and will
produce results similar to results shown in Figure 2
and Figure 3. Once the SP enters the stable state, the
new algorithm will disable the boosting and notify the
application about the state change. The controller
tracks the participation of mini-columns overall seen
patterns. After the controller notices that all mini-
columns are approx. uniformly used and all seen
SDRs are encoded with the approx. the same number
of active mini-columns, the SP has entered the stable
state. From that moment the SP will leave the new-
born stage and continue operating as usual but
without the boosting.
3 RESULTS
To approve of the Spatial Pooler algorithm can be
improved to reliably generate a stable state with the
help of the Homeostatic Plasticity controller, the
following experiment was designed. The experiment
(see Listing 1) executes 25000 iterations and presents
100 scalar values to the SP. The scalar encoder used
in line 11 is configured with the set of parameters
(line 5) described in Table 2.
Every input value (0-100) will be encoded as the
vector of 200 bits. Also, every single value from the
specified range will be encoded with 15 non-zero bits
as shown in Figure 1 - right.
Listing 1: Using of improved SP - Pseudo code.
0 function Experiment( inputSet )
1 begin ( 𝚰 )
2 | p // Set of SP parameters.
3 | hp,enp // Set of HPC and encoder parameters
6 | isStable = false
5 | en←create(enp)
6 | hpc ←create(hp, onStateChange);
7 | sp ←create(i, hpc);
8 | FOR i = 0; i<25000
9 | FOREACH i IN inputSet
10 | // Generate SDR for the input.
11 | o ← sp.compute(encode(i));
12 | IF isStable = true
13 | // new-born stage exited
14 | // Use stable SDRs. Custom code here.
15 | ENDIF
16 | ENDFOREACH
17 | ENDFOR
18 | end
19 |
20 | function onStateChange(state)
21 | begin
22 | isStable = true // Indicate the stable state
23 | end
The instance of the Spatial Pooler (line 7) with the
common set of parameters (line 3) has been created.
The same configuration was used in the experiment
described in the previous section, that produced
results shown in Figure 2 and Figure 3.
As next, the Homeostatic Plasticity Controller
(line 6) is typically attached to the Spatial Pooler
instance (line 7, second argument) and used inside of
the compute method.
The Homeostatic Plasticity Controller requires
the callback
function (line 6, second argument),
which is invoked when the controller detects the
stable state of the Spatial Pooler. The experiment is
designed to execute any number of training iterations
(line 8 defines 25000 iterations).
In every iteration, the Spatial Pooler is trained
with the whole set of input values 𝚰 line 9.
The spatial input is trained in line 11. The output
of the training step in line 11 is an SDR code (set of
active mini-columns) associated with the encoded
input value i. Before presented to the Spatial Pooler,
the input value i is encoded by the Scalar Encoder
configured with the named set of parameters shown
in Table 2. The encoder is represented as a function e
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
102

that converts the given scalar value to the binary
array:
𝑒: ℝ ⟶ 0,1
The computation inside of HTM operates
exclusively on binary arrays as the neo-cortex does it.
The existing SP compute algorithm is extended to
invoke the Compute method of the Homeostatic
Plasticity Controller (HPC) shown in Algorithm 1.
The HPC computation takes places after the Spatial
Pooler has computed the iteration.
The HPC Algorithm 1 starts with two inputs. The
first one is the binary array of encoded input pattern
and the second one is the SDR as calculated by the SP
for the given input.
Table 2: Scalar Encoder parameters.
Parameters Value
W – Bits for coding of the single value 15
N – Input bits 200
MinVal 0
MaxVal 100
On the beginning, the algorithm does not perform any
change in the SP. This period is called the newborn
stage. The Homeostatic Plasticity Controller will
disable the boosting in the Spatial Pooler after the
minimum required the number of iterations m is
reached (line 15). When the iteration number is larger
than m, the boosting is disabled by setting parameters
DUTY_CYCLE_PERIOD and MAX_BOOST to
zero. These parameters update the boost factors for
every single column in every iteration. The boost
factors are used in the Spatial Pooler to increase the
number of connected synapses (overlap) of inactive
columns. Increased overlap of inactive column
improves the chance of the column to become active.
After disabling of boosting the algorithm starts
tracking all seen patterns and their associated SDRs.
To avoid the saving of entire input dataset
internally, the function ℎ𝑎𝑠ℎ calculates the hash
value (line 6) over the sequence of bits of the input in
the current iteration. The calculated hash-value is a
sequence of bytes defined as a set H.
In line 8 the tuple of the input’s hash value H and
the number of active columns of the corresponding
SDR is associated with the set Ε. The set Ε
remembers p tuples of every input.
As discussed in the previous section, the goal is to
keep the number of active columns (non-zero bits)
uniform across all generated SDRs. The value 𝛿 is the
average change of the number of active cells per SDR
in the interval p (line 9).
Algorithm 1: Computation in HPC.
01 input: i // Set of neural cells. I.e. sensory input.
02 output: o // Set of active columns - SDR
03 configuration:
04 b // SP max boost
05 d // SP min pct. overlap duty cycles
06 begin
| // Calculate the hash value of the input of N bits.
07 | H ←ℎ𝑎𝑠ℎ(i);
| // Calculate the sum of active columns in SDR
08 | Ε ←H,
∑
𝑖
𝑜
∈𝒐)
| // The average change of num. of the act. columns
09| 𝛿 ←
∗
∑
|
ℇ
ℇ
| ℇ
∈ Ε
| // Calculate the correlation.
10| 𝑐 𝑐𝑜𝑟𝑟𝒐′, 𝒐 | 𝒐′ ∈ ℋ
| // Store input-hash and SDR pair
11| ℋ←H, o
| // Increment the counter of stable iterations for i.
12| Γ← γ
1𝛿 0, 𝑐 𝜃|0.9 𝜃 1, γ
∈ Γ
| // Fire stabe state event
13| StableState γ
𝜏,∀ γ
∈ Γ, 𝜏 ∈𝐍
| // Reset the counter of stable iterations for i.
14| Γ← 0
𝑐𝜃
|
0.9 𝜃 1.0
| // Disable boost after specified num. of iterations.
15| boost=off 𝑖𝑡𝑒𝑟𝑎𝑡𝑖𝑜𝑛 𝑚
16| end
The interval p is the number of previous iterations
used to calculate the 𝛿 . In most experiments, this
value was set to five.
The value 𝛿 is calculated as an average sum of
deltas ℇ
ℇ
in the last p iterations for the
given input hash value H.
𝛿 =
∗
∑
|
ℇ
ℇ
| ℇ
∈ Ε
Having this value zero is the first condition of the
stability of the new Spatial Pooler. This value is zero
if the number of active columns of the SDR of the
same input does not change over time defined by the
number of iterations p.
The second condition for stability of the Spatial
Pooler is the achieving of the constant SDR for every
input seen by the Spatial Pooler during the entire
training process. For this reason, the set ℋ is used to
keep tuples (H,o) of input hash values and their SDRs.
SDRs of inputs in upcoming iterations override the
previously-stored tuple of the current input. There is
always a single tuple (H,o) for every input inside of
ℋ. Tuples in ℋ are used to calculate the correlation
between previous and the current SDR of the given
input (lines 10, 11).
Improved HTM Spatial Pooler with Homeostatic Plasticity Control
103

If the correlation between the last SDR 𝒐′ and the
new (current) SDR 𝒐 of the given input i is larger then
the specified threshold 𝜃 (typically near 100%) and
the first condition 𝛿0 is fulfilled, then the counter
of stable iterations of the given input i is incremented
(line 12).
The second condition that corresponds to the
stable state of the Spatial Pooler is fulfilled if the γ
(number of stable iterations) reach the defined
threshold 𝜏 (line 13) for every seen input during the
training process. In most experiments, the chosen
value was between 15 and 150. Every time the
correlation value is less than threshold 𝜏 the counter
of stable iterations γ
for the given input is reset.
After entering the stable state all generated SDR-
s should remain unchanged for the entire lifetime of
the Spatial Pooler instance. The SP is defined as
stable if both described conditions are satisfied:
- uniform number of active cells in all SDRs and
- required number of stable iterations for all SDRs
is reached.
The implementation of the algorithm of HPC
(Dobric, 2020) continues to track the stability after
the SP has reached a stable state.
Some experiments show that SP can also get
unstable shortly after entering the stable state. If that
happens the unstable state will get stabilized soon in
typically few iterations. This behaviour is still under
investigation.
Figure 6: Spatial Pooler in the stable state representing two
SDRs of two input pattern examples with the activated
Homeostatic Plasticity Controller.
The experiment in Listing 1 was executed many
times (1000+) for various configurations and input
patterns previously discussed in this section.
As mentioned, the described Homeostatic
Plasticity Controller algorithm is injected in the
Spatial Pooler in line 7 in Listing 1.
Results show that the extended Spatial Pooler
with HPC algorithm gets always stable with the
uniformly distributed number of active columns for
all SDRs.
Figure 6 shows SDRs of two coincidently used
spatial input samples. Values ‘0’ and ‘1’ are both
encoded with the stable SDR after approx. 300
iteration. As shown in the figure, generated SDRs are
unstable in the first 300 hundred iterations. Active
columns which encode SDRs are in first 300 steps
continuously changed. This iteration interval is called
HTM new-born stage and it is defined by the
parameter m (line 15). In this stage the boosting is
active and SDRs of all inputs are changing during the
learning process.
After 300 cycles the HPC disables the boosting
and SDRs converge to very quickly to the stable state,
which remains during the life cycle of the Spatial
Pooler. In this experiment, tests were done with up to
30000 iterations. The SP remains stable with one
exception. As already mentioned, the SP can
sometimes leave the stable state shortly after entering
it. This instability is according to the design of the
HPC algorithm caused changed SDR of the currently
processing input. The HPC will in this case reset the
counter of stable iterations for the given input
(line14), which will declare the SP as unstable. When
this exception occurs, the learning can continue until
the SP enters the stable state again for the entire life
cycle of the SP instance. This unwanted behaviour
occurs when the chosen number of minimum required
iterations m is too small. Choosing larger values form
solves this exceptional behaviour but it takes a longer
time to leave the newborn stage and enters the stable
state. Application developers should choose a
reasonable value for their specific use case. Even if
this value is not ideally selected, the HPC will notify
the application when the SP gets instable. With this,
any required action can be performed inside of the
application.
Figure 7 shows this exceptional behaviour. The
HPC was configured in this experiment to use very
low minimum iteration required value m=25. This is
typically a very short new-born stage. The SP has not
enough time to uniformly activate all columns. The
SP entered the stable state but, in some iterations,
some mini-columns get deactivated and some new
mini-columns get activated. The red arrow in the
figure shows that last instability iteration. After the
iteration marked with the arrow, the SP gets stable
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
104

and remains stable. The figure shows 100 iterations
only due to the limited space.
Figure 7: Spatial Pooler soon after entering the stable state
become instable for some input patterns. After a few
iterations, the SP become stable again and it remains in the
stable state.
4 CONCLUSIONS
The Hierarchical Temporal Memory algorithm is
inspired by the neo-cortex and implements many
known features that have roots in neuro-sciences.
Nowadays many results show that the algorithm is
very flexible and can solve different kind of
problems. However, the reverse engineering of the
neo-cortex is still a complex and unsolved task. Many
design decisions in the algorithm base on assumptions
and work in progress. This paper focuses on the
instability issue of the HTM Spatial Pooler algorithm,
which has a task to memorize spatial patterns in an
unsupervised way. As discussed, the original Spatial
Pooler already integrates some sort of homeostatic
plasticity mechanism discovered in previous work in
neurosciences. However, the existing solution causes
instability in the learning process, which makes very
difficult to build applications. This work briefly
documented the named issue and offered the solution
by extending the existing SP algorithm with the new
component called Homeostatic Plasticity Controller.
The extended version of the SP is motivated by
finding in neurosciences, that documents the activity
of this mechanism during the development of the
species. Inspired with this finding the new
Homeostatic Plasticity Controller defines the
newborn stage of the Spatial Pooler. In this stage, the
SP stimulates the boosting of mini-columns and first
allows the instability in the learning process. After
the specified number of iterations, the HPC switches
off the boosting and waits for the SP to enter the
stable state. With this approach the SP converges to
the stable state and applications can be notified about
the state of the SP. This improves the quality of the
learning of the SP and enables the implementation of
more reliable solutions. Another work in progress in
this context is related to the design of the parallel
version of the HTM. The new HPC algorithm needs
to be validated for parallel implementation (Dobric,
Pech, Ghita and Wennekers, 2019).
REFERENCES
Davis, Graeme. (2006). Homeostatic Control of Neural
Activity - From Phenomenology to Molecular Design.
Annu. Rev. Neurosci. doi:10.1146
Davis, Graeme. (2013). Homeostatic Signaling and the
Stabilization of Neural Function. Neuron, 09.044.
Dobric. (2020). Implementation of Homeostatic Plasticity
Controller. Retrieved from GitHub - NeoCortexApi
repository: https://github.com/ddobric/neocortexapi/
blob/master/NeoCortexApi/NeoCortexApi/Homeostati
cPlasticityController.cs
Dobric, D. (2018). GitHub. Retrieved from NeoCortexAPI:
https://github.com/ddobric/neocortexapi
Dobric, Pech, Ghita, Wennekers. (2019). SCALING THE
HTM SPATIAL POOLER. International Journal of
Artificial Intelligence, 11(4).
Hawkins, Subtei. (2016). Why Neurons Have Thousands of
Synapses, a Theory of Sequence Memory in Neocortex.
Frontiers in neural circuts. doi:10.3389/
fncir.2016.00023
Hawkins, Subutai, & Cui. (2017). A Theory of How
Columns in the Neocortex Enable Learning the
Structure of the World. Frontiers in Neural Circuits,
11, 81-81. Retrieved 10 17, 2020, from
https://frontiersin.org/articles/10.3389/fncir.2017.0008
1/full
Maffei, Nelson, Turrigiano. (2004). Selective
reconfiguration of layer 4 visual cortical circuitry by
visual. Nature neuroscience, 1353-9.
Mountcastle. (1997). The columnar organization of the
neocortex. Journal of neurology, 120, 701-22.
Subutai, Hawkins. (2016). How do neurons operate on
sparse distributed representations? A mathematical
theory of sparsity, neurons and active dendrites.
ResearchGate.
Tien, Kerschensteiner. (2018). Homeostatic plasticity in
Improved HTM Spatial Pooler with Homeostatic Plasticity Control
105

neural development. ND - Neural Development, 13/9.
doi:10.1186
Turrigiano, Nelson. (2004). Homeostatic plasticity in the
developing nervous system. Nature Reviews
Neuroscience, 97–107.
Yuwei; Subutai; Hawkins. (2017). The HTM Spatial
Pooler, A Neocortical Algorithm for Online Sparse
Distributed Coding. Frontiers in computational
neurosciences, 11, 111.
APPENDIX
All experiments described in this paper are
implemented in C#/.NET Core 31. The Hierarchical
Temporal Memory framework with the Spatial Pooler
used in experiments is based on the open-source
project NeocortexApi. The source code and
documentation can be found at the GitHub (Dobric,
GitHub, 2018).
The experiment related to the stability of the
Spatial Pooleris implemented in a form of the
UnitTest inside of the Microsoft Unit Testing
framework integrated in Visual Studio. The test used
for the stability experiment is called
SpatialPooler_Stability_Experiment_3. It is
implementedin the source file SbStability.cs. This
code generatesthree output CSV files:-
ActiveColumns.csv,
-ActiveColumns-plotlyinput.csv and
-Oscilations.csv.
ActiveColumns files hold the same information in
a slightlydifferent format than ActiveColumns-
plotlyinput.csv. Bothfiles contain active columns
(SDR) for every trained digit in every iteration.
ActiveColumns-plotlyinput.csv can be used as the
input for the Python script to generate diagrams that
represent activecolumns shown in figure 6.
The script used go generate the diagram is called
draw_figure.py and can be found at the following
location:
/Python/ColumnActivityDiagram/draw_figure.py
Further information about running the script can
be foundin the Pyhton script
The file Oscilations.csv file is used to generate the
diagramshown in Figure 1. This diagram was
generated by Microsoft Excel.
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
106
