
Dreaming of Keys: Introducing the Phantom Gradient Attack
Åvald Åslaugson Sommervoll
a
Institute of informatics, University of Oslo, Problemveien 7, 0315 Oslo, Norway
Keywords:
Phantom Gradient Attack, Key Recovery, Neuro-cryptanalysis, Backpropagation, Neural Network,
Replacement Function.
Abstract:
We introduce a new cryptanalytical attack, the phantom gradient attack. The phantom gradient attack is a key
recovery attack that draws its foundations from machine learning and backpropagation. This paper provides
the first building block to a full phantom gradient attack by showing that it is effective on simple cryptographic
functions. We also exemplify how the attack could be extended to attack some of ASCONs’ permutations,
the cryptosystem that won CAESAR the competition for authenticated encryption: security, applicability, and
robustness.
1 INTRODUCTION
Neural networks have the past decade seen a wide ar-
ray of academic and commercial applications. One
notable exception is cryptography
1
. A reason is that
neural networks rely on gradients of differentiable
functions, while encryption and decryption typically
rely on discrete functions. Our contribution is to
replace these discrete functions with piecewise dif-
ferentiable functions, thereby allowing for a neural
network-based key-recovery. We dub this the phan-
tom gradient attack, which aims to link the step-wise
training of neural networks to key-recovery. The at-
tack can be used to attack almost any cryptosystem.
We attack some basic cryptographic functions and
show how the attack could be extended to attack more
complex cryptosystems like ASCON.
In 2015 Google released DeepDream, popularized
the idea of "training"
2
the input using a pre-trained
network. The phantom gradient attack builds on this
idea by representing a cryptosystem as a neural net-
work. This way, the cryptosystem acts as a pre-trained
network, and we use it to train on our input. This
training aims to recover the secret key. However, a lot
of cryptographic functions are discrete and thereby do
not have gradients. An essential part of our attack is
to replace the discrete functions with piecewise dif-
a
https://orcid.org/0000-0001-5232-5630
1
Neural networks have shown promise in side channel
attacks, but not on an algorithmic level.
2
We write "training" in quotation since we are updating
on the input and not the weights.
ferentiable ones. These functions have gradients, and
we call these the phantom gradients of the original
discrete function. The choice of the piecewise differ-
entiable function is crucial, and we will refer to these
functions as replacement functions
3
. Moreover, we
will highlight some choices that correlate with suc-
cessful attacks and state some general principles for
good replacement functions.
In symmetric key encryption, there is a secret key,
k, which is used for encryption and decryption. In
this case, we can view the encryption as a function f
k
and decryption as its inverse f
−1
k
. Finding this f
−1
k
is trivial if k is known, but it is intentionally hard if k
is unknown. The phantom gradient attack presented
in this paper attempts to recover this k. More specifi-
cally, the phantom gradient attack attempts to recover
an input that would result in a specified output. In
other words, given f (x) = y, it searches for an x
∗
such
that f (x
∗
) = y, given that the function f and output y
are known. If we look at our encryption we have:
Enc
k
(p) = f
k
(p) = f (k, p) = c, (1)
where p is the plaintext and c is the ciphertext. How-
ever, as the plaintext is unknown in this case, we
would recover both k
∗
and p
∗
. Furthermore, since
|k| + |p| is likely to be much larger than |c|, the re-
covered k
∗
would most likely
4
be different from k.
3
These replacement functions can often be viewed as ex-
tensions to their discrete counterpart, as they typically act
the same for valid discrete inputs. However, this is not a
requirement.
Sommervoll, Å.
Dreaming of Keys: Introducing the Phantom Gradient Attack.
DOI: 10.5220/0010317806190627
In Proceedings of the 7th International Conference on Information Systems Security and Privacy (ICISSP 2021), pages 619-627
ISBN: 978-989-758-491-6
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
619

Therefore we assume that the plaintext is known so
the plaintext can act as a constant. This way, we
may only focus on finding a k
∗
. In order to find such
a k
∗
, we have to take a closer look at the function
5
f
p
. As already mentioned, we wish to represent this
f
p
as a neural network. To do this, we look at the
individual functions that take part in the encryption
and find piecewise differentiable functions to replace
them. These replacement functions are of great im-
portance, as their derivatives are what we use to re-
cover the key.
The remaining paper is organized as follows: Sec-
tion 2 discusses related work. Next, section 3 pro-
vides some details regarding implementations and an
application of our attack on the XOR function. In sec-
tion 4, we briefly introduce ASCON and its basic per-
mutations, p
C
, p
S
, and p
L
. We show that the input is
easily recovered for the first two, whereas p
L
is less
susceptible to our phantom gradient attack. Finally,
we conclude our findings in section 5 and cover pos-
sible future work in section 6.
2 RELATED WORK
Our phantom gradient attack has a clear connec-
tion to the field of neuro-cryptology. A field that
was first formally described by Dourlens in his 1996
masters dissertation (Dourlens, 1996), where he de-
scribed the possibility of neuro-cryptography and
neuro-cryptanalysis. Since then, we have seen the ad-
dition of a neural cryptosystem in 2002 by Kinzel and
Kanter (Kinzel and Kanter, 2002). They synchro-
nized two neural networks by sending the networks’
outputs through a public channel and training on
them. Unfortunately, this cryptosystem was not com-
pletely secure, as Klimov et al. (Klimov et al., 2002)
published a paper the same year that broke it three
different ways. In neuro-cryptanalysis, Alini success-
fully applied an attack on DES and Triple-DES using
neuro-Cryptanalysis in 2012s (Alani, 2012). He, like
us, was working in the known-plaintext case. How-
ever, he is not interested in key-recovery. Instead,
he simulates the decryption of DES and Triple-DES
under a specific key. In this effort, his inputs are
ciphertexts, and his reference outputs are plaintexts
and train the weights accordingly. This procedure is
in great contrast to our implementation, which trains
no weights, uses the ciphertext as reference output,
4
The phantom gradient attack could be fed multiple ci-
phertexts to increase this probability - more on this in sec-
tion 6.
5
The p is subscript because it is assumed to be constant
and is not an argument for the function.
and a guessed key as input. His implementation re-
quired an average of 2
11
plaintext ciphertext pairs for
DES and 2
12
for Triple-DES. In the phantom gradi-
ent attack implementation put forward in this paper,
we only train on plaintext ciphertext pair, as we only
want to recover a possible key. However, more train-
ing samples could help us avoid stagnation and ensure
that the key recovered is the correct key; this may be
fruit for future work. With his network trained to pre-
dict the ciphertext given the plaintext, he attempts to
use his network to predict the ciphertext for new mes-
sages with some success
6
. Greydanus also attempts
to use neural networks to simulate cryptosystems in
his work, Learning the Enigma with Recurrent Neu-
ral Networks. This work exemplified some of the dif-
ficulty of simulating and learning a cipher with re-
current neural networks, even an outdated cryptosys-
tem like Enigma (Greydanus, 2017). This work con-
tributed to the phantom gradient attack introduced in
this paper to only focus on a stateless FFNN repre-
sentation instead of recurrent neural networks, which
can be more memory efficient. Long before the pop-
ularization of Googles DeepDream in 1988 Lewis
in his work Creation By Refinement: A Creativity
Paradigm for Gradient Descent Learning Networks
(Lewis, 1988) exemplified the idea of training on in-
puts. He trained a classification network to judge is a
sequence of 5 music notes where valid or not. Then
he used the trained network to generate music notes
using backpropagation. Like Alani, (Alani, 2012),
he first trains the network’s weights, while the phan-
tom gradients are predefined. This approach differs
from the phantom gradient because his gradients are
found through training of the neural network, while
the phantom gradients are predefined. This defini-
tion gives the phantom gradients a larger degree of
freedom, but at the cost of having perhaps unsuitable
gradients. In terms of image generation and visualiza-
tions, there are many more works (Portilla and Simon-
celli, 2000; Erhan et al., 2009; Simonyan et al., 2013).
In these works, they always train on the entire input.
However, our phantom gradient attack will often be
used to attack only a specific part of the input. For
example, in ASCON, we know a lot about the initial
state of the sponge duplex construction (Dobraunig
et al., 2016). Some techniques for generating adver-
sarial examples also attack specific parts of the input,
like One Pixel Attack for Fooling Deep Neural Net-
works by Su et al. There they change just one pixel in
an image to fool a pre-trained network into misclassi-
fying the image. BriarPatches: Pixel-Space Interven-
tions for Inducing Demographic Parity by Gritsenko
6
The average number of wrong bits in the unseen pair is
8.3% for DES and 11.4% for Triple-DES.
ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy
620

et al. does something similar; however, their interven-
tion is on a larger area of the image but constrained to
be a small patch (Gritsenko et al., 2018). An alterna-
tive to representing the discrete cryptographic func-
tions to continuous ones is to use the discrete func-
tions, and train using binarized networks (Zhu et al.,
2019). Networks that train on bit operations without
proper gradients see considerable speedup compared
to traditional networks, but at the cost of their accu-
racy.
3 IMPLEMENTATION AND
RESULTS
Punishment. The loss function tells us if our train-
ing brings us closer to the actual output. However, it
is not built into the loss function to take into account
whether or not the predicted values are in the correct
range. As we aim to recover bits, values larger than
1 and less than 0 are meaningless
7
. To prevent values
from becoming increasingly negative or much greater
than one, we introduce an additional punishment for
such values. We choose a ridge regression like pun-
ishment measure: Our experiments found that a pun-
ishment closely related to that of a ridge regression
worked well:
punish
ridge
(x) =
1
2
(x − 1)
2
for x > 1
0 for 0 ≤ x ≤ 1
1
2
x
2
for x < 0
. (2)
This allows the learning to take values outside the
range [0,1] but should help keep the values close to
proper bit values. We also introduce a scalar λ
punish
,
which we use to adjust the punishment in relation to
the loss.
Rounding. At the end of our run, the guessed key k
∗
typically consists exclusively of floating-point num-
bers. Therefore if we have reached our final iteration,
we round the guessed key, k
∗
, to force it to assume
integer values. This rounding at the end is primarily
to polish the recovered key, but may in some cases,
allow us to take the final leap to a candidate key k
∗
.
Momentum, Gradient Clipping and Decay. We
may add momentum to our gradient descent by up-
dating our input x
i
like so: x
new
i
= x
i
− η · (
∂loss
∂x
i
+
7
Numbers between 0 and 1 can be interpreted as prob-
abilities. Numbers above 0.5 may be viewed as it is more
likely to be a one than a zero.
momentum ·
∂loss
old
∂x
old
i
). Furthermore, to take incremen-
tally smaller steps, we introduce a decay to the learn-
ing rate: Each iteration, the learning rate, eta, is up-
dated: η =
η
1+decay
. This way, decay = 0 gives no de-
cay. To avoid overly large gradients, we introduce a
negative minimum gradient and a positive maximum
gradient. We clip gradients smaller or larger than this
threshold, a common technique to combat exploding
gradients (Zhang et al., 2019).
Remap Input. Some initial experiments showed
that even with ridge punishment, the inputs could be
led astray by the phantom gradients. Furthermore,
we found that typically with phantom gradients from
eq. (10), if a bit became overly positive, its true value
was typically 0. Similarly, if the bit value became
overly negative, its true bit value was typically 1. To
combat these stray gradients, we remap the inputs, so
that overly positive bits are set to 0, and overly nega-
tive bits are set to 1. We define overly positive to be at
1.5 and overly negative to be at -0.5. This way, when
we round at the end of the run, we force the network to
make a valid guess restricted to valid bit values, and
at the same time, we allow the bits to explore some
values outside the valid range of 0 and 1. To indi-
cate when this stricter boundary is used, we write that
remap is true. We also tried input clipping, but this
technique was much better at combating stagnation in
the learning, as it also forces the algorithm to change
its guess.
3.1 Phantom Gradient Attack on XOR
Practically all modern cryptosystems work exclu-
sively on bits. Therefore, the use of binary functions
in encryption is widespread. Perhaps most common
is the XOR function, which takes two bits and returns
their sum modulo 2. By itself, XOR can be used to
provide perfect security (Shannon, 1949) by using the
encryption function:
Enc
k
(p) = k ⊕ p = c, (3)
where p is the plaintext, k is the key, and ⊕ is used
to symbolize bitwise addition modulo 2. Each bit in
the key k is random and independent of the other bits,
with a 50 % probability of 0 and a 50% probability
of 1. This provides perfect security since the proba-
bility of observing the ciphertext c is independent of
the plaintext p, in other words: P(c|p) = P(c). How-
ever, that does not mean that the plaintext p holds no
significance. If we assume that the plaintext is known
to the attacker, he can recover the key by computing
c ⊕ p. This trivial case where we know the plaintext
p and the ciphertext c can also effectively be attacked
Dreaming of Keys: Introducing the Phantom Gradient Attack
621

by the phantom gradient attack. This case can be rep-
resented as the network seen in fig. 1. Here g
p
i
is used
to represent our piecewise differentiable function that
we use to represent XOR with the i-th bit value in the
plaintext. A natural thought when choosing g
p
i
is to
let it be bitwise addition paired with a sine activation
function to constrain it to modulo 2. However, the
unpublished work by Parascandolo et al. (Parascan-
dolo et al., 2016) showed some of the complications
of learning with a sine activation function. Therefore
we choose to instead separate XOR with constant 1
and XOR with the constant 0 into:
g
p
i
(x) =
(
1− x for p
i
= 1
x for p
i
= 0.
(4)
It must be stressed that this choice is just one among
many. For any gradient descent, we need a loss func-
tion; for this paper, we will use a square error:
loss =
1
2
n
∑
i
(c
∗
i
− c
i
)
2
, (5)
where c
∗
i
is the predicted output bit in the i-th posi-
tion, and c
i
is the true bit value of the ciphertext in the
i-th position. With this replacement function, this loss
function, and input a, and learning rate η = 1, this
replacement function can always recover the full key
in one step. Formally, by recovering the full key, we
mean that all the bits in the key are correct; similarly,
if one or more bits are incorrect, the full key has
not been recovered. Since all inputs are independent
we can illustrate all possible outcomes by letting
~p = [1, 0,1,0] and the targets be ~c = [1, 1, 0, 0].
Then we can construct the neural network based on
fig. 1 and eq. (4). On such a network, a single iteration
k
1
g
p
1
(x)
c
1
k
2
g
p
2
(x)
c
2
k
n
g
p
n
(x)
c
n
where n is the number of bits in the plaintext p, and g
p
i
is
the reduction of f
p
that only works on a single bit instead
of a bit sequence.
Figure 1: XOR with a constant as a FFNN.
would be:
k
∗
0
= k
∗
0
− η ·
∂loss
∂k
∗
0
= a − 1·
∂loss
∂c
∗
0
∂c
∗
0
∂k
∗
0
= 0 (6)
k
∗
1
= k
∗
1
− η ·
∂loss
∂k
∗
1
= a − 1·
∂loss
∂c
∗
1
∂c
∗
1
∂k
∗
1
= 1 (7)
k
∗
2
= k
∗
2
− η ·
∂loss
∂k
∗
2
= a − 1·
∂loss
∂c
∗
2
∂c
∗
2
∂k
∗
2
= 1 (8)
k
∗
4
= k
∗
4
− η ·
∂loss
∂k
∗
4
= a − 1·
∂loss
∂c
∗
4
∂c
∗
4
∂k
∗
4
= 0. (9)
We observe that the recovered
~
k
∗
is correct and was
found independently from the initial input a. The key
can also found with an η smaller than 1; this would
just take more iterations.
3.2 XOR between Two Inputs
XOR between two inputs is also common in mod-
ern cryptosystems, especially in the construction of S-
boxes
8
. Like previously, we have to represent XOR
as a piecewise continuous function. One approach is
to build on the previous replacement function and cre-
ate the nonlinear function:
f (x, y) = x + y − 2xy, (10)
which has all the desired XOR properties, and it col-
lapses to the cases in eq. (4) if one of the bits in ques-
tion are constant. The derivatives of this function is
∂ f
∂x
= 1 − 2y and
∂ f
∂y
= 1 − 2x, which means that the
gradient is 0 for x =
1
2
or y =
1
2
. The vanishing gra-
dients at 0.5 is a potential weakness as this value may
act as a barrier preventing movement from values be-
low 0.5 to move above 0.5 and vice versa. A way to
address this concern is to have gradient descent with
momentum. Additionally, the full gradient may not
be 0 at 0.5 since the loss typically depends on many
outputs, such as out1 and out2 in eq. (12).
Example: The simplest example, in this case, is just
two bits as input, which are XOR-ed, as shown in
fig. 2. As in section 3.1, we want to train on the initial
x
1
f (x
1
,x
2
)
out
1
x
2
out
2
Figure 2: Example FFNN for XOR between two inputs.
8
S-boxes stands for substitution boxes, and are often
computed by a network so that the substitution can go fast
in hardware.
ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy
622

(a) Input history (1,1) (b) Contour plot (1, 1)
(c) Input history (
1
2
,
1
2
) (d) Contour plot (
1
2
,
1
2
)
Figure 3: XOR between inputs learning success.
(a)+(c): The y-axis gives the guessed input bit, and the x-
axis counts the number of iterations. The blue line is for the
guessed bit for x
1
, and the green line gives the guessed bit
for x
2
. (b)+(d): In the contour plot, we have plotted x
1
, x
2
,
and the loss against each other. Each dot corresponds to a
guess, and the iteration number of the guess is written next
to the dot. As the number of iterations increases, the dots
color change from blue to red, and the target is shown as a
black dot.
guessed inputs; we call these inputs x
1
,x
2
. We see
that x
1
is xor-ed with x
2
, while x
2
is left unaltered,
meaning that we get the following gradients:
∂loss
∂x
1
=
∂loss
∂out1
·
∂out1
∂x
1
(11)
∂loss
∂x
2
=
∂loss
∂out1
·
∂out1
∂x
2
+
∂loss
∂out2
·
∂out2
∂x
2
. (12)
It must be noted that even in this simple example, of
phantom gradient attack can fail. If try to recover
x
1
= x
2
= 0, and start with initially random x
1
and x
2
we get a recovery rate of 96% (9599 out of 10000). In
other words, the starting point can hold great signif-
icance for the success of our attack. To analyze this,
we look at two cases, initial input [1,1] and [0.5, 0.5],
as can be seen in fig. 3. We see that in fig. 3b, the
phantom gradients lead the input astray, and it gets
stuck in a repeating pattern. However, with a better
starting point like [0.5,0.5], learning is easy, and the
solution is found almost instantly. A possible pitfall
may be that the phantom gradients lead our guesses
astray by moving them outside the range of 0 and 1;
in section 6, we discuss ways to prevent this.
4 ATTACK ON ASCON’s
UNDERLYING FUNCTIONS
ASCON is a cryptography system for lightweight au-
thenticated encryption and hashing. It has entered two
competitions:
1. The Competition for Authenticated Encryption:
Security, Applicability, and Robustness (CAE-
SAR) (Dobraunig et al., 2016).
2. NIST’s Lightweight Cryptography standardiza-
tion competition (Dobraunig et al., 2019).
So far in the competitions, it has won CAE-
SAR (Bernstein, 2019) and is currently a third-
round qualifier of the NIST standardization compe-
tition (NIST, 2020). ASCON has many different ver-
sions; for this paper, we will investigate its most cur-
rent iteration, ASCON v1.2. Furthermore, within AS-
CON v1.2, there are some variants. We will only be
looking at encryption and decryption using ASCON-
128 within ASCON v1.2. From this point on, when
we refer to ASCON encryption and ASCON permuta-
tion, we refer to them as they are in ASCON-128 v1.2,
details in table 1. Full ASCON encryption uses a se-
cret state of 320 bits that undergo a series of permuta-
tions. Only 64 bits are observed before the state is per-
muted again. This segmentation of the observed out-
put means that if one were to attack the ASCON en-
cryption using the phantom gradient attack, we would
only get gradients from 64 bits to attack a 128-bit key.
We can use additional 64-bit blocks, recover possible
intermediate states, and work backward from these
possible intermediate states. However, in this paper,
we will only be looking at ASCON’s three permuta-
tions; p
C
, p
S
, and p
L
. To clarify the individual steps,
we divide p
S
into p
S
1
, p
S
2
, and p
S
3
. Furthermore,
when running our neural networks, we use the set-
tings seen in table 2.
4.1 p
C
Permutation
The first permutation in ASCON is the p
C
permuta-
tion, which only consists of an XOR with a constant
9
.
Table 1: ASCON-128 specifications.
Number of bits # rounds
key nonce tag S
r
S
c
p
a
p
b
128 128 128 64 256 12 6
(This table is heavily influenced by table 1 in the ASCON
v1.2 submission to CAESAR (Dobraunig et al., 2016).)
9
This constant varies with p
b
and p
a
and how many per-
mutations that have taken place.
Dreaming of Keys: Introducing the Phantom Gradient Attack
623
In section 3.1, we saw that this could be easily solved
using the phantom gradient attack.
4.2 p
S
Permutation
The p
S
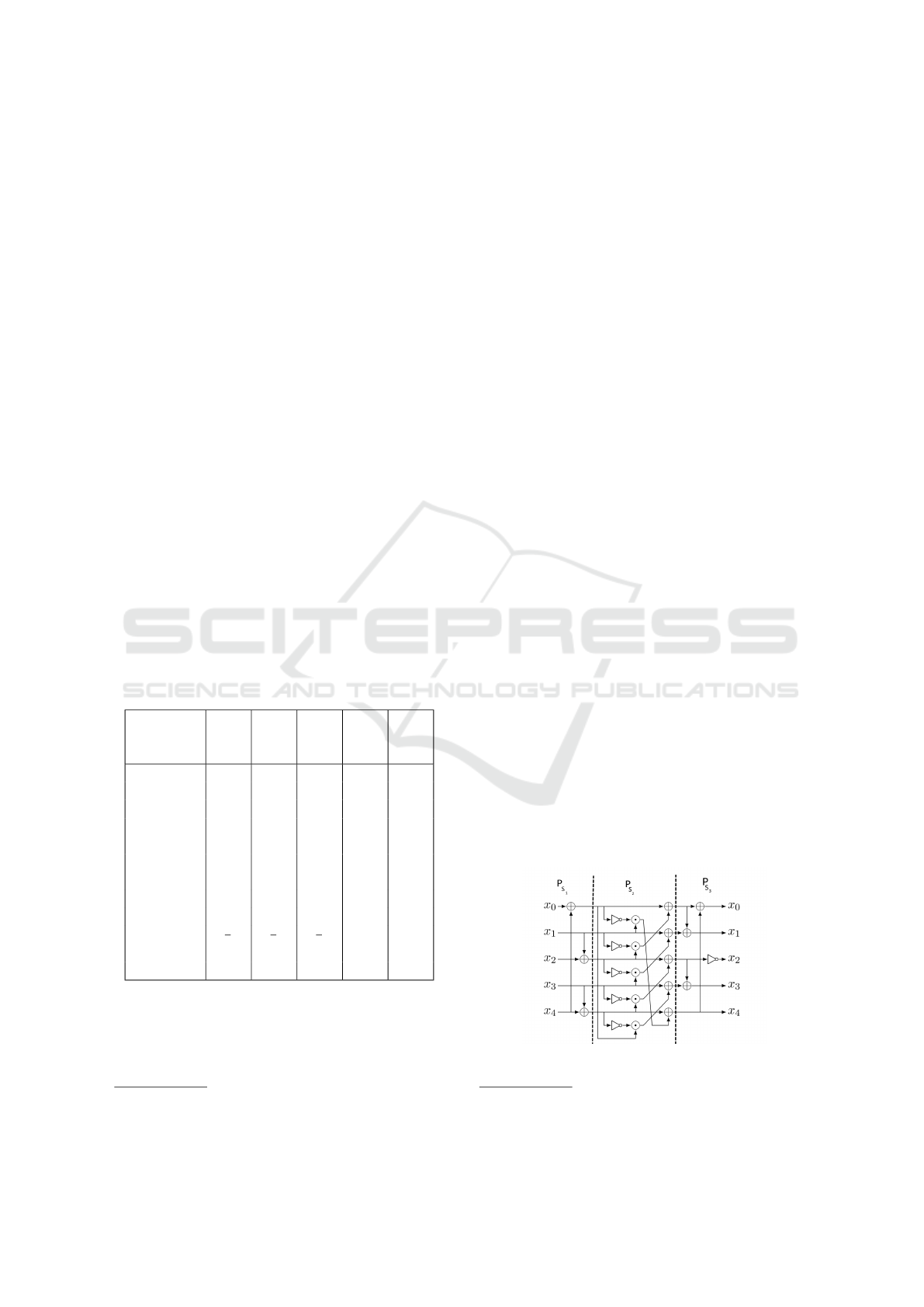
permutation defines a 5-bit substitution. As it
only works on 5 independent bits, we can reduce the
problem from 320 bits down to 5 without losing any
complexity. This reduction allows us to check phan-
tom gradient attacks recovery capabilities on any of
the possible 32 (2
5
) different inputs. This substitu-
tion can be expressed as a series of XOR-, AND- and
NOT- gates. To further simplify this network, we di-
vide it into three parts p
S
1
, p
S
2
, and p
S
3
, as shown in
fig. 4.
4.2.1 p
S
1
Permutation
For p
S
1
we have the following mapping:
p
S
1
x
0
x
1
x
2
x
3
x
4
=
x
0
⊕ x
4
x
1
x
2
⊕ x
1
x
3
x
4
⊕ x
3
.
The p
S
1
permutation only uses three XOR’s, all
10
of
which we can represent with eq. (10). With phantom
gradients from eq. (10) and settings as in table 2, we
recover the input in all 32 cases.
Table 2: Settings for backpropagation.
parameter p
C
p
S
1
p
S
2
and
p
S
3
p
S
Σ
1
and
Σ
2
η 1 0.01 0.2 0.02 0.2
momentum 0 0.01 2e-3 0.2 0.9
decay 0 10
−3
10
−4
10
−9
1
max gra-
dient
∞ ∞ 7 7 7
min gra-
dient
−∞ −∞ −7 -7 -7
λ
punish
0 0 4e-3 0.04 0.04
remap False False False True True
Initial in-
put
{
1
2
}
5
{
1
2
}
5
{
1
2
}
5
.4,.6 na
Iterations 1000 1000 1000 1000 1000
4.2.2 p
S
2
Permutation
The p
S
2
permutation can be expressed as:
10
We just have to make sure that x
4
⊕ x
3
happens after
x
0
⊕ x
4
.
p
S
2
x
0
x
1
x
2
x
3
x
4
=
x
0
⊕ (NOT (x
1
) · x
2
)
x
1
⊕ (NOT (x
2
) · x
3
)
x
2
⊕ (NOT (x
3
) · x
4
)
x
3
⊕ (NOT (x
4
) · x
0
)
x
4
⊕ (NOT (x
0
) · x
1
)
.
We replace the NOT gate
11
with 1 − x
1
, and the ⊕
function with eq. (10):
f (x
i
,x
j
,x
k
) = x
i
+ (1− x
j
) ∗ x
k
− 2∗ x
i
∗ (1− x
j
) ∗ x
k
,
(13)
where j = i + 1(mod5) and k = i + 2(mod5). This
means that bitwise rotations should act equivalently,
that is a bit sequence [b
0
,b
1
,b
2
,b
3
,b
4
] should be-
have similarly to [b
1
,b
2
,b
3
,b
4
,b
0
], [b
2
,b
3
,b
4
,b
0
,b
1
],
[b
3
,b
4
,b
0
,b
1
,b
2
] and [b
4
,b
0
,b
1
,b
2
,b
3
]. The equiv-
alent permutation groups are shown in table 3. To
achieve full key recovery for any key, we use the set-
tings as seen in table 2. All the inputs that belong
to the same group recovered their bit sequence after
the same number of iterations. However, perhaps sur-
prisingly, group 4 and group 6 need 199 and 159 it-
erations, while the slowest of the remaining groups
finish in 48 iterations. This wide gap is a little sur-
prising. It can be related to the fact that groups 4 and
6 are the two groups containing the only two-bit alter-
nating sequences: 01010 and 10101. This fact may be
a coincidence, but it seems like our phantom gradients
struggle a little with such alternating bit sequences at
p
S
2
.
4.2.3 p
S
3
Permutation
The p
S
3
is defined as:
p
S
3
x
0
x
1
x
2
x
3
x
4
=
x
0
⊕ x
4
x
1
⊕ x
0
1 − x
2
x
3
⊕ x
2
x
4
We see that this permutation only consists of previ-
ously defined functions: XOR between two indices,
Figure 4: Binary network for the S-box in p
S
permutation
divided into p
S
1
, p
S
2
, and p
S
3
.
11
Note that this is the same as our replacement function
of XOR with 1 in eq. (4).
ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy
624

eq. (10), and NOT (XOR with 1, eq. (4)). We achieve
full key recovery
12
by reusing the settings p
S
2
, table 2.
The maximum number of iterations required for our
attack on p
S
3
is higher than the worst-case we ob-
served for group 4 in p
S
2
. This is as expected as p
S
3
is a simpler permutation. However, perhaps surpris-
ing is that the smallest number of iterations required
for p
S
3
, 58, is higher than the smallest number of iter-
ations required for p
S
2
, 12.
The full p
S
permutation is, of course, more compli-
cated than its components. However, we achieve full
key recovery using the settings seen in table 2. The
most notable difference is that we no longer guess
[
1
2
,
1
2
,
1
2
,
1
2
,
1
2
] as the gradient is zero for this input. We,
therefore, assume that like in ASCON that x
0
,x
3
, and
x
4
are known,
13
and we only recover x
1
and x
2
.
4.3 p
L
Permutation
The p
L
permutation is a combination of bitwise ro-
tation and a three-way XOR on each 64-bit block.
In this paper, we will only be looking at Σ
1
and Σ
2
as they affect the same blocks as the key started in.
However, all the blocks are treated similarly. Based
on eq. (10) we create the following formula for this
three-way XOR:
f (x, y, z) = x + y + z − 2xy − 2xz − 2yz + 4xyz (14)
which means that for Σ
1
and Σ
2
we get:
Σ
1
: f (x
1,i
,x
1,(i+61(mod64))
,x
1,(i+39(mod64))
)
Σ
2
: f (x
2,i
,x
2,(i+01(mod64))
,x
2,(i+06(mod64))
)
In contrast to earlier XOR examples, all the bits are
affected by XOR at the same time. This means that
the weakness of the vanishing derivative at 0.5 is even
Table 3: p
S
2
permutation groups.
group1 group2 group3 group4
00000 00001 00011 00101
10000 10001 10010
01000 11000 01001
00100 01100 10100
00010 00110 01010
group5 group6 group7 group8
00111 01011 01111 11111
10011 10101 10111
11001 11010 11011
11100 01101 11101
01110 10110 11110
12
Full key recovery means that all the bits in guessed key
are correct.
13
x
0
is a constant and [x
3
,x
4
] are nonces, like a times-
tamp.
more of an obstacle. Therefore we do two things to
aid the learning: 1. We let the initial η be large to
build momentum initially, but we have a large decay
so that it only moves fast in the beginning. To ensure
that we have some learning rate for later iterations,
we bound the minimal η value to a small value. In
this case, we set the boundary to η
min
= 0.02. 2: To
help cross during later iterations, we choose a random
index that is closer than some ε
xor
to 0.5. Then we
add:
λ
xor
· sign(
∂ f (x
i
,x
i61
,x
i39
)
∂x
i
), (15)
to the diagonal position corresponding to this index,
where λ
xor
is a predefined constant and symbolizes
addition under modulo 64. The other matrix cells that
impact this input are scaled-down by with λ
xor
to en-
sure that 0.5 avoided. We call this a gradient jump,
and we set ε
xor
to 0.01 and λ
xor
to 5. In contrast to the
p
C
permutation, where we proved that we could al-
ways recover the input, and the p
S
permutation where
we could test for all 32 possible inputs, we cannot
test for all 2
64
≈ 10
19
possible inputs. Furthermore,
we do not achieve full key recovery on Σ
1
and Σ
2
.
To analyze our performance on these permutations,
we reduce the complexity by dropping leading bits.
This way, we can adjust the number of bits to be be-
tween 1 bit and 64 bits. To analyze our performance,
we start doing a 100 runs on 1 bit and iteratively in-
crease the number of bits until we reach the full 64
bits. We use the settings as seen in table 2, where our
initial guess has the same number of bits we wish to
recover. Each element in our initial guess is randomly
chosen to be either 0.4 or 0.6, as our initial experi-
ments showed that this improved performance. For
both Σ
1
and Σ
2
, we do this with and without gradi-
ent jump.For almost all runs, the algorithm performs
better with gradient jump. However, both of them per-
form poorly and have 0 successes on the full 64 bits.
So even the gradient jump could not properly com-
pensate for this suboptimal gradient. There is room
for future work to investigate replacement functions
that provide better phantom gradients.
5 CONCLUSION
We have shown that the phantom gradient attack
works on simple cryptographic functions. It also
shows some promise on attacking ASCON’s permuta-
tions, but as used in this paper, the attack is unsuccess-
ful on ASCON’s third permutation p
L
. The two other
permutations, p
C
and p
S
, were effectively attacked.
The phantom gradient attacks failure on p
L
is likely
our replacement functions whose gradients are 0 at
1
2
Dreaming of Keys: Introducing the Phantom Gradient Attack
625

for XOR. It must be stressed that there is nothing in-
herently different from p
L
, which renders it immune
to the phantom gradient attack. It is most probably a
question of finding the correct work around this "one-
half"-challenge. These first results hold promise, as
it shows that gradual learning of neural networks can
also be applied to key recovery in cryptology.
6 FUTURE WORK
There is much room for future work on the phan-
tom gradient attack. In particular, research regarding
good replacement functions. Ideally, the replacement
function should keep as many as the properties of tra-
ditional XOR. For example: (x ⊕ y) ⊕ x should ide-
ally be y in the replacement function as well. More
generally, there is much room for attempting to at-
tack other cryptosystems. For example, if we use the
phantom gradient attack to attack a public cryptogra-
phy scheme, we can use the public key to generate
as many training samples as needed. Then we can
use the phantom gradient attack to attack the decryp-
tion function: f
c
(k
private
) = p, The subscript c is the
generated ciphertext, k
private
is the secret private key,
and p is the chosen plaintext. We subscript c since,
for each iteration, we assume that it is constant like
we did with the plaintext in this work. The attack
may also be extended even to work when the plaintext
is unknown; however, this will likely require many
training samples. As the phantom gradient attack is a
new cryptanalytical attack, there is room for studying
how to protect against it. Since it draws its founda-
tion from neural networks, one could draw from cases
where neural networks struggle. For example, learn-
ing works better on deep networks rather than wide
networks. A cryptosystem that has to be represented
as a wide network may be less vulnerable to a phan-
tom gradient attack. For training the network, we tried
gradient descent and gradient descent with momen-
tum in this paper. However, other optimizers remain
untested. Two natural candidates are the neural net-
work optimizers ADAM and RMSProp. Moreover, it
is not obvious that square error is the most suited loss
function. Testing different optimizers and loss func-
tions are low hanging fruits for future research.
ACKNOWLEDGMENTS
The author wishes to give a special thanks to Audun
Jøsang and Thomas Gregersen for valuable discussion
and words of encouragement.
REFERENCES
Alani, M. M. (2012). Neuro-cryptanalysis of des and triple-
des. In International Conference on Neural Informa-
tion Processing, pages 637–646. Springer.
Bernstein, D. J. (2019). Crypto competitions: Cae-
sar submissions. https://competitions.cr.yp.to/
caesar-submissions.html. (Accessed on 03/19/2020).
Dobraunig, C., Eichlseder, M., Mendel, F., and Schläffer,
M. (2016). Ascon v1.2. Submission to Round 3 of the
CAESAR competition.
Dobraunig, C., Eichlseder, M., Mendel, F., and Schläffer,
M. (2019). Ascon v1.2. Submission to Round 1 of the
NIST Lightweight Cryptography project.
Dourlens, S. (1996). Applied neuro-cryptography and
neuro-cryptanalysis of des. Master Thesis. Advisor:
Riesner, Christian.
Erhan, D., Bengio, Y., Courville, A., and Vincent, P. (2009).
Visualizing higher-layer features of a deep network.
University of Montreal, 1341(3):1.
Greydanus, S. (2017). Learning the enigma with recurrent
neural networks. arXiv preprint arXiv:1708.07576.
Gritsenko, A. A., D’Amour, A., Atwood, J., Halpern, Y.,
and Sculley, D. (2018). Briarpatches: Pixel-space in-
terventions for inducing demographic parity. arXiv
preprint arXiv:1812.06869.
Kinzel, W. and Kanter, I. (2002). Neural cryptography. In
Proceedings of the 9th International Conference on
Neural Information Processing, 2002. ICONIP’02.,
volume 3, pages 1351–1354. IEEE.
Klimov, A., Mityagin, A., and Shamir, A. (2002). Analysis
of neural cryptography. In International Conference
on the Theory and Application of Cryptology and In-
formation Security, pages 288–298. Springer.
Lewis, J. P. (1988). Creation by refinement: a creativity
paradigm for gradient descent learning networks. In
ICNN, pages 229–233.
NIST (2020). Lightweight cryptography | csrc. https://
csrc.nist.gov/projects/lightweight-cryptography. (Ac-
cessed on 03/19/2020).
Parascandolo, G., Huttunen, H., and Virtanen, T. (2016).
Taming the waves: sine as activation function in deep
neural networks.
Portilla, J. and Simoncelli, E. P. (2000). A parametric tex-
ture model based on joint statistics of complex wavelet
coefficients. International journal of computer vision,
40(1):49–70.
Shannon, C. E. (1949). Communication theory of se-
crecy systems. The Bell System Technical Journal,
28(4):656–715.
Simonyan, K., Vedaldi, A., and Zisserman, A. (2013).
Deep inside convolutional networks: Visualising im-
age classification models and saliency maps. arXiv
preprint arXiv:1312.6034.
Zhang, J., He, T., Sra, S., and Jadbabaie, A. (2019).
Analysis of gradient clipping and adaptive scaling
with a relaxed smoothness condition. arXiv preprint
arXiv:1905.11881.
ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy
626

Zhu, S., Dong, X., and Su, H. (2019). Binary ensemble neu-
ral network: More bits per network or more networks
per bit? In Proceedings of the IEEE/CVF Conference
on Computer Vision and Pattern Recognition (CVPR).
Dreaming of Keys: Introducing the Phantom Gradient Attack
627
