
On Explanation of Propositional Logic-based Argumentation System
Teeradaj Racharak and Satoshi Tojo
School of Information Science, Japan Advanced Institute of Science and Technology, Ishikawa, Japan
Keywords:
Deductive Argumentation, Argumentation System, Explainable Artificial Intelligence, Natural Deduction.
Abstract:
We present a characterization about argumentation and proof in logic. Indeed, we show that proof for a
claim α from a set of premises Φ can be deemed as a structured form of an argument for that claim. Due to the
expressivity of classical propositional logic (PL), this work considers that the knowledge-base is represented in
PL, in which the semantics and proof systems for individual arguments are studied and utilized. We show that
natural deduction (ND) can be used as a basis of proof for an argument and also for modeling counterarguments
in the form of canonical undercut. We reveal that ND does not merely enable for the construction of arguments
but also paves the way naturally for a human-understandable form of argumentative reasoning. Finally, we
demonstrate that our approach gives the feasibility of developing explainable artificial intelligence systems
that can offer human-friendly explanations to the users.
1 INTRODUCTION
Argumentation is an important aspect of human in-
telligence. Humans always search for pros and cons
of arguments as well as their consequences when at-
tempting to understand a facing situation for mak-
ing decisions. This argumentative reasoning can be
formalized by utilizing a logical language for the
premises and an appropriate consequence relation
for showing that claims logically follow from the
premises (a.k.a. logic-based argumentation).
There are a number of proposals for logic-based
formalization of argumentation (cf. (Besnard and
Hunter, 2018; Ches
˜
nevar et al., 2000; Vreeswijk
and Prakken, 2001) for the existing literature).
These works allow the representation of arguments
for claims, the representation of counterarguments
against them, and the relationships between the argu-
ments. Despite the diversity, an argument in logic-
based argumentation is commonly defined as a pair
of which the first item is a set of formulae that proves
the second item (i.e. a logical formula). There have
been several investigation of and success with the use
of proof techniques in logic. For instance, (Prakken
and Sartor, 1997) developed proof procedures to find
acceptable arguments in Dung’s semantics from a de-
feasible logic knowledge-base. As an example in
propositional logic knowledge-base, (Efstathiou and
Hunter, 2011) proposed to generate arguments and
counterarguments using the resolution principle and
connected graph (Kowalski, 1975; Kowalski, 1979).
Unfortunately, these approaches do not concretely of-
fer computational content of an argument in a form
that is understandable by naive users. This is a vital
aspect of developing explainable artificial intelligence
systems; reasoners should provide understandable ex-
planations in order to facilitate the process of evolv-
ing the theory between explainers and explainees (i.e.
a group of people who receive the explanations).
Here, we suppose that a knowledge-base ∆ is rep-
resented by classical propositional logic (PL); thereby
proof theories in PL are investigated for construc-
tion of arguments and counterarguments from ∆. For-
mally, finding an argument for claim α involves seek-
ing for a consistent subset Φ of ∆ which can logically
derive α, i.e., one can prove the validity of α from Φ
using some proof systems. This basically amounts to
investigate well-established proof theories of the base
logic towards arguments’ construction. Figure 1 (a)
depicts an example of applying the resolution tech-
nique (as adopted in (Efstathiou and Hunter, 2011)) to
prove that q is a valid consequence from {p, ¬p ∨q},
in which {} denotes the empty clause.
Researchers have put an essentially great deal
of effort into development of structured argumenta-
tion framework, but addressing understandable com-
puted content of argumentation models have received
less attention. Nevertheless, we might utilize proce-
dures which offer to generate an adequate explana-
tion for a developed argument. Considering Figure
Racharak, T. and Tojo, S.
On Explanation of Propositional Logic-based Argumentation System.
DOI: 10.5220/0010318103230332
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 2, pages 323-332
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
323
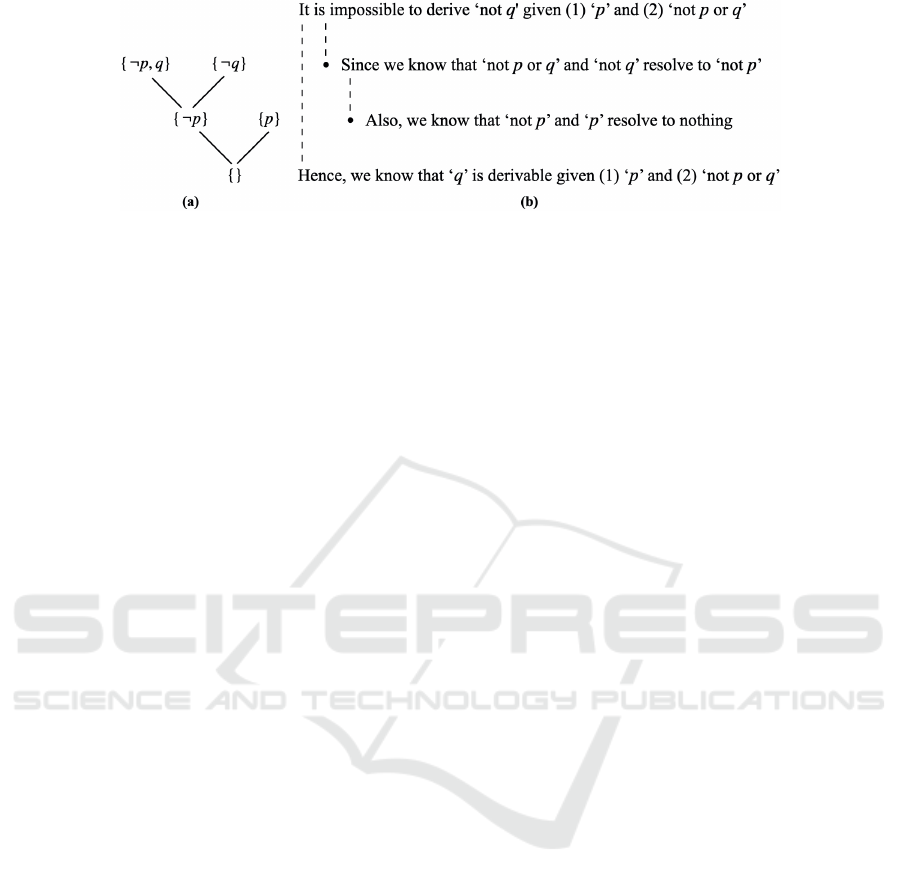
Figure 1: (a) A resolution proof for claim q given assumptions p and ¬p ∨ q; (b) A corresponding explanation of the proof.
1 (b) as a motivating example, one may observe that
an argument developed from the resolution carry too
much information than the need for a meaningful ex-
planation of why ‘q’ given assumptions ‘p implies q’
and ‘q’. While there exist more diverse procedures in
logic (e.g. analytic tableaux (Smullyan, 1995) and se-
quent calculus (Takeuti, 2013)), this work argues for
using natural deduction (ND) (Gentzen, 1935), taken
as a mean to identify an argument’s structure from
proof. We demonstrate that the pattern represented by
ND is close to what humans can perceive as an ar-
gument drawing a conclusion from any conjunction
that it contains. We elaborate upon our formalization
based on ND proof in Section 3.
It is worth mentioning that current studies on
logic-based argumentation have mostly concerned on
exploiting logic for modeling structured argumenta-
tion such as (Besnard and Hunter, 2018); however,
how it contributes to the development of explainable
artificial intelligence (XAI) systems is not fully in-
vestigated. Thus, this work aims at bridging this gap
between argumentation and its applications on XAI.
The contribution in this paper is that we introduce
an approach to modeling arguments based on ND cal-
culus towards the development of XAI systems. Our
approach offers three main advantages: (1) explicit
information used to build up arguments, (2) a trans-
parent connection between the supports and the claim
corresponding to the consequence relation, and (3)
obvious translation for generating a human-friendly
argument from the proposed formalization. The use
of ND supports explanation generation from the com-
puted deductive arguments; and also, the use of ar-
gumentative proof procedure coincides with everyday
explanations used by humans (cf. Section 4). We
review the basic elements in (Dung’s) abstract argu-
mentation and classical propositional logic including
the natural deduction in Section 2. Section 5 relates
our approach to others. Finally, Section 6 provides a
conclusion and discussion of future directions.
2 PRELIMINARIES
2.1 Abstract Argumentation
Abstract argumentation (AA) provides a good start-
ing point for formalizing argumentation in human rea-
soning. In (Dung, 1995), an AA framework is a pair
hA, R i of which A represents a set of arguments and
R ⊆ A × A represents attack between arguments. Ar-
guments may attack each other and thereby their sta-
tuses are subject to an evaluation. Semantics for AA
returns sets of arguments called extensions, which are
conflict-free and defend themselves against attacks.
Formally, a set S ⊆ A of arguments is conflict-
free iff there are no arguments A, B ∈ S such that
(A, B) ∈ R . Moreover, S defends A ∈ A iff, for any
argument B ∈ A, (B, A) ∈ R implies an existence of
C ∈ S such that (C, B) ∈ R . A conflict-free set S is
admissible iff each argument A ∈ S is defended by
S. These conflict-freeness and admissibility proper-
ties form the basis of all AA semantics as follows.
Let Defended(S)
:
= {A | S defends A} be a function
which yields a set of arguments defended by a cer-
tain set. Then, set S is a complete extension iff S is
conflict-free and S = Defended(S); set S is a grounded
extension iff it is the minimal complete extension
(w.r.t. set inclusion); set S is a preferred extension iff
it is a maximal complete extension (w.r.t. set inclu-
sion); and set S is a stable extension iff S is conflict-
free and S attacks every argument which is not in S.
2.2 Propositional Logic and Proof
In AA, the structure and meaning of arguments and
attacks are abstract. On the one hand, the abstract
definition enables to study properties which are in-
dependent of any specific aspects (Baroni and Gia-
comin, 2009). On the other hand, this generality fea-
tures a limited expressivity and can be hardly adopted
to model practical target situations. To fill out this
gap, less abstract formalisms were considered, deal-
ing in particular with the construction of arguments
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
324

and the conditions for an argument to attack another
e.g. ASPIC
+
(Modgil and Prakken, 2014), DeLP
(Garc
´
ıa and Simari, 2004), and assumption-based ar-
gumentation (ABA) (Dung et al., 2009). There have
also been some investigation of logic-based argumen-
tation in which well-established logical frameworks
are used to model arguments and the relationship be-
tween them (cf. Section 5). Since the expressivity of
classical propositional logic (PL) allows for model-
ing sufficient knowledge-base, this work focuses on a
knowledge-base expressible in PL. Some preliminary
definitions are provided below for self-containment.
Let L be a PL language obtained from a given set
of atoms with ¬, ∧, ∨, and → as connectives. Though
all PL formulae can be formulated by using only ¬
and ∧, we also include others to simplify the presen-
tation of our approach. We also assume that L con-
tains the special symbol ⊥ representing inconsistency.
To show that a sentence is derivable (or provable), we
use the following natural deduction (ND) rules for any
φ, ψ ∈ L (Van Dalen, 2004):
φ ψ
φ ∧ ψ
(∧I)
φ ∧ ψ
φ
(∧E)
φ ∧ ψ
ψ
(∧E)
φ ¬φ
⊥
(¬E)
⊥
φ
(⊥)
[¬φ]
.
.
.
.
⊥
φ
(RAA)
[φ]
.
.
.
.
ψ
φ → ψ
(→ I)
φ → ψ φ
ψ
(→ E)
φ
φ ∨ ψ
(∨I)
ψ
φ ∨ ψ
(∨I)
φ ∨ ψ
[φ]
.
.
.
.
σ
[ψ]
.
.
.
.
σ
σ
(∨E)
Derived consequences result from applying these
ND rules in sequence and we denote Φ ` φ if φ is
derivable from Φ. This search can be performed in
the forward direction, from Φ to φ, in the backward
direction, from φ to Φ, or even from both directions
concurrently (Ferrari and Fiorentini, 2015). Our defi-
nition of argument (cf. Section 3) insists on the back-
ward generation of arguments by applying ND rules
with formulae in a knowledge-base.
Example 2.1. For a knowledge-base ∆
:
= {b →
a, c → b, c ∧ b}, where a, b, c represents ‘avoid
steroids’, ‘get vaccine against hepatitis B’, and ‘plan
to visit Africa’, respectively. In the following, we
show that ∆ ` a:
b → a
c ∧ b
b
a
Naturally, reading this deduction tree from top
to bottom corresponds to the following explanation;
noted that one can also read the tree from bottom to
top to obtain a similar natural language sentence:
1. It is assumed that c and b;
2. So is b from #1;
3. It is also assumed that b implies a;
4. So is a from #2 and #3.
Hence, we show that assuming ‘b implies a’ and ‘c
and b’ derives ‘a’.
3 NDSA FRAMEWORK: ND FOR
STRUCTURED
ARGUMENTATION
Observe that a derivation in Example 2.1 corresponds
to querying ‘should we avoid steroids and why if so?’.
Hence, it is quite natural to deem that ND for formula
α represents a logical argument for claim α supported
by a corresponding set of premises. Indeed, reading a
ND tree from top to bottom (also, from bottom to top)
yields an interpretation of a logical argument, allow-
ing to extract naturally a human-friendly explanation
as to why the claim α is so.
Definition 3.1 (ND Argument). Given a PL
knowledge-base ∆, an argument for claim α sup-
ported by Φ ⊆ ∆ (denoted by hΦ, αi) is a ND proof
tree such that α is derivable (backwards) from α to Φ
and ¬α is not derivable from Φ.
Set Φ is called supports or assumptions; and also,
α is called a claim of an argument. Observe that Defi-
nition 3.1 imposes consistency constraint to avoid the
construction of illogical arguments (such as via ex
falso quodlibet).
Unlike several other work, e.g. those of (Besnard
and Hunter, 2018) and (Garc
´
ıa and Simari, 2004), we
do not impose the restriction that the support of an
argument be minimal. For instance, the same conse-
quence as in Example 2.1 can be derived; however
more verbose, as follows:
b → a
c → b
c ∧ b
c
b
a
This ND proof tree corresponds to the following log-
ical argument for explaining why we should avoid
steroids (a) given the assumptions (reading from top
to bottom of the ND proof tree):
1. We know that c and b by our assumptions;
On Explanation of Propositional Logic-based Argumentation System
325

2. So is c from #1;
3. We also know that c implies b by our assumptions;
4. So is b from #2 and #3;
5. We also know that b implies a by our assumptions;
6. So is a from #4 and #5.
Though the above argument is not minimal, it is
also relevant in the sense that their supports contribute
to deducing the conclusion. Minimal checking is one
way to ensure relevancy but may come at a compu-
tational cost. Nonetheless, our arguments are guar-
anteed to be relevant without imposing on minimality
due to the backward generation of ND proof trees.
It is worth mentioning that applying ND is advan-
tageous for us since the hypotheses appear only on
top layers of a deduction tree, that suffices our prime
goal of yielding human-friendly arguments. In com-
parison to other formalisms, a Hilbert-style axiomati-
zation requires us to supply many axioms in the midst
of a proof tree. As for the analytic tableau method,
we need to show our goal to prove first on the top line,
that is against our objective. Gentzen’s sequent calcu-
lus (Kleene et al., 1952) might be the most polished
style of deduction; however, each sequent becomes a
long and messy sequence of formulae and is thus dif-
ficult for proof’s visualization.
Given two arguments, it is possible to compare
which argument is more general than one another.
The following definition captures this relation be-
tween two arguments from a knowledge-base.
Definition 3.2. An argument hΦ, αi is comparable to
and more concise than an argument hΨ, βi iff Φ ⊂ Ψ
and α ≡ β.
From the above definition, one can say that argu-
ment h{b → a, c ∧ b}, ai is comparable to and more
concise than argument h{b → a, c → b, c ∧ b}, ai.
Equipping argumentation into knowledge-base
reasoning enables to deal with existence of inconsis-
tent premises; derived conclusions of a knowledge-
base are the claims of arguments in a concerned ex-
tension. Since a knowledge-base may be inconsistent,
logical arguments constructed from the knowledge-
base may be conflicting with each other. To define
counterarguments, we consider the notion classical
direct undercut (Besnard and Hunter, 2018), which
is largely applied in the literature.
Definition 3.3. Let A
:
= hΦ, αi and B
:
= hΨ, βi be
arguments. Then, we say that argument A attacks ar-
gument B iff ∃φ ∈ Ψ such that α ≡ ¬φ.
It is worth noticing that if an argument is attacked
by another argument, then other arguments which are
less concise than it will also be attacked by the same
counterargument. Hence, it is redundant to account
for less concise arguments in argumentative reason-
ing and is omitted to show in our running examples.
Following this idea, we are now ready to instantiate
an abstract argumentation framework from a (possi-
bly inconsistent) PL knowledge-base.
Figure 2 illustrates an instantiated abstract argu-
mentation framework, in which each triangle repre-
sents an argument corresponding to each ND deriva-
tion. At each argument, the bottom part represents the
claim, the top part denotes its supports, and arrows
represent argument-counterargument relationship.
The proposed approach gives a straightforward
way for instantiating an abstract argumentation
framework from a PL knowledge-base. However, ap-
plying these definitions may cause infinite construc-
tion of arguments; thereby causing the attack rela-
tion among them to be also infinite. For instance,
if an instantiated abstract argumentation framework
contains argument h{a}, ai, it also means that the in-
stantiated framework contains arguments h{a}, a ∨bi,
h{a}, a ∨ b ∨ ci, and so on using the ∨I-ND rule. This
kind of infinite abstract argumentation frameworks
may be hardly used and requires a special treatment
to deal with the infinite construction. In the follow-
ing, we consider a core of an argumentation frame-
work (Amgoud et al., 2011) which can be identified
by the following notions.
Definition 3.4 (Structural Equivalence of Argu-
ments). Arguments A
:
= hΦ, αi and B
:
= hΨ, βi are
structurally equivalent iff Φ = Ψ and α ≡ β.
Definition 3.5. Let F
0
:
= hA
0
, R
0
i and F
:
= hA, R i
represent different AA frameworks. Then, F
0
is a
core of F iff A
0
and R
0
are finite; and, for any A ∈ A,
there exists A
0
∈ A
0
such that A
0
and A are structurally
equivalent and A
0
satisfies the following conditions:
• For any argument B ∈ A such that (B, A) ∈ R ,
there also exists argument B
0
∈ A
0
such that
(B
0
, A
0
) ∈ R
0
, and
• For any argument B ∈ A such that (A, B) ∈ R ,
there also exists argument B
0
∈ A
0
such that
(A
0
, B
0
) ∈ R
0
.
When multiple arguments are structurally equiva-
lent, it is adequate to choose exactly one argument of
them in an instantiated abstract argumentation frame-
work. Restricted our attention on structurally equiva-
lent arguments, one can identify a core of an argumen-
tation framework. For instance, it can be shown that a
core of an instantiated abstract argumentation frame-
work in Example 2.1 contains three arguments as in
Figure 3 in which A
1
denotes a derivation for c from
c ∧ b, A
2
denotes a derivation for b from c ∧ b, and
A
3
denotes a derivation for a from c ∧ b together with
b → a. At implementation, this imposition can be re-
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
326
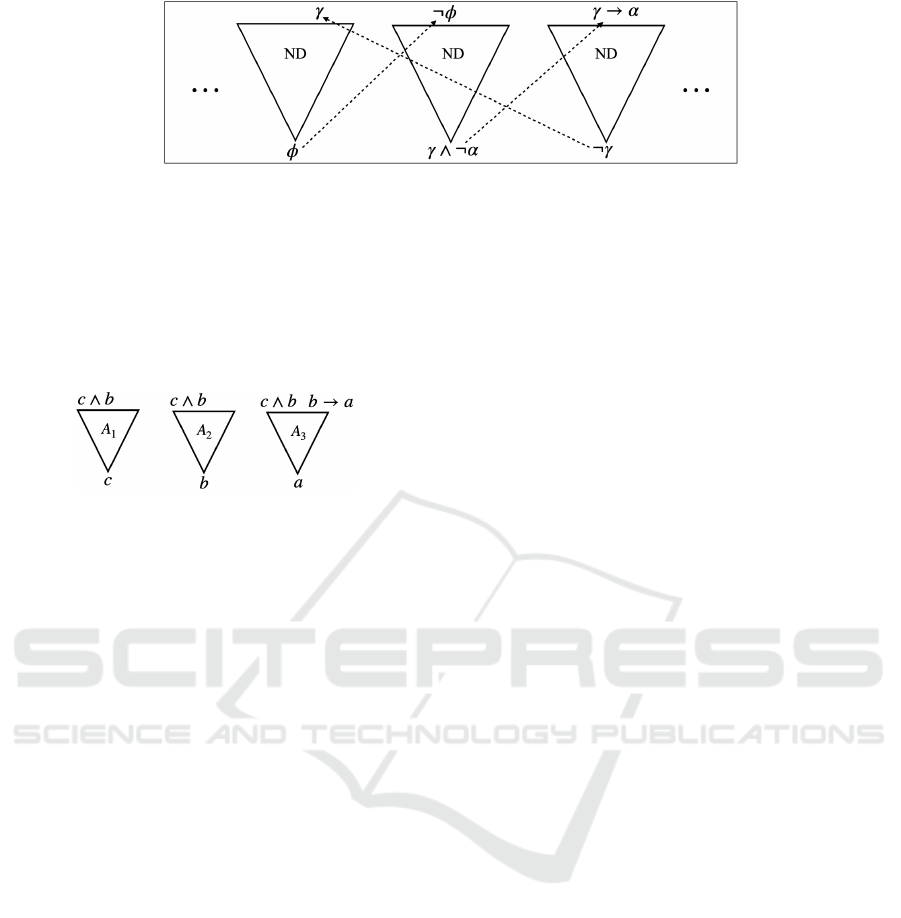
Figure 2: An instantiated abstract argumentation framework.
duced to checking whether α ∧¬β and β∧ ¬α are un-
satisfiable by any Boolean satisfiability (SAT) solver,
although checking if two logical formulae are equiv-
alent may come with a computational cost. Some
more heuristic techniques for performance improve-
ment may also be investigated and are remained as
our future tasks.
Figure 3: A core of an instantiated abstract argumentation
framework.
To complete our earlier definitions of argument
and attack, we formally give a definition of our natural
deduction-based structured argumentation (NDSA)
framework as follows.
Definition 3.6 (NDSA). A NDSA framework is a
triple hL, ∆, `
ND
i, where L is a PL language, ∆ is
a knowledge-base modeled based upon language L,
and `
ND
is a consequence relation represented by the
natural deduction proof calculus.
Proposition 3.1. Let F
:
= hA, R i be an AA frame-
work built according to NDSA. Then, F
0
:
= hA
0
, R
0
i
is a core of F if it is constrained from F as follows:
• For each set A ⊆ A of structurally equivalent
arguments, only one argument A of A is non-
deterministically included in A
0
and all attacks
of arguments A \ A are excluded from hA, R i to
yield hA
0
, R
0
i .
Proof. We show that the above construction yields
a core of any argumentation framework hA, R i. Fix
any A ⊆ A of structurally equivalent arguments, we
show if an argument A of A is non-deterministically
in A
0
, then the following conditions hold:
• (Condition 1) Fix any argument B ∈ A \ A such
that (B, A) ∈ R , we show that there exists an ar-
gument B
0
∈ A
0
such that (B
0
, A) ∈ R
0
. Since A
is a set of structurally equivalent arguments, then
(B, A) ∈ R
0
. This means B
0
= B. Therefore, this
condition trivially holds.
• (Condition 2) Fix any argument B ∈ A \ A such
that (A, B) ∈ R , we show that there exists an ar-
gument A
0
∈ A
0
such that (A
0
, B) ∈ R
0
. Since A is
a set of structurally equivalent arguments and A is
a singleton, then we know A
0
= A. Therefore, this
condition also trivially holds.
The above proposition provides us an algorithmic
procedure to indicate a core of an abstract argumenta-
tion framework. In the following, we illustrates an-
other (but less trivial) example about identifying a
core of an abstract argumentation framework. It also
highlights that the proposed framework can be used
in multi-agent reasoning, in which all agents possess
their own consistent set of the knowledge (but, their
integration is inconsistent). For instance, it often oc-
curs that witnesses in jurisdictions may hold differ-
ent consistent sets of beliefs but integration among
those beliefs turns to be inconsistent. This shows that
NDSA allows to represent an argumentation dialogue
and to detect the argument-counterargument interac-
tion between each agent’s utterance.
Example 3.1. Let ∆
A
:
= {a, a → b} and ∆
B
:
=
{¬b, a → b} represent different knowledge-bases pos-
sessed by Agents A and B, respectively, in which a de-
notes ‘plan to visit Africa’ and b denotes ‘get vaccine
against hepatitis B’. For the integrated knowledge-
base ∆
:
= ∆
A
∪ ∆
B
, it can be shown that a core of an
AA framework built from ∆ according to NDSA is
presented as in Figure 4.
Noted that, in the figure, A
1
represents a deriva-
tion for h{a}, ai, A
2
represents a derivation for
h{¬b}, ¬bi, A
3
represents a derivation for h{a →
b}, a → bi, A
4
represents a derivation for h{a, ¬b}, a∧
¬bi, A
5
represents a derivation for h{¬b, a → b}, ¬ai,
and A
6
represents a derivation for h{a, a → b}, bi.
4 ACCEPTABILITY AND
EXPLANATIONS OF NDSA
Since NDSA instantiates an AA framework from a
knowledge-base, all semantics for determining the
‘acceptability’ of arguments in AA also apply to ND
arguments. As a common approach in logic-based ar-
gumentation, consequences of a knowledge-base are
claims of those arguments in a concerned extension.
Definition 4.1. Let hL, ∆, `
ND
i be a NDSA frame-
work and ext(F ) be an extension of an AA frame-
On Explanation of Propositional Logic-based Argumentation System
327

Figure 4: A core of an instantiated abstract argumentation framework.
work F built from the NDSA. Then, a set of conse-
quences from ∆ w.r.t. ext(F ) (denoted by Con
ext(F )
)
is defined as: Con
ext(F )
:
= {α | hΦ, αi ∈ ext(F )}.
For instance, considering Example 3.1, applying
stable semantics (cf. Subsection 2.1) yields three ex-
tensions: {A
1
, A
3
, A
6
}, {A
2
, A
3
, A
5
}, and {A
1
, A
2
, A
4
}.
Hence, there are three sets of accepted consequences
w.r.t. the stable semantics from this knowledge-base:
{a, a → b, b}, {¬b, a → b, ¬a}, and {a, ¬b, a ∧ ¬b}.
Proposition 4.1. Let F
0
:
= hA
0
, R
0
i and F
:
= hA, R i
represents AA frameworks. If F
0
is a core of F , then
the following holds for any concerned extension:
• For any α ∈ Con
ext(F
0
)
, there exists β ∈ Con
ext(F )
such that α ≡ β; and
• For any β ∈ Con
ext(F )
, there exists α ∈ Con
ext(F
0
)
such that α ≡ β.
Proof.
• (Condition 1) Fix any α ∈ Con
ext(F
0
)
, we show
that there exists β ∈ Con
ext(F )
such that α ≡ β.
By assumption, we know that, for any A ∈ A,
there exists A
0
∈ A
0
such that A
0
and A are struc-
turally equivalent. Therefore, this condition triv-
ially holds by Definitions 3.4 – 3.5.
• (Condition 2) Fix any β ∈ Con
ext(F )
, we show
that there exists α ∈ Con
ext(F
0
)
such that α ≡ β.
By assumption, we know that, for any A ∈ A,
there exists A
0
∈ A
0
such that A
0
and A are struc-
turally equivalent. Therefore, this condition triv-
ially holds by Definitions 3.4 – 3.5.
Notice that incorporating the computation of ac-
ceptability in AA together with ND in PL knowledge-
base naturally represents formal reasoning used by
humans, as (Gentzen, 1935)
1
and (Dung, 1995) aimed
at this. Furthermore, separating levels of proof of-
fers non-monotonic behavior for PL (which is a
monotonic logic) since adding/removing arguments
can surpass the acceptance of some arguments and
1
“First, I wished to construct a formalism that comes as
close as possible to actual reasoning. Thus, arose a calculus
of natural deduction”, quoted from (Gentzen, 1935).
thereby the corresponding claims are prevailed. Due
to the well-investigated computational models of ar-
gumentation and ND proof in PL, we can outline an
implementation of our proposed approach as shown
in Algorithm 1. This algorithm finds all acceptable
arguments w.r.t. a concerned extension.
Algorithm 1 : Finding accepted arguments in a NDSA
framework hL, ∆, `
ND
i.
1: input: a knowledge-base ∆, an AA semantics s
2: output: sets of acceptable arguments w.r.t. s
3: function ACCEPTEDARGUMENTS(∆, s)
4: Let G be an empty directed graph.
5: G
:
= Construction of an abstract argumenta-
tion framework based on Definitions 3.1 – 3.3.
6: Indicate a core of G based on Proposition 3.1.
7: Remove irrelevant arguments and attack rela-
tions (that are not part of the core) in G.
8: exts
:
= Sets of acceptable arguments w.r.t. the
semantics s in G.
9: return exts
10: end function
Regarding the tasks of providing their explana-
tions, NDSA considers two-level interpretation on a
core of an argumentation framework:
1. Explain why arguments are acceptable w.r.t. AA
semantics;
2. Explain why accepted arguments are logically de-
rived based on ND.
These two levels correspond to macro-scoping and
micro-scoping explanations, respectively, for an ac-
cepted argument. The first level interpretation can be
viewed as a debate between two fictitious agents (i.e.
the proponent and the opponent) arguing why argu-
ments in an extension should be accepted. On the
other hand, for the second level interpretation, one can
specifically zoom into a ND derivation of an argument
as a basis for serving an explanation.
The following ND deduction proof exemplifies
this intuition by explaining why argument A
6
(in Ex-
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
328

ample 3.1) for claim ‘get vaccine against hepatitis B’
is derivable in the first stable extension:
a a → b
b
This inferential step enables to yield the following ex-
planations to the users. As aforementioned, it corre-
sponds to the micro-scoping level of explanation:
1. Given that ‘plan to visit Africa’ (a) and ‘planning
to visit Africa implies to get vaccine against hep-
atitis B’ (a → b);
2. Hence, ‘get vaccine against hepatitis B’ (b).
We discuss more about the generation process of
explanations on our two levels of explanations (cf.
Subsection 4.1) and the evaluation of explanations in
an aspect of good explanations based upon the view-
point of human cognition in social science (cf. Sub-
section 4.2) in the following subsections.
4.1 Generation of Explanations for
Claims of NDSA Arguments
This subsection briefly introduces the idea of provid-
ing explanations from NDSA, which basically com-
prise two forms of explanation as follows.
4.1.1 Dialogical Explanations
This explanation corresponds to the macro-scoping
interpretation of our proposed framework. Indeed,
given an abstract argumentation framework hA, R i
instantiated from NDSA, one can explain the outcome
of a concerned extension dialogically by reinterpret-
ing a dispute tree T of an argument A ∈ A, which can
be constructed by the following procedure:
1. Every node of T is of the form [L : B] where L is
either proponent (P) or opponent (O) and B ∈ A,
2. The root node of T is always labeled by [P : A],
3. For every node [P : B] of T with B ∈ A, and for
every C ∈ A with (C, B) ∈ R , there exists a child
of [P : B] which is labeled by [O : C],
4. For every node [O : B] of T with B ∈ A, there
exists exactly one child of [O : B] which is labeled
by [P : C] with (C, B) ∈ R ,
5. There are no other nodes in T except #1 – #4.
The proponent wins if he/she can counter-attack
against every attacking argument by the opponent.
The set of all arguments belonging to the proponent
nodes in T is called the defence set of T (Dung et al.,
2006). This defence set represents a reason for why a
certain claim should be accepted.
Note that a branch in a dispute tree may be either
finite or infinite. A finite branch represents a win-
ning sequence of arguments that ends with an argu-
ment by the proponent in which the opponent is un-
able to attack. An infinite branch represents a winning
sequence of arguments that the proponent counter-
attacks every attack of the opponent ad infinitum.
Several studies (Dung et al., 2006; Modgil and Cami-
nada, 2009) have put an essentially great deal of effort
into investigation of its winning strategies in order to
help determining the membership of arguments in an
extension of any abstract argumentation framework.
Definition 4.2. Let hA, R i be an abstract argumenta-
tion framework. A dispute tree T for A ∈ A is admis-
sible iff no argument labels both P and O;
Theorem 4.1 ((Dung et al., 2009)). Let hA, R i be an
abstract argumentation framework. We know:
1. If T is an admissible dispute tree for an argument
A ∈ A, then the defence set of T is admissible;
2. If A ∈ S for an admissible set S ⊆ A, then there ex-
ists an admissible dispute tree for A with defence
set S
0
such that S
0
⊆ S and S
0
is admissible;
This work does not focus on the strategies; but rather,
we employ this notion for explanation in a contrafac-
tual argumentative situation for the consequences de-
rived by NDSA (cf. Definition 4.1).
Intuitively, this form explains as a debate between
a proponent P seeking to establish the acceptance of
an argument in an extension and an opponent O seek-
ing to withdraw such acceptance. For example, one
can unfold the debate for the acceptance of A
1
in a sta-
ble extension {A
1
, A
3
, A
6
} in Example 3.1 as follows
(cf. Figure 5). First, P moves argument A
1
repre-
senting the acceptability of A
1
. Then, O puts forward
argument A
5
representing the attack on a support of
A
1
. Then, P has to counter-argue O’s argument by
putting forward argument A
6
as it defends A
1
. Next,
O puts forward argument A
4
representing the attack
on a support of A
6
. It is in turn provided that this ar-
gument is counter-attacked by the same argument A
6
of P. We note that the same arguments A
4
, A
5
put for-
ward by O can also counter-attack A
6
of P; however,
this attack and counter-attack relationship represents
two winning sequences of arguments that the propo-
nent counterattacks every attack of the opponent ad
infinitum. We can handle this situation of an infinite
branch by disabling its repetition on the dispute tree
(cf. the dot lines in Figure 5). Since the arguments
forwarded by P are unattacked by O, these sequences
of argument moves indicate the acceptance of argu-
ment A
1
. Dialogical explanations for other arguments
in the extension can be obtained similarly.
On Explanation of Propositional Logic-based Argumentation System
329
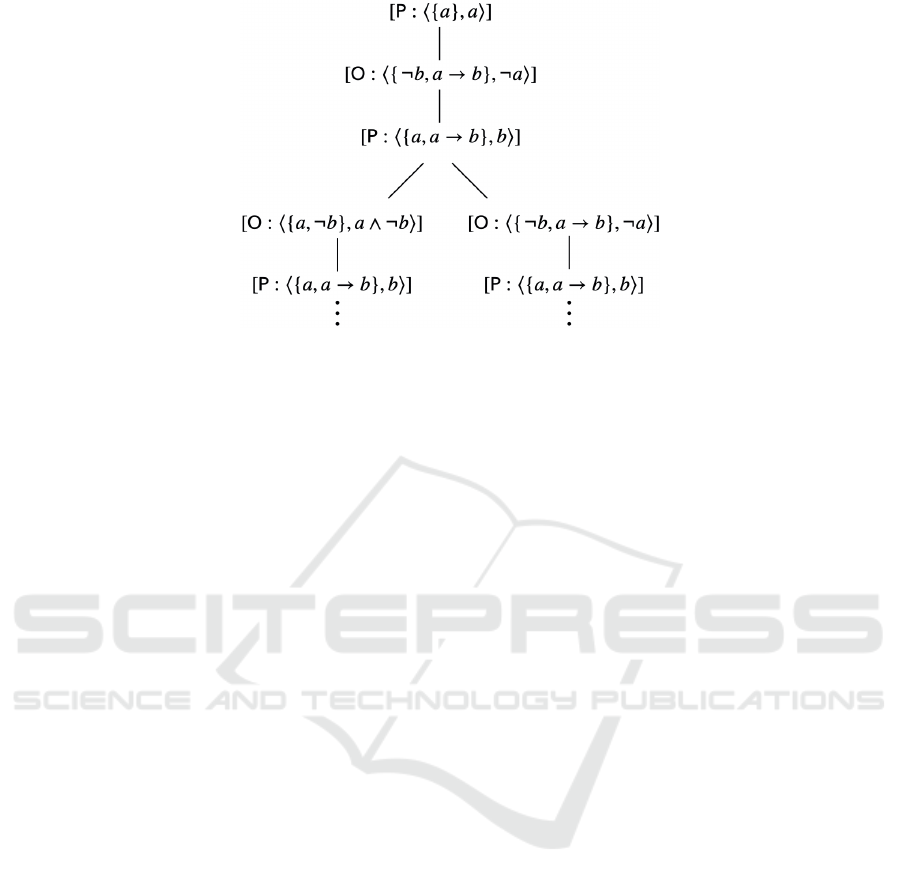
Figure 5: A dispute tree for argument h{a}, ai w.r.t. the NDSA framework in Example 3.1.
4.1.2 Logical Explanations
This explanation corresponds to the micro-scoping
interpretation of our proposed framework. As we
demonstrate earlier, the computational content of ND
can facilitate to generate human-friendly logical ex-
planations on theorem hood in a theory. It is worth
noting that other proof systems may also be used as a
basis to explanation generation; nonetheless, we ob-
serve that they may carry more information and ex-
press less intuitively to human interpretation. The
idea to unfold explanations from a ND derivation is
as follows. We trace on a ND proof tree from top
to bottom (toward the conclusion of the proof) by a
procedure that generates text corresponding to each
inference step and tries not to repeat conjunctive par-
ticles (e.g. if – then, thus, hence, etc.). After that, we
put together phrases derived from each subproof.
4.2 Evaluation of Explanations for
Claims of NDSA Arguments
To evaluate the explanations generated from NDSA,
we compare and relate with major findings on charac-
teristics of good explanations in philosophy, cognitive
psychology/science, and social psychology. Early on,
most works devoted for explainable artificial intelli-
gence use only the researchers’ intuition of what con-
stitutes a good explanation (Miller, 2019) and over-
look the important insights from these research fields.
We fill in this gap by reviewing relevant work and
demonstrating that NDSA can support XAI systems
to develop human-like explanations, i.e. contrastive
explanations (Subsubsection 4.2.1) and selected ex-
planations (Subsubsection 4.2.2). In other words, an
important outcome of this work is to draw a closer
connection between argumentation theory and its ap-
plications towards the development of XAI systems.
4.2.1 Contrastive Explanations
Humans always seek in response to particular coun-
terfactual cases (Hilton, 1990; Lipton, 1990). Re-
search in related fields especially the social science
shows that people do not explain the causes for an
event per se, but rather explain the cause of an event
relative to some other event that does not occur; that
is, an explanation is of the form ‘why α rather than
β?’, in which α represents the final conclusion and β
represents an opposite outcome.
It is worth observing that our dialogical explana-
tions are inherently contrastive by the construction;
that is, to explain that α must occur, the explainer (the
proponent) deliberates that a counterfactual β is not
necessarily the case to the explainee (the opponent) by
finding a counterargument to β. For instance, given a
question “why should we plan to visit Africa?”, the
explainer may try to answer “why should not we plan
to visit Africa?”. To answer this negated question,
the explainer can answer it by showing that “not visit-
ing Afriva (¬a)” is not necessarily the case, i.e., with
an answer “because we plan to visit Africa (a) and if
we plan to visit Africa, then we get vaccine against
hepatitis B (a → b)”. This indicates that our explana-
tions satisfy this form of good explanations by natu-
rally reinterpreting from the dialogical explanation.
4.2.2 Selected Explanations (w.r.t. a Context)
Research results on social psychology and cognitive
science show that humans rarely expect an explana-
tion to consist of both an actual and complete cause of
a decision. But rather, they select one or two causes
from a (possibly infinite) number of causes to be the
explanation for the explainee (Hilton, 2017). Indeed,
while a decision may have many argumentative claim-
backings, often the explainee cares only about a small
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
330

subset (relevant to the context). That is, the explainer
selects a subset of the possible explanations (based on
different criteria), and the explainer and the explainee
may interact and argue about these explanations.
It is worth observing that the generation of dia-
logical explanations can be tailored to selected expla-
nations if the context of the explainee is given. For
that, we consider only a branch in a dispute tree for
the argument in which the selected branch coincides
with the criteria specified in the context; the context
may mean a concerned formula indicated by the ex-
plainee, the length of a considering branch of the dis-
pute tree, and etc. For instance, according to Figure
5, there might be two possible selected explanations
to be transmitted to a receiver of the explanation for
why argument h{a}, ai as the dispute tree has two
branches. This indicates that our forms of explanation
also enable to create selected explanations by manip-
ulating on the generation of dialogical explanations.
5 COMPARISON WITH THE
STATE OF THE ART WORK
This section compares our approach described in this
paper with existing work on logic-based argumenta-
tion where the knowledge-base is formulated by PL.
(Efstathiou and Hunter, 2011) adopt the idea of
connection graph (Kowalski, 1975; Kowalski, 1979)
to model arguments from a knowledge-base ∆ of
clauses where each claim is a literal. At a high level,
each node in a connection graph represents a clause
in ∆; and, each edge connects nodes φ, ψ if there is a
disjunct in b ∈ φ with its complement being a disjunct
¬b ∈ ψ. To find an argument for claim α, the authors
considered the set of complements of the disjuncts of
α together with ∆. Then, for any clause φ in the graph,
if there is a disjunct b ∈ φ and there are no edges con-
necting φ, ψ where the complement of b is a disjunct
in ψ, then the clause φ is deleted together with edges
involving φ. This process of deletion is continued un-
til no more clauses can be identified for deletion. If
the resulting graph is non-empty, then it contains a
set of formulae that entails α. Though the idea of
connection graph can be used to find arguments, our
proposed approach can model logical arguments more
naturally where connections between the claim and its
supporting premises are visualized explicitly; thereby
our approach enables to extract explanation as more
human-friendly arguments for non-technical users.
(Dung et al., 2009) introduced a more concrete
framework for instantiating abstract argumentation
called assumption-based argumentation, in which ar-
guments can be constructed deductively from infer-
ence rules and the notion of attack is defined based
on the contrary of an argument’s claim. It is worth
observing that the authors’ proposal was also similar
to ours in a sense that their arguments were modeled
by applying modus ponens on inferential knowledge-
base whereas our approach models arguments by ap-
plying ND rules to prove a claim (i.e. ND proof trees
as logical arguments). The fact that we do not only fo-
cus on just one rule enables to model deductive argu-
ments in a way that can be understood by naive users.
(Kakas et al., 2014) developed argumentation
logic (AL), which can be viewed as an extension of
PL. AL re-interpreted and extended PL to deal with
inconsistency by modeling arguments from a set of
PL formulae. Attack between two arguments in AL
was defined based on a proof for inconsistency (in-
spired by Reductio ad Absurdum in ND) between
two sets of PL formulae representing arguments. As
for entailment, an argument is said to hold if it can
be successfully defended and it cannot be success-
fully objected against. AL does not follow conven-
tional semantics in AA; hence, the framework may
infer different results to ours. For instance, let ∆
:
=
{α, β, α ∧ β, ¬α ∨ ¬β}, the knowledge-base does not
entail α in AL; however, our approach flavors ND for
modeling arguments from sets of PL formulae and
evaluates the acceptability of arguments based on se-
mantics in AA. For example, α may be inferred from
∆ if stable semantics is used or otherwise if grounded
semantics is considered.
6 CONCLUSION AND FUTURE
DIRECTIONS
This work presents an approach to a logic-based ar-
gumentation framework for reasoning with an (incon-
sistent) PL knowledge-base, especially in multi-agent
reasoning in which each agent holds different set of
(mutually inconsistent) knowledge, with an aim at the
introduction of human-friendly explanations in argu-
mentative reasoning. We show that good explanations
investigated in cognitive science and social psychol-
ogy can be formalized as a NDSA framework to de-
velop an explainable artificial intelligence system.
Our approach exploits two main aspects of for-
malisms: (1) the naturalness of natural deduction and
(2) argumentative semantics in AA. First, we utilize
natural deduction proof in PL for finding valid argu-
ments in a knowledge-base. While we are inspired
by ND for modeling arguments from the knowledge-
base, our approach can also be applied with other
proof systems even though verbose explanations may
be generated due to the proof procedure (cf. Figure
On Explanation of Propositional Logic-based Argumentation System
331

1). Indeed, a derivation for a formula is re-interpreted
as an argument supporting that formula; and also, ar-
guments supporting the contrary of the premises are
seen as its attack. Second, when modeled arguments
are in conflict, the notion of acceptability and se-
mantics in AA are used to handle inconsistency. We
believe that the computational content which brings
together these two formalisms can generate human-
friendly explanations on theorem hood in a theory.
It is widely accepted by now that answers of an
intelligent systems should be able to explain for why
to the users. Therefore, in the future, we would like to
extend this idea for other logics (e.g. description logic
and modal logic) and develop argumentation-based
reasoning engines that offer human-friendly explana-
tions to naive users for applying on real-world appli-
cations such as legal reasoning and ontology merging.
ACKNOWLEDGEMENTS
The authors would like to thank anonymous reviewers
for valuable comments. This study was supported by
JSPS KAKENHI Grant Number 17H02258.
REFERENCES
Amgoud, L., Besnard, P., and Vesic, S. (2011). Identify-
ing the core of logic-based argumentation systems. In
2011 IEEE 23rd International Conference on Tools
with Artificial Intelligence, pages 633–636. IEEE.
Baroni, P. and Giacomin, M. (2009). Semantics of abstract
argument systems, pages 25–44. Springer US, Boston,
MA.
Besnard, P. and Hunter, A. (2018). A review of argumen-
tation based on deductive arguments. Handbook of
Formal Argumentation, pages 437–484.
Ches
˜
nevar, C. I., Maguitman, A. G., and Loui, R. P. (2000).
Logical models of argument. ACM Computing Sur-
veys (CSUR), 32(4):337–383.
Dung, P. M. (1995). On the acceptability of arguments
and its fundamental role in nonmonotonic reasoning,
logic programming and n-person games. Artif. Intell.,
77(2):321–358.
Dung, P. M., Kowalski, R. A., and Toni, F. (2006). Dialec-
tic proof procedures for assumption-based, admissible
argumentation. Artif. Intell., 170(2):114–159.
Dung, P. M., Kowalski, R. A., and Toni, F. (2009).
Assumption-based argumentation. In Simari, G. R.
and Rahwan, I., editors, Argumentation in Artificial
Intelligence, pages 199–218. Springer.
Efstathiou, V. and Hunter, A. (2011). Algorithms for gen-
erating arguments and counterarguments in proposi-
tional logic. International Journal of Approximate
Reasoning, 52(6):672–704.
Ferrari, M. and Fiorentini, C. (2015). Proof-search in
natural deduction calculus for classical propositional
logic. In International Conference on Automated Rea-
soning with Analytic Tableaux and Related Methods,
pages 237–252. Springer.
Garc
´
ıa, A. J. and Simari, G. R. (2004). Defeasible logic
programming: An argumentative approach. Journal of
Theory and Practice of Logic Programming, 4(2):95–
138.
Gentzen, G. (1935). Untersuchungen
¨
uber das logische
schließen. i. Mathematische zeitschrift, 39(1):176–
210.
Hilton, D. (2017). Social attribution and explanation.
Hilton, D. J. (1990). Conversational processes and causal
explanation. Psychological Bulletin, 107(1):65.
Kakas, A. C., Toni, F., and Mancarella, P. (2014). Argu-
mentation logic.
Kleene, S. C., De Bruijn, N., de Groot, J., and Zaanen,
A. C. (1952). Introduction to metamathematics, vol-
ume 483. van Nostrand New York.
Kowalski, R. (1975). A proof procedure using connection
graphs. Journal of the ACM (JACM), 22(4):572–595.
Kowalski, R. (1979). Logic for problem solving, volume 7.
Ediciones D
´
ıaz de Santos.
Lipton, P. (1990). Contrastive explanation. Royal Institute
of Philosophy Supplement, 27:247–266.
Miller, T. (2019). Explanation in artificial intelligence: In-
sights from the social sciences. Artificial Intelligence,
267:1–38.
Modgil, S. and Caminada, M. (2009). Proof Theories and
Algorithms for Abstract Argumentation Frameworks,
pages 105–129. Springer US.
Modgil, S. and Prakken, H. (2014). The ASPIC
+
frame-
work for structured argumentation: A tutorial. Argu-
ment and Computation, 5(1):31–62.
Prakken, H. and Sartor, G. (1997). Argument-based ex-
tended logic programming with defeasible priorities.
Journal of applied non-classical logics, 7(1-2):25–75.
Smullyan, R. M. (1995). First-order logic. Courier Corpo-
ration.
Takeuti, G. (2013). Proof theory, volume 81. Courier Cor-
poration.
Van Dalen, D. (2004). Logic and structure. Springer.
Vreeswijk, G. and Prakken, H. (2001). Logical systems for
defeasible argumentation. Handbook of Philosophical
Logic,, 4:219–318.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
332
