Multi-product, Multi-supplier Order Assignment and Routing for an

e-Commerce Application in the Retail Sector

Louis Rivi

ere

, Christian Artigues

, Azeddine Cheref

, Nicolas Jozefowiez

, Marie-Jos

e Huguet

Sandra U. Ngueveu

and Vincent Charvillat

3,4

CNRS, LAAS-CNRS, Universit

e de Toulouse, INSA, INP, France

LCOMS EA 7306, Universit

e de Lorraine, Metz 57000, France

Universit

e de Toulouse, IRIT, INP, France

U Devatics, Toulouse, France

Keywords:

e-Commerce, Retail Market, Order Assignment, Vehicle Routing, Genetic Algorithms.

Abstract:

With the rise of virtualization, the share of e-commerce in the retail market continues to grow in an omnichan-

nel context. We consider an existing software tool, developed by the Devatics company, for pooling inventories

in stores to meet online orders. The problem which arises therefore consists in seeking the optimal allocation

of a set of customers to stores. In this paper we consider a variant of the ofﬂine problem corresponding to an

evolution of the existing software, consisting of assigning a set of predeﬁned orders when the transportation

cost depends on a delivery tour to the customer locations. We show that the problem corresponds to a vehicle

routing problem with additional but standard attributes. A mixed-integer linear programming formulation is

given and several heuristics are proposed : a giant tour-based genetic algorithm, a simple cluster-ﬁrst, route

second heuristic and an assignment-based genetic algorithm. Preliminary computational results on a set of

realistic problem instances suggest that the assignment-based genetic algorithm better scales as the problem

size increases.

1 INTRODUCTION

With the rise of virtualization, the share of e-

commerce in the retail market continues to grow in an

omnichannel context. One of the services offered by

the Devatics company is Onestock

, a tool for pool-

ing inventories to meet online orders. The problem

which arises therefore consists in seeking the opti-

mal allocation of a set of customers to stores. Two

modes of assignment are possible. Indeed, we can

consider the ”Online” assignment mode, consisting

of the allocation of each order as they are declared,

and the ”Ofﬂine” assignment which consists of as-

signing all the orders in a single large block. In this

paper we consider the ofﬂine problem. The Onestock

software solves a variant where the transport cost are

ﬁxed. In this paper we consider an evolution of the

problem towards a variant where the transport costs

depend on delivery tours to the customer locations.

We propose an mixed-integer linear programming for-

mulation (MILP) of the problem. On realistic data

https://www.onestock-retail.com/

instances, we compare several heuristics and meta-

heuristics. We show that a cluster-ﬁrst, route-second

based genetic algorithm obtains the best results. The

problem formulation is given in Section 2. The real-

istic data extraction approach that we use to generate

the data instances is then presented in Section 3. Sec-

tion 4 ﬁrst gives a quick state of the art review of efﬁ-

cient metaheuristics for vehicle routing problems and

propose adaptations for the considered E-commerce

problem. Section 5 provides a computational compar-

ison of the proposed exact and heuristic approaches.

Concluding remarks are drawn in Section 6.

2 MODELING THE PROBLEM

The problem considers a ﬁxed set of online orders D

for a set of products P. Each order d ∈ D asks for

an amount q

d p

of product p ∈ P. We have a set M of

stores, and each store m ∈ M has a stock s

of prod-

uct p ∈ P. The problem is then to meet the demand

in products of each order by using the store stocks

438

Rivière, L., Artigues, C., Cheref, A., Jozefowiez, N., Huguet, M., Ngueveu, S. and Charvillat, V.

Multi-product, Multi-supplier Order Assignment and Routing for an e-Commerce Application in the Retail Sector.

DOI: 10.5220/0010318304380445

In Proceedings of the 10th International Conference on Operations Research and Enterprise Systems (ICORES 2021), pages 438-445

ISBN: 978-989-758-485-5

with the possibility to split the demand across differ-

ent stores. Then, each store must deliver the ordered

packages to the customers in a single tour.

Although in the OneStock software the orders are

served online upon receipt, the ofﬂine problem has

concrete applications. Indeed, most real orders take

place in the evening, and therefore cannot be pro-

cessed before the stores open on next morning. In this

case, we have a given number of orders to process at

a time. Another application of interest is the estima-

tion of a ”regret”, i.e. the difference in performance

between the immediate allocation of successive or-

ders and the optimal allocation of these orders. In

this paper, we wish to minimize the distance traveled

on tours. The trucks have no capacity, so each store

only has to deliver the products in at most one tour.

However, a customer can be served by several stores

and therefore by several routes. This model therefore

explicitly incorporates the “assignment + routing” as-

pect.

2.1 Input Data

D : set of orders.

M : set of stores.

P : set of products.

N = M ∪ D : set of nodes.

V = {(i, j) | i, j ∈ N

} set of arcs.

R : set of r

i j

∈ R : cost of arc from i to j

Q : set of q

d p

∈ N : amount of product p ∈ P in order

d ∈ D.

S : set of s

∈ N : stock of product p ∈ P in store

m ∈ M.

2.2 Variables

X : set of x

dmp

∈ N : number of products p sent from

store m for order d.

Y : set of y

∈ {0, 1} : indicates whether a package

is sent from store m for order d.

Z : set of z

i j

∈ {0, 1} : indicates whether the tour of

store m takes arc (i, j).

U : set of u

∈ N : number assigned to node i in the

tour of store m (to avoid subtours).

2.3 Objective

min

∑

m∈M

∑

(i, j)∈V

i j

(1)

2.3.1 Constraints

∑

m∈M

dmp

≥ q

d p

, ∀d, p ∈ D, P (2)

∑

d∈D

dmp

≤ s

, ∀m, p ∈ M, P (3)

dmp

≤ y

min(q

d p

, s

), ∀d, m, p ∈ D, M, P (4)

∑

i∈N

≥ y

, ∀d, m ∈ D, M (5)

∑

i∈N

≥ y

, ∀d, m ∈ D, M (6)

∑

i∈N

i j

∑

k∈N

, ∀m, j ∈ M, N (7)

− u

+ |D|z

i j

≤ |D| − 1, (8)

∀i, j ∈ V \ {m}, i 6= j, ∀m ∈ M

Objective (1) is this time to minimize the total dis-

tance traveled by the store deliverers.

Constraints (2) guarantees that each order is sufﬁ-

ciently supplied. Constraints (3) guarantee that stocks

are sufﬁcient for shipments and constraints (4) ensure

that the number of products p sent from store m to

customer d is set to 0 if no package is sent from m to

d. Constraints (5) and (6) guarantee that the tour of

store m passes through customer d and by store m if

this allocation has been decided, respectively. Con-

straints (7) ensure ﬂow conservation while (8) guar-

antees that only cycles including store m are allowed.

3 REALISTIC DATA INSTANCE

GENERATION

To best stick to reality, we use statistics extracted

from real instances of a Devatics customer. An of-

ﬂine problem generator uses these statistics to create

datasets with an arbitrary number of orders.

Figures 1 and 2 show that for the ﬁrm considered

the distribution of orders is not egalitarian.Wednesday

is the busiest day with around 200 orders on average,

with peaks of orders on sales days that do not exceed

1000 orders for a day.

For each product, its popularity is given by the

sum of its purchases. In addition, a matrix of co-

occurrence indicates for each pair of products the

number of orders that include both. We notice that

the popularity of the products is distributed in a way

approaching a Pareto distribution.

We can therefore generate a semi-realistic n-sized

order from the data, ﬁrst choosing a product randomly

based on its popularity, then adding products accord-

ing to their co-occurrences with the products already

Multi-product, Multi-supplier Order Assignment and Routing for an e-Commerce Application in the Retail Sector

439

Figure 1: Number of orders per day over a three-month pe-

riod.

Figure 2: Average number of orders per day of the week.

present until we have n products. We also have in-

formation regarding the size distribution of n orders

with an almost binomial distribution of the quantity

of product ordered. We notice that the average order

gathers 2.8 products, or roughly 1% of the available

products (203 in total).

Once the orders are composed, we need to provide

stores to ensure the feasibility of the problem. To do

this, we are inspired by the overall distribution of the

stock of products as well as quantities of stocks of

each product in each store. We noticed that more than

30% of the stock is in the warehouse, while all the

other stores roughly share the rest.

For each unit of product ordered we select a store

to receive a unit of stock of this product. If it is the

ﬁrst unit of this product in stock, a stock margin of

two units is added. This margin value, given by De-

vatics, corresponds to the risk aversion of stores that

report a quantity of stock below reality to avoid short-

age. We generate a set of problems constituting a test

bench on which we vary the values of the number of

orders and of the stock margin.

4 PROPOSED METHODS

The modeling of the routing problem, in particular

the constraints that eliminate subtours, do not allow

a MILP solver to solve the problem effectively, which

justiﬁes the use of heuristics. This problem is very

close to several well studied problems such as the

traveling salesman problem (TSP) the location and

routing problem (LRP) and in particular the vehicle

routing problem (VRP). Classically, the latter consists

of minimizing the cost of visiting all customers with-

out exceeding a given capacity of the truck. One can

consider that our problem corresponds to the VRP

with additional classical attributes (no capacity on

trucks, multi-products, capacity on stocks, several

warehouses, multiple deliveries, one truck per ware-

house). The VRP as well as many variations involving

some of these attributes are very studied problems for

their many practical applications in the ﬁeld of logis-

tics. In (Abdulkader et al., 2018; Martins et al., 2020),

heuristics are proposed for a related omnichannel re-

tail problem with the difference that vehicles are not

attached to stores but located in a central depot and

perform pick up and delivery tours. We ﬁrst review

the efﬁcient metaheuristics designed for the VRP be-

fore describing our solution approaches.

4.1 The Properties of Efﬁcient

Metaheuristics for Vehicle Routing

Problems

Vidal et al. (Vidal et al., 2014b) proposed a uniﬁed

heuristic framework to solve ta family of VRP with

many attributes. The approach consists in categoriz-

ing the attributes (additional constraints) of the VRP

to be able to offer solutions adapted to each of these

categories. In addition, others works (Vidal et al.,

2013) try to extract from the profusion of the meth-

ods the main characteristics which make the success

of an approach. Although empirical, this analysis can

guide us in creating our method. Two tracks inspired

by the methods of LRP solution approach emerge. On

the one hand, the giant tour method, which focuses on

the ”routing” aspect of the problem, and on the other,

an approach highlighting the ”assignment” aspect of

the problem.

4.2 Giant Tours: Route-ﬁrst,

Cluster-second Approach

The giant tour method is proposed for the ﬁrst time

for the VRP by Beasley (Beasley, 1983). Prins (Prins,

2004) integrates this technique with a memetic algo-

rithm (genetic algorithm with a local search phase).

ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems

440

Vidal et al. (Vidal et al., 2014b) among others pro-

posed an efﬁcient variant able to solve a large set of

routing problems with various constraints. In this sec-

tion we ﬁrst recall the principle of the giant tour and

the SPLIT operator for the VRP. Then, we describe the

adaptation of the SPLIT operator to our problem and

we ﬁnally describe the proposed giant tour based hy-

brid genetic algorithm that uses a MILP-based repair

operator.

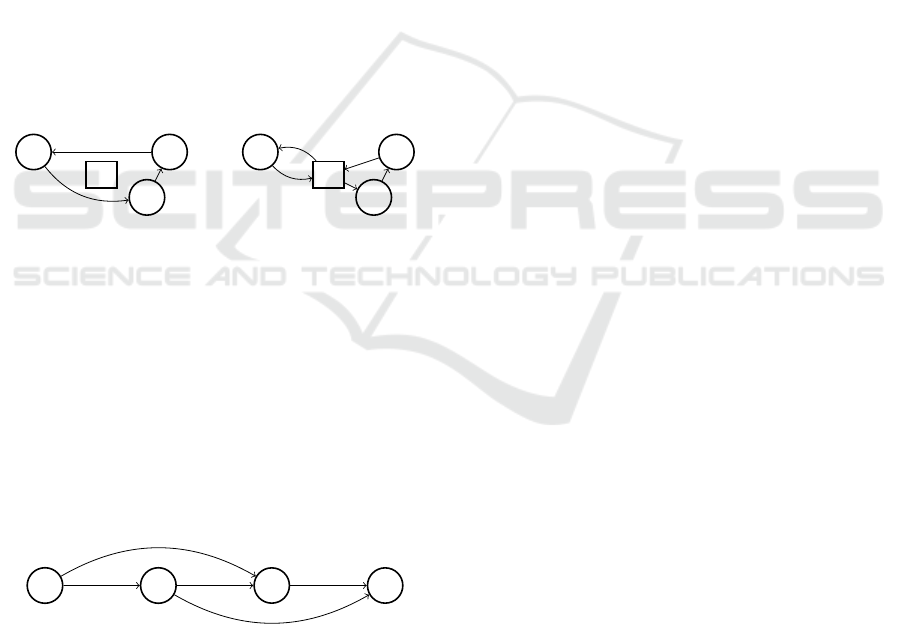
The Principle of the Giant Tour. The representa-

tion by giant tour consists for the classic VRP to con-

sider, instead of explicit solutions, ”giant tours”, a

kind of concatenation of real tours, representing all

the ways to cut this tour in order to respect the ca-

pacity constraint of the trucks. The idea is that if we

know how to quickly ﬁnd the best solution for this

subset, it is faster to consider ”macro solutions”. An

illustration of the giant tour is given in Fig. 3. In this

ﬁgure, a giant tour of size 3: [3,1,2] must be cut for

a truck capacity of 2. The different possible cuts are

therefore [3 — 1 — 2], [3,1 — 2] and [3 — 1,2]where

”—” represents a return to the depot.

⇒

Figure 3: Giant tour [3,1,2] and associated solution.

Finding an optimal division of the giant tour into

subtours is polynomial, as a shortest path algorithm.

Figure 4 shows how this cutting operator (commonly

called SPLIT) determines the optimal solution. It con-

sists in ﬁnding the shortest path in a graph whose

nodes are the ordered points visited by the giant tour

and whose arcs each represent a grouping. Each arc

cannot group more points than the capacity of the

trucks and the cost associated with an arc is the cost

of the grouping it represents.

0 3

1 2

[3]

[3,1]

[1]

[1,2]

[2]

Figure 4: Subgraph for cutting by SPLIT the giant tour

[3,1,2] with capacity 2.

Adapting the Split Operator to Our Problem. To

adapt the method to our problem and its attributes,

we ﬁrst observe the adaptations considered for these

attributes taken individually. In the literature, to adapt

the method to problems with split-delivery, (Boudia

et al., 2007) brings two changes:

• A node can appear several times in a giant tour.

• Each occurrence of a node is associated with the

quantity of delivered products. The sum of the

delivered quantity must match the request.

The SPLIT operator is also slightly modiﬁed since

when a sub-tour is considered, visiting several times

the same node is meaningless. The sum of the de-

livered quantities is therefore carried over to a sin-

gle occurrence of the node. Experience shows that

the choice of this node, if it can be difﬁcult to deter-

mine optimally, can be done deterministically (the lo-

cal search carried out thereafter rectifying a possible

bad choice). In addition to the loss of optimality, the

ﬁrst of these changes complicates the cutting, in fact,

in a giant tour, a node can appear up to M times if it is

served by all stores. We switch from a ﬁxed size |D|

to a variable size up to |D|.|M|. Especially since in a

multi-product context and with capacities on stocks,

the information associated with the quantity delivered

for each product can be voluminous and, as we will

see later, does not by itself guarantee the existence of

a solution by the SPLIT operator. Indeed, even if the

sum of the delivered products corresponds to the de-

mand for each product, it is still necessary that stores

have stocks to deliver these products. This feasibil-

ity of a sub tour is itself difﬁcult to determine since it

depends on the other sub-routes selected.

Vidal et al. (Vidal et al., 2014a) show how the

giant tour can be adapted to multiple depots. The

change is restricted to the SPLIT method, in which the

costs associated with a sub-tour becomes the cost of

allocating the tour to the best depot. In our case with

capacities, it is not possible to determine the ”best”

assignment independently of other assignments. We

must therefore create for each assignment of a sub-

tour to a store m, an arc with a corresponding cost.

The number of route assignments to be considered be-

comes O(|M|

) in the worst case where n is the size

of the giant tour since we do not limit the capacity of

the trucks.

A SPLIT operator adapted to the case of deliv-

eries with capacities is presented by Duhamel et al.

(Duhamel et al., 2010). The authors use a Bellman

algorithm with several labels per node to keep the

stocks available when searching for the shortest path.

A dominance rule between labels makes it possible

to discard some of them, but the method remains too

slow for large instances. Several improvements are

proposed to speed it up, in particular, limiting the

number of labels considered during the evaluation (a

parameter to be set). Despite these complications, one

of the properties of our problem, which can simplify

Multi-product, Multi-supplier Order Assignment and Routing for an e-Commerce Application in the Retail Sector

441

the SPLIT procedure, is that each store performs only

one tour. In this case, the resource whose labels must

report the usage is no longer the stock, but the prior

use or not of a store. However, the giant tour cut

this way represents a less important set of solutions.

So we have a trade-off between speed of cutting and

search efﬁciency.

From this analysis, a giant tour for our problem

is thus a sequence S of at most |D|.|M| nodes, each

node k corresponding to an order δ(k) associated to

a delivered amount λ

(k) such that the sum of deliv-

ered amount for the nodes corresponding to the same

order equals the total required quantity for each prod-

uct, which correspond to the following invariant:

|S|

∑

k=1

δ(k)=d

(k) = q

d p

∀d ∈ D, p ∈ P (9)

The SPLIT operator we propose is synthesized in

Algorithmm 1. A solution is represented by a chain

of labels. a label L labels is composed of a node

L.nodein the giant tour S, a score L.score, a store

L.store and a set of available stores L.available m,

and a parent label L.parent. A Label represent

the subsequence from the successor of L. parent to

L.node assigned to store m of cost L .score and such

that the set of stores available for delivering the suc-

cessors of L.node in S is stored in L.available

. The

notation µ

i j

denotes the sub-tour comprising nodes

i + 1 up to j in S. To save the propagation of un-

necessary labels, the procedure ADDLABELTONODE

uses a standard dominance rule. A label L

dominates

a label L

(noted L

 L

) if it uses fewer resources

for a better score. Formally:

.score < L

.score and

.available m ⊆ L

.available m

.score ≤ L

.score and

.available m ⊂ L

.available m

One must notice that the SPLIT operator may fail

in obtaining a feasible set of tours. Indeed, it is

possible that all active label at some points fail to

satisfy the condition at Line 8. This condition ex-

press the fact that the stock in store m must be suf-

ﬁcient to deliver all amounts λ

(k) of each order k

in the µ

i j

subsequence for all products p. But if the

(k) atttached to the giant tour satisfy invariant (9),

which ensure that the customer demand is satisﬁed,

they are not necessarily compatible with the stock. In

this case, the best set of tours computed by the SPLIT

operator is incomplete.

Algorithm 1: The SPLIT procedure.

1 //Insert start label;

2 L ← (node = 0; cost = 0; available store =

M; parent = nil);

3 ADDLABELTONODE(0, L);

4 for i ∈ {0, .., |S|} do

5 for L

∈ {Labels on node i} do

6 for j ∈ {i, .., |N|} do

7 for m ∈ L

.available m do

8 if s

≥

∑

k=i+1

(k), ∀p ∈ P

then

9 L.score ← L

.score +

route cost(µ

i j

, m);

10 L.available ←

.available m \ {m};

11 L.node = j;

12 L.store = m;

13 L.parent = L

;

14 ADDLABELTONODE( j, L);

15 end

16 end

17 end

18 end

19 end

The Giant Tour-based Hybrid Genetic Algorithm.

Given the SPLIT operator, Algorithm 2 describes the

genetic algorithm. Individuals are giant tours. In Line

1, a population of giant tours is initialized randomly

via function INITPOPGT. The a standard tournament

selection is performed to select two parent individuals

I1 and I2 (Line 3, function CHOOSEPARENTSGT).

An adaptation of the classic one point crossover op-

erator is used on the selected giant tours I1 and I2 at

Line 4 with function CROSSOVERGT, which yields

offspring I3. Recall that a giant tour is deﬁned by a

sequence of nodes k and associated λ

(k) delivered

values for each product p ∈ P. For the nodes up to the

crossover point, λ

(k) values in I3 are the same as in

I1. After the crossover point, the λ

(k) values for the

nodes k duplicated from I2 are set so that invariant (9)

is satisﬁed. If there is not enough nodes for a given

order to satisfy its demand, nodes are duplicated at

the end until the invariant is satisﬁed. Then, at Line

5, the SPLIT operator is applied to obtain a set T of

tours (one for each store).

If tour T is incomplete (see reasons above), a

MILP-based repairing operator is used (Line 6).

Based on tour T , the repair operator searches to com-

pute a new feasible tour for each store with optimized

cost. Let ¯y the current assignment of orders to stores

ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems

442

Algorithm 2: Giant tour-based genetic algorithm.

1 Pop = InitPopGT (n);

2 while True do

3 I1, I2 =CHOOSEPARENTSGT(Pop);

4 I3 =CROSSOVERGT(I1, I2);

5 T =SPLIT(I3);

6 T =MILPREPAIR(T );

7 T =LOCALSEARCH(T );

8 I3 =GETGT(T );

9 Pop = Pop + I3;

10 if |Pop| > α then

11 Pop =SELECTSURVIVORSGT(Pop);

12 end

13 if it stale > β then

14 Pop =DIVERSIFYGT(Pop);

15 end

16 end

as stated by tour T such that ¯y

= 1 if store m de-

livers at least a part of order d and ¯y

= 0 if no part

of order d is delivered by store m. A new feasible

assignment of orders to stores is ﬁrst computed by

solving a variant of multi order, multi product facility

location problem issued from MILP (1–8) while re-

placing the routing constraints by estimated removal

proﬁts and insertion costs. Let T

denote the tour on

machine m and T

for k = 1, . . . |T

| the kth order

visited by tour T

. The repair MILP has variables y

and x

dmp

∈ {0, 1} for all d ∈ D, m ∈ M, d ∈ D and the

following objective and constraints.

min

∑

m∈M

∑

d∈D

¯y

−

∑

m∈M

∑

d∈D

¯y

−

(10)

subject to constraints (2–4), where

= min

k=1,...,|T

|−1

+ R

m,k+1

− R

m,k+1

is the insertion cost of d (in the case where it is the

only order inserted in the tour on machine m) and

−

represents symmetrically the proﬁt of removing

d from T

Then function MILPREPAIR, use the standard best

insertion algorithm to build the route of each store

given the orders assigned to the stores. A two-opt

local search algorithm (function LOCALSEARCH at

Line 7) further improves tours T . Finally, the gi-

ant tour offpring I3 is rebuilt by deriving the gi-

ant tour from the sequence of tours on T (function

GETGT). The SELECTSURVIVORSGT keeps the best

giant tours in the population up to a maximal number

α. The DIVERSIFYGT diversiﬁcation function sim-

ply reinitializes part of the population randomly.

4.3 Cluster-ﬁrst, Route Second

Approaches

Another common approach, in opposition to the giant

tour method, ﬁrst selects the store assignments to cus-

tomers, then chooses the best routes for visits. The

idea is that once the allocation ﬁxed, the problem is

reduced to an instance of the TSP for each store hav-

ing to visit customers to whom it was assigned. In

the worst case, each customer should be visited, but it

can be expected that in general a store will only visit

a small number of customers; and, due to the combi-

natorial nature of the problem, solving a set of small

problems is much faster than solving a single bigger

problem.

Cluster-ﬁrst, Route-second Heuristic. In an arti-

cle by Fisher (Fisher and R.Jaikumar, 1981), a heuris-

tic of this type is proposed for the ﬁrst time for a vari-

ant of the VRP and we adapt this method to our prob-

lem. It solves a general assignment problem to de-

termine the assignments and then solves the resulting

TSP. Intuitively, the problem of allocation resembles

the problem of clustering; indeed, if the sets of cus-

tomers to be visited are located around the stores, we

can hope that the associated routing is of good quality.

Among all the existing clustering criteria, we choose

to minimize the sum of the distances between cus-

tomers and their associated stores (potentially several)

such that the allocation is valid. This criterion has

the merit of being simple and of adapting well to the

strong constraints on stocks. Other criteria such as

minimizing the greatest distance between a customer

and a linked store are not adapted since if an assign-

ment happens to be necessary (for example in the case

where only one store has a given product) yielding

a high cost A, the assignment of other customers to

stores becomes indifferent to the cost as long as it is

less than A. Once the assignment of orders to stores

is made, we use the the MILP (1–8) with ﬁxed vari-

ables y

and x

pdm

, which amounts to solve |M| small

TSPs.

Hybrid Genetic Assignment Algorithm. In addi-

tion to the previously mentioned heuristic, another ge-

netic algorithm based on solving the underlying as-

signment problem is proposed (Algorithm 3). The so-

lutions (or individuals) are represented by a set of |M|

chromosomes, each corresponding to a store tour. The

population is initialized randomly (INITPOP), then,

at each iteration, two individuals are selected to be

crossed (function CHOOSEPARENTS). The classic

one point crossover operator is used on each of the

store tour pairs since it has the advantage of keeping

Multi-product, Multi-supplier Order Assignment and Routing for an e-Commerce Application in the Retail Sector

443

part of the parents’ route ( CROSSOVER). Each indi-

vidual offspring is not not always viable because of

the product stock in the stores and the MILPREPAIR

function is then used to repair the offspring.

The offspring is then inserted into the population.

If the population size exceeds a given threshold, a se-

lection procedure (SELECTSURVIVORS) determines

which individuals are deleted. To choose the sur-

vivors, we compare of course the solution scores, but

we also take into account their diversity, using a mea-

sure based on the average Hamming distance between

an individual and his closest neighbors. When the

search stagnates during a given number of iterations,

the population is diversiﬁed (DIVERSIFY). The op-

eration consists in destroying the current solutions by

removing certain visits before applying a random re-

pair of individuals. To do this, we use a random vari-

ant of MILPREPAIR.

Algorithm 3: Assignment based genetic algorithm.

1 Pop = INITPOP(n);

2 while True do

3 T 1, T 2 = CHOOSEPARENTS(Pop);

4 T 3 = CROSSOVER(T 1, T 2);

5 T 3 =MILPREPAIR(T 3);

6 T 3 =LOCALSEARCH(T 3);

7 Pop = Pop + T 3;

8 if |Pop| > α then

9 Pop =SELECTSURVIVORS(Pop);

10 end

11 if it stale > β then

12 Pop =DIVERSIFY(Pop);

13 end

14 end

5 PRELIMINARY

COMPUTATIONAL RESULTS

We compare the four solution methods (MILP us-

ing the IBM Cplex solver, Cluster-ﬁrst heuristic,

Assignement-based Genetic algorithm, Giant tour-

based Genetic algorithm) on randomly generated

problem instances for given dimensions. Figure 5

presents the performances of the methods compared

to the best solution among the four. A single 15 min

run was performed for each algorithm. Each point

correspond to the average score on 3 instances of the

given size. So a score of 1 corresponds to the best

solution found and a score of 0.5 corresponds to a so-

lution twice as expensive.

As you would expect, The MILP formulation,

even if it ﬁnds the optimal solution for small in-

stances, is quickly outperformed when it comes to

solving larger instances. The assignment-based ge-

netic (named AG affectation in Fig. 5) algorithm is

more efﬁcient than the one based on giant tours, es-

pecially for the larger instances with a realistic size

of 100 orders, 10 stores and 10 products. In third po-

sition, the assignment heuristic obtains surprisingly

honorable scores (about 1.25 times higher than the

best score). As parameter tuning was handcrafted and

only single runs were performed, these preliminary

computational experiments should be extended in the

future but they suggest good scaling properties of the

assignment-based genetic algorithm.

6 CONCLUSION

We have considered an industrial problem problem

consisting in ﬁnding the optimal allocation and rout-

ing of a set of customer orders to stores, a vari-

ant of the location routing problem / vehicle routing

problem with complicating constraints. We proposed

mixed-integer linear programming formulations and

several heuristics for the problem. Our hybrid genetic

algorithm based on assigning customers to store ﬁrst

and routing the order second with MILP-based repair

operators showed good scaling properties on prelimi-

nary computational experiments. Regarding the rout-

ing problem, further improvements can be made in

the conﬁguration of genetic algorithms. In particular,

the Split operator could be improved as in (Duhamel

et al., 2011). An idea to experiment would be not

to ﬁx the quantities of products, but that each label

contains a MILP model, enriched with each alloca-

tion of a sub-tour, which determines the feasibility of

an assignment. A simple local search integrating the

cluster-ﬁrst, route-second phases using combined tour

improvement neighborhoods and assignment neigh-

borhoods deserves also to be tested.

ACKNOWLEDGEMENTS

This research was carried out in the context of the

”One Stock Performance” project, funded by the

EASYNOV program (FEDER / Midi-Pyr

ees re-

gion), in partnership with DEVATiCS.

We also thank the anonymous referees for their

enlightening suggestions.

ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems

444

Figure 5: Performance of the different methods compared to the best solution.

REFERENCES

Abdulkader, M. M. S., Gajpal, Y., and ElMekkawy, T. Y.

(2018). Vehicle routing problem in omni-channel re-

tailing distribution systems. International Journal of

Production Economics, 196:43–55.

Beasley, J. (1983). Route ﬁrst - cluster second methods for

vehicle routing. Omega, 11(4):403–408.

Boudia, M., Prins, C., and Reghioui, M. (2007). An effec-

tive memetic algorithm with population management

for the split delivery vehicle routing problem. In Inter-

national Workshop on Hybrid Metaheuristics, pages

16–30. Springer.

Duhamel, C., Lacomme, P., C.Prins, and C.Prodhon (2010).

A GRASPxELS approach for the capacitated location-

routing problem. Computers & Operations Research,

37(11):1912–1923.

Duhamel, C., Lacomme, P., and Prodhon, C. (2011). Com-

puters & Operations Research, 38(4):723–739.

Fisher, M. and R.Jaikumar (1981). A generalized as-

signment heuristic for vehicle routing. Networks,

11(2):109–124.

Martins, L. d. C., Bayliss, C., Juan, A. A., Panadero, J.,

and Marmol, M. (2020). A savings-based heuristic

for solving the omnichannel vehicle routing problem

with pick-up and delivery. Transportation Research

Procedia, 47:83–90.

Prins, C. (2004). A simple and effective evolutionary algo-

rithm for the vehicle routing problem. Computers and

Operations Research.

Vidal, T., Crainic, T., Gendreau, M., and Prins, C. (2013).

Heuristics for multi-attribute vehicle routing prob-

lems: A survey and synthesis. European Journal of

Operational Research, 231(1):1–21.

Vidal, T., Crainic, T., Gendreau, M., and Prins, C. (2014a).

Implicit depot assignments and rotations in vehicle

routing heuristics. European Journal of Operational

Research, 237(1):15–28.

Vidal, T., Crainic, T., Gendreau, M., and Prins, C. (2014b).

A uniﬁed solution framework for multi-attribute ve-

hicle routing problems. European Journal of Opera-

tional Research, 234(3):658–673.

Multi-product, Multi-supplier Order Assignment and Routing for an e-Commerce Application in the Retail Sector

445