An Effective Driver Intention and Trajectory Prediction for Autonomous

Vehicle based on LSTM

Fatimetou El Jili

Altran Prototypes Automobiles, Research Departement, 02 rue Paul Dautier, 78140, France

Keywords:

Artiﬁcial Intelligence, Intention Prediction, Trajectory Prediction, Deep Learning, Long Short Term Memory,

CARLA Simulator, Autonomous Driving.

Abstract:

In order to make the navigation system of autonomous vehicle more robust and safe in urban environment we

propose in this paper a model for driver intention prediction and trajectory prediction. The proposed model

is based on LSTM (long short term memory). The model was trained on database of features collected from

the driving simulator CARLA. This paper treats four type of intentions, turn left, turn right, go straight and

stopping intention. Two cases were treated, the ﬁrst case is to predict intention before it occurs, the second

case corresponds to intention recognition, where the driver already starts maneuvering the intention. Both

cases are treated by the same model. The model shows better performances for the second case than the ﬁrst

case with small differences. The main strength of our model is that it gives good performances with a small set

of features. The accuracy of the model is 96% for intention prediction and 97% for the intention recognition.

The proposed method for trajectory prediction reach an accuracy of 99.9%. Those accuracies are higher than

what we found in state of art.

1 INTRODUCTION

Autonomous driven is a very complex system that re-

quires a lot of constraints to perform as the best hu-

man driving or better. In order to make a robust and

safe navigation system, understanding other driver’s

intentions is one of the most important task. By pre-

dicting the surrounding vehicles intentions, the au-

tonomous vehicle can plan its trajectory in a way that

it can avoid collision with other vehicles. In gen-

eral collisions happen due to a false identiﬁcation

of driver’s intentions or a lack of attention from the

driver.

In this paper we propose a method for driver in-

tention prediction and recognition for self driving ve-

hicles at several type of intersection (tree way, two

way and four way intersections), where intentions are

turn left and turn right, go straight and, stop, it also

gives intention on one way where in ideal case in-

tentions are stopping or going straight. This method

also gives the direction the vehicle is fellowing to ma-

noeuvre the intention. We also propose a method for

trajectory prediction. These methods can be used for

ADAS systems.

More recently in the last decade with the appari-

tion of autonomous vehicle and ADAS system, driver

intention prediction has been a topic of interest of

researchers. A variety of approches were proposed

for driver intention prediction. Some statistical meth-

ods (L.R Rabiner, 1986), (Streubel and Hoffmann,

2014), (Hou and al., 2011) were proposed to solve

this problem. Some machine learning methods like

SVM (Support Vector Machines) in (B. Tang, 2015)

and GP (Gaussian Process) (Laugier and al., 2011)

were also used to solve this problematic. Most of

these work needs a huge datasets to train their model

and some complex features, like when lane detection

is required, these additional tasks related to those fea-

tures computational time give rise to the model com-

putational time increasement. Whereas, our model

use a small dataset and a small set of features which

doesn’t need any additional tasks or complex artiﬁcial

intelligence algorithms to compute those features.

In (Hou and al., 2011) authors used CHMM (Con-

tinuous Hidden Markov Model ) for driver intention

prediction which gives an accuracy of 95% for in-

tention recognition, while in (B. Tang, 2015) SVM

gives an accuracy of 90% 1.6 s before the intersec-

tion and an accuracy of 93% at intersection for a gen-

eralized method for driver intention prediction at in-

tersection. There are other approches based on deep

learning specially RNN (Recurrent Neural Network)

(A. Zyner and Nebot, 2018), LSTM (Long-Short

Term Memory) (Sepp Hochreiter, 1997), (Hao Xue

1090

El Jili, F.

An Effective Driver Intention and Trajectory Prediction for Autonomous Vehicle based on LSTM.

DOI: 10.5220/0010321710901096

In Proceedings of the 13th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2021) - Volume 2, pages 1090-1096

ISBN: 978-989-758-484-8

 2021 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved

and Reynolds, 2018), (Derek J. Phillips and Kochen-

derfe, 2017), deep inverse reinforcement learning

(Zhang and al., 2018) and deep convolutional net-

work in (Djuric and al., 2019). In (Derek J. Phillips

and Kochenderfe, 2017) the LSTM model gives 95%

on dataset regrouping all kind of intersections. In

(B. Tang, 2015) authors proposed a method based

on HMM (Hidden Markov Model) for prediction of

driver intended path which gives an accuracy up to

90% 7 seconds before entering the intersection area.

Our model gives a higher accuracy than what we

found in state of art. This model doesn’t require any

information about roads and the map. Section 2 illus-

trates the LTSM(Sepp Hochreiter, 1997) model used

in this work to perform the prediction. In section 3 we

present an overview of the proposed method. Section

4 exhibits the model selection and datasets collection

details.

2 LSTM: LONG SHORT TERM

MEMORY

LSTM (Long Short Term Memory) (Sepp Hochre-

iter, 1997) is a novel architecture of recurrent neural

network (A. Zyner and Nebot, 2018) with an appro-

priate gradient based learning algorithm. The RNN

(Recurrent Neural Network) can use past information

when the time gap between past and present is short,

whereas when the time gap become long the RNN

can not learn exact information from the past.LSTM

was designed to remediate this problem so it can learn

from the past even when the time gap between past

and present is long, it also can learn when the input

data is incomprehensible due to noise. It is useful for

sequential data, time series data, speech processing,

etc ...

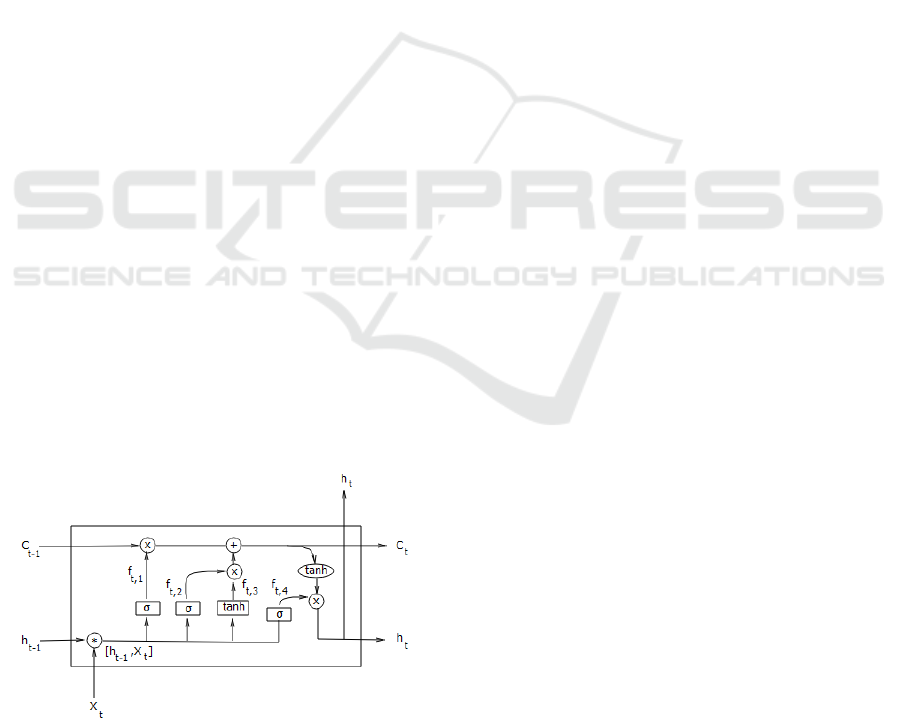
Figure 1: LSTM variant.

Figure 1 illustrate an exemple of LSTM variant at step

t of the model, or in other words when the input of

the model is the sequence of data collected at time

t. There is many variants of LSTM, researchers have

shown that almost all variants have the same perfor-

mances. The variables X

, C

t−1

and h

t−1

are respec-

tively the input of the network at the step t, the mem-

ory cell at the step t −1 and the output of the network

at the step t −1. These variables are given as the input

of the network at the step t to compute the output h

and the memory cell C

. The memory cells stores the

information about the past at each step of the model

in order to be used as input of the next step. For the

variant in ﬁgure 1, the memory cell C

and the output

are given by the following equations:

= f

t,1

t−1

+ f

t,2

t,3

, (1)

= f

t,4

tanh(C

), (2)

Where f

t,1

, f

t,2

, f

t,3

and f

t,4

are given by the equations

below :

t,1

= σ(W

t,1

t−1

, X

] + B

t,1

), (3)

t,2

= σ(W

t,2

t−1

, X

] + B

t,2

), (4)

t,3

= tanh(W

t,3

t−1

, X

] + B

t,3

), (5)

t,4

= σ(W

t,4

t−1

, X

] + B

t,4

), (6)

t,i

and W

t,i

, 1 ≤ i ≤ 4, correspond respectively to the

biais vector and the weight matrix, and σ the softmax

function.

3 THE PROPOSED METHOD FOR

DRIVER INTENTION AND

TRAJECTORY PREDICTION

This paper focus mainly on intention prediction,

recognition, and trajectory prediction. The term

recognition is used when the intention already oc-

curred or its manoeuvre already starts. In this work

intention prediction is treated as a classiﬁcation prob-

lem. Given the past information : starting from the

present back to the past though a given interval of

time, we predict or recognize the driver intention.

Trajectory prediction is a regression problem. In this

paper the prediction task needs information from the

past to perform the prediction. The state of art shows

that the LSTM (Sepp Hochreiter, 1997) is one of the

strongest model for this kind of problem.

3.1 Intention Prediction

This work focus on predicting driver’s intention

mainly turn right, turn left, stop and go straight ac-

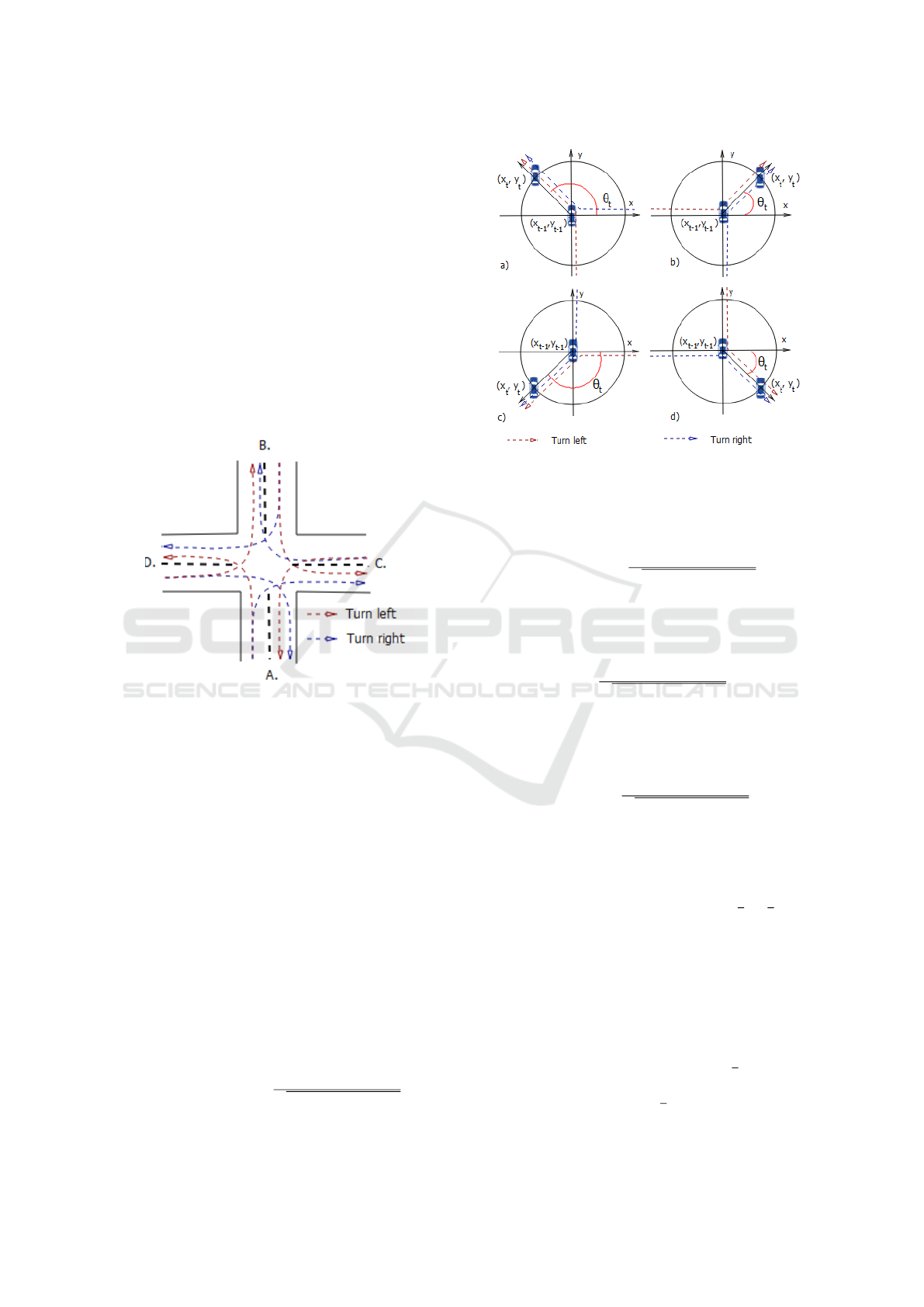
tion. Figure 2 illustrate all possible actions in a four

way intersection, we observe 8 kind of action depend-

ing to driver direction. The two remaining actions

An Effective Driver Intention and Trajectory Prediction for Autonomous Vehicle based on LSTM

1091

which are stopping and going straight whom are not

presented in this ﬁgure. Thus for this task we have

in total 10 intentions to predict or recognize, which

means we have 10 classes, let C = {C

, 1 ≤ j ≤ 10}

be the set of classes. Those actions can be maneu-

vered at any other kind of roads ( 2 ways intersection,

3 ways intersections, etc ...). Some of this actions can

be forbidden according to the type of the road and the

traﬁc regulation rules.

Datasets corresponding to each action were col-

lected during a given interval of time, this interval

starts few seconds before the action occurs and it ends

few seconds after it occurs. The datasets collected

before the actions occurrence were used for different

time window size, to predict drivers’s intentions.

Figure 2: Four ways intersection.

3.1.1 Features

In addition to classical features (position, accelera-

tion, velocity, etc...) we’ve deﬁned an important fea-

ture that are effective for the prediction task. This

feature made the model perform better, specially the

recognition, we named it the directional tilt angle of

the vehicle, we denote θ

this angle. This angle is cre-

ated between the abscissa axis and the vector created

by the past position (x

t−1

, y

t−1

) and the present posi-

tion (x

, y

) of the vehicle.

The angle θ

varies according to the vehicle di-

rection, in other words it depends on the positions

t−1

, y

t−1

) and (x

, y

) of the vehicle. Figure 3 illus-

trates how the angle is created for different cases, the

angle θ

is given by the fellowing equations:

• If x

< x

t−1

and y

≥ y

t−1

, this corresponds to the

case a) of ﬁgure 3, where θ

is given by:

= 180 −arccos



−x

t−1

√

−x

t−1

)

+(y

−y

t−1

)



(7)

Figure 3: The directional tilt angle of the vehicle.

• If x

> x

t−1

and y

≥ y

t−1

, this corresponds to the

case b) of ﬁgure 3, where θ

is given by :

= arccos



−x

t−1

√

−x

t−1

)

+(y

−y

t−1

)



(8)

• If x

≤ x

t−1

and y

< y

t−1

, this corresponds to the

case c) of ﬁgure 3, where θ

is given by :

= arccos



−x

t−1

√

−x

t−1

)

+(y

−y

t−1

)



−180 (9)

• If x

≥ x

t−1

and y

< y

t−1

, this corresponds to the

case d) of ﬁgure 3, where θ

is given by :

= −arccos



−x

t−1

√

−x

t−1

)

+(y

−y

t−1

)



(10)

For the remaining case where, x

= x

t−1

and y

= y

t−1

which correspond to stopping action, x

−x

t−1

= y

−

t−1

= 0, in this case θ

can’t be computed using the

arccos function. For this sake θ

is set to 1. For going

straight intention θ

can take the value 0,

, −

, or π

depending on the direction of the vehicle.

For the remaining intention maneuvering the an-

gle θ

takes value in the interval ] −π, π]. Let’s take

the case a) of ﬁgure 3, if we refer to the ﬁgure 2 we

can observe that we have two possible intentions be-

side going straight an stopping intentions: the inten-

tion of going from A to D and the intention of going

from C to B. The ﬁrst intention corresponds to a turn

left for this case the angle θ

varies from

to π, while

the second intention corresponds to a turn right, where

the angle θ

varies from π to

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

1092

3.1.2 The Model

The model used in this paper is a four layers LSTM

with tree hidden layers of 128 neurones each and an

output layer with 10 neurones corresponding each to

a given class C

, 1 ≤ j ≤ 10. The hidden layers use

the rectiﬁed linear unit (ReLU) as activation function.

The output layer use the softmax function to compute

the probability that the observation is the in a given

class. This model use as loss function the categorical

crossentropy given by the fellowing equation:

L(Y,

Y ) = −

∑

i=1

∑

j=1

∈C

log(P(o

∈C

)) (11)

Where, N is the number of classes, M the number of

observation, o

the ith observation, Y vector of the

truth labels, and

Y the vector of predicted labels.

To ﬁnd the minimum of the loss function or ap-

proximate it the model uses a stochastic optimization

method called the Adam optimized (D. P. Kingma,

2015). The model is trained on dataset for differ-

ent time windows size and different number of fea-

tures in order to select the those that gives the best

performances. The model was tested on data coming

from time windows situated at different time to inten-

tion occurrence values, to evaluate its performances

in term of it.

3.2 Trajectory Prediction

The trajectory prediction method use the same fea-

tures as the intention prediction one. Since the trajec-

tory prediction is mainly about predicting a sequence

of the vehicle’s positions in future, we denote

T the

predicted trajectory,

T = {( ˆx

, ˆy

) ∈ R

: m +1 ≤k ≤

K + m}, where K is the number of the predicted po-

sitions, and m is the length of the previous time win-

dow used to prediction (x

, y

), let L be the size of the

window in second L =

, where f

= 10 Hz is the

frequency of data collection.

Since (x

, y

) are in R

, this means we are facing

a regression task. To predict trajectories we use the

same model used for intention prediction with differ-

ent loss function and different output layer. The loss

function in this case is the mean squared error. The

model was trained on different time window size for

different number of features in order to select those

which give better performances.

3.2.1 Prediction of One Point of the Trajectory

To predict the point (x

, y

) of the trajectory, the model

takes as input, the previous m sequence of features

collected during the past time window of size L. Let

= [ f

1,t

, ..., f

n,t

] be the sequence of features at time t

and n the number of features, the model uses the pre-

vious m sequences of features to predict the vector F

The ﬁrst two features of each vector of features cor-

responds to the position of the vehicle. In this part

we are just interested in predicting only the next posi-

tion of the vehicle, thus there is no need to predict all

features.

3.2.2 Prediction of a Sequence of Points

To predict a sequence of positions T ( trajectory to

be predicted), we ﬁrst start by predicting the ﬁrst next

point (x

, y

) of the trajectory by predicting F

. As in

the previous case the model takes the previous m se-

quence of the feature as input to perform the predic-

tion. To predict the position (x

, y

) of a vehicle, the

model takes a sequences of features as input, for this

reason and in order to be able to predict the following

position (x

t+1

, y

t+1

) of the vehicle, the model predict

the sequence F

of features.

The predicted sequence of features F

and the last

m −1 sequences of features are given to the model

as input to predict the following sequence F

t+1

which

contains the point (x

t+1

, y

t+1

) of the trajectory

T , this

step is repeated till we predict all points of the trajec-

tory. The disadvantage of this technic is that the error

made on predicting F

will affect the prediction of the

next sequence of features F

t+1

thus it will affect the

prediction of (x

t+1

, y

t+1

4 EXPERIMENT

In this section we use the 3/4 of the database to train

the model and the remaining data is used as valida-

tion set. Datasets with different time windows size

were constituted. In this part we compare the model

performances by varying time window size and the

number of features used to train the model, for both

trajectory prediction and intention prediction. For in-

tention prediction we study the model performances

according to time to intention occurrence.

4.1 Data Collection

Our model use data collected from the driving simu-

lator CARLA (A. Dosovitskiy and V. Koltun, 2017).

CARLA is an open source software developed by

Alexey Dosovitski and al. at the computer and vi-

sion center of Barcelona. The CARLA simulator use

a virtual environment which represents maps of vir-

tual towns. These maps use a cartesian coordinate

An Effective Driver Intention and Trajectory Prediction for Autonomous Vehicle based on LSTM

1093

system which allows us to locate vehicles and get its

positions in time. Data collection code have been run

on the town 01 of CARLA which contains two, three

and four ways intersections, red lights and some traﬁc

signs.

Several vehicles have been spawned on the town

01 of CARLA, with an autopilots which generates the

trajectory of each vehicle and follow it. Vehicle’s data

is collected for a constant time step of 0.1 s in other

words data is collected at a frequency of f

=10 Hz.

Only data corresponding to intentions that we are in-

terested in is stored.

4.2 Model Selection and Feature

Selection

To evaluate the model performances, several compar-

isons were done on the model trained on different

time window size and different number of features to

select those that give the best performances.

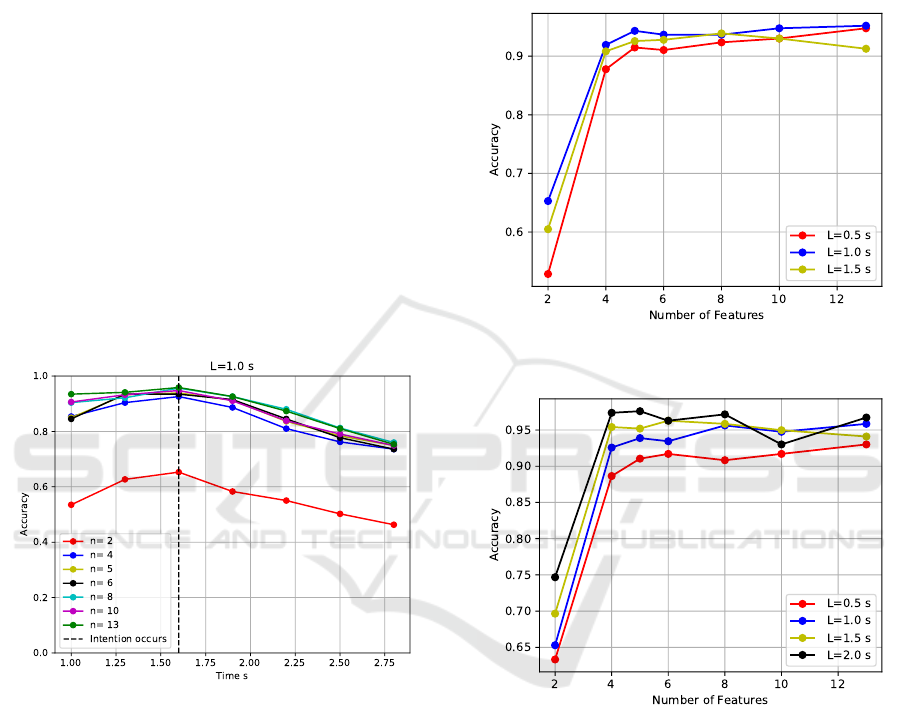
Figure 4: Accuracy of the model trained on time window of

1 s vs time, for different number of features n.

Figure 4 illustrates the accuracy of the model for dif-

ferent time to intention occurrence, for a time win-

dow of size L=1 s. We can observe that the model

trained on n = 5 features which are the positions, the

velocity and the directional tilt angle of the vehicle,

and the model trained on n = 13 features, which con-

tains some road characteristics like traﬁc light and the

type of the road at a given distance, have almost the

same the performances. The accuracy of each model

depends on the time to intention occurrence and the

number of features. We can observe on this ﬁgure

that if the model is trained just on the vehicle posi-

tions as features (n = 2) its accuracy become weak,

while when the model is trained on more features its

performances become better.

The accuracy of intention prediction increase

when time to intention occurrence decreases despite

the number of features. After the intention occur-

rences and the end of its maneuvering, the accuracy

decrease which is normal because we didn’t give the

model the following intentions labels.

Figure 5: Intention prediction: Model accuracy vs the num-

ber of feature.

Figure 6: Intention recognition: Model accuraracy vs the

number of feature.

Figure 5 and ﬁgure 6 show respectively the accuracy

of the model for intention prediction and intention

recognition, where the model was trained on differ-

ent time window size for different number of features.

We can observe that intention recognition performs

better with long time window, where the accuracy can

reach 97% for a time window of 2 s, while for in-

tention prediction the accuracy reach 96% for a time

window of 1 s.

Figure 7 illustrates the accuracy of the trajectory

prediction model for one point prediction, for differ-

ent time window size. Curves show that the model

performs better with small set of features and long

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

1094

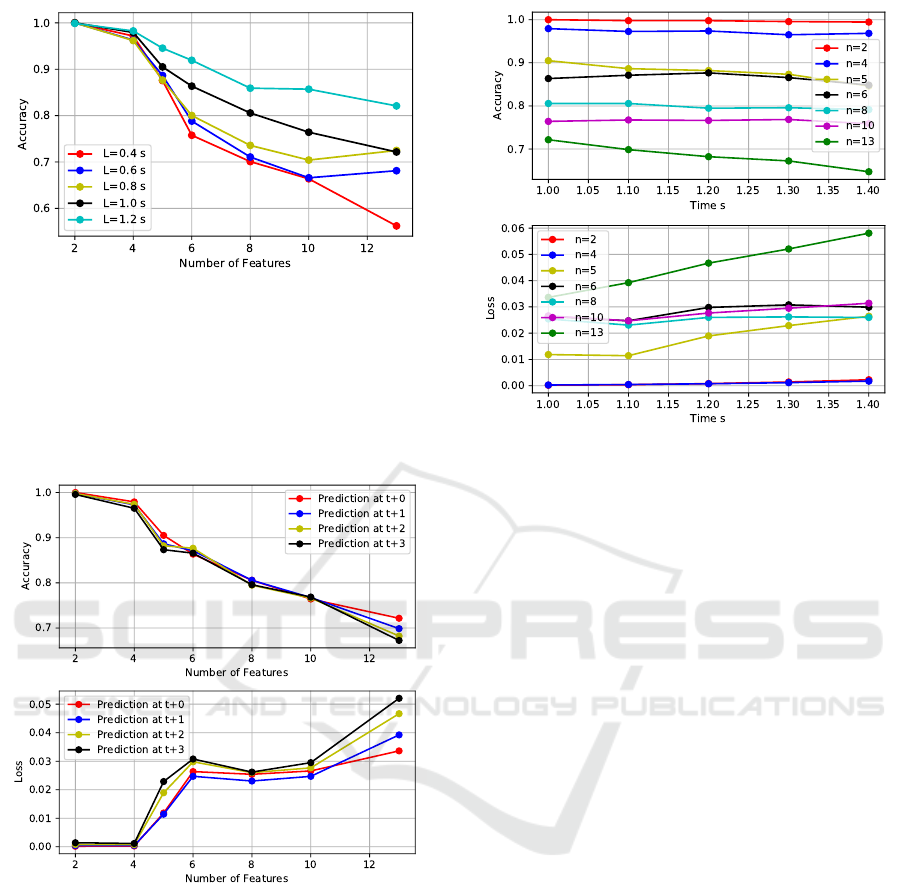
Figure 7: Prediction of one point of the future trajectory:

model accuracy vs the number of feature, for different time

window size L..

time window. We have an accuracy of 99.9% for the

model trained only on vehicles positions (number of

features n = 2), when the number of features increases

the accuracy of the model decreases.

Figure 8: Trajectory prediction: model accuracy and loss vs

n the number of features , for a time window of L=1 s..

Figure 8 present the accuracy of the model, where we

predict a sequence (x

, y

), (x

t+1

, y

t+1

),... of future po-

sitions that constitute the predicted trajectory

T . By

observing the ﬁgure 8, we can conclude that the tra-

jectory prediction accuracy decreases when the num-

ber of features increases which is normal due to errors

made on features prediction. When the number n of

features is high, it become difﬁcult to predict all of

those features without making errors.

Figure 9 illustrate the accuracy of the model at

each step (prediction of a sequence of features) of the

trajectory prediction, which is the accuracy variation

according to time of prediction. We can observe that

Figure 9: Trajectory prediction: model accuracy and loss vs

time of prediction, for a time window of L=1 s..

the error made on predicting the sequence F

at each

time t in the process of trajectory prediction doesn’t

affect that much the performances of the prediction

model. The accuracy is almost stable for low num-

ber of features while for high number of features the

accuracy decreases slowly with time.

5 CONCLUSIONS

In this paper, we propose a method for driver inten-

tion prediction and recognition, and a method for tra-

jectory prediction. With only a small set of features (4

or 5 features), this method gives high accuracy hence

it performs in real time unlike the methods proposed

in state of art, where a plenty of complex features are

used to get good performances, which makes them

greedy in term of computational time. This method

will prevent collisions occurrence, whether it is used

by a self-driving vehicle system or an ADAS sys-

tems. Trajectory prediction can be used for inten-

tion prediction where the predicted trajectory and fea-

tures will be given as input to the intention prediction

model to perform the intention prediction. We have

shown in this paper that modeling this problem of

prediction leads us to select the right features, which

increases our model performances. Our feature se-

lection method makes the model perform better with

small dataset. By introducing the directional tilt an-

gle of the vehicle as a feature our model performances

increases. The proposed method gives an accuracy of

97% for intention recognition and an accuracy of 96%

on intention prediction, whereas other work gets in

An Effective Driver Intention and Trajectory Prediction for Autonomous Vehicle based on LSTM

1095

general 95% or less. The trajectory prediction model

gives an accuracy of 99.9% just by using vehicle’s po-

sitions and it gets 98% when the number of features

is equal to 4. Thus for trajectory prediction when the

number of predicted features increases the accuracy

of the model decreases. This work will be extended

to predict intentions at a roundabout and to predict the

lane change intention, where the database will be up-

dated with data coming from driver behavior for these

intentions maneuvering.

REFERENCES

A. Dosovitskiy, G. Ros, F. C. A. L. and V. Koltun, C. (2017).

Carla: An open urban driving simulator. 1st Confer-

ence on Robot Learning.

A. Zyner, S. W. and Nebot, E. (2018). Naturalistic driver in-

tention and path prediction using recurrent neural net-

works. IEEE Transactions on Intelligent Transporta-

tion Systems.

B. Tang, S. Khokhar, R. G. (2015). Turn prediction at gen-

eralized intersections. IEEE Intelligent Vehicles Sym-

posium (IV).

D. P. Kingma, J. Lei Ba, A. (2015). A tutorial on

mpeg/audio compression. ICLR.

Derek J. Phillips, T. A. W. and Kochenderfe, M. J. (2017). A

tutorial on mpeg/audio compression. IEEE Intelligent

Vehicles Symposium (IV).

Djuric, N. and al. (2019). Multimodal trajectory predictions

for autonomous driving using deep convolutional net-

works. IEEE International Conference on Robotics

and Automation (ICRA).

Hao Xue, D. Q. H. and Reynolds, M. (2018). Ss-lstm:a

hierarchical lstm model for pedestrian trajectory pre-

diction. IEEE Winter Conference on Applications of

Computer Vision.

Hou, H. and al. (2011). Driver intention recognition method

using continuous hidden markov model. International

Journal of Computational Intelligence Systems, 4.

Laugier, C. and al. (2011). Probabilistic analysis of dynamic

scenes and collision risks assessment to improve driv-

ing safety. IEEE Intelligent Transportation Systems,

3:4–19.

L.R Rabiner, B. J. (1986). An introduction to hidden

markov models. IEEE ASSP Magazine, 3:4–16.

Sepp Hochreiter, J. S. (1997). Long short-term memory,

neural computation. IEEE Multimedia, 9:1735–1780.

Streubel, T. and Hoffmann, K. H. (2014). Prediction of

driver intended path at intersections. IEEE Intelligent

Vehicles Symposium (IV).

Zhang, Y. and al. (2018). Integrating kinematics and en-

vironment context into deep inverse reinforcement

learning for predicting off-road vehicle trajectories.

2nd Conference on Robot Learning.

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

1096