
Sparse Image Reconstruction for the SPIDER Optical Interferometric
Telescope
Luke Pratley
1,2 a
and Jason D. Mcewen
2 b
1
Dunlap Institute for Astronomy and Astrophysics, University of Toronto, Toronto, ON M5S 3H4, Canada
2
Mullard Space Science Laboratory (MSSL), University College London (UCL), Holmbury St. Mary, Surrey RH5 6NT, U.K.
Keywords:
Optical, Photonic Circuits, Interferometry, Imaging, Convex Optimization.
Abstract:
The concept of a recently proposed small-scale interferometric optical imaging device, an instrument known
as the Segmented Planar Imaging Detector for Electro-optical Reconnaissance (SPIDER), is of great interest
for its possible applications in astronomy and space science. Due to low weight, low power consumption, and
high resolution, the SPIDER telescope could replace the large space telescopes that exist today. Unlike tradi-
tional optical interferometry the SPIDER accurately retrieves both phase and amplitude information, making
the measurement process analogous to a radio interferometer. State of the art sparse radio interferometric im-
age reconstruction techniques have been gaining traction in radio astronomy and reconstruct accurate images
of the radio sky. In this work we describe algorithms from radio interferometric imaging and sparse image
reconstruction and demonstrate their application to the SPIDER concept telescope through simulated obser-
vation and reconstruction of the optical sky. Such algorithms are important for providing high fidelity images
from SPIDER observations, helping to power the SPIDER concept for scientific and astronomical analysis.
1 INTRODUCTION
The Hubble Space Telescope (HST) has changed the
way astronomers have looked at the Universe. The
number of astronomical studies that have used obser-
vations from the HST make it one of the most im-
portant observatories in history. More than 15,000
articles that have used HST data, in total collecting
738,000 citations.
1
However, telescopes such as the
HST and its scientific successor, the James Webb
Space Telescope (JWST), are extremely heavy and
large, while being expensive in cost and power con-
sumption. Nevertheless such next generation optical
telescopes like JWST are critical to address astron-
omy and cosmology science goals such as answering
questions about dark matter through weak lensing and
understanding the history and formation of our uni-
verse.
Recently, the concept of an instrument known as
the Segmented Planar Imaging Detector for Electro-
optical Reconnaissance (SPIDER) has been devel-
a
https://orcid.org/0000-0002-4716-9933
b
https://orcid.org/0000-0002-5852-8890
1
See https://www.nasa.gov/mission pages/hubble/story/
index.html
oped (Kendrick et al., 2013; Duncan et al., 2015). The
SPIDER is a small-scale interferometric optical imag-
ing device that first uses a lenslet array to measure
multiple interferometer baselines, then uses photonic
integrated circuits (PICs) to miniaturize the measure-
ment acquisition. The goal of the SPIDER is to re-
duce the weight, cost, and power consumption of op-
tical telescopes. Furthermore, additional designs have
been proposed that could increase the efficiency of
imaging using fewer measurements (Liu et al., 2017;
Liu et al., 2018). Recent visibility measurements us-
ing lenslet arrays and PICs have shown to match theo-
retical predictions (Su et al., 2017). Unlike traditional
optical interferometry, the SPIDER telescope can ac-
curately retrieve both phase and amplitude informa-
tion (Su et al., 2017), making the measurement pro-
cess analogous to a radio interferometer. Accurate in-
terferometric image reconstruction methods from ra-
dio astronomy can thus be applied to image SPIDER
observations.
Radio astronomy has a long history of using in-
terferometry to push beyond the limits of resolution
and size, at the computational cost of image recon-
struction (Ryle and Hewish, 1960). An interferometer
is a device that measures the cross-correlation func-
tion of the signals. Interferometric imaging in the ra-
104
Pratley, L. and Mcewen, J.
Sparse Image Reconstruction for the SPIDER Optical Interferometric Telescope.
DOI: 10.5220/0010322601040109
In Proceedings of the 9th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2021), pages 104-109
ISBN: 978-989-758-492-3
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

dio has proven to be a popular approach between 50
MHz and 100 GHz, with telescopes such as the Very
Large Array (VLA) that have antenna arrays spread
over 36 kilometers (Thompson et al., 2008). The
cross-correlation between voltages from each pair of
antenna is computed to interfere the complex valued
measurements known as visibilities. A visibility rep-
resents a Fourier coefficient for the sky brightness,
with the Fourier coordinate determined by the antenna
pair separation. Typically an antenna pair is known as
a baseline, with the baseline length corresponding to
the antenna separation (Thompson et al., 2008).
Recently, sparse image reconstruction algorithms
that exploit developments from the field of convex op-
timization have shown to improve the quality of re-
constructed observations from radio interferometers
considerably, on both simulations and real data (Prat-
ley et al., 2018; Cai et al., 2018b; Pratley et al., 2019a;
Pratley et al., 2019b; Pratley, 2019). In this article
we take recent developments from radio interferomet-
ric imaging and sparse image reconstruction, and put
them into the context of the proposed SPIDER instru-
ment. Such methodology would prove useful in fu-
ture space based telescopes and space missions based
on the SPIDER technology (e.g. aerial observations
of planetary surfaces). Ultimately it is evident that
recent algorithmic developments for radio interfero-
metric imaging can be directly applied to the SPIDER
optical interferometer.
In Section 2 we introduce the background and cur-
rent developments behind the SPIDER concept. Sec-
tion 3 discusses the calculation of the SPIDER mea-
surement equation. Section 4 introduces the sparse
image reconstruction formalism. Section 5 shows im-
age reconstruction from a simulated SPIDER obser-
vation.
2 SPIDER
Key to the concept design of the SPIDER is the use of
lenslets to collect signals from incoming light. These
signals are combined using a PIC to produce an inter-
ferometric measurement (visibility), i.e. a Fourier co-
efficient of the observation. The Fourier coordinates,
(u,v), are determined by the separation size in wave-
lengths (baseline length) between the lenslets that
were used to generate the measurement, with larger
separations resulting in higher resolution measure-
ments. However, unlike radio interferometry where
all possible pairs of antennas in an array can be com-
bined in an observation, lenslets can only be paired
once. If there are N
l
lenslets, the lenslet array will pro-
duce N
l
/2 correlations. This differs to the N(N −1)/2
Table 1: SPIDER configuration parameters adopted from
(Kendrick et al., 2013).
Parameter Value
Spectral Coverage 500-900 nm
Lenslet Diameter 8.75 mm
Longest Baseline 0.5 m
Number of Lenslets per PIC spoke 24
Number of PIC spoke 37
Number of Spectral Bins 10
FoV at 500 (900) nm 35
00
(65
00
)
Maximum Resolution at 500 (900) nm 0.7
00
(1.2
00
)
Total Measurements 4440
correlations expected from a radio array (Thompson
et al., 2008; Liu et al., 2018). To compensate for
this lenslets can be combined with the PIC to split
the signal into spectral bins (channels), allowing for
increased sampling coverage due to variation of base-
line length over wavelength. This strategy has been
successful in radio astronomy for decades, and is
known as multi-frequency synthesis (Thompson et al.,
2008).
The concept design of the SPIDER proposed in
(Kendrick et al., 2013) is to put a linear array of
lenslets onto a PIC card. The PIC cards are mounted
as radial spokes on a disc, producing a radial sampling
pattern in the uv-plane (however, other sampling pat-
terns are considered in (Kendrick et al., 2013)). The
proposed operating wavelengths are between 500 nm
and 900 nm. The operating wavelength divided by
the size of a lenslet (8.75 mm) determines the field
of view to be approximately between 0.5 and 1 arc
minutes. The longest baseline along a spoke is 0.5
m, which is sensitive to resolutions between 0.65 and
1.2 arcseconds. Parameters of the SPIDER design
adopted from (Kendrick et al., 2013) are listed in Ta-
ble 1, which leads to the (u,v) sampling coverage
shown in Figure 1.
3 SPIDER MEASUREMENT
MODEL
The SPIDER is an interferometric instrument operat-
ing at optical wavelengths. It follows from (Zernike,
1938) that the measurement equation will have the
form of a Fourier Transform
y(u,v) =
Z
∞
−∞
x(l,m)a(l,m)e
−2πi(lu+mv)
dldm , (1)
where (l, m) is the coordinates of the image intensity
x, a is the sensitivity of the instrument over the field
of view, and (u,v) is the separation vector between
two lenslets and the Fourier coordinate of the mea-
surement (Thompson et al., 2008). Due to the lim-
ited number of lenslets it is not possible to sample the
Sparse Image Reconstruction for the SPIDER Optical Interferometric Telescope
105
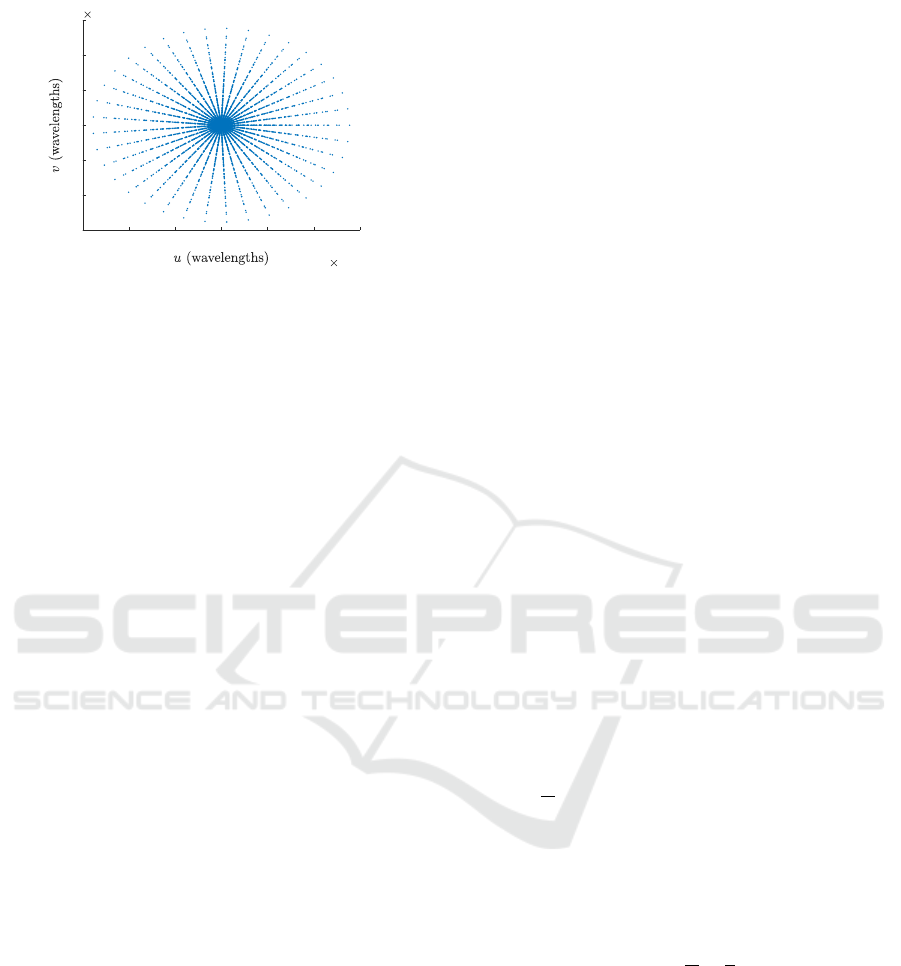
-6 -4 -2 0 2 4 6
10
5
-6
-4
-2
0
2
4
6
10
5
Figure 1: The sampling pattern of SPIDER in the uv-plane
in units of wavelengths using 24 lenslets over 37 PIC cards
for the combined coverage of 10 spectral bins. The sam-
pling pattern was generated using the parameters in Ta-
ble 1. Since the Fourier coordinates are relative to wave-
length, using the spectral bins (channels) will increase the
uv-coverage of the instrument substantially. The number
of measurements in the single channel corresponds to 444,
which makes 4440 measurements over the entire band.
entire (u, v) domain, leading to an ill-posed inverse
problem. However, the measurement equation is lin-
ear, and we can represent the measurement equation
as a linear operator
y = Φx + n, (2)
with measurements y
k
= y(u
k
,v
k
) for a sampling pat-
tern (u, v) and intensity values x
i
= x(l
i
,m
i
) for pix-
els of an image (l,m) and n is independent and iden-
tically distributed (i.i.d.) Gaussian noise.
The measurement operator requires performing a
Fourier transform. However, the sampling pattern of
SPIDER does not lie on a regular grid so it is not
possible to use the speed of the standard Fast Fourier
Transform (FFT). Instead, a non-uniform FFT can be
used to evaluate the measurement equation, where an
FFT is applied, and the visibilities are interpolated off
of the FFT grid. This is known as the non-uniform
FFT (NUFFT) but is commonly known as degrid-
ding in radio astronomy (Fessler and Sutton, 2003;
Thompson et al., 2008).
In a discrete setting, let x ∈ R
N
and y ∈C
M
. Due
to the limited field of view for x, the values of y
can be estimated using interpolation off the FFT grid.
Sinc interpolation suppresses repeating artifacts from
outside the imaged region appearing in the model x.
These artifacts are known as aliasing error, this be-
comes more difficult to suppress for bright sources
outside the field of view. However, Sinc interpolation
requires convolution of the FFT grid with a Sinc func-
tion for each measurement y
i
, which requires a large
support. In general, it is possible to replace the Sinc
function with an interpolation kernel with minimal
support such as a Kaiser-Bessel or Gaussian kernel
(Fessler and Sutton, 2003), with appropriate apodiza-
tion correction in the image domain.
A NUFFT can be represented by the following lin-
ear operations
Φ = WGFZS , (3)
where S represents scaling required due to the attenu-
ation of the interpolation kernel but also scaling due to
the sensitivity of the instrument over the field of view,
Z is a zero padding operation of the image to up sam-
ple the Fourier domain, F is an FFT, G represents the
convolution constructed from the interpolation kernel
used to interpolate measurements off of the grid, and
W are noise weights applied to the measurements, i.e
W
kk
= 1/σ
k
for a variance of σ
2
k
. This measurement
operator is described in detail in (Pratley et al., 2018)
where it is applied to radio interferometric imaging. Φ
has its adjoint operator Φ
†
, which consists of apply-
ing adjoints of these operators in reverse. In this work
we assume that y are the weighted measurements and
that the dirty map is defined as Φ
†
y.
3.1 Interpolation Kernels
The sparse degridding matrix G can be constructed in
1d from a kernel d(u) by
G
i,{k
i
+ j}
K
= d(u
i
−(k
i
+ j)), (4)
where i is the index of the measurement y
i
, k
i
is the
closest integer to visibility coordinate u
i
− J/2 (in
units of pixels) and is found by the flooring opera-
tion, and j = 1 ...J are the possible non-zero entries
of the kernel. {·}
K
is the modulo-K function, where
K = α
√
N is the dimension of the Fourier grid in 1-D
(for notational sake, the 2d Fourier grid is comprised
of K ×K samples). For a separable anti-aliasing ker-
nel, it is straight forward to extend the 1d kernel to 2d.
The diagonal operator S is calculated in a similar way
by
S
i,i
= s
i
K
−
1
2
, (5)
where s(x) is the reciprocal of the inverse Fourier
transform of d(u). In practice, S can be computed an-
alytically if the inverse Fourier transform of the con-
volution kernel is known.
The Kaiser-Bessel kernel has shown to perform
well as an interpolation kernel while using a mini-
mal support size (Fessler and Sutton, 2003; Pratley
et al., 2018). More examples of interpolation kernels
are provided in (Jackson et al., 1991) and (Thompson
et al., 2008). For this work we use the Kaiser-Bessel
kernel that was used in (Pratley et al., 2018).
PHOTOPTICS 2021 - 9th International Conference on Photonics, Optics and Laser Technology
106

4 SPARSE IMAGE
RECONSTRUCTION
The Bayesian statistical inference framework can be
used to address the inverse problem (2), as shown in
(Cai et al., 2018a). From Bayes’ theorem, the poste-
rior can then be expressed as
p(x|y) ∝ exp
−ky −Φxk
2
`
2
/2σ
2
exp
−γkΨ
†
xk
`
1
,
(6)
where Ψ
†
x represents wavelet coefficients, k·k
`
1
is
the sum of absolute values, and k·k
`
2
is the Euclidean
norm. Maximum a posteriori (MAP) estimation is
found by choosing the estimate of x that will maxi-
mize the posterior, which is equivalent to minimizing
the negative log posterior, i.e.
argmax
x
p(x|y) =
argmin
x
n
ky −Φxk
2
`
2
/2σ
2
+ γkΨ
†
xk
`
1
o
.
(7)
This minimization problem is known as regularized
least squares, with the regularization term in the anal-
ysis setting being kΨ
†
xk
`
1
. In many cases kΨ
†
xk
`
1
is chosen to penalize the number of parameters that
determine x and reduce over fitting; moreover, it can
also be used to enforce other properties for x like
smoothness. Furthermore, it is possible to add indi-
cator functions as a prior that can restrict our solu-
tion to be real or positive valued, as is done in the
constrained problem below. MAP estimation can be
solved efficiently using the Forward Backward Split-
ting algorithm (e.g. (Cai et al., 2018b)).
An issue of using MAP estimation to perform
sparse regularization is choosing a proper regulariza-
tion parameter γ (although there are ways to address
this; (Pereyra et al., 2015)). The choice of γ, however,
can be avoided after moving from the unconstrained
problem in MAP estimation to the constrained prob-
lem
argmin
x
kΨ
†
xk
`
1
+ ι
B
ε
(y )
(Φx) + ι
R
N
+
(x), (8)
where ι is the indicator function that restricts Φx to
the set B
ε
(y) = {q : ky −qk
`
2
≤ ε}, ε is the error tol-
erance, and ι
R
N
+
restricts the solution to be positive.
4.1 ADMM
In the constrained problem the `
2
-norm is replaced
with an indicator function that restricts the solution
to the `
2
-ball of radius ε. This indicator function is
non-differentiable and it is not possible to apply the
Forward Backward method to obtain a solution.
Let f (Φx) = ι
B
ε
(y )
(Φx) and g(x) = kΨ
†
xk
`
1
+
ι
R
N
+
(x). We can then consider the optimization prob-
lem
min
x∈R
N
f (Φx) +g(x). (9)
Problem (9) can be addressed by the alternating direc-
tion method of multipliers (ADMM) algorithm (Boyd
et al., 2011; Yang and Zhang, 2011; Onose et al.,
2016). Starting from an augmented Lagrangian, vari-
ables x and v are minimized alternatively while up-
dating the dual variable z (using the dual accent
method; (Boyd et al., 2011)) to ensure that the con-
straint v = Φx is met in the final solution, i.e.
llx
(k)
= argmin
x∈R
N
g(x) +
1
2λ
kΦx −(v
(k)
−z
(k)
)k
2
`
2
(10)
v
(k+1)
= argmin
v∈R
K
f (v) +
1
2λ
kv −(Φx
(k)
+ z
(k)
)k
2
`
2
(11)
z
(k+1)
= z
(k)
+ (Φx
(k)
−v
(k+1)
). (12)
The above iterations can be evaluated using a com-
bination of proximal operators and the Dual Forward
Backward algorithm (allowing the use of more than
one wavelet basis). See (Pratley et al., 2019b) for a
detailed description of the ADMM algorithm applied
here.
5 RECONSTRUCTIONS
In this section we demonstrate reconstruction of sim-
ulated SPIDER observations using the ADMM algo-
rithm, where a solution is found from the constrained
problem. We use the software package PURIFY
2
to
perform interferometric image reconstruction, pow-
ered by the convex optimization package SOPT
3
.
To generate the measurement operator used to
simulate the observation we use the Kaiser-Bessel
kernel with a support size J = 8 pixels to reduce alias-
ing error in the ground truth measurements. For re-
construction, we use a measurement operator with a
kernel support size of J = 4 pixels. The number of
pixels in x are determined by the ground truth image,
x
GroundTruth
∈ R
N
+
. We do not include the decrease in
sensitivity of the SPIDER instrument away from the
center of the field, but this can be included in simula-
tions if it is well characterized. To simulate the obser-
vation we follow (Pratley et al., 2018) and add i.i.d.
Gaussian noise to the observational data. We define
2
https://github.com/astro-informatics/purify
3
https://github.com/astro-informatics/sopt
Sparse Image Reconstruction for the SPIDER Optical Interferometric Telescope
107

Figure 2: Simulation of observation and reconstruction of
the spiral galaxy M51 using ADMM implemented with PU-
RIFY, including the ground truth (top left), the observed
image (top right), the PURIFY reconstruction (bottom left),
and the residuals (bottom right). We used an ISNR of 30dB,
a pixel size of 0.3
00
, and an image size of 256 by 256 pixels,
with the sampling pattern for 10 spectral bins as shown in
Figure 1 resulting in 4440 measurements. The structure of
the spiral arms and point sources are recovered well using
PURIFY.
an input signal to noise ratio (ISNR) to determine the
standard deviation of the Gaussian noise, where this
standard deviation is defined as
σ
i
=
kΦx
GroundTruth
k
`
2
√
M
×10
−
ISNR
20
. (13)
The Fourier sampling pattern of the observation (i.e.
the uv-coverage) is determined by the design of the
SPIDER instrument and the optical spectral coverage.
By combining the entire spectra it is possible to in-
crease the sampling coverage, as explained in Section
2. We use the configuration of Table 1 (shown in Fig-
ure 1).
The results presented in Figure 2 show that an
observation using the proposed SPIDER design can
be effectively reconstructed using PURIFY. Recon-
struction was performed using a Dirac basis and
Daubechies wavelets 1 to 8. While we have used the
design from (Kendrick et al., 2013), where the base-
lines lie on radial spokes, different baseline configu-
rations may lead to higher quality reconstruction. De-
pending on the structures in the ground truth sky, dif-
ferent baseline configurations will be more effective
at sampling the sky, leading to more effective recon-
struction of objects and their details. It was recently
shown that the theory of compressive sensing might
lead to more efficient designs (Liu et al., 2018).
In summary, we adapt recent developments in ra-
dio interferometric imaging, leveraging sparsity and
convex optimisation, and show that they are effective
for imaging SPIDER observations. Moreover, recent
developments in efficient uncertainty quantification
for radio interferometric imaging can also be adapted
for use with SPIDER (Cai et al., 2018b). The compu-
tational performance of these algorithms can be fur-
ther increased using GPU multi-threading and distri-
bution across nodes of a computing cluster (as imple-
mented in PURIFY already; (Pratley et al., 2019b)).
REFERENCES
Boyd, S. et al. (2011). Distributed optimization and statis-
tical learning via the alternating direction method of
multipliers. Found. Trends Mach. Learn., 3(1):1–122.
Cai, X., Pereyra, M., and McEwen, J. D. (2018a). Uncer-
tainty quantification for radio interferometric imaging
- I. Proximal MCMC methods. MNRAS, 480:4154–
4169.
Cai, X., Pereyra, M., and McEwen, J. D. (2018b). Uncer-
tainty quantification for radio interferometric imag-
ing: II. MAP estimation. MNRAS, 480:4170–4182.
Duncan, A. et al. (2015). SPIDER: Next Generation
Chip Scale Imaging Sensor. In Advanced Maui Opti-
cal and Space Surveillance Technologies Conference,
page 27.
Fessler, J. A. and Sutton, B. P. (2003). Nonuniform fast
fourier transforms using min-max interpolation. IEEE
Transactions on Signal Processing, 51:560–574.
Jackson, J. I., Meyer, C. H., Nishimura, D. G., and Macov-
ski, A. (1991). Selection of a convolution function
for fourier inversion using gridding [computerised to-
mography application]. IEEE Transactions on Medi-
cal Imaging, 10(3):473–478.
Kendrick, R. et al. (2013). Flat Panel Space Based Space
Surveillance Sensor. In Advanced Maui Optical and
Space Surveillance Technologies Conference, page
E45.
Liu, G., Wen, D., and Song, Z. (2017). Rearranging the
lenslet array of the compact passive interference imag-
ing system with high resolution. In AOPC 2017:
Space Optics and Earth Imaging and Space Naviga-
tion, volume 10463 of Society of Photo-Optical In-
strumentation Engineers (SPIE) Conference Series,
page 1046310.
Liu, G., Wen, D.-S., and Song, Z.-X. (2018). System de-
sign of an optical interferometer based on compressive
sensing. MNRAS, 478:2065–2073.
Onose, A. et al. (2016). Scalable splitting algorithms for
big-data interferometric imaging in the SKA era. MN-
RAS, 462:4314–4335.
Pereyra, M., Bioucas-Dias, J. M., and Figueiredo, M. A. T.
(2015). Maximum-a-posteriori estimation with un-
known regularisation parameters. In 2015 23rd Eu-
PHOTOPTICS 2021 - 9th International Conference on Photonics, Optics and Laser Technology
108

ropean Signal Processing Conference (EUSIPCO),
pages 230–234.
Pratley, L. (2019). Radio Astronomy Image Reconstruc-
tion in the Big Data Era. Doctoral thesis (Ph.D), UCL
(University College London).
Pratley, L., Johnston-Hollitt, M., and McEwen, J. D.
(2019a). A Fast and Exact w-stacking and w-
projection Hybrid Algorithm for Wide-field Interfer-
ometric Imaging. ApJ, 874(2):174.
Pratley, L., McEwen, J. D., d’Avezac, M., Cai, X., Perez-
Suarez, D., Christidi, I., and Guichard, R. (2019b).
Distributed and parallel sparse convex optimization
for radio interferometry with PURIFY. arXiv e-prints,
page arXiv:1903.04502.
Pratley, L., McEwen, J. D., et al. (2018). Robust sparse
image reconstruction of radio interferometric obser-
vations with purify. MNRAS, 473:1038–1058.
Ryle, M. and Hewish, A. (1960). The synthesis of large
radio telescopes. MNRAS, 120:220.
Su, T. et al. (2017). Experimental demonstration of inter-
ferometric imaging using photonic integrated circuits.
Opt. Express, 25(11):12653–12665.
Thompson, A., Moran, J., and Swenson, G. (2008). Inter-
ferometry and Synthesis in Radio Astronomy. Wiley.
Yang, J. and Zhang, Y. (2011). Alternating direction algo-
rithms for l1-problems in compressive sensing. SIAM
Journal on Scientific Computing, 33(1):250–278.
Zernike, F. (1938). The concept of degree of coherence and
its application to optical problems. Physica, 5:785–
795.
Sparse Image Reconstruction for the SPIDER Optical Interferometric Telescope
109
