
Improving Decision-Making-Process for Robot Navigation
Under Uncertainty
Mohamed Ibn Khedher
1
, Mallek Sallami Mziou
2
and Makhlouf Hadji
1
1
IRT - SystemX, 8 Avenue de la Vauve, 91120 Palaiseau, France
2
CEA, The French Alternative Energies and Atomic Energy Commission, France
Keywords:
Uncertainty in AI, Neural Network Robustness, Data Augmentation, Abstract Interpretation, Pareto Front.
Abstract:
Designing an autonomous system is a challenging task nowadays, and this is mainly due to two challenges such
as conceiving a reliable system in terms of decisions accuracy (performance) and guaranteeing the robustness
of the system to noisy inputs. A system is called efficient, if it is simultaneously reliable and robust. In
this paper, we consider robot navigation under uncertain environments in which robot sensors may generate
disturbed measures affecting the robot decisions. We aim to propose an efficient decision-making model,
based on Deep Neural Network (DNN), for robot navigation. Hence, we propose an adversarial training step
based on data augmentation to improve robot decisions under uncertain environment. Our contribution is
based on investigating data augmentation which is based on uncertainty noise to improve the robustness and
performance of the decision model. We also focus on two metrics, Efficiency and Pareto Front, combining
robustness and performance to select the best data augmentation rate. In the experiment stage, our approach is
validated on a public robotic data-set.
1 INTRODUCTION
The autonomy of a system is its ability to analyze the
environment, make decisions and perform actions in
order to achieve goals assigned beforehand.
Decision-Making Process (DMP) is, then, one of
the key elements in the conception of autonomous
systems in order to have successful behavior. It re-
quires an accurate and adequate representation of the
environment to choose the optimal decision. Often,
the environment is uncertain due to external factors
that highly impact the system. Generally, these diffi-
culties are related essentially to the fact that: i) per-
ception environment is absent or partially observable
and ii) sensors values are false or disturbed due to a
software or hardware anomalies.
In this context, it is important to study the behav-
ior of the DMP in uncertain environment, i.e given
noisy inputs. In fact, nowadays, the difficulty is not
only to construct a reliable decision-making model in
terms of decision accuracy (Performance), but also
the challenge is to construct a robust decision-making
model in terms of stability to noisy inputs (Robust-
ness). For a clearer definition of the robustness, it
consists in checking the capacity of the neural net-
work to take the same label for all similar inputs even
if they are noisy.
In this paper, we focus on the impact of data
augmentation on the decision model behavior against
noisy inputs. Our intuition leads us to study the capac-
ity of data augmentation to improve the performance
and/or the robustness of decision model. Hence, given
a decision model based on Deep Neural Networks
(DNN), several data augmentation rates are applied.
For each rate, the model performance and robustness
are evaluated. To measure the robustness, we pro-
pose to use the Abstract Interpretation that aims to
check systems for resistance to unsatisfied specifica-
tions (Cousot, 2008). Its principle consists in check-
ing that DNN still output the same label even if inputs
are noisy.
To the best of our knowledge, this is the first paper
dealing with the fusion of Performance and Robust-
ness to select the best decision model. We propose to
investigate two metrics: Efficiency based on F-score
measure (Chinchor, 1992) and Pareto front (Ehrgott,
2005) metric.
Pareto front metric is often used for preferences’
comparison when each preference is represented by
vectors containing at least two scores. It is based on a
set of decision points that are not dominated by other
points. Further mathematical details and formulations
Khedher, M., Mziou, M. and Hadji, M.
Improving Decision-Making-Process for Robot Navigation Under Uncertainty.
DOI: 10.5220/0010323311051113
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 2, pages 1105-1113
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
1105

on Pareto front points and the notion of Dominance
will be provided in next sections. In our case, Pareto
front solution will be used to select solutions that meet
the multiple objectives or criteria such as robustness
and performance trade-offs.
The rest of the paper is organized as follows. In
section 2, a state of the art is presented. The structure
of our approach is described in section 3. Sections 4
and 5 detail respectively the decision-making model
construction and decision-making model evaluation.
Section 6 includes the experimental results and sec-
tion 7 concludes the paper.
2 STATE OF THE ART
In this section, the state of the art is split into two ma-
jor topics: i) the first is about the solutions proposed
to construct a DMP model for autonomous systems
and ii) the second concerns approaches to verify the
robustness of a constructed DMP model based on neu-
ral networks.
2.1 Decision-making Approaches
Decision-making approaches can be roughly classi-
fied into two major approach categories: i) Learning-
free approaches and ii) Learning-based approaches.
Regarding Learning-free approaches, system de-
cisions are taken without any prior trained model
(Khedher et al., 2012; Khedher and El Yacoubi,
2015). Mostly, it is based on the use of rules, cost
functions and graphs. First, Finite State Machines
(FSM) and Rule Based manual programming ap-
proaches are the simplest. Physically, states corre-
spond to system behaviors and transitions are the rules
(or constraints) to transit from one state to another.
Second, decision-making can be performed by defin-
ing a cost function. It consists in evaluating each ac-
tion or sequence of actions using optimization algo-
rithms in order to find the one with the lowest cost. Fi-
nally, decision-making can be modeled using graphs.
Mostly, a tree-like graph is created to model different
decisions and their consequences in order to select the
optimal action.
In (Kammel et al., 2009; Aleluya et al., 2018),
a FSM-based approaches are proposed. The team
AnnieWay, authors of (Kammel et al., 2009), uses
FSM for autonomous driving decisions where states
included driving behavior and transitions are defined
according to a manually written conditions. The au-
thors of (Aleluya et al., 2018) use FSM to control a
robot in soccer-playing context. It models the process
of selecting the optimal robot-action according to its
environment.
In (Vitus and Tomlin, 2013), the authors proposed
a Chance Controlled Optimization approach to solve
lane change overtaking in urban areas. The objective
function minimizes, in the one hand, the traditional
objectives such as minimization of fuel, and in the
other hand, the nominal planned trajectory prediction
against potential crashes.
Regarding Learning-based approaches, a prior
decision-making model is trained (Jmila et al., 2017).
Among these models, we quote Support Vector Re-
gression (Zhang et al., 2017), Deep Learning (Shabbir
and Anwer, 2018) and reinforcement learning (Hoel
et al., 2018).
In (Zhang et al., 2017), a Support Vector Regres-
sion is proposed to model the driving decisions. It
takes as input the environment parameters (e.g. vehi-
cle states, road conditions, etc.) and retrieves the driv-
ing decision (e.g. steering angle, speed, etc.). Using
the same technique, authors of (Abdessemed, 2012)
propose the use of Support Vector Machine (Vapnik,
1995) to achieve the tracking trajectory task of a robot
manipulator.
In the other hand, Deep Learning (DL) approaches
have been gaining popularity in recent years across a
variety of applications (Khedher et al., 2018; Jmila
et al., 2019) such as decision-making. In (Shab-
bir and Anwer, 2018), a survey of Deep Learning
techniques for mobile robot applications including
decision-making is proposed. In (Gallardo et al.,
2017), authors use Deep Learning techniques to help
the navigation of a driverless car through an urban en-
vironment.
Besides, the authors of (Hoel et al., 2018) for-
mulate the decision-making task as a reinforcement
learning problem. The goal is to learn a policy
that aims to automatically generate a decision-making
function to handle speed and lane change decisions.
2.2 Neural Networks Verification
Approaches
The Neural Network Verification (NNV) is the task
studying the evolution of its outputs in uncertain envi-
ronment. Otherwise, it consists of checking the neural
network capacity to take the same output for all sim-
ilar inputs even if they are noisy. The principle of a
NNV system consists in: i) first calculating, from the
input data, all possible inputs that can be obtained by
adding noises and ii) second, checking that the prop-
erties of the input data is kept for noisy data. The
properties are fixed beforehand and, for example, they
can be defined as range of values, as an object class,
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
1106

etc.
To verify a Neural Network (NN), several ap-
proaches have been proposed, mainly: i) satisfiability
approaches and ii) reachability approaches.
Regarding satisfiability approaches, it consists
in transforming the NN into a feasibility problem
to prove the existence of a counter-example. If a
counter-example has been found, the NN is not se-
cure, else if no counter-example has been found, the
NN is secure.
In (Katz et al., 2017), the authors propose an ex-
tension of the simplex algorithm, a standard algorithm
for solving linear programming (LP) instances, to
support non-linear ReLU activation function (ReLU
for " Rectified Linear Unit"). The algorithm is called
Reluplex, i.e. ReLU with the simplex method. Relu-
plex uses the simplex algorithm to search a feasible
activation pattern that leads to an in-feasible output.
The authors of (Ehlers, 2017) propose PLANET (for
"a Piece-wise LineAr feed-forward NEural network
verification Tool"). It consists first on replacing the
non-linear functions of the NN by a set of linear equa-
tions. Then, it tries to find a solution for the resulting
system of equations.
Regarding the reachability approaches, it consists
in calculating the reachable set (outputs) of all inputs
and checking if it is included in the desired set. Given
a neural network N and an input set
~
X, the reach-
ability set
~
Y is defined as all the possible outputs:
~
Y = {~y,~y = N(~x),∀~x ∈
~
X}. If the reachable set is in-
cluded in the desired set, the NN is declared secure,
else if the reachable set is not included, totally or par-
tially, in the desired set, the NN is not secure.
The calculation of the reachable set can be exact
(Xiang et al., 2017b) or approximate (Xiang et al.,
2017a; Gehr et al., 2018).
In (Xiang et al., 2017b), authors compute the ex-
act reachable set for a neural network includes only
ReLU activation. In fact, they assume that if the input
is a union of polytopes, then the output reachable set
is also a union of polytopes. In their paper, the entries
of the NN are represented by the union of polyhedra
(a polyhedron is an example of the more general poly-
tope in any number of dimensions). Moreover, any
over-approximation is applied. Hence, the number of
polytopes grows exponentially with each layer.
In (Gehr et al., 2018), authors propose AI2 (for
"Abstract Interpretation for Artificial Intelligence")
that approximates the reachable set. The main idea
is to over-approximate inputs by a set of zonohedron
(a special case of the polyhedron geometric form).
Then, a set of abstract operators are defined to follow
the evolution of the zonohedron through the layers of
the network.
The satisfiability approaches does not adopt any as-
sumptions, however their execution time grows expo-
nentially with the augmentation of NN hidden layers
(depth). In the other hand, reachability approaches are
based on over-approximation but are more scalable
to a large NN. Since the importance of the execution
time in our study, our approach lies to the reachability
approaches.
3 OUR APPROACH
Figure 1 shows the flowchart of our approach. The
input is a dataset composed of ultrasound sensor mea-
surements collected from a mobile robot during its
movement inside a room. The output is an efficient
decision model under uncertainly sensor measures.
Our approach considers three stages described as fol-
lows:
• Data-set augmentation
• Decision model construction
• Decision model evaluation
We start by a data augmentation algorithm which is
applied to increase the variety of the training dataset.
The original dataset is composed of i) ultrasound sen-
sor measurements and ii) the corresponding robot de-
cision (label). The data augmentation algorithm con-
sists in injecting a Gaussian noise to generate noisy
inputs. In this work, several data augmentation rates
are used.
Next, a decision model is trained on the aug-
mented training dataset, based on Deep Neural net-
works. The trained model learns the robot decision
depending on sensor measurements.
Hence, for each data augmentation rate, the de-
cision model robustness is evaluated by adapting the
Abstract Interpretation algorithm to heterogeneous in-
puts.
Finally, two metrics are proposed to evaluate the
decision model taking into account its performance
and robustness. The metric is used to select the best
model in terms of performance and robustness trade-
offs.
4 DECISION-MAKING MODEL
CONSTRUCTION
Our decision model is based on a Deep Neural Net-
work. In this section, DNN principle and its applica-
tion in robot decision-making are presented.
Improving Decision-Making-Process for Robot Navigation Under Uncertainty
1107

Figure 1: Proposed approach.
4.1 Deep Neural Network Principles
A Deep Neural Network is a extension of neural net-
work with several hidden layers. It consists of three
typical types of layers: i) an input layer, ii) hidden
layers of neuron computations and iii) an output layer.
Each neuron is a simple processing element that re-
sponds to the weighted inputs it received from other
neurons.
The action of a neuron depends on its activation
function, which is described by:
y
i
= f
n
∑
j=1
w
i j
× x
j
+ θ
i
!
(1)
where x
j
is the j
th
input of the i
th
neuron, w
i j
is the
weight from the j
th
input to the i
th
neuron, θ
i
is the
bias of the i
th
neuron, y
i
is the output of the i
th
neu-
ron and f (.) is the activation function. The activation
function is, mostly, a nonlinear function describing
the reaction of i
th
neuron according to inputs.
4.2 Model Construction
Our DNN architecture consists of N fully-connected
layers, each of them are followed by an activation
function and a dropout layer, and a final softmax layer
indicating robot decision. As activation function, we
used the non-linear function "Rectified Linear Units
(ReLU)" defined by:
R(x) = max(0,x) (2)
The dropout layer is used to prevent over-fitting
(Krizhevsky et al., 2012). Figure 2 shows the detailed
architecture of our DNN. It takes, as input, vectors of
dimension 24 components and outputs a probability
distribution vector of 4 components (the number of
decisions in the dataset).
4.3 Data Augmentation
Data augmentation is the process of modifying the
available data in a realistic and randomized method.
This is used to increase the dataset variety. In this pa-
per, we propose to enhance the training dataset by in-
jecting a Gaussian noise. Our intuition that injecting
noise during training phase makes the decision model
more efficient. This intuition should be confirmed ex-
perimentally.
In this paper, we propose to inject a Gaussian
noise based on the sensor uncertainty. It consists in
adding noisy samples x
noise
to the training set with
the following manner: for an input sample x
init
, we
generate: x
noise
= x
init
± ε, where ε follows a Gaus-
sian distribution centred on [-∆X,∆X]. ∆X is the sen-
sor uncertainty computed as following: For N multi-
ple sensor measures x
i
with average x, ∆X is given by
Eq.3.
∆X =
s
1
N − 1
N
∑
i=1
(x
i
− x)
2
(3)
In our work, the robot is equipped with 24 ultrasound
sensors. Hence, the dimension of x
init
is 24 where
each component is associated with a sensor measure.
Moreover, each sensor i has its own (∆X)
i
. To form
x
noise
, each component is disrupted independently of
the others by adding the term ε
i
∈ [−(∆X)
i
,(∆X)
i
].
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
1108

Figure 2: Our DNN architecture.
To prevent overfitting, only a randomly R% of the
training dataset is noisy and injected in the training
process. R is a hyper-parameter of our data augmen-
tation algorithm.
5 DECISION MODEL
EVALUATION BASED ON
ABSTRACT INTERPRETATION
The evaluation of the decision model is based on the
abstract interpretation. In this section, abstract inter-
pretation principles and its application in the context
of robot navigation are presented.
5.1 Principles of Abstract
Interpretation
The abstract interpretation is a technique used for ana-
lyzing specifications and checking programs for resis-
tance to specification unsatisfaction (Cousot, 2008).
In (Gehr et al., 2018; Singh et al., 2018), authors have
reused the abstract interpretation for verifying the ro-
bustness of neural networks. This approach lies in the
reachability approaches.
The formulation of verifying the robustness of a
neural network is detailed as following. Given x
I
a
sample input and x
N
generated from x
I
by applying a
perturbation A, verifying the robustness R
(x
I
,A)
con-
sists of checking the robustness condition over the
whole possible x
N
resulting from x
I
. The robustness
condition is defined as: «the neural network outputs
the same label for x
N
and x
I
i.e. x
N
and x
I
belongs the
same class ».
The condition R
(x
I
,A)
is checked and two cases are
possible:
• if all possible x
N
verified R
(x
I
,A)
, the neural net-
work is called robust to the perturbation A given
the input x
I
.
• if at least one x
N
not verified R
(x
I
,A)
, the neural
network is called not robust to the perturbation A
given the input x
I
.
5.2 Robustness Evaluation based on the
Abstract Interpretation
To measure the robustness of the decision model, the
abstract interpretation is applied to each sample from
the test dataset (Only samples correctly classified by
the decision model are used). Hence, each sample is
represented by a polyhedra. Later should includes all
possible samples resulting by adding perturbation re-
lated to sensor uncertainty. In other words, the shape
should include all possible sample ∈ [low, upper]
(where low = sample − ∆X, upper = sample + ∆X,
∆X is the sensor uncertainty defined in section 4.3).
We recall that (∆X)
i
associated with the i
th
sensor is
different from one sensor to another.
Then, the shape is propagated through the abstract
transformer of each layer, obtaining a new shape. Fi-
nally, the final shape should be checked if they kept
the the same label as the original sample.
Mathematically, the robustness is formulated as
follows. Given M the number of correctly classified
samples, the robustness is provided by:
Robust =
1
M
M
∑
i=1
verified(Net, s
i
) (4)
where:
• verified(Net, s
i
) = 1, if the neural network Net re-
turns the same label for all points of the shape gen-
erated from s
i
.
• Otherwise, verified(Net, s
i
) = 0.
5.3 Evaluation Metrics
Our goal in this phase is to select the best model in
terms of performance (Per f ) and robustness (Robust).
• Per f : is defined as the rate of correct decisions
predicted by the neural network.
• Robust: is defined as the rate of samples keeping
their original labels after perturbation (Eq.4).
The proposed metrics are used to combine the two
characteristics of the model (performance and robust-
ness) in order to select the best one. The proposed
metrics are: the model efficiency and Pareto front.
Improving Decision-Making-Process for Robot Navigation Under Uncertainty
1109
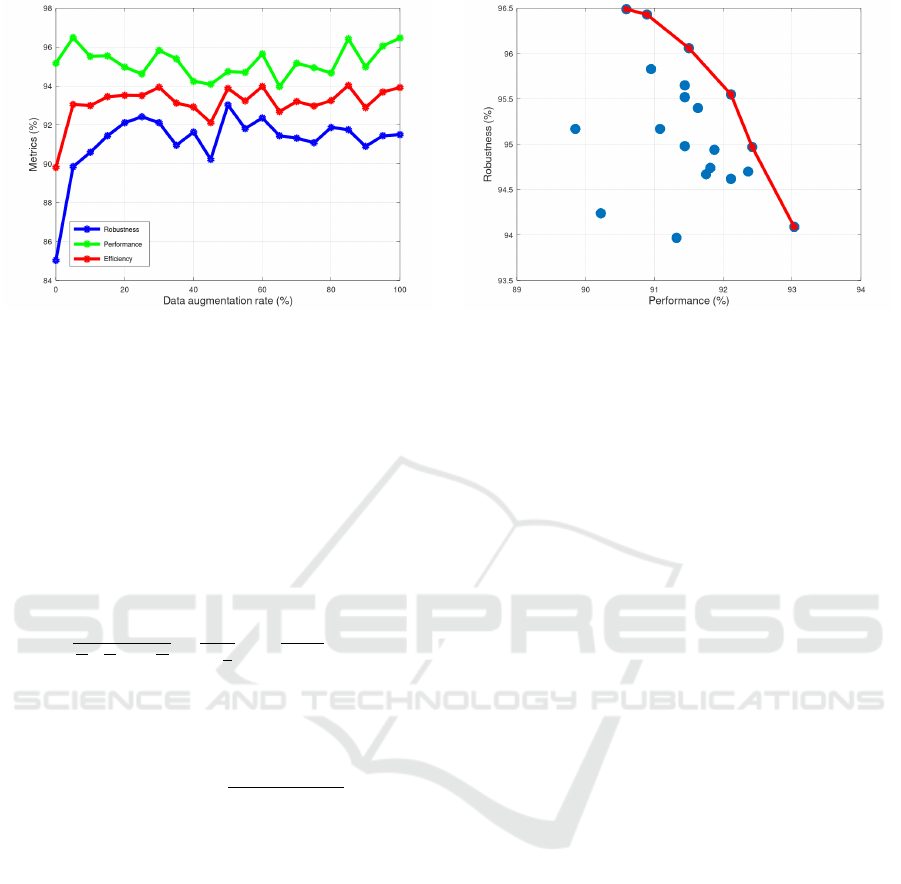
(a) Performance and robustness (b) Pareto Front
Figure 3: Decision-making model evaluation.
5.3.1 Efficiency Metric
The efficiency metric is based on the F
1
score (Chin-
chor, 1992) that is the harmonic mean of the perfor-
mance and robustness.
Mathematically, the harmonic mean is one of sev-
eral types of average, and in particular, one of the
Pythagorean means. The harmonic mean H of given
positive real numbers x
1
,x
2
,. .. ,x
n
is defined by:
H =
n
1
x
1
+
1
x
2
+···+
1
x
n
=
n
n
∑
i=1
1
x
i
=
n
∑
i=1
x
−1
i
n
−1
In this work, the efficiency metric E f f iciency corre-
sponds to the harmonic average of the performance
and robustness (Eq.5).
E f f iciency = 2 ∗
Per f ∗ Robust
Per f + Robust
(5)
The highest possible value of E f f iciency is 1, indi-
cating perfect performance and robustness, and the
lowest possible value is 0, if either the performance
or the robustness is close to zero.
5.3.2 Pareto Front Metric
Pareto ranking is often used for vectors or tensors
comparison with multiple criteria. This metric can be
embedded and used easily for evaluation process of a
given algorithm.
We first define the concept of dominance that is
important to assess the quality of the solutions and to
make sure that the best solutions are selected.
Definition 1 (Dominance). For a given problem iden-
tified by a vector
~
f = ( f
1
,. .. , f
n
) under a set of de-
fined constraints. Then, vector ~u dominates vector ~v
if and only if
∀i ∈ {1,. .. ,n}, u
i
≤ v
i
∧ ∃ j( j 6= i)u
j
< v
j
This is denoted by ~u ~v.
The above definition reports that a vector is dom-
inated if and only if another vector exists which is
better in at least one objective, and at least as good
in the remaining objectives. In our work, these objec-
tives are represented by robustness and performance
scores. A set of dominant points are representing the
Pareto front set.
Pareto front method is based on the dominance
strategy considering the bi-dimensional vector of
points. This approach is agnostic to the generation
of the considered points and will not change for new
generated datasets.
6 EXPERIMENTAL RESULTS
6.1 Dataset and Evaluation Protocol
To validate our approach, we use the experimental
sensor dataset proposed in (Freire et al., 2009) for
wall-following robot navigation. The dataset is a
collection of sensor readings obtained by the mobile
robot «SCITOS G5» during its navigation inside a
room. To navigate, 24 ultrasound (US) sensors were
used, and arranged circularly around its waist with an
arc distance of 15 degrees. The dataset file contains
5456 rows. Each raw values corresponds to the mea-
surements of all 24 US and the corresponding deci-
sion label (i.e. direction where the robot should nav-
igate next). All the 24 US readings are synchronized
(i.e collected at the same time step). The possible de-
cisions of the robot are: 1) Move-Forward, 2) Slight-
Right-Turn, 3) Slight-Left-Turn and 4) Sharp-Right-
Turn.
For the evaluation, 70% of the available data is
used for training and the resting 30% for evaluation.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
1110

6.2 Results
To assess our decision model, several data augmenta-
tion rates R are evaluated as described in section 4.3.
In our study, R varies from 0% to 1000% by step of
5%. For each rate, performance and robustness are
computed to measure the two proposed metrics.
The behavior of our decision model according to
the two metrics is presented in Fig.3. Figure 3a shows
the evaluation in terms of three indicators: model per-
formance, model robustness and the efficiency metric
(Eq.5). Figure 3b shows the evaluation of our model
according to the Pareto front metric. It shows the cou-
ples (Per f ormance,Robustness) as well as the pareto
front.
Table 1 shows the evolution of model perfor-
mance, robustness and efficiency according to the
data augmentation rate.
6.3 Discussion
The standard experience, where no data augmentation
is applied, achieves a performance of 85.03%. More-
over, an improvement of 8% is obtained by augment-
ing the training dataset by 50%. This improvement is
significant given the large size of the test dataset (8%
is equivalent to 131 robot decisions) and proves the
importance to augment the training dataset by inject-
ing noisy inputs. Afterwards, the decision model per-
formance decreases with the augmentation of training
dataset (R > 50%). This is explained by the fact that
when the reference dataset is significantly augmented,
it becomes slightly different from the test dataset.
Table 1 shows that augmenting the training dataset
by 10% led to a stable robustness. Then, by augment-
ing more the training dataset (R > 10%), the robust-
ness is decreasing. From a data augmentation of 90%
(R >= 90%), the robustness attains its initial value
(before data augmentation). These results lead us to
two remarks: 1) the dataset augmentation is very im-
portant to improve the performance of the neural net-
work face to sensor uncertainty perturbation however
2) the data augmentation rate should be controlled to
keep a acceptable robustness level.
In the following, we discuss and show the conflict-
ing behavior of robustness and performance accord-
ing to the data augmentation rate. Taking the experi-
ence of a data augmentation of 30%, the performance
is improved by 7.08% however, the robustness is de-
creased by 1.85%. Table 1 illustrates results accord-
ing to the efficiency metric that combines robustness
and performance. Experimentally, data augmentation
has a slight impact on the efficiency metric. Table 1
shows that augmenting training dataset by 50% leads
to the best model in terms of efficiency. In fact, aug-
menting the training dataset by 50%, the efficiency is
improved by 3.08%.
Figure 3b depicts the results of the Pareto front
metric. This metric allowed us to select rapidly few
Pareto efficient points (on the Pareto front) dominat-
ing the reminder points.
In this Pareto front, the lowest value for the ro-
bustness is close to 94.2% while the performance is
close to 93%. A major set of points indicated by F-
Score metric are dominated by the Pareto Front set.
We can conclude that for the considered data set, the
Pareto Front set allows to easily eliminating domi-
nated points while considering performance and ro-
bustness trade-offs.
7 CONCLUSION AND
PERSPECTIVES
In this paper, we examined the efficiency of a robot
system navigation against sensors uncertainty. We
are interested in the case where the robot decision is
based on deep neural network. Our challenge was the
impact of noisy inputs on robot decision. To cope
with this issue, we proposed to enhance the training
dataset by injecting noisy inputs. From one side, An
adversarial training based on data augmentation has
improved the decision model efficiency by 3.17%,
and from the other side the efficiency metric is in-
sufficient to conclude on the best data augmentation
rate. The Pareto Front allows us to select a wider
value range of data augmentation rates. It allowed us
to consider only non dominated points combining the
robustness and performance scores at the same time.
In the future work, we plan to study the correlation
between sensor measurements. The goal is to select
sensors disturbing more the decision-making process.
This selection will help experts to replace faulty sen-
sors. Moreover, we plan to validate our proposed ap-
proach on several datasets in different contexts.
ACKNOWLEDGMENT
This research work has been carried out in the frame-
work of IRT SystemX, Paris-Saclay, France, and
therefore granted with public funds within the scope
of the French Program Investissements d’Avenir. This
work is a part of the project EPI project (EPI for "AI-
based Decision Making Systems’ Performance Eval-
uation").
Improving Decision-Making-Process for Robot Navigation Under Uncertainty
1111

Table 1: Decision-making model evaluation.
Data augmentation rate (R%) Performance (%) Robustness (%) Efficiency (%)
No augmentation 85.03 96.47 90.39
10 90.59 96.49 93.45
20 92.11 95.55 93.80
30 92.11 94.62 93.35
40 91.63 95.40 93.47
50 93.03 94.09 93.56
60 92.36 94.70 93.52
70 91.32 93.97 92.63
80 91.87 94.94 93.38
90 90.89 96.43 93.58
100 91.50 96.06 93.72
REFERENCES
Abdessemed, F. (2012). Svm-based control system for a
robot manipulator. International Journal of Advanced
Robotic Systems, 9(6):247.
Aleluya, E. R., D. Zamayla, A., and Lyle M. Tamula, S.
(2018). Decision-making system of soccer-playing
robots using finite state machine based on skill hier-
archy and path planning through bezier polynomials.
Procedia Computer Science, 135:230–237.
Chinchor, N. (1992). Muc-4 evaluation metrics. In In Pro-
ceedings of the Fourth Message Understanding Con-
ference, pages 22–29.
Cousot, P. (2008). The Verification Grand Challenge and
Abstract Interpretation, pages 189–201. Springer
Berlin Heidelberg, Berlin, Heidelberg.
Ehlers, R. (2017). Formal verification of piece-
wise linear feed-forward neural networks. CoRR,
abs/1705.01320.
Ehrgott, M. (2005). Multicriteria optimization.
Freire, A. L., Barreto, G. A., Veloso, M., and Varela, A. T.
(2009). Short-term memory mechanisms in neural
network learning of robot navigation tasks: A case
study. In 2009 6th Latin American Robotics Sympo-
sium, pages 1–6.
Gallardo, N., Gamez, N., Rad, P., and Jamshidi, M. (2017).
Autonomous decision making for a driver-less car. In
2017 12th System of Systems Engineering Conference
(SoSE), pages 1–6.
Gehr, T., Mirman, M., Drachsler-Cohen, D., Tsankov, P.,
Chaudhuri, S., and Vechev, M. (2018). Ai2: Safety
and robustness certification of neural networks with
abstract interpretation. In 2018 IEEE Symposium on
Security and Privacy (SP), pages 3–18.
Gehr, T., Mirman, M., Drachsler-Cohen, D., Tsankov, P.,
Chaudhuri, S., and Vechev, M. (2018). Ai2: Safety
and robustness certification of neural networks with
abstract interpretation. In 2018 IEEE Symposium on
Security and Privacy (SP), pages 3–18.
Hoel, C., Wolff, K., and Laine, L. (2018). Automated
speed and lane change decision making using deep re-
inforcement learning. CoRR, abs/1803.10056.
Jmila, H., Ibn Khedher, M., Blanc, G., and El Yacoubi,
M. A. (2019). Siamese network based feature learn-
ing for improved intrusion detection. In Gedeon, T.,
Wong, K. W., and Lee, M., editors, Neural Informa-
tion Processing, pages 377–389, Cham. Springer In-
ternational Publishing.
Jmila, H., Khedher, M. I., and El-Yacoubi, M. A. (2017).
Estimating VNF resource requirements using machine
learning techniques. In Liu, D., Xie, S., Li, Y., Zhao,
D., and El-Alfy, E. M., editors, Neural Information
Processing - 24th International Conference, ICONIP
2017, Guangzhou, China, November 14-18, 2017,
Proceedings, Part I, volume 10634 of Lecture Notes
in Computer Science, pages 883–892. Springer.
Kammel, S., Ziegler, J., Pitzer, B., Werling, M., Gindele,
T., Jagzent, D., Schöder, J., Thuy, M., Goebl, M., von
Hundelshausen, F., Pink, O., Frese, C., and Stiller, C.
(2009). Team AnnieWAY’s Autonomous System for
the DARPA Urban Challenge 2007, pages 359–391.
Springer Berlin Heidelberg, Berlin, Heidelberg.
Katz, G., Barrett, C. W., Dill, D. L., Julian, K., and Kochen-
derfer, M. J. (2017). Reluplex: An efficient SMT
solver for verifying deep neural networks. CoRR,
abs/1702.01135.
Khedher, M. I. and El Yacoubi, M. A. (2015). Local sparse
representation based interest point matching for per-
son re-identification. In Arik, S., Huang, T., Lai,
W. K., and Liu, Q., editors, Neural Information Pro-
cessing, pages 241–250, Cham. Springer International
Publishing.
Khedher, M. I., El-Yacoubi, M. A., and Dorizzi, B. (2012).
Probabilistic matching pair selection for surf-based
person re-identification. In 2012 BIOSIG - Proceed-
ings of the International Conference of Biometrics
Special Interest Group (BIOSIG), pages 1–6.
Khedher, M. I., Jmila, H., and Yacoubi, M. A. E. (2018).
Fusion of interest point/image based descriptors for
efficient person re-identification. In 2018 Interna-
tional Joint Conference on Neural Networks (IJCNN),
pages 1–7.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-
agenet classification with deep convolutional neural
networks. In Advances in Neural Information Pro-
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
1112

cessing Systems 25, pages 1097–1105. Curran Asso-
ciates, Inc.
Shabbir, J. and Anwer, T. (2018). A survey of deep learn-
ing techniques for mobile robot applications. CoRR,
abs/1803.07608.
Singh, G., Gehr, T., Mirman, M., Püschel, M., and Vechev,
M. (2018). Fast and effective robustness certification.
In Advances in Neural Information Processing Sys-
tems 31, pages 10825–10836. Curran Associates, Inc.
Vapnik, V. N. (1995). The Nature of Statistical Learning
Theory. Springer-Verlag, Berlin, Heidelberg.
Vitus, M. P. and Tomlin, C. J. (2013). A probabilistic ap-
proach to planning and control in autonomous urban
driving. In 52nd IEEE Conference on Decision and
Control, pages 2459–2464.
Xiang, W., Tran, H., and Johnson, T. T. (2017a). Out-
put reachable set estimation and verification for multi-
layer neural networks. CoRR, abs/1708.03322.
Xiang, W., Tran, H., and Johnson, T. T. (2017b). Reachable
set computation and safety verification for neural net-
works with relu activations. CoRR, abs/1712.08163.
Zhang, J., Liao, Y., Wang, S., Han, J., Zhang, J., Liao,
Y., Wang, S., and Han, J. (2017). Study on Driving
Decision-Making Mechanism of Autonomous Vehicle
Based on an Optimized Support Vector Machine Re-
gression. Applied Sciences, 8(1):13.
Improving Decision-Making-Process for Robot Navigation Under Uncertainty
1113
