Mathematical Programming Approach for Adversarial Attack Modelling
Hatem Ibn-Khedher
1
, Mohamed Ibn Khedher
2
and Makhlouf Hadji
2
1
Universit
´
e de Paris, LIPADE, F-75006 Paris, France
2
IRT - SystemX, 8 Avenue de la Vauve, 91120 Palaiseau, France
Keywords:
Neural Network, Adversarial Attack, Linear Programming (LP).
Abstract:
An adversarial attack is defined as the minimal perturbation that change the model decision. Machine learning
(ML) models such as Deep Neural Networks (DNNs) are vulnerable to different adversarial examples where
malicious perturbed inputs lead to erroneous model outputs. Breaking neural networks with adversarial attack
requires an intelligent approach that decides about the maximum allowed margin in which the neural network
decision (output) is invariant. In this paper, we propose a new formulation based on linear programming
approach modelling adversarial attacks. Our approach considers noised inputs while reaching the optimal
perturbation. To assess the performance of our approach, we discuss two main scenarios quantifying the
algorithm’s decision behavior in terms of total perturbation cost, percentage of perturbed inputs, and other
cost factors. Then, the approach is implemented and evaluated under different neural network scales.
1 INTRODUCTION
The past decade has witnessed the great rise of Ar-
tificial Intelligence (AI) and especially Deep Learn-
ing (DL). The success of deep learning, as Machine
Learning (ML) classifier, has drawn great attention
in the recent, particularly in computer vision appli-
cations(Khedher et al., 2018) , telecommunications
(Jmila et al., 2017; Jmila et al., 2019) and control of
autonomous systems (Bunel et al., 2018; Rao and Fr-
tunikj, 2018; Kisacanin, 2017). A classifier is an ML
model that learns a mapping function between inputs
and a set of classes (Khedher et al., 2012; Khedher
and El Yacoubi, 2015). For instance, an anomaly de-
tector is a classifier taking as inputs a network traffic
features and assigning them to the normal or abnor-
mal class.
Despite the success of DNN deployment in real
time applications, it shows a vulnerability to integrity
attacks. Such attacks are often instantiated by adver-
sarial examples: legitimate inputs altered by adding
small, often imperceptible, perturbations to force a
learned classifier to misclassify the resulting adver-
sarial inputs, while remaining correctly classified by
a human observer. In the automotive context, the per-
turbation of environment can be caused by the failure
of perception sensors. So to ensure operational safety
and road safety, it is crucial to assure the robustness of
these systems faced sensor uncertainty. In fact, know-
ing the smallest disturbance gives us an idea of the
level of robustness of DL in the face of adversary at-
tacks (Cao et al., 2019; Sharif et al., 2016; Carlini and
Wagner, 2018).
To illustrate, consider the following images, po-
tentially consumed by an autonomous vehicle (Aung
et al., 2017), these images appear to be the same to hu-
mans. In fact, our biological classifiers (vision) iden-
tify each image as a limit speed sign to 20 km/h. The
image on the left is indeed an ordinary image of a
limit speed sign. We produced the image on the right
by adding a precise perturbation, blurring, that forces
a particular DNN to classify it as a yield sign, i.e., as
a limit speed sign to 80 km/h (Aung et al., 2017).
Here, an adversary could potentially use the al-
tered image to cause a car without failsafes to behave
dangerously. This attack would require modifying the
image used internally by the car through transforma-
tions of the physical traffic sign. It is thus conceivable
that physical adversarial traffic signs could be gen-
Figure 1: Adversarial attacks. left: initial image, right:
Blurring (Aung et al., 2017).
Ibn-Khedher, H., Ibn Khedher, M. and Hadji, M.
Mathematical Programming Approach for Adversarial Attack Modelling.
DOI: 10.5220/0010324203430350
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 2, pages 343-350
ISBN: 978-989-758-484-8
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
343

erated by maliciously modifying the sign itself, e.g.,
with stickers or paint. It is worth mentioning here that
in most application fields, the predicted decision of
neural networks (i.e., detecting the presence/absence
of a pedestrian, changing or keeping the lane, etc.)
has a serious impact on the safety of the driver, the
safety of passengers and other users of the road. For
the sake of clarity, detecting the absence of the pedes-
trian while he is actually present can cause a serious
accident.
In this paper, we contribute to the search of adver-
sarial attack. Compared to the state of the art, most
of proposed approaches follow an iterative procedure
where from one iteration to another, we are getting
closer to the adversarial example. At the end of pro-
cedure, we are not sure to get an adverse example.
Contrary, our approach consists in finding the small-
est perturbation that changes the decision on DNN,
i.e., an adverse example.
Our novel attack strategy is to convert the map-
ping between outputs and inputs to a linear system of
equations. Our approach is based on linear program-
ming (LP) technique and iteration process. Through
the first LP optimization technique, we are going
to formulate an exact algorithm based on a mathe-
matical model. In the proposed solution, we elimi-
nate the non-linearity by encoding them with the help
of binary variables. Then, the iterative process can
search a smallest perturbation in order to broke the
input/output constraints.
The rest of the paper is organized as follows. In
Section 2, the principles of feed-forward neural net-
works and adversarial attacks are presented. In the
Section 3, a state of the art of adversarial attacks
methods is discussed. The structure of our proposed
approach is described in Section 4. Section 5 includes
the experimental results and Section 6 concludes the
work.
2 BACKGROUNDS
In this Section, we highlight the main architectures
used in DNN and adverse attacks fields.
2.1 Deep Neural Networks
A Deep Neural Network (DNN) consists of a set of
several hidden layers, in addition to an input and out-
put layer. Each layer contains a set of neurons. Each
of the neurons is connected to those of the neurons of
the previous layer. Each neuron is a simple process-
ing element that responds to the weighted inputs it re-
ceived from other neurons (Shrestha and Mahmood,
2019).
There are several types of DNNs. In this paper,
we are focusing on Feed-Forward Neural Network
where each neuron in a layer is connected with all the
neurons in the previous layer. These connections are
not all equal: each connection may have a different
strength or weight. The weights on these connections
encode the knowledge of a network.
The action of a neuron depends on its activation func-
tion, which is described as:
y
i
f
n
j 1
w
i j
x
j
θ
i
(1)
where x
j
is the j
th
input of the i
th
neuron, w
i j
is the
weight from the j
th
input to the i
th
neuron, θ
i
is the
bias of the i
th
neuron, y
i
is the output of the i
th
neu-
ron and f . is the activation function. The activation
function is, mostly, a nonlinear function describing
the reaction of i
th
neuron with inputs.
2.2 Adversarial Attacks
An adversarial example is an instance with small
perturbation that cause a machine learning model to
make a false prediction. There are different ways to
find an adversarial example. Most of them rely on
minimizing the distance between the adverse example
and the original one while making sure that the pre-
diction is wrong. Attacks can be classified into two
categories: white-box attacks and black-box attacks
(Chakraborty et al., 2018),(Akhtar and Mian, 2018).
• White-box Attack: To generate a white-box at-
tack, the attacker should have full access to the
architecture and parameters of the classifier (gra-
dient, loss function, etc.)
• Black-box Attack: To generate a black-box at-
tack, the attacker does not have complete access
to the classifier. In a black-box setting, the classi-
fier parameters are unknown.
For simplicity, we consider X as the set of classifier
inputs and Y the set of classifier outputs along K pos-
sible classes, Y 1, . . . , K . Finally, we note C x
x
1
x
2
H
1
H
2
y
1
1
1
-1
1
-1
Figure 2: Example of neural network.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
344

the class of x by the neural network F . Regardless
of the type of attack, it is important to distinct between
targeted and non-targeted attack.
• Untargeted Attack: an untargeted attack aims to
misclassify the benign input by adding adversar-
ial perturbation so that the predicted class of the
benign input is changed to some other classes in
Y without a specific target class.
• Targeted Attack: a targeted attack aims to mis-
classify the benign input x to a targeted (specific)
class y Y by adding an adversarial perturbation.
3 RELATED WORK: NEURAL
NETWORK ATTACKS FIELD
In this Section, we highlight the relevant work about
Neural Network Attacks (NNA) methods.
3.1 Fast Gradient Sign Method (FGSM)
Goodfellow et al. (Goodfellow et al., 2015) have
developed a method for generating adverse sample
based on the gradient descent method. Each compo-
nent of the original sample x is modified by adding or
subtracting a small perturbation ε. The adverse func-
tion ψ is expressed as following:
ψ : X Y X
x, y ε∇
x
L x, y
Thus, the loss function of the classifier will decrease
when the class of the adverse sample is chosen as y.
We then wish to find x adverse sample of x such as:
x x
p
ε.
It is clear that the previous formulation of FGSM is
related to targeted attack case where y corresponds to
the target class that we wish to impose on the original
input sample. However, this attack can be applied in
the case of untargeted attack, by considering the fol-
lowing perturbation:
ρ : X X
x ψ x, C x
Thus, the original input x is modified in order to in-
crease the loss function L when the classifier retains
the same class C x . This attack only requires the
compute of the loss function gradient, which makes
it a very efficient method. On the other hand,vε is
a hyper parameter that affect the x class: if ε is too
small, the ρ x perturbation may have little impact on
the x class.
3.2 Basic Iterative Method (BIM)
Kurabin et al. (Kurabin et al., 2017) proposed an ex-
tension of the FGSM attack by iteratively applying
FGSM. At each iteration i, the adverse sample is gen-
erated by applying FGSM on the generated sample at
the i 1
th
iteration. The BIM attack is generated as
the following:
x
0
x
x
i 1
x
i
ψ x
i
, y
where y represents, in the case of a targeted attack,
the class of the adverse sample and y C x
N
in the
case of an untargeted attack. Moreover, ψ is the same
function defined in the case of FGSM attack.
3.3 Projected Gradient Descent (PGD)
The PGD (Madry et al., 2017) attack is also an ex-
tension of the FGSM and similar to BIM. It con-
sists in applying FGSM several times. The major
difference from BIM is that at each iteration, the
generated attack is projected on the ball B x, ε
z X : x z
p
ε . The adverse sample x asso-
ciated with the original one x is then constructed as
following:
x
0
x
x
i 1
Π
ε
x
i
ψ x
i
, y
where Π
ε
is the projection on the ball B x, ε and ψ is
the perturbation function as defined in FGSM. Like-
wise, y refers to the target label you wish to reach, in
the case of targeted attack, or it refers to C x
N
in the
case of an untargeted attack.
3.4 Jacobian Saliency Map Attack
(JSMA)
This attack differs from the previous ones, since
Parpernot et al. (Papernot et al., 2015) did not rely
on a gradient descent to build an adverse example but
the idea is to disturb a minimal number of pixels, in
the case of image input, according to a criterion. Ini-
tially proposed for a targeted attack, JSMA consists in
controlling the number of pixels of an input image x
(or the number of components of an input vector) that
should be modified in order to obtain an adverse im-
age associated with a target class y. Iteratively, JSMA
consists in modifying pixels until the target class is
obtained.
The idea behind is to, on one hand, increase F
y
x
the probability of the target class y and on the other
hand, decrease the probabilities of the other classes.
Mathematical Programming Approach for Adversarial Attack Modelling
345

To do this, authors introduced the Saliency Map ma-
trix as following:
S x, y i
0 si
F
y
x
x
i
0 ou
k y
F
k
x
x
i
0
F
y
x
x
i
k y
F
k
x
x
i
otherwise
The Saliency Map is used as criterion to select pix-
els which should be modified. In fact, the way that
Saliency Map is computed, allows to reject pixels that
will not increase the probability of the target class y or
will not decrease the probabilities of the other classes;
for these pixels, the criterion is set to 0.
Indeed, for a pixel x
i
, if
F
y
x
x
i
0 means F
y
will
be decreasing by adding a positive term to pixel x
i
and thus tend to decrease the probability of the target
class y. Similarly, for the pixel x
i
, if
k y
F
k
x
x
i
0
means
k y
F
k
will be increasing by adding a positive
term to x
i
in x
i
and increase the probability of the other
classes.
As described below, the proposed criterion acts on a
single pixel. Nevertheless, another version of JSMA
is proposed by authors and consists in considering a
pair of pixels rather than single pixels. At each itera-
tion, pair of pixels (i
max
and j
max
) is found that satisfy
:
argmax
p, q
i p, q
F
y
x
x
i
i p, q
k y
F
k
x
x
i
(2)
As show above, an adversarial attack requires an
enticed algorithm that decides about the maximum
allowed perturbation after which the neural network
model is no robust. Hereafter we introduce our pro-
posed approaches using linear programming tech-
nique.
4 EXACT APPROACH FOR
ADVERSARIAL ATTACK
USING BIG-M
Most of the approaches consist in converging itera-
tively towards an adverse example. Obtaining this ad-
verse example is not guaranteed at the end of the ap-
plication of the algorithm. In fact, it depends on the
number of iterations. Compared to the state of the art,
our approach consists in determining and in an exact
way, after a single iteration the minimum disturbance
that disturbs the Neural Network.
The approach takes as input a given neural net-
work. It is encoded as series of data inputs ranging
from lower to upper bounds. Neural network nodes
have activation functions applied at the output of an
artificial neural node in order to transform the incom-
ing flow into another domain. It is worth mention-
ing here that the considered activation function is the
ReLU function. For sake of clarity, ReLU function is
defined as follows: ReLU X max X; 0 , where X
represents the incoming flow at that artificial node.
The ReLU is a non-linear activation function.
Therefore, we propose to consider the bigM tech-
nique as an automated encoder that linearizes the hid-
den constraint. It is a mixed integer linear program-
ming transformation that exactly transforms non-
linear constraints into linear inequalities. More details
on bigM are given in the sequel.
After converting the neural network to a linear
program, the second stage of our approach it find the
small perturbation ε E
n
that change the decision
of neural network, where n the dimension of input.
Moreover we are interesting in minimizing the num-
ber of the perturbed inputs. The approach based on
formulating the neural network using linear equation
that maps the output classes to the inputs. It is worth
mentioning here that introducing perturbation to each
inputs may change the decision of the neural network.
Therefore, we propose optimal adversarial attack ap-
proach using linear programming techniques. Here-
after we describe the problem formulation, decision
variables and algorithm constraints.
4.1 Adversarial Attack Problem
Formulation
Let we consider a neural network with m layers noted
by L
1
, L
2
, . . . , L
m
. In each layer, we consider n neu-
rons represented by nodes in Fig. 2. There exists an
arc i, j between each neuron i in a layer L
s
and j in
a different layer L
t
(s t). This arc is weighted by
w
i j
as depicted by Fig. 2. Moreover, for each neuron
j (node in the graph of Fig. 2), we consider two main
variables a
in
j and a
out
j given by the following:
1. if j L
1
, hence we have the two following inputs:
• a
in
j x
j
• a
out
j x
j
2. if j L
k
where 2 k m 1, hence we have:
• a
in
j
i Γ j
w
i j
a
out
i
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
346

• a
out
j max a
in
j ; 0
3. if j L
m
(last layer in our neural network):
• a
in
j
i Γ j
w
i j
a
out
i
• a
out
j max a
in
j ; 0 : not concerned in our
scenarios;
where Γ j indicates the set of predecessor nodes of
j in the considered neural network.
4.2 Decision Variables
We introduce the following decision variables:
• The binary decision variables y indicates if the
data input x
j
, j N, is perturbed. It is defined as
follows
y
i
1 if the data input x
j
is perturbed
0 otherwise
(3)
• The real variable ε decides about the perturbation
value. It indicates the maximum value that does
not change the decision (the ground truth in our
case). It is defined as follows
ε
j
0 if x
j
is perturbed
0 otherwise
(4)
4.3 Algorithm Constraints
According to the previous formulations and inequali-
ties linearization, we summarize in the following the
whole constraints of our model:
• First layer constraint: introducing perturbation to
the input neurons re-transforms the previous vari-
ables of the first layer as follows:
j L
1
: a
in
j x
j
ε
j
(5)
j L
1
: a
out
j x
j
ε
j
(6)
• Hidden layer constraint: the data inputs to a layer
m 1 depends on the output of the previous layer
m. It is formulated as follows:
j L
k
2 k m 1 : a
in
j
i Γ j
w
i j
a
out
i
(7)
j L
k
2 k m 1 : a
out
j max a
in
j ; 0
(8)
• Output layer constraint: the output flow of the last
layer is bounded by β. It is formulated as follows:
j L
m
: a
in
j
i Γ j
w
i j
a
out
i (9)
j L
m
: a
in
j
i Γ j
w
i j
a
out
i β (10)
• Data inputs boundary: It is implied before and af-
ter perturbation and formulated as follows
a
0 j
x
j
b
0 j
(11)
where a
0 j
and b
0 j
represent lower and upper
bounds for each neuron j N
• Perturbation constraint: decisions related to the
data to be perturbed and the values of the pertur-
bation are formulated as follows
ε
j
y
j
b
0 j
x
j
(12)
ε
j
y
j
a
0 j
x
j
(13)
• Perturbation boundary: the data values after the
perturbation decision should not exceed the data
inputs boundary mentioned above:
a
0 j
x
j
ε
j
b
0 j
x
j
(14)
• Non negativity of decision variables: While ε is a
real variables, y
j
is bounded as follows
y
j
0, 1 (15)
4.4 Objective Function Formulation
Considering different DNN use cases, the main objec-
tive functions in our proposed model is to minimize
the number of perturbed data inputs while maximiz-
ing each perturbation (if it exists). It is formulated as
follows:
minZ
j n
y
j
j n
ε
j
(16)
4.5 Algorithm Constraints
Linearization
The previous inequalities using to determine the max-
imum between 0 and a
in
j (for a given neuron j) are
non-linear and necessitate to be linearized to facilitate
solving the model in negligible times. In the sequel,
we propose a linearization approach based on Big-M
technique to totally eliminate non-linear equalities in
the mathematical formulation. We consider, for in-
stance, the following non-linear equality (for a given
j):
a
out
j max a
in
j ; 0 (17)
We introduce a new binary variable θ 0, 1 to dis-
cuss the different cases that can be resulted from (17).
In fact, we consider :
a
out
j
a
in
j , if a
in
j 0
0, otherwise
Mathematical Programming Approach for Adversarial Attack Modelling
347

Table 1: Neural Network Configuration Setting.
Simulation Parameters Values
m from 50 to 500 which models most of the neural networks (Carlini and
Wagner, 2018)
n 10 and 20 neurons
Type Fully connected feed-forward neural network
M or Big M infinity
x
j
j 1, . . . , n normalized and scaled data inputs
Decision Variables Definitions
y
j
Indicates if the data input x
j
is perturbed
ε
j
perturbation associated with the input x
j
θ Binary decision variable used for constraints linearization(0 or 1)
Hence, we propose:
a
out
j θ 1 M a
in
j
a
out
j 1 θ M a
in
j
a
out
j θ M
a
in
j θ 1 M
a
in
j θ M
θ 0, 1
(18)
Using the formulation 18, one can verify, according
to the values of θ, that we can attend the same results
than those of equation (17).
5 PERFORMANCE EVALUATION
5.1 Optimization Scenarios and Key
Performance Indicators
We have considered a feed-forward neural network ar-
chitecture with two neural networks scales N and
different hidden layers M . Table 1 summarizes the
used simulation parameters in our models.
For the interest of assessing the efficiency of the exact
ILP algorithm, we used CPLEX optimization tool
1
for the adversarial attack optimization in small neural
network scale.
Further, in order to compare the Big-M based ad-
versarial attack algorithm, we proposed two scenar-
ios: 1 Linear objective function, and 2 Quadratic
objective function. The two approaches are defined
as follows:
• In linear objective function, the linear distance be-
tween perturbed and original inputs is minimized.
• In quadratic objective function, the Euclidean dis-
tance (i .e ., the l
2
norm) between perturbed and
original inputs is minimized.
1
https://pypi.org/project/cplex/
Figure 3: Total Perturbation Cost.
In addition, we propose Total Perturbation Cost
(TPC) and Percentage of Perturbed Inputs (PPI) as
key metrics to assess the behavior of the proposed al-
gorithm. They can be defined as follows:
T PC
j n
y
j
j n
ε
j
(19)
PPI
j n
y
j
N
100 (20)
5.2 Obtained Results
Since we focused on the total perturbation cost as in-
dicated in the above objective functions, we measure
this cost in the two scenarios as shown in Fig. 3. The
result shows that the linear approach is slightly effi-
cient in terms of perturbation cost compared to the
quadratic objective function.
Fig. 4 illustrates the obtained results in terms of
percentage of perturbed inputs using the two men-
tioned objective functions or metrics. It is clear and
with no surprises that the linear approach outper-
forms the quadratic one, as it necessitates less than
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
348

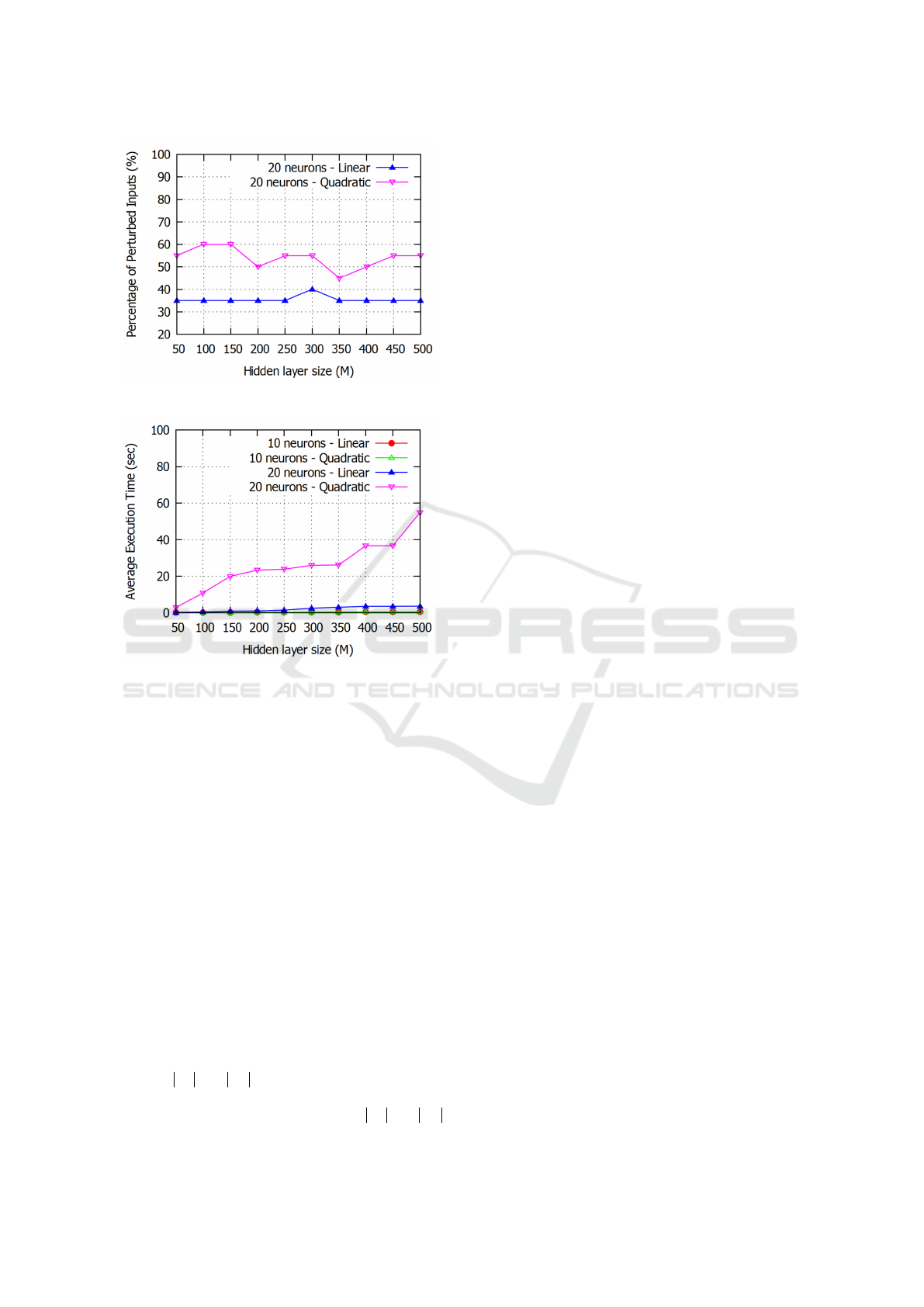
Figure 4: Percentage of Perturbed Inputs (%).
Figure 5: Average Execution Time.
40% of PPI, compared to 60% of PPI when using the
quadratic formulation.
The efficiency and feasibility of our adversarial
attack algorithm, leveraging an Integer Linear Pro-
gramming approach, is depicted in Fig. 5. In other
words, the average execution time does not exceed
1 minute in the worst scenario (Quadratic objective
function with 20 neurons as input). The average time
for searching an adversarial image (for instance) is
linearly increasing for a hidden layer number ranging
from 50 to 500.
6 CONCLUSION
We proposed in this paper a new optimization tech-
nique for adversarial attack process. We considered
in our optimization the integration of new constraints
such as the number of perturbed inputs. Moreover, an
optimal optimization algorithm is proposed and eval-
uated for N and M changes according to predeter-
mined scenarios (linear and quadratic). Performance
evaluation is investigated to confirm that N and M
have significant impact on the average execution time,
TPC, and PPI. Finally, our results show the efficiency
of the linear algorithm compared to the quadratic ap-
proach.
We considered in this paper only feed-forward
neural network. As a future work, we plan to ex-
tend our modelling to other deep learning architec-
tures such as Convolutional Neural Network (CNN)
and Long Short-Term Memory (LSTM) . Moreover,
we plan to validate our proposed approach on real use
cases such as image classification, self-driving, etc.
REFERENCES
Akhtar, N. and Mian, A. (2018). Threat of adversarial at-
tacks on deep learning in computer vision: A survey.
CoRR, abs/1801.00553.
Aung, A. M., Fadila, Y., Gondokaryono, R., and Gonzalez,
L. (2017). Building robust deep neural networks for
road sign detection. CoRR, abs/1712.09327.
Bunel, R., Turkaslan, I., Torr, P. H., Kohli, P., and Kumar,
M. P. (2018). A unified view of piecewise linear neu-
ral network verification. In Proceedings of the 32Nd
International Conference on Neural Information Pro-
cessing Systems, NIPS’18, pages 4795–4804, USA.
Curran Associates Inc.
Cao, Y., Xiao, C., Cyr, B., Zhou, Y., Park, W., Rampazzi,
S., Chen, Q. A., Fu, K., and Mao, Z. M. (2019). Ad-
versarial Sensor Attack on LiDAR-based Perception
in Autonomous Driving. In Proceedings of the 26th
ACM Conference on Computer and Communications
Security (CCS’19), London, UK.
Carlini, N. and Wagner, D. (2018). Audio adversarial ex-
amples: Targeted attacks on speech-to-text. In 2018
IEEE Security and Privacy Workshops (SPW), pages
1–7.
Chakraborty, A., Alam, M., Dey, V., Chattopadhyay, A.,
and Mukhopadhyay, D. (2018). Adversarial attacks
and defences: A survey. CoRR, abs/1810.00069.
Goodfellow, I. J., Shlens, J., and Szegedy, C. (2015). Ex-
plaining and harnessing adversarial examples. ICLR,
1412.6572v3.
Jmila, H., Khedher, M. I., Blanc, G., and El-Yacoubi, M. A.
(2019). Siamese network based feature learning for
improved intrusion detection. In Gedeon, T., Wong,
K. W., and Lee, M., editors, Neural Information
Processing - 26th International Conference, ICONIP
2019, Sydney, NSW, Australia, December 12-15, 2019,
Proceedings, Part I, volume 11953 of Lecture Notes in
Computer Science, pages 377–389. Springer.
Jmila, H., Khedher, M. I., and El-Yacoubi, M. A. (2017).
Estimating VNF resource requirements using machine
learning techniques. In Liu, D., Xie, S., Li, Y., Zhao,
D., and El-Alfy, E. M., editors, Neural Information
Processing - 24th International Conference, ICONIP
2017, Guangzhou, China, November 14-18, 2017,
Proceedings, Part I, volume 10634 of Lecture Notes
in Computer Science, pages 883–892. Springer.
Mathematical Programming Approach for Adversarial Attack Modelling
349

Khedher, M. I. and El Yacoubi, M. A. (2015). Local sparse
representation based interest point matching for per-
son re-identification. In Arik, S., Huang, T., Lai,
W. K., and Liu, Q., editors, Neural Information Pro-
cessing, pages 241–250, Cham. Springer International
Publishing.
Khedher, M. I., El-Yacoubi, M. A., and Dorizzi, B. (2012).
Probabilistic matching pair selection for surf-based
person re-identification. In 2012 BIOSIG - Proceed-
ings of the International Conference of Biometrics
Special Interest Group (BIOSIG), pages 1–6.
Khedher, M. I., Jmila, H., and Yacoubi, M. A. E. (2018).
Fusion of interest point/image based descriptors for
efficient person re-identification. In 2018 Interna-
tional Joint Conference on Neural Networks (IJCNN),
pages 1–7.
Kisacanin, B. (2017). Deep learning for autonomous vehi-
cles. In 2017 IEEE 47th International Symposium on
Multiple-Valued Logic (ISMVL), pages 142–142.
Kurabin, A., Goodfellow, I. J., and Bengio, S. (2017).
Adversarial examples in the physical world. ICLR,
1607.02533v4.
Madry, A., Makelov, A., Schmidt, L., Tsipras, D., and
Vladu, A. (2017). Towards deep learning models re-
sistant to adversarial attacks.
Papernot, N., McDaniel, P., Jha, S., Fredrikson, M.,
Berkay Celik, Z., , and Swami, A. (2015). The limi-
tations of deep learning in adversarial settings. IEEE,
1511.07528v1.
Rao, Q. and Frtunikj, J. (2018). Deep learning for self-
driving cars: Chances and challenges. In 2018
IEEE/ACM 1st International Workshop on Software
Engineering for AI in Autonomous Systems (SEFA-
IAS), pages 35–38.
Sharif, M., Bhagavatula, S., Bauer, L., and Reiter, M. K.
(2016). Accessorize to a crime: Real and stealthy at-
tacks on state-of-the-art face recognition. In Proceed-
ings of the 2016 ACM SIGSAC Conference on Com-
puter and Communications Security, CCS ’16, pages
1528–1540, New York, NY, USA. ACM.
Shrestha, A. and Mahmood, A. (2019). Review of deep
learning algorithms and architectures. IEEE Access,
7:53040–53065.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
350