Exploring Narrative Economics: An Agent-based-modeling Platform
that Integrates Automated Traders with Opinion Dynamics
Kenneth Lomas
a
and Dave Cliff
b
Department of Computer Science, University of Bristol, Bristol BS8 1UB, U.K.
Keywords:
Economic Agent Models, Intelligent Auctions & Markets, Multi-agent Systems.
Abstract:
In seeking to explain aspects of real-world economies that defy easy understanding when analysed via conven-
tional means, Nobel Laureate Robert Shiller has since 2017 introduced and developed the idea of Narrative
Economics, where observable economic factors such as the dynamics of prices in asset markets are explained
largely as a consequence of the narratives (i.e., the stories) heard, told, and believed by participants in those
markets. Shiller argues that otherwise irrational and difficult-to-explain behaviors, such as investors partici-
pating in highly volatile cryptocurrency markets, are best explained and understood in narrative terms: people
invest because they believe, because they have a heartfelt opinion, about the future prospects of the asset,
and they tell to themselves and others stories (narratives) about those beliefs and opinions. In this paper we
describe what is, to the best of our knowledge, the first ever agent-based modelling platform that allows for
the study of issues in narrative economics. We have created this by integrating and synthesizing research
in two previously separate fields: opinion dynamics (OD), and agent-based computational economics (ACE)
in the form of minimally-intelligent trader-agents operating in accurately modelled financial markets. We
show here for the first time how long-established models in OD and in ACE can be brought together to en-
able the experimental study of issues in narrative economics, and we present initial results from our system.
The program-code for our simulation platform has been released as freely-available open-source software on
GitHub, to enable other researchers to replicate and extend our work.
1 INTRODUCTION
In his influential 2017 paper (Shiller, 2017), later
expanded into the successful 2019 book Narrative
Economics: How Stories Go Viral and Drive Ma-
jor Economic Events (Shiller, 2019), Nobel Laure-
ate Robert Shiller introduced the concept of narrative
economics as an overlooked factor in understanding
market trends. In brief, Shiller argues that in many
markets the movement and maintenance of prices are
driven to a significant extent by the stories – i.e., the
narratives – that market participants tell each other.
Shiller draws comparisons between the spread of nar-
ratives and the transmission of infectious diseases,
and argues that financial bubbles and crashes (most
notably in cryptocurrency markets) can plausibly be
accounted for as primarily driven by the narratives
that traders tell each other, even when those narratives
make little sense to outside observers.
a
https://orcid.org/0000-0003-2279-1782
b
https://orcid.org/0000-0003-3822-9364
The narratives told in and about a market are ex-
ternalisations, verbalizations, of the participants’ inte-
rior beliefs or opinions. In this paper, we present the
first results from a novel synthesis of two previously
separate fields that both rely on agent-based mod-
elling: our work combines practices from minimal-
intelligence agent-based computational economics
(ACE) with ideas developed separately in the research
field known as opinion dynamics. We show here for
the first time how existing well-known and widely-
used ACE models of trader-agents can be extended so
that each trader also holds its own independent opin-
ion, which is our minimal approximation model of
Shiller’s notion that real traders are influenced by the
narratives that they hear, read, and tell. In our work,
an individual trader’s opinion may be influenced to
varying degrees by the opinions of other traders that
it interacts with; and the trader’s own opinion also di-
rectly influences its individual trading activity, i.e. the
sequence of bids and/or offers that it quotes into a sin-
gle central financial exchange that all traders in our
model interact with. Our model financial exchange is
Lomas, K. and Cliff, D.
Exploring Narrative Economics: An Agent-based-modeling Platform that Integrates Automated Traders with Opinion Dynamics.
DOI: 10.5220/0010337101370148
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 1, pages 137-148
ISBN: 978-989-758-484-8
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
137

technically a continuous double auction (CDA) mar-
ket operating with a limit order book (LOB), which
is exactly the structure of existing financial markets
such as the New York Stock Exchange, and all other
major national and international financial exchanges.
In keeping with the spirit of minimalism that moti-
vates much ACE work, We show here for the first time
how zero-intelligence (ZI) and minimal-intelligence
(MI) trader-agents can be extended so that each trader
also holds its own independent opinion. For consis-
tency with prior work in opinion dynamics (OD) re-
search, we model each trader’s opinion as a signed
scalar real value, e.g. as a number in the continuous
range [−1.0, +1.0]: this approach is long-established
in OD research, a field that over its multi-decade his-
tory has seen developed a succession of models intro-
duced to explore and/or account for observable pat-
terns of opinion dynamics in human societies. In
our work we have explored the integration of ZI/MI
traders with the following previously-established OD
models: the Bounded Confidence model (Krause,
2000; Hegselmann and Krause, 2002); the Rela-
tive Agreement model (Deffuant et al., 2002; Mead-
ows and Cliff, 2012); and the Relative Disagreement
model (Meadows and Cliff, 2013). We refer to these
three opinion dynamics models as the BC, RA, and
RD models respectively.
The trader-agents that we extend by addition
of these OD models are Gode & Sunder’s (1993)
Zero Intelligence Constrained (ZIC), and the Near-
Zero-Intelligence (NZI) trader agents of (Duffy and
Utku nver, 2006) which minimally extend Gode &
Sunder’s ZI approach in such a way that markets pop-
ulated by NZI traders can exhibit asset-price bubbles.
We refer to the extended agent designs as opinionated
agents: we name our opinionated version of ZIC as
OZIC, and our opinionated version of NZI as ONZI.
For both OZIC and ONZI agents, the bounds of the
probability distribution used to randomly generate a
trader’s bid or offer prices is dependent at least in part
on the current value of that agent’s opinion-variable;
and that opinion variable can change over time as
a consequence of interactions with other traders in
the market, thereby modelling Shiller’s notion of nar-
rative economics: in our system opinions can drive
prices, and prices can alter opinions. To the best of
our knowledge, we are the first authors to report on
such a system, a synthesis of opinion dynamics and
market-trading agents, and so the primary contribu-
tion of this paper is the modelling platform that we
describe for the first time here. The source-code for
our system has been placed in the public domain as a
freely-available open-source release on GitHub.
1
1
github.com/ken-neth/opinion dynamics BSE.git
We evaluate and test the performance of these
trading agents, contrasting and comparing the BC,
RA, and RD opinion dynamics models, using as our
financial-market simulator BSE, a long-established
open-source simulator of a LOB-based financial ex-
change for a single asset, and freely available in the
public domain since 2012 (Cliff, 2018). This paper
summarises (Lomas, 2020), which contains extensive
further visualization and discussion of additional re-
sults that are not included here.
In Section 2 we summarise relevant prior aca-
demic literature. Section 3 describes near-zero-
intelligence traders in more depth. Section 4 then in-
troduces our innovation, the addition of opinions to
trading-agent models, giving opinionated traders, and
results from simulation studies running on our plat-
form are presented in Section 5.
2 BACKGROUND
2.1 Opinion Dynamics
People are complicated. In particular, how ideas are
formed and conveyed to others are difficult to model
as there are numerous factors that could affect the be-
haviour of individuals. Nevertheless we can say, with
some degree of certainty, that people hold opinions
and these opinions are changed by interacting with
the world. Taking this a step further, people commu-
nicate and at some point during or after the commu-
nication their opinions may alter as a consequence.
Given a sufficiently large population we can design
models for how their opinions will change over time,
i.e. models of the system’s opinion dynamics (OD).
Of course these models make clear assumptions and
may not fully encapsulate the inner workings of a per-
son but can nevertheless be useful in understanding
problems relying on the opinions of large populations.
One early OD model is given in (DeGroot, 1974).
In this model, a group of experts have different opin-
ions on a subject and want to reach a consensus. The
experts decide on a format of structured debate where
each individual expert has a turn to express their opin-
ion, taking the form of a real number, and at the end
every expert updates their own individual opinion, us-
ing a fixed weight. The experts continue to take turns
sharing their opinions until a consensus is reached.
(DeGroot, 1974) proves that they will always reach a
consensus given positive weights.
A number of later works have analysed the DeG-
root model. In (Chatterjee and Seneta, 1977) the De-
Groot model’s treatment of the consensus problem is
related to the ergodicity problem in probability theory,
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
138

which concerns stochastic state spaces where from a
given state all possible states are reachable and hence
backwards traversal of the state space is difficult.
The DeGroot model was subsequently analysed
by (Friedkin, 1999), who described experiments to
understand how the model’s mean opinions change
over time. Choice-shifts are shown by the difference
between the final group mean opinion and their ini-
tial mean opinion. These experiments showed how
individuals in the population could have greater influ-
ence on the overall consensus, and Friedkin argued
that choice shifts are an inherent problem in discus-
sions of issues where influence is not balanced.
2.1.1 Bounded Confidence
A variation on the DeGroot model was described in
(Krause, 2000) and named the Bounded Confidence
(BC) model. In this, all agents in a fixed-size popula-
tion hold an opinion that is represented as a real num-
ber. The agents share their opinions and only update
their opinions if they are closer than a given devia-
tion threshold. The reasoning for this is that humans
are less likely to have their opinions swayed by some-
one whose opinion heavily deviates from their own.
A formal specification of the BC model is given in
(Hegselmann and Krause, 2002) and summarised as
follows: given a population of size n, x
i
(t) represents
the opinion of expert i at time t. This is updated by:
x
i
(t + 1) = a
i1
x
1
(t) + a
i2
x
2
(t) + ... +a
in
x
n
(t),
where a
i j
is the confidence factor between experts i
and j. Crucially the confidence factor between two
experts can be zero if the difference in their opinions
are too great. Since at each time step opinions change,
it is possible that at a much later time step two agents
that initially held too-distant opinions can come to be
within a sufficiently close range to start to agree.
At the beginning of a simulation, all opinions
should be distributed over [−1, +1] ⊂ R , with any in-
dividuals holding opinions less than or greater than a
certain extreme value parameter regarded as extrem-
ists. As time progresses, experts whose opinions de-
viate by less than the deviation threshold move closer
together according to a confidence factor. The opin-
ions of the experts will converge until the simulation
reaches a stable state with do further changes.
2.1.2 Relative Agreement
Another well-known Opinion Dynamics model, the
Relative Agreement (RA) model was proposed by
(Deffuant et al., 2000). In the RA model experts hold
opinions, that are each represented as a real number,
but with the difference that they also hold an uncer-
tainty, which acts like a range around their opinion.
The experts communicate and provided the overlap
of their uncertainties exceeds the expert’s individual
uncertainty then they update their opinion and uncer-
tainty by a weight parameter and a Relative Agree-
ment value.
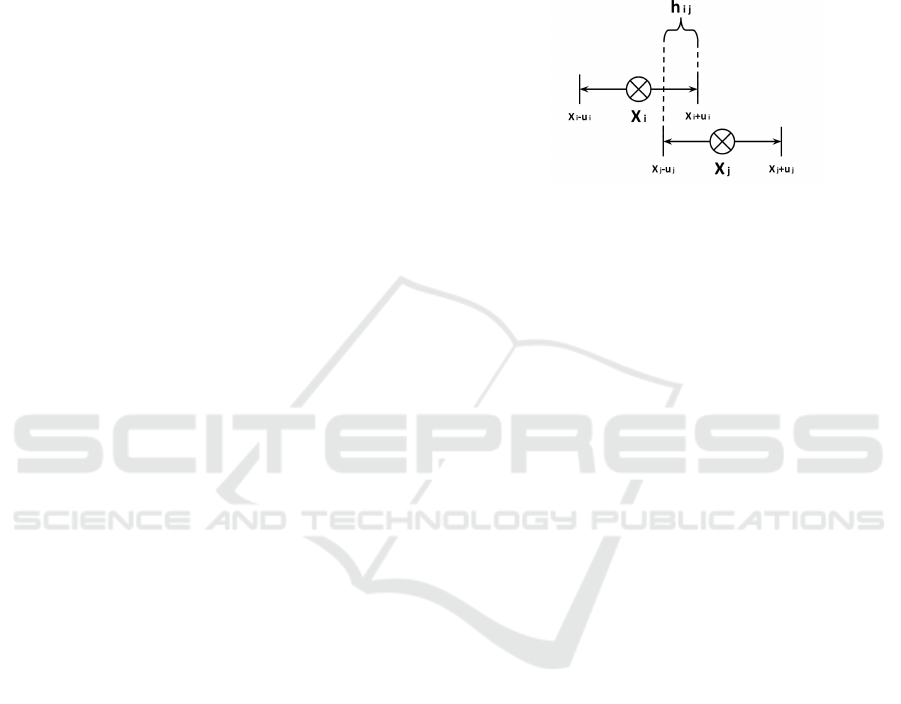
Figure 1: Overlap h
i j
for experts i and j with opinions X
i
and X
j
and uncertainties u
i
and u
j
respectively.
According to the RA model definition in the Def-
fuant et al. 2000 paper, opinions are updated as fol-
lows: a pair of experts i and j are chosen at random
from the population of experts. Firstly, calculate the
overlap h
i j
, as illustrated in Figure 1,
h
i j
= min(x
i
+ u
i
,x
j
+ u
j
) − max(x
i
− u
i
,x
j
− u
j
),
where x
i
is the real number representation of the opin-
ion of expert i, and u
i
is the uncertainty of expert i in
their own opinion. Then, subtract the size of the non-
overlapping part 2u
i
−h
i j
so the total agreement of the
two experts is given by:
h
i j
− (2u
i
− h
i j
) = 2(h
i j
− u
i
),
and so the RA between i and j is given by:
RA
i j
= 2(h
i j
− u
i
)/2u
i
= (h
i j
/u
i
) − 1
Then if h
i j
> u
i
, the update is given by:
x
j
:= x
j
+ µRA
i j
(x
i
− x
j
)
u
j
:= u
j
+ µRA
i j
(u
i
− u
j
)
where µ is a constant parameter for convergence, sim-
ilar to the confidence factor in the BC model. (Def-
fuant et al., 2000) show that the RA model converges
to an average of n = w/2u opinions as opposed to the
BC model that converges to n = floor(w/2u) opin-
ions.
Extremists were added by (Deffuant et al., 2002),
which also describes three modes of convergence that
occur with the RA model: central convergence; bipo-
lar convergence; and single-extreme convergence. As
with BC, at the beginning of an RA simulation all
opinions are randomly distributed over [−1, +1] ⊂ R .
Central convergence appears as all of the opinions
converge towards a stable single central value, around
Exploring Narrative Economics: An Agent-based-modeling Platform that Integrates Automated Traders with Opinion Dynamics
139

zero. In the case where the opinions converge to-
wards two separate values and reach a stable state,
we have bipolar convergence. When all opinions
converge towards an extreme value and reach a sta-
ble state, exceeding a given extreme parameter, we
have single-extreme convergence. In a later paper
(Deffuant, 2006), an asymmetric influence rule is de-
scribed where agents that are more convinced of their
own opinion exert greater influence upon others.
In (Deffuant et al., 2002) a metric is used to mea-
sure the influence of extremists in a population called
the y metric. The y metric, or indicator, is given by
the formula:
y = p
2
+
+ p
2
−
,
where p
+
denotes the proportion of experts that were
initially moderate but held a positive extreme opin-
ion by the end of the simulation, and p
−
denotes the
proportion of experts that were initially moderate but
held a negative extreme opinion by the end of the sim-
ulation. Deffuant et al. use the y metric as an indicator
of convergence type, i.e. central convergence at y = 0,
bipolar convergence at y = 0.5, and single extreme
convergence at y = 1.
2.1.3 Relative Disagreement
The RA model has been shown to successfully simu-
late useful convergences in populations with extrem-
ists initialized. A more recent model, introduced in
(Meadows and Cliff, 2013), and called the Relative
Disagreement (RD) model improves on the RA model
by introducing probability λ of an update occurring
and the idea of reactance. In (Meadows and Cliff,
2013) the RD model was shown to achieve the same
opinion convergences as the RA model without the
need for initialising the population with extremists.
Reactance is the motivation to disagree with an
opinion. In psychology it has been rationalised as a
desire to exercise freedom when that freedom is un-
der threat (Steindl et al., 2015). It is an important part
of how people behave and how they come to hold cer-
tain opinions. The RD model incorporates the idea
of reactance by having individuals’ opinions diverge
when they disagree to enough of a degree. In con-
trast to h
i j
in RA, g
i j
is the non overlapping distance
calculated by:
g
i j
= max(x
i
− u
i
,x
j
− u
j
) − min(x
i
+ u
i
,x
j
+ u
j
)
Subtract the extent of the overlap 2u
i
− g
i j
to give
the total disagreement:
g
i j
− (2u
i
− g
i j
) = 2(g
i j
− u
i
)
The RD between i and j is given by:
RD
i j
= 2(g
i j
− u
i
)/2u
i
= (g
i j
/u
i
) − 1
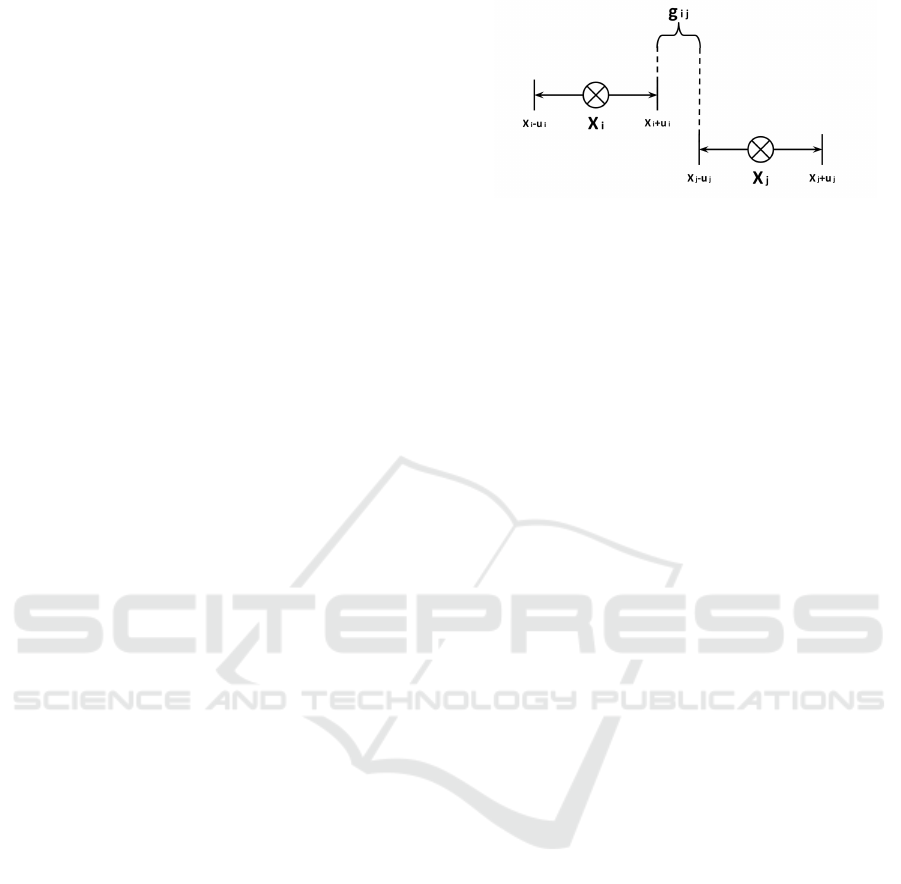
Figure 2: Illustration of non overlapping distance g
i j
for
experts i and j with opinions X
i
and X
j
and uncertainties u
i
and u
j
respectively.
If g
i j
> u
i
, update the opinions and uncertainties with
probability λ, where λ is a parameter.
x
j
:= x
j
+ µRD
i j
(x
i
− x
j
)
u
j
:= u
j
+ µRD
i j
(u
i
− u
j
)
2.2 Markets and Traders
The famous 18th-Century Scottish economist Adam
Smith included a description of what he called The
Invisible Hand in his landmark book (Smith, 1759);
Smith used the term to embody the unintended posi-
tive effects of selfish behaviour in a market. This idea
forms the basis for allocative efficiency, sometimes
thought as the “fairness” of a market. Where utility
is the measure of the usefulness a person gets from
a product, the allocative efficiency of a market is the
total utility gained from trade, expressed as a percent-
age of the maximum possible utility to be gained.
Understanding the details of how selfish interac-
tions among competitive traders in a market can give
rise to desirable outcomes, such as efficient alloca-
tion of scarce resources between producers and con-
sumers, has been a desire of economists ever since
Adam Smith. A major step forward was taken by
American economist Vernon Smith who in the late
1950s started a program of experimental studies of
human traders interacting in markets under repeatable
laboratory conditions – a field that became known as
experimental economics, the founding and growth of
which resulted in Vernon Smith being awarded the
Nobel Prize in Economics in 2002. Much of Smith’s
experimental work studied the dynamics of markets
in which human traders, either buyers announcing
bid-prices or sellers announcing ask-prices, interacted
with one another via a market mechanism known as
the continuous double auction (CDA) which is the
basis of almost all of the world’s major financial mar-
kets. In a CDA a buyer can announce a bid at any time
and a seller can announce an offer at any time, and
any buyer is free to accept an ask at any time while
any seller is free to accept a bid at any time.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
140

In establishing experimental economics research,
Vernon Smith had devised experimental CDA auc-
tions for teaching purposes and later as a tool to ob-
serve how traders in a market act according to differ-
ent specified conditions (Smith, 1962). Vernon Smith
and his fellow experimental economists focused en-
tirely on the interactions among human traders in their
market laboratories but in 1993, inspired by Vernon
Smith’s work, the economists Gode & Sunder devised
experiments to compare the allocative efficiency of
minimally-simple automated trading systems against
human traders. Gode & Sunder’s automated traders
we so simple that they were, entirely justifiably, re-
ferred to as zero-intelligence (ZI) traders. Most no-
tably, in (Gode and Sunder, 1993) the authors de-
scribe the design of a ZI trader known as ZIC (for
ZI-Constrained) which generated random bid or ask
prices, subject to the single budget constraint that the
prices generated should not lead to loss-making deals:
ZIC is constrained by a limit price and so draws its bid
quote price from a uniform random distribution below
the limit price, and its ask quote price from a uniform
random distribution above the limit price.
To everyone’s surprise the allocative efficiency
scores of CDA markets populated by ZIC traders
was demonstrated to be statistically indistinguishable
from those of comparable CDA markets populated
by human traders. Gode & Sunder’s result indicated
to many people that the high intelligence of human
traders was irrelevant within the context of a CDA-
based market, and a research field formed, with var-
ious authors publishing details of automated trading
systems that refined and extended the ZI approach.
Often these early automated traders involved some
means of making the trader adaptive, so that it could
adjust its response to changing market conditions. As
adaptivity to the environment is seen by some as a
minimal signifier of intelligence, adaptive ZI-style au-
tomated trading agents became known as minimal-
intelligence (MI) traders.
Numerous variations on ZI/MI traders have been
proposed to test the limits of their trading perfor-
mance and to provide more human-like trader to test
new trading strategies against. A notable work, which
extended a MI trading strategy to enable the study
of asset price bubbles and crashes, is (Duffy and
Utku nver, 2006), discussed in more detail below.
The primary contribution of this paper is to com-
bine the Opinion Dynamics models with ZI/MI auto-
mated traders, creating a new class of automated trad-
ing strategies: ones that are still zero- or minimal- in-
telligence, but which also hold opinions.
In the 27 years since Gode and Sunder published
their seminal 1993 paper on ZIC, the field of agent-
based computational economics (ACE) has grown
and matured. For reviews of work in this field, see
(Chen, 2018; Hommes, C. and LeBaron, B., 2018).
ACE is a subset of research in agent-based modelling
(ABM), which uses computational models of inter-
acting agents to study various phenomena in the nat-
ural and social sciences: see (Cooks and Heppenstall,
2011) for more details.
2.3 The BSE Financial Exchange
We used the BSE open-source simulator of a contem-
porary financial exchange populated with a number
of automated trading systems. The BSE project is
open source and publicly available on Github, at:
https://github.com/davecliff/BristolStockExchange
(Cliff, 2018).
BSE is a simulated CDA-based financial market,
which is populated by a user-specifiable configura-
tion of various automated-trader systems; it includes
a number of predefined classes of automated trader
each with unique trading strategies.
BSE’s implementation of a CDA, like real-world
financial exchanges, requires buyers and sellers to
submit bid and ask prices simultaneously and contin-
uously onto an exchange mechanism that publishes
the orders to a Limit Order Book, (LOB), each order
(each bid or ask) specifies a price and a quantity. A
transaction will go through when a buyer’s bid price
and a seller’s ask price are the same or ’cross’, i.e. if
a buyer’s bid exceeds a seller’s ask, or a seller’s ask is
less than a buyer’s bid. When the transaction is com-
plete, the orders have been filled hence they are re-
moved from the LOB. On a Limit Order Book (LOB),
the bids and asks are stacked separately on ordered
lists each sorted from best to worst: the best bid is the
highest-priced one and the remaining bids are listed
in decreasing-price order below it; the best ask is the
lowest-priced one and the remaining asks are listed in
ascending-price-order below it.
BSE comes with several types of ZI/MI automated
traders built-in, including Gode & Sunder’s ZIC,
and also Vytelingum’s AA trader (Vytelingum, 2006)
which was demonstrated by (De Luca and Cliff, 2011)
to outpefrom human traders, so an experimental mar-
ket can readily be set up and populated with some
number of traders of each type. However BSE does
not include the Near-Zero Intelligence (NZI) trader-
type introduced by (Duffy and Utku nver, 2006), so
we created our own implementation of that and added
it to BSE: the source-code for that implementation
is available in our GitHub repository, the location of
which was given in the footnote in Section 1. In the
next section we describe NZI traders in more detail.
Exploring Narrative Economics: An Agent-based-modeling Platform that Integrates Automated Traders with Opinion Dynamics
141

3 NEAR-ZERO-INTELLIGENCE
TRADERS
In (Duffy and Utku nver, 2006), NZI traders are de-
fined to mimic the behaviour of traders in markets
where asset prices bubble and crash, i.e. where the
price of a tradeable asset rises quickly and falls pre-
cipitously. As the name implies, NZI traders are sim-
ilar to Gode and Sunder’s ZI traders but have some
added features. The following is a summary of key
aspects of NZI traders.
3.1 The Weak Foresight Assumption
Firstly, Duffy and nver define the weak foresight as-
sumption (WFA) which gives the traders knowledge
that the trading session is coming to an end. This in-
volves two variables:
¯
D
T
t
and π
t
, both of which are
explained further below.
A trading period is defined as 240 seconds where
at the end of a trading period the traders earn a div-
idend per unit of the asset they own. The dividend
amount is a random variable drawn from a uniform
distribution with support: d
1
,d
2
,d
3
,d
4
where {0 ≤
d
1
< d
2
< d
3
< d
4
}. Hence the expected dividend is
given by:
¯
d =
1
4
4
∑
i=1
d
i
At the start of each simulation of T trading peri-
ods, a trader i has a balance of x
i
and owns a number y
i
of units of the tradeable asset. Before the first trading
period, t = 1, we have the equation:
x
i
+
¯
D
T
1
y
i
= c
where c is a constant for all i.
During the simulation of the market sessions,
¯
D
T
t
decreases as t → T . It represents the fundamental
market price or the default value of the asset at pe-
riod t which earns zero profit. It is calculated by the
equation:
¯
D
T
t
=
¯
d(T − t +1) +
¯
D
T
T +1
¯
D
T
t
is a value that decreases by
¯
d each trading period
t, this makes up the first part of the WFA.
The second part of the WFA is π
t
, the probability
of a trader being a buyer in trading period t. It is given
by the equation:
π
t
= max{0.5 − ϕt,0}
where ϕ ∈ [0, 0.5/T ). Since 0 ≤ ϕ <
0.5
T
then 0 < π
t
≤
0.5, and as t → T , the probability of a trader being a
buyer decreases over time; therefore traders are less
likely to buy as time goes by. The combination of
a reduction in tendency to buy, caused by π
t
, and a
decrease in the default value of the asset,
¯
D
T
t
, results
in traders having a “weak” awareness of the future
hence, the name “weak foresight assumption”.
3.2 The Loose Budget Constraint
In (Gode and Sunder, 1993), their ZIC trader has a no
loss constraint. That constraint on ZIC traders forces
them to buy and sell at prices bounded by the intrinsic
value, and transacting at that price would not result in
asset price inflation.
In contrast to Gode and Sunder’s work, (Duffy
and Utku nver, 2006) propose a “loose” budget con-
straint: if trader i is a seller and has an asset, submit
an ask price; and if trader i is a buyer and has suffi-
cient cash balance, submit a bid price:
if trader i is a seller and trader i has an asset then
submit ask
else if trader i is a buyer then
submit min(balance, bid)
end if
3.3 The “Anchoring Effect”
Another departure from (Gode and Sunder, 1993) is
that Duffy & nver’s NZI traders are not entirely zero-
intelligence. In fact they have knowledge of the mean
transaction price from the previous trading period, de-
noted ¯p
t−1
, which is used to calculate the trader’s ini-
tial quote price in a trading period – thus the trader’s
quote price is to some extent “anchored” by the previ-
ous period’s prices. In the first session, ¯p
t−1
= 0, and
the traders submit low quote prices.
3.4 Formal Specification
Simulations involve T market periods or sessions,
t ∈ [1,T ], and within each iteration of each market
session a trader i is chosen to submit an order in se-
quence S, s ∈ S. The uniform random variable u
i
t,s
is
calculated using
¯
D
T
t
via:
u
i
t,s
∈ [ε
t
,
¯
ε
t
]
where ε
t
= 0,
¯
ε
t
= k
¯
D
T
t
and k > 0 is a parameter. The
upper bound of u
i
t,s
,
¯
ε
t
, will decrease over time since
¯
D
T
t
decreases. Therefore the range for u
i
t,s
becomes
smaller and with an average of
1
2
k
¯
D
T
t
, the value of u
i
t,s
should decrease.
If a trader is a seller then offer the ask price a
i
t,s
,
a
i
t,s
= (1 − α)u
i
t,s
+ α
¯
P
t−1
,
where α ∈ (0,1) is a constant parameter. Using the
loose budget constraint so a buyer can only offer as
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
142

much money as they possess, if a trader is a buyer
then offer the bid price b
i
t,s
,
b
i
t,s
= min{(1 − α)u
i
t,s
+ α
¯
P
t−1
,x
i
t,s
}
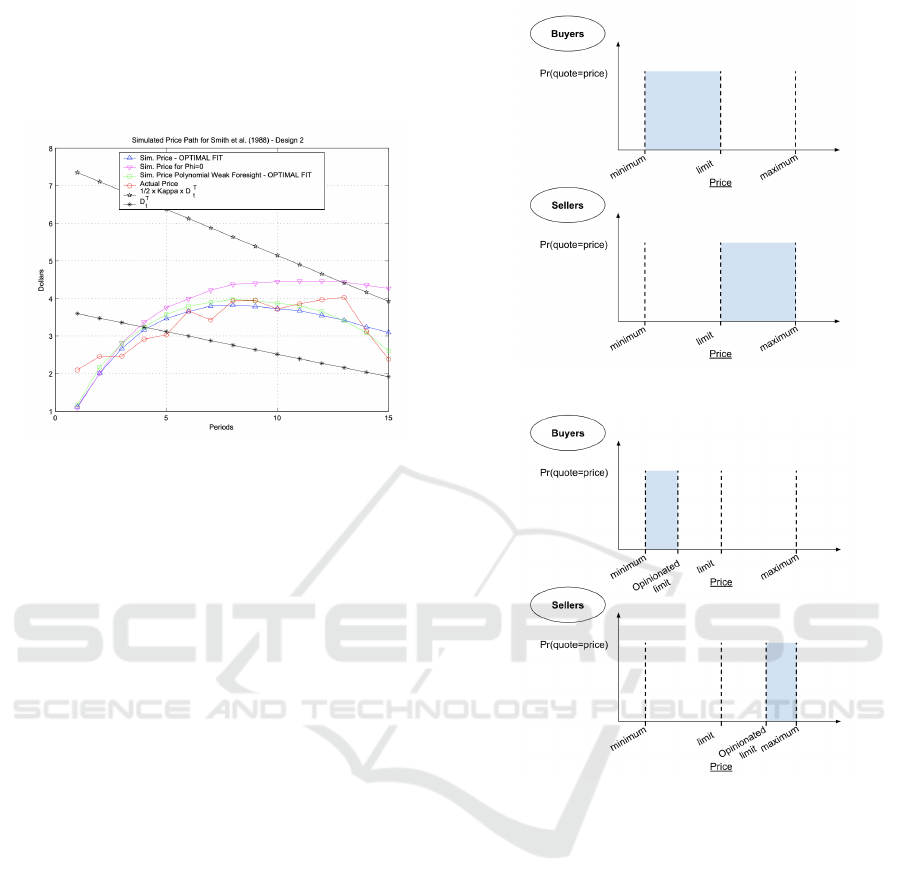
Figure 3: Comparison of mean transaction price path in
the simulations and actual data from (Duffy and Utku nver,
2006).
The combination of a decreasing
¯
D
T
t
value and an
anchoring to the mean transaction price of the pre-
vious trading period
¯
P
t−1
results in a humped shape
pattern in the transaction history. This hump is the
model’s endogenous rise in price, i.e. the ‘bubble’,
followed by a fall or ‘crash’. The mean transac-
tion price per trading period increases initially due to
the high
¯
D
T
t
value which increases the bid and ask
prices above the previous mean transaction price
¯
P
t−1
.
Eventually as the value of
¯
D
T
t
decreases, the mean
transaction price levels out closer to α
¯
P
t−1
which is
less than or equal to
¯
P
t−1
.
4 OPINIONATED TRADERS
We introduce a new variation on the ZIC trader
model, from (Gode and Sunder, 1993), called the
Opinionated-ZIC (i.e., OZIC) trader, that submits
quote-prices affected by its opinion.
The BSE simulator (Cliff, 2018) contains an im-
plementation of the ZIC trader, which has knowledge
of the Limit Order Book (LOB), it sets its minimum
quote price to the worst bid on the LOB, its maxi-
mum quote price to the best ask price on the LOB,
and its limit price to that specified by the customer
order currently being worked on. If the ZIC trader
is a buyer then it submits orders with a quote price
generated from a random draw between the minimum
quote price and the limit price. Otherwise, if the ZIC
trader is a seller then it submits orders with a quote
price generated from a random draw between the limit
(a) Quote price range of ZIC traders.
(b) Quote price range of OZIC traders.
Figure 4: Diagrams of quote price range for Gode & Sun-
der’s Zero Intelligence Constrained (ZIC) Traders in 4a and
for our Opinionated-ZIC (OZIC) Traders in 4b. The shaded
region represents the uniform distribution that the traders’
quote prices are drawn from.
price and the maximum quote price. The quote price
distribution for ZIC traders are illustrated in Figure
4a, with the buyers’ quote price distribution on the left
and the sellers’ quote price distribution on the right.
The Opinionated Zero-Intelligence-Constrained
(OZIC) trader model submits quote prices that vary
according to its opinion. If the OZIC trader is a buyer
and its opinion is negative then it submits a low bid,
and if its opinion is positive then it submits a bid that
is higher but still capped at its limit price. On the other
hand if the OZIC trader is a seller and its opinion is
negative then it submits a low ask, and if its opinion
is positive then it submits a high ask. This models
Exploring Narrative Economics: An Agent-based-modeling Platform that Integrates Automated Traders with Opinion Dynamics
143

the idea that traders will submit quote prices close to
what they believe the actual value of the stock to be,
and if a traders holds a positive opinion of the stock
they would believe the value of the stock to be greater
than a trader holding a negative opinion of the stock.
As illustrated in Figure 4b, the quote price range
for OZIC buyers are between the minimum price and
their opinionated limit, and the quote price range for
OZIC sellers are between their opinionated limit and
the maximum price.
If the OZIC trader i is a buyer then calculate the
opinionated limit OL
i
by:
OL
i
= f (x) =
L(1 + x
i
) + M(1 − x
i
)
2
,
where L is the limit price, M is the minimum price,
and x
i
is the opinion of OZIC trader i: this gives
f (−1) = M; f (0) =
L+M
2
: and f (1) = L. Then gen-
erate a bid quote price as a random draw from the
interval [M, OL
i
].
If the OZIC trader i is a seller then calculate the
opinionated limit OL
i
by:
OL
i
= f
0
(x) =
L(1 − x
i
) +
¯
M(1 + x
i
)
2
,
where L is the limit price,
¯
M is the maximum price,
and x
i
is the opinion of OZIC trader i: this gives
f
0
(−1) = L; f
0
(0) =
L+
¯
M
2
; and f (1) =
¯
(M). Then
bid quote prices are generated as a random draw from
the interval [OL
i
,
¯
M].
4.1 Opinionated NZI Traders
We also introduce here an Opinionated Near-Zero-
Intelligence (ONZI) trader based on the near-zero-
intelligence (NZI) trader model of (Duffy and
Utku nver, 2006). The ONZI trader model offers the
possibility of price bubbles dependent on the prevail-
ing opinions of the population, i.e. if the opinions are
mostly positive then the bubble should be greater than
if the opinions were mostly negative.
4.2 Recreating NZI Trader Model
Duffy & Utku nver’s NZI trader model uses a random
component u
i
t,s
, given by u
i
t,s
∈ [0,k
¯
D
T
t
], where i is
the index of the trader, t is the current trading period
out of T periods, s is the order of the trader in the
sequence that the traders submit orders, k is a constant
parameter, and
¯
D
T
t
is the default value of the asset.
The ask price a
i
t,s
is calculated using u
i
t,s
as described
in Section 3.
In (Duffy and Utku nver, 2006), optimal param-
eter values were calibrated to best match their sim-
ulated data with the data collected from experiments
with human traders. The values are as follows: k
∗
=
4.0846, α
∗
= 0.8480, φ
∗
= 0.01674, and S
∗
= 5. We
use the optimised parameter values k
∗
and α
∗
here-
after, however we have not used φ
∗
because in our
work the buyers and sellers do not change specifica-
tion and we have not used S
∗
as small values of S do
not show opinion convergences in large populations
very well. The ask and bid price of traders are calcu-
lated in such a way that they require the default value
¯
D
T
t
of the asset and the mean transaction price of the
previous trading period
¯
P
t−1
. To get the default value
of
¯
D
T
t
for each trading period t, the expected divi-
dend amount
¯
d is calculated by the average of divi-
dends [0,1,2,3] which is 1.5 and the final value is set
¯
D
T
T +1
= 40. These values form a similar gradient for
¯
D
T
t
over time to that shown in (Duffy and Utku nver,
2006).
4.3 Opinionated Limit
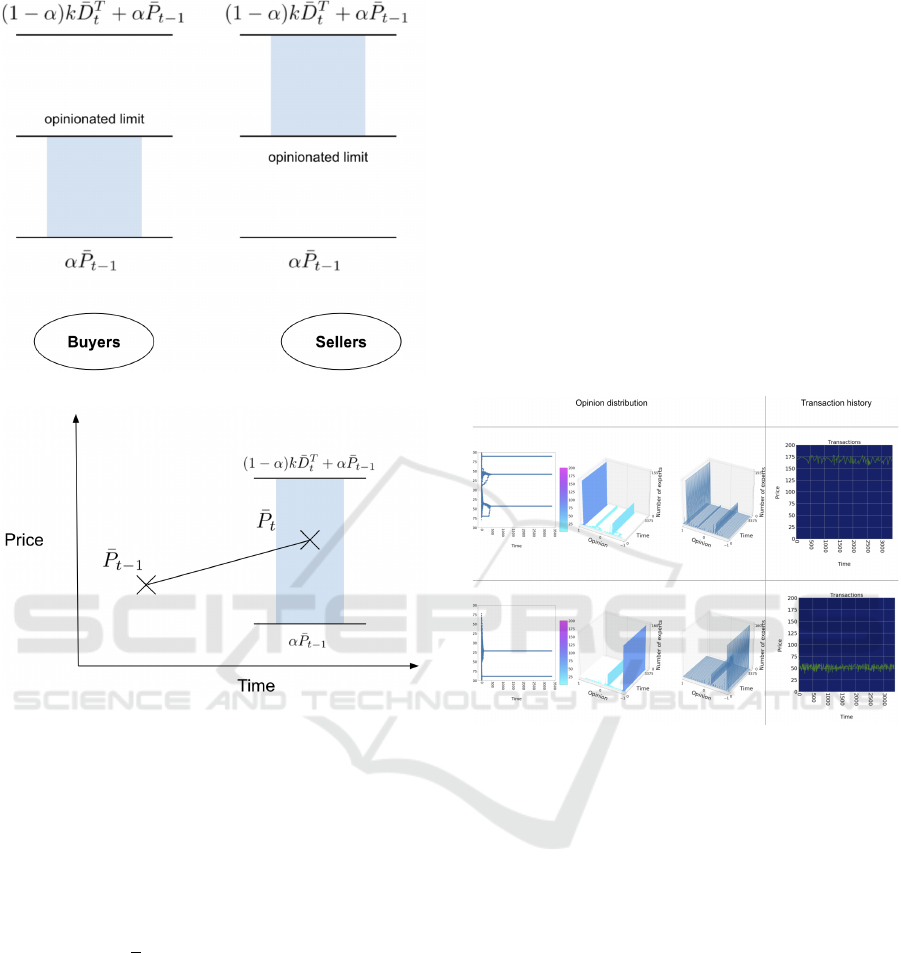
We created an opinionated limit to integrate trader
opinions with the NZI strategies. Similarly to the
opinionated limit calculation in our OZIC trader
model, the opinionated limit of the ONZI trader
model can be calculated from between α
¯
P
t−1
and
(1 − α)k
¯
D
T
t
+ α
¯
P
t−1
, as shown in Figure 5a, because
the maximum u
i
t,s
value is k
¯
D
T
t
. So for an ONZI trader
i, with opinion x
i
, the opinionated limit OL
i
is calcu-
lated by:
OL
i
=
(1 − α)(k
¯
D
T
t
+ α
¯
P
t−1
)(1 + x
i
) + (α
¯
P
t−1
)(1 − x
i
)
2
This form is closest to that of OZIC traders but is eas-
ier to read when expressed in terms of the opinion-
ated uncertainty OU
i
t,s
, based on the definition of u
i
t,s
,
which is given by:
OU
i
t,s
∈ [0,
1
2
k
¯
D
T
t
(1 + x
i
)]
Then the quote price a
i
t,s
is calculated by:
a
i
t,s
= (1 − α)OU
i
t,s
+ α
¯
P
t−1
The effect of the opinionated uncertainty u
i
t,s
is il-
lustrated in Figure 5b, where the value of
¯
P
t
is the
mean transaction price for trading period t. Dur-
ing trading period t, every trader will submit quotes
between α
¯
P
t−1
and (1 − α)k
¯
D
T
t
+ α
¯
P
t−1
so if there
are n transactions that take place at the maximum
(1 − α)k
¯
D
T
t
+ α
¯
P
t−1
then the average
¯
P
t
will be:
1
n
n
∑
((1 − α)k
¯
D
T
t
+ α
¯
P
t−1
) = (1 − α)k
¯
D
T
t
+ α
¯
P
t−1
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
144

(a)
(b)
Figure 5: Diagram of quote price range for Opinionated
near-zero-intelligence (ONZI) Traders in 5a and an illus-
tration of the possible range for the mean transaction price
¯
P
t
of trading period t in relation to the previous mean trans-
action price
¯
P
t−1
in 5b.
Similarly if all transactions in trading period t occur
at the minimum α
¯
P
t−1
, then the average
¯
P
t
will be:
1
n
n
∑
(α
¯
P
t−1
) = α
¯
P
t−1
The shaded region in Figure 5b represents the
range that
¯
P
t
can be in, i.e. between α
¯
P
t−1
and
(1 − α)k
¯
D
T
t
+ α
¯
P
t−1
. The value of
¯
D
T
t
will decrease
hence the range for
¯
P
t
decreases however will roughly
remain centered. In contrast, a population of ONZI
traders will submit high quote prices, close to the
maximum, when they hold positive opinions and will
submit low quote prices, close to the minimum, when
they hold negative opinions.
5 RESULTS
5.1 OZIC Traders
5.1.1 Baseline Results
The more useful results are in the extreme cases of
opinion distribution, i.e. when all the traders hold
extremely positive opinions or negative opinions. In
Figure 6, we have shown the effects of extremely pos-
itive opinion distribution on the transaction history
which is quite high, whereas for an extremely nega-
tive opinion distribution the transaction history shows
very low prices. The results use the RA model with
pe = 0.5 and w = 0.5, and a function that specifies the
distribution of extremists.
Figure 6: OZIC traders with extreme opinions. Upper row
of plots is for traders with extremely positive opinions;
lower row is for traders with extremeley negative opinons.
The plot at far left shows the convergence of opinion values
in the population over time, in the 2D style used by (Def-
fuant et al., 2002) among others – the population converges
to a situation where all traders hold one of three opinions;
the two central plots display the same opinion-distribution
data as 3D plots (heatmap-colored on the left; uncoloured
on the right), which gives a better indication of the number
of traders that hold each converged-upon opinion. The dark-
background plot at far right in each row os the transaction-
price time series from this experiment.
In Figure 7, we have plotted the transaction histo-
ries of OZIC traders with extremely positive opinions,
in orange, and extremely negative opinions, in green.
When compared this way it is clear that the traders
with extremely positive opinions trade at much higher
prices than traders with extremely negative opinions.
5.1.2 Extreme Opinion Shift
We initialise a given proportion of extremists to be ex-
tremely positive or negative initially and switch them
Exploring Narrative Economics: An Agent-based-modeling Platform that Integrates Automated Traders with Opinion Dynamics
145

Figure 7: Comparison of OZIC trader transaction histories
with extremely negative and positive opinions.
to the polar opposite opinion half way through the du-
ration of the simulation. Figure 8 shows the results for
a population of 100 OZIC buyers and 100 OZIC sell-
ers using the RA model with proportion of extremists
pe = 0.5, confidence factor µ = 0.5, and uncertainty
in the range [0.2,2.0].
Figure 8: OZIC traders with extreme shifts in opinion at the
start of Period 6; format as for Figure 6.
The results show a clear change in mean trans-
action price in relation to opinion distribution. For
a positive to negative opinion shift, the traders start
selling and buying at high prices and after t = 1350
drastically shift to lower prices. Similarly for a nega-
tive to positive opinion shift, the traders begin trading
at low prices and after t = 1350 trade at higher prices.
5.2 ONZI Trader Results
5.2.1 Baseline Results
The same rationality for testing the extreme opin-
ion distributions for ONZI traders applies to testing
ONZI traders. With extremely positive opinions, the
shape of the transaction history peaks higher and has
a greater initial gradient than that of ONZI traders
with extremely negative opinions. ONZI traders with
extremely negative opinions show a shorter hump
shaped pattern than the ONZI traders with extremely
positive opinions.
Figure 9: ONZI trader transaction histories with extreme
positive and negative opinions; format as for Figure 6.
In Figures 10 and 11, inspired by a graph in (Duffy
and Utku nver, 2006), we have plotted the transac-
tion histories of the ONZI trader, in orange, against
an ordinary near-zero-intelligence (NZI) trader’s re-
sults, in green. We have also plotted
¯
D
T
over time and
1/2κ
¯
D
T
over time to illustrate the effect it has on the
transaction price over time. The average transaction
price per trading period is also shown to encapsulate
the overall behaviour of the market trends, in red. The
simulated data for NZI traders, in green, tapers off and
does not crash because we are not using a decreasing
proportion of buyers in the population.
The transaction price data for ONZI traders with
extremely positive opinions is very close to the sim-
ulated transaction history of near-zero-intelligence
traders, as shown in Figure 10. On the other hand,
the transaction price data for ONZI traders with ex-
tremely negative opinions is much lower than the sim-
ulated transaction history of near-zero-intelligence
traders, as shown in Figure 11.
5.2.2 Extreme Opinion Shift
Figure 12 shows ONZI traders with extremely posi-
tive opinions until half way through the simulation,
i.e. t = 1350, when the opinions shift to extremely
negative, and vice versa. The opinion dynamics
model used is RA with confidence factor µ = 0.5 and
proportion of extremists pe = 0.5 for both initializa-
tions of extremists. Similarly to the results in Figures
13 and 14, we have plotted the transaction histories of
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
146

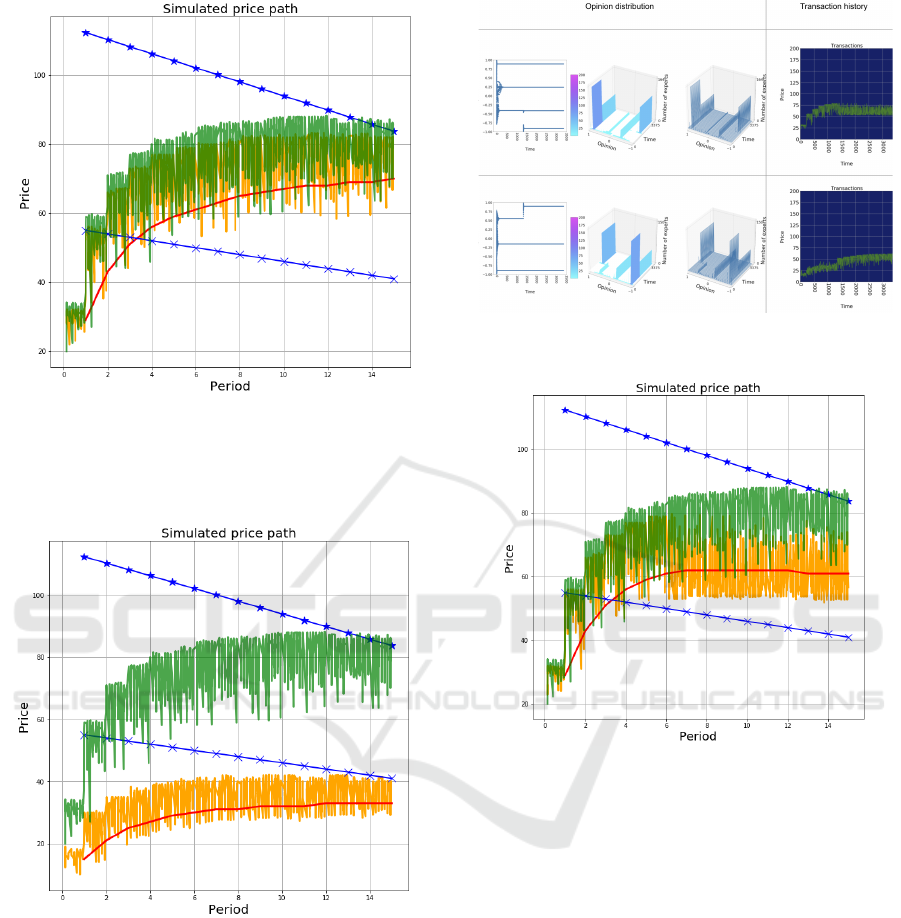
Figure 10: ONZI trader transaction history with extremely
positive opinions; compared to the original NZI results
shown in Figure 3. Yellow lines show transaction history
of traders with extreme positive opinions; green lines are
baseline comparison; red line shows mean transaction price.
Figure 11: ONZI trader transaction history with extremely
negative opinions; compared to the original NZI results as
shown in Figure 3. Color-coding of lines is as for Figure 10.
ONZI traders with drastically shifting opinion distri-
butions against the ordinary NZI traders, the default
value
¯
D
T
, the expected uncertainty 1/2κ
¯
D
T
, and the
mean transaction price per trading period. The mean
transaction price per trading period, in red, is a use-
ful indicator of the trends generated from the opinion
distribution, as the average transaction price over time
increases and decreases according to positive and neg-
ative opinions respectively.
Figure 12: ONZI extreme opinion shifts; format as for Fig-
ure 6.
Figure 13: ONZI traders with extremely positive opinions
drastically shifting to negative opinions at the start of Period
6. Color-coding of lines is as for Figure 10.
6 CONCLUSIONS
In this paper we have described what we believe to be
the first ever system that integrates ideas from opinion
dynamics into well-established trader-agent models,
and in doing so we have created the first platform for
the experimental exploration of agent-based models
of narrative economics. In his seminal work on narra-
tive economics, Nobel Laureate Robert Shiller argues
for a program of empirical research, gathering data on
the stories, the narratives, that humans tell each other
about economic affairs, which shape and change their
opinions about future economic events, and where
those opinions are themselves also significant factors
in the dynamics of economic affairs. Our work opens
up an experimental approach that is complementary
to the one proposed by Shiller: using our platform,
Exploring Narrative Economics: An Agent-based-modeling Platform that Integrates Automated Traders with Opinion Dynamics
147

Figure 14: ONZI traders with extremely negative opinions
drastically shifting to positive opinions at the start of Period
6. Color-coding of lines is as for Figure 10.
experimentalists can now also run agent-based sim-
ulations to better understand the dynamic interplay
between opinions, expressions of those opinions, and
subsequent economic outcomes.
ACKNOWLEDGEMENTS
The work described here was orally presented in Oc-
tober 2020 at an international conference on Zero-
and Minimal-Intelligence Trading Agents held virtu-
ally at the Yale School of Management, Connecticut,
USA. We are grateful to the participants of that meet-
ing for their insightful questions and comments, and
for awarding this work the Best Student Paper prize.
REFERENCES
Chatterjee, S. and Seneta, E. (1977). Towards Consensus:
Some Convergence Theorems on Repeated Averag-
ing. Journal of Applied Probability, 14(1):88–97.
Chen, S. H. (2018). Agent-based computational eco-
nomics: How the idea originated and where it is go-
ing. Routeledge.
Cliff, D. (2018). BSE : A Minimal Simulation of a Limit-
Order-Book Stock Exchange. Proc. European Mod-
elling and Simulation Symposium, pages 194–203.
Cooks, A. and Heppenstall, A. (2011). Introduction to
Agent-Based Modelling. Agent-Based Models of Ge-
ographical Systems, pages 85–105.
De Luca, M. and Cliff, D. (2011). Human-agent auction
interactions: Adaptive-aggressive agents dominate. In
Proceedings of the Twenty-Second International Joint
Conference on Artificial Intelligence.
Deffuant, G. (2006). Comparing Extremism Propagation
Patterns in Continuous Opinion Models. Journal of
Artificial Societies and Social Simulation, 9(3):8.
Deffuant, G., Neau, D., and Amblard, F. (2000). Mixing
Beliefs Among Interacting Agents. Advances in Com-
plex Systems, 3:87–98.
Deffuant, G., Neau, D., and Amblard, F. (2002). How
can extremism prevail? A study based on the rela-
tive agreement interaction model. Journal of Artificial
Societies and Social Simulation, 5(4):1.
DeGroot, M. (1974). Reaching a Consensus. Journal of the
American Statistical Association, 69(345):118–121.
Duffy, J. and Utku nver, M. (2006). Asset Price Bubbles and
Crashes with Near-Zero-Intelligence Traders. Eco-
nomic Theory, 27:537–563.
Friedkin, N. (1999). Choice Shift and Group Polarization.
American Sociological Review, 64(6):856–875.
Gode, D. and Sunder, S. (1993). Allocative Efficiency of
Markets with Zero-Intelligence Traders: Market as a
Partial Substitute for Individual Rationality. Journal
of Political Economy, 101(1):119–137.
Hegselmann, G. and Krause, U. (2002). Opinion dynamics
and bounded confidence: models, analysis and simu-
lation. Journal of Artificial Societies and Social Sim-
ulationn, 5(3):2.
Hommes, C. and LeBaron, B., editor (2018). Computa-
tional Economics: Heterogeneous Agent Modeling.
North-Holland.
Krause, U. (2000). A discrete nonlinear and non-
autonomous model of consensus formation. Proc. 4th
Int. Conf. on Difference Equations, pages 27–32.
Lomas, K. (2020). Exploring narrative economics: A novel
simulation platform that integrates automated traders
with opinion dynamics. Master’s thesis, University of
Bristol Department of Computer Science.
Meadows, M. and Cliff, D. (2012). Reexamining the Rela-
tive Agreement Model of Opinion Dynamics. Journal
of Artificial Societies and Social Simulation, 15(4):4.
Meadows, M. and Cliff, D. (2013). The Relative Disagree-
ment Model of Opinion Dynamics: Where Do Ex-
tremists Come From? 7th International Workshop on
Self-Organizing Systems (IWSOS), pages 66–77.
Shiller, R. (2017). Narrative Economics. Technical Report
2069, Cowles Foundation, Yale University.
Shiller, R. (2019). Narrative Economics: How Stories Go
Viral & Drive Major Economic Events. Princeton Uni-
versity Press.
Smith, A. (1759). The Theory of Moral Sentiments. Penguin
Classics.
Smith, V. (1962). An Experimental Study of Competi-
tive Market Behaviour. Journal of Political Economy,
70(2):111–137.
Steindl, C., Jonas, E., Sittenhaler, S., Traut-Mattausch, E.,
and Greenberg, J. (2015). Understanding Psychologi-
cal Reactance. Zeitschrift fr Psychologie, 223(4):205–
214.
Vytelingum, P. (2006). The Stucture and Behavior of the
Continuous Double Auction. PhD thesis, University
of Southampton.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
148