Distributed Framework for Reversible Merging of Heterogeneous

Robot Maps

Ilze Andersone

Riga Technical University, Kalku Street 1, Riga, Latvia

Keywords: Multi-robot Systems, Robot Map Merging, Heterogeneous Robot Maps, Occupancy Grids.

Abstract: Studies have shown that multi-robot mapping has the benefit of faster environment exploration when

compared to single robot mapping. However, when multiple robots explore the environment simultaneously,

a new problem arises – how to merge the individual robot maps. While there are many map merging methods

developed for homogeneous maps, heterogeneous robot map merging is still a new research area. Another

relatively little researched aspect of map merging is how to deal with an error in the map merging decision.

This paper proposes a map merging framework for the distributed merging of heterogeneous robot maps and

offers two approaches for the further mapping with an emphasis on map merging process reversibility.

1 INTRODUCTION

The environment mapping is a fundamental problem

in the mobile robotics. When multiple robots explore

the environment simultaneously, it is possible to

speed up the mapping process by sharing the maps

between the robots. If the maps are shared, then the

map merging problem must be solved: the match

between the maps must be found and the maps must

be fused together.

Many researchers have dealt with the map

merging problem from the perspective of the map

matching – the search of transformation between the

two source maps. Some examples of such research are

occupancy grid matching (Ko et al, 2003; Carpin,

2008; Li et al, 2012; Liu et al, 2013), feature map

matching (Lakaemper et al, 2005; Dinnissen et al,

2012), and grid-based map matching (Dedeoglu and

Sukhatme, 2000; Bonanni et al, 2017).

However, only few have addressed the problem

of merging heterogeneous maps, which are defined in

(Andersone, 2019) as “two maps are considered to be

heterogeneous in respect to one another, if their

representations of the same environment part are

different, and the differences are caused at least

partially by the robot mapping system (such as map

format, map scale or used sensors)”.

https://orcid.org/0000-0003-1711-9393

Mostly the heterogeneous map merging research

considers the matching of different resolution

occupancy grid maps (Topal et al, 2010; Park et al,

2016). Besides heterogeneous occupancy grid

matching, most other research addresses the fusion of

sparse/dense 3D point clouds, or fusion of a robot

map with prior CAD map (Andersone, 2019).

However, these methods only address specific

map merging steps, but do not consider the

heterogeneous map merging problem as a whole.

Besides the necessity for the appropriate matching

and fusion algorithms there are several additional

aspects that should be considered when merging

heterogeneous maps: such as distributed merging,

decision making about merging attempt, choice of the

map merging method and map quality considerations.

These are addressed in the development of the

proposed map merging framework.

Another little researched aspect of map merging

is the map merging reversibility – a process that

includes dealing with errors in map merging decision.

Some proposed solutions are multi-level map storage

where multiple maps are maintained simultaneously

(Huang and Beevers, 2005, Andersone and

Nikitenko, 2014) or arranging robot meetings to

confirm map merging decisions (Ko et al, 2003).

These are valid solutions, but multiple map

maintenance can be computationally costly, and the

relative position determination is impossible if the

422

Andersone, I.

Distributed Framework for Reversible Merging of Heterogeneous Robot Maps.

DOI: 10.5220/0010342404220430

In Proceedings of the 13th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2021) - Volume 1, pages 422-430

ISBN: 978-989-758-484-8

necessary sensors are unavailable. Therefore, a way

to discard the data integrated from the other robot

without maintenance of multiple maps can be

beneficial, if it is possible without losing significant

data acquired after the map merging.

This paper proposes a map merging framework

for distributed and reversible merging of

heterogeneous robot maps. The most important

contributions of this paper are the following two:

 This paper proposes a general map merging

framework for distributed and reversible

merging of heterogeneous robot maps.

 A special emphasis is put on the reversibility of

the map merging decision. To address this

problem, two approaches how to proceed with

the mapping are offered. For each approach,

both the way to recognize the merging failure

and the approach to exclude the other robot

map’s data is proposed.

The rest of the paper is organized in the following

way. Section 2 gives an overview of the proposed

framework and its main components. Section 3

describes the proposed approaches for further

mapping along with similarity metrics for map

merging error detection. Section 4 is dedicated to the

presentation of the experimental results. Section 5

contains Discussion about the findings, and Section 6

concludes the work and outlines the future work.

2 THE PROPOSED MAP

MERGING FRAMEWORK

To address the problem of reversible and distributed

merging of heterogeneous robot maps, a map merging

framework is proposed with the main steps listed in

Figure 1:

1. Decision making about the map merging

attempt (described in section 2.1);

2. Map matching – the search for transformation

between the maps (described in section 2.2);

3. Map fusion – the incorporation of the other

robot’s map data in the current map if the

matching is successful (described in section

2.2);

4. Further mapping with periodic verification –

the mapping is continued, and it is periodically

checked whether the similarity of merged

maps is still high enough (described in section

2.3);

5. Discarding of the other robot’s map data

(implementation of reversibility) – if the error

in merging is discovered, the other robot’s

map data or part of it is discarded (described

briefly in sections 2.3 and Section 3 in more

detail).

Figure 1: The main steps of the map merging framework.

2.1 Decision Making about the Map

Merging

Depending on the metadata (map types, relative

positions, exchanged data) an appropriate procedure

is chosen for the matching and fusion, or the merge is

rejected if such procedure is not available.

To make a merging decision, a decision table can

be created, where the appropriate procedures for

various parameters are listed. The priority of the

chosen procedure can be determined by the order of

the records in the table, or a priority value may be

assigned to each record. If there is no record in the

table that corresponds to the received metadata, then

the map merging attempt is rejected.

2.2 Map Matching and Fusion

To ensure the distributedness of the map matching

and fusion process, the map matching and fusion must

Distributed Framework for Reversible Merging of Heterogeneous Robot Maps

423

be performed by each robot separately, i.e. the map

from the other robot is fused in the current robot map,

assuming that the map matching is successful. The

robots must be capable of exchanging metadata and

the map data at least once during the mapping.

It should be noted that various algorithms can be

used for both map matching and map fusion

depending from several factors (identified in

(Andersone, 2019): representations of both maps,

mapping algorithm employed by the robot, data and

knowledge about robot’s relative positions. A

detailed review of both homogeneous and

heterogeneous map matching and fusion algorithms

can be found in (Andersone, 2019).

In the case of heterogeneous maps, the integration

of data from lower quality map can decrease the

quality of the higher quality map. To reduce this

problem, the map fusion should take into account the

quality of individual maps by using quality evaluation

methods such as one in (Andersone, 2020).

2.3 Further Mapping and Reversibility

After the map matching and fusion step each robot

continues the exploration independently. During the

continued exploration process the robots should be

able to identify whether the merged maps are still

consistent, or an erroneous fusion has been

performed.

An error the map fusion can happen if a wrong

match of similar environment areas is found between

the two maps. Such errors most often happen when

the environment contains many similar areas (e.g.

similar length and width corridors).

There are two approaches proposed for the further

mapping after the map merging decision is made

(described in more detail in Section 3): further

mapping with multiple maps and further mapping

with a single map.

3 PROPOSED APPROACHES

FOR MERGING

REVERSIBILITY

To support the map merging reversibility two

approaches are proposed:

 Further mapping with multiple maps (multi-

level mapping) similarly to (Huang and

Beevers, 2005, Andersone and Nikitenko,

2014). The concept of this approach is

described in Section 3.1.

 Further mapping with a single map (described

in Section 3.2). In this case, algorithms must

discard the other robot’s data from the merged

map, if the error in merging is found.

Additionally, the use of two metrics to detect map

merging error are proposed in Section 3.3.

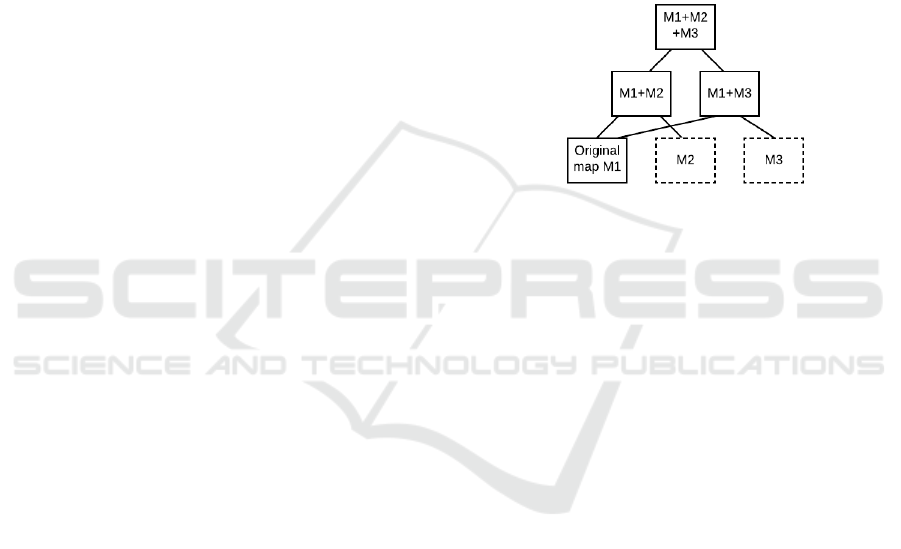
3.1 Mapping with Multiple Maps

The further mapping with multiple maps maintains

separate maps for all updates after map fusion both

for map before merging and after merging (see Figure

2). Additionally, the other maps can be stored for

repeated merging if necessity arises.

Figure 2: Multi-level mapping map hierarchy with 3 maps.

Continuous lines represent updated maps; dashed lines

represent maps, which are stored but not updated.

Mapping with multiple maps has the advantage of

simple recovery from a wrong map merging. If the

dissimilarity is identified, then the merged map can

be discarded without losing any data collected after

the fusion, and only the original map is further

updated. The main drawback of the multi-level

mapping is the necessity to maintain multiple maps at

once, which can be computationally costly.

3.2 Mapping with Single Map

The mapping with single map updates only one map,

which is the fusion of all merged maps. This approach

has the advantage that only one map is updated, and

the computational cost remains manageable.

The main problem with this approach is the

restoration of the original map if the map merging

error is discovered and the discovery of such errors.

To address this problem for occupancy grids, the

author proposes to introduce a local update map (see

Figure 3), where the cells updated at least once by the

robot are marked. Together with original merged

maps, it is easy to determine, which regions have been

affected exclusively by the map whose data should be

discarded due to wrong merging.

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

424

Figure 3: Single-map mapping. Only the merged map and

local update map is maintained.

It is not a perfect solution due to some remaining

data of the wrong merging in areas visited by the

robot, but most often these traces are relatively

insignificant, because the merging decision was made

when the overlap of the maps had high similarity and

the differences were discovered later in the further

mapping.

3.3 Metrics for Map Merging Error

Detection

For the detection of map merging error use of two

metrics is proposed: map similarity metric (SM) and

map distance metric (DM).

The similarity metric SM from (Birk and Carpin,

2006) counts the similar and dissimilar cells in the

common parts of the maps to calculate the overall

similarity of the map (Equation 1).

𝑆𝑀 

𝑠𝑖𝑚𝑖𝑙𝑎𝑟_𝑐𝑒𝑙𝑙𝑠

𝑠𝑖𝑚𝑖𝑙𝑎𝑟_𝑐𝑒𝑙𝑙𝑠  𝑑𝑖𝑠𝑠𝑖𝑚𝑖𝑙𝑎𝑟_𝑐𝑒𝑙𝑙𝑠

(1)

The main drawback of the similarity metric is that

it only considers whether the cells have the same

value (‘occupied’ or ‘free’), but doesn’t take into

account the distance to the closest same value cell in

the other map in the case of dissimilarity. This is

especially problematic if the maps are heterogeneous

and have significant local differences even when the

map merging is performed correctly. Another

problem is the relatively low impact of occupied cells,

which are generally much lower in count.

Another metric in (Birk and Carpin, 2006) based

on distance maps is proposed to aid in the heuristic

search process for map transformations. The map

distance metric DM represents the average Manhattan

distance to the nearest same value cell in the other

map. It is calculated by first creating four distance

maps representing the Manhattan distances to free or

occupied cells in both maps (Figure 4), and then

calculating the average distances between the

significant cells. The occupied cell and free cell

metrics are calculated separately and then summed,

which gives the same weight for free and occupied

cells disregarding their total count.

The map distance metric allows to distinguish

between small and large transformation errors, but it

was created to help in the search process and not to

evaluate the map similarity (Birk and Carpin, 2006).

To adapt the metric for similarity evaluation, a new

step was added – marking of unknown cells (Figure

4.d). Instead of calculating the distance to the nearest

same value cell in the other map for all cells, only the

distances that have significant (not ‘unknown’) value

in both maps are considered.

Figure 4: The main steps of the modified distance map

calculation.

4 EXPERIMENTAL RESULTS

To demonstrate the heterogeneous map merging

process and the merging reversibility, an example

was implemented with the following assumptions:

 The robot maps are occupancy grid maps of the

same environment, and these occupancy grids

have different resolutions. Occupancy grids

represent the environment as an array, where

each cell represents the probability that the

corresponding environment area is occupied by

an obstacle.

 The environment maps are globally accurate

(Schwertfeger and Birk, 2013): the features are

accurately positioned in the global reference

frame. There may be local inaccuracies in

individual maps.

4.1 The Map Matching and Fusion

Algorithms

For the map matching the occupancy grid algorithm

developed by Carpin (Carpin, 2008) was

implemented and used. It was chosen because it is

fast, deterministic, and well suited for the matching

of indoor environment maps. For the maps of

Distributed Framework for Reversible Merging of Heterogeneous Robot Maps

425

different resolution, a map resolution transformation

was performed before the merging.

The maps were fused by Binary Bayes filter cell

update algorithm (Thrun, 2005) with a quality

evaluation method from (Andersone, 2020).

Depending on the quality differences of both map

regions, the Binary Bayes filter update is applied 0-3

times. An example of one map merging attempt is

shown in Figure 5.

Figure 5: An example of a map merging result.

4.2 Data Generation and Experimental

Setup

For the experiments, the map data from the Pre-2014

Robotics 2D-Laser Dataset was used

(http://www.ipb.uni-bonn.de/datasets/) (Haehnel, D).

Maps were updated with a Binary Bayes filter scan

update (Thrun 2005) (the positions are available in

the corrected log files).

From the log files partial maps of two different

resolutions were generated: 7x7cm and 10x10cm

resolutions (further referred to as 0.07 and 0.1

resolutions). Each individual partial map was

generated from 30 consecutive scans with a random

starting point. The map data from (Haehnel, 2003)

contains places that are visited several times, so the

same area with slight differences can be generated

from different scans contributing to heterogeneity of

the maps.

Map merging attempts with three different

resolution combinations were performed: 0.07-0.07,

0.07-0.1 and 0.1-0.07. For each resolution

combination, 20 map mergings were performed with

successful results (correct transformation) and 20

mergings with failed results (wrong transformation).

All mergings had map similarity metric threshold of

0.9 (only results with higher than 90% similar cells

were accepted).

After the map merging, the mapping was

continued by integrating the next 10 scans in either

the merged map (case of further mapping with one

map) or both merged and original map (case of further

mapping with multiple maps).

For each map merging attempt, the similarity

metric (SM) and distance metric (DM) was calculated

both before and after the integration of the additional

10 scans that represent the further mapping:

 In the case of further mapping with multiple

maps both metrics are calculated between the

original map and the other robot’s map.

 In the case of further mapping with single map

both metrics are calculated between the merged

map and the other robot’s map (as the updated

original map is not available).

The goal of similarity metric calculations is to

determine whether failed merging cases can be

correctly identified and reversed.

4.3 Map Merging Results

The acquired map merging results are summarized in

the Tables 1-3. Each value in all tables represents the

average value from 20 merging attempts. The average

metric values both for mapping with single map (1M)

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

426

and two (multiple) maps (2M) are given. The same

partial map sets are used for both cases, so that the

results of map update times are comparable.

Table 1: The similarity metric (SM) and distance metric

(DM) evaluations for 0.07-0.07 resolution maps.

Correct

(

)

Correct

(

)

Wrong

(

)

Wrong

(

)

Initial SM 0,995 0,979 0,990 0,923

End SM 0,986 0,977 0,974 0,910

Initial DM 0,419 1,251 2,485 14,950

End DM 0,883 1,462 5,006 14,570

. time 6,816 10,516 9,512 12,289

Table 2: The similarity metric (SM) and distance metric

(DM) evaluations for 0.07-0.1 resolution maps.

Correct

(

)

Correct

(

)

Wrong

(

)

Wrong

(

)

Initial SM 0,992 0,970 0,991 0,913

End SM 0,982 0,968 0,970 0,896

Initial DM 0,329 1,229 2,202 14,604

End DM 0,754 1,702 4,532 14,656

d. time 7,384 10,709 9,221 12,600

Table 3: The similarity metric (SM) and distance metric

(DM) evaluations for 0.1-0.07 resolution maps.

Correct

(1M)

Correct

(2M)

Wrong

(1M)

Wrong

(2M)

Initial SM 0,989 0,966 0,994 0,909

End SM 0,973 0,956 0,976 0,864

Initial DM 0,518 1,313 2,055 9,979

End DM 1,094 1,678 3,298 10,249

Upd. time 3,395 5,106 4,757 6,321

It can be observed in Tables 1-3 that the average

values of the similarity metric are higher (better) for

the mapping with single map, and the average

distance metrics are higher (worse) for the mapping

with two maps. These results were expected and show

higher similarity for the mapping with single map,

because the metrics are calculated for the other

robot’s map and the merged map, in which the other

robot’s map is already integrated. These differences

demonstrate that the similarity and distance metrics

should be evaluated in the context of the chosen

further mapping approach – single map approach

requires higher similarity values.

The update time comparison in Tables 1-3 show

that the map updates with two maps on average take

longer than the map updates with one map, which

illustrates the point that multi-level map maintenance

is more computationally costly than single map.

Table 4 represents the ranges of similarity and

distance metrics at the end of the further mapping for

both mapping approaches.

Table 4: Similarity and Distance metric ranges for 0.07-

0.07 maps after the further mapping.

Correct

(

)

Wrong

(

)

Correct

(

)

Wrong

(

)

End SM 0,964-

0,999

0,945-

0,996

0,954-

0,999

0,853-

0,956

End DM 0,248-

2,382

0,784-

9,029

0,270-

4,545

3,874-

20,946

It can be seen in Table 4 that both similarity (SM)

and distance metric (DM) ranges for correct and

wrong merges have low overlap for the mapping with

multiple maps (2M), and both metrics can be used for

map merging error detection.

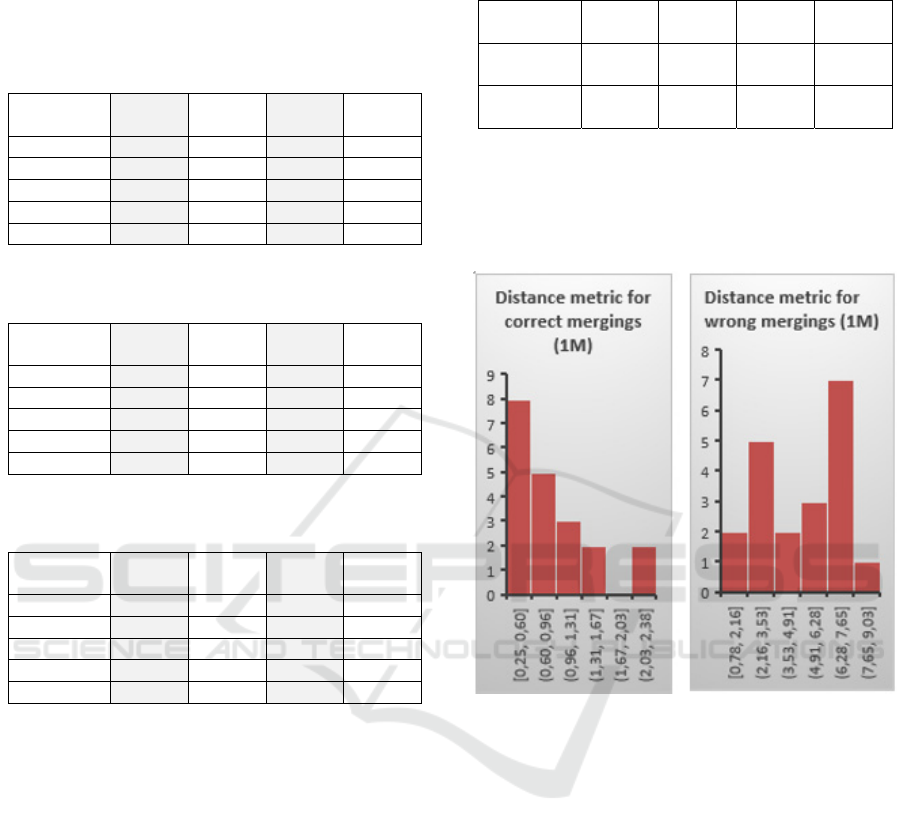
Figure 6: Distance metric histograms for 0.07-0.07 maps

after the further mapping with single map.

On the other hand, similarity metric ranges are

very similar for single map mapping (1M) and

therefore are not useful for the identification of wrong

merges. Instead, the distance metric should be used

for the merging error detection (histograms of

distance metric distribution are shown in Figure 6.

While some false positives and/or false negatives

are present no matter the distance metric threshold,

wrong mergings can be identified relatively

accurately when compared to the use of similarity

metric.

To show the differences between the single and

multi-level mapping reversibility, illustrative

example is given in Figures 7-9. Figure 7 shows the

original maps and their merging result, which is

wrong but exceeds the acceptance threshold of 95%

same value cells. The resolution of the maps M1 and

M2 are 0.07 and 0.1.

Distributed Framework for Reversible Merging of Heterogeneous Robot Maps

427

Figure 7: Example of the original maps and the merging

result. Top: Map1 and Map2; Bottom left: The merging.

Figure 8 shows the two maps maintained by both

mapping approaches after the updates: multi-level

mapping updates both original and merged map while

single map approach only updates the merged map

(top map in Figure 8).

Figure 8: Example of the maintained maps for multi-level

mapping after the updates. Top: The original Map1 with

updates after the merging; Bottom: The Map1 and Map2

merging result with updates after the merging.

Figure 9 shows the resulting maps after the data

of M2 is discarded from the original map M1.

For multi-level approach (Figure 9 top part) that

means that the merged map is discarded and only

original map with updates is kept. For single map

approach (Figure 9 bottom part) the data of M2 is

discarded from the merged map – value of all the cells

not updated locally are reset to ‘unknown’.

It can be seen that the results are quite similar with

only some areas of the single mapping approach

containing corrupted data. This shows that the single

Figure 9: Comparison of the resulting maps without

merging (top) and after single map mapping and reversing

the merging (bottom).

map mapping approach is a valid alternative to the

maintenance of multiple maps if the latter is not

possible due to computational restrictions.

5 DISCUSSION

The experiments and case study shows that it is

possible to implement distributed and reversible

merging of heterogeneous robot maps within the

proposed framework.

While there is no universal solution for

heterogeneous map merging and the experiments

were performed with different resolution occupancy

grid maps, the framework can be used for any type of

heterogeneous map merging as long as the following

requirements are met:

 It must be possible to match the chosen types

of maps. For that, map type-specific matching

algorithms are required, or the match may be

acquired by estimating the robot relative

positions.

 It must be possible to fuse the chosen types of

maps. Specific algorithms must be developed

to fuse different types of heterogeneous maps.

If possible, then the quality evaluation of each

map should be considered when performing the

fusion. For occupancy grid map quality

evaluation and comparison an approach

proposed in (Andersone, 2019) can be used.

 A method to discard the other robot’s data

without significant loss of data collected after

the merging should be available. If such a

method does not exist for the particular map

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

428

type and mapping algorithm, then the map

merging should only be performed when there

is a high certainty about its correctness. This is

especially important with heterogeneous maps,

where the chance of an incorrect match is

higher than for homogeneous maps.

6 CONCLUSIONS

In this paper a map merging framework for

distributed merging of heterogeneous robot maps and

a method for reversible map merging are proposed.

The experimental results with different resolution

occupancy grid maps demonstrate that the framework

can be successfully used for distributed and reversible

heterogeneous map merging.

The research can be continued by developing new

algorithms for the merging of other robot map types,

such as feature maps. For the heterogeneous

occupancy grid map merging the next research

direction is the adaptation of the proposed approach

for various mapping algorithms, such as particle filter

algorithms and graph-based algorithms.

Another area of further research is how to reliably

determine the thresholds for similarity and distance

metrics for both single and multiple map mapping

approaches so that minimal count of false positives

and false negatives is achieved. The main problem is

that these thresholds may vary as they depend on

resolutions and quality of the merged maps.

ACKNOWLEDGEMENTS

This work has been supported by the European

Regional Development Fund within the Activity

1.1.1.2 “Post-doctoral Research Aid” of the Specific

Aid Objective 1.1.1 “To increase the research and

innovative capacity of scientific institutions of Latvia

and the ability to attract external financing, investing

in human resources and infrastructure” of the

Operational Programme “Growth and Employment”

(No. 1.1.1.2/VIAA/1/16/030).

REFERENCES

Andersone I., Nikitenko A., 2014. Reliable multi-robot map

merging of inaccurate maps. In International

Conference on Practical Applications of Agents and

Multi-Agent Systems (PAAMS), pp. 13-24

Andersone I., 2019. Heterogeneous Map Merging: State of

the Art. MDPI Robotics, 8.3:74

Andersone I., 2020. Quality Evaluation of the Occupancy

Grids without Ground Truth Maps. In Proceedings of

the 12th International Conference on Agents and

Artificial Intelligence (ICAART), Vol.1, pp. 319-326

Birk A. and Carpin S., 2006. Merging occupancy grid maps

from multiple robots. Proceedings of the IEEE, vol. 94,

no. 7, pp. 1384-1397.

Bonanni T.M., Della Corte B., Grisetti G., 2017. 3-D map

merging on pose graphs. IEEE Robotics and

Automation Letters, 2, pp. 1031–1038.

Carpin S., 2008. Fast and accurate map merging for multi-

robot systems. Autonomous Robots, 25, no. 3, pp. 305-

316.

Dedeoglu G., Sukhatme G.S., 2000. Landmark-based

matching algorithm for cooperative mapping by

autonomous robots. Distributed Autonomous Robotic

Systems, 4, pp. 251–260.

Dinnissen P., Givigi S.N., Schwartz H.M., 2012. Map

merging of multi-robot slam using reinforcement

learning. In Proceedings of the 2012 IEEE

International Conference on Systems, Man, and

Cybernetics (SMC), Seoul, Korea, pp. 53–60.

Haehnel D., 2003. Intel Research Lab Robotics 2D-

Laserdata set. http://www.ipb.uni-bonn.de/datasets/

Huang W.H., Beevers K.R., 2005. Topological map

merging. The International Journal of Robotics

Research, 24, pp. 601-613.

Kang L., Ye P., Li Y., and Doermann D., 2014.

Convolutional neural networks for no-reference image

quality assessment. In Proceedings of the IEEE

conference on computer vision and pattern recognition,

pp. 1733-1740.

Ko J., Stewart B., Fox D., Konolige K., Limketkai, B.,

2003. A practical, decision-theoretic approach to multi-

robot mapping and exploration. In Proceedings of the

2003 IEEE/RSJ International Conference on Intelligent

Robots and Systems (IROS 2003), Las Vegas, NV,

USA, Volume 4, pp. 3232–3238.

Lakaemper R., Latecki L.J., Wolter D., 2005. Incremental

multi-robot mapping. In Proceedings of the 2005

IEEE/RSJ International Conference on Intelligent

Robots and Systems, Edmonton, AB, Canada, pp.

3846–3851.

Li H. and Nashashibi F., 2012. A new method for

occupancy grid maps merging: Application to multi-

vehicle cooperative local mapping and moving object

detection in outdoor environment. In Proceedings of the

2012 12th International Conference on Control

Automation Robotics and Vision, Guangzhou, China,

pp. 632–637.

Liu, Y.; Fan, X.; Zhang, H. A fast map merging algorithm

in the field of multirobot SLAM. Sci. World J. 2013,

169635.

Ma X., Guo R., Li Y., Chen W., 2008. Adaptive genetic

algorithm for occupancy grid maps merging. In

Proceedings of the 2008 7thWorld Congress on

Intelligent Control and Automation, Chongqing, China,

pp. 5716–5720.

Park J., Sinclair A.J., Sherrill R.E., Doucette E.A., Curtis

J.W., 2016. Map merging of rotated, corrupted, and

Distributed Framework for Reversible Merging of Heterogeneous Robot Maps

429

different scale maps using rectangular features. In

Proceedings of the 2016 IEEE/ION Position, Location

and Navigation Symposium (PLANS), Savannah, GA,

USA, pp. 535–543.

Schwertfeger S., and Birk A., 2013. Evaluation of map

quality by matching and scoring high-level, topological

map structures. In 2013 IEEE international conference

on robotics and automation, pp. 2221-2226.

Thrun S., Burgard W., Fox D., 2005. Probabilistic Robotics,

MIT Press: Cambridge, MA, USA.

Topal S., Erkmen D., Erkmen A.M., 2010. A novel map

merging methodology for multi-robot systems. In

Proceedings of the World Congress on Engineering and

Computer Science 2010, San Francisco, CA, USA,

Volume I, pp. 383–387.

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

430