Privacy Preserving Services for Intelligent Transportation Systems with

Homomorphic Encryption

Aymen Boudguiga

, Oana Stan

, Abdessamad Fazzat

, Houda Labiod

and Pierre-Emmanuel Clet

Université Paris-Saclay, CEA-List, 91120, Palaiseau, France

INFRES, Telecom Paris, Institut Polytechnique de Paris, 91120 Palaiseau, France

Keywords:

Privacy, C-ITS, Homomorphic Encryption.

Abstract:

With the advent of intelligent transportation systems, vehicles will connect continuously to the Internet via the

vehicular core network or the cellular network. Opening vehicles systems to the Internet aims at improving

vehicles safety and comfort via the development of remote services for drivers assistance. Such services are for

example infotainment applications, software update over the air, remote diagnostics and adaptive insurance.

However, some of these services come with an inherent problem of privacy as they require as inputs the

private data from the vehicles. In this work, we investigate the use of homomorphic encryption for ensuring

the conﬁdentiality of vehicles private data. We study the conﬁdentiality of data, which are treated by external

service providers such as cars manufacturers, their stakeholders and insurances. Our protocol ensures, by

design, the private treatment of vehicles data thanks to homomorphic encryption properties. We validate our

proposal by studying drivers behaviour using a simple neural network that takes as input drivers pictures and

tells whether a driver is concentrated or distracted. Indeed, we rely on a 3 layers network for classifying

drivers behavior in 10 different classes from normal to dangerous. We use a quadratic activation function

for intermediate layers which contain 20 and 10 units, respectively. Meanwhile, we use a sigmoid activation

function for the last layer which contains 10 units, one per label. Our classiﬁcation takes 11 seconds with a

classiﬁcation accuracy of 86% and 25 seconds with a classiﬁcation accuracy of 92%.

1 INTRODUCTION

Nowadays, transportation systems are evolving to-

wards autonomous driving. They will beneﬁt from

wireless car-to-car and car-to-infrastructure connec-

tivities provided by upcoming Cooperative Intelligent

Transportation System (C-ITS). The combination of

wireless connectivity and automatic driving capabili-

ties is creating new services not only targeting vehicle

and driver safety but also providing new infotainment

applications. Most of these services rely on collected

data about drivers and their vehicles, and raise new

challenges for personal privacy.

In this work, we target the privacy of drivers us-

ing remote services that collect data from their con-

nected vehicles. The collected data serve to propose

a dedicated remote service to the vehicle driver. By

data, we refer to vehicle position, acceleration peri-

ods, braking frequencies, and in general, all the in-

formation that come from the internal network of a

vehicle (e.g., electronic controllers, drivers installed

applications, vehicle conﬁguration and drivers pref-

erences,. . . ). These data can be exported to exter-

nal entities such as insurances, Original Equipment

Manufacturers (OEM) and their stakeholders or ser-

vice providers. An OEM can be for example Ford

or BMW, a stakeholder entity can be represented by

Bosch or Valeo, and a service provider can be Google

or Apple as they provide Android Auto and Apple

Carplay, respectively.

For example, in the case of a remote service

hosted by an insurance company, the collected data

from the vehicles serve to adapt insurance fees for

a driver if he/she subscribes to a pay-how-you-drive

service. That is, the insurance will compute a driving

proﬁle associated to each driver, using the data col-

lected from his/her vehicle as inputs. Then, the insur-

ance fee is determined by the computed driver proﬁle.

As such, a cautious driver will have a reduction of

his/her insurance fees, while a dangerous driver will

have higher insurance fees.

The collected data from vehicles can also be used

by the OEMs and their stakeholders for vehicle re-

mote diagnostics (e-diagnostics) and for proposing

684

Boudguiga, A., Stan, O., Fazzat, A., Labiod, H. and Clet, P.

Privacy Preserving Services for Intelligent Transportation Systems with Homomorphic Encryption.

DOI: 10.5220/0010349706840693

In Proceedings of the 7th Inter national Conference on Information Systems Secur ity and Privacy (ICISSP 2021), pages 684-693

ISBN: 978-989-758-491-6

software updates over the air. For example, the e-

diagnostics service classiﬁes drivers as good or bad

with respect to the state of wear of their vehicles.

This classiﬁcation serves to predict possible damages

that will happen to vehicles and so, these service

providers will adapt accordingly their offer to their

clients. In addition, OEMs are interested in collect-

ing data from several vehicles simultaneously to make

statistics about breakdowns that touch a common de-

vice in their produced vehicles.

The Software update over the air is a critical ser-

vice as it discloses information about the current ver-

sion of software installed in vehicles’ controllers.

This information is too valuable for hackers as it al-

lows them to choose with scrutiny their attacks with

respect to the current software vulnerabilities.

Finally, the collected data from vehicles can also

be used by vehicular service providers such as Google

and Apple to create proﬁles of drivers. These proﬁles

will then serve to target drivers with personalized ap-

plications.

Problem Statement. The major problem of vehicu-

lar services is the sensitiveness and the privacy of the

collected data from vehicles. For example, this infor-

mation can be used by a malicious entity to recover

drivers home location or their habits of traveling. In

addition, current regulation efforts regarding the con-

ﬁdentiality of personal data such as the EU 2016/679

General Data Protection Regulation (GDPR) consider

collected data from connected vehicles as private and

so their treatment must be conﬁdential and must pro-

tect drivers and passengers privacy.

Contribution. In this work, we propose to use ho-

momorphic encryption to ensure the conﬁdentiality

of the remote treatment of vehicles private data and

so, ensure drivers and passengers privacy. We investi-

gate two deployment options. First, we make each

vehicular service provider compute a function over

the driver’s encrypted inputs, and then return an en-

crypted result to the concerned driver. Second, we ex-

tend the existing connected vehicle architecture with

honest-but-curious third parties that will be in charge

of homomorphic computation. These third parties

will analyse a vehicle private data and return a re-

sult to the interested entity (e.g. an OEM or an in-

surance). That is, the OEMs, the stakeholders or the

insurances will never have access to the private data

collected from vehicles. Finally, we give some per-

formance indicators about current homomorphic en-

cryption schemes when they are used for drivers data

analysis. To do so, we consider as example a remote

service for detecting distracted drivers. We rely on

an open access dataset with different drivers videos

to train a simple neural network for drivers behaviors

classiﬁcation

. Once the training is ﬁnished, we clas-

sify drivers using their encrypted features.

Paper Organization. Section 2.1 reviews the main

components of a C-ITS architecture. Section 2.2 de-

ﬁnes the basic concepts of homomorphic encryption.

Section 2.3 presents the related works on privacy-

preserving services for ITS and vehicular networks.

Section 3 speciﬁes our protocol for ensuring privacy-

preserving vehicular services. Section 4 presents the

experiments conducted to validate our proposal and

discusses the obtained performance results. Finally,

Section 5 concludes the paper with future perspectives

and improvements.

2 BACKGROUND

In this section, we ﬁrst describe the Cooperative In-

telligent Transportation System (C-ITS) architecture.

Then, we introduce homomorphic encryption. In ad-

dition, we review the state of the art on privacy pre-

serving vehicular services. Finally, we present the no-

tations followed in this work.

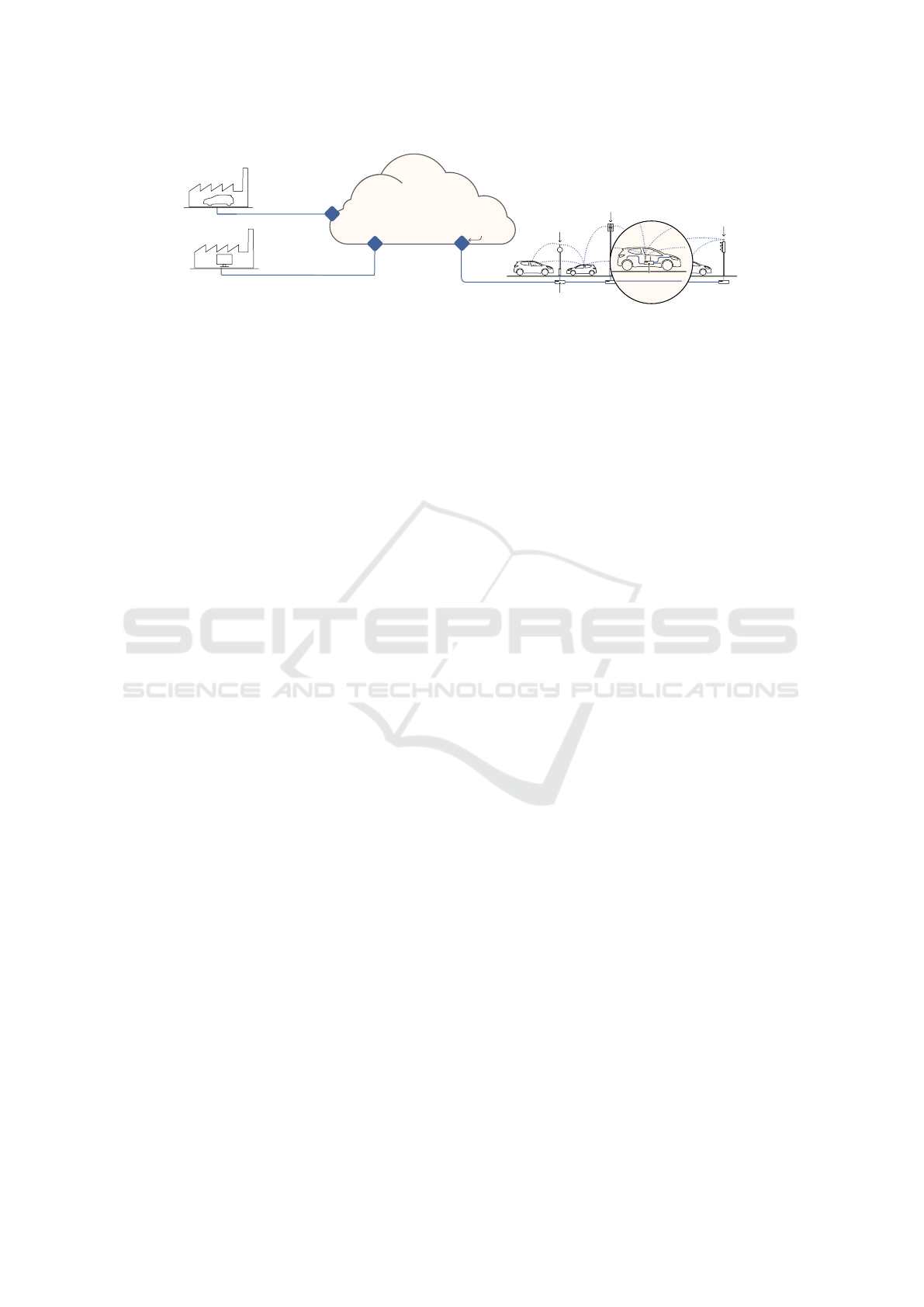
2.1 ITS Architecture

Figure 1 depicts the components of a Cooperative In-

telligent Transportation System (C-ITS). C-ITS re-

lies on two types of access points: Road Side

Units (RSUs) installed on roads and On-Board Units

(OBUs) embedded in cars. RSUs are gateways to

the core network. Meanwhile, OBUs are gateways to

vehicles internal networks that connect several Elec-

tronic Control Units (ECUs). An OBU serves also as

interface to the extra-vehicle network such as 4G/5G,

GPS or IEEE802.11p (IEEE standard 802.11p, 2010).

The vehicle embedded network is formed by vari-

ous communication buses such as automotive Ether-

net (IEEE Std 100 Base T1, 2018), FlexRay (FlexRay,

2010), MOST (Grzemba, 2011), LIN (ISO-17987-3,

2016) and CAN (Bosch, 1991).

Intelligent vehicles will communicate either with

other vehicles (V2V) or with the roadside infras-

tructure (V2I) using IEEE802.11p or LTE/5G-V2X

(IEEE standard 802.11p, 2010; Molina-Masegosa

et al., 2020; Sharma et al., 2019). V2X communi-

cations provide road safety and improve trafﬁc con-

We use the State Farm dataset pro-

vided by Kaggle (https://www.kaggle.com/c/

state-farm-distracted-driver-detection). State Farm is

an insurance that works on improving alarming to better

insure its customers’ safety. For example, State Farm

studied whether dashboard cameras can help on detecting

distracted drivers.

Privacy Preserving Services for Intelligent Transportation Systems with Homomorphic Encryption

685

Internet

Onboard Unit (OBU)

Road Side Units (RSU)

4G/5G

802.11p

Gateway

Intelligent Transport System

Original Equipment

Manufacturer (OEM)

Insurances,

stackholders,...

Vehicular Service Providers (VSP)

Figure 1: Cooperative Intelligent Transportation System Architecture.

ditions. V2X messages must come from trustworthy

parties and only authorized entities can access their

contents. Indeed, the standard IEEE1609.2 (IEEE Std

1609.2, 2016) speciﬁes the security requirements for

V2X communications. It provides messages integrity

and non-repudiation thanks to the use of digital signa-

tures and ensures drivers privacy by using pseudony-

mous certiﬁcates. However, using pseudonymous cer-

tiﬁcates will not prohibit Vehicular Service Providers

(VSP) from accessing drivers personal data at the ap-

plication level. Indeed, pseudonymous certiﬁcates

serve mainly to thwart network level attacks such as

drivers tracking using V2X messages.

In this work, we demonstrate that homomorphic

encryption can be an effective solution to the inherent

privacy problem of vehicular services. Indeed, these

services are strongly dependant on the driver proﬁle

and require access to his/her personal data. Fortu-

nately, homomorphic encryption allows computation

over encrypted data and so, can serve to implement

privacy-preserving vehicular services. In addition, as

vehicular services such as pay-how-you-drive or e-

diagnostics do not have hard real-time constraints, the

use of homomorphic encryption seems convenient.

Recent works introduced Unmanned Aerial Vehi-

cles (UAV) as part of the C-ITS architecture (Mes-

sous et al., 2017; Garg et al., 2018). UAVs provide

vision as a service for vehicles. They offer better traf-

ﬁc trajectory and load analysis. In addition, they are

supported by the use of Edge servers which extend

the C-ITS cloud. Indeed, it is impractical to trans-

mit data from millions of vehicles to data centers in

the cloud for processing due to latency and band-

width constraints. The use of Edge servers ensures

faster information analysis, decision making and a

quick response to vehicles. That is, instead of carry-

ing their complex computation in a dedicated server

on the cloud, intelligent vehicles will ofﬂoad their

computations to the neighboring Edge nodes. The

use of Edge servers is advantageous for homomor-

phic encryption applications, as these nodes can carry

out some cumbersome homomorphic operations such

as tranciphering, i.e. a cryptographic technique for

switching from symmetrically encrypted data to ho-

momorphic data without access to the clear messages

(see details below). This allows not only to delegate a

part of the computation from the homomorphic com-

putation servers but also to keep a lightweight sym-

metric encryption on the vehicles side (with usually

limited embedded resources) and moreover to save on

the network bandwidth.

2.2 Homomorphic Encryption

In 2009, Gentry (Gentry et al., 2009) made a break-

through in cryptography by proposing the ﬁrst Fully

Homomorphic Encryption (FHE) scheme. That is,

Gentry speciﬁed a homomorphic encryption scheme

E that computes E(m

+ m

) and E(m

× m

) from

encrypted messages E(m

) and E(m

). Then, many

leveled HE and FHE schemes have been proposed in

the literature (Brakerski and Vaikuntanathan, 2011;

Brakerski et al., 2012; Fan and Vercauteren, 2012;

Van Dijk et al., 2010; López-Alt et al., 2012; Chillotti

et al., 2016; Cheon et al., 2016). In practice, a

public key homomorphic encryption scheme HE =

(HE.Keygen, HE.Enc, HE.Dec, HE.Eval) is deﬁned

by a set of probabilistic polynomial-time algorithms

with respect to the security parameter k:

• (pk,evk, sk) ← HE.Keygen(1

): outputs an en-

cryption key pk, a public evaluation key evk and

a secret decryption key sk. The evaluation key is

used during homomorphic operations. This key

evk corresponds to the relinearization key in lev-

eled homomorphic schemes such as BFV (Fan

and Vercauteren, 2012) or to the bootstrapping

key in gate boostrapped schemes such as TFHE

(Chillotti et al., 2016).

• c ← HE.Enc

(m): encrypts a message m into a

ciphertext c using the public key pk.

• m ← HE.Dec

(c): decrypts a message c into a

plaintext m using the secret key sk.

• c

← HE.Eval

evk

(f,c

,.. .,c

): evaluates the func-

tion f on the encrypted inputs c

,.. .,c

using the

evaluation key evk.

ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy

686

Nowadays, we can mix several FHE schemes (e.g.

BFV, TFHE, CKKS (Cheon et al., 2016), etc.) using

the CHIMERA framework (Boura et al., 2018). As

for the overhead induced by the size of the homomor-

phic ciphertexts during their transmission and stor-

age, we can use transciphering (Canteaut et al., 2015;

Albrecht et al., 2016; Hoffmann et al., 2020). This

cryptographic technique changes the data encryption

algorithm from a classical symmetric encryption to

a HE scheme, without decrypting the data. Let m

be a plaintext, SYM a symmetric scheme with key

k, SYM.Enc

(m) the encryption of m with SYM,

and HE a homomorphic encryption scheme. With

the transciphering, it is enough to run in homomor-

phic domain the decryption circuit of SYM.Dec using

the homomorphic encryption of the symmetric key

HE.Enc

(k) to obtain the message encrypted with

pk:

HE.Eval

evk

(SYM.Dec

HE.Enc

(k)

(SYM.Enc

(m))) =

HE.Enc

(m)

Tranciphering is well ﬁtted to the C-ITS architec-

ture as the intelligent vehicles can encrypt their pri-

vate data using a lightweight symmetric encryption

scheme. Then, they outsource the cumbersome ho-

momorphic encryption to a more resource abundant

party such as an RSU, an Edge server or a honest-but-

curious third party.

As for the application of the homomorphic tech-

niques to the private inference step of neural networks

notable works include, in a non-exhaustive way,

CryptoNets (Dowlin et al., 2016), DiNN (Bourse

et al., 2018), nGraph-HE (Boemer et al., 2018),

LOLA (Brutzkus et al., 2019), TAPAS (Sanyal et al.,

2018), Faster CryptoNets (Chou et al., 2018). Most

of these work are validated over MNIST dataset and

none of them addresses our considered use-case.

2.3 C-ITS Privacy State of the Art

The main privacy concern in the ITS context is re-

maining anonymous and untraceable at the network

level (Petit and Kargl, 2018). The standardization

solution to this issue is signing V2X messages with

short-term pseudonym certiﬁcates which are managed

by a dedicated Public Key Infrastructure (PKI). Vehi-

cles will change periodically their certiﬁcates from a

small pool of pseudonyms. A larger pseudonym pool

size enhances privacy but weakens efﬁciency and re-

sistance against Sybil attacks.

Neven et al., (Neven et al., 2017) proposed a

generic approach for C-ITS authentication based on

privacy-preserving Attribute-Based Credential that

generates pseudonyms locally on the vehicle. Their

approach enhances the frequency of pseudonym

changing while keeping a low exposure against Sybil

attacks. Unfortunately, their scheme does not meet

the efﬁciency requirements of real-world C-ITS sce-

narios such as data latency and bandwidth saturation.

Other solutions have been proposed to ensure lo-

cation privacy (Kido et al., 2005; Wang et al., 2019;

Zhao and Wagner, 2019; Asuquo et al., 2018). Their

approaches consist mainly in using anonymization

and obfuscation techniques. For example, Ghane et

al., (Ghane et al., 2020) addressed the issue of loca-

tion privacy when the data transportation infrastruc-

ture between C-ITS stations is untrusted. They pro-

posed a Differentially Private Data Streaming (DPDS)

system. DPDS consists of adding a correlated noise

to data before their exchange.

Let us consider now the state of the art regard-

ing the privacy of vehicular services at the applica-

tion level. In 2011, Troncoso et al., (Troncoso et al.,

2011) proposed to install a secure hardware, namely

a black box in vehicles to compute the insurance fees

locally. The obtained fees are transmitted later to in-

surances for billing. As such, vehicles private data are

kept secret from insurances. The authors also deﬁned

a black box auditing mechanism to verify that neither

the insurance nor the owner of the vehicle attempted

to modify the calculated fees. Indeed, they store the

data used to calculate insurance costs on an auxiliary

storage. The data are encrypted using a split key be-

tween the vehicle owner and the insurance. In case of

a dispute, the vehicle owner and the insurance com-

bine their split key to decrypt the auxiliary storage and

check how the insurance fee has been computed.

In 2013, Kargl et al., (Kargl et al., 2013) used dif-

ferential privacy techniques to protect Floating Car

Data (FCD). Höfer et al., (Höfer et al., 2013) pro-

posed a privacy preserving charging for electrical ve-

hicles called POPCORN. They relied on group signa-

ture and anonymous credentials to enhance the ISO

15118 norm that speciﬁes protocols for smart charg-

ing. POPCORN ensure the privacy of vehicles loca-

tion.

In 2015, Rizzo et al., (Rizzo et al., 2015) proposed

a technique to train a decision tree to classify drivers

behavior (as aggressive or defensive), while preserv-

ing the privacy of collected data and the conﬁden-

tiality of the decision tree computed by the insurance

company. They used a secure version of the ID3 al-

gorithm to build the decision tree by using the homo-

morphic properties of Paillier’s cryptosystem (Pail-

lier, 1999). They also relied on Paillier’s cryptosys-

tem homomorphic properties during the classiﬁcation

phase. In 2019, El Ormi et al., (Omri et al., 2019)

proposed a privacy preserving k-means clustering for

driving style recognition. They relied on multiparty

Privacy Preserving Services for Intelligent Transportation Systems with Homomorphic Encryption

687

computation for computing the distances to clusters

centroids. Meanwhile, they used Paillier’s cryptosys-

tem during the computation of the new centroids.

That is, as for Rizzo et al., they only needed an ho-

momorphic additive scheme to add ciphertexts.

Also an approach using semi-private function

evaluation and based on Yao’s Garbled circuits is pro-

posed in (Günther et al., 2019) for the calculation

of tariff of car insurance companies while hiding the

user’s data as well as the insurance’s private data.

In this work, we beneﬁt from the properties of

fully homomorphic encryption to evaluate drivers

classiﬁcation algorithms using a simple neural net-

work with quadratic and sigmoid activation functions.

2.4 Notations

In the following sections, we denote vectors by bold

letters, for example x. Each vector x of n elements

can be represented as: x = (x

,.. .,x

). The trans-

pose of a vector x is denoted x

. As such the dot

product between two vector x and y is expressed as:

hx,yi = x

·y. We denote by M

m,n

(K) the set of matri-

ces with m rows and n columns with entries sampled

in K. Matrices are represented by capital letters. X

the transpose of the matrix X.

3 PRIVACY PRESERVING

SERVICES FOR C-ITS

In this section, we ﬁrst present our considered threat

model. Then, we specify our privacy preserving pro-

tocol for the private treatment of a vehicle’s data.

3.1 Threat Model

In this work, we consider a honest-but-curious model

(also called the semi-honest model). In this model,

many entities (E

,.. .,E

), having as secret informa-

tion (s

, . . . , s

), participate to a protocol P to com-

pute a function F(s

,.. .,s

). Each entity E

i,i∈[1,n]

honest and must follow each step of P. However,

i,i∈[1,n]

is curious. That is, E

i,i∈[1,n]

will try to ﬁnd

information about other entities secrets s

j,j6=i

. P is se-

cure in the honest-but-curious model if each E

i,i∈[1,n]

has no other information than F(s

,.. .,s

) at the end

of the protocol.

In the honest-but-curious model, the adversary

cannot inject modiﬁed message as in the Dolev and

Yao model (Dolev and Yao, 1981). In addition, using

a honest-but-curious adversary avoids message mod-

iﬁcation attacks against homomorphically encrypted

data. Indeed, as homomorphic encryption schemes

are malleable by deﬁnition, a malicious adversary is

able to modify the content of encrypted data.

In this work, vehicle service providers (VSP) will

be honest-but-curious. We discuss hereafter two ways

for the deﬁnition of our privacy preserving service for

C-ITS:

1. Each vehicle encrypts its own data using its public

key before sending them to the VSP. The VSP will

then compute the required output on encrypted

data. Finally, the VSP sends the computation re-

sult to the vehicle for decryption. It is up to the

vehicle to send the decryption result to the VSP.

One disadvantage of this approach is that each ve-

hicle will have to maintain a pair of public and

private keys for homomorphic encryption. That

is, we will need to deploy a public key infrastruc-

ture dedicated to managing the homomorphic en-

cryption keys needed by millions of vehicles.

2. Each vehicle encrypts its own data using the

VSP public key before sending them to a honest-

but-curious Homomorphic Computation Server

(HCS). The latter is in charge of evaluating the

VSP algorithm over the encrypted data. Then, the

HCS sends the encrypted output to VSP which re-

covers the result in clear after decryption. In this

case, we assume that the VSP and the HCS do

not collude. Indeed, if they collude, they recover

the vehicles data. Note that a HCS can perform

several homomorphic computations on behalf of

different VSP, simultanouesly.

We prefer this approach because it has the advan-

tage of restricting the deployment of homomor-

phic encryption keys only to VSPs.

We consider that all vehicles are honest entities.

If we consider that vehicles are semi-honest (i.e.

honest-but-curious), a vehicle may try a passive attack

against the computed function by the HCS. Indeed, a

semi-honest vehicle can use the HCS as a computa-

tion black box. The semi-honest vehicle provides it

with inputs and recovers an associated output. If the

computed function is simple, the semi-honest vehicle

may attempt to approximate it by computing an in-

terpolation with its stored inputs and their associated

outputs.

Finally, we assume that the used homomorphic en-

cryption schemes are well implemented and do not

suffer from implementation errors as those pointed by

Peng (Peng, 2019). In addition, we focus here on en-

suring the conﬁdentiality of data in use and do not

consider other security properties such as entities au-

thentication or message integrity validation. We con-

sider that "classical" cryptographic mechanisms are

ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy

688

sufﬁcient to provide such properties

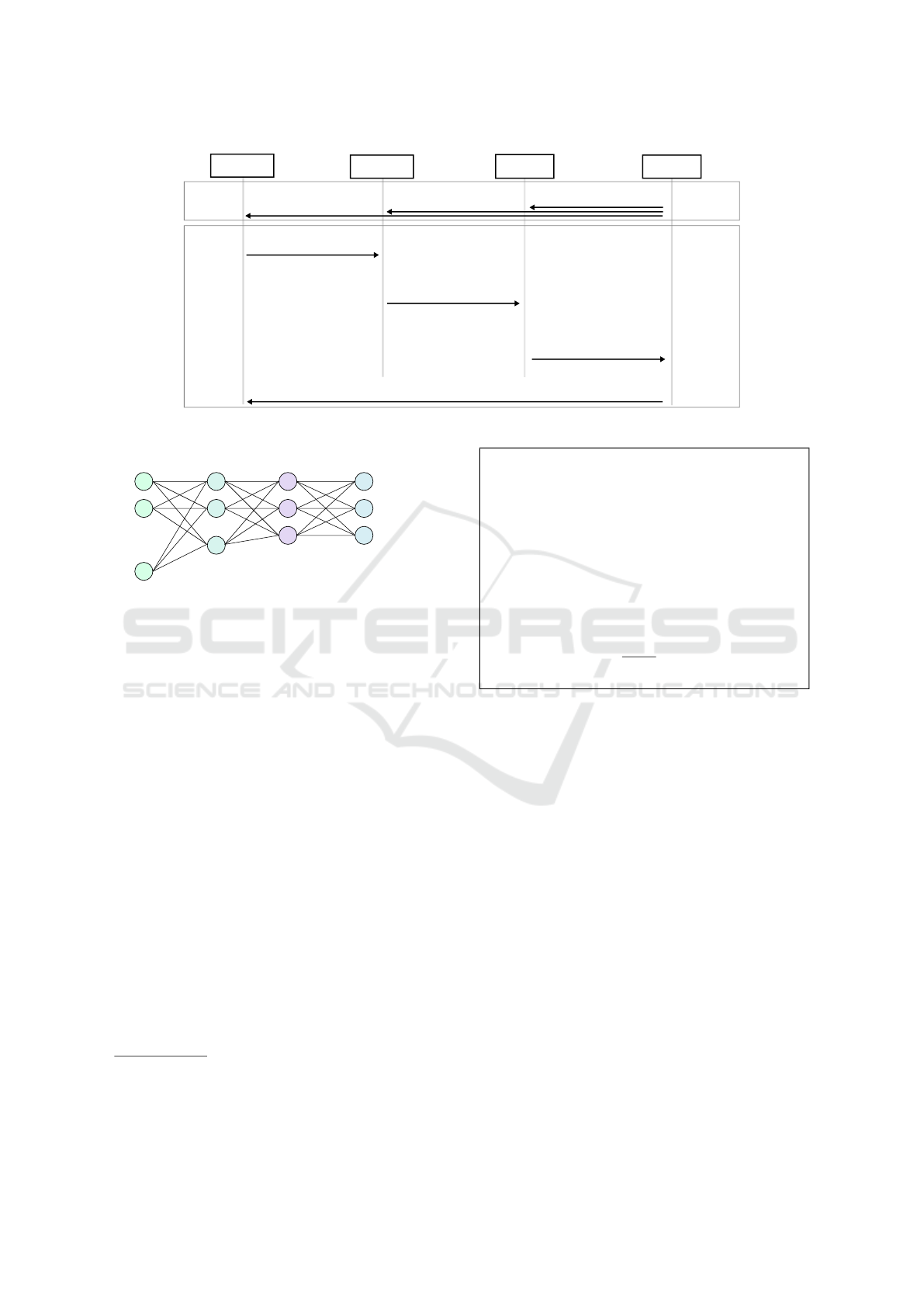
3.2 Protocol Description

We specify in this section our protocol for providing

a privacy preserving C-ITS service. Our main idea is

to add a Homomorphic Computation Server (HCS) to

the C-ITS architecture. The HCS does computation

on vehicles encrypted data on behalf of different Ve-

hicle Service Providers (VSP).

In Figure 2, we present the four entities participat-

ing to our protocol: the vehicle, the Road Side Unit

(RSU), the HCS and the VSP.

First, the VSP runs HE.Keygen and gets pk, evk

and sk. Then, it transmits pk and evk to the HCS and

the RSU, while the vehicle receives only pk.

The vehicle selects a symmetric key k for a

homomorphic-friendly symmetric scheme (Canteaut

et al., 2015; Albrecht et al., 2016; Hoffmann et al.,

2020). This key is renewed from every protocol run.

In step 2, the vehicle encrypts the symmetric key

k using the homomorphic public key HE.Enc

(k).

It also encrypts its data d

with the symmetric key

SYM.Enc

). Then, the vehicle sends HE.Enc

(k)

and SYM.Enc

) to the RSU. In step 3, the RSU

recrypts d

as HE.Enc

) without access to the ve-

hicle data in clear. Indeed, the RSU applies the tran-

ciphering presented in section 2.2 to SYM.Enc

)

using HE.Enc

(k). Note that in practice, RSUs are

only used for V2X communications. So, it is advan-

tageous to delegate the transciphering to them instead

of doing it at the HCS level. As such, we distribute

computation over the different players of the proto-

col. Finally, the RSU sends HE.Enc

) to the HCS

in step 4.

In step 5, the HCS applies the service S to the ho-

momorphically encrypted inputs HE.Enc

). The

obtained result of this analysis HE.Enc

) is sent

to the VSP in step 6. Note that r

= S(d

). The VSP

obtains r

after decryption with its own secret key sk

(step 7). Based on the value of r

, the VSP returns an

adapted service s

to the vehicle (step 8). If the re-

turned s

is a conﬁdential information (e.g. an insur-

ance fee), the VSP can encrypt it with the symmetric

key k. Of course, in this case, we make the RSU send

HE.Enc

(k) to the VSP (red information in Figure

2).

We refer, for example, to message authentication codes

to provide message integrity

4 PERFORMANCE

In this section, we present an example of a service for

classifying drivers as concentrated or distracted us-

ing a dataset of drivers pictures. Such classiﬁcation

can be used during drivers insurance fees computa-

tion. We show how to turn it private thanks to the use

of homomorphic encryption. The dataset is provided

by the State Farm insurance on Kaggle

. The dataset

speciﬁes 10 different classes of drivers. Concentrated

drivers have their 2 hands on the steering wheel and

keep their eyes on the road. Meanwhile, distracted

drivers are talking on the phone, drinking coffee or

doing makeup.

We use the aforementioned dataset to train a 3

layers neural network where the 2 ﬁrst layers have

a quadratic activation function (Figure 3). Mean-

while, the last layer has a sigmoid activation function.

The ﬁrst layer contains 20 units while the second and

third layers contain 10 units each. We choose to use

the quadratic activation function as it is easily imple-

mented in the homomorphic domain (no need for its

approximation by interpolation as for other non-linear

activation functions).

4.1 Neural Network Training

We use Python 3 and the Tensorflow framework for

the dataset preprocessing and for encoding our neural

network (NN) model.

For the training step, we choose 90% of the 22424

labelled records of the dataset randomly. Each en-

try of this dataset is an RGB picture of the shape

480 × 640 × 3. First, we compress each picture either

to 52 × 52 × 3 or to 64 × 64 × 3. Then, we vectorize

these 3 dimensional matrices. That is, we represent

each picture by a vector of 8112 features or 12288

features, respectively. In addition, we scale all the

features by 255. Finally, we train our NN on clear

data using a learning rate of 0.0001, minibatches of 32

elements and 100 epochs. We use the sigmoid cross

entropy as a cost function.

4.2 Classiﬁcation of Clear Inputs

Once the training is ﬁnished, we run the prediction on

the test set of 2243 records (i.e. the remaining 10% of

the dataset). The prediction consists in running Algo-

rithm 1 where W

i,i∈{1,2,3}

are the matrices of weights

and b

i,i∈{1,2,3}

are the biases vectors per layer.

With the NN settings of Section 4.1, we obtain a

training accuracy of 88,953% and a classiﬁcation ac-

https://www.kaggle.com/c/

state-farm-distracted-driver-detection

Privacy Preserving Services for Intelligent Transportation Systems with Homomorphic Encryption

689

RSU

HCS

VSP

1. k = SYM.Keygen(1

)

3. HE.Eval

evk

(SYM.Dec

HE.Enc

(k)

(SYM.Enc

))

= HE.Enc

)

5. HE.Eval

evk

(S, HE.Enc

))

= HE.Enc

) = HE.Enc

(S(d

))

6. HE.Enc

), HE.Enc

(k)

7. HE.Dec

(HE.Enc

)) = r

HE.Dec

(HE.Enc

(k)) = k

8. s

or SYM.Enc

)

1. (pk, evk, sk) = HE.Keygen(1

)

pk, evk

Oﬄine

Online

Vehicle

2. HE.Enc

(k), SYM.Enc

)

4. HE.Enc

), HE.Enc

(k)

pk, evk

Figure 2: Protocol for providing privacy preserving services for C-ITS.

...

20 units

10 units

Inputs

=(a

,...,a

)

=(W

.x+b

)

=(a

,...,a

)

=(W

)

=(a

,...,a

)

=sigmoid(z

)

=sigmoid(W

)

x=(x

,...,x

)

n=8112 or 12288

Figure 3: Trained neural network structure.

curacy value of 86,223% for inputs with 8112 fea-

tures. Accuracy is deﬁned as the ratio between the

predicted values and the real ones. In our case, we

can improve accuracy by increasing the number of

features of the pictures of the dataset. For example,

if we compress images to a size of 64 × 64 × 3 (i.e.

using 12288 features), we get a training accuracy of

94,247% and a test accuracy of 92,866%.

However, using more features impacts the de-

gree of the cyclotomic polynomial

used for ho-

mormophic encryption and batching (Smart and Ver-

cauteren, 2011).

4.3 Classiﬁcation of Encrypted Inputs

In this section, we use the trained NN from section 4.1

to make private classiﬁcation of input vectors. Indeed,

we encrypt the input vectors as they present driver

sensitive data. In addition, we encrypt the NN weights

and biases as they are private knowledge of the insur-

ance and are shared with the HCS.

We remind that the cyclotomic polynomial f(x) is an

irreducible polynomial over Z which is used to specify the

polynomial ring R = Z(x)/(f(x)). Ciphertexts are polyno-

mials in R .

input : x a column vector of features, where

x ∈ M

n,1

(R) and n ∈ {8112,12288}

output: c

i,i∈[0,9]

the class of x

1 z

= W

.x + b

where W

∈ M

20,n

(R) and

∈ M

20,1

(R)

2 a

= z

3 z

= W

+ b

where W

∈ M

10,20

(R) and

∈ M

10,1

(R)

4 a

= z

5 z

= W

+ b

where W

∈ M

10,10

(R) and

∈ M

10,1

(R)

6 a

= sigmoid(z

) =

1+e

−z

7 c

= argmax(a

)

Algorithm 1: NN prediction algorithm.

To classify a vector x without revealing any x

, we

ﬁrst encrypt it as one poylnomial [x] with the API for

CKKS encryption scheme (Cheon et al., 2016) from

Microsoft SEAL library. We use batching to acceler-

ate the computation and encode all the x

in the same

polynomial x before its encryption as [x]. Batching al-

lows parallel operations in a Simple Instruction Mul-

tiple Data (SIMD) fashion (refer to (Smart and Ver-

cauteren, 2011) for details on batching).

Then, we use the updated prediction algorithm 2:

1. In step 1, we encrypt the element of x in a unique

polynomial [x]. If we use 8112 features per dataset

entry, we specify in SEAL a cyclotomic polyno-

mial of degree 16384. As such, we can pack

8192 slots in the same ciphertext polynomial us-

ing CKKS. Meanwhile, if we use 12288 fea-

tures per dataset entry, we specify a cyclotomic

polynomial of degree 32768 so that we can pack

16384 slots in the same ciphertext polynomial us-

ing CKKS.

In addition, we encrypt each row W

as a packed polynomial to obtain an en-

ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy

690

crypted column vector of 20 polynomials [W

] =

([W

],.. .,[W

]). The dot product [W

].[x] re-

sults in a column vector of 20 polynomials. The

dot product is computed by multiplying [x] by the

polynomial [W

],∀i ∈ [1,20] and adding all the

slots of the resulting polynomial. Adding all the

slots of a batched polynomial requires log

(N/4)

rotations and additions, where N is the degree of

the chosen cyclotomic polynomial. Finally, we

encrypt each element b

of b

in a separate packed

polynomial [b

]. As such, we obtain the encrypted

vector [b

] = ([b

],.. .,[b

]). At the end of step

1, we obtain an encrypted vector of 20 polynomi-

als [z

] = ([z

],.. .,[z

]). Each [z

] contains in its

slots the same encrypted value corresponding to

the plaintext z

= W

.x + b

2. In step 2, we just square element-wise the en-

crypted vector of polynomials [z

] to get the en-

crypted vector [a

3. In step 3, we proﬁt from the format of [a

] to

compute the dot product [W

].[a

] in a different

way. Indeed, we pack the column vectors of W

in 20 polynomials. Each column vector has 10 el-

ements and so will use 10 slots per batched poly-

nomial. We multiply the obtained vector [W

]

element-wise with [a

]. Then, we add the re-

sulting 20 polynomials together. Finally, we add

the obtained result to the batched and encrypted

polynomial [b

] that corresponds to the vector b

We obtain one batched polynomial [z

] that en-

crypts in each of its slots the following plaintext:

= W

+ b

where i ∈ [1,10].

4. In step 4, we just square the encrypted polynomial

] to obtain the encrypted polynomial [a

5. In step 5, we use the same method as in step 1 to

compute the encrypted vector of polynomials [z

The HCS computes [z

] and adds a random noise

e to it in order to avoid leaking information to

the VSP when deciphering the NN outputs. The

noise vector e is added in clear. In addition, each

of its components must maintain the order of the

encrypted values (e.g., [W

].[a

] + [b

]). The or-

der is important as the VSP deciphers [z

] and

gets the class of [x] by taking the argmax(z

For this work, we took e as the vector formed

by the same random value α repeated 10 times,

i.e., e = (e

= α,. . ., e

= α). For the futur work,

we will investigate other methods for noise setting

and leakage avoidance such as interactive encryp-

tion as stated in (Boemer et al., 2020).

We implemented Algorithm 2 on an Intel Core i7

and we ran the tests in 1 CPU cadenced at 3,9GHz.

The used security parameters respect the default secu-

input : [x] an encrypted polynomial

corresponding to the vector x ∈ M

n,1

(R)

output: [z

] an encrypted vector of polynomials

corresponding to the logits [z

],i ∈ [0, 9]

1 [z

] = [W

].[x] + [b

]

2 [a

] = [z

]

3 [z

] = [W

].[a

] + [b

]

4 [a

] = [z

]

5 [z

] = [W

].[a

] + [b

] + e

Algorithm 2: NN prediction algorithm with encrypted in-

puts, weights and biases.

rity level provided by SEAL which is equal to 128bits.

It took 2.368 seconds for data pre-processing and en-

cryption, and 11.664 seconds for the classiﬁcation of

a vector of 8112 features. Meanwhile, it took 4.759

seconds for data pre-processing and 25.667 seconds

for the classiﬁcation of a vector of 12288 features.

The difference in classiﬁcation times depends on the

the number of features of the input. Indeed, the num-

ber of features dictates the degree of the cyclotomic

polynomial to be used for ciphertext representation.

In our case, when we used inputs with 8112 features,

the degree of the cyclotomic polynomial was 16384.

Meanwhile, it was 32768 for inputs with 12288 fea-

tures. That is, we used bigger ciphertexts to pack in-

puts with more features, and using bigger ciphertexts

results in longer computation times. That is why the

classiﬁcation time was longer for longer input vec-

tors. In addition, we computed the accuracy of the

classiﬁcation with encrypted inputs. We noticed that

we got the same classiﬁcation accuracy as for clear

inputs presented in section 4.2.

5 CONCLUSION

In this work, we speciﬁed a ﬁrst version of a privacy-

preserving protocol for C-ITS services. We made ve-

hicle service providers delegate their computation on

vehicle private data to a semi-honest homomorphic

computation server. Indeed, the latter is in charge of

running services over encrypted data which ensures

data conﬁdentiality in use. In addition, we showed

that a simple neural network classiﬁcation of driver

behavior using encrypted features and parameters can

be effective and may run in reasonable times when we

do not have hard real-time constraints. In the future,

we plan to:

• study in depth state of the art solutions for apply-

ing homomorphic encryption to non-linear activa-

tion function such as ReLu. Of course, being able

to use other non-linear activation function is im-

Privacy Preserving Services for Intelligent Transportation Systems with Homomorphic Encryption

691

portant as it can improve the NN accuracy. An

interesting solution seems to combine homomor-

phic encryption with MPC as presented recently

in the MP2ML framework (Boemer et al., 2020;

Juvekar et al., 2018).

• investigate output layer data randomization to

avoid data leakage to the vehicle service provider

as discussed by (Boemer et al., 2020; Juvekar

et al., 2018).

• improve execution times by investigating hard-

ware algorithmic acceleration for homomorphic

schemes such as using GPU for polynomial mul-

tiplication acceleration with FFT as proposed by

nuFHE

REFERENCES

Albrecht, M., Rechberger, C., Schneider, T., Tiessen, T.,

and Zohner, M. (2016). Ciphers for mpc and fhe.

Cryptology ePrint Archive, Report 2016/687. https:

//eprint.iacr.org/2016/687.

Asuquo, P., Cruickshank, H., Morley, J., Ogah, C. P. A.,

Lei, A., Hathal, W., Bao, S., and Sun, Z. (2018). Secu-

rity and privacy in location-based services for vehic-

ular and mobile communications: An overview, chal-

lenges, and countermeasures. IEEE Internet of Things

Journal, 5(6):4778–4802.

Boemer, F., Cammarota, R., Demmler, D., Schneider, T.,

and Yalame, H. (2020). Mp2ml: A mixed-protocol

machine learning framework for private inference.

Cryptology ePrint Archive, Report 2020/721. https:

//eprint.iacr.org/2020/721.

Boemer, F., Lao, Y., and Wierzynski, C. (2018). ngraph-he:

A graph compiler for deep learning on homomorphi-

cally encrypted data. CoRR.

Bosch (1991). CAN Speciﬁcation Version 2.0.

Boura, C., Gama, N., Georgieva, M., and Jetchev, D.

(2018). Chimera: Combining ring-lwe-based fully ho-

momorphic encryption schemes. Cryptology ePrint

Archive, Report 2018/758. https://eprint.iacr.org/

2018/758.

Bourse, F., Minelli, M., Minihold, M., and Paillier, P.

(2018). Fast homomorphic evaluation of deep dis-

cretized neural networks. In Proceedings of CRYPTO

2018. Springer.

Brakerski, Z., Gentry, C., and Vaikuntanathan, V. (2012).

(Leveled) Fully Homomorphic Encryption Without

Bootstrapping. In Proceedings of the 3rd Innovations

in Theoretical Computer Science Conference, ITCS

’12, pages 309–325.

Brakerski, Z. and Vaikuntanathan, V. (2011). Fully Homo-

morphic Encryption from Ring-LWE and Security for

Key Dependent Messages. In CRYPTO, volume 6841

of Lecture Notes in Computer Science, pages 505–

524. Springer.

https://github.com/nucypher/nufhe

Brutzkus, A., Oren Elisha, O., and Gilad-Bachrach, R.

(2019). Low latency privacy preserving inference. In

Proceedings of the 36th International Conference on

MachineLearning, Long Beach, California, PMLR 97.

Canteaut, A., Carpov, S., Fontaine, C., Lepoint, T., Naya-

Plasencia, M., Paillier, P., and Sirdey, R. (2015).

Stream ciphers: A practical solution for efﬁcient

homomorphic-ciphertext compression. Cryptology

ePrint Archive, Report 2015/113. https://eprint.iacr.

org/2015/113.

Cheon, J. H., Kim, A., Kim, M., and Song, Y. (2016).

Homomorphic encryption for arithmetic of approxi-

mate numbers. Cryptology ePrint Archive, Report

2016/421. https://eprint.iacr.org/2016/421.

Chillotti, I., Gama, N., Georgieva, M., and Izabachène,

M. (2016). Faster fully homomorphic encryption:

Bootstrapping in less than 0.1 seconds. In Advances

in Cryptology–ASIACRYPT 2016: 22nd International

Conference on the Theory and Application of Cryp-

tology and Information Security, Hanoi, Vietnam, De-

cember 4-8, 2016, Proceedings, Part I 22, pages 3–33.

Springer.

Chou, E., Beal, J., Levy, D., Yeung, S., Haque, A., and Fei-

Fei, L. (2018). Faster cryptonets: Leveraging sparsity

for real-world encrypted inference. CoRR.

Dolev, D. and Yao, A. C. (1981). On the security of pub-

lic key protocols. In Proceedings of the 22nd An-

nual Symposium on Foundations of Computer Sci-

ence, SFCS ’81, page 350–357, USA. IEEE Computer

Society.

Dowlin, N., Gilad-Bachrach, R., Laine, K., Lauter, K.,

Naehrig, M., and Wernsing, J. (2016). Cryptonets:

Applying neural networks to encrypted data with high

throughput and accuracy. Technical Report MSR-TR-

2016-3.

Fan, J. and Vercauteren, F. (2012). Somewhat practical fully

homomorphic encryption. IACR Cryptology ePrint

Archive, 2012:144.

FlexRay (2010). FlexRay Communications System Proto-

col Speciﬁcation Version 3.0.1.

Garg, S., Singh, A., Batra, S., Kumar, N., and Yang,

L. T. (2018). Uav-empowered edge computing envi-

ronment for cyber-threat detection in smart vehicles.

IEEE Network, 32(3):42–51.

Gentry, C. et al. (2009). Fully homomorphic encryption

using ideal lattices. In STOC, volume 9, pages 169–

178.

Ghane, S., Jolfaei, A., Kulik, L., Ramamohanarao, K., and

Puthal, D. (2020). Preserving privacy in the internet of

connected vehicles. IEEE Transactions on Intelligent

Transportation Systems, pages 1–10.

Grzemba, A. (2011). MOST-The Automotive Multimedia

Network. Electronics Library.

Günther, D., Kiss, A., Scheidel, L., and Schneider, T.

(2019). Poster: Framework for semi-private function

evaluation with application to secure insurance rate

calculation. In Proceedings of the 2019 ACM SIGSAC

Conference on Computer and Communications Secu-

rity, CCS ’19, page 2541–2543, New York, NY, USA.

Association for Computing Machinery.

ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy

692

Höfer, C., Petit, J., Schmidt, R., and Kargl, F. (2013). Pop-

corn: Privacy-preserving charging for emobility. In

Proceedings of the 2013 ACM Workshop on Security,

Privacy & Dependability for Cyber Vehicles, CyCAR

’13, page 37–48, New York, NY, USA. Association

for Computing Machinery.

Hoffmann, C., Méaux, P., and Ricosset, T. (2020). Transci-

phering, using ﬁlip and tfhe for an efﬁcient delegation

of computation. Cryptology ePrint Archive, Report

2020/1373. https://eprint.iacr.org/2020/1373.

IEEE standard 802.11p (2010). IEEE Standard for In-

formation technology– Local and metropolitan area

networks– Speciﬁc requirements– Part 11: Wireless

LAN Medium Access Control (MAC) and Physical

Layer (PHY) Speciﬁcations Amendment 6: Wireless

Access in Vehicular Environments. IEEE Std 802.11p-

2010 (Amendment to IEEE Std 802.11-2007), pages

1–51.

IEEE Std 100 Base T1 (2018). Iso/iec/ieee international

standard - part 3: Standard for ethernet - amendment

1: Physical layer speciﬁcations and management pa-

rameters for 100 mb/s operation over a single balanced

twisted pair cable (100base-t1). ISO/IEC/IEEE 8802-

3:2017/Amd 1:2017(E), pages 1–92.

IEEE Std 1609.2 (2016). Ieee standard for wireless access

in vehicular environments–security services for appli-

cations and management messages. IEEE Std 1609.2-

2016 (Revision of IEEE Std 1609.2-2013), pages 1–

240.

ISO-17987-3 (2016). Road vehicles - Local Interconnect

Network (LIN) - Part 3: Protocol speciﬁcation.

Juvekar, C., Vaikuntanathan, V., and Chandrakasan, A.

(2018). Gazelle: A low latency framework for secure

neural network inference. CoRR, abs/1801.05507.

Kargl, F., Friedman, A., and Boreli, R. (2013). Differential

privacy in intelligent transportation systems. In Pro-

ceedings of the sixth ACM conference on Security and

privacy in wireless and mobile networks, pages 107–

112. ACM.

Kido, H., Yanagisawa, Y., and Satoh, T. (2005). An anony-

mous communication technique using dummies for

location-based services. In ICPS ’05. Proceedings. In-

ternational Conference on Pervasive Services, 2005.,

pages 88–97.

López-Alt, A., Tromer, E., and Vaikuntanathan, V. (2012).

On-the-ﬂy multiparty computation on the cloud via

multikey fully homomorphic encryption. In Proceed-

ings of the forty-fourth annual ACM symposium on

Theory of computing, pages 1219–1234. ACM.

Messous, M., Arfaoui, A., Alioua, A., and Senouci, S.

(2017). A sequential game approach for computation-

ofﬂoading in an uav network. In GLOBECOM 2017

- 2017 IEEE Global Communications Conference,

pages 1–7.

Molina-Masegosa, R., Gozalvez, J., and Sepulcre, M.

(2020). Comparison of ieee 802.11p and lte-v2x: An

evaluation with periodic and aperiodic messages of

constant and variable size. IEEE Access, 8:121526–

121548.

Neven, G., Baldini, G., Camenisch, J., and Neisse, R.

(2017). Privacy-preserving attribute-based credentials

in cooperative intelligent transport systems. In 2017

IEEE Vehicular Networking Conference (VNC), pages

131–138.

Omri, O. E., Boudguiga, A., Izabachene, M., and Klaudel,

W. (2019). Privacy-preserving k-means clustering: an

application to driving style recognition. In Liu, Joseph

K.and Huang, X., editor, Network and System Se-

curity, pages 685–696, Cham. Springer International

Publishing.

Paillier, P. (1999). Public-key cryptosystems based on com-

posite degree residuosity classes. In International

Conference on the Theory and Applications of Cryp-

tographic Techniques, pages 223–238. Springer.

Peng, Z. (2019). Danger of using fully homomorphic

encryption: A look at microsoft SEAL. CoRR,

abs/1906.07127.

Petit, Jonathanand Dietzel, S. and Kargl, F. (2018). Pri-

vacy of Connected Vehicles, pages 229–251. Springer

International Publishing, Cham.

Rizzo, N., Sprissler, E., Hong, Y., and Goel, S. (2015). Pri-

vacy preserving driving style recognition. In Con-

nected Vehicles and Expo (ICCVE), 2015 Interna-

tional Conference on, pages 232–237. IEEE.

Sanyal, A., Kusner, M., Gascón, A., and Kanade, V. (2018).

In ICML.

Sharma, V., You, I., and Guizani, N. (2019). Security of 5g-

v2x: Technologies, standardization and research di-

rections.

Smart, N. and Vercauteren, F. (2011). Fully homomorphic

simd operations. Cryptology ePrint Archive, Report

2011/133. https://eprint.iacr.org/2011/133.

Troncoso, C., Danezis, G., Kosta, E., Balasch, J., and Pre-

neel, B. (2011). Pripayd: Privacy-friendly pay-as-

you-drive insurance. IEEE Transactions on Depend-

able and Secure Computing, 8(5):742–755.

Van Dijk, M., Gentry, C., Halevi, S., and Vaikuntanathan, V.

(2010). Fully homomorphic encryption over the inte-

gers. In Annual International Conference on the The-

ory and Applications of Cryptographic Techniques,

pages 24–43. Springer.

Wang, W., Min, M., Xiao, L., Chen, Y., and Dai, H. (2019).

Protecting semantic trajectory privacy for vanet with

reinforcement learning. In ICC 2019 - 2019 IEEE

International Conference on Communications (ICC),

pages 1–5.

Zhao, Y. and Wagner, I. (2019). On the strength of privacy

metrics for vehicular communication. IEEE Transac-

tions on Mobile Computing, 18(2):390–403.

Privacy Preserving Services for Intelligent Transportation Systems with Homomorphic Encryption

693