
A Method for Estimating Potential Knowledge Increase after Updating
Ontology Mapping
Adrianna Kozierkiewicz
a
, Marcin Pietranik
b
and Karolina Kania
Faculty of Computer Science and Management, Wroclaw University of Science and Technology,
Keywords:
Ontology Alignment, Ontology Evolution, Knowledge Management.
Abstract:
In the modern days, users cannot expect that ontologies in their initial states won’t remain static throughout the
lifespan of their application, therefore a tool for managing appearing alterations is necessary. In our previous
work, we have prepared a solid, formal, and flexible foundation that can be used to express changes that
appear while maintained ontologies evolve. This paper contains a description of the process of constructing a
method assessing knowledge increase after an ontology alignment update. Our developed measure estimates
how ontology evolution influenced the increase of knowledge for two input ontologies. The developed method
has been experimentally verified by simulating random ontology evolutions ad the obtained results have been
statistically analyzed. Due to the limitation of this paper, we focus only on the concept level.
1 INTRODUCTION
In large and distributed systems the knowledge is dis-
persed between multiple nodes in a large infrastruc-
ture. It is not uncommon that ontologies are used as
the underlying knowledge representation. They are
usually defined as a formal specification of conceptu-
alization and are one of the foundations of modern
semantic applications. To facilitate communication
between them, so-called ontology alignment can be
used, which informally can be described as creating
a bridge between two ontologies. This tool provides
the ability to translate the content of one ontology into
the content of another one.
However, in such an environment, one cannot ex-
pect that business requirements won’t change over
time. This entails that if some underlying ontology
changes, the exchange of information between par-
ticipating services may become compromised. To
remedy this situation, a sound procedure for updat-
ing the ontology alignment is required. Such a pro-
cedure should start with identifying a situation when
changes applied to ontologies are significant enough
to potentially invalidate the alignment between on-
tologies. Then, a sound algorithm for alignment reval-
idation should be applied. Up until now in our pre-
a
https://orcid.org/0000-0001-8445-3979
b
https://orcid.org/0000-0003-4255-889X
vious research, we have developed and verified sev-
eral approaches to described tasks ((Kozierkiewicz
and Pietranik, 2019), (Kozierkiewicz and Pietranik,
2020)), decomposing them into the level of concepts,
relations, and instances. Using them entails that the
communication between two knowledge-based sys-
tems can be reinstated.
However, there is still an open question. Two
aligned ontologies are easy to merge and carry some
synergic knowledge potential. Modifications done to
such ontologies are frequently followed by modifica-
tions of their mappings. So how much both of those
modifications influence the aforementioned knowl-
edge potential? Do the applied changes increased or
decrease it? In this paper, we present a measure that
can be used to estimate how much knowledge about
the interoperability of two ontologies has been ac-
quired through the process of updating the ontology
alignment. Due to the limited space, we will focus
only on a concept level available in ontologies.
The remaining part of this article is organized as
follows. In the next section, a summary of related
work is given. Section 3 provides the most important
definitions that will be used to develop a method for
assessing knowledge growth. Section 4 describes the
main task we want to solve- a method definition of as-
sessing knowledge increase after ontology alignment
update. In Section 5 results of the conducted exper-
iment are provided. Section 6 gives brief summary
Kozierkiewicz, A., Pietranik, M. and Kania, K.
A Method for Estimating Potential Knowledge Increase after Updating Ontology Mapping.
DOI: 10.5220/0010362001730180
In Proceedings of the 16th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2021), pages 173-180
ISBN: 978-989-758-508-1
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
173

and overviews our upcoming research plans.
2 RELATED WORKS
Ontology alignment is a widely discussed topic,
frequently investigated in the available literature
((Shvaiko et al., 2018), (Shvaiko and Euzenat, 2011)).
The variety of (e.g. (Kolyvakis et al., 2018)) ap-
proaches usually define mappings between ontologies
as sets of pairs of complementary elements from two
ontologies. In other words, pairs of those elements
from ontologies describe the same part of the universe
of discourse. Those sets are then validated by means
of Precision and Recall measures ((Algergawy et al.,
2019)) using preprepared mappings treated as a refer-
ence.
This approach, despite being perfectly valid, has
two downsides. The first one is it measures only the
correctness of mappings in relation to the aforemen-
tioned references. Using Precision and Recall mea-
sures is impossible in practical applications, due to the
fact that no reference alignment exists. The second
disadvantage is the fact that such assessment takes
into account solely mappings, omitting the content of
ontologies that are matched.
There some research addressing the raised issues
by noticing those flaws and attempted to overcome
them (Thiéblin et al., 2020). In (Dragisic et al., 2016)
authors provide a survey on involving users in mea-
suring the quality of automated alignment algorithms.
Three aspects of human-centric evaluation are espe-
cially investigated: the profile of the user, the services
of the alignment system, and the user interface while
in (Leal et al., 2017) authors attempt to utilize the so-
called Ontology of Enterprise Interoperability to as-
sess different aspects of interoperability.
A similar approach can be found in (Ivanova et al.,
2017). The article proposes a "human-in-the-loop"
approach to overcome the difficulties when reference
alignments are unavailable. The main idea is based
on a tool called Matrix Cubes, which is used for visu-
alizing dense dynamic networks, this further supports
the interactive exploration of multiple ontology align-
ment in order to assess their quality. The research is
further extended in (Li et al., 2019).
The research found in (Solimando et al., 2017)
presents detecting and minimizing the violations
of the "conservativity principle". This is a situa-
tion where novel subsumption entailments between
classes from one of the mapped ontologies are marked
as unwanted.
This paper focuses on a different issue. While
approaches described above all focus on evaluating
the designated ontology alignments in order to check
their correctness, we attempt to address the change
factor of ontology alignments. Obviously, when
mapped ontologies evolve, it requires that their align-
ment evolve as well. Therefore, we would like to
provide a method for assessing how much knowl-
edge about the interoperability between ontologies
has been gained or lost. We claim that such a tool
can become very useful in practical applications of
ontologies and ontology alignment. Especially, when
large-scale ontologies (e.g. in (Kiourtis et al., 2019))
are mapped the knowledge about the degree to which
they can cooperate can be invaluable.
3 BASIC NOTIONS
Our research focuses on a mathematical model of an
ontology. We assume that a real world is defined as
a pair (A, V ) where: A is a finite set of attributes that
can be used to describe objects, V is a set of their
valuations (domains) such that V =
S
(a∈A)
V
a
, V
a
is a
domain of a particular attribute a. The following quin-
tuple defines an ontology as a (A, V)-based ontology:
O = (C, H, R
C
, I, R
I
) (1)
where: C is a set of concepts; H is a concepts’ hierar-
chy; R
C
is a set of relations between concepts, R
C
=
{r
C
1
, r
C
2
, ..., r
C
n
}, n ∈ N, such that r
C
i
∈ R
C
(i ∈ [1, n]) is
a subset of C × C; I is a set of instance identifiers;
R
I
= {r
I
1
, r
I
2
, ..., r
I
n
} is a set of relations between con-
cepts’ instances.
A concept’sc ∈ C structure from (A, V )-based on-
tology is defined as:
c = (id
c
, A
c
, V
c
, I
c
) (2)
where id
c
is an identifier of the concept c, A
c
is a set of
its attributes, such that A
c
⊆ A, V
c
is a set of attributes
domains (formally: V
c
=
S
(a∈A
c
)
V
a
), I
c
is a set of
instances of the concept c. We write a ∈ c to denote
that an attribute a belongs to concept c set of attributes
A
C
.
The hierarchy of concepts H is a distinguished re-
lation between concepts. Formally, hierarchy is a set
concept pairs (H ⊂ C ×C), where a single pair of con-
cepts (c
1
, c
2
) ∈ H represents the fact that c
1
is an an-
cestor of c
2
. The position of a concept in a hierar-
chy allows us to deduce how much specific knowl-
edge it carries a concept. Thus, concept c
2
is more
detailed than c
1
. This remark will be used for esti-
mating knowledge increase. Based on hierarchy H
we can define subtree in the following way:
Definition 1. For given ontology O, and c ∈ C by
Subtree(O, c) we call a subtree of H such that ¬∃c
0
∈
{x|(x, x
0
) ∈ Subtree(O, c)} : (c
0
, c) ∈ Subtree(O, c).
ENASE 2021 - 16th International Conference on Evaluation of Novel Approaches to Software Engineering
174

The subtree definition allows to define the depth
properties:
Definition 2. For a given subtree S = Subtree(O, c
r
)
and the subtree’s root classes c
r
∈ C, the depth of
class c ∈ C denoted as Depth(S , c)) in the subtree S is
the number of subsumption relationships between c
r
and c.
We define an auxiliary notion S
UNDUP
that for
a subtree S = Subtree(O
1
, c
1
), c
1
∈ C
1
returns this
subtree with removed concepts (and their descen-
dants) which have complementary mappings within
the alignment Align(O
1
, O
2
).
S
UNDUP
(S, Align(O
1
, O
2
)) =
S \
[
(c,c
0
)∈Align(O
1
,O
2
)
(S ∩ Subtree(O
1
, c))
(3)
As it was mentioned, we assume that ontolo-
gies may change over time. Therefore, we need to
introduce a formal notion of time. In our work,
time is represented as a timeline, which is treated
as an ordered set of moments, defined as T L =
{t
n
|n ∈ N}. By T L(O) we denote a subset of time-
line, with only elements from T L during which the
ontology O has changed. A superscript O
(m)
=
(C
(m)
, H
(m)
, R
C(m)
, I
(m)
, R
I(m)
) is used to denote the
ontology O in a selected moment in time t
m
∈ T L(O).
A symbol ≺ is denotes a fact that O
(m−1)
is an earlier
version of O than O
(m)
(O
(m−1)
≺ O
(m)
). A reposi-
tory of an ontology O, is an ordered set of its succes-
sive versions, It is defined as Rep(O) =
O
(m)
|∀m ∈
T L(O)
.
Between two independent (A, V )-based ontologies
O
1
and O
2
there may exist some correspondences
called alignment. Of course, for each ontology level
like concepts, instances and relations it is possible to
determine separate set of correspondences. However
in this paper we will focus only on concept level, so
we formally define a set Align(O
1
, O
2
) containing tu-
ples of the form (c
1
, c
2
, λ
C
(c
1
, c
2
), r) where: c
1
, c
2
are
concepts from O
1
and O
2
respectively, λ
C
(c
1
, c
2
) is
a real value representing a degree to which concept
c
1
can be aligned into the concept c
2
, r is a rela-
tion’s type connecting c
1
and c
2
(equivalency, gener-
alization). λ
C
(c
1
, c
2
) can be designated using one of
the matching methods described in i.e.(Shvaiko et al.,
2018). A vast majority of alignments between two on-
tologies include only mappings of concepts that are
equivalent with 100% certainty. Therefore, for sim-
plicity, we can reduce the definition of Align(O
1
, O
2
)
to only pairs of concepts:
Align(O
1
, O
2
) =
{(c
1
, c
2
)|(c
1
, c
2
) ∈ C
1
×C
2
∧ λ
C
(c
1
, c
2
) = 1}
(4)
The above notation can be easily extended to in-
clude the notion of time, by analogously usage of
superscripts. For example, Align(O
(m)
1
, O
(n)
2
) repre-
sents an alignment of the two ontologies O
1
and O
2
in their states in moments m and n respectively, where
m, n ∈ T L.
4 A METHOD FOR ESTIMATING
THE POTENTIAL
KNOWLEDGE INCREASE
In our research, we have noticed that the value of
depth for a given concept is related to the detailed
knowledge stored in this concept. These remarks have
been used for developing a measure for estimating the
potential knowledge increase. For a given concept
c
r
∈ C
1
of some ontology O
1
its knowledge potential
is calculated as:
λ(O
1
, c
r
) =
∑
c
s
∈C
1
Depth(S
UNDUP
(S, Align(O
1
, O
2
)), c
s
)
(5)
where: S = Subtree(O
1
, c
r
). Figure 1 represents two
examples of the same ontology however for different
alignments. The mapped concepts are marked in yel-
low color. The value of λ for particulars concepts are
assigned to each of them:
Equation 5 allows us to calculate the knowledge
potential of complementary mappings in the align-
ment Align(O
1
, O
2
):
σ(c
r1
, c
r2
) = λ(O
1
, c
r1
) + λ(O
2
, c
r2
) (6)
where: c
r1
∈ C1, c
r2
∈ C2, (c
r1
, c
r2
) ∈ Align(O
1
, O
2
).
Thus, for estimating the knowledge potential of the
whole alignment Align(O
1
, O
2
) we should repeat the
calculation for each pair mapped concepts:
γ(O
1
, O
2
) =
∑
(c,c
0
)∈Align(O
1
,O
2
)
σ(c, c
0
) (7)
By Root(O) let’s denote a set of classes in ontol-
ogy O which are direct children of the abstract class
Thing. In other words- this is a set of concepts that
are in the highest level of the taxonomy. Then, let us
introduce an auxiliary notion:
η(O
1
) =
∑
c
d
∈Root(O
1
)
λ(O
1
, c
d
) (8)
Lets denote by µ(O
1
, O
2
) a knowledge potential of
two mapped ontologies O
1
and O
2
. It needs to fulfill
the following postulates:
A Method for Estimating Potential Knowledge Increase after Updating Ontology Mapping
175

Figure 1: The example of calculating λ.
• µ(O
1
, O
2
) = 0 ⇐⇒
∀
(c
r1
,c
r2
)∈Align(O
1
,O
2
)
σ((c
r1
, c
r2
) = 0 (in other
words: concept c
r1
and c
r2
has empty set
Subtree(O, c
r1
) and Subtree(O, c
r2
), respectively)
• µ(O
1
, O
2
) = 0 ⇐⇒ Align(O
1
, O
2
) =
/
0 (in other
words, the alignment of O
1
and O
2
is empty)
• µ(O
1
, O
2
) = 1 ⇐⇒ ∀
(c
r1
,c
r2
)∈Align(O
1
,O
2
)
(c
r1
∈
Root(O
1
) ∧ c
r2
∈ Root(O
2
)) (in other words - all
of the alignments connect only top level concepts
in both ontologies)
Therefore, the knowledge potential of two mapped
ontologies is normalized to set [0, 1], and calculated
as according to the equation below:
µ(O
1
, O
2
) =
γ(O
1
, O
2
)
η(O
1
) + η(O
2
)
(9)
Example ontologies with a minimal value of µ are
presented in Figure 2, while ontologies with the max-
imal value of µ are presented in Figure 3.
Equation 9 can be used to assess the knowledge
potential for two mapped ontologies assuming that
they are constant and unchanging in time. However,
in the real world, changes applied in ontologies and
alignments between could be more or less significant.
In our work, we would like to know how the
changes applied to two ontologies which entail up-
dating the alignment between them influence their
knowledge potential. In other words, for ontologies
O
(n)
1
O
(n)
2
and the alignment between them in moment
of time n and two ontologies after changes and up-
dated alignment between them in the moment of time
m such that O
(n)
1
≺ O
(m)
1
and O
(n)
2
≺ O
(m)
2
. The poten-
tial knowledge increase after updating ontology map-
pings is calculated as follows:
δ(O
(m)
1
, O
(m)
2
, O
(n)
1
, O
(n)
2
) = (
µ(O
(m)
1
, O
(m)
2
)
µ(O
(n)
1
, O
(n)
2
)
−1)∗100%
(10)
We assume that µ(O
(n)
1
, O
(n)
2
) 6= 0 because if the
knowledge increase in the initial state of the ontology
is equal to 0 then we have no reference value to re-
fer to. δ ∈ [−100%, ∞) and values greater than 0 will
symbolize the growth of knowledge in comparison to
the earlier state. Values lower than 0 means the de-
crease of knowledge stored in two ontologies.
5 THE RESULTS OF
EXPERIMENTS
For our experiment, we used ontologies provided
by OAEI (Ontology Alignment Evaluation Initiative)
(oae, 2020). It is an organization that annually or-
ganizes a campaign aiming at assessing the strengths
and weaknesses of ontology matching systems and
comparing their performances. To determine align-
ments, we used a widely known tool LogMap (log,
2020), which is a highly scalable ontology matching
solution with integrated reasoning and inconsistency
repair capabilities. More importantly, LogMap earned
high positions in subsequent OAEI campaigns.
The main aim of our experiment was to verify the
developed measure of δ and its applicability in the
case of evolving ontology. From the benchmark set
of ontologies, we have chosen pairs of ontologies pre-
sented in Table 1.
For each pair, the first ontology has been modified
by randomly adding or deleting some concepts. Such
an approach allows us to simulate the ontology evolu-
tion process. We formulated nine different scenarios
of such evolution:
1. Adding about 20% random new concepts,
all satisfying the following condition: for
each new concept c
new
added to ontology O
1
∃c
r1
∈ C
1
and c
r2
∈ C
2
, where (c
r1
, c
r2
) ∈
Align(O
1
, O
2
) and (c
r1
, c
new
) ∈ Subtree(O
1
, c
r1
)
and Depth(S, c
new
= 1) for a given subtree S =
Subtree(O, c
r1
)
2. Adding about 20% new random concepts,
all satisfying the following condition: for
ENASE 2021 - 16th International Conference on Evaluation of Novel Approaches to Software Engineering
176
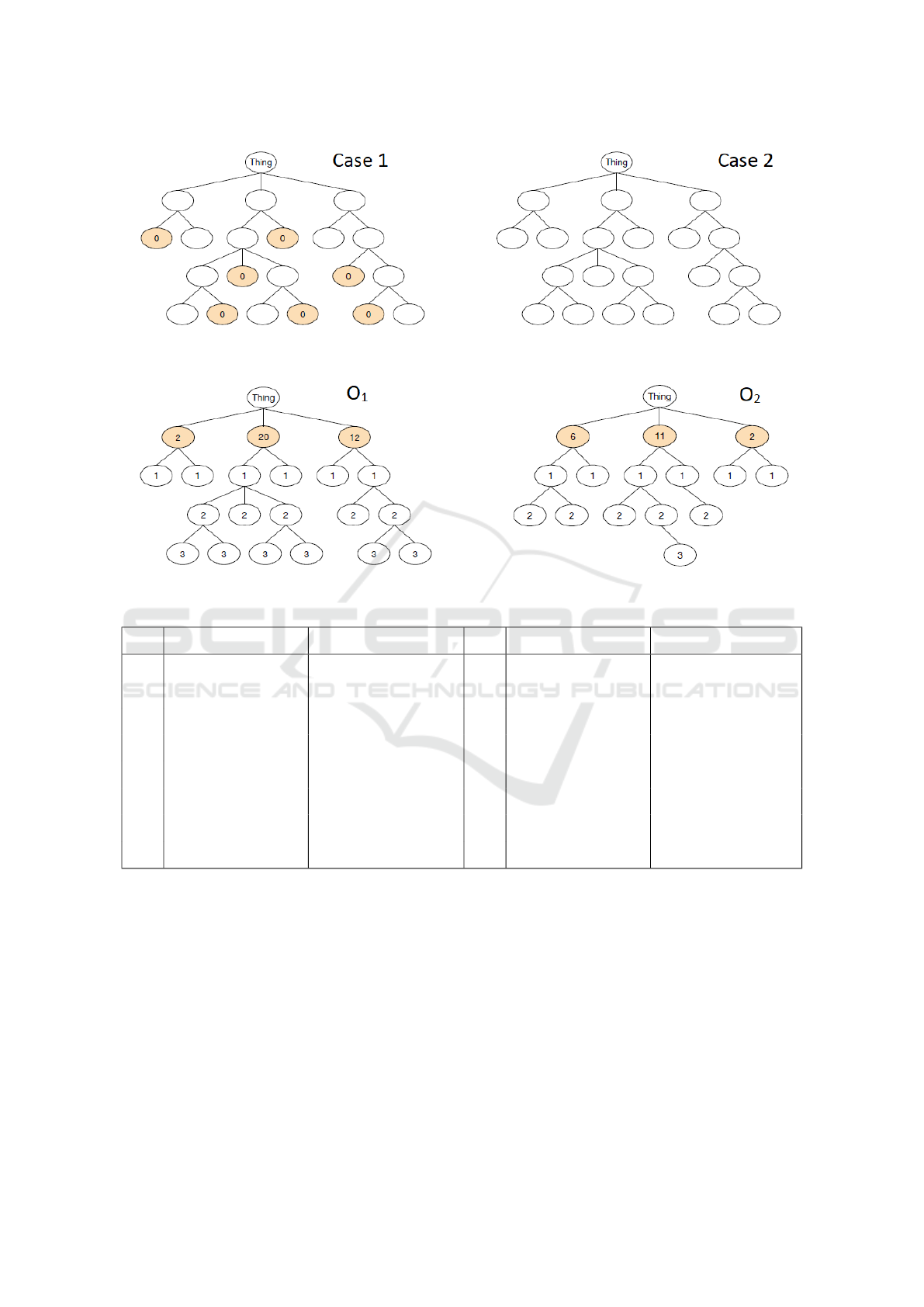
Figure 2: The ontologies with the minimal value of µ.
Figure 3: The ontologies with maximal value of µ.
Table 1: The pair of ontologies used in experiment.
No. Name of ontologies Number of Concepts No. Name of ontologies Number of concepts
1 Cocus/Iasted 55/ 140 2 ConfTool/Sofsem 38/ 60
3 Ekaw/Sigkdd 74/ 49 4 Cmt/Paperdyne 36/ 47
5 Edas/Iasted 104/ 140 6 Sofsem/Confious 60/ 57
7 OpenConf/Ekaw 62/ 74 8 Edas/Sofsem 104/ 60
9 openConf/Cocus 62/ 55 10 Edas/Conftool 104/ 38
11 Cosus/Pcs 55/ 23 12 Ekaw/MyRieview 74/ 39
13 Confios/Sigkdd 57/ 49 14 Iasted/OpenConf 140/ 62
15 Ekaw/Paperdyne 74/ 47 16 Paperdyne/Sofsem 47/ 60
each new concept c
new
added to ontology O
1
∃c
r1
∈ C
1
and c
r2
∈ C
2
where (c
r1
, c
r2
) ∈
Align(O
1
, O
2
), and (c
r1
, c
new
) ∈ Subtree(O
1
, c
r1
)
and Depth(S, c
new
= 1 or Depth(S, c
new
= 2 for a
given subtree S = Subtree(O, c
r1
)
3. Adding about 20% random new concepts, all sat-
isfying the following condition: for each new con-
cept c
new
added to ontology O
1
∃c
r1
∈ C
1
and
c
r2
∈ C
2
where (c
r1
, c
r2
) ∈ Align(O
1
, O
2
), and
(c
r1
, c
new
) ∈ Subtree(O
1
, c
r1
)
4. Adding about 20% random new concepts, all sat-
isfying the following condition: for each new con-
cept c
new
added to ontology O
1
¬∃c
r1
∈ C
1
and
¬∃c
r2
∈ C
2
such that (c
r1
, c
r2
) ∈ Align(O
1
, O
2
)
and (c
new
, c
r1
) ∈ Subtree(O
1
, c
r1
)
5. Adding about 10% random new concepts, all sat-
isfying the following condition: for each new con-
cept c
new
added to ontology O
1
∃c
0
∈ C
1
where
(c
new
= c
0
).
6. Adding about 10% random new concepts, all sat-
isfying the following condition: for each new con-
cept c
new
added to ontology O
1
∃c
r1
∈ C
1
and
∃c
r2
∈ C
2
such that (c
r1
, c
r2
) ∈ Align(O
1
, O
2
), and
(c
r1
, c
new
) ∈ Subtree(O
1
, c
r1
) and ∃c
0
∈ C
2
where
A Method for Estimating Potential Knowledge Increase after Updating Ontology Mapping
177

(c
new
= c
0
).
7. Randomly removing about 5% of concepts, such
that each removed concept c
rem
from ontology O
1
satisfies the following condition: ∃c
r1
∈ C
1
and
∃c
r2
∈ C
2
such that (c
r1
, c
r2
) ∈ Align(O
1
, O
2
), and
(c
r1
, c
rem
) ∈ Subtree(O
1
, c
r1
)
8. Randomly removing about 5% of concepts, such
that each removed concept c
rem
from ontology O
1
satisfies the following condition: ∃c
r1
∈ C
1
and
∃c
r2
∈ C
2
such that (c
r1
, c
r2
) ∈ Align(O
1
, O
2
) and
λ(O
1
, c
r1
) is maximal.
9. Removing only 2 concepts and their subtrees
which satisfy the following condition: for each re-
moved concept c
rem
from ontology O
1
∃c
r1
∈ C
1
and ∃c
r2
∈ C
2
where (c
r1
, c
r2
) ∈ Align(O
1
, O
2
),
for which λ(O
1
, c
r1
) is maximal.
For all modified ontologies (according to the evolu-
tion scenarios described above), values of δ have been
designated. The results, shown in Table 2, demon-
strate that the developed measure δ returns intuitive
values. The evolution scenarios have been designed
such that in the case of Scenario 1, 2, 3, and 5 we
expected the growth of knowledge. Scenarios 7, 8,
and 9 are based on removing concepts- it is related to
knowledge decrease. Knowledge increase in Scenar-
ios 4 and 6 is not expected. On the one hand, we add
concepts. On the other hand, in Scenario 4 we added
concepts in such a place in an ontology that there is
no effect on the growth of knowledge. In Scenario
6, new concepts are copied from one ontology to an-
other, therefore, one ontology becomes similar to the
other. This entails that the level of knowledge stored
in ontologies does not increase. Most of the values
of δ are in line with our expectations. However, δ
measures evaluate knowledge increase from the per-
spective of entire ontologies. Single or not significant
changes do not influence the δ values, and results are
invalid in terms of the direction of change (an increase
or a decrease).
The results of the experiments have been statis-
tically analyzed. We accepted a significance level
α = 0.05. We decided to verify a correlation between
δ values and the percentages of changes applied in
ontologies. We assumed, that the changes have been
calculated as the number of added/removed concepts
divided by the number of all concepts in the initial
state of an ontology. In the case of adding concepts,
the obtained score is multiplied by 100%, and in the
case of removing concepts by -100%.
In the first step, we have checked the normal dis-
tribution of the analyzed samples. We rejected the hy-
pothesis about the normal distribution of the sample,
so we have calculated Spearman’s rank correlation
coefficient, and we obtain a value equal to 0.603969
and p-value equals 1.13e
−15
. It allows us to conclude
that there exists a moderate positive correlation be-
tween δ value and the percentage number of changes
applied in ontologies. It proved the correctness of our
assumption and allows us to conclude that changes in
ontologies and their mappings influence the assess-
ment of knowledge increase.
The results allow us to decide which alignment is
the most valuable. If we need need to choose for ex-
ample for EDAS ontology the most important map-
pings we need to analyze pairs: 8, 10, and 5. As we
can see, the biggest value of µ = 0.6 is for the pair:
Edas-Sofsem. The alignment for this pair of ontolo-
gies should be maintained and frequently validated.
6 FUTURE WORKS AND
SUMMARY
Two ontologies that can be aligned by a set describing
mappings of their elements can be easily merged into
one unified knowledge structure. Therefore, they both
carry some synergic knowledge potential. However,
in modern days it is impossible to expect that ontolo-
gies will not change in time. Their evolution influ-
ences their mappings and in consequence their syner-
gic knowledge. In this paper, we presented a measure
that can be used to estimate how much knowledge
about interoperability of two ontologies has been ac-
quired or lost through the process of updating ontolo-
gies and their alignment.
The paper contains both formal, mathematical
definitions, and verification of the developed measure.
The experiment involved simulating ontology evolu-
tion according to the predefined scenarios. It has been
conducted using widely accepted benchmark ontolo-
gies provided by Ontology Alignment Evaluation Ini-
tiative. Collected results have been statistically ana-
lyzed, which proved the correctness of our ideas and
intuitiveness of the developed measure.
In the future, we plan to extend the proposed
methods to other levels of ontologies, namely rela-
tions and instances. We will also perform more exten-
sive experiments that will involve larger ontologies,
possibly from a medical domain.
ACKNOWLEDGEMENTS
This research project was supported by grant No.
2017/26/D/ST6/00251 from the National Science
Centre, Poland.
ENASE 2021 - 16th International Conference on Evaluation of Novel Approaches to Software Engineering
178

Table 2: The results of experiment.
No. of evolution sce-
nario
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
No changes µ =
(O
(0)
1
, O
(0)
2
)
0.3451 0.5205 0.4612 0.278 0.272 0.1524 0.2648 0.6001 0.2545 0.4371 0.1705 0.3516 0.043 0.125 0.3523 0.5347
δ(O
(1)
1
, O
(1)
2
, O
(0)
1
, O
(0)
2
) 12.88 1.23 -0.2 -1.74 20.99 64 13.66 -3.44 17.68 6.97 77.92 34.29 297.36 50.88 16.05 6.4
δ(O
(2)
1
, O
(2)
2
, O
(0)
1
, O
(0)
2
)
21.24 56.55 47.95 28.57 36.45 29.41 32.8 60.52 33.62 50 36.92 50 22.35 22.27 43.88 59.46
δ(O
(3)
1
, O
(3)
2
, O
(0)
1
, O
(0)
2
) 29.79 7.92 11.04 20.81 50.44 120.68 33.37 4.01 47.12 21.44 253.24 49.3 552.13 109.18 32.22 17.92
δ(O
(4)
1
, O
(4)
2
, O
(0)
1
, O
(0)
2
) -8.87 -10.98 -13.08 -12.7 -16.07 -21.53 -20.44 -12.18 -28.88 -21.84 -21.43 -18.39 -33.9 -22.31 -1.97 -22.99
δ(O
(5)
1
, O
(5)
2
, O
(0)
1
, O
(0)
2
) -2.06 17.33 6.36 2.65 65.1 24 105.03 34.02 28.65 10.35 140 19.25 647.23 301.02 36.92 3.9
δ(O
(6)
1
, O
(6)
2
, O
(0)
1
, O
(0)
2
) 4.05 -9.52 9.43 -23.79 39.28 -3.53 87.4 23.75 0.35 -3.06 107.78 9.49 489.47 332.85 22.22 -20.93
δ(O
(7)
1
, O
(7)
2
, O
(0)
1
, O
(0)
2
) -0.14 -9.32 21.15 -35.6 -22.57 -100 -13.73 -9.23 -49.24 -13.23 -20.56 -11.8 -100 50.38 -14.16 -27.69
δ(O
(8)
1
, O
(8)
2
, O
(0)
1
, O
(0)
2
) -3.72 8.06 -6.55 -28.15 -13.45 -36.1 -4.05 -4.45 -4.91 -5.63 -28.46 2.51 -100 -33.14 7.19 1.13
δ(O
(9)
1
, O
(9)
2
, O
(0)
1
, O
(0)
2
) -65.12 -8.9 -5.13 -32.22 -36.15 -81.65 -46.9 -16.79 -88.02 -50.68 22.79 -14.85 -59.66 -74.76 -1.03 -41.02
A Method for Estimating Potential Knowledge Increase after Updating Ontology Mapping
179

REFERENCES
((accessed June 17, 2020)). LogMap. https://www.cs.ox.ac.
uk/isg/tools/LogMap/.
((accessed June 17, 2020)). OAEI. http:
//engineering.purdue.edu/~mark/puthesihttp:
//oaei.ontologymatching.org/.
Algergawy, A., Faria, D., Ferrara, A., Fundulaki, I., Harrow,
I., Hertling, S., Jiménez-Ruiz, E., Karam, N., Khiat,
A., Lambrix, P., et al. (2019). Results of the ontology
alignment evaluation initiative 2019. In CEUR Work-
shop Proceedings, volume 2536, pages 46–85.
Dragisic, Z., Ivanova, V., Lambrix, P., Faria, D., Jiménez-
Ruiz, E., and Pesquita, C. (2016). User validation in
ontology alignment. In International Semantic Web
Conference, pages 200–217. Springer.
Ivanova, V., Bach, B., Pietriga, E., and Lambrix, P. (2017).
Alignment cubes: Towards interactive visual explo-
ration and evaluation of multiple ontology alignments.
In International Semantic Web Conference, pages
400–417. Springer.
Kiourtis, A., Mavrogiorgou, A., Menychtas, A., Maglogian-
nis, I., and Kyriazis, D. (2019). Structurally mapping
healthcare data to hl7 fhir through ontology align-
ment. Journal of Medical Systems, 43(3):62.
Kolyvakis, P., Kalousis, A., Smith, B., and Kiritsis, D.
(2018). Biomedical ontology alignment: an approach
based on representation learning. Journal of biomedi-
cal semantics, 9(1):1–20.
Kozierkiewicz, A. and Pietranik, M. (2019). Updating on-
tology alignment on the concept level based on ontol-
ogy evolution. In European Conference on Advances
in Databases and Information Systems, pages 201–
214. Springer.
Kozierkiewicz, A. and Pietranik, M. (2020). Updating on-
tology alignment on the relational level based on on-
tology evolution. In Proceedings of the 15th Interna-
tional Conference on Evaluation of Novel Approaches
to Software Engineering - Volume 1: ENASE, pages
241–248.
Leal, G. S., Guédria, W., Panetto, H., and Proper, E. (2017).
Towards a semi-automated tool for interoperability as-
sessment: An ontology-based approach. In Inter-
national Conference on Software Process Improve-
ment and Capability Determination, pages 241–254.
Springer.
Li, H., Dragisic, Z., Faria, D., Ivanova, V., Jiménez-Ruiz,
E., Lambrix, P., and Pesquita, C. (2019). User valida-
tion in ontology alignment: functional assessment and
impact. The Knowledge Engineering Review, 34.
Shvaiko, P. and Euzenat, J. (2011). Ontology matching:
state of the art and future challenges. IEEE Transac-
tions on knowledge and data engineering, 25(1):158–
176.
Shvaiko, P., Euzenat, J., Jiménez-Ruiz, E., Cheatham, M.,
and Hassanzadeh, O. (2018). Ontology matching:
Om-2018: Proceedings of the iswc workshop.
Solimando, A., Jimenez-Ruiz, E., and Guerrini, G. (2017).
Minimizing conservativity violations in ontology
alignments: Algorithms and evaluation. Knowledge
and Information Systems, 51(3):775–819.
Thiéblin, E., Cheatham, M., Trojahn, C., and Zamazal, O.
(2020). A consensual dataset for complex ontology
matching evaluation. The Knowledge Engineering Re-
view, 35.
ENASE 2021 - 16th International Conference on Evaluation of Novel Approaches to Software Engineering
180
