Towards Repairing Scenario-Based Models with Rich Events

Guy Katz

The Hebrew University of Jerusalem, Jerusalem, Israel

Keywords:

Scenario-Based Modeling, Program Repair, Model Checking, Constraint Solvers, SMT Solvers.

Abstract:

Repairing legacy systems is a difﬁcult and error-prone task: often, limited knowledge of the intricacies of

these systems could make an attempted repair result in new errors. Consequently, it is desirable to repair

such systems in an automated and sound way. Here, we discuss our ongoing work on the automated repair

of Scenario-Based Models: fully executable models that describe a system using scenario objects that model

its individual behaviors. We show how rich, scenario-based models can be model-checked, and then repaired

to prevent various safety violations. The actual repair is performed by adding new scenario objects to the

model, and without altering existing ones — in a way that is well aligned with the principles of scenario-based

modeling. In order to automate our repair approach, we leverage off-the-shelf SMT solvers. We describe the

main principles of our approach, and discuss our plans for future work.

1 INTRODUCTION

Modeling complex systems is a painstaking and dif-

ﬁcult task. Even once a suitable model has been

created, and the system in question has been imple-

mented and deployed, the model may still need to be

changed as part of the system’s life cycle — for exam-

ple, if bugs are discovered, or if the speciﬁcation of

the system is changed. This post-deployment altering

of systems and models, which we refer to as repair, is

a challenging undertaking: even if the desired change

is small, i.e. if it only affects a small portion of the

system’s operations, attempting a ﬁx could have un-

desirable consequences. For example, dependencies

between various system components, which have not

been property modeled or documented, could make

changing one component affect other components in

unintended ways. This problem is typically com-

pounded by lack of knowledge — because the engi-

neers who developed the system are unavailable, or

have forgotten crucial details. Thus, as program re-

pair is frequently needed, we require formalisms and

tools that will allow us to automatically repair sys-

tems and models in a safe and convenient way.

One promising approach for tackling this dif-

ﬁculty is through modeling techniques that fa-

cilitate model repair. Scenario-Based Modeling

(SBM) (Damm and Harel, 2001; Harel and Marelly,

2003; Harel et al., 2012b) is a notable candidate that

ﬁts this description. In SBM, systems are modeled

through the speciﬁcation of scenario objects: objects

that represent individual behaviors of the system be-

ing modeled. Each of these objects describes either

behavior that the system should uphold, or behavior

that it should avoid. Although each object is only

tasked with governing a narrow aspect of the over-

all system behavior, the resulting model is fully exe-

cutable — i.e., the various objects can be composed

together and executed, in a way that achieves the over-

all system goals. This execution is performed by an

event selection mechanism, which is in charge of ex-

ecuting the objects simultaneously and synchronizing

them in a way that produces cohesive behavior. Stud-

ies have shown that SBM is nicely aligned with how

humans perceive systems, and that it consequently

fosters abstract programming (Gordon et al., 2012;

Alexandron et al., 2014).

Although SBM was designed as a general model-

ing framework, not particularly geared towards model

repair, prior work has shown its compatibility with

various formal analysis techniques, such as model-

checking (Harel et al., 2011) and automated re-

pair (Harel et al., 2014). This compatibility stems

from the fact that scenario objects in a scenario-based

(SB) model interact through the well deﬁned interface

of the event selection mechanism, making it possible

to automatically construct a model of the full, com-

posite system, and then analyze it. Tools and tech-

niques have been devised to model-check and repair

safely and liveness violations in SB models (Harel

et al., 2011; Harel et al., 2011), to automatically

optimize and distribute these models (Harel et al.,

362

Katz, G.

Towards Repairing Scenario-Based Models with Rich Events.

DOI: 10.5220/0010373403620372

In Proceedings of the 9th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2021), pages 362-372

ISBN: 978-989-758-487-9

 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved

2013a; Harel et al., 2015a; Steinberg et al., 2017), and

to identify emergent properties thereof (Harel et al.,

2018).

Recently, it has been observed that while SBM

is well equipped for modeling reactive systems, it is

sometimes inadequate for modeling systems that han-

dle data — for example, robotics and autonomous ve-

hicle systems (Katz et al., 2019; Katz, 2020), which

involve various mathematical computations in addi-

tion to their reactivity. To this end, researchers have

extended the SBM principles, allowing the event se-

lection mechanism to support rich events, i.e. events

that carry various types of data. These enhancements

have proven quite useful for modeling more complex

systems, but are unfortunately incompatible with ex-

isting formal analysis and repair techniques for SBM,

which rely on the simplistic nature of the event selec-

tion mechanism. This has raised the following ques-

tion: are the automated analysis beneﬁts afforded by

SBM limited to the simple models, or do these carry

over when SBM is used in richer settings?

Here, we begin to answer this question, by de-

vising analysis techniques for rich SBM. Speciﬁcally,

we focus on program repair: we show how, using ap-

propriate extensions, the automated repair techniques

proposed for SBM carry over when richer events are

introduced and more complex systems are modeled.

At the core of our proposed extension is the abil-

ity to automatically extract the underlying transition

graphs of SB models with rich events, through the

use of SMT solvers — a powerful family of auto-

mated solvers that can reason about ﬁrst order logic

theories, such as arithmetic. We propose an SMT-

based method for constructing SBM transition graphs,

which effectively reduces sets of inﬁnitely many pos-

sible events into a ﬁnite set of possibilities that need to

be explored. Although our work is focused primarily

on program repair, we believe it will allow the exten-

sion of other automated analysis techniques to the rich

SBM setting.

The rest of this paper is organized as follows. In

Section 2 we provide the necessary background on

SBM, and its extension to handle rich events. Next, in

Section 3 we present our core technique for automat-

ically extracting the underlying transition graphs of

SB models with rich events. We then show how this

technique enables us to automatically model-check

and repair SB models with rich events in Section 4.

We discuss related work in Section 5, and conclude in

Section 6.

2 BACKGROUND

2.1 Vanilla Scenario-Based Modeling

The multiple variants of SBM that have been pro-

posed typically include a set of scenario objects that

are run in parallel, and repeatedly synchronize with

each other. the most commonly used synchronization

idioms (Harel et al., 2012b) include:

1. requesting events: a scenario object can request

event e, indicating that it wishes that e be trig-

gered. Intuitively, e represents some desirable be-

havior that the system should now perform.

2. waiting-for events: a scenario object may wait-for

an event, i.e. state that it wishes to be notiﬁed

when that event is triggered. However, the object

does not actively request this event. The waiting-

for idiom is useful, for example, when an object

is waiting for some sequence of external events to

mark that it should perform some actions in re-

sponse.

3. blocking events: when a scenario object blocks

event e, it prevents the overall system from trig-

gering it — even if e was requested by another

object. Intuitively, this is how components can in-

dicate undesirable behavior, which the system is

forbidden from performing.

We refer to the SBM variant that consists of these id-

ioms as vanilla SBM, or vSBM, for short. in vSBM,

each scenario object deﬁnes a set of synchronization

points, and in each of these points it declares its sets of

requested, waited-for and blocked events. The event

selection mechanism collects these declarations from

all objects; selects for triggering one enabled event,

i.e. an event that is requested and not blocked; and

then informs all the objects that requested or waited-

for this event about the selection. These objects then

progress to their next synchronization point, and the

process is repeated as the execution continues.

A toy example, borrowed from (Harel et al.,

2014), is depicted in Fig. 1. The model that appears

therein belongs to a system that controls the water

level in a tank. Adding water can be done from ei-

ther a hot water tap or a cold water tap. The various

scenario objects are each depicted as a transition sys-

tem: the nodes represent the object’s synchronization

points, and they are labeled with the events that are re-

quested, waited-for and blocked in those points. The

scenario object ADDHOTWATER repeatedly waits for

WATERLOW events and requests three times the event

ADDHOT; and the scenario object ADDCOLDWATER

performs a symmetrical operation with cold water. If

Towards Repairing Scenario-Based Models with Rich Events

363

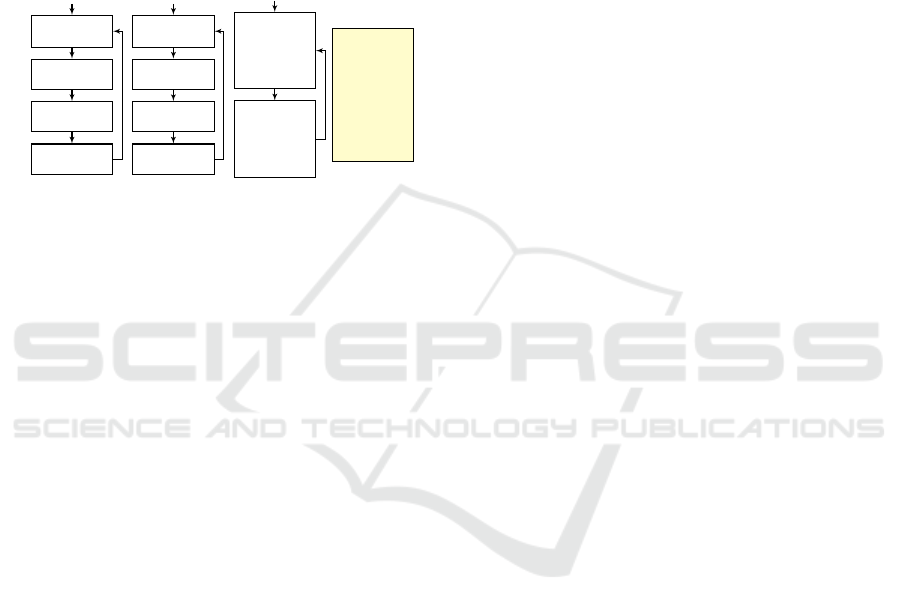
the model only includes these two objects, ADDHOT-

WATER and ADDCOLDWATER, the three ADDHOT

events and three ADDCOLD events may be triggered

in any order when the model is executed. If, for exam-

ple, we wish to maintain a steady water temperature,

we may add the scenario object STABILITY in order to

enforce the interleaving of ADDHOT and ADDCOLD

events, by using event blocking. The execution trace

of the resulting model (with all three objects) is de-

picted in the event log.

wait for

WATERLOW

request

ADDHOT

request

ADDHOT

request

ADDHOT

ADDHOTWATER

wait for

WATERLOW

request

ADDCOLD

request

ADDCOLD

request

ADDCOLD

ADDCOLDWATER

wait for

ADDHOT

while

blocking

ADDCOLD

wait for

ADDCOLD

while

blocking

ADDHOT

STABILITY

···

WATERLOW

ADDHOT

ADDCOLD

ADDHOT

ADDCOLD

ADDHOT

ADDCOLD

···

EVENT LOG

Figure 1: (From (Harel et al., 2014)) A scenario-based

model of a system that controls the water level in a tank

with hot and cold water taps.

We follow the deﬁnitions of (Katz, 2013), and for-

malize the vSBM framework as follows. Given some

ﬁnite event set E, we deﬁne a scenario object O as the

tuple O = hQ,δ,q

,R,Bi, where the interpretation of

the components is as follows:

• Q is a set of states. Each state represents a prede-

termined synchronization point.

• q

∈ Q is the initial state.

• R and B are mappings, R,B : Q → 2

. They map

states to set of events requested (R) and blocked

(B) at those states.

• δ : Q×E → 2

is a transition function. It indicates

how the object reacts when an event is triggered,

i.e. if q

∈ δ(q,e) then the object can transition to

state q

when event e is triggered in state q.

We sometimes refer to this tuple as the underlying

transition graph of scenario object O.

The composite model speciﬁed by a set of sce-

nario objects is deﬁned using a composition oper-

ator, which combines two scenario objects into a

single, larger scenario object, as follows. For two

scenario objects O

= hQ

,δ

i and O

,δ

i, both over a common event set

E, we deﬁne the composite scenario object O

k O

as O

k O

= hQ

× Q

,δ,hq

i,R

∪ R

∪ B

where:

• The transition relation is deﬁned element-wise,

i.e. h ˜q

, ˜q

i ∈ δ(hq

i,e) if and only if ˜q

∈

,e) and ˜q

∈ δ

,e).

• The labeling of a composite state is the union

of the element-wise labeling, i.e. e ∈ (R

∪

)(hq

i) if and only if e ∈ R

) ∪ R

and e ∈ (B

∪ B

)(hq

i) if and only if e ∈

) ∪ B

Finally, we deﬁne a behavioral model M as a collec-

tion of scenario objects O

,... ,O

. The execu-

tions of M are then deﬁned to be the executions of

the composite scenario object O = O

k O

k . .. k O

Each execution of M starts from the initial state of O,

and in each state q along the run it selects for trigger-

ing an enabled event, i.e., an event e ∈ R(q) − B(q)

(if no such event exists, the execution terminates in

a deadlock). Then, the execution moves to a state

˜q ∈ δ(q, e), and so on.

In practice, users very seldom describe models

by providing the transition graphs of their scenario

objects. Instead, SBM has been implemented in

a variety of tools, either as dedicated frameworks

(e.g., the Play-Engine tool for Live Sequence Charts

(LSC) (Harel and Marelly, 2003) or the Scenari-

oTools (Greenyer et al., 2017) engine), or on top

of popular programming languages, such as JavsS-

cript (Bar-Sinai et al., 2018), Python, Java (Harel

et al., 2010) and C++ (Harel and Katz, 2014). SBM

has been used in modeling complex systems, such

as robotic controllers (Elyasaf et al., 2019; Gritzner

and Greenyer, 2018), web-servers (Harel and Katz,

2014), smart buildings (Elyasaf et al., 2018), a nano-

satellite (Bar-Sinai et al., 2019), and cache coherence

protocols (Harel et al., 2016a).

2.2 Scenario-Based Modeling with Rich

Events

Although vanilla SBM has been successfully used in

various contexts, in recent years it was shown that it

may fall short in expressing various complex inter-

actions between scenario objects (Katz et al., 2019;

Katz, 2020; Elyasaf, 2020). Speciﬁcally, the sim-

ple event declaration mechanism — a ﬁnite set of

events E, and a ﬁnite set of requested, waited-for and

blocked events in every state, may be inadequate for

expressing more complex behaviors.

For example, consider a drone that needs to turn

left or right by a certain degree. Degrees are repre-

sented as real numbers, and an attempt to express this

using vanilla SBM would require either some loss of

precision, e.g. by discretizing the set of possible de-

grees; or the use of various hacks that circumvent the

SBM event selection mechanism, thus going against

the grain of SBM.

In line with the notions in (Katz et al., 2019), we

deﬁne rich SBM (rSBM) as follows: instead of dis-

MODELSWARD 2021 - 9th International Conference on Model-Driven Engineering and Software Development

364

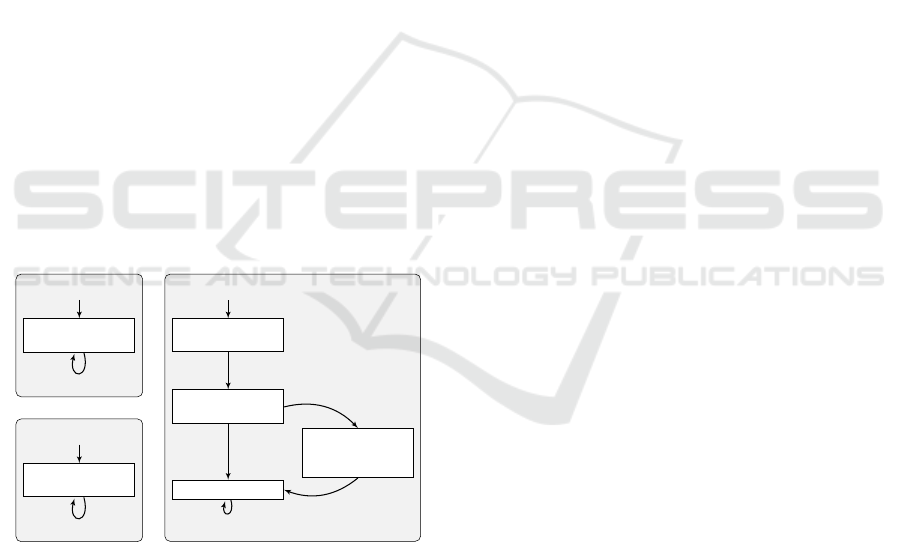
crete events, the event set E now contains a set of

real-valued variables. Each scenario object can now

request that certain variables in E be assigned cer-

tain values, and block certain variables from being as-

signed other values. Event selection then consists of

choosing a variable assignment that satisﬁes at least

one request, and violates none of the blocked assign-

ments.

An example appears in Fig 2. The model depicted

therein belongs to a system controlling a drone. The

event set E contains two real variables, E = {v, h},

representing the vertical and horizontal angular veloc-

ities of the drone, respectively. Each round of event

selection assigns new values to these variables. Sce-

nario object 1 poses hard limits of v, due to mechan-

ical limitations in the drone; and scenario object 2

poses similar constraints on h. Scenario object 3, in

charge of navigating the drone to its destination, re-

quests an ascent at an angular velocity of at least 2

degrees per second (v ≥ 2), while not turning left or

right (h = 0). Afterwards, it requests a right turn at

10 degrees per second or more (h ≥ 10), while block-

ing the drone from changing altitude or turning left

(v 6= 0 ∨ h < 0). Depending on the actual right turn

that was performed, the object might request an ad-

ditional right turn at 10 degrees per second, this time

forcing the drone to turn by blocking all other possi-

ble assignments. Finally, the object reaches its goal

state, and requests nothing more.

Block

h ≤ −20 ∨ h ≥ 20

true

Block

v ≤ −5 ∨ v ≥ 5

true

Request

v ≥ 2 ∧ h = 0

Request h ≥ 10

Block v 6= 0 ∨ h < 0

v ≥ 2 ∧h = 0

Request true

h ≥ 10

Request h ≥ 10

Block

h < 10 ∨ v 6= 0

h < 10

h ≥ 10

true

OBJECT 1

OBJECT 2

OBJECT 3

Figure 2: A model for controlling a drone, comprised of

three scenario objects. Each state lists the requested and

blocked assignment for that state; and the transitions are

given as guard formulas, where a transition can be traversed

if and only if the triggered assignment satisﬁes the guard.

Observe that the model in Fig. 2 again depicts the sce-

nario objects as transition systems. Further, the edges

do not list the (possibly inﬁnite) set of assignments

that trigger the transition, but instead list guard for-

mulas: an edge may be traversed only if the triggered

assignment satisﬁes the edge’s guard.

We formalize rich SBM as follows. The set E is

no longer a discrete set of events, but is instead a set of

real-valued variables E = {x

,... ,x

}. A scenario ob-

ject O is a tuple O = hQ,δ,q

,R,Bi, where Q is again

a set of states and q

∈ Q is an initial state. The label-

ing functions now map each state q ∈ Q into a ﬁrst-

order, linear real arithmetic formula. Speciﬁcally,

these formulas can impose linear constraints on the

variables e.g., x

≥ 5 or x

≤ x

, and can have ar-

bitrary Boolean structure: e.g., (x

≥ 5) → (x

≤

∨ x

< 7). The transition function δ : Q × R

→ 2

now deﬁnes how the state transitions for every possi-

ble assignment α that assigns a real value to each of

the variables x

,... ,x

For two scenario objects O

= hQ

,δ

and O

= hQ

,δ

i, both over a common

variable set E, we deﬁne the composite scenario ob-

ject O

k O

as O

k O

= hQ

× Q

,δ,hq

i,R

∨

∨ B

i. As before, the transition relation is de-

ﬁned element-wise, i.e. h ˜q

, ˜q

i ∈ δ(hq

i,e) if and

only if ˜q

∈ δ

,e) and ˜q

∈ δ

,e). The compos-

ite formulas that represent the requested and blocked

events are deﬁned as the disjunctions of the element-

wise formulas: R

∨ R

(hq

i) = R

) ∨ R

)

and B

∨ B

(hq

i) = B

) ∨ B

The rich behavioral model M is now deﬁned as a

collection of rich scenario objects O

,... ,O

. The

executions of M are then deﬁned to be the executions

of the composite scenario object O = O

k O

k . .. k

. Each execution of M starts from the initial state

of O, and in each state q along the run it selects for

triggering a variable assignment α, that satisﬁes the

formula

R(q) ∧ ¬B(q).

In other words, the selected assignment satisﬁes the

request of at least one component object, and does not

contradict the blocking declarations issued by any ob-

ject. Then, the execution moves to a state ˜q ∈ δ(q,α),

and so on.

In practice, the discovery of an assignment that

satisﬁes the given constraints can be performed us-

ing various automated solvers, such as LP or SMT

solvers (Harel et al., 2020). Because we restrict

our constraints to ﬁrst-order, quantiﬁer-free linear

real arithmetic, they can be resolved in polynomial

time (Barrett and Tinelli, 2018).

3 FORMALLY ANALYZING RICH

SCENARIO-BASED MODELS

Much work has been put into performing formal, au-

tomated analysis of SB models (e.g., (Harel et al.,

2011; Katz, 2013; Harel et al., 2018)). The cor-

Towards Repairing Scenario-Based Models with Rich Events

365

nerstone of these techniques is the automated ex-

traction of the underlying transition graph of an SB

model M = {O

,... ,O

} given in some high-level

language, such as C++. Intuitively, this is done in two

steps (Katz, 2013):

1. The underlying transition graph of each sce-

nario object O

is extracted independently, di-

rectly from its code. This process is performed by

iteratively exploring the object’s synchronization

points. Starting at the initial state q

, each non-

blocked event e ∈ E is triggered, and the object’s

reaction to e is recorded. If the object transitions

to some state q, then the edge q

→ q is added

to its transition graph. If q is a previously unvis-

ited state, it is added to a queue for later inspec-

tion. The process repeats until all possible events,

in all reachable states, have been considered and

mapped.

2. Once the transition graph for each scenario object

has been extracted, these graphs are composed

to produce the composite transition graph of M

(according to the composition operator deﬁned in

Section 2).

A key point in this construction is that the event set

E is ﬁnite. In particular, in Step 1 this allows us to

exhaustively trigger each non-blocked event in each

state, and check how the object transitions. In order

to apply a similar technique to rSB models, this step

needs to be adjusted; speciﬁcally, in an rSB model,

the discrete set of enabled events is replaced with a

variable assignment, and because there are inﬁnitely

many such assignments, enumerating them is impos-

sible. Step 2, on the other hand, remains unchanged

also when reasoning about rSBM, and can be applied

to construct the composite transition graph.

The method that we propose for extracting the

transition graph from a scenario object is as follows.

We make the observation that although there are in-

ﬁnitely many variable assignments that the object

needs to react to, these are typically grouped into a

ﬁnite number of possibilities that the object handles

in the same way. Consider, for example, the follow-

ing code snippet that deﬁnes a rich scenario object in

some high-level language:

sync ( request=(x < 5) );

if ( x ≥ 2 )

A();

else

B();

Here, the object synchronizes (using the sync key-

word) and requests that x be assigned a value less than

5. Then, when the synchronization call returns, i.e.

when x has been assigned a value smaller than 5, the

object performs A() if x ≥ 2, and B() otherwise. Thus,

there is no difference between x = 3 and x = 4, as far

as the underlying transition graph is concerned; in ei-

ther case, the object will transition into the same state

(the next synchronization point in A). Additionally,

the relevant predicates, i.e. (x ≥ 2) in this case, are

already available to us: we can ﬁnd them by simply

parsing the code of the scenario object, and collecting

all the predicates that appear therein.

We thus propose the following approach. Given

a scenario object O in some high-level language, we

ﬁrst parse its code and produce the set P

of all pred-

icates that appear in O — either as formulas within

its synchronization points, or elsewhere in the code.

Next, at every state q of O, we observe the power-set

, and for each element hϕ

,... ,ϕ

i ∈ 2

we use

an SMT solver to come up with a concrete assignment

for which ϕ =

i=1

holds. If such an assignment α

exists, we trigger it at state q, and record

→ q

in our transition graph. The full algorithm appears as

Alg. 1.

Algorithm 1: Extract Transition Graph(O).

1: P ← all predicates in O

2: Q.push(q

)

3: while Q not empty do

4: q ← Q.pop()

5: for hϕ

,... ,ϕ

i ∈ 2

6: ϕ ←

i=1

7: α ← SMT(ϕ)

8: if α 6= ⊥ then

9: Invoke α in state q, mark new state as q

10: Add q

→ q

to transition graph

11: if q

not previously visited then

12: Q.push(q

)

13: end if

14: end if

15: end for

16: end while

For soundness, we have the following lemma. The

proof, by induction on the path length, is straightfor-

ward and is omitted.

Lemma 1. Let M be an rSB model, and let G be its

transition graph constructed by Alg. 1. Then any ex-

ecution path q

,... of M, either ﬁnite or inﬁnite,

corresponds to a path s

,... in G, and vice versa.

A natural concern is about the size of the power

set, 2

. We argue that this size is quite manage-

able: indeed, scenario objects tend to be short and

MODELSWARD 2021 - 9th International Conference on Model-Driven Engineering and Software Development

366

concise, as they deal only with speciﬁc aspects of the

system in question. Thus, spanning the individual

transition graphs should be doable, even for large sys-

tems. Of course, computing the composite transition

graph in Step 2 might suffer from the infamous state

explosion problem, which is common in veriﬁcation.

Here, one possible solution is to break the model up

into sub-models, and reason about each of them sep-

arately; there exist techniques for doing this (Harel

et al., 2013a), but they are out of our scope here.

Example. Observe the following pseudo-code, which

represents Object 3 from Fig. 2:

sync ( request = (v ≥ 2 ∨ h = 0) );

sync ( request = (h ≥ 10), block = (v 6= 0 ∨ h < 0));

if ( h < 10 )

sync ( request = (h ≥ 10),

block = (v 6= 0 ∨ h < 10) );

sync ( request = (true) );

In this case, syntactically constructing the set P

yields:

= {v ≥ 2,h = 0,h ≥ 10, v = 0, h < 0}

(we do not need to consider a predicate and its nega-

tion, e.g. h ≥ 10 and h < 10, twice). Thus, the power

set 2

has 32 elements. One of these elements is

hv ≥ 2,h = 0i. Passing the constraint v ≥ 2 ∧ h = 0

to an SMT solver yields a concrete assignment, e.g.

v = 3,h = 0. Finally, triggering this assignment in

state q

, which is the ﬁrst synchronization point of

this scenario object, reveals a new state which cor-

responds to the second synchronization point. How-

ever, triggering the element {v = 0} does not result

in reaching a new state: the scenario object did not

request this assignment, and so it does not wake up

from the synchronization call.

Repeating this process to saturation produces a

transition graph equivalent to the one depicted in

Fig. 2. (In order to reduce clutter in the resulting

graph, some transitions can then be merged together

by additional invocations of the SMT solver; applying

this approach is part of our ongoing work.)

4 FORMALLY ANALYZING rSBM

Model Checking Rich SBM. Given Lemma 1, it is

straightforward to devise a model-checking algorithm

for rSBM models. Given a model M and a safety

property ϕ, we can construct the transition graph G

of M, compose it with ϕ, and then check whether

there are any reachable states that violate ϕ. The

rSBM formalism is sufﬁciently expressive to formu-

late the property ϕ itself as a scenario object that sim-

ply marks some of its states as bad. Then, the same

techniques from Section 3 can be used to extract the

composite transition graph.

We demonstrate this process with an example. Let

us review again the model from Fig. 2, and let us con-

sider a safety property stating that it is forbidden for

the drone to turn sharply, either vertically or horizon-

tally, twice in a row. This property can be encoded as

the scenario object that appears in Fig. 3. This object

never requests or blocks anything; it only waits for

two consecutive events in which the horizontal or ver-

tical angular velocities were high (|h| ≥ 18 or |v| ≥ 4,

respectively). If such two consecutive events are de-

tected, the object marks the state as bad.

Request

Block

Request

Block

Bad

|v| ≥ 4 ∨|h| ≥ 18

|v| < 4 ∧|h| < 18

Figure 3: Encoding a safety property as an rSBM scenario

object.

By composing this new scenario object with the

model depicted in Fig. 2 and searching for reach-

able bad states (e.g., using BFS), we can determine

that a safety violation is possible. Further, using the

concrete variable assignments returned by the SMT

solver, we can provide a counter-example that demon-

strates this, e.g.: the triggering of hv = 5,h = 0i

and then of hv = 0,h = 20i, which is allowed by the

model.

Repairing Rich SBM Modes. Given an rSB model

M and a violated safety property ϕ, we now seek to re-

pair M so that ϕ becomes satisﬁed. Our goal is to cut

off any bad states in the underlying transition graph

G, so that they become unreachable from the initial

state q

. Further, we wish to cut off only paths that

lead, or are guaranteed to lead, to a violating state;

that is, we do not wish to remove any runs that are not

violating.

To this end, we follow an approach proposed

for repairing vSBM (Harel et al., 2014) and utilize

the blocking idiom to create patch scenario objects.

Speciﬁcally, we propose to add to the scenario-based

model an additional scenario object that will apply

blocking at selected points during the execution, so as

to cut off the reachable bad states from the transition

graph. The algorithm for performing this repair has

the following steps: (i) given a behavioral model M

Towards Repairing Scenario-Based Models with Rich Events

367

and a scenario object for a violated safety property ϕ,

we extract the composite transition graph of M and ϕ,

as previously described. We then apply BFS to iden-

tify the set B of all reachable bad states in this graph;

(ii) next, we iteratively search for states currently not

in B, i.e. q /∈ B, such that all of their outgoing edges

lead to B, i.e. q → q

⇒ q

∈ B. Any such state is guar-

anteed to eventually lead to a violating state, and so is

added to B, i.e. B := B∪{q}. This process is repeated

until we reach a ﬁxed point, and no new states can be

added to B; (iii) ﬁnally, we add a new scenario object

to the model that keeps track of the execution, and

blocks precisely those edges that lead to states in B.

Intuitively, this process cuts off precisely those states

that are either bad themselves, or are guaranteed to

lead to a bad state in a ﬁnite number of steps. Thus,

we only remove runs that violate the safety property

in question, and no others. Additionally, we create no

new bad runs, and do not introduce any deadlocks.

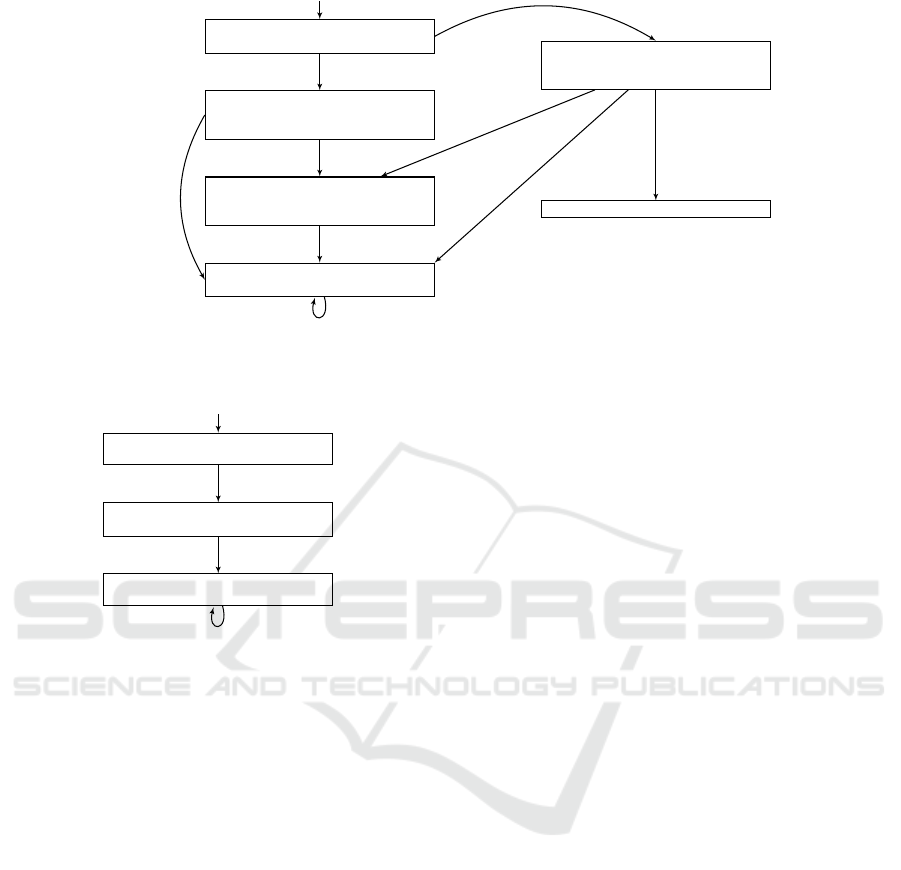
We demonstrate this process using the rSB model

from Fig. 2 and the violated safety property from

Fig. 3. The full, composite transition graph of this

model (including the safety property) is depicted in

Fig. 4. Unsurprisingly, there is a reachable bad state

in this model (state q

). Our repair algorithm thus

starts from state q

, i.e. B = {q

}, and identiﬁes all

states with edges leading to q

; in this case, state q

Because state q

has edges leading also to states not

marked as bad (states q

and q

), it is not added to the

set B of bad states. Thus, the algorithm generates a

new scenario object such that, when composed with

the existing scenario objects, will apply blocking to

prevent state q

from transitioning into state q

This new scenario object is depicted in Fig. 5. It

merely waits for the sequence of events that would

send the original model into state q

, namely an as-

signment that satisﬁes v ≥ 4 ∧ h = 0; then blocks the

assignments that would send the original model into

state q

, namely h ≥ 18; and then does nothing else

for the remainder of the run.

For soundness, we have the following lemma

(proof omitted):

Lemma 2. Let M be an rSB model with reachable

bad states, and let M

be this model augmented with a

patch scenario object, as explained above. The set of

runs of M

is then precisely the set of runs of M, with

all violating runs removed.

We note that, while we have focused here on

model checking and repairing safety violations in rSB

models, similar operations can be performed also for

liveness properties. Given a liveness property ϕ, for-

mulated as a scenario object that marks some states as

good, we can check whether there exists a reachable

cycle in the composite rSB model that does not con-

tain any good states (Baier and Katoen, 2008). Fur-

ther, if we detect such a cycle, a patch scenario object

can be added to the model to prevent it, again using

the blocking idiom (Harel et al., 2014). We leave treat-

ment of this case for future work.

5 RELATED WORK

The general research question that this paper ad-

dresses, namely how to effectively model complex

systems and then repair these models, has been stud-

ied extensively. Here, we focused on the scenario-

based modeling paradigm, in which system behaviors

are modeled as scenarios (Damm and Harel, 2001;

Harel and Marelly, 2003; Harel et al., 2012b). There

are numerous related approaches for modeling event-

driven reactive systems: notable examples include Es-

terel (Berry and Gonthier, 1992), Lustre (Halbwachs

et al., 1991), Signal (Le Guernic et al., 1991), and

Petri Nets (Holloway et al., 1997). Similar concepts

appear also in component based programming lan-

guages, such as BIP (Basu et al., 2006). Some of our

repair techniques may be carried over to these frame-

works, provided that the blocking idiom, which is cru-

cial to our approach, is present or can be achieved

using other idioms. More broadly, scenario-based

modeling is adequate for modeling discrete event sys-

tems (Cassandras and Lafortune, 2009); and the re-

pair of SB models is related to the supervisory con-

trol problem of such systems (Ramadge and Wonham,

1987; Ramadge and Wonham, 1989).

Prior work has demonstrated how scenario-based

models may be automatically repaired (Katz, 2013;

Harel et al., 2014; Harel et al., 2012a), and here we

generalized and extended this approach to scenario-

based models with rich events — which are neces-

sary for modeling more complex systems (Katz et al.,

2019; Katz, 2021; Elyasaf et al., 2018; Bar-Sinai

et al., 2019). The automated repair problem in other

modeling and programming paradigms has also been

studied extensively: some examples include fault lo-

calization and automatic repair by identifying sets

of malfunctioning components and synthesizing re-

placement components (Staber et al., 2005b; Staber

et al., 2005a; Jobstmann et al., 2005); program repair

via semantic analysis (Nguyen et al., 2013); the au-

tomatic repair of concurrency-related bugs by analyz-

ing execution traces associated with bug reports (Jin

et al., 2011); applying genetic-programming to repair

legacy C programs (Weimer et al., 2010); combining

genetic-programming with co-evolution of test cases

until a bug is repaired (Arcuri and Yao, 2008); and

leveraging information regarding previous repairs (Le

MODELSWARD 2021 - 9th International Conference on Model-Driven Engineering and Software Development

368

Request v ≥ 2 ∧ h = 0

Block h ≤ −20 ∨h ≥ 20 ∨v ≤ −5 ∨v ≥ 5

Request h ≥ 10

Block v 6= 0 ∨ h < 0∨

h ≤ −20 ∨ h ≥ 20 ∨ v ≤ −5 ∨ v ≥ 5

2 ≤ v < 4 ∧h = 0

Request h ≥ 10

Block v 6= 0 ∨ h < 10∨

h ≤ −20 ∨ h ≥ 20 ∨ v ≤ −5 ∨ v ≥ 5

h < 10

Request true

Block h ≤ −20 ∨h ≥ 20 ∨v ≤ −5 ∨v ≥ 5

h ≥ 10

Request h ≥ 10

Block v 6= 0 ∨ h < 0∨

h ≤ −20 ∨ h ≥ 20 ∨ v ≤ −5 ∨ v ≥ 5

v ≥ 4 ∧h = 0

10 ≤ h < 18

h < 10

true

Bad

h ≥ 18

Figure 4: The composite transition graph of the model from Fig. 2, composed also with the scenario object for the safety

property form Fig. 3.

Request

Block

Request

Block h ≥ 18

v ≥ 4 ∧h = 0

Request

Block

true

Figure 5: The composite transition graph of the model from

Fig. 2, composed also with the scenario object for the safety

property form Fig. 3.

et al., 2016). Naturally, work on automatic-repair of

models and programs can be considered a particular

case of program synthesis (Pnueli and Rosner, 1989;

Bloem et al., 2012; Alur et al., 2013).

Scenario-based models have been automatically

analyzed in a variety of ways that go beyond re-

pair. Notable examples include compositional veriﬁ-

cation (Harel et al., 2013b; Harel et al., 2015c; Harel

et al., 2015b; Katz et al., 2015), automated optimiza-

tion (Greenyer et al., 2016b; Steinberg et al., 2018),

synthesis (Greenyer et al., 2016a), and speciﬁcation

mining (Marron et al., 2016; Harel et al., 2016b). It

will be interesting to extend these approaches to the

rSBM setting, using the techniques we have outlined

here.

Our proposed approach relies on constraint

solvers in order to construct the model’s underly-

ing transition graph. The use of such solvers in

the context of software modeling is expending, with

common use-cases typically revolving around formal

methods. Some examples include symbolic execu-

tion (P

areanu and Visser, 2009), bounded model-

checking (Biere et al., 1999), and concolic test-

ing (Sen, 2007). The aforementioned techniques, and

many others, showcase the beneﬁts that automated

solvers afford in the context of the various tasks that

arise as part of a software model’s life cycle.

6 CONCLUSION

Scenario-based modeling is promising approach for

designing and implementing complex systems: on

one hand, it is intuitive and well-aligned with human

perception of models, and on the other it is compat-

ible with automated analysis and repair of models.

Our initial results demonstrate that extending SBM to

support rich events, which may be required for mod-

eling various real-world systems, does not harm this

compatibility: speciﬁcally, it is still possible to span

the underlying transition systems of models, and use

these transition systems for model-checking and au-

tomated repair.

We regard this paper as a ﬁrst step in the direc-

tion of creating automated analysis tools for rSBM.

As part of our ongoing work we are pursuing sev-

eral directions: (i) implement our repair technique

on top of an existing rSBM platform, and evaluate

it on varied benchmarks; (ii) leverage our technique

for spanning rSBM transition graphs to automate ad-

ditional aspects of the system’s life cycle, such as op-

timization (Harel et al., 2015a) and speciﬁcation min-

ing (Harel et al., 2018); and (iii) further improve the

scalability of our technique for transition graph span-

ning. We hope that these lines of work will promote

the use of rSBM in additional systems and settings.

Towards Repairing Scenario-Based Models with Rich Events

369

ACKNOWLEDGEMENTS

The project was partially supported by grants from

the Binational Science Foundation (2017662) and the

Israel Science Foundation (683/18).

REFERENCES

Alexandron, G., Armoni, M., Gordon, M., and Harel, D.

(2014). Scenario-Based Programming: Reducing the

Cognitive Load, Fostering Abstract Thinking. In Proc.

36th Int. Conf. on Software Engineering (ICSE), pages

311–320.

Alur, R., Bodik, R., Juniwal, G., Martin, M., Raghothaman,

M., Seshia, S., Singh, R., Solar-Lezama, A., Torlak,

E., and Udupa, A. (2013). Syntax-Guided Synthesis.

Proc. of the IEEE, pages 1–8.

Arcuri, A. and Yao, X. (2008). A Novel Co-evolutionary

Approach to Automatic Software Bug Fixing. In Proc.

10th IEEE Congress on Evolutionary Computation

(CEC), pages 162–168.

Baier, C. and Katoen, J.-P. (2008). Principles of Model

Checking. MIT Press.

Bar-Sinai, M., Elyasaf, A., Sadon, A., and Weiss, G. (2019).

A Scenario Based On-Board Software and Testing En-

vironment for Satellites. In Proc. 59th Israel Annual

Conf. on Aerospace Sciences (IACAS), pages 1407–

1419.

Bar-Sinai, M., Weiss, G., and Shmuel, R. (2018). BPjs: An

Extensible, Open Infrastructure for Behavioral Pro-

gramming Research. In Proc. 21st ACM/IEEE Int.

Conf. on Model Driven Engineering Languages and

Systems (MODELS), pages 59–60.

Barrett, C. and Tinelli, C. (2018). Satisﬁability Modulo

Theories. In Clarke, E., Henzinger, T., Veith, H.,

and Bloem, R., editors, Handbook of Model Check-

ing. Springer.

Basu, A., Bozga, M., and Sifakis, J. (2006). Modeling Het-

erogeneous Real-time Systems in BIP. In Proc. 4th

IEEE Int. Conf. on Software Engineering and Formal

Methods (SEFM), pages 3–12.

Berry, G. and Gonthier, G. (1992). The Esterel syn-

chronous programming language: design, semantics,

implementation. Science of Computer Programming,

19(2):87–152.

Biere, A., Cimatti, A., Clarke, E., and Zhu, Y. (1999). Sym-

bolic Model Checking without BDDs. In Proc. 5th Int.

Conf. on Tools and Algorithms for the Construction

and Analysis of Systems (TACAS), pages 193–207.

Bloem, R., Jobstmann, B., Piterman, N., Pnueli, A., and

Saar, Y. (2012). Synthesis of Reactive(1) Designs.

Journal of Computer and System Sciences, 78(3):911–

938.

Cassandras, C. and Lafortune, S. (2009). Introduction to

Discrete Event Systems. Springer Science & Business

Media.

Damm, W. and Harel, D. (2001). LSCs: Breathing Life

into Message Sequence Charts. Journal on Formal

Methods in System Design (FMSD), 19(1):45–80.

Elyasaf, A. (2020). Context-Oriented Behavioral Program-

ming. Technical Report. https://arxiv.org/abs/2005.

02373.pdf.

Elyasaf, A., Marron, A., Sturm, A., and Weiss, G. (2018).

A Context-Based Behavioral Language for IoT. In

Proc. 5th Int. Workshop on Model-driven Robot Soft-

ware Engineering (MORSE), pages 485–494.

Elyasaf, A., Sadon, A., Weiss, G., and Yaacov, T. (2019).

Using Behavioral Programming with Solver, Con-

text, and Deep Reinforcement Learning for Playing

a Simpliﬁed RoboCup-Type Game. In Proc. 22nd

ACM/IEEE Int. Conf. on Model Driven Engineering

Languages and Systems Companion (MODELS-C),

pages 243–251.

Gordon, M., Marron, A., and Meerbaum-Salant, O. (2012).

Spaghetti for the Main Course? Observations on

the Naturalness of Scenario-Based Programming. In

Proc. 17th Conf. on Innovation and Technology in

Computer Science Education (ITICSE), pages 198–

203.

Greenyer, J., Gritzner, D., Gutjahr, T., K

onig, F., Glade,

N., Marron, A., and Katz, G. (2017). ScenarioTools

— A Tool Suite for the Scenario-based Modeling and

Analysis of Reactive Systems. Journal of Science of

Computer Programming (J. SCP), 149:15–27.

Greenyer, J., Gritzner, D., Katz, G., and Marron, A.

(2016a). Scenario-Based Modeling and Synthesis for

Reactive Systems with Dynamic System Structure in

ScenarioTools. In Proc. 19th ACM/IEEE Int. Conf.

on Model Driven Engineering Languages and Systems

(MODELS), pages 16–23.

Greenyer, J., Gritzner, D., Katz, G., Marron, A., Glade,

N., Gutjahr, T., and K

onig, F. (2016b). Distributed

Execution of Scenario-Based Speciﬁcations of Struc-

turally Dynamic Cyber-Physical Systems. In Proc.

3rd Int. Conf. on System-Integrated Intelligence: New

Challenges for Product and Production Engineering

(SYSINT), pages 552–559.

Gritzner, D. and Greenyer, J. (2018). Synthesizing Exe-

cutable PLC Code for Robots from Scenario-Based

GR(1) Speciﬁcations. In Proc. 4th Workshop of

Model-Driven Robot Software Engineering (MORSE),

pages 247–262.

Halbwachs, N., Caspi, P., Raymond, P., and Pilaud, D.

(1991). The Synchronous Data-Flow Programming

Language LUSTRE. Proc. of the IEEE, 79(9):1305–

1320.

Harel, D., Kantor, A., and Katz, G. (2013a). Relaxing Syn-

chronization Constraints in Behavioral Programs. In

Proc. 19th Int. Conf. on Logic for Programming, Arti-

ﬁcial Intelligence and Reasoning (LPAR), pages 355–

372.

Harel, D., Kantor, A., Katz, G., Marron, A., Mizrahi, L.,

and Weiss, G. (2013b). On Composing and Proving

the Correctness of Reactive Behavior. In Proc. 13th

Int. Conf. on Embedded Software (EMSOFT), pages

1–10.

Harel, D., Kantor, A., Katz, G., Marron, A., Weiss, G., and

Wiener, G. (2015a). Towards Behavioral Program-

ming in Distributed Architectures. Journal of Science

of Computer Programming (J. SCP), 98:233–267.

MODELSWARD 2021 - 9th International Conference on Model-Driven Engineering and Software Development

370

Harel, D. and Katz, G. (2014). Scaling-Up Behavioral Pro-

gramming: Steps from Basic Principles to Applica-

tion Architectures. In Proc. 4th Int. Workshop on Pro-

gramming based on Actors, Agents, and Decentral-

ized Control (AGERE!), pages 95–108.

Harel, D., Katz, G., Lampert, R., Marron, A., and Weiss, G.

(2015b). On the Succinctness of Idioms for Concur-

rent Programming. In Proc. 26th Int. Conf. on Con-

currency Theory (CONCUR), pages 85–99.

Harel, D., Katz, G., Marelly, R., and Marron, A. (2016a).

An Initial Wise Development Environment for Behav-

ioral Models. In Proc. 4th Int. Conf. on Model-Driven

Engineering and Software Development (MODEL-

SWARD), pages 600–612.

Harel, D., Katz, G., Marelly, R., and Marron, A. (2016b).

First Steps Towards a Wise Development Environ-

ment for Behavioral Models. Int. Journal of Informa-

tion System Modeling and Design (IJISMD), 7(3):1–

22.

Harel, D., Katz, G., Marelly, R., and Marron, A. (2018).

Wise Computing: Toward Endowing System Devel-

opment with Proactive Wisdom. IEEE Computer,

51(2):14–26.

Harel, D., Katz, G., Marron, A., Sadon, A., and Weiss, G.

(2020). Executing Scenario-Based Speciﬁcation with

Dynamic Generation of Rich Events. Communica-

tions in Computer and Information Science (CCIS),

1161.

Harel, D., Katz, G., Marron, A., and Weiss, G. (2012a).

Non-Intrusive Repair of Reactive Programs. In Proc.

17th IEEE Int. Conf. on Engineering of Complex Com-

puter Systems (ICECCS), pages 3–12.

Harel, D., Katz, G., Marron, A., and Weiss, G. (2014). Non-

Intrusive Repair of Safety and Liveness Violations in

Reactive Programs. Transactions on Computational

Collective Intelligence (TCCI), 16:1–33.

Harel, D., Katz, G., Marron, A., and Weiss, G. (2015c). The

Effect of Concurrent Programming Idioms on Veri-

ﬁcation. In Proc. 3rd Int. Conf. on Model-Driven

Engineering and Software Development (MODEL-

SWARD), pages 363–369.

Harel, D., Lampert, R., Marron, A., and Weiss, G. (2011).

Model-Checking Behavioral Programs. In Proc. 11th

Int. Conf. on Embedded Software (EMSOFT), pages

279–288.

Harel, D. and Marelly, R. (2003). Come, Let’s Play:

Scenario-Based Programming Using LSCs and the

Play-Engine. Springer.

Harel, D., Marron, A., and Weiss, G. (2010). Program-

ming Coordinated Scenarios in Java. In Proc. 24th

European Conf. on Object-Oriented Programming

(ECOOP), pages 250–274.

Harel, D., Marron, A., and Weiss, G. (2012b). Behav-

ioral Programming. Communications of the ACM,

55(7):90–100.

Holloway, L., Krogh, B., and Giua, A. (1997). A Survey

of Petri Net Methods for Controlled Discrete Event

Systems. Discrete Event Dynamic Systems, 7(2):151–

190.

Jin, G., Song, L., Zhang, W., Lu, S., and Liblit, B. (2011).

Automated Atomicity-Violation Fixing. In Proc. 32nd

ACM SIGPLAN Conf. on Programming Language De-

sign and Implementation (PLDI), pages 389–400.

Jobstmann, B., Griesmayer, A., and Bloem, R. (2005). Pro-

gram Repair as a Game. In Proc. 17th Int. Conf. on

Computer Aided Veriﬁcation (CAV), pages 226–238.

Katz, G. (2013). On Module-Based Abstraction and Re-

pair of Behavioral Programs. In Proc. 19th Int. Conf.

on Logic for Programming, Artiﬁcial Intelligence and

Reasoning (LPAR), pages 518–535.

Katz, G. (2020). Guarded Deep Learning using Scenario-

Based Modeling. In Proc. 8th Int. Conf. on

Model-Driven Engineering and Software Develop-

ment (MODELSWARD), pages 126–136.

Katz, G. (2021). Augmenting Deep Neural Networks with

Scenario-Based Guard Rules. Communications in

Computer and Information Science (CCIS).

Katz, G., Barrett, C., and Harel, D. (2015). Theory-Aided

Model Checking of Concurrent Transition Systems. In

Proc. 15th Int. Conf. on Formal Methods in Computer-

Aided Design (FMCAD), pages 81–88.

Katz, G., Marron, A., Sadon, A., and Weiss, G. (2019).

On-the-Fly Construction of Composite Events in

Scenario-Based Modeling Using Constraint Solvers.

In Proc. 7th Int. Conf. on Model-Driven Engineering

and Software Development (MODELSWARD), pages

143–156.

Le, X., Lo, D., and Le Goues, C. (2016). History Driven

Program Repair. In Proc. IEEE 23rd Int. Conf.

on Software Analysis, Evolution, and Reengineering

(SANER), pages 213–224.

Le Guernic, P., Gautier, T., Le Borgne, M., and Le Maire,

C. (1991). Programming Real-Time Applications with

Signal. Proceedings of the IEEE, 79(9):1321–1336.

Marron, A., Arnon, B., Elyasaf, A., Gordon, M.,

Katz, G., Lapid, H., Marelly, R., Sherman, D.,

Szekely, S., Weiss, G., and Harel, D. (2016). Six

(Im)possible Things before Breakfast: Building-

Blocks and Design-Principles for Wise Computing. In

Proc. 19th ACM/IEEE Int. Conf. on Model Driven En-

gineering Languages and Systems (MODELS), pages

94–100.

Nguyen, H., Qi, D., Roychoudhury, A., and Chandra, S.

(2013). Semﬁx: Program Repair via Semantic Analy-

sis. In Proc. 35th Int. Conf. on Software Engineering

(ICSE), pages 772–781.

Pnueli, A. and Rosner, R. (1989). On the Synthesis of a Re-

active Module. In Proc. 16th ACM Symposium Princi-

ples of Programming Languages (POPL), pages 179–

190.

areanu, C. and Visser, W. (2009). A Survey of New

Trends in Symbolic Execution for Software Testing

and Analysis. Int. Journal on Software Tools for Tech-

nology Transfer, 11(4):339–353.

Ramadge, P. and Wonham, W. (1987). Supervisory Control

of a Class of Discrete Event Processes. SIAM Journal

on Control and Optimization, 25(1):206–230.

Ramadge, P. and Wonham, W. (1989). The Control of Dis-

crete Event Systems. Proc. of the IEEE, 77(1):81–98.

Sen, K. (2007). Concolic Testing. In Proc. 22st IEEE/ACM

Int. Conf. on Automated Software Engineering (ASE),

pages 571–572.

Towards Repairing Scenario-Based Models with Rich Events

371

Staber, S., Jobstmann, B., and Bloem, R. (2005a). Diagno-

sis is Repair. In Proc. 16th Int. Workshop on Princi-

ples of Diagnosis (DX), pages 169–174.

Staber, S., Jobstmann, B., and Bloem, R. (2005b). Find-

ing and Fixing Faults. Correct Hardware Design and

Veriﬁcation Methods, 3275:35–49.

Steinberg, S., Greenyer, J., Gritzner, D., Harel, D., Katz,

G., and Marron, A. (2017). Distributing Scenario-

Based Models: A Replicate-and-Project Approach. In

Proc. 5th Int. Conf. on Model-Driven Engineering and

Software Development (MODELSWARD), pages 182–

195.

Steinberg, S., Greenyer, J., Gritzner, D., Harel, D., Katz,

G., and Marron, A. (2018). Efﬁcient Distributed Exe-

cution of Multi-Component Scenario-Based Models.

Communications in Computer and Information Sci-

ence (CCIS), 880:449–483.

Weimer, W., Forrest, S., Le Goues, C., and Nguyen, T.

(2010). Automatic Program Repair with Evolutionary

Computation. Communications of the ACM (CACM),

53:109–116.

MODELSWARD 2021 - 9th International Conference on Model-Driven Engineering and Software Development

372