
Converting Image Labels to Meaningful and Information-rich
Embeddings
Savvas Karatsiolis
a
and Andreas Kamilaris
b
Research Centre on Interactive Media, Smart Systems and Emerging Technologies (RISE), Nicosia, Cyprus
Keywords: Convolutional Neural Networks, Disentangled Latent Space, Representation Learning, Siamese Network.
Abstract: A challenge of the computer vision community is to understand the semantics of an image that will allow for
higher quality image generation based on existing high-level features and better analysis of (semi-) labeled
datasets. Categorical labels aggregate a huge amount of information into a binary value which conceals
valuable high-level concepts from the Machine Learning models. Towards addressing this challenge, this
paper introduces a method, called Occlusion-based Latent Representations (OLR), for converting image labels
to meaningful representations that capture a significant amount of data semantics. Besides being information-
rich, these representations compose a disentangled low-dimensional latent space where each image label is
encoded into a separate vector. We evaluate the quality of these representations in a series of experiments
whose results suggest that the proposed model can capture data concepts and discover data interrelations.
1 INTRODUCTION
Deep Learning (DL) advancements during the last
years offer powerful frameworks for mapping dataset
instances to binary labels and thus allow the building
of powerful classifiers for several seemingly difficult
tasks (Touvron et al., 2019), (Simonyan & Zisserman,
2015), (K. He et al., 2016), (Szegedy et al., 2017).
Classification models are usually simpler and more
successful in their task than generative models.
Likewise, transforming the instances of a dataset to
meaningful representations is harder than
transforming them into binary vectors because it
requires the preservation of data semantics.
Compressing the dataset instances into binary
numbers results in the condensation of data
interrelations to a degree that they become
undetectable and not re-constructible anymore. For
example, the value of a binary label can be calculated
by a classifier by combining the features detected
during the forward propagation of the data through
the model’s layers. At the level where the label is
calculated (i.e., the model’s output) every feature and
data characteristic has already been processed into
some high-level data abstraction. More importantly,
the high-level concepts do not contain qualitative
a
https://orcid.org/0000-0002-4034-7709
b
https://orcid.org/0000-0002-8484-4256
information or any other statistical information that
describes the degree based on which some instance
complies with a specific label. On the contrary, a label
described by a distribution instead of a binary label
mitigates the problem of blurred-out statistics and
context unawareness. The contribution of this paper
involves the investigation of suitable DL models
which allow the calculation of meaningful vectors
from the labels of a dataset with the information
provided by a classifier trained with these labels. For
this purpose, a Siamese neural network is employed,
where the information of the classifier combined with
input image occlusion enables the Siamese model to
extract discriminating features and calculate
meaningful label distributions. We call our method
Occlusion-based Latent Representations (OLR). This
work’s main contribution is a simple but effective
methodology for learning appropriate label
distributions that contain enough semantic
information and can be exploited in various ways as
demonstrated in a series of experiments. OLR builds
latent representations in a supervised manner (using
labels) that have a major advantage: latent subspaces
disentanglement. Each latent representation links
directly to one problem label and automatically
constitutes that label’s set of exclusive factors of
variation.
Karatsiolis, S. and Kamilaris, A.
Converting Image Labels to Meaningful and Information-rich Embeddings.
DOI: 10.5220/0010375801070119
In Proceedings of the 10th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2021), pages 107-119
ISBN: 978-989-758-486-2
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
107

The rest of the paper is organized as follows:
Section 2 describes related work. Section 3 describes
the methodology followed while Section 4 presents
various experiments assessing the quality and
effectiveness of the approach. Then, Section 5
discusses the results and Section 6 concludes the paper.
2 RELATED WORK
Different studies applied a variety of strategies for
label enhancement and/or efficient separation of the
effect that each label has on the data.
2.1 Label Distribution Learning and
Label Enhancement
Hinton et al. (2015) suggested raising the temperature
coefficient of the SoftMax units at the output of the
classifier to increase the entropy of the labels’
distribution. In this way, label distribution becomes
less stringent and reveals otherwise unobservable
instance properties. Of course, this strategy can be
applied only after the model is trained and it allows
instance representation with relaxed class
probabilities, i.e., a vector containing the probability
of each class. Label distribution learning (LDL)
(Geng, 2016) aims at a similar outcome, i.e., a vector
representing the degree to which each label describes
an instance. LDL maps each instance to a label
distribution space but requires the availability of the
actual label distribution before-hand, something
which is highly impracticable in real-world
applications. Label enhanced multi-label learning
(LEMLL) (Shao et al., 2018) suggests a framework
incorporating regression of the numerical labels and
label enhancement that does not require the
availability of the label distribution. LEMLL jointly
learns the numerical labels and the predictive model
taking advantage of the topological structure in the
feature space (label enhancement).
2.2 Attribute-editing Models
Attribute-editing models are also relevant, in the
sense that they target specific attributes of the
instances. Some recent attribute-editing models
manipulate face attributes and generate images with a
set of desired (or undesired) characteristics while
preserving at the same time almost all other image
details. Given an image and the desired
characteristics (labels), an image is generated that
satisfies the given characteristics while resembling
the initial image in every other detail. Fader networks
(Lample et al., 2017) enforce an adversarial process
that makes the latent space of the labels invariant to
the attributes. Generally, the attribute-independent
latent representation is very restrictive, leading to
blurriness and distortion (Lample et al., 2017). Shen
and Liu (Shen & Liu, 2017) proposed a model that
learns the difference between images before and after
the manipulation, i.e., a residual image holding the
difference of the pixel values due to attribute-editing.
An interesting approach applying an encoder-decoder
architecture is by (Guo et al., 2019), which
compresses the original image to a latent
representation that has predefined placeholders for
the different problem classes. The model is trained
using different image pairs, editing the individual
placeholders according to the corresponding binary
labels of each image, preserving only the ones that are
set in the image label vector, and making zero every
other. Edited representations pass through the
decoder to reconstruct the original image. Besides the
two edited representations, MulGan created two more
representations by exchanging the editable
placeholders between the two representations. The
representations with the attributes exchanged pass
through a label classifier and a real/fake
discriminator. The latter uses an adversarial loss
aiming to produce more realistic images. AttGan (Z.
He et al., 2019) uses an encoder-decoder architecture
but additionally applies conditional decoding of the
latent representation based on the desired attributes
(i.e., class labels). AttGan also applies a
reconstruction, using both classification and
adversarial loss. The reconstruction preserves the
attribute-excluding details, classification loss
guarantees correct attribute manipulation while
adversarial loss aims to achieve realistic image
generation. Authors of AttGan also suggested that
symmetric skip connections between the encoder and
the decoder, like the U-Net architecture (Ronneberger
et al., 2015), improved their model’s performance.
Liu et al. (M. Liu et al., 2019) made some significant
modifications to the AttGan architecture for further
improving the results obtained. The authors of
STGAN, after conducting several experiments,
suggested that skip connections can improve the
reconstruction of the original image but at the same
time may harm attribute-editing. Their effect can be
driven to a win-win compromise using selective
transfer units that control the information flow from the
encoder to the decoder. They also suggested using a
difference attribute vector instead of the whole actual
target attribute vector (having a −1 for removing an
attribute and a +1 for adding an attribute).
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
108

2.3 Disentangled Representations
According to Bengio (Y. Bengio, 2013), a change in
one dimension of a disentangled representation
causes a change in one variation factor while being
relatively invariant to changes in other factors.
Disentangled representations have been studied both
in the context of semi-supervised learning (Hsu et al.,
2017), (Denton & Birodkar, 2017), and unsupervised
learning (Higgins et al., 2017), (Kurutach et al.,
2018), (Kim & Mnih, 2018). Semi-supervised
approaches require knowledge about the underlying
factors of the data which is a significant limitation. β-
VAE (Higgins et al., 2017) is a disentangling
approach based on the Variational Autoencoder
(VAE) (Kingma & Welling, 2014) and achieves
latent space disentanglement by applying a slightly
different VAE objective function with a larger weight
on the Kullback–Leibler (KL) divergence between
the posterior and the prior. While the β-VAE is
appealing mainly because it relies on the elegant
framework of the VAE, it offers disentanglement to
the cost of generated image quality. Kim and Mnih
(Kim & Mnih, 2018) proposed encouraging the
VAE’s representations distribution to be factorial
which improves upon β-VAE. InfoGAN (Kurutach et
al., 2018) is a popular alternative that enhances the
mutual information between the latent codes and the
generated images.
3 METHODOLOGY
Our approach for turning the problem labels to
distributions involves the use of information from a
model trained on the classification task. Such a
classifier compresses the information of an image
down to labels and outputs probabilities of label
occurrence for an input image. We further use a
Siamese network (Neculoiu et al., 2016),(Sahito et
al., 2019),(Mueller & Thyagarajan, 2016),(Benajiba
et al., 2019) which receives two images and the
product of their label probabilities to adapt its output
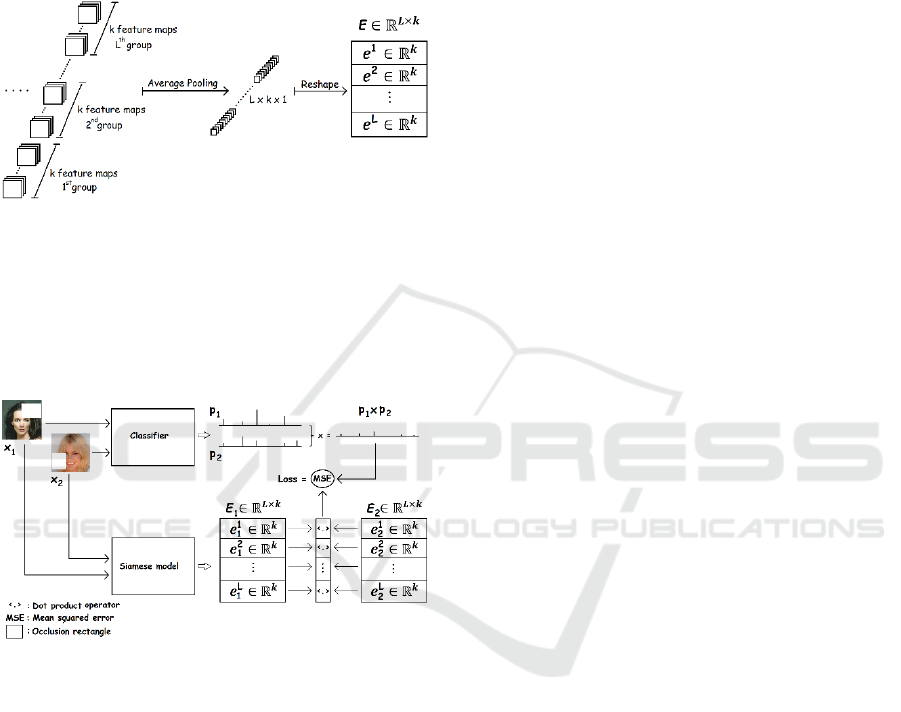
𝐸 accordingly, as illustrated in Figure 1. The output
of the Siamese network
comprises L vectors of size k,
with L being the number of problem labels and 𝑒
∈
𝑅
being the row vector component of E
corresponding to label 𝑙. Effectively, the Siamese
output is a matrix holding much less information than
the original input 𝑥∈𝑅
××
, where h, w are the
height and width of the 3 channels of the image
respectively. We generally assume that 𝐿×𝑘≪ℎ×
𝑤×3. The output consists of L distributions in vector
form, one for each problem label. Since these vectors
constitute compressed representations of the input,
we will refer to them as image embeddings from this
point on.
For the Siamese model to learn the embeddings
properly, we sample pairs of images from the dataset
calculating their label probabilities using a classifier
previously trained on recognizing the labels. The
probability outcomes of the two images are multiplied
in an element-wise fashion to obtain a value for the
overall probability of each label being evident in the
image pair. Each training example comprises a triplet
of two images and the joint probability vector of their
labels (the product of the classifier’s probabilities for
the two images). The Siamese network receives the
two images of each triplet and calculates two
embeddings, one for each image. Then, it calculates
the dot products between the vector components 𝑒
of
the two embeddings. Assuming the two embeddings
matrices 𝐸
,𝐸
∈𝑅
×
, the dot product is calculated
between the rows of the two matrices resulting in a
vector 𝑢
⃗
∈𝑅
. The loss function of the Siamese
model is equal to the Mean Squared Error (MSE)
between 𝑢
⃗
and the joint probability vector in the
triplet. In other words, the dot product between the
label embeddings of the two images should be equal
to the joint probability vectors as calculated by the
classifier. This means that images that share a
common label should produce embeddings of the
specific class that have a high dot product.
Regarding the proposed approach, there are two
main issues to address. The first has to do with the
Siamese model architecture and the way it is designed
to have an output in the form of matrix E. The second
issue concerns the calculation of appropriate joint
probability vectors. Regarding the Siamese
architecture, after several convolutional and pooling
layers, we apply a special layer that comprises several
feature maps that form label-specific groups. The
number of groups is equal to the number of problem
labels so that each label is represented by a certain
number of feature maps 𝑘. The number of feature
maps representing a label is equal to the
dimensionality of each embedding’s vector 𝑘 and the
size of the special layer is 𝑓×𝑓×
(
𝐿×𝑘
)
, with f
being the width/height of the feature maps. At the
output of this layer, an average pooling layer is
applied which calculates the average value of each
feature map. Consequently, the output of the average
pooling layer is 𝐿×𝑘×1 and through a reshaping
operation, the output can be transformed to the
embedding’s shape L × k. The last layers of the
Siamese network are displayed in Figure 1.
Converting Image Labels to Meaningful and Information-rich Embeddings
109
The concern for calculating appropriate joint-
probability vectors is related to the classifier’s
tendency to output a high probability (close to 1) for
the correct class and a low probability (close to 0) for
the incorrect classes. This results in calculating joint
probabilities that are either close to 1 or 0 which does
not empower the Siamese model to learn the data
Figure 1: Final layers of the Siamese model. After several
convolutional and pooling layers, the label-specific layer
consists of L groups of k feature maps. The next layer is an
average pooling layer followed by a reshape operation
which formats the output matrix to a shape of 𝐿×𝑘, so that
there is a vector (embedding) of size k for each of the L
classes. According to the architecture, each problem label
has its feature maps which represent its statistics.
Figure 2: Training process of the Siamese model. Two
images are randomly chosen from the dataset and occlusion
rectangles are applied at random positions on them. These
rectangles are of different dimensions and have a height and
width randomly chosen from a range of values that are
between 0.33 and 0.66 of the image height and width (the
occlusion rectangles shown in the figure are smaller for
cosmetic reasons). Next, the two occluded images are
classified, and the resulting label probabilities are
multiplied to form a joint label probability. The two
occluded images and the joint probability vector form a
triplet that is used for the training of the Siamese model.
Both images go through the model and produce two image
embeddings 𝐸
,𝐸
. A dot product operation applies to the
vector components of the embeddings resulting in a vector
of L elements. The MSE between the joint probability of the
triplet (obtained from the classifier) and the dot product of
the embeddings’ vectors constitutes the loss of the training
procedure.
interrelations. The Siamese model becomes
inefficient when its training relies on over-confident
or binary vectors. Additionally, when joint
probabilities lie close to the extreme probability
values (0 or 1) the Siamese model is more prone to
overfitting and thus may not properly consider feature
correlations and interactions. Two ways for raising
the entropy of the classifier’s output were considered:
a) The first applies a strategy used in model
distillation (Hinton et al., 2015) by raising the
temperature parameter of the SoftMax function at the
output of the classifier which relaxes the label
distribution and communicates more information
about the input b) The second approach is based on
applying random partial occlusion to the input to
make the classifier less confident about its
predictions. Experiments showed that occlusion
works better in the sense that it prevents the Siamese
model from overfitting and encourages the discovery
of feature correlations and the calculation of more
expressive distributions. The degree of the occlusion
on the images of each triplet (the percentage of the
occluded image surface) can be determined
experimentally for the problem at hand. We
discovered that randomly selected occlusion
rectangles of width and height ranging from 33% to
66% of the image dimensions have a positive effect
on the training of the Siamese model. Figure 2 shows
the training process of the Siamese model.
4 RESULTS
We evaluate the proposed method on the CelebA
dataset (Z. Liu et al., 2015). The dataset contains
more than 200,000 images of faces, each annotated
with 40 binary labels (either an attribute exists or not).
Images are cropped and resized to 178 × 178 × 3
pixels. In several cases, cropping removes part of the
person’s neck thus 2 labels requiring view on the
specific (low) image region are not considered:
“wearing necklace” and “wearing necktie”. This
reduces the number of problem labels to 38.
Randomly selected 190,000 images are used in the
training set (≈ 95%) while the remaining images are
kept for the test set (≈ 5%). No pre-processing has
been applied to the images. Each label embedding has
a size of 32 which means that each image is
compressed to a representation of size 38 × 32. After
training the model and calculating the embeddings for
each image in the dataset the quality of the
embeddings is evaluated through various experiments
discussed in the following sub-sections.
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
110

4.1 Using the Embeddings to Train a
Linear Classifier
A linear classifier was trained based on the CelebA
dataset using the calculated embeddings, to assess
their quality. The performance of the convolutional
classifier that the Siamese model relies on for its
training was used as a baseline. This comparison can
provide some useful insights on whether the
calculated embeddings are indeed capturing the data
relations. The linear classifier for this experiment has
a single layer comprising of 38 neurons representing
the classes of the dataset. Each of these neurons uses
the sigmoid activation. The embeddings calculated by
the Siamese model 𝐸∈𝑅
××
(N is the size of the
training set) are used as input to this linear model. The
linear classifier has a classification success rate of
91.6% on the test set while the convolutional
classifier has a success rate of 94.2%. This slight
performance decrease is the cost of obtaining
embeddings that capture data inter-relations, as will
be shown briefly.
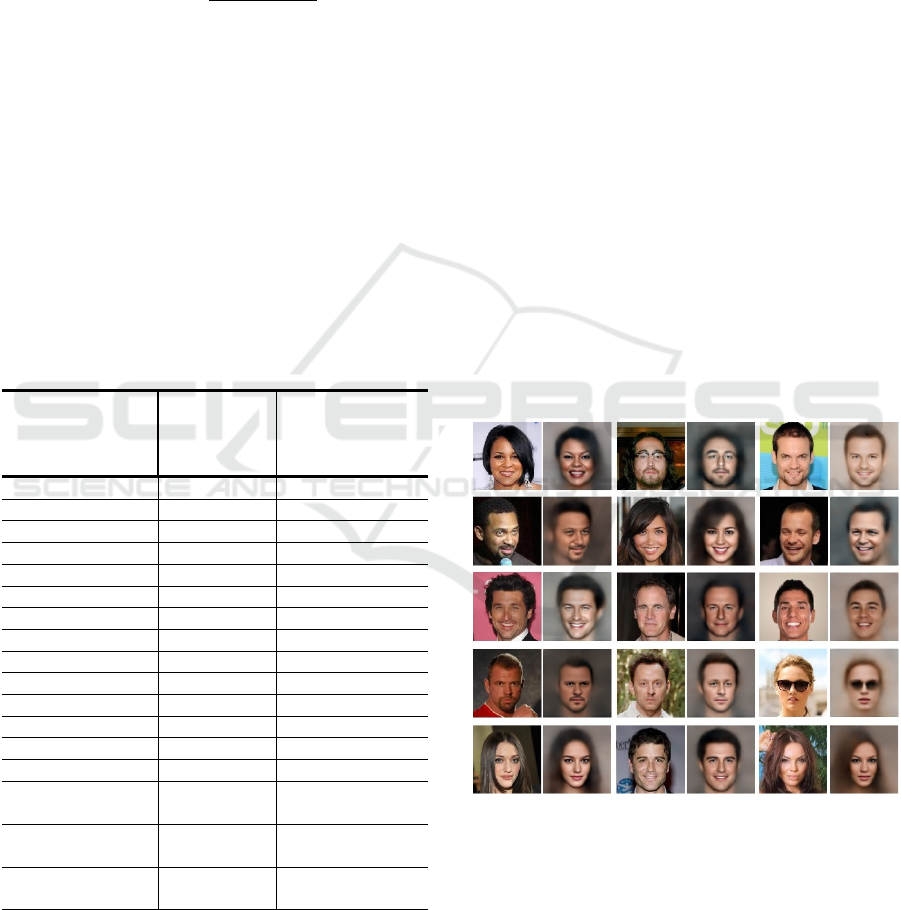
Figure 3: Examples of original CelebA images that are
accompanied by vague labels, shown under the images.
OLR does not adopt this labeling. Generally, the Siamese
embeddings are more resilient to such cases than a
convolutional classifier in the sense that they adopt a label
only if they discover strong feature correlations with other
images having the corresponding label.
The patterns classified incorrectly by the linear
model (trained on the embeddings) but, at the same
time, classified correctly by the convolutional
classifier were further analyzed. In essence, these
cases belong to the 2.6% of the test set that reflects
the success rate difference of the classifiers in
comparison. It turns out that the CelebA dataset
contains several wrong or ambiguous labels that the
Siamese embeddings did not adopt. Some examples
of questionable cases are shown in Figure 3. The
Siamese model seems to be reluctant to associate
vague labels with false evidence (features). On the
contrary, the convolutional classifier tends to learn
the ambiguous labels acting obediently in an eager to
satisfy fashion.
4.2 Correlations between the
Embeddings’ Distributions
In this experiment, the correlations between the
embeddings were examined to investigate
empirically whether the depicted label distributions
are meaningful. Figure 4 shows the Pearson
correlation coefficients between the distributions’
norm value. When a label is detected, the
corresponding embedding’s norm-value tends to
increase, reflecting the presence of such a
characteristic, otherwise, the norm-value is very
small. The high values of the vector reveal an attempt
to describe the evident label through the calculated
distribution. Some interesting and well-anticipated
correlations are revealed, for example, the positive
effect that big lips (0.3) and wearing lipstick (0.7)
may have on considering a person being attractive.
Other interesting correlations are between baldness
and attractiveness (−0.2), double chin and gray hair
(+0.5), being young and bald (−0.3), high cheekbones
and attractiveness (0.3), being male and having a big
nose (0.6), being male and having a heavy makeup
(−0.8) and the tendency to consider a smiling person
attractive (0.2). Small steps towards the pursuit of
beauty are being made here.
4.3 Principal Components Analysis of
the Embeddings’ Distribution
Principal component analysis (PCA) was applied to
the embeddings focusing on the label “Mouth slightly
open”, to further analyze the results and evaluate the
characteristics of the distribution as obtained from
OLR. This specific label was selected because almost
half of the images in the dataset contain it, hence there
is much information available for analysis. Moreover,
this label can be effortlessly detected in an image and
its detection does not rely on subjective judgment, for
example, the label regarding “attractiveness”. The
PCA applied on the “Mouth slightly open”
embeddings of all images in the dataset revealed that
the first component (eigenvector) explains 67.5% of
the data variance while the second component
explains another 4.1% of the data variance. Given the
large quantity of variance explained by the first
component, only this component was selected in this
Converting Image Labels to Meaningful and Information-rich Embeddings
111

Figure 4: The Pearson correlation table between the vectors' norm value. The norm value of a specific label vector tends to
increase when a positively correlated label is evident in the same pattern. Likewise, it tends to decrease in the presence of a
negatively correlated label.
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
112

experiment. The projections of the “Mouth slightly
open” embeddings of all images in the dataset on this
single component were sorted in increasing order of
magnitude. This results in a list of projections and
their corresponding images, starting from images that
have a smaller projection on the first principal
component moving towards images that have a larger
projection and thus comply with the selected label
“Mouth slightly open”. Figure 5 shows some ordered
images from this experiment. A higher value of the
principal component projection signifies more
confidence in the label “open mouth” being evident.
Figure 5: Images corresponding to different projection
values of the “Mouth slightly open” embeddings on the first
principal component of the specific label’s embeddings set
(displayed in increasing order). In the top row, the images
correspond to ranking locations which are 20,000 positions
apart (ranking positions 0-80,000). From that point on,
images satisfy the “Mouth slightly open” attribute (almost
50% of the images in the dataset have the specific label).
The second row shows images corresponding to the ranking
positions 100,000-180,000. The actual projection value is
shown on top of each image.
4.4 Using the Embeddings for
Reconstructing the Images
In this experiment, each image is compressed to its
representation. If a label is evident in an image, its
corresponding vector output imprints the phenotype
of the specific label in the image. Each dataset image
has an average of eight non-zero labels, which means
that the average embeddings’ size effectively
describing an image is 8×32 = 256 out of the total
38×32 = 1216 numbers of the model’s output. The
validity of this analysis relies on the fact that any label
not evident in an image is described with a zero (or
near zero) vector, so only the active labels get a non-
zero vector value. Given the input image sizes
(178×178×3 = 95052 ), the model compresses the
input by more than 370 times, representing the images
with only 𝑝̅ ×32 numbers, where 𝑝̅ is the average
number of evident labels in the images (nonzero
labels). Due to the huge compression rate,
reconstructing the image in a way that the imprinted
face is recognized as being the same face shown in
the input image is a challenging task. The Mean
Squared Error (MSE) loss for the image
reconstruction process has some interesting
properties but also tends to create blurry images and
annoying artifacts (Wang & Bovik, 2009) (Zhao et
al., 2017). The very large compression factor applied
in the embeddings amplifies these disadvantages. The
MSE or any other norm-based distance error does not
account for the structure and the characteristics of an
image, such as the statistics among pixel values. On
the contrary, such losses produce reconstructions
which, in the general case, only approximate the raw
pixel values in the training images. A better
reconstruction could be obtained by using a loss
function that accounts for pixel statistics reflecting
the structure of the images like the structural
similarity loss function (SSIM) (Wang et al., 2004).
The SSIM loss function considers three basic image
components: luminance, contrast, and structure.
SSIM is a perceptual-based loss function that
considers some factors that are closer to what humans
perceive when they look at an image. It seems
unlikely that humans perceive an image’s content by
making pixel-level calculations in a way like what
norm-based losses do. In practice, the SSIM loss
function measures the similarity between two images
based on factors that encode the perceived change in
structural information. The SSIM between two
images x and y is calculated on various windows of
size N as follows:
𝑆𝑆𝐼𝑀
(
𝑥,𝑦
)
=
(1)
with 𝑐
and 𝑐
stabilizing the division and 𝜇
, 𝜇
, 𝜎
,
𝜎
and 𝜎
calculated as:
𝜇
=
1
𝑁
𝑥
, 𝜇
=
1
𝑁
𝑦
𝜎
=
∑(
𝑥
−𝜇
)
, 𝜎
=
∑
𝑦
−𝜇
𝜎
=
2𝜎
𝜎
+𝑐
𝜎
+𝜎
+𝑐
SSIM acts on the luma (brightness) of the images
and does not consider chrominance. For that reason,
SSIM is applied separately on each of the three color
channels of the image. To achieve even better
chromatic reconstruction, the MSE loss was also used
in conjunction with the SSIM, in a way that allows
relative freedom to each loss function’s application.
This degree of freedom is accomplished by applying
the two losses on different layers of the reconstruction
model, allowing both SSIM and MSE to operate on
different value scales. More specifically, the SSIM
Converting Image Labels to Meaningful and Information-rich Embeddings
113
loss is applied first to the output of layer Conν2D
out
,
which has a size of 176 × 176 × 3 as shown in Table
1. A pixel was removed from each side (top/bottom
height and left/right width) of the dataset images to
match the size of the model’s output. Next, a rescaling
layer (Rescale) puts the pixel values back to the range
y ∈ [0,1] by applying the following operation on the
output of the previous layer x:
𝑦
=
(
)
(
)
()
(2)
Then, the MSE loss is applied at the last layer after
the SSM loss is scaled by a factor α. The total loss
function between the reconstructed image y and the
original image x that corresponds to an input
embedding e is:
𝐿
= 𝛼 SSIM
(
𝑥,
Conv
2𝐷
)
+
(
1−𝛼
)
MSE
(
𝑥,𝑅𝑒𝑠𝑐𝑎𝑙𝑒
)
(3)
The reconstruction model is trained with the
RMSProp optimizer and a learning rate of 1×10
.
Parameter 𝑎 of equation (3) is set to 0.5. Some
reconstructions based on the test set embeddings are
shown in Figure 6 next to the original images that
produced the embeddings.
Table 1: Architecture of the reconstruction model.
Layer Output
Size (map
height,
channels)
Parameters
1
(kernel, channels,
stride, padding)
Flatten (1216)
Dense (18432)
Reshape (6,512)
Conv2DT (12,128) (3,128,2,same)
Conv2D (12,64) (3,64,1,same)
Conv2DT (24,64) (3,64,2,same)
Conv2D (22,64) (3,64,1,valid)
Conv2DT (44,64) (3,64,2,same)
Conv2D (44,64) (3,64,1,same)
Conv2DT (88,64) (3,64,2,same)
Conv2D (88,64) (3,64,1,same)
Conv2DT (176,64) (3,64,2,same)
Conv2D (176,32) (3,32,1,same)
Conv2D
(176,3) (3,3,1,same)
SSIM
(x
2
, Conv2D
)
1
Rescale
(Conv2D
)
(176,3)
MSE
(x
2
, Rescale)
1
1
All activation functions are ReLUs.
2
Input image
The reconstructions suggest that the embeddings
hold significant information from the original images,
despite the huge compression. More specifically, the
reconstructions generally tend to preserve the general
facial structure, individual characteristics, pose, and
facial expressions. This behavior is interesting for the
following reasons:
a. The reconstruction model and the Siamese
network (which is responsible for extracting
the embeddings) are separately trained with
different objective functions and there is no
co-adaptation between their tasks. However,
these models can be joined to form an implied
underdetermined autoencoder that
significantly compresses the original image to
a small internal representation (embedding)
and then decode it to reconstruct the original
image.
b. All images illustrated in Figure 6 belong to the
test set which means that the models
(embeddings’ extraction model and
reconstruction model) have never seen them
before. These images were not used during the
training of these models.
It must be noted that the image embeddings
contain significantly less information than the
original image (∼ 370 times less information). The
model maintains an important degree of similarity
between the reconstructions and the original images
despite the high compression ratio.
Figure 6: Several embeddings’ reconstructions compared to
the original images that produced the embeddings. Each
pair of images consists of the original image on the left and
the reconstruction on the right (3 pairs per row). Most
reconstructions tend to preserve facial structure and
characteristics, pose, and facial expression information.
The original images belong to the test set and were not used
during the training of the Siamese model or the
reconstruction model.
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
114

4.5 Using the Embeddings for
Image-editing
Since the calculated embeddings are converted to a
distribution (or distributions of the various problem
labels), we can extract and apply inferred statistical
properties to the data. More specifically, it is assumed
that the 32-dimensional (32−d) vectors representing a
specific class (out of the 38 dataset classes) are points
on a normal probability distribution. Then, all 32−d
vectors corresponding to a specific class are used to
calculate the distribution function of the specific
problem label. For example, the embeddings’
distribution of the “wearing eyeglasses” class is
calculated from the group of images that satisfy the
specific label. Let 𝐸
be the embedding of an image
having a size of 38×32 and 𝑒
be the 32−d vector
component that corresponds to a single class 𝑙 from
the 38 classes described by the embedding. The mean
of the distribution formed by the class 𝑙 vector
components 𝑒
of all N images in the dataset that
satisfy the specific label (𝑦
= 1) is calculated by
𝜇
=
∑
∑
𝑒
{
}
(4)
where {.} is a qualifier function that allows
consideration only of terms that satisfy the enclosed
condition. The covariance matrix of the normal
distribution 𝛴∈𝑅
×
, where k is the vector
dimensionality (32), is calculated in a matrix form
with:
𝛴 = 𝑐𝑜𝑣
𝑋,𝑋
=𝐸
(
𝑋−𝐸
𝑋
)(
𝑋−𝐸
𝑋
)
= 𝐸
𝑋𝑋
−𝐸
𝑋
𝐸
𝑋
(5)
Approximating the distribution of each class with a
normal distribution allows drawing samples of
candidate vectors representing an instance of the
specific class. Such vectors can replace the values in
the embedding’s placeholder 𝑒
of the specific class 𝑙
in an image embedding 𝐸
. The reconstruction of the
modified embedding resembles a possible instance of
the dataset that belongs to the specific class. For
example, the embedding of an image that does not
satisfy the label “mouth slightly open” may be
modified by inserting a vector 𝑥⃗ sampled from the
embeddings’ distribution of the label “mouth slightly
open” to the placeholder 𝑒
that corresponds to the
specific label 𝑙. After making the assignment 𝑒
:=𝑥⃗,
passing the modified embedding through the
reconstruction model generates an image like the
original image which additionally satisfies the
specific label. In other words, the face in the image
remains very similar but additionally has the “mouth
Figure 7: Examples of generating images with a property
removed or added. The original image is shown on the left
column, the reconstruction of its unmodified embedding in
the 2nd column, and the reconstruction of its modified
embedding in the 3rd column. The desired property added
or removed by modifying the embedding is shown in the
rightmost column. A plus (“+”) prefix indicates the
replacement of the appropriate embedding’s placeholder
with a vector sampled from the normal distribution of the
embeddings that satisfy the specific characteristic (label). A
minus (“-”) prefix indicates the replacement of the
appropriate embedding’s placeholder with a zero vector.
The images belong to the test set.
Converting Image Labels to Meaningful and Information-rich Embeddings
115

slightly open” property. Respectively, the phenotype
of a label can be removed by filling the embedding’s
placeholder that corresponds to the specific label with
zeros or by replacing the values of the placeholder
with a vector sampled from the distribution of the
specific label after being scaled down to a small norm
value. Vector upscaling can also be applied when
adding a specific property to an embedding by
replacing a placeholder with an upscaled vector. In
this way, the effect of adding a specific property is
increased and the phenotype change can be more
evident. Figure 7 shows several cases of sampling the
embeddings distributions for generating images with
specific characteristics or for removing specific
characteristics from images.
Interestingly, the modified embeddings generate
images of faces that are very similar to the
reconstructed images when using the original
unaltered embeddings. Additionally, the new image
has the desired characteristic added to the embedding
of the image. This experiment suggests that the 32-d
vector components of 𝑒
encode the various image
properties in an effective manner.
The degree of an edited characteristic can also be
controlled by adjusting the magnitude of the sampled
vector. For example, to add an emphasized phenotype
of a specific label to an image, the magnitude of the
sampled vector may be increased by multiplying the
vector with a scaling factor 𝑠>1. The opposite
(reduction of the vector’s magnitude) tends to add
mild phenotypes. Figure 8 shows that increasing the
magnitude of the sampled vectors makes the edited
characteristic more evident.
Figure 8: The edited characteristics become more evident
when the added vector is upscaled by a certain factor to
increase its magnitude. In the first row, a vector is sampled
from the “chubby” distribution and used to edit the original
image. The rightmost image shows the result of editing the
embeddings with a vector multiplied with a scaling factor
𝑠=1.5. In the second row, the editing vector is sampled
from the “narrow eyes” distribution.
5 DISCUSSION
OLR aims to calculate the representations of each
problem label while preserving the evident label
correlations. It does not explicitly address attribute-
editing nor representing the instances in terms of
single-value class probabilities. In a sense, OLR has
some similarity with MulGan (Guo et al., 2019) in the
way specific labels get a fixed placeholder in the
latent distribution. It is different from AttGan (Z. He
et al., 2019) and STGAN (M. Liu et al., 2019) in the
sense that the latent distribution of our model
comprises solely of label representations and does not
contain any other components that encode general
image details. Essentially, OLR encodes all image
information in the label distributions while preserving
the attribute correlations. Moreover, OLR constructs
the label distributions without utilizing an adversarial,
reconstruction, or classification loss. It does this by
simply applying a supervision signal sourced from the
actual image labels. Avoiding the use of a
reconstruction loss enables the model to maintain the
correlations between the labels and to depart from
adapting according to specific image details. Various
experiments were performed (see Sections 4.1-5), to
demonstrate that OLR tends to build an understanding
of the semantics of the data distribution.
Regarding the experiment of training a linear
classifier (Section 4.1), using a dot product for
applying the labeling on the calculated features of the
Siamese model is the key operation that differentiates
OLR from the conventional way of making the
classification with a fully connected classifier
attached to a convolutional feature extractor. Usually,
the classifier consists of many neurons and accepts as
input the features detected from the preceding
convolutional layers and forms complex non-linear
relations to satisfy the output labeling. In other words,
the fully connected layers at the end of the
conventional classifier combine the calculated
features in uncontrolled and arbitrary ways under one
criterion: fitting the labels available. On the other
hand, the embeddings calculated by OLR satisfy a
probabilistic criterion: images that share labels
produce embeddings’ distributions that are similar in
the dot-product sense. The proposed method produces
label distributions that have non-zero values only if
specific features are detected in images having the
same label. In this way, the proposed approach
validates its perception of images and its decisions
regarding the conformance of each image to a label.
This conformance must be “justified” in the sense that
the compressed content vector of a specific label must
have a considerable probability of occurrence in other
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
116

images having the same label.
The correlation results between the embeddings
(Section 4.2) suggest that OLR can calculate
embeddings that capture the relations between the
different problem labels. While these interrelations
are seemingly easy for humans to infer, establishing
these logical links is not an easy task for machine
learning (ML) models. Further, principal components
analysis on the embeddings (Section 4.3)
demonstrates that the projection on the principal
component of the embeddings’ set of each label
reflects the way the phenotype of the specific
characteristic is imprinted on the data.
Moreover, image reconstruction from the
embeddings (Section 4.4) demonstrates that the
learned representations can be transformed back to
the images that produced them. Despite the very small
size of the embeddings in comparison to the original
data and the discard of a huge amount of information,
the calculated embeddings are still able to maintain
enough information to reproduce a decent version of
the input. Finally, using the embeddings for image
editing (Section 4.5) shows that the proposed method
provides label distributions that can be exploited in
various ways for semantically-aware image editing:
an instance of a characteristic may be sampled from
the specific distribution and added to an image while
another characteristic may be removed from an image
by significantly reducing (or eliminating) the
magnitude of the respective distribution. The
phenotype of the edited characteristic (characteristic
intensity) can be controlled by modifying the
magnitude of the sampled instance.
While nothing is restraining the OLR from
working with problems that have fewer labels or a
single label per image, its full potential unravels when
dealing with problems having many labels per image.
However, despite that OLR indirectly uses labels, it
is still limited due to its reliance on supervisory
information. Another limitation arises from the fact
that, during the experiments, the image embeddings
were not allowed to adapt and were used as input data
rather than intermediate/learnable features. As such,
they did not adapt depending on the task of each
experiment and therefore they were not specialized in
tackling the specific problems. On one hand, using
unspecialized representations for a variety of tasks
stresses their quality, but on the other hand, it
produces worse results which makes the task-specific
assessment of the model more difficult. For example,
a comparison between the results of the attribute-
editing experiment (Section 4.5) and the results of
analogous models is highly unfair because our
experimental model uses embeddings that have been
learned without considering the task under study.
Future work aspires to address this limitation.
Finding a latent space in which we are fully aware
of what each variable controls, is a step forward in the
research direction of semantically-aware deep
learning and computer vision in general. OLR applies
latent space factors’ disentanglement, which is
derived from its architecture and training procedure.
Every latent representation has a non-zero magnitude
only if its respective label is evident in an image.
Occlusion-based supervision drives the model into
building representations that reflect its degree of
belief that an image complies with a label. More
importantly, these representations encapsulate image
semantics as suggested by the conditional
reconstruction experiment (Section 4.5). Converting
labels to meaningful vectors is especially useful in
many aspects. Both main ML regimes (supervised
and unsupervised learning) can benefit from
exploiting the information distilled in label
representations. As shown in the experiments
conducted, OLR builds label embeddings with
appealing properties that may be harvested by ML
methods.
In future work, we plan to add an adversarial loss
(Goodfellow et al., 2014) to the training of the
decoder to improve the quality of the reconstructed
images. Specifically, a discriminator will be added at
the output of the decoder and trained with real and
generated images. Optimization of a loss based on
both MSE and real/fake adversaries has been used
before. FSRGAN (Chen et al., 2018) uses this
technique and achieves the current perceptual state-
of-the-art in face super-resolution task for x8
upscaling. Another interesting direction would be to
modify the model for directly outputting distributions
instead of plain representations. This would resemble
variational autoencoders (Kingma & Welling, 2014)
which use a (normal) distribution for their latent
space. Converting the image labels to distributions
would be helpful for the attribute editing application
in terms of sampling an attribute point and controlling
the degree of the attribute phenotype in the generated
image (high probability samples of an attribute should
produce an emphasized attribute in the output image).
6 CONCLUSIONS
We have presented a simple method for calculating
effective representations of labels that capture the
relations among them, using a Siamese network and
a dataset of human faces. Several experiments were
conducted revealing the potential of the proposed
Converting Image Labels to Meaningful and Information-rich Embeddings
117

methodology and its ability to provide meaningful
label embeddings. The results of the experiments
suggest that the small size of the calculated
embeddings does not prevent them from maintaining
sufficient information regarding the semantics of the
data. Moreover, the experiments performed indicate
the big potential of methods that transform labels into
information-rich vectors.
REFERENCES
Benajiba, Y., Sun, J., Zhang, Y., Jiang, L., Weng, Z., &
Biran, O. (2019). Siamese Networks for Semantic
Pattern Similarity. 13th IEEE International Conference
on Semantic Computing, ICSC 2019, CA, USA, 191–
194. https://doi.org/10.1109/ICOSC.2019.8665512
Bengio, Y. (2013). Deep learning of representations:
Looking forward. Lecture Notes in Computer Science
(Including Subseries Lecture Notes in Artificial
Intelligence and Lecture Notes in Bioinformatics), 7978
LNAI, 1–37. https://doi.org/10.1007/978-3-642-39593-
2_1
Chen, Y., Tai, Y., Liu, X., Shen, C., & Yang, J. (2018).
FSRNet: End-to-End Learning Face Super-Resolution
with Facial Priors. 2018 IEEE/CVF Conference on
Computer Vision and Pattern Recognition, 2492–2501.
Denton, E., & Birodkar, V. (2017). Unsupervised learning
of disentangled representations from video. Advances
in Neural Information Processing Systems, 2017-
December, 4415–4424. http://arxiv.org/abs/1705.10
915
Geng, X. (2016). Label Distribution Learning. IEEE Trans.
Knowl. Data Eng., 28(7), 1734–1748.
Goodfellow, I., Pouget-Abadie, J., & Mirza, M. (2014).
Generative Adversarial Networks. CoRR, abs/1406.2.
Guo, J., Qian, Z., Zhou, Z., & Liu, Y. (2019). MulGAN:
Facial Attribute Editing by Exemplar. CoRR,
abs/1912.1.
He, K., Zhang, X., Ren, S., & Sun, J. (2016). Deep Residual
Learning for Image Recognition. Conference on
Computer Vision and Pattern Recognition (CVPR),
770–778.
He, Z., Zuo, W., Kan, M., Shan, S., & Chen, X. (2019).
AttGAN: Facial Attribute Editing by Only Changing
What You Want. IEEE Transactions on Image
Processing, 28(11), 5464–5478.
Higgins, I., Matthey, L., Pal, A., Burgess, C., Glorot, X.,
Botvinick, M., Mohamed, S., & Lerchner, A. (2017).
beta-VAE: Learning Basic Visual Concepts with a
Constrained Variational Framework. ICLR (Poster
Session).
Hinton, G. E., Vinyals, O., & Dean, J. (2015). Distilling the
Knowledge in a Neural Network. Computing Research
Repository (CoRR). http://arxiv.org/abs/1503.02531
Hsu, W.-N., Zhang, Y., & Glass, J. R. (2017). Unsupervised
Learning of Disentangled and Interpretable
Representations from Sequential Data. In I. Guyon, U.
von Luxburg, S. Bengio, H. M. Wallach, R. Fergus, S.
V. N. Vishwanathan, & R. Garnett (Eds.), Advances in
Neural Information Processing Systems 30: Annual
Conference on Neural Information Processing Systems
2017, 4-9 December 2017, Long Beach, CA, {USA} (pp.
1878–1889).
Kim, H., & Mnih, A. (2018). Disentangling by factorising.
In J. G. Dy & A. Krause (Eds.), 35th International
Conference on Machine Learning, ICML 2018 (Vol. 6,
pp. 4153–4171). PMLR.
Kingma, D. P., & Welling, M. (2014). Auto-Encoding
Variational Bayes. In Y. Bengio & Y. LeCun (Eds.),
2nd International Conference on Learning
Representations, ICLR 2014, Conference Track
Proceedings. http://arxiv.org/abs/1312.6114
Kurutach, T., Tamar, A., Yang, G., Russell, S., & Abbeel,
P. (2018). Learning plannable representations with
causal infogan. In S. Bengio, H. M. Wallach, H.
Larochelle, K. Grauman, N. Cesa-Bianchi, & R.
Garnett (Eds.), Advances in Neural Information
Processing Systems (Vols. 2018-Decem, pp. 8733–
8744).
Lample, G., Zeghidour, N., Usunier, N., Bordes, A.,
Denoyer, L., & Ranzato, M. (2017). Fader Networks:
Manipulating Images by Sliding Attributes. In I.
Guyon, U. von Luxburg, S. Bengio, H. M. Wallach, R.
Fergus, S. V. N. Vishwanathan, & R. Garnett (Eds.),
NIPS (pp. 5967–5976).
Liu, M., Ding, Y., Xia, M., Liu, X., Ding, E., Zuo, W., &
Wen, S. (2019). STGAN: A Unified Selective Transfer
Network for Arbitrary Image Attribute Editing. CoRR,
abs/1904.0.
Liu, Z., Luo, P., Wang, X., & Tang, X. (2015). Deep
Learning Face Attributes in the Wild. Proceedings of
International Conference on Computer Vision (ICCV).
Mueller, J., & Thyagarajan, A. (2016). Siamese Recurrent
Architectures for Learning Sentence Similarity. In D.
Schuurmans & M. P. Wellman (Eds.), AAAI (pp. 2786–
2792). AAAI Press.
Neculoiu, P., Versteegh, M., & Rotaru, M. (2016). Learning
Text Similarity with Siamese Recurrent Networks. In P.
Blunsom, K. Cho, S. B. Cohen, E. Grefenstette, K. M.
Hermann, L. Rimell, J. Weston, & S. W. tau Yih (Eds.),
Rep4NLP@ACL (pp. 148–157). Association for
Computational Linguistics.
Ronneberger, O., Fischer, P., & Brox, T. (2015). U-Net:
Convolutional Networks for Biomedical Image
Segmentation. International Conference of Medical
Image Computing and Computer-Assisted Intervention
18 (MICCAI), 234–241.
Sahito, A., Frank, E., & Pfahringer, B. (2019). Semi-
supervised Learning Using Siamese Networks. In J. Liu
& J. Bailey (Eds.), Australasian Conference on
Artificial Intelligence (Vol. 11919, pp. 586–597).
Springer.
Shao, R., Xu, N., & Geng, X. (2018). Multi-label Learning
with Label Enhancement. ICDM, 437–446.
Shen, W., & Liu, R. (2017). Learning Residual Images for
Face Attribute Manipulation. CVPR, 1225–1233.
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
118

Simonyan, K., & Zisserman, A. (2015). Very deep
convolutional networks for large-scale image
recognition. In 3rd International Conference on
Learning Representations, ICLR 2015 - Conference
Track Proceedings.
Szegedy, C., Ioffe, S., Vanhoucke, V., & Alemi, A. A.
(2017). Inception-v4, Inception-ResNet and the Impact
of Residual Connections on Learning. In S. P. Singh &
S. Markovitch (Eds.), Proceedings of the Thirty-First
AAAI Conference on Artificial Intelligence, February
4-9, 2017, San Francisco, California, USA (pp. 4278–
4284). AAAI Press.
Touvron, H., Vedaldi, A., Douze, M., & Jégou, H. (2019).
Fixing the train-test resolution discrepancy. In H. M.
Wallach, H. Larochelle, A. Beygelzimer, F. d’Alché
Buc, E. B. Fox, & R. Garnett (Eds.), Advances in
Neural Information Processing Systems (NeurIPS) (pp.
8250–8260).
Wang, Z., & Bovik, A. C. (2009). Mean squared error: Love
it or leave it? A new look at Signal Fidelity Measures.
IEEE Signal Process. Mag., 26(1), 98–117.
Wang, Z., Bovik, A. C., Sheikh, H. R., & Simoncelli, E. P.
(2004). Image quality assessment: from error visibility
to structural similarity. IEEE Transactions on Image
Processing, 13(4), 600–612.
Zhao, H., Gallo, O., Frosio, I., & Kautz, J. (2017). Loss
Functions for Image Restoration With Neural
Networks. IEEE Trans. Computational Imaging, 3(1),
47–57.
Converting Image Labels to Meaningful and Information-rich Embeddings
119
