Cloud-based Private Querying of Databases by Means of Homomorphic

Encryption

∗

Yassine Abbar

, Pascal Aubry

, Thierno Barry

, Sergiu Carpov

, Sayanta Mallick

, Mariem Krichen

Damien Ligier

, Sergey Shpak

and Renaud Sirdey

Capgemini DEMS France - Research & Innovation, France

CEA LIST, Universit

e Paris-Saclay, France

Wallix, France

Inpher, Switzerland

p.aubry@cea.fr, {nsurname}@wallix.com, {name}@inpher.io

Keywords:

Private Database Querying, Homomorphic Encryption, Privacy-by-Design.

Abstract:

This paper deals with several use-cases for privately querying corpora of documents in both settings where

the corpus is public or private with respect to an honest-but-curious infrastructure executing the query. We

address these scenarios using Fully Homomorphic Encryption (FHE) hybridized with other techniques such

as Symmetric Searchable Encryption (SSE) and Private Information Retrieval (PIR) to achieve acceptable

system level performances. The paper also presents the prototypes developed to validate the approach and

reports on the performances obtained as well as their capacity to scale.

1 INTRODUCTION

This paper addresses issues related to database query

in concrete setups where a client wishes to privately

perform general queries remotely to a database stored

on a server. The database can be either stored in clear

form (in which case it is public to the server) or en-

crypted. As examples, a user may wish to query a

database which mirrors the open (say, medical) liter-

ature but without revealing his or her query contents

(public database case) or may want to retrieve a selec-

tion of private encrypted corporate documents whose

(encrypted) storage has been outsourced to a cloud

platform.

The goal of the work presented in this paper is

to investigate how emerging privacy enhancing tech-

nologies can help addressing real-world database re-

lated scenarios in need for stronger privacy properties.

As a sound set of cryptographic primitives for per-

forming general calculations directly over encrypted

data, we have mainly used Fully Homomorphic En-

cryption (FHE) as a yardstick to address the speciﬁc

use-cases presented in this paper. In order to do so, we

have used the open-source Cingulata compiler envi-

∗

This Work Has Been Funded by the French FUI

Project ANBLIC.

ronment

which allows to write general programs and

then execute them over either the BFV (Fan and Ver-

cauteren, 2012) or the TFHE (Chillotti et al., 2016)

homomorphic schemes. Yet, using FHE to practically

address database query scenarios does not come with-

out challenges in terms of performance, scaling and

system architecture impacts. These applications re-

quire to deal with a large amount of data. Treating

as much data on the ciphertext domain implies a lot

of process even for simple tasks. Moreover, database

query scenario involves often reactivity needs. Com-

bining these imperatives with the FHE execution is

also an important issue.

This paper is organized as follows. Sect. 2

presents the system architectures of our two concrete

use-cases, how FHE ﬁts and impacts them as well as

the other cryptographic tools it had to be paired with

in order to be able to hope for practical performances.

Then, Sect. 3 didactically presents an example of al-

gorithm that had to be implemented over FHE and the

FHE-speciﬁc optimizations that had to be done on it.

Lastly, Sect. 4 presents experimental results.

www.github.com/CEA-LIST/Cingulata

Abbar, Y., Aubry, P., Barry, T., Carpov, S., Mallick, S., Krichen, M., Ligier, D., Shpak, S. and Sirdey, R.

Cloud-based Private Querying of Databases by Means of Homomorphic Encryption.

DOI: 10.5220/0010378801230131

In Proceedings of the 6th International Conference on Internet of Things, Big Data and Security (IoTBDS 2021), pages 123-131

ISBN: 978-989-758-504-3

123

2 APPLICATION SCENARIOS

AND ARCHITECTURES

2.1 Private Text Search on Public

Medical Literature Databases

(PSPMD)

2.1.1 Use Case Objectives and Outcomes

We ﬁrst consider a setup which requires to perform

private queries over an unencrypted database. This

use-case comes from a system under development by

the company of some of the paper authors and, as

such, can be considered a real-world scenario.

Public search engines are used by medical profes-

sionals, insurers and pharmaceutical laboratories on

public bibliographic databases. These professionals

often seek information from open databases on the

internet using clear queries. However query data can

leak sensitive corporate information related to intel-

lectual property, R&D or marketing strategies. For

example, when employees of a pharmaceutical ﬁrm

seek documents on the drug toxicity of a speciﬁc

molecule for personalized medicine and targeted ther-

apies, it may leak the fact that the company is con-

sidering the development of a new drug based on

it. Of course, although our prototype system targets

corporate users and corporate privacy, its core tech-

nology can also be relevant to address personal pri-

vacy issues as, in this context, query data can also

be used for person identiﬁcation, to feed some ad-

vanced monitoring algorithm or extract sensitive per-

sonal information related to medical condition, ethnic

origin or sexual orientations. As a result, this use-case

addresses the problem of information retrieval doc-

uments ranking by using encrypted user queries on

open data search environment. The use-case goal is

to allow the ﬁnal user to encrypt sensitive query terms

before sending them to the public search server, then

the ﬁnal user will obtain the ranking documents re-

sults with the minimum of information leakage. The

server side will rank the documents using the TF-

IDF (Term Frequency–Inverse Document Frequency)

ranking model. To achieve this goal, we have built a

prototype which show the use of privacy driven text

search environment using FHE (Fully homomorphic

encryption) and PIR (Private information retrieval).

The reason of FHE and PIR techniques combination

is to reduce FHE computations and transfer of FHE-

encrypted data which means that FHE is used to com-

pute the TF-IDF of the documents to ﬁnd the most rel-

evant ones but returns only document id information.

Then, the PIR protocol is further used to fetch the en-

tire relevant documents from the server without re-

vealing which were fetched. The high level architec-

ture of the PMSPD use-case follows the client-server

model, each system entity has a predeﬁned role. The

system goal is to minimize the user query information

leakage to the server and the FHE computation.

2.1.2 Client-side

The client application performs four main tasks:

• FHE public and secret keys generation.

• FHE query terms ids encryption using the FHE

public key.

• FHE documents scores decryption with their cor-

responding ids using the FHE secret key.

• Perform the subsequent PIR request to privately

fetch the most relevant documents from the public

database from the ids.

2.1.3 Server-side

The server-side contains two main services : an FHE

service and an indexing service which communicate

with two databases, a public documents database for

the latter and digested corpus database for the for-

mer. The public documents database contains the raw

open data sources (medical publications, biomedical

articles, medicals record, etc ). The digested corpus

database contains the plaintext values needed for FHE

computation (e.g. tokenized data, with keywords re-

placed by hashes, etc. in order to FHE operations to

proceed). Then, the FHE service performs three main

tasks :

• Read data from the digested corpus.

• Compute similarity between encrypted user query

and the plaintext document digests using TF-IDF

ranking model and FHE.

• Execute PIR server to fetch documents from the

raw document database.

Lastly, the indexing service performs the following

three main tasks:

• Public documents database indexing.

• FHE-friendly documents data formatting.

• Corpus update: e.g., add or delete documents

from the database.

2.1.4 Security Model and Communication

between System Entities

The main system security requirement concerns the

end user query sensitive information privacy. Thus,

IoTBDS 2021 - 6th International Conference on Internet of Things, Big Data and Security

124

in the context of a public environment search, the

end user client application needs to hide the user

query sensitive terms before sending it to the server-

side. Then, The FHE service computes the documents

ranking, in the encrypted domain, according to the

documents (encrypted) score values. Finally, a PIR

protocol is used to privately fetch the entire docu-

ments from the database.

Figure 1: High level architecture of PMSPD use-case.

2.2 A Platform for Conﬁdential Search

in End-to-End Encrypted Data

2.2.1 Use-case Objectives and Outcomes

We now consider a setup which requires to perform

private queries over an encrypted database. As for

the preceding one, this use-case comes from a cloud

platform under development by the company of some

(other) authors of the paper and, as such, can be con-

sidered a real-world scenario in which end-to-end-

encryption (E2EE) needs to be integrated as seam-

lessly as possible into applications to harden their se-

curity.

However, E2EE with “traditional” cryptography

faces a number of barriers, the most obvious being

that, without granting a decryption ability, any legit-

imate encrypted data exploitation is hopeless. As an

example, one of the usages that are impossible to hold

over encrypted data is key word Search.

Fully Homomorphic Encryption provides an an-

swer to this problem by enabling the possibility to

store data, on Cloud or “on Premise”, in an encrypted

form and, yet, to exploit them for legitimate purposes

without any decryption taking place. As such, the Key

word Search on Encrypted Data capability is meant

to be a high added value feature for an E2EE plat-

form.Retrieving the most relevant documents from a

corpus given a user query is a common operation for

search engines. A search engine ranks the documents

regarding the importance of the keywords from the

user query to documents contents and returns results

to the client. Currently, search engines require access

to the corpus and to the keywords in the query for this

operation. However, it poses a security risk if a client

wants to perform a keyword search on conﬁdential or

sensitive data. To address this problem we propose to

use FHE to allow a server to rank documents in the

case of an encrypted query over an encrypted corpus.

2.2.2 High-level Architecture

A server that wants to rank documents where both the

query and the corpus are encrypted using FHE, needs

to:

1. Calculate the importance of terms from the query

to every document in its database. In this pa-

per, this is done by means of the term frequency-

inverse document frequency (TFIDF) statistic to

estimate the importance of a term in a document.

2. Sort the documents by the statistic calculated in

the ﬁrst step in the order of decreasing impor-

tance.

As a result, the server returns the n ﬁrst (most

relevant) documents to the client. Depending, on

performance and security trade-off of the setup, we

can optimize the process for example by means of

a SSE-based preprocessing step which could consist

in ﬁrst retrieving the documents which contain the

query terms and pass them (and only them) to the

FHE server for ranking. There are several options to

associate SSE and FHE, which we now discuss.

Also note that (Shen et al., 2018) uses a similar

approach to perform searching and ranking in an en-

crypted corpus; however, the proposed solution does

not allow to sort the retrieved documents ranks at

server side. Using FHE allows us to overcome this

limitation.

Mainly, there are three possible architectures to

model this use-case.

First Model. First, if no SSE is used, then the TF-

IDF computation has to be performed for all database

records and the whole database has to be sorted based

on ranking. When SSE is put into the picture then

there are two options depending on whether or not

the indices of the records matching the SSE request

are disclosed to the FHE server or only their number.

Second Model. If these indices are disclosed, then

the FHE server can compute the TF-IDF only for a

(presumably small) subset of the database records and

then perform the sorting only on that subset. This

is the most favorable case in terms of decreasing the

FHE computation footprint, but it induces some infor-

mation leakage – for example, it reveals if two queries

Cloud-based Private Querying of Databases by Means of Homomorphic Encryption

125

concern the same (encrypted) records at the SSE step.

The main drawback of this model is that we leak a

very important information while the main advantage

is that the FHE Server could directly select the docu-

ments for which it will compute TF-IDF.

Third Model. If the indices are not disclosed but

only their number is, then the FHE server will have

to compute the TF-IDF for all of the database records

but sorting will be performed only for the documents

which have their indices in the SSE response (al-

though the server is not able to identify them). De-

pending on the size of the SSE response, this model

could be more or less interesting. We will detail this

in section IV.

2.2.3 Communication between System Entities

To isolate different parts of the system we chose the

model where the SSE server and the FHE server do

not communicate (that is the second model above).

The communications between the client and the

servers are shown in Figure 2.

Figure 2: Communications during the query phase consid-

ering a system with FHE and SSE Servers.

2.2.4 Security Model

The principal requirement to the system in the context

of data security is the conﬁdentiality of the document

contents stored server-side as well as the client rank-

ing requests.

FHE Server. We use an IND-CPA secure FHE

scheme for the use-case and we assume the honest-

but-curious security model for the server. Therefore,

encryption operations performed on the data does not

leak any information about cleartext values. As the

FHE server calculates TF-IDF, it knows the number

of documents in the corpus.

SSE Server. As the data, which is stored server-

side, and the client queries are encrypted, the contents

of the documents and the ranking request terms are

not exposed to an unauthorized party. However, we

should consider the potential data leakage due to the

analysis of the terms usage in insert and rank queries.

The system should guarantee the data forward pri-

vacy. This security characteristic means that indexing

a new document against the server does not leak the

information on terms that the document contains. We

cannot require the backward privacy, i.e. the security

characteristic that means that deleting a document re-

moves the information on the keywords that the doc-

ument contained. To our knowledge, there is no efﬁ-

cient SSE scheme that allows to fulﬁll the backward-

privacy requirement. Nevertheless, the SSE server

should delete the documents when required by the

client.

3 IMPLEMENTING TF-IDF OVER

FHE

In this section, we focus, as an example, on the im-

plementation of a TF-IDF ranking following an en-

crypted query over a clear database by means of a

levelled-FHE. Note that although the database is not

encrypted, the result is necessarily encrypted. Note

also that the FHE formalism can easily handle mixed

clear/encrypted data calculations (the results always

being encrypted). Thus, this section intends to illus-

trate the kind of programming mindset and techniques

that have to be used to implement a given algorithm

towards an (as) efﬁcient (as possible) execution in

the encrypted domain. Unitary performance results

a given throughout the section using the BFV scheme

to illustrate our purpose. Overall performance results,

using several FHE cryptosystems, are given in Sect.

So let us consider the following usual formula for

the computation of the score of a document d ∈ D

(Salton and Buckley, 1988),

score(q, d) = coord (q, d).

∑

t∈q

tf(t, d) .idf

(t)

where q ⊆ T is the subset of terms from the ﬁxed

vocabulary T in the query. As, in the present case,

the database is public, pre-computations can be done

in the clear-domain to minimize the footprint of en-

crypted domain calculations. In particular, this ap-

plies to the product of the term frequency tf (t, d) and

the square of the inverse document frequency idf(t)

The term frequency is the number of occurrences of

IoTBDS 2021 - 6th International Conference on Internet of Things, Big Data and Security

126

a term t

T in a document d ∈ D. The inverse docu-

ment frequency is computed as follows:

idf(t) = log



|D|

1 + n



where n

the number of documents containing the

term t. Let α be the matrix of tf.idf

. As the FHE for-

malism allows only to manipulate integers, we deﬁne

α(t, d) as dtf (t, d).idf(t)

c (to increase precision, it

is possible to apply a scaling factor before rounding).

Additionally, χ is the matrix which indicates the pres-

ence of a term in a document, i.e.,

χ(t, d) =



1 if tf(t, d) > 0

0 else

As a result, the score expression can be rewritten

in much more “FHE-friendly” form as,

score(q, d) =

∑

t∈q

χ(t, d) .

∑

t ∈q

α(t, d)

The last step consists in reformulating the above equa-

tion as

score(q, d) =

∑

t∈T

(q)

χ(t, d) .

∑

t∈T

(q)

α(t, d)

where x

(q)

is set to 1 iff q ∈ T and 0 otherwise. As

such, the x

(q)

are the |T | encrypted variables repre-

senting the query

which then interact with the clear-

text data χ (t, d) and α (t, d) to produce an encrypted

score(q, d).

3.1 Pseudocode

Algorithm 1 describes how to compute the scores and

return the results sorted by score. First, we com-

pute the score using the pre-calculated matrix α. For

each document, we then calculate the product of 2

sums, acc and coord, where acc is the sum of the

relevant α’s and coord is the sum of the relevant χ’s

for each term in the query. Note that the outter loop

is obviously parallel. When all the scores are com-

puted, we sort the documents by score by means of

the FHE-optimized algorithm described in (Chatter-

jee and Sengupta, 2015).

Implicitly, this reformulation assumes that the number

of terms is relatively small since |T | encrypted bits have to

be sent from the client to the server. Other approaches are

possible for encoding the query when this is not the case,

which results in a larger computational burden on the server

(and which also require revealing the number of terms in

the query, while this is not necessarily an issue).

Algorithm 1: Algorithm for retrieving document ranking by

score.

Require: num terms – number of terms in the dictio-

nary

Require: num docs – number of documents in the

database

Require: α [term id][doc id] – t f .id f

calculated

for the document identiﬁed by doc id and the term

identiﬁed by term id

Require: χ [term id][doc id] – 1 if term with

term id is in the document with doc id, 0 else

Require: query [term id] – 1 if term in the query, 0

else (secret)

Require: num results – number of results

Ensure: Res – Vector of results of the length

num results

for i in 1 : num

docs do

coord = 0 and acc = 0

for j in 1 : num terms do

acc = acc + query [ j].α [ j][i]

coord = coord + query [ j].χ[ j][i]

end for

score[i] = acc.coord

end for

Res =SORTBYSCORE(score)

return Res

3.2 Multiplicative Depth

Characterization

Algorithm 1 has been implemented using the Cin-

gulata toolchain. Cingulata is a compiler toolchain

and RTE for running C++ programs over encrypted

data by means of fully homomorphic encryption tech-

niques (https://github.com/CEA-LIST/Cingulata). In

the present case, we have conﬁgured Cingulata

in order to use the Fan-Vercauteren(Fan and Ver-

cauteren, 2012) schemes as the FHE backend. Under

this scheme, the execution performances are highly

multiplicative-depth dependant. The multiplicative

depth is the maximal number of sequential homomor-

phic multiplications which have to be performed on

fresh ciphertexts such that once decrypted we retrieve

the result of these multiplications.

With respect to this, the algorithm for retrieving

document ranking by score can be split in two parts:

score computation and sort algorithm. The score

computation is a product of coord and acc. The mul-

tiplicative depth of multiplication depends on the bit

width of the entries size int . According to (Buescher

et al., 2016), the multiplicative depth of multipli-

cation is minimized with the Wallace tree compo-

sition(Wallace, 1964). The multiplication can thus

be performed with a depth of dlog

(size int)e + 1.

Cloud-based Private Querying of Databases by Means of Homomorphic Encryption

127

Table 1: Execution of Algorithm 1 in function of num docs

and num terms.

# terms # docs mult. depth exec. time (s)

4 4 4 0.18

4 20 5 0.79

10 10 16 74.02

10 20 17 251.86

20 20 17 315.46

30 30 17 688.66

50 50 18 2175.77

50 100 20 None

60 60 18 3090.57

70 70 20 6299.17

80 80 20 None

100 20 17 617.06

100 50 18 2732.67

150 20 17 800.92

150 50 18 3241.01

200 50 18 3794.28

300 50 18 5042.98

400 50 18 None

500 50 18 None

As described in (Chatterjee and Sengupta, 2015),

the multiplicative depth of sort algorithm is equal to

dlog

(size int + 1)e + dlog

(num docs − 1)e + 1.

Thus, the overall algorithm multiplicative depth is

dlog

(size int)e + dlog

(size int + 1)e

+dlog

(num docs − 1)e + 2

3.3 Unitary Benchmarks

We produced different benchmarks in order to eval-

uate the performances of FHE executions of Algo-

rithm 1. For this purpose, we generated randomly the

term frequency matrices T F for different values of

num docs and num terms (note that FHE execution

timings are by necessity data-independant, so work-

ing on dummy or real data does not change the ob-

served performances). For the different tests, the size

of integer size int is 8. As FHE execution is per-

formed on arithmetic or boolean circuits, it is intrinsi-

cally parallelizable. Thus, we can use multiprocessor

architectures to accelerate the execution time (some-

thing Cingulata nicely does for free). The following

benchmarks have been achieved on a 16-core Intel

Xeon Bronze 3106s calculation server, all cores be-

ing activated.

In Table 1, #terms and #docs are the number

of terms and the number of documents respectively.

Also, mult.depth represents the multiplicative depth

of the application and exec.time denotes the execution

times in seconds. Except for low values of num

docs,

the multiplicative depth follows the equation in sub-

section 3.2. Above 64 documents, the multiplicative

depth becomes 20 instead the 19 expected. This is due

to the way Cingulata generates the Boolean circuit.

Indeed, Cingulata is not using the Wallace decompo-

sition but instead several optimization to reduce mul-

tiplicative depth after a ﬁrst Boolean circuit is gener-

ated. With lines 3, 4 and 5 of Table 1, we see that the

execution time increases faster with higher number

of documents than with higher number of terms. We

were not able to execute tests with a number of docu-

ments above 70 as the memory of the workstation sat-

urated before the FHE execution was complete. We

also increased the number of terms in order to ﬁnd the

maximal num terms possible with num docs = 50.

3.4 Optimizing Performance

In (Aubry et al., 2020) and in (Carpov et al., 2017),

the authors propose several heuristics to automati-

cally reduce the multiplicative depth of Boolean cir-

cuits toward improving FHE execution performances.

These methods deﬁne several local rewriting opera-

tors which preserve the semantics of the Boolean cir-

cuit. We applied these heuristics to lower the mul-

tiplicative depth of our benchmark circuits, as we

wanted to measure the performance gains using these

heuristics. We managed to reduce the multiplicative

depth by 1 or 2 which lead to an average speed-up of

1.15 for the present benchmark.

Note that in these unitary tests we consider only

queries with a single term to decrease the multiplica-

tive depth and lower the computational time of appli-

cations. Indeed, less operations are required to rank

the documents by score if the number of terms in the

query is one. Let id term be the index of the term in

the query. coord is equal to 1 if α (id term, d) 6= 0

and 0 else. Hence, only α (id term, d) is required

to perform the score of the document. Moreover, as

idf(id term) is the same for all the documents, this

metric does not inﬂuenced the rank of the documents.

Hence, only t f is required to compute α (id term, d).

As the score computation only consists in retrieving

the α(id term, d) for each document d ∈ D, we con-

sider only the multiplicative depth of the sort algo-

rithm. Then, the minimal multiplicative depth of the

sorting algorithm is :

dlog

(size int + 1)e + dlog

(num docs − 1)e + 1

The maximal execution time was below 40s for

all the tests. So if we restrict ourselves to single-

term queries, then the response time can be reason-

able. Note that this restriction might be interesting in

practice as it is possible that several services cohabit

in a given system e.g. fast one term queries and slower

multi-term ones.

The main issues we encountered was compilation

one. Whereas we had reasonable execution times, the

IoTBDS 2021 - 6th International Conference on Internet of Things, Big Data and Security

128

compilation time was very long. In practice, this is

not a real issue, as we need to compile the code only

once and this compilation phase is done ofﬂine.

4 PERFORMANCE

EVALUATIONS

High-level abstractions and tools are provided in or-

der to facilitate the implementation and the execution

of privacy-preserving applications.

4.1 Private Search on Public Medical

Literature Database

Table 2 provides the execution timings obtained with

Cingulata using TFHE as the backend cryptosystem

for various small numbers of documents and vocabu-

lary terms. At present, we did not yet integrated the

PIR (Private Information Retrieval) step in our pro-

totype. This will be done by means of well know

PIR libraries such as XPIR (Melchor et al., 2016) or

SealPIR (Angel et al., 2017) to fetch the top ranked

documents privately. In Table 2 the time (s) represents

user time for computing the score and performing the

subsequent sort in Cingulata. The #gates columns

provides the total number of AND and XOR gates.

With TFHE, the time per gate is a constant which de-

pends only on the processor.

Table 2: TFHE execution timings (in secs) for various num-

bers of documents and terms in the context for the private

search on public data use-case.

#doc #terms #gates time (s)

7 10 3201 47

8 15 4948 109

10 17 7299 149

13 23 13125 229

12 18 10043 211

17 31 22994 645

23 35 39292 572

22 25 31616 501

16 33 21796 350

21 31 33617 556

26 55 57339 1043

50 100 214060 3591

20 100 58792 850

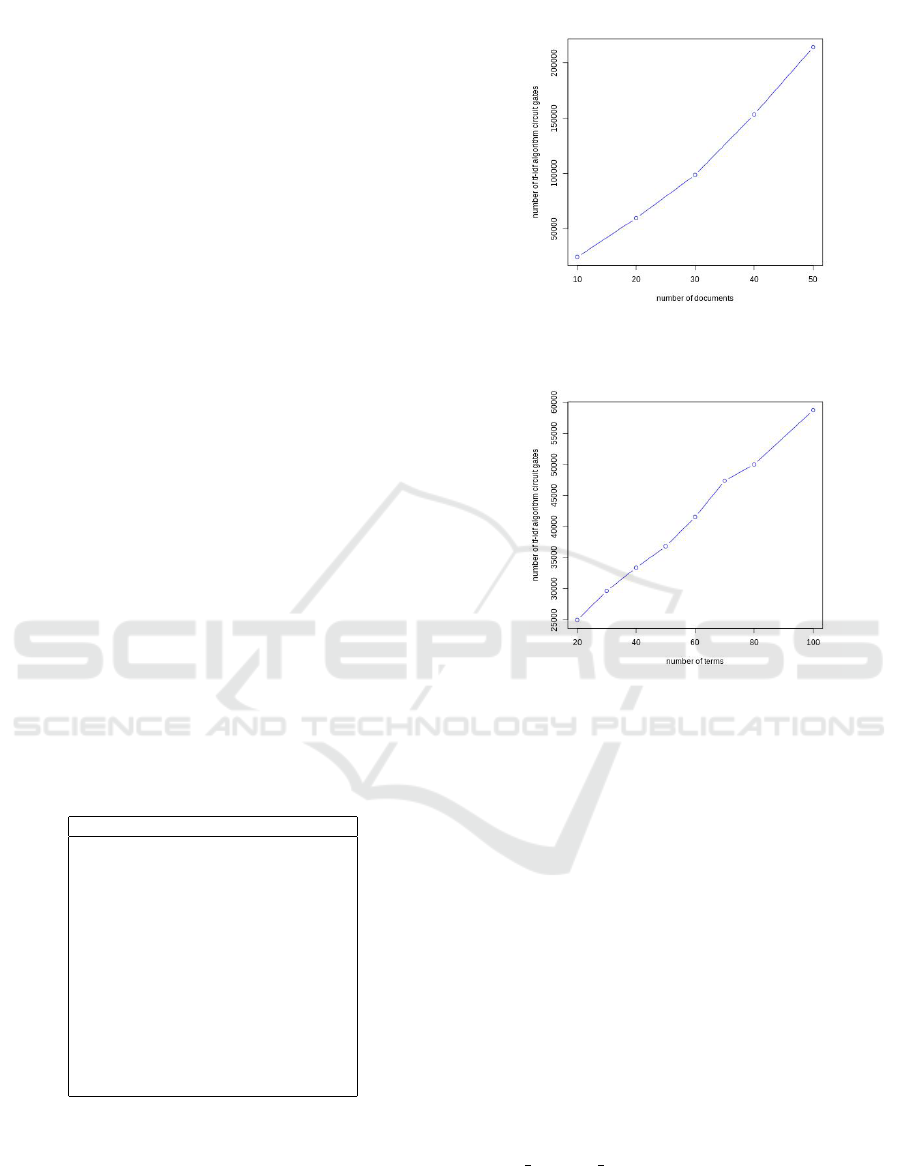
Figure 3 shows the number of total gates for a

dictionary of 100 terms varying the number of doc-

uments in the corpus and Figure 4 shows the number

of total gates for a corpus of 20 documents varying the

size of terms in the dictionary. In order to get coarse

estimates with respect to how these ﬁgures will scale,

we assume that there is a linear relation between the

Figure 3: (number of gates varying the size of documents

corpus with a dictionary of 100 terms.

Figure 4: Number of gate varying the size of dictionary

terms with 20 documents corpus.

number of gates and the numbers of documents and

terms. There is also a linear relation between the

number of gates and the execution timing because (in

TFHE) the execution time of unitary gates (AND or

XOR) is constant.

4.1.1 PSPMD Use-case Scaling Estimation

Thus, by preforming a bi-linear regression (based on

the data of Table 2 between the number of documents,

number of terms and number of gates we can estimate

the number of gates for larger corpus sizes and, since

the time/gates is a constant, also obtain estimates for

the associated execution timings. Thus, we can ob-

tain an approximate scaling formula between number

of documents, the number of terms and the execution

timing:

seq time = t gate.(a

.docs + a

.terms + a

) (1)

with a

= 1681, 008 , a

= 509, 4045 , a

−18014, 7.

Lastly, we also assume that linear multicore

speedups are achievable (from past experience with

Cloud-based Private Querying of Databases by Means of Homomorphic Encryption

129

Table 3: Estimation of TFHE sequential execution timings

(in mins) for various numbers of documents and terms high

sizes in the context of PSPMD use-case using the estimation

equation(1). For the last column, 100 cores are assumed.

# doc # terms # gates time (s) // time (s)

100 500 404788 6071 75

1000 1000 2172397 32585 407

10000 1000 17301465 259521 3244

10000 10000 21886105 328291 4103

100000 10000 173176784 2597651 32470

other kinds of FHE calculations) according to the fol-

lowing formula

parallel time =

seq time

0.8.nb o f core

(2)

which domain validity ranges up to around 200 cores

(which corresponds to the largest multicore machines

with a uniﬁed shared memory).

Hence, given the empirical equation 2 between

parallel execution timing and sequential execution

timing in TFHE mode and the equation 1, we obtain

scaling estimation equation 3 of the score and sort al-

gorithm using multi-core processor machines:

parallel

time =

t gate.(a

.docs + a

.terms + a

)

0.8.nb o f core

(3)

Thus, with an expected latency for query response

of around 3 mins and 100 CPU cores on a single com-

puter node, we will approximately cover an corpus of

240 documents and 500 terms. With a 2000 docu-

ments corpus and 500 terms we almost reach 10 min

of latency in the same conditions. In terms of com-

munications, the client sends an encrypted query of

size 1 Mo and receives the 10 most relevant ranked

documents (encrypted) ids which account for 160

Ko. Both ﬁgures and scaling estimation shows the

scalability limitation in FHE encrypted computations

for documents searching without parallelism exploita-

tion.

4.2 Conﬁdential Search in End-to-End

Encryption Platform

4.2.1 Execution Time Gain using SSE

The main purpose of using SSE is to reduce the FHE

computation time as discussed in Sect. 2.2.2. The

FHE server receives a request from the client with

encrypted terms and encrypted documents indices

(found during the SSE phase). Then, although the

TF-IDF computation has to be performed for all doc-

uments in the database

, the FHE server only stores

As the FHE server cannot “trigger” the TF-IDF com-

putation conditionally, it performs it for all documents in

(and sorts) as many TF-IDF results as there are docu-

ment indices in the SSE response.

Thus, using the SSE server induces an execution

time gain that tightly depends on the number of the

returned document indices. Figure 5 highlights the

FHE computation time in seconds considering differ-

ent lengths of the SSE response. We do not take into

consideration the time needed by the SSE server to ﬁl-

ter documents. In this case, we considered an instance

with 8-bit integers, 10 documents in the corpus, 8

terms in the dictionary and a query with 3 terms.

Figure 5: FHE execution time considering different lengths

of the SSE response.

Figure 5 shows a quadratic dependency of the ex-

ecution time on the number of terms returned by the

SSE.

We tried to improve the ranking time by perform-

ing the documents ranking using a modiﬁed parallel

merge sort. We tried to achieve the performance gain

by splitting the SSE response into batches, sorting

them in parallel and getting only k ﬁrst elements out

of the response of the length h, n > k. However, FHE

does not allow to extract only k ﬁrst elements during

the merge phase, making it computationally expen-

sive and cancelling out the performance gain. As

a result sorting the whole response with Cingu-

lata’s standard sorting function is more efﬁcient.

4.2.2 Execution Times

In order to deploy our documents ranking system, we

need to setup the cryptographic tools related to the

FHE and SSE deployment. This phase allows the

client to have the cryptographic keys for the FHE

system and for the SSE system in order for her to

be able to send encrypted data related to the docu-

ments corpus to the server(s). We give in this section

some execution time graphics necessary for the setup

and the query phases. Note that NBDOC refers to

the number of documents in the corpus, NBTERM

the database, though some results are “not used” (or, rather,

have no effect in the clear domain but the FHE server cannot

by-construction distinguish when this is the case.

IoTBDS 2021 - 6th International Conference on Internet of Things, Big Data and Security

130

refers to the number of word in the dictionary and

ﬁnally NBREQ refers to the number of words in a

request. Figure 6 shows the execution time of both

phases where we vary the number of documents from

10 to 50 and where we consider NBTERM=10 and

NBREQ=2. Figure 7 shows the execution time of

both phases where we vary the number of terms in

the dictionary from 10 to 35 and where we consider

NBDOC=10 and NBREQ=2.

Figure 6: Execution time varying the number of documents.

Figure 7: Execution time varying the number of the query

terms.

Additionally, Figure 6 shows that for a database

of 50 documents, the setup and the query will take al-

most 17 minutes to be processed (sequentially). Fig-

ure 7 shows that for a dictionary of 35 terms, it takes

more than 5 minutes to sequentially process a two

terms query in a database of 10 documents. In this

case the sizes of the requests sent to the FHE server

and its responses are of the order of 90 kB and 20

kB respectively. Both ﬁgures show the limits of FHE

computation for word searching in an encrypted cor-

pus when it comes to scalability, unless heavy paral-

lelism is used. These results also shows that running

encrypted queries over encrypted data is more chal-

lenging than running encrypted queries overs clear

data.

5 CONCLUSION

In this paper, we have studied real-life scenarios of

performing encrypted queries over clear or encrypted

data. Indeed, we have investigated the impact of inte-

grating FHE in the system architectures of these use-

cases as well as optimized the involved algorithms to-

wards FHE-friendlyness and FHE execution perfor-

mances. Although we obtained acceptable perfor-

mances on small database sizes, our experimental re-

sults still suggest that scaling our observed sequen-

tial execution timings to larger database sizes remains

a challenge. Still, parallelism and hardware accel-

eration of FHE operators on FPGA offer short and

medium terms perspectives to achieve better scaling.

REFERENCES

Angel, S., Chen, H., Laine, K., and Setty, S. (2017). Pir

with compressed queries and amortized query pro-

cessing. In International Conference on Security and

Privacy in Communication Systems. The University of

Texas at Austin New York University and Microsoft

Research.

Aubry, P., Carpov, S., and Sirdey, R. (2020). Faster homo-

morphic encryption is not enough: improved heuristic

for multiplicative depth minimization of boolean cir-

cuits. In CT-RSA, pages 345–363.

Buescher, N., Holzer, A., Weber, A., and Katzenbeisser, S.

(2016). Compiling low depth circuits for practical se-

cure computation. In ESORICS, pages 80–98.

Carpov, S., Aubry, P., and Sirdey, R. (2017). A multi-

start heuristic for multiplicative depth minimization of

boolean circuits. In IWOCA, pages 275–286.

Chatterjee, A. and Sengupta, I. (2015). Searching and sort-

ing of fully homomorphic encrypted data on cloud.

IACR Cryptology ePrint Archive, 2015:981.

Chillotti, I., Gama, N., Georgieva, M., and Izabach

ene, M.

(2016). Faster fully homomorphic encryption: Boot-

strapping in less than 0.1 seconds. In ASIACRYPT,

pages 3–33.

Fan, J. and Vercauteren, F. (2012). Somewhat practical fully

homomorphic encryption. IACR Cryptology ePrint

Archive, 2012:144.

Melchor, C. A., Barrier, J., Fousse, L., and Killijian, M.-O.

(2016). XPIR: Private information retrieval for every-

one. POPETS, 2016(2):155–174.

Salton, G. and Buckley, C. (1988). Term-weighting ap-

proaches in automatic text retrieval. Information pro-

cessing & management, 24(5):513–523.

Shen, P., Chen, C., and Zhu, X. (2018). Privacy-preserving

relevance ranking scheme and its application in multi-

keyword searchable encryption. In SecureComm, page

128.

Wallace, C. S. (1964). A suggestion for a fast multiplier.

IEEE Transactions on electronic Computers, 1:14–17.

Cloud-based Private Querying of Databases by Means of Homomorphic Encryption

131