
SLPRNet: A 6D Object Pose Regression Network by Sample Learning
Zheng Zhang
a
, Xingru Zhou
b
and Houde Liu
c
Center for Artificial Intelligence and Robotics, Shenzhen International Graduate School,
Tsinghua University, 518005, Shenzhen, China
Keywords:
Robot Manipulation, Point Cloud Sampling, Object Pose Regression.
Abstract:
Visual grasping holds important implications for robot manipulation situations. As a core procedure in such
grasping tasks, pose regression has attracted lots of research attention, among which point cloud based deep
learning methods achieve relatively better result. The usual backbone of such network architectures includes
sampling, grouping and feature extracting processes. We argue that common sampling techniques like Farthest
Point Sampling(FPS), Random Sampling(RS) and Geometry Sampling(GS) hold potential defectiveness. So
we devise a pre-posed network which aims at learning to sample the most suitable points in the whole point
cloud for a downstream pose regression task and show its superiority comparing to the above-mentioned
sampling methods. In conclusion, we propose a Sample Learning Pose Regression network (SLPRNet) to
regress each instances pose in a standard grasping situation. Meanwhile, we build a point cloud dataset to
train and test our network. In experiment, we reach an average precision(AP) up to 89.8% on dataset generated
from Silane and an average distance(ADD) up to 91.0% on YCB. Real-world grasp experiments also verify
the validity of our work.
1 INTRODUCTION
In the robot industry, grasping tasks are really com-
mon and important. Given different kinds of instances
in a scene, robots are required to pick the exact target
out. During this process, the executor should have
accurate information as input, which contains targets
translation and rotation information basically. Stan-
dard translation information is represented by a 3 di-
mensional vector including x y and z values in carte-
sian space, while rotation information contains three
Euler angles α β and γ which also form a 3 dimen-
sional vector. Combining these two vectors together,
a pose regression task mainly aims to get the 6Dof
representation of a particular instance.
Previous approaches usually treat this regression
problem as a feature matching problem (et al., 2012;
Deng et al., 2010), where an original template is re-
quired to search matching features. But these meth-
ods are not accurate enough when applied to clut-
tered and occluded scenes. Therefore, recent works
always turn to deep learning method (Xiang et al.,
2018) and treat this problem in an end-to-end man-
a
https://orcid.org/0000-0001-8195-9624
b
https://orcid.org/0000-0002-2796-2264
c
https://orcid.org/0000-0002-7314-3366
ner. The work (Xiang et al., 2018) takes RGB im-
ages as input and uses convolutional neural networks
to solve the pose regression problem. However, with
the growth of the input scale, especially in 3D scenes,
RGB-based methods show their deficiency. RGB im-
ages are always divided into regular pixels in grid
space, which could not reflect the actual relationship
among points in 3D space. Thus, point cloud based
deep leaning methods (Qi et al., 2017a) are proposed
recently, which outperform RGB-based ones to a con-
siderable degree, particularly in 3D scenes.
In point cloud based method, limited by the com-
puting power, the usual treatment to point cloud P is
to sample some representative points constituting a
subset S first. The most common used approaches in-
clude Random Sampling(RS) and Farthest Point Sam-
pling(FPS) (Moenning and Dodgson, 2003). FPS
holds the idea that taking into account the structure
of a point cloud, points that are far away with each
other may represent the point cloud better compar-
ing with those points gathering in a small area. Many
deep learning methods use FPS to handle their origi-
nal point cloud (Qi et al., 2017a). However, it is ob-
vious that different sampled subsets should contribute
differently to a particular task. Thus, draw on the idea
of (Dovrat et al., 2019), we design a sample network
to choose a best subset for pose regression task using
Zhang, Z., Zhou, X. and Liu, H.
SLPRNet: A 6D Object Pose Regression Network by Sample Learning.
DOI: 10.5220/0010385912331240
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 2, pages 1233-1240
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
1233

deep learning method.
The SLPRNet mainly contains two parts: the first
part is a sample-learning network which takes raw
point cloud P as input and outputs a particular sub-
set S for pose regression task; the second part is a
pose-regression network which takes S as input and
outputs the exact 6Dof pose of each instance in the
original point cloud P. Architecture of SLPRNet is
shown in Fig.1. During this process, we also create a
new dataset based on Silane and YCB to validate our
performance, which contains the 6Dof pose informa-
tion of the object that each point belongs to.
In summary, this work mainly contributes in the
following aspects:
(a) We devise a sample-learning network to sam-
ple the raw point cloud to a best-suitable subset for
pose regression task;
(b) We propose a pose-regression network to
regress the 6Dof pose of each instance from a point
cloud. Combining with the sample-learning network,
we achieve a better pose regression result—an AP up
to 89.8% and ADD up to 91.0%—than current non-
learning sampling methods;
(c) We create a synthetic dataset on which
our network can be trained and validated,
which is also publicly available at Kaggle:
https://www.kaggle.com/shawnzhengzhang/slprnet-
dataset.
The rest of the paper is organized as follows: Sec
II reviews related works about pose regression and
sampling on point clouds. Sec III introduces the struc-
ture of our network and method in detail. Sec IV
shows some experiment results of our method. And
Sec V includes the conclusion and future work.
2 RELATED WORK
In this section, we mainly review some typical work
on pose regression and point cloud sampling.
2.1 Pose Regression
Typically, pose regression is based on point cloud reg-
istration, which aims to find a spatial transformation
that aligns two point sets. Rusu (R. B. Rusu and
Beetz, 2009) proposed a coarse registration approach
SAC-IA, which exploits hand-crafted local features
FPFH for point pair matching and uses RANSAC for
pose hypotheses. Coarse alignment can then be re-
fined by ICP based methods (Besl and McKay, 1992).
Drost (Deng et al., 2010) proposed to use Point Pair
Features for building a hash table as model global de-
scriptors and retrieve poses from scene point cloud
via voting scheme, which is then extended by (Hin-
terstoisser et al., 2016) for better performance under
noise and occlusion.
In recent years, with the progress of deep learn-
ing, network based pose regression methods becomes
more popular. Among these methods, point cloud
data instead of RGB or RGB-D data has gradually
dominated the area thanks to the pioneer work of
Pointnet (Qi et al., 2017a) and Pointnet++ (Qi et al.,
2017b). Pointnet (Qi et al., 2017a) can extract fea-
tures from raw point cloud directly using symmetry
function such as max pooling. And Pointnet++ (Qi
et al., 2017b) porposed the classical hierachical archi-
tecture including sampling layer, grouping layer and
feature extracting layer, in which way furthermore
improve the network performance. Many works han-
dling object detection or segmentation use Pointnet++
as their backbone and achieve impressive effect, such
as (Aoki et al., 2019; Zhang et al., 2020; Z et al.,
2019).
The work (Qi et al., 2019) is a more representa-
tive work. Kaiming He combines Pointnet and hough
voting (Gall and Lempitsky, 2009) together and gets
3D bounding boxes from the raw point cloud, which
contains the pose information of an instance. Work
(Qi et al., 2019) verifies the effectiveness of hough
voting in pose regression tasks. Our pose-regression
network also uses the thought of hough voting, but to
be more specific, we execute hough voting to each of
the sampled points and get better results.
2.2 Point Cloud Sampling
Several techniques for point cloud sampling have
been proposed in the literature. The most com-
monly used sampling method (Moenning and Dodg-
son, 2003) Farthest Point Sampling(FPS) was adopted
in the work of Moenning as a means to simplify point
clouds of geometric shapes, in a uniform as well
as feature-sensitive manner. Recently, Chen (Chen
et al., 2018) employed graph-based filters to extract
per point features. Points that preserve specific in-
formation are likely to be selected by their sampling
strategy. The desired information is assumed to be
beneficial to a subsequent application.
Other point cloud sampling methods include Ran-
dom Sampling(RS) and Geometry Sampling(GS). RS
is a rather direct and simple method which just ran-
domly samples required number of points from a raw
point cloud without considering the relative position
of the sampled points. Intutively, RS holds very
low computational complexity, whereas sacrifices the
sampling quality. GS takes the geometry information
of the point cloud into account and uses the angle be-
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
1234
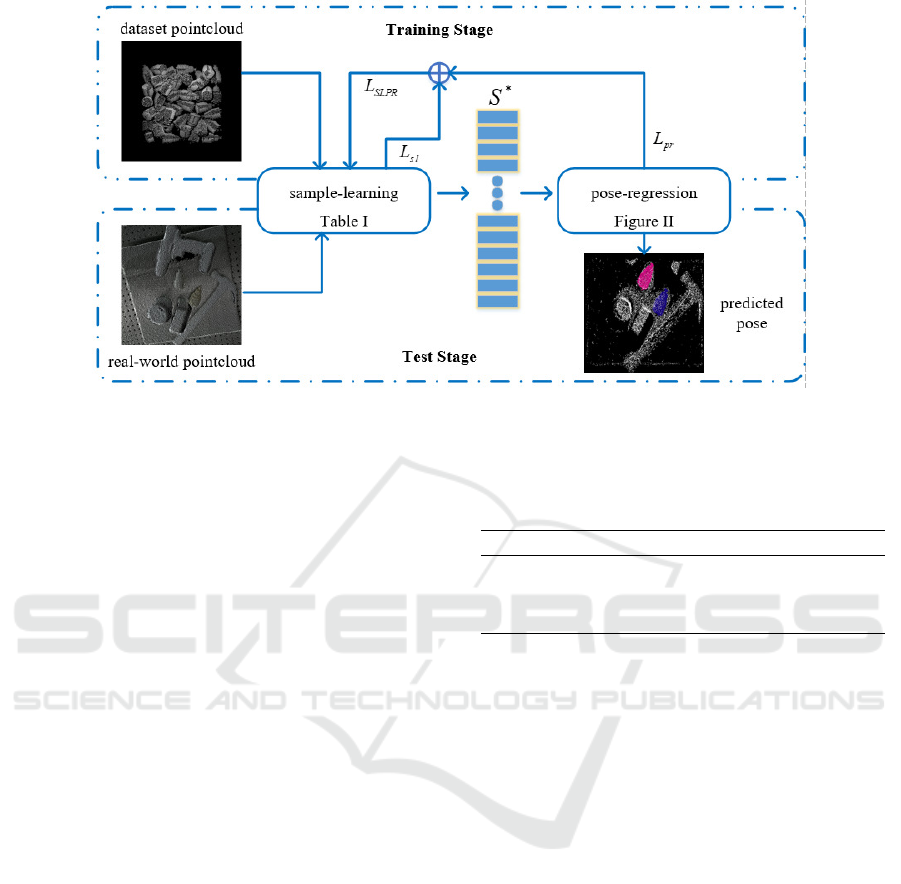
Figure 1: Architecture of SLPRNet. SLPRNet contains two parts: (a) sample-learning network which learns to sample a
suitable subset of input point cloud to a fixed size and (b) pose-regression network. which takes sampled point cloud as
input and regresses the pose of target instance. SLPRNet is trained on our proposed dataset and generats well in real-world
applacations in test stage.
+
represents a weighted sum as Eq. (11).
tween normals of neighber points as the approximate
curvature. By comparing these curvatures with a pre-
set threshhold, geometry regions and non-geometry
regions are seprated. In each region, a different sam-
ple ratio is employed. As a result, more points will be
sampled in regions with richer geometry information,
thus the sampled subset preserves higher quality than
uniform sampling methods (e.g. RS and FPS).
However, the above-mentioned sampling methods
do not consider the objective of the following task.
Dovrat first proposed the thought of learning-based
sampling method (Dovrat et al., 2019), which opti-
mizes the sampled subsets for a downstream task. In
this paper, we design a sampling network following
Dovrats idea.
3 APPROACH
In this section, we mainly discuss the mathematical
details and the concrete structure of our SLPRNet.
Specifically, SLPRNet is consisted by two parts:
sample-learning network and pose-regression net-
work. In this section, we describe our work in the
following manner: sub-section III-A describes the
sample-learning network; sub-section III-B describes
the pose-regression network; sub-section III-C intro-
duces how we generate the dataset used for our pose
regression task.
Table 1: Architecture of sample-learning network.
NO. of Layer Layer Description Output Size and Feature
1-4 1×1 convs(bn, relu) n×1024
5 max pooling 1×1024
6-9 deconvs(bn, relu) k×96
10-13 fully connected k×3
3.1 Sample-learning Network
To find a suitable subset in a given point cloud to per-
form a downstream task (here it means the pose re-
gression task), we can define the problem as follows:
Given a point cloud P ={p
i
∈ R
3
, i = 1, 2, · · · , n},a
sample size k ≤ n and a task network T, find a sub-
set S
∗
of k points that minimizes the task networks
objective function f :
S
∗
= argmin
S
f (T (S)), S ∈ P, |S| = k ≤ n (1)
The architecture of the proposed sample-learning net-
work is inpired by Pointnet (Qi et al., 2017a). The
input points undergo a set of 1×1 convolution layers,
resulting in a per point feature vector. Then, a sym-
metric feature-wise max pooling operation is used to
obtain a global feature vector. After this, deconvolu-
tional layers are used to decode the feature vector to a
suitable size. Finally, we use several fully connected
layers to get the output: a generated point set S. Table
1 shows the details of sample-learning network archi-
tecture.
During training, we define the loss function of
sample-learning network as Eq.(2). Here weights in
L
sl
will be given in experiment implementation detail
SLPRNet: A 6D Object Pose Regression Network by Sample Learning
1235

section. And items in L
sl
are illustrated in the next
3 equations. L
a
and L
w
keep the points in S close
to those in P in average and worst cases respectively,
while L
s
keeps the points in S well spread among P.
L
sl
= L
a
+ γL
w
+ (η + σ|S|)L
s
(2)
L
a
=
1
|S|
∑
s∈S
min
p∈P
k
s − p
k
2
2
(3)
L
w
= max
s∈S
min
p∈P
k
s − p
k
2
2
(4)
L
s
=
1
|P|
∑
p∈P
min
s∈S
k
s − p
k
2
2
(5)
Through this network, a point set S is obtained
from point set P in reference stage. But it is not
guaranteed that the point set S is strictly one of the
subsets of the original point set P, for including this
condition will change the loss function into a discrete
form which is difficult for the network to train. So
we perform a matching stage by Earth Mover’s Dis-
tance(EMD) between point set S and P so as to gen-
erate a real sub-set S
∗
of P which is further applied to
a downstream task.
3.2 Pose-regression Network
The proposed pose-regression network takes Point-
net++ (Qi et al., 2017b) as its backbone. It first feeds
a sampled point set S of N
s
points through a feed-
forward network for feature extraction. And then
Pointnet++ (Qi et al., 2017b) is capable for extract-
ing both global and local features from point set S.
The output feature F
e
is the size of N
s
× N
e
, in which
each row represents the high dimensional features of
each point. After acquiring the feature F
e
, we use
MLP to further obtain three different metrics: seman-
tic segmentation, transformation regression and visi-
bility prediction. Corresponding to each metric, we
design three kind of losses which are aggregated to-
gether as the final loss of the pose-regression network.
The over-all architecture of pose-regression network
is depicted in Fig.2.
Semantic Segmentation Loss. Semantic segmen-
tation is vital in cluttered scenes where multiple types
of objects exits. The purpose of semantic segmenta-
tion is to perform classification for each point. We
pass extracted features F
e
of size N
s
× N
e
through
an MLP and produce the semantic prediction of size
N
s
× N
c
, where N
c
is the number of different object
classes. This semantic prediction indicates the type
of object to which each point belongs, and we de-
note it as S
e
. Each element S
e
(i, j) represents the
probability that ith point belongs to object of class
j. The semantic segmentation loss L
se
is the sum of
the cross entropy soft-max loss between predicted S
e
and ground truth labels. After getting the semantic
segmentation result, we concatenate S
e
to F
e
to form
feature F
se
based on a simple idea that semantic la-
bel may be beneficial for other learning tasks such as
transformation regression.
Transformation Regression Loss. We use feature
F
se
as input, applying two separate MLPs to regress
center position and rotation separately. Here, to en-
sure a translation invariance, for each point p, we
regress the relative coordinate between p and the cen-
ter position of its corresponding object. And we use
Euler angle to represent rotation due to its conve-
nience. Thus, a transform τ can be formulated by
combining these two parts. For a rigid body, τ corre-
sponds to a unique pose P, and P can be represented
in Euclidean space as a finite set of points R
P
at most
12 dimensions as work (Bregier et al., 2018) illus-
trates. Also, to obtain a loss function with relavant to
the pose of rigid bodies, we should define the distance
between two poses in pose sapce. Thanks to the work
(Bregier et al., 2018) which proposed a method to
measure the distance between different poses in both
symmetry and non-symmetry situation, we can build
our tranformation regression loss L
tr
as Eq. (6) where
R(P
pred
) represents the prediction pose and R(P
gt
)
represents the ground truth pose. For readers who
are interested in the concrete mathematical expres-
sion that dist represents, please refer to (Bregier et al.,
2018) for we quote it without modificaion.
L
tr
=
∑
S
dist(R(P
pred
, R(P
gt
))) (6)
Visibility Loss. Visibility is a common problem in
grasping tasks. Always, low visible objects also suffer
a low possibility to be grasped, thus they are not the
focus targets when executing detection and grasping.
Let N
i
denotes the number of points of the instance
to which ith point belongs and N
max
denotes the num-
ber of point of instance with most points in the scene.
In this manner, the visibility of the ith point can be
defined simply as follows:
V
i
=
N
i
N
max
(7)
And the visibility loss L
v
could naturally be written
as:
L
v
=
∑
S
V
pred
i
−V
gt
i
2
2
(8)
Total Loss of Pose-regression Network. To in-
troduce visibility effect to tranformation regression
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
1236
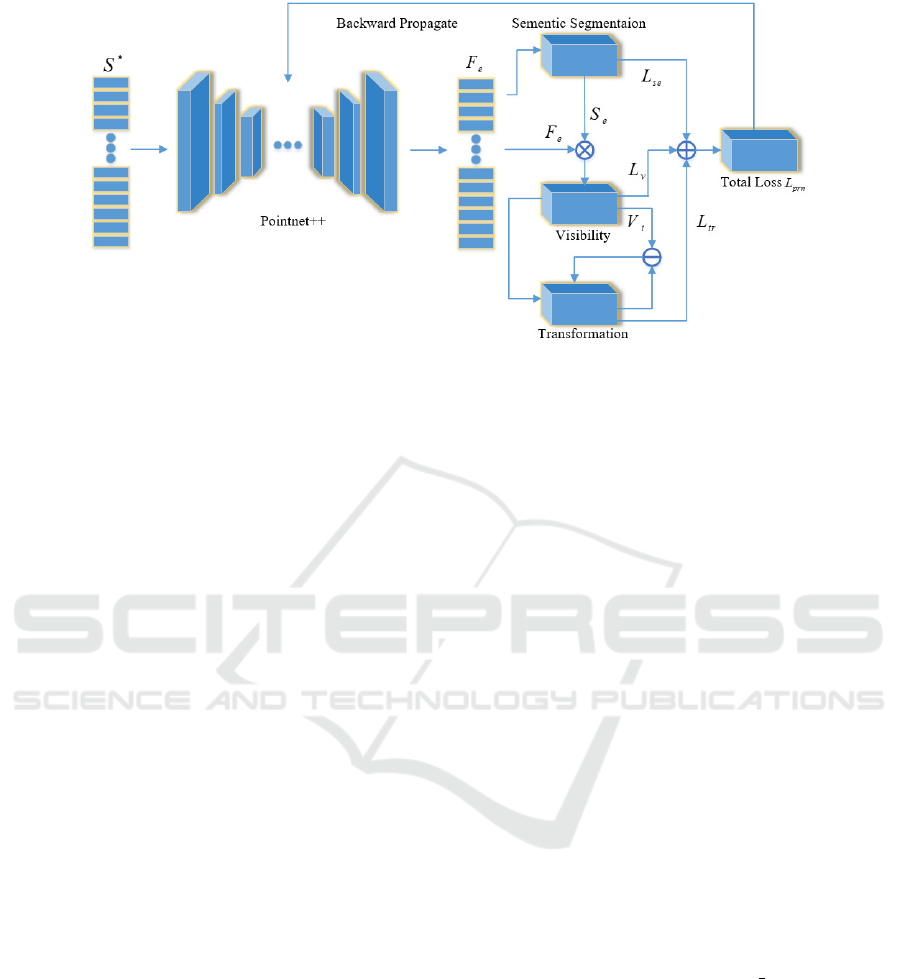
Figure 2: Architecture of Pose-regression Network.
—
represents the operation of Eq. (9).
+
represents a weighted sum as
Eq. (10).
×
represents concatenation.
branch, loss L
tr
can be modified with V
i
as Eq. (9).
L
tr
=
∑
S
V
gt
i
× dist(R(P
pred
, R(P
gt
))) (9)
In this way, we assign a higher transformation regres-
sion loss to those objects with higher visibility. In
this manner, our network can focus more on those in-
stances that are lying on the top of the box, and as
a result improve the average accuracy. To conclude,
after defining the three specific losses as above, we
can finally define the total loss of our pose-regression
network in a weighted summation manner as
L
pr
= L
se
+ αL
tr
+ βL
v
(10)
Now, we have introduced the two parts of our net-
work in details. But to make our whole network an
end-to-end solution, it is necessary to combine these
two parts together. Remember that the goal of our
sample-learning network is to optimize the point sam-
pling result corresponding to a specific downstream
task, which is the pose regression task here, we further
add a wighted L
pr
to L
sl
to form the loss of SLPRNet
as Eq.(11) shows.
L
SLPR
= L
sl
+ φL
pr
(11)
3.3 Generating Dataset
We mainly use the physics engine Bullet to simulate
different instances randomly dropping into a bin and
use Blender to perform scene rendering. Taking the
result poses of different instances generated by Bullet
as input, Blender can produce RGB-D images, which
are furthermore converted into point cloud. More de-
tails on how we generate the dataset can be found on
https://www.kaggle.com/shawnzhengzhang/slprnet-
dataset.
4 EVALUATION
In this section, we present some experiment results of
our proposed SLPRNet.
Section IV-A gives the implementation details in
our experiment and the metric we use to evaluate the
network. Section IV-B compares the average preci-
sion(AP) with other state-of-the-art methods. The re-
sult shows that SLPRNet outperforms previous meth-
ods to some extent. Section IV-C discusses the effect
of sample-learning network to emphasis the impor-
tance of suitable sampling derived by auto-learning
method. And in section IV-D we conduct a real-
world grasp task to demonstrate the effectiveness of
our work.
4.1 Implementation Details and Metric
Implementation Details. We evaluate our network
on two datasets: Silane dataset and YCB dataset.
Silane dataset does not provide training data for
deep learning based approaches, so we choose five
objects from Silane dataset(object 4e, bunny, pep-
per, tless-20 and candlestick) to generate synthetic
training data of our own as section III-C illustrates.
As for YCB dataset, we directly perform section
III-C (c) to the RGB-D images it provides. During
training reference, we set N
e
to 128 and use a
batch-size of 32. The network is prototyped with
Tensorflow 1.3 with Nvidia GTX 2080Ti GPU on a
Ubuntu 16.04 system. Training the whole network
on our synthetic dataset takes about 14 hours. The
hyper-parameters mentioned earlier in the article
are listed in Table 2 (including dataset generation
hyper-parameters which are described in detail on
SLPRNet: A 6D Object Pose Regression Network by Sample Learning
1237

Table 2: Hyper-parameters in network foundation and
dataset generation.
Parameter Value Meaning
box lenght 60cm length of containing box
box width 60cm width of containing box
box height 30cm height of containing box
min obj num 5 minimum object number dropped into box
max ojb num 45 maximum object number dropped into box
sim round 100 rounds when simulating per-object
num point 16384 number of points sampled from depth image to point cloud
α β 5 1 wights in pose-regression network loss
γ η σ 1 1 0.5 wights in sample-learning network loss
φ 0.3 wight when constructing whole network loss
https://www.kaggle.com/shawnzhengzhang/slprnet-
dataset).
Metric. Performance of pose regression is mea-
sured by average precision(AP) on Silane dataset,
which consists in area under the precision-recall
curve, given the goal of retrieving instances with rel-
ative complete appearance. Appearance complete-
ness is parameterized by occlusion rate, here we take
50% as threshold. A pose hypothesis is considered
as a true positive if its pose distance to ground-truth
is smaller than 0.1 times the diameter of the small-
est bounding sphere. On YCB dataset, we naturally
use ADD(for non-symmetric objects) and ADD-S(for
symmetric objects) metric as PoseCNN (Xiang et al.,
2018) proposed. To calculate the ADD or ADD-S
metric with respect to a specific object in YCB, we
simply calculate the mean value among the scores of
the same object in different scenes.
4.2 Pose Regression Result
Table 3 summarizes the AP scores of different meth-
ods applied to our synthetic dataset based on Silane.
And Table 4 summarizes the ADD or ADD-S scores
of SLPRNet, PoseCNN (Xiang et al., 2018) and some
3D coordinate based methods (Brachmann et al.,
2014; Brachmann et al., 2016; Michel et al., 2017)
on YCB dataset. It is obvious that our work outper-
forms the referred non-learning methods by a large
margin(Linemod and PPF). This is reasonable for
deep learning methods naturally hold superiority. It
is worth noting that our work also achieves bet-
ter AP scores than existing deep learning based ap-
proaches(Sock’s and PPRnet) which validates the ef-
fectiveness of SLPRNet. Our pose-regression net-
work applies similar processing pipline with PPRnet
but is more powerful according to the experiment.
We argue that this mainly results from the sample-
learning network which is capable to sample a more
suitable point set for pose regression task. This will
be discussed in another experiment shown in section
IV-C.
Table 3: AP scores of different methods on Silane dataset.
method
AP
object 4e bunny pepper tless-20 candlestick
Lienmod (et al., 2012) 0.23 0.39 0.04 0.25 0.38
Linemod+ (Aldoma et al., 2012) 0.26 0.45 0.03 0.31 0.49
PPF (Deng et al., 2010) 0.30 0.29 0.06 0.20 0.16
PPF+ (Aldoma et al., 2012) 0.35 0.37 0.12 0.23 0.22
Sock et al. (J. Sock and Kim, 2018) 0.62 0.74 0.43 - 0.64
PPRnet+ICP (Z et al., 2019) 0.85 0.89 0.84 0.85 0.95
Ours+ICP 0.90 0.90 0.89 0.88 0.90
Table 4: ADD(-S) scores of different methods on YCB
dataset.
method
ADD ADD-S
banana mug bowl large clamp
3D coordinate+ICP (Michel et al., 2017) 0.74 0.67 0.80 0.75
PoseCNN+ICP (Xiang et al., 2018) 0.92 0.81 0.78 0.75
Ours+ICP 0.90 0.92 0.92 0.90
Note that in experiments above, we all perform
iterative closest point(ICP) algorithm after the men-
tioned methods get the 6Dof pose.
4.3 Discussion on Sample Learning
PPRnet (Z et al., 2019) follows Pointnet++ (Qi et al.,
2017b) structure, which contains sampling, group-
ing and feature extracting layers. In sampling stage,
farthest point sampling(FPS) is adopted. In sec-
tion IV-B, we have shown that our work outperforms
PPRnet (Z et al., 2019). To demenstrate that this
mainly benefits from the proposed sample-learning
network, we conducted another experiment. First, we
trained our pose-regression network on an oject 4e
single-class-object dataset with different number of
points(by modifying parameter: num point) sampled
by FPS, RS, GS, and sample-learing network respec-
tively. And in test stage, we fed pose-regression net-
work with a point cloud sampled to the same size as
that during training to get the predicted 6Dof object
pose. AP scores are summarized in Table 5. And
Fig.4 is a more intutive presentation. As the sampled
point cloud gets sparser, our method not only holds
the best AP score, but also keeps it decrease in a rela-
tively gentler manner comparing to other methods.
RS can not guarantee the sampled points spread
well in the whole point cloud, thus underperforms
when the sampled point sets are sparse. GS holds
some superiority when adopted on detection or clas-
sication tasks where sampling is taken on the object,
because in such occastions geometry primitives on
object are very essantial. However, when we should
sample points from a whole scene, the motivation of
GS is hardly to come into effect. FPS is a widely
used technique in point cloud sampling, and many
works have verify the validity of the algorithm. How-
ever, we can also see a significant decline in pose re-
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
1238

Table 5: AP scores with different sampling methods and
scales on object 4e.
num point
AP
RS FPS GS sample-learning network
16384 0.84 0.85 0.83 0.90
8192 0.84 0.85 0.82 0.89
4096 0.82 0.80 0.79 0.86
2048 0.75 0.78 0.76 0.82
1024 0.67 0.72 0.70 0.79
512 0.42 0.56 0.50 0.65
Figure 3: Performance of Different Methods Applied on
Multi-scale Point Cloud.
gression precision when the sampled point sets turn
sparser. This is reasonable since FPS tends to sam-
ple points that are far away from each other without
considering some representative points whose rela-
tionship may help to regress the poses to a consider-
able degree. This is what the sample-learning network
solves. By automatically learning which points con-
tribute to the regression task most, sample-learning
network succeed to counteract the influence of infor-
mation loss caused by small scale sampling. As a re-
sult, we can search for a balance between regression
precision and sampling scale, which will significantly
influence training efficiency and calculating pressure.
4.4 Real-world Grasp Task
We conduct a grasp task in real world to show SL-
PRNet could correctly regress the 6Dof pose of target
objects in a scattered scene which is shown in Fig.5.
The grasp executer is a Robotiq 2-fingered manip-
ulator connected by a fixed joint to a 6Dof robotic
arm UR5. We capture the scenes using a Kinect V2
camera into RGB-D images which are transferred into
point cloud as input of SLPRNet. Output object poses
are then performed transformation from camera coor-
dinate to world coordinate and the ik f ast inverse ki-
netic algorithm is adopted to calculate the six joint
(a) (b)
(c) (d)
Figure 4: Real-word Grasping Experiment. (a) our experi-
ment platform. (b) point cloud captured by kinect V2. (c)
regressed pose of target objects(object 4e). (d) UR5 per-
froms grasping.
angles of UR5. Finally, we use RRT
∗
to plan an ex-
ecutable obstacal-free path for performing a grasp by
UR5. The above-mentioned procedures are first simu-
lated in ROS and then transferred into real movement
of UR5 through Moveit!. Experiment shows that our
pipeline is able to pick the target instances with a high
success rate.
5 CONCLUSIONS
In this work, we proposed a novel architecture, SL-
PRNet, to accomplish pose regression task with in-
put scene information in point cloud data format. The
sampling process in most other networks to achieve
this goal is replaced from FPS to an auto-learning
framework. In this way, we find the performance is
lifted in many aspects including precision, times cost
and resistance to sparse distribution of input point
cloud. At meantime, we generate a publicly avail-
able synthetic dataset in which each point is labled by
the 6Dof pose of the object it belongs to. Real-world
experiment is conducted to verify the effectiveness of
the proposed work. In the future, we will (a) keep to
update our dataset and (b) search for a probability to
simplify our network to a more lightweight manner.
ACKNOWLEDGEMENTS
This research was performed in Center for Arti-
ficial Intelligence and Robotics under Shenzhen
SLPRNet: A 6D Object Pose Regression Network by Sample Learning
1239

International Graduate School, Tsinghua Univer-
sity. And this work was supported by National
Natural Science Foundation of China (No.61803221
and No.U1813216) and the Basic Research Pro-
gram of Shenzhen (JCYJ20160301100921349,
JCYJ20170817152701660). We thank our partners
who provided helpful feedback and suggestions,
in particular Jian Ruan, Sicheng Liu, Anshun Xue,
Kangkang Dong, and Xiaojun Zhu.
REFERENCES
Aldoma, A., Tombari, F., Stefano, L. D., and Vincze, M.
(2012). A global hypotheses verification method for
3d object recognition. In Proceedings of the Euro-
pean Conference on Computer Vision (ECCV), vol-
ume 7574, page 511524.
Aoki, Y., Goforth, H., Srivatsan, R. A., and Lucey, S.
(2019). Pointnetlk: Robust efficient point cloud regis-
tration using pointnet. In IEEE Conference on Com-
puter Vision and Pattern Recognition (CVPR), page
71567165.
Besl, P. J. and McKay, N. D. (1992). A method for registra-
tion of 3-d shapes. IEEE Trans. Pattern Anal. Mach.
Intell., 14:239256.
Brachmann, E., Krull, A., Michel, F., Gumhold, S., Shotton,
J., and Rother, C. (2014). Learning 6d object pose
estimation using 3d object coordinates.
Brachmann, E., Michel, F., Krull, A., Yang, M. Y.,
Gumhold, S., and Rother, C. (2016). Uncertainty-
driven 6d pose estimation of ob- jects and scenes from
a single rgb image.
Bregier, R., Devernay, F., Leyrit, L., and Crowley, J. L.
(2018). Defining the pose of any 3d rigid object and
an associated distance. In Int. J. Comput. Vis., volume
126, page 571596.
Chen, S. H., Tian, D., Feng, C., Vetro, A., and Kovacevic,
J. (2018). Fast resampling of three-dimensional point
clouds via graphs. In Ieee Trans. Signal Process., vol-
ume 66, page 666681.
Deng, J., Dong, W., Socher, R., Li, L.-J., Li, K., and Fei-Fei,
L. (2010). Model globally, match locally: Efficient
and robust 3d object recognition. In 2010 IEEE Con-
ference on Computer Vision and Pattern Recognition,
pages 998–1005. IEEE.
Dovrat, O., Lang, I., and Avidan, S. (2019). Learning to
sample. Proceedings of the IEEE Conference on Com-
puter Vision and Pattern Recognition (CVPR), pages
2760–2769.
et al., S. H. (2012). Technical demonstration on model
based training, detection and pose estimation of
texture-less 3d objects in heavily cluttered scenes. In
Proceedings of the European Conference on Com-
puter Vision (ECCV), pages 593–596. IEEE.
Gall, J. and Lempitsky, V. (2009). Class-specific hough
forests for object detection. In IEEE Conference on
Computer Vision and Pattern Recognition (CVPR),
pages 1022–+.
Hinterstoisser, S., Lepetit, V., Rajkumar, N., and Konolige,
K. (2016). Going further with point pair features.
In Proceedings of the European Conference on Com-
puter Vision (ECCV), volume 9907, pages 834–848.
J. Sock, K. I. Kim, C. S. and Kim, T.-K. (2018). Multi-task
deepnetworks for depth-based 6d object pose and joint
registration in crowd scenarios. The British Machine
Vision Conference.
Michel, F., Kirillov, A., Brachmann, E., Krull, A.,
Gumhold, S., Savchynskyy, B., and Rother, C. (2017).
Global hypothesis generation for 6d object pose esti-
mation.
Moenning, C. and Dodgson, N. (2003). A new point cloud
simplification algorithm. In Proc. Int. Conf. Vis. Imag-
ing, page 810.
Qi, C. R., Litany, O., Kaiming, H., and Guibas, L. (2019).
Deep hough voting for 3d object detection in point
clouds. In IEEE International Conference on Com-
puter Vision (ICCV), page 92769285.
Qi, C. R., Su, H., Mo, K., and Guibas, L. J. (2017a). Point-
net: Deep learning on point sets for 3d classification
and segmentation. In Proceedings of the IEEE Con-
ference on Computer Vision and Pattern Recognition,
pages 652–660.
Qi, C. R., Yi, L., Su, H., and Guibas, L. J. (2017b). Point-
net++: Deep hierarchical feature learning on point sets
in a metric space. In Advances in neural information
processing systems, pages 5099–5108.
R. B. Rusu, N. B. and Beetz, M. (2009). Fast point feature
histograms (fpfh) for 3d registration. In Ieee Interna-
tional Conference on Robotics and Automation, page
18481853.
Xiang, Y., Schmidt, T., Narayanan, V., and Fox, D. (2018).
Posecnn: A convolutional neural network for 6d ob-
ject pose estimation in cluttered scenes.
Z, D., ann Zhou. T, L. S., H, C., L, Z., YuXing.Y, and
Liu.HD (2019). Ppr-net: Point-wise pose regression
network for instance segmentation and 6d pose es-
timation in bin-picking scenarios. In International
Conference on Intelligent Robots and Systems (IROS),
pages 1773–1780. IEEE.
Zhang, D. J., He, F. Z., Tu, Z. G., Zou, L., and Chen, Y. L.
(2020). Pointwise geometric and semantic learning
network on 3d point clouds. In Integr. Comput. Aided.
Eng., volume 27, page 5775.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
1240
