Measuring Centers of Special Targets in Digital Still Images and

Movie Frames: Approach and Evaluation

Shakhzod Takhirov

Department of Civil and Environmental Engineering, University of California, Berkeley, U.S.A.

Keywords: Image Correlation, Digital Still Images, Digital Movie Frames, Non-contact Displacement Measurements,

Best Fitting, Evaluation.

Abstract: Digital cameras are undergoing explosive developments. As a result, high-resolution digital cameras have

become very affordable, especially with the latest growth in smart phone technologies. Hence, the usage of

existing measuring technologies and the development of new measuring technologies utilizing digital cameras

is in high demand. This paper utilizes special black and white patterns, the so-called targets, to measure the

relative displacement between two points. The paper introduces a new approach in measuring the location of

their centers that is based on best fitting the transition zones to straight lines. The intersection of these lines

produces the location of the center with sub-pixel accuracy. A special experimental rig was designed and built

to evaluate the approach and compare the measurements to those obtained by a conventional position

transducer connected to a data acquisition system. In the first part of the paper, the accuracy of the position

transducer and the experimental setup is discussed. It is shown that the accuracy of the setup is much greater

than the measurement expected from the digital images. Based on this, it was used as a reference system to

evaluate the approach. In the second half of the paper, the approach is evaluated based on monitoring two

targets. One of them is fixed and serves as a reference point, whereas another one is floating. The latter can

move along the linear bearing system axis, which is orthogonal to the axis of the camera lens. The

displacements of the floating target in respect to the fixed target were measured by a position transducer

connected to a data acquisition system. The relative displacement of the floating target is captured by the

digital camera and is based on the current location of the floating and fixed targets. This paper shows adequate

accuracy of the approach and provides recommendations on the ways of keeping it at high accuracy for

practical applications in experimental earthquake engineering.

1 INTRODUCTION

Digital still imaging cameras are commonly used as

an affordable tool for measuring surface deformations

and displacements of test specimens in experimental

studies. Digital still images can also be extracted from

digital movies as individual frames. This provides an

opportunity to use digital cameras in quasi-static and

dynamic experiments as well. Certainly, in the latter

case the main limitation is going to be the number of

frames per second. With the current development in

digital cameras, access to high-resolution cameras

with rates greater than the normal 30 frames per

second is rapidly increasing. In addition, the cost of

cameras is dramatically decreasing because of high

demand by several industries: autonomous cars,

https://orcid.org/0000-0002-4396-7946

surveillance monitoring cameras, and smart phones,

to name a few. Therefore, the usage of digital still

images or movie frames is steadily increasing in

many fields, including experimental earthquake

engineering. A digital imaging camera has become an

affordable and easy to access tool for monitoring

surface deformations and relative displacements

(Ogorzalek et al 2017, as an example). In addition, it

represents one of the most cost-effective ways of

measuring the relative displacements of a complex

system with several moving parts. An example is

presented in Figure 1. This image shows a typical

suspended ceiling system consisting of a grid and lay-

in panels. Because of the gap between the grid and the

panels, the movements of the grid are different from

those of the panels. To monitor all these displacement

136

Takhirov, S.

Measuring Centers of Special Targets in Digital Still Images and Movie Frames: Approach and Evaluation.

DOI: 10.5220/0010392901360142

In Proceedings of the 9th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2021), pages 136-142

ISBN: 978-989-758-492-3

differences, an installation of many position

transducers is needed, which is not practical. In

addition, conventional instrumentation is not

preferred because it can alter the system performance

due to the added weight of instrumentation. This can

be addressed by utilizing measurement techniques

based on the digital images. In this case, the

movements of the panels and the grid can be

monitored by these non-contact measurements.

Figure 1: Monitoring grid and panel displacements in

testing of suspended ceiling system.

2 MOTIVATION

The main motivation was to develop a reliable

technique of non-contact displacement measurements

when installation of many position transducers is not

practical or too expensive. In addition, accuracy

estimation is crucial for achieving high quality of test

data and such, needs to be provided for the analysis

of the experimental data. Recommendations on the

position of the camera in respect to the experimental

setup required to achieve higher accuracy are very

valuable too. In addition, the proper selection of

settings in digital cameras is also very important to

achieve high-quality measurements.

3 EXPERIMENTAL SETUP AND

REFERENCE INSTRUMENT

A special experimental setup was developed and

assembled to evaluate the accuracy of the monitoring

conducted by the targets. As shown in Figure 2, the

targets were installed on two vertical boards located

in the same plane. Each target represents a special

black and white pattern printed on a sheet of paper

and attached to the surface to be monitored. Quite a

few patterns are used in practical applications with a

recent extensive review of their specifics summarized

in (Janßen et al 2019).

Figure 2: Front view of experimental setup.

Each board shown in Figure 2 was attached to a

different carriage of a linear bearing system as shown

in Figure 3. One of them was fixed and the other was

free to slide along the rail of the linear bearing system.

The latter was called a floating carriage. The axis of

the linear bearing system was orthogonal to the axis

of the camera’s lens. As a result, due to the presence

of the linear bearing system, both boards were

restrained to move in the same plane orthogonal to the

camera’s lens.

Figure 3: Top view of experimental setup: linear bearing

system with carriages.

The relative displacement between the fixed and

floating carriages was monitored by a position

transducer as shown in Figure 4. This position

transducer was used as a reference. The setup utilized

TR0050 (Novotechnik U.S., Inc., 2014), a position

transducer with a specified linearity of 0.15% of full

Measuring Centers of Special Targets in Digital Still Images and Movie Frames: Approach and Evaluation

137

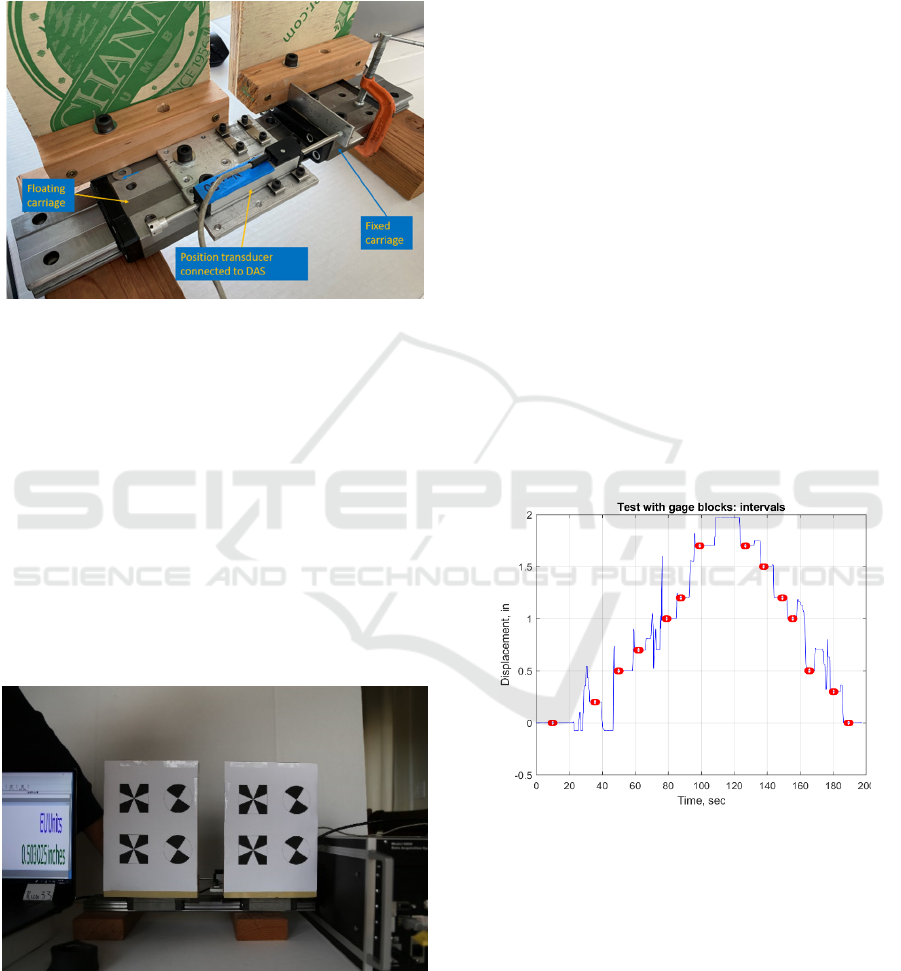
scale. The transducer had a full stroke of 50 mm or

about 2 inches. The readings of the position

transducer were acquired by PI-6008U, a data

acquisition system (DAS) from Pacific Instruments,

Inc. (Pacific Instruments, Inc, 2017).

Figure 4: Reference position transducer to monitor relative

displacement.

A few targets were installed on the boards as

presented in Figure 5. One of them is a black and

white target commonly used for laser scanning (see

Takhirov, 2010, as an example). The second one, is a

target similar to the so-called BOTA8 proposed by

(Janßen et al 2019). The target used in this study

utilized an opposite colouring pattern when compared

to BOTA8. For the purposes of this paper, the

discussion of the approach and its evaluation are

discussed only for the round target. A full-frame

digital camera, Canon EOS 6D DSLR in this

particular case, was installed on a tripod to capture the

movements of the floating targets.

Figure 5: Typical image frame.

A typical still image of the targets is presented in

Figure 5. It shows the floating and fixed boards on the

right and left sides, respectively. In addition, to

achieve real-time correlation to the reference

displacement, the latter was displayed on the left side

of the screen as shown in Figure 5. Presence of the

reference displacement in the same image with the

targets is especially important for movie frames

because then no time correlation is needed.

4 EVALUATION OF

REFERENCE ACCURACY

Prior to evaluating the target monitoring accuracy

approach, accuracy of the reference position

transducer was measured. It was performed in the

following way. High-precision steel calibration

blocks were used (Mitutoyo, 2016). The blocks were

Grade 0 which ensures that their tolerance is about a

few micro-inches (or about 0.0001 mm). The position

transducer was calibrated at two points and its

readings were checked with several gage blocks at

many other displacement points as presented in

Figure 6. This plot shows the readings collected by

DAS when the position transducer is displaced by

various gage blocks. The collected data was averaged

over 400 points to obtain a reading of the reference

position transducer with a certain gage block. Those

points are shown as red circles in Figure 6.

Figure 6: Displacement of position transducer with various

high-precision gage blocks.

Each averaged reading was compared to the

corresponding gage block and the error between the

two values was calculated. It is presented in Figure 7.

As it is shown in this plot, the error does not exceed

0.015 mm. Based on the specifications of the position

transducer, the expected linearity is 0.15% of full-

scale, which equals to 0.075 mm for the 50 mm

instrument used herein. Hence, based on this accuracy

measurement, it was concluded that the accuracy of

this particular transducer is much better than the

PHOTOPTICS 2021 - 9th International Conference on Photonics, Optics and Laser Technology

138

specifications established for their mass production.

It is worth noting that the accuracy measurement

included possible uncertainties associated with the

data acquisition system and DAS accessories (a cable,

for example).

These preparatory steps show that this

experimental setup has an adequate accuracy for the

evaluation of the accuracy of monitoring by targets

introduced in this paper.

Figure 7: Error of position transducer with respect to gage

blocks.

5 RESULTS OF IMAGE

REDUCTIONS: CLOSE

PROXIMITY

Figure 8: Step 1: find target’s pattern in image.

All image manipulations were conducted in the

Matlab environment (MathWorks, 2016). The image

reduction was based on utilization of the target’s

specific pattern. It was conducted in two steps. In the

first step, the location of the target’s pattern shown in

Figure 8 was identified based on Fast Normalized

Cross-Correlation, FNCC, (Lewis, 1995a and 1995b).

In this step, the location of the target’s center is

estimated with pixel accuracy.

In the second step, the transition points between

the black and white zones are determined. Based on

the target pattern, points for two subsets are separated

from each other. One subset corresponds to a slope of

less than 90 degrees whereas another one corresponds

to a slope greater than 90 degrees. These subsets are

best fit to straight lines as presented in Figure 9.

Figure 9: Step 2: Target’s center as intersection of two

straight lines best fit to the transition points.

As it was noted earlier, step 1 serves as an

intermediate step to identify an approximate location

of the target’s center. This step helps to speed up the

calculation of a more accurate estimation of the

target’s center. The difference between the results of

the two steps is presented in Figure 10.

Figure 10: Target’s center: step 1 (red cross) and step 2

(magenta circle).

As it can be seen from Figure 10, step 2 estimates

the target’s center with a subpixel accuracy. Now, if

the correlation between the pixels and the engineering

Measuring Centers of Special Targets in Digital Still Images and Movie Frames: Approach and Evaluation

139

units is defined, this approach estimates the location

of the center in mm with a much higher accuracy than

the one based on the FNCC procedure.

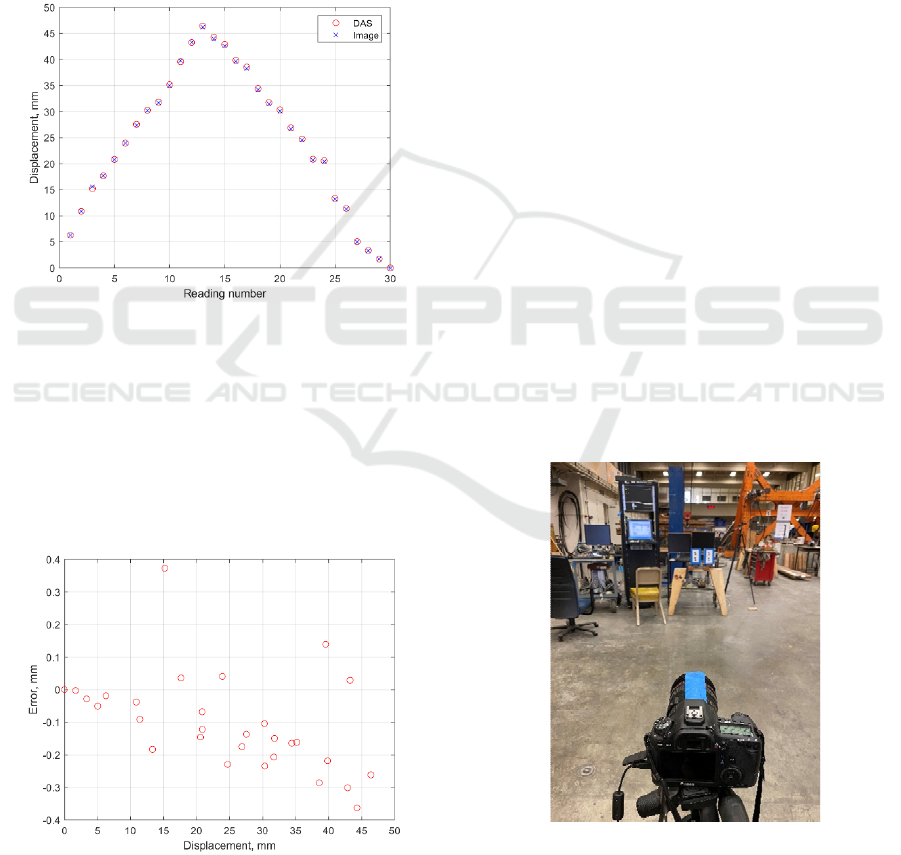
The correlation between the pixels and

engineering units, mm in this case, was based on

measurements of the target’s radius in both pixels and

mm. A comparison between the measurements of the

position transducer and the moving target monitored

by the still images, is presented in Figure 11. The plot

shows close correlation between the two

measurements. It is worth noting that this discussion

and this plot is based on the estimation of the relative

displacements between the fixed and floating targets.

Figure 11: Displacements of target compared to that of the

reference position transducer.

An error or the difference between the two

measurements does not exceed 0.4 mm as presented

in Figure 12. This error is shifted towards negative

values when the image measurement is less than the

displacement measured by the position transducer.

Hence, in this particular case, the displacement

measured from the image is underestimated.

Figure 12: Error of target’s center estimation with respect

to the reference position transducer.

It is worth noting that the size of each target was

about 0.7% of the 3648 pixels by 5472 pixels images

taken by this camera. A lens with variable focal

distance was used and for this test the focal distance

of the images was 32 mm.

The error of 0.4 mm is well below the accuracy of

the experimental setup discussed earlier. The

accuracy can be increased by correcting the images

for the lens distortion and other means. Some of the

possible ways of improving the accuracy are

discussed below.

6 RESULTS OF IMAGE

REDUCTIONS: CAMERA

PLACED FURTHER AWAY

To evaluate the approach, a number of tests were

conducted with the camera placed further away from

the targets. In the first case described above, the

camera was placed about 1 meter away from the

targets. As a result, the target occupies a relatively

large portion of the overall image. By placing the

camera further away, the targets occupy a much

smaller portion of the image. For the second case

considered here, the camera was placed about 5

meters away as presented in Figure 13.

A typical image taken by the camera at this

distance is presented in Figure 14. The focal distance

of the lens was set at 65 mm. As a result, each target

occupies about 0.06% of the 3648 pixels by 5472

pixels image’s area.

Figure 13: Camera placed at further way distance.

A smaller relative target size is very important in

experimental studies because then the larger surface

PHOTOPTICS 2021 - 9th International Conference on Photonics, Optics and Laser Technology

140

of a test specimen can be included in the same frame

for simultaneous visual monitoring.

Figure 14: Targets occupy very small portion of the image.

To avoid any possibility of relative movement of

the camera, the camera was placed on the strong floor

of the test laboratory and all triggering was done

remotely. The latter ensures that small but unexpected

movements of the camera resulting from pushing the

triggering button on top of the camera are completely

avoided.

The same experimental setup was utilized as the

in the previous case of the closely placed camera. The

direct correlation between the actual displacement of

the target and image was achieved by combining the

displacement output of the DAS into the same image

with targets as presented in Figure 15.

Figure 15: The reference displacement is combined into

each image.

A correlation between the pixels and engineering

units, mm in this case, were based on measurements

of the distance between the top and bottom targets in

both pixels and mm. A comparison between the

displacement measured by the reference position

transducer and the displacement measured from the

image is presented in Figure 16.

Figure 16: Comparison of the displacement measured from

images to that of the reference position transducer.

The error between the two measurements is

presented in Figure 17. As presented in the plot, the

error between the displacements measured from the

images and from the position transducer does not

exceed ±0.5 mm. It is worth reminding that this

accuracy was achieved from a distance of about 5m,

which is quite remarkable. The result is consistent

with the one obtained earlier when the camera was

placed much closer to the targets.

Figure 17: Error between the displacements measured from

images and that of the reference position transducer.

This accuracy was achieved based on the

following measures. First, the relative size of the

target was reduced to about 0.07% of the overall

image area. This reduces the effects of the lens

distortion. Second, the camera was triggered

remotely, so any contact with the camera was

excluded to avoid any undesired movements of the

camera by pushing on the triggering button. Third, the

focal distance of the lens was increased to reduce the

effect of the lens distortion. Fourth, a calibration

Measuring Centers of Special Targets in Digital Still Images and Movie Frames: Approach and Evaluation

141

factor converting pixels into engineering units was

based on a relatively larger distance, a distance

between the top and bottom targets. In this case, a

small error in the distance measurements will not

result in a large error in conversion of pixels into mm.

For future applications of the approach in

experimental studies, these measures are

recommended to be used so adequate accuracy of the

measurements can be achieved.

Some other variables affecting the measurements

will be studied in future investigations.

7 CONCLUSIONS

This paper utilizes special black and white patterns,

the so-called targets, to measure the relative

displacement between two points. The paper

introduces a new approach in measuring the location

of their centers that is based on best fitting the

transition zones to straight lines. An intersection of

these lines produces the location of the center with

sub-pixel accuracy. A special experimental rig was

designed and built to evaluate the approach and

compare the measurements to those obtained by a

conventional position transducer connected to a data

acquisition system. In the first part of the paper, the

accuracy of the position transducer and the

experimental setup is estimated. It is shown that the

accuracy of the setup is much greater than the

measurement expected from the digital images. Based

on this, it was used as a reference system to evaluate

the approach. In the second half of the paper, the

approach is evaluated based on monitoring two

targets. One of them is fixed and serves as a reference

point whereas another one is floating. The latter can

move along the linear bearing system axis which is

orthogonal to the axis of the camera lens. The

displacements of the floating target in respect to the

fixed target were measured by a position transducer

connected to a data acquisition system. The relative

displacement of the floating target is captured by the

digital camera and is based on the current location of

the floating and fixed targets. The paper shows

adequate accuracy of the approach and provides

recommendations on the ways of keeping it at a high

accuracy for practical applications in experimental

earthquake engineering.

ACKNOWLEDGEMENTS

Special thanks are due to Sensor Fusion and

Monitoring Technologies, LLC for providing access

to the PI-6008U data acquisition system which was

crucial for achieving the objectives of the paper.

Special thanks are due to Ms. Lola Takhirov of UC

Berkeley for editing the paper.

REFERENCES

Janßen, J., Medic, T., Kuhlmann H., and Holst, C. (2019).

Decreasing the Uncertainty of the Target Center

Estimation at Terrestrial Laser Scanning by Choosing

the Best Algorithm and by Improving the Target

Design. Remote Sensing. 11, 845;

doi:10.3390/rs11070845.

Lewis, J. P. (1995a). Fast Template Matching, Vision

Interface, p. 120-123,1995.

Lewis, J. P. (1995b). Fast Normalized Cross-Correlation,

Industrial Light & Magic.

http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.

1.1.21.6062&rep=rep1&type=pdf.

MathWorks (2016). Matlab Version R2016b.

Mitutoyo (2016). https://www.mitutoyo.com/wp-

content/uploads/2016/09/E-section-Gage-Blocks.pdf

last retrieved on 11/23/20.

Novotechnik U. ., Inc. (2014).

https://www.novotechnik.com/pdfs/TRTRS.pdf last

retrieved on 11/23/20.

Kenneth A. Ogorzalek, Blake W. Dilsworth and Shakhzod

M. Takhirov (2017). ‘Experimental Program for

Historic and Contemporary Strengthening of Wood

Connections and Advanced Measurements by Laser

Scanning and Image Tracking’. PROHITECH2017, 3rd

International Conference on Protection of Historical

Constructions, 12-15 July 2017, Lisbon, Portugal.

Pacific Instruments, Inc. (2017).

http://catalog.pacificinstruments.com/Asset/6008U_En

closure%204-slot%2012V%20DC%20USB%

20Control%20&%20Data%20Interface.pdf last

retrieved on 11/23/20.

Takhirov, S. M. (2010). Laser Scanners in Structural

Assessment and FE modeling, 2010 Structures

Congress, Orlando, Florida, May 12-15, 2010.

PHOTOPTICS 2021 - 9th International Conference on Photonics, Optics and Laser Technology

142