
Scalable Stochastic Path Planning under Congestion
Kamilia Ahmadi and Vicki H. Allan
Computer Science Department, Utah State University, Logan, Utah, U.S.A.
Keywords:
Stochastic Path Planning, Multi-Agent Systems, Congestion-aware Modeling, Community Detection
Methods, Distance Oracles, Approximation, Route Planning Under Uncertainty.
Abstract:
In this work, we propose a city scale path planning framework when edge weights are not fixed and are
stochastically defined based on the mean and variance of travel time on each edge. Agents are car drivers
who are moving from one point to another point in different time of the day/night. Agents can pursue two
types of goals: first, the ones who are not willing to take risk and look for the path with highest probability of
reaching destination before their desired arrival time, even if it may take them longer. The second group are
the agents who are open to take a riskier decision if it helps them in having the shortest en-route time. In order
to scale the path planning process and make it applicable to city scale, pre-computation and approximation
has been used. The city graph is partitioned to smaller groups of nodes and each group is represented by one
node which is called exemplar. For path planning queries, source and destination pair are connected to the
respective exemplars correspond to the direction of source to destination and path between those exemplars is
found. Paths are stored in distance oracles for different time slots of day/week in order to expedite the query
time. Distance oracles are updated weekly in order to capture the recent changes in traffic. The results show
that, this approach helps in having a scalable path finding framework which handles queries in real time while
the approximate paths are at least 90 percent as good as the exact paths.
1 INTRODUCTION
This paper focuses on a practical scalable algorithm
for stochastic path planning under congestion. The
approach uses stochastic path planning framework
and improves the query time utilizing pruning, graph
clustering, pre-processing and approximation tech-
niques.
In modeling a city scale graph, congestion
changes throughout the day which results in having
uncertain costs on the road segments (Nikolova, 2010;
Geisberger et al., 2012; Rus, 2020). In the stochas-
tic path planning framework, the city is modelled as
a graph and the graph’s edge weights are the mean
and variance of a travel time random variable on each
edge. Two types of agents have been modelled: a) the
ones that look for the path with highest probability
of reaching destination before a desired arrival time,
and b) the agents who look for the smallest en-route
time. A path planner satisfies the agents’ goals by
minimizing the path costs over the travel time ran-
dom variable. To make it clearer, one good example
of these kind of agents’ goals is in the context of a
package delivery system. For example, suppose that
we guarantee the delivery of a package by 4 PM, oth-
erwise the customer doesn’t accept the delivery and
we lose the shipping costs. In that case, we are in-
terested in picking a path that has the highest chance
of reaching destination before the deadline to avoid
losing the shipping cost. The other possible case is
delivering perishable products. For example, if we
promised the delivery of perishable products before 6
PM to the customers, we are interested to pick a path
that has the shortest en-route time due to the nature of
our package. In this case, we are flexible in leaving
anytime, but we do need to have the shortest en-route
path while still making the destination before 6 PM.
The main objective of this work is to minimize
the query time in order to handle the large scale of re-
quests in the real world domain. In the scalable path
finding, the whole idea is to find small (region based)
clusters in the city graph and get an exemplar of each
cluster that is used to represent the nodes of that clus-
ter. Then instead of planning a path from a source
node to the destination node, we connect each node
to the closest exemplar aligned with the direction to
the destination and find a path between exemplars. In
pre-processing phase, all of the paths from every pair
of exemplars for every time slot of each day of the
week is being stored in distance oracles. Therefore,
454
Ahmadi, K. and Allan, V.
Scalable Stochastic Path Planning under Congestion.
DOI: 10.5220/0010394104540463
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 2, pages 454-463
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

in the query time, a source and destination are con-
nected to their corresponding exemplar, and the path
from two exemplars is retrieved.
Our data is the historical traffic logged data of
one year and distance oracles are being updated ev-
ery week with respect to the preceding 12 months in
order to reflect the recent traffic pattern changes such
as seasonality, events, and weather condition on the
congestion of each edge. Changes on the city network
traffic is represented as mean and variances of travel
time on edges. While mean shows the average traffic
on the edge, variance reflects how far the values are
spread out from their average value with respect to all
of the changes and uncertainties in network conges-
tion.
2 LITERATURE REVIEW AND
CONTRIBUTION
There are few approaches on solving the stochastic
path planning problems in scale. One approach is
to calculate the optimal a-priori path in query time.
Nie and Wu (Nie and Wu, 2009) proposed a multi-
criteria label-correcting algorithm by generating all
non-dominated paths based on the first-order stochas-
tic dominance (FSD) condition. While the algo-
rithm provides an approximate solution in pseudo-
polynomial time in the best case, the solution is ex-
ponential in the worst-case run time since the num-
ber of FSD non-dominated paths grows exponentially
with network size. Nikolova et. al. (Nikolova, 2010)
showed how to solve the problem in n
log(n)
time when
the link travel time distributions are Gaussian.
The second approach selects the best next direc-
tion at each junction using local information such as
transit nodes (Bast et al., 2007) and SHARC (Bauer
et al., 2016). Fan et al. (Fan and Nie, 2006) used
stochastic dynamic programming problem and solved
it using a standard successive approximation algo-
rithm. On road networks with cycles, their algorithm
has no finite bound on the maximum number of it-
erations to converge. Samaranayake et al. (Sama-
ranayake et al., 2012) presented a label-setting ap-
proach to speed up the computation based on zero-
delay convolution, and localization techniques for de-
termining an optimal order of policy computation.
While this approach enhances the run time, it is still
too slow to be implemented in scalable navigation
systems. In a real world path planning, it is not prac-
tical to use an adaptive algorithm which selects the
best next direction at each junction due to urgency in
having a quick and fixed response to the queries.
The other speed up technique in scalabale path
planning utilizes bi-directional search. Algorithms
such as contraction hierarchies (Geisberger et al.,
2012) and arc-flags (Bauer et al., 2016) use bidirec-
tional search in pre-processing. However, speedup
techniques that rely on bidirectional search are not ap-
plicable to the stochastic path planning problem, be-
cause the final and intermediate solutions are a func-
tion of the remaining time budget and remaining time
budget is not deterministic. When performing a bidi-
rectional search, the reverse search needs to stochasti-
cally estimate the time budget at each step, hence bi-
directional search might never converge (Sabran et al.,
2014).
Another technique for speeding up the stochastic
planning process is pruning the search region which
are used in ’reach’ and ’arc-flags’. In reach (Gut-
man, 2004), a node is expanded if its reach value is
larger than some amount. To have a high value of
reach, a vertex must lie on a shortest path that ex-
tends a long distance in both directions from the ver-
tex. Arc-flag acceleration method (Bauer et al., 2016)
uses a partition of the graph to pre-compute informa-
tion on whether an arc is useful for a shortest path
search by dividing the graph into a set of regions and
a Boolean vector representing each region which the
value is true if the edge is used by at least one path
ending in the corresponding region. During the pre-
processing phase, any edge without the Boolean cor-
responding to the region that the destination belongs
to is pruned from the graph. One of the major limi-
tations of both mentioned methods is it takes a long
time to reflect any possible change of the network
due to the vast amount of computation, even in pre-
processing phase.
Lim et. al. (Rus, 2020) showed how to solve
the scalable stochastic path finding in Θ(nlog
n
) time
where n is number of nodes in the network and when
travel time distributions are Gaussian. They provide a
method that answers stochastic shortest-path queries
using a data structure that occupies space roughly
proportional to the size of the network utilizing pre-
computation and distance oracles. Their approach is
quasi-polynomial with a rate of growth between poly-
nomial and exponential.
In this work, we propose a framework that can
answer large scale stochastic path planning queries
in real time using graph clustering, pruning, pre-
computation, and approximation. The framework first
finds the suitable way of clustering the city among
community-based methods, clustering and grid-based
methods. It also handles two types of agents’ goals:
a) agents with the goal of getting the paths with max-
imum probability of reaching destination before their
deadline, and 2) agents that look for the path with
Scalable Stochastic Path Planning under Congestion
455

shortest en-route time. The framework reflects the
changes of traffic in different time slots of a day
in each days of the week and pre-computed paths
are updated every week in order to reflect the recent
changes. It is computationally efficient as it leverages
the pre-computation step and hence provides accept-
able accuracy in comparison to exact paths.
3 FRAMEWORK
The whole idea of scaling the path planning process
is to cluster the city to smaller parts and get an ex-
emplar of each cluster that can represent the nodes
of the cluster. Then instead of planning a path from
each source node to a destination node, we connect
each node to one of the neighboring exemplars and
find path between the exemplars.
3.1 Open Street Map
For building the city graph, we used Open Street Map
data (Frederik Lardinois, 2011). Open Street Map
is a free editable map with data structure including
nodes (a single point defined by latitude and longi-
tude), ways (list of nodes), and relations (which re-
lates two or more data elements like a route, turn re-
striction, traffic signal or an area). Open Street Map
represents physical entities on the ground like build-
ings, roads, intersections, bridges and so on. It uses
the basic data structure of entities and tags for describ-
ing the characteristics of that entity.
3.2 Modeling City and Edge Weights
We model the city as a weighted directed graph in-
cluding a set of vertices (V ) representing road inter-
sections and edges (E) representing road segments
connecting vertices. Edge weights are represented as
a tuple of mean and variance of the expected travel
time on each edge which follows an independent
Gaussian random variable (Ahmadi and Allan, 2017;
Rus, 2020).
For finding the mean and variance of the expected
travel time on edges, we summarize yearlong traffic
data in 10 minutes time segments for each day of a
week on Salt Lake City, Utah. The monitored traf-
fic data is from Utah Department of Transportation
(UDOT) (Utah Traffic, 2020) which is logged in 10
minute basis.
We assume edge weights are independent. If we
want to consider stochastic dependency between ad-
jacent edges, one way is to transform the graph and
add extra edges between dependent edges. Here, we
don’t transform the graph and the assumption is, the
dependence between edges affects the variance of the
consecutive edges. For example, if edge A, has strong
dependency with edge B and congestion on edge A
causes congestion on edge B, then the variance on
edge B is high enough to represent this dependence
(Rus, 2020; Nikolova, 2010; Niknami and Sama-
ranayake, 2016; Ahmadi and Allan, 2017).
The mean of a path is the sum of the means of
all edges included in the path (Equation 1) which t is
query time and δ is the time takes to reach to any edge
from query time.
m
path
(t) =
∑
e∈path
m
e
(t + δ) (1)
(Equation 2) shows how to calculate the variance of
the path. Since we assume edge weights are indepen-
dent from each other, then cov(X
i
, X
j
)=0 for i 6= j and
Equation 3 is the result. Based on Equation 3, the
variance of a path is the sum of variance of all edges
included in the path shown in Equation 4 (Rus, 2020;
Nikolova, 2010).
var(
n
∑
i=1
X
i
) = E([
n
∑
i=1
X
i
]
2
) −[E(
n
∑
i=1
X
i
)]
2
(2)
var(
n
∑
i=1
X
i
) =
n
∑
i=1
n
∑
j=1
cov(X
i
, X
j
) =
n
∑
i=1
cov(X
i
, X
j
) =
n
∑
i=1
var(X
i
) (3)
v
path
(t) =
∑
e∈path
v
e
(t + δ) (4)
For finding the mean and variance of a path, sliding
time window has been considered to imply the cost of
each edge in the path depends on the amount of time
that took to reach it, not just the initial departure time.
For example, if we look at the path at time a and take
δ to reach the forth edges, the cost of the forth edge is
considered at the time of a + δ.
3.3 Agents
Agents are car drivers which can pursue different
goals: First, the ones who are not willing to take
risk and look for the path with highest probability
of reaching destination before a desired arrival time,
even if it may take them longer. Secondly, the agents
who are open to take a riskier decision if it helps them
in having the shortest en-route time. These agents
are flexible in leaving anytime while they still need
to make the trip. We can technically model any type
of agents’ goals, hence, we picked these two goals as
they have interesting characteristics in path planning
domain and some other goals can be incorporated in
their formulations.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
456

3.4 Base Path Planning Framework
For path planning, the goal is to find the path between
two nodes of the city graph that satisfies the agent’s
goal with the minimum cost associated with it. The
first step is to find the set of candidate paths that can
possibly satisfy the agents’ goals as considering all of
the paths between two nodes is computationally in-
tractable (3.4.1). Then, from those paths, we select
(path selection) the one with the least cost aligned
with the goal of the agents (3.4.2).
3.4.1 Pruning
In a city scale graphs, there are many paths between
two nodes and considering all of them is not computa-
tionally tractable. Therefore, a pruning step is needed
in order to consider the paths with the closest charac-
teristics to the agents goals and query’s deadline. For
finding the candidate paths between source and des-
tination, we start from the source node and expand
until we reach the destination. In expansion phase,
we utilize a heuristic based on the approximate path
from that node to destination which tells us whether
the mean of the approximate path is greater than the
provided deadline in query time or not. And if it is
greater, then the node is not expanded.
The approximate path from a node N to destina-
tion D uses the exemplars of the graphs. We partition
the graph and each partition includes a set of nodes
and it is represented by its exemplar which is the node
with highest traffic in the partition. Partitioning the
city graph and getting the exemplars are discussed in
details in 3.5. After finding the partitions and getting
the exemplars, we run A* (Hart et al., 1968) algorithm
on exemplars instead of all the nodes from source to
destination. In each step of A*, the next exemplar is
picked based on the smallest g(n)+h(n) value, where
g(n) is the shortest-length path from current exemplar
to the neighboring exemplar. For estimating h(n), we
use the direct distance heuristic from the neighboring
exemplar to the destination. Shortest-length paths be-
tween adjacent exemplars are pre-computed and they
are retrieved to build the approximate shortest-length
path. Figure 1 shows the approach.
3.4.2 Paths Cost Definition and Selecting Best
Path
The basis of path cost definition and path selection ap-
proach is extended from (Ahmadi and Allan, 2017).
In modelling city graph, edge weights are represented
based on mean and variance of the traffic flow on
those edges. Hence, paths are represented as nodes
(m
p
,v
p
) in the mean-variance plane. When we have
Figure 1: Finding an approximate shortest-length path from
N (a middle node in expansion) to destination D using A∗
algorithm through exemplars. Red circles are exemplars.
g(n) is the shortest-length path from current exemplar to
the neighboring exemplar. h(n) is the heuristic of direct
distance from neighboring exemplar to destination.
the candidate paths between two nodes, a cost func-
tion is used to model the cost of each path in expected
cost formula shown in Equation 5. The goal is to pick
the path with minimum cost. Path cost minimization
is a reward function here in order to make the plan-
ner take informed decisions in picking the best path
which is aligned with agents’ goals.
For modelling paths’ costs, we used step cost
function, but generally any type of cost function can
be used in 5 to estimate the expected cost of a path.
Step cost function considers the cost in the interval of
[−∞, d] as zero and wants to penalize the agent if it
reaches the destination after deadline. In 5, t
path
is the
expected arrival time of the path and d is the deadline
the agent has to make.
expected cost =Cost(t
path
, d)∗ f
path
(t
path
|m, δ
2
path
)
=
Z
+∞
−∞
u(t −d) f
path
(t
path
)dt
path
=
Z
+∞
d
f
path
(t
path
)dt
path
(5)
Based on 5, the whole cost is equal to the Cumulative
Density Function (CDF) of Standard Normal Distri-
bution. CDF generates a probability of the random
variable (travel time in this case) when distribution
is normal to be less than a specific value which is d
(deadline) here. Then, maximizing the Θ value, ul-
timately results in having a path that maximizes the
probability of reaching the destination before dead-
line (shown in equation 6) which is aligned with the
first type of agents goal mentioned above.
Θ(path) =
deadline −m
path
√
v
path
(6)
The second type of agents’ goal is to look for the
shortest en-route time while still the agent reaches
destination before deadline. Therefore, we need to
select a path that provides shortest en-route time. In
equation 6, we can re-write the deadline as the differ-
ence of desired arrival time and departure time. De-
sired arrival time is fixed, but departure time is flex-
ible. Therefore, we can transform the equation 6 to
Scalable Stochastic Path Planning under Congestion
457

equation 7 and all we need to do is to minimize the
left-hand side of 7. In 7, φ is the argument of Gaus-
sian CDF that makes the CDF equal to the probability
of making the trip before deadline which in our case
is 90 percent.
desired arrival time −departure time =
m
path
+ Φ(path)∗
√
v
path
i f departure time ⊂ [τ1, τ2] (7)
For finding the best departure time, first step is to find
what is the latest possible departure time (τ
2
) that if
the agent departs by that time, it still can make the
trip before deadline. Then, considering the query time
as the earliest possible departure time as τ
1
, the inter-
val of [τ
1
, τ
2
] is the time frame that includes the best
departure time. Then, we divide the interval to 10-
minute segments and for each segment, the path that
minimizes the equation 7 is selected. Afterward, we
pick the ”time segment” which has the minimum cost
path (based on 7) in comparison to other time seg-
ments. The found minimum cost path with this ap-
proach, is the path that has the least en-route time.
3.5 City Graph Clustering
For partitioning the city graph, we investigate three
possible approaches: 1) using community detection
methods, 2) unsupervised learning (clustering), and
3) manually dividing city graphs (grid-based). After
partitioning the city graph, the exemplar of each par-
tition is the node with highest traffic for that region.
3.5.1 Community Detection Methods
Community structure refers to the group of nodes in
a network that are more densely connected internally
than with the rest of the network. The goal is to put
each node into one and only one community. Depend-
ing on the type of the community detection methods,
the city graph can be partitioned differently. For our
use case, the goal is to see almost evenly distributed
partitions. Details on how many partitions are needed
are explained here 4.1. We tried many community de-
tection methods on the graph of Salt Lake City and
among them all, Infomap (Edler et al., 2017), Lead-
ing Eigenvector (Ruaridh Clark, 2018), Label prop-
agation (Garza and Schaeffer, 2019), and Multilevel
(Yang et al., 2016) methods are the ones with better
results for our case.
Infomap. In Infomap (Edler et al., 2017), commu-
nity is defined as a group of nodes among which in-
formation flows quickly. Using the Infomap algo-
rithm, the network is decomposed into modules by
their probability flow of random walks in a way that
a random walker spends a long period of time in one
module before departing for another module. To find
the best such partition, the traffic flow over the all
possible partitions is minimized to find the best set of
partitions. As Figure 2 shows, Infomap found 22929
communities on total of 56753 nodes of main nodes
of Salt Lake City, Utah. Community sizes are in the
range of 2 to 5 with majority of them with size 2.
Figure 2: Infomap community detection approach on the
main nodes of OSM data from Salt Lake City.
In Infomap, basically a random walker exploring the
network with the probability that the walker transi-
tions between two nodes given by its Markov transi-
tion matrix. Since our graph is a city graph which
is planar and all nodes are connected to each other,
the random walker easily walk from one region to an-
other. That’s why, the formed communities are com-
posed of few nodes.
Leading Eigenvector. A good community is when
the edges inside the group are dense while the num-
ber of edges outside the group is significantly smaller.
This notion is called modularity. Leading Eigenvector
approach (Ruaridh Clark, 2018) is based on maximiz-
ing the ’modularity’ over possible divisions of a net-
work in terms of the eigen-spectrum of the modularity
matrix in order to detect communities. Spectrum of a
matrix is the set of its eigenvalues.
As it can be seen from Figure3, using the Leading
Eigenvector approach, we got the total of 21 commu-
nities with 48398 of nodes in one community which is
the main area of the Salt Lake City. Based on the dis-
tribution of result, this method is not an appropriate
method in our case due to uneven city partitioning.
Label Propagation. In Label propagation (Garza
and Schaeffer, 2019) every node is initialized with a
unique label, and at every step each node adopts the
label of most of its neighbors. In this iterative process,
densely connected groups of nodes form a consensus
on a unique label to form communities. Label propa-
gation gives us 2007 communities on the 56753 main
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
458

Figure 3: Distribution of communities in Leading Eigen-
vector approach.
nodes of Salt Lake City graph with the distribution as
shown in figure 4. The distribution looks like a trun-
cated normal distribution, having most of the commu-
nity sizes of the range of 10 to 40 which makes this
approach a good candidate for our case.
Figure 4: Left: Distribution of communities in Label Prop-
agation approach. The dots represent communities.
Multilevel. Multilevel (Yang et al., 2016) approach
proposes a heuristic-based method that is based on
modularity optimization. Based on modularity opti-
mization, a good division of a network into commu-
nities is when the edges inside the group are dense
while the number of edges between groups is signifi-
cantly lower.
The algorithm is divided in two phases that are re-
peated, iteratively. It first starts with assigning a dif-
ferent community to each node of the network. Then,
for each node i and its neighbors, the gain of modu-
larity is calculated by removing i from its own com-
munity and by placing it in the community of j. The
node i is then placed in the community for which this
gain is maximum but only if this gain is positive. If
no positive gain is possible, i stays in its original com-
munity. This process is applied repeatedly and se-
quentially for all nodes until no further improvement
can be achieved and the first phase is then complete.
It gave us 157 communities on 56753 main nodes of
Salt Lake City (Figure 5).
Figure 5: Left: Distribution of communities in Multilevel
approach. The dots represent communities.
3.5.2 K-means Clustering
Graph clustering is the task of grouping the vertices of
the graph into clusters. Generally, a cluster refers to
a collection of data points aggregated together due to
the certain similarities using unsupervised methods.
There are various clustering methods to be used on
graphs and in this work, we used k-means.
The K-means clustering (Macqueen, 1967) aims
to partition n observations into k clusters in which
each observation belongs to the cluster with the near-
est mean of distance, serving as the centroid of the
cluster. The K-means algorithm starts with a first
group of randomly selected centroids, which are used
as the beginning points for every cluster, and then per-
forms iterative calculations to optimize the positions
of the centroids. It ends when there is no change in the
value of centroids or the defined number of iterations
has been achieved.
In K-means, for determining the optimal K (the
number of clusters), we used ’elbow’ method (Mac-
queen, 1967) which fits the model with a range of
values for K and looks at the percentage of variance
inside clusters versus the number of clusters. If the
point of inflection on the curve is seen, then it is a
good indication that the underlying model fits best at
that point. After clustering the city graph using k-
means method, the node with highest traffic in that
region is used as exemplar of the nodes in that cluster.
As Figure 6 shows, K-means gives us the total of 151
clusters.
Figure 6: Left: Distribution of main nodes in each cluster of
K-means clustering approach. Right: Visualization of clus-
ters on Salt Lake City. Each color represents one cluster.
Red points represent main ways of the city.
Scalable Stochastic Path Planning under Congestion
459

Figure 7: Left: Distribution of main nodes in each partition.
Right: Visualization of partitions on Salt Lake City. Each
color represents one partition.
3.5.3 Grid based City Partitioning
In this approach, we partition the city based on a sim-
ple gird of 10 * 15 to have 150 partitions. Figure 7
shows the distribution of partitions. Grid based parti-
tioning is used as a baseline in our experiments as it
provides almost an even distribution of nodes in par-
titions.
3.6 Pre-processing: Building Distance
Oracles
Pre-processing helps in quickly finding paths between
each two nodes and minimizes the time for querying
in a motion planning graph. At each time step of up-
date (which is every week), distance oracles are ex-
ecuted, and the values are used for all types of path
finding solutions. Given an n-vertex weighted planar
graph G, a distance oracle for G is a data structure that
efficiently answers distance queries between pairs of
vertices (u, v) in G. One way is to simply store an
n ×× n-distance matrix for a n-vertex graph. In that
case, each query can be answered in constant time,
but the space requirement is large. Therefore, we are
looking for a solution which answers queries in real
time and efficient in terms of space.
Approximation is a way of making distance or-
acles more compact. Approximate solutions aim to
find the solutions which are not exact but clearly
close. Besides, the solution is space and time effi-
cient. Approximation in our model utilizes the exem-
plars and instead of finding an exact path from source
to destination, it plans a approximate oath through ex-
emplars (details of approach is explained in 3.7).
Distance oracles store the best path for each type
of agent goals between every pair of exemplars for
different time slots of each day of week. In our case,
the whole graph is reduced to exemplars that repre-
sent regions of the graph and we use the path finding
approach explained in 3.4 to find paths between ex-
emplars for each time slot of day/week.
Distance Oracles are updated every week, in or-
der to reflect recent traffic patterns on the edges of
Figure 8: Blue circles are exemplars of regions. Green cir-
cles are the typical source and destination.
the city. In every update, data is considered based on
the preceding year data from the date of updating dis-
tance oracle. We store distance oracles for all days of
the week, every 10 minutes time slots and have them
updated weekly. The process of updating distance or-
acles are offline.
3.7 Scalable Algorithm
When a path finding request comes, based on the time
of the day, agent’s goal and deadline, source and des-
tination nodes are connected to the respective exem-
plars. Each node has up to nine exemplars around
it, one candidate is the exemplar of the region it is
located and the others are the exemplars of neighbor-
ing regions. Based on the hypothetical direct path be-
tween source and destination, the nodes get connected
to the exemplars with closest similarity to the direc-
tion of that hypothetical path.
For finding a path that connects source, destina-
tion nodes to their own exemplar, we consider short-
est length path. Then, the best path between the two
exemplars are fetched from the distance oracles and
final paths is sent as the result of the query. The path
between exemplars may have other exemplars in the
way, but it does not necessarily need to go through
other exemplars. Figure 8 illustrates the typical path
between source and destination.
4 EXPERIMENTS AND RESULTS
Our experiments are designed to answer the following
questions: 1) how accurate are the approximate paths
in comparison with the exact paths and 2) how much
time we save when we use approximate paths instead
of exact paths.
For the purpose of experiments, we choose 1000
source, destination pairs randomly among all of the
possible source, destination pairs to represent the path
planning universe at different time slots of weekdays
including peak hours and non-peak hours. For each
path planning query, we have the following inputs:
a) source, b) destination, c) time of query, d) dead-
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
460

line and, e) agent’s goal. Then, first we find the best
path using ’exact’ path planning approach explained
in 3.4 and then using the ’approximate’ path planning
approach explained in 3.7 which works on the set of
exemplars found by a) community detection, b) clus-
tering and c) grid approaches.
4.1 How Many Partitions is Needed?
In picking the right community detection method, the
main consideration is the number of partitions it gen-
erates and the number of nodes the method put in each
partition. Partitioning is mainly used to reduce the
number of nodes in the large scale graph in order to
improve the query time. Obviously, the more the par-
titions the more accurate the results. Hence, we don’t
want to deviate too much from the goal which is sum-
marizing the large scale graph while keeping the ac-
curacy in the acceptable range.
For checking the effect of number of partitions
on accuracy of approximate path planning method,
we use grid-based partitioning as baseline and played
with the number of partitions for one of the agents’
goals. Accuracy of approximate path planning is mea-
sured by its deviation from exact path for each source
and destination for the 1000 samples.
Figure 9 shows the mean difference of travel time
of exact and approximate paths for the agents goal of
highest probability path for the variation of partitions
of the city using grid-based method. As it shows, the
more the partitions the more accurate the paths are.
However, having more partitions increases the node
size which leads in larger distance oracles. Based on
figure 9, having 150 to 200 partitions looks reason-
able number of partitions with the mean difference of
travel time of exact and approximate paths around 6
percent for peak and non-peak hours.
Figure 9: Number of partitions vs the mean difference of
travel time of exact and approximate path.
Figure 10: Relative difference of mean and variance of
travel time of paths for exact and approximate approach
for peak and non-peak hours for the agent’s goal of high-
est probability path.
4.2 Which Community Detection
Method is Used?
Among the four community detection methods that
we used,’Label propagation’ 3.5.1 and ’Multilevel’
3.5.1 were the two good candidates for our case.
Label propagation partitions Salt Lake City to 2007
communities which most of the communities have
roughly 20 to 40 nodes in them. Multilevel divides
the city to 157 communities and in average each com-
munity includes 200 to 400 nodes in it. For a city
like Salt Lake City, Multi-level provides a good dis-
tribution of clusters, hence we select this approach for
community-based graph partitioning.
4.3 How Accurate Are the Approximate
Paths?
Highest Probability Path. Figure 10 shows the rel-
ative difference of mean and variance of travel time
of paths between exact and approximate path plan-
ning approaches for peak and non-peak hours. As it is
shown, Multi-level community approach is the closest
to exact paths in comparison to clustering (k-means)
and grid-based partitioning. The relative difference
of travel time of all of the approximate approaches is
more significant in peak hour in comparison to non-
peak hour. As in non-peak time, the traffic is not high,
both approximate and exact approach are almost the
same. These graphs show that in peak hour, the mean
of travel time of the approximate path using commu-
nity approach is just 8 percent longer than the exact
path and the variance is just 7 percent away.
Figure 11 shows among all of the 1000 source-
destination samples of the experiment, how many
Scalable Stochastic Path Planning under Congestion
461
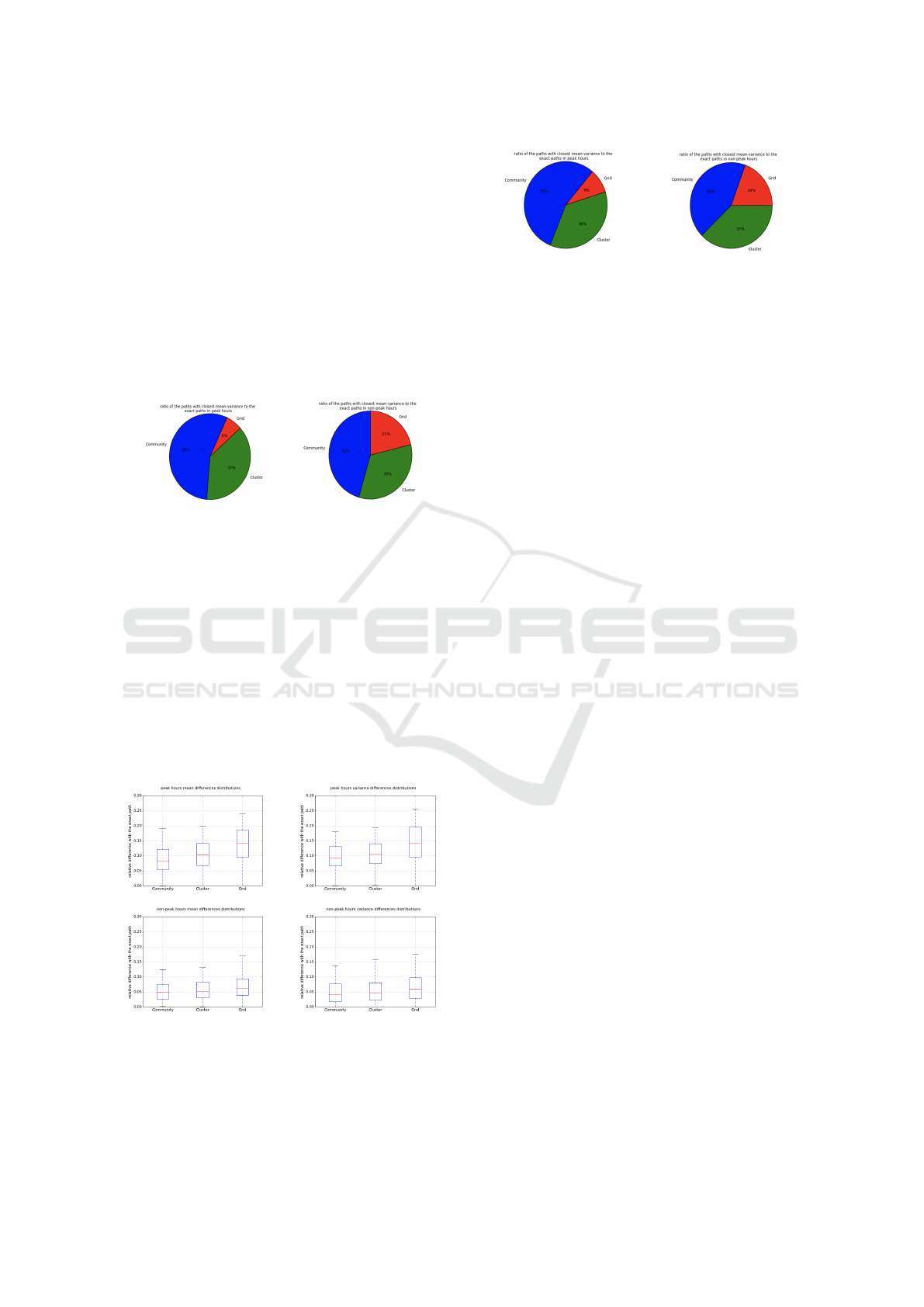
times each of the approximate path planning ap-
proaches (community, cluster and grid) has the clos-
est (mean, variance) of travel time to the exact paths.
Based on figure 11, in peak hour, 55 percent of the
closest paths to the exact were from community ap-
proach. As it can be seen, in peak hour, most of
the closest paths in both peak and non-peak hour are
found either by community approach or cluster ap-
proach, with some small fraction of grid approach.
While in non-peak hour the ratio is similar for com-
munity, cluster and grid approach. This emphasizes
the fact that, having an accurate graph clustering ap-
proach is crucial in the time of high traffic.
Figure 11: Ratio of paths with the closest mean-variance
to the exact path in peak and non-peak hour for the agent’s
goal of highest probability path.
Shortest Travel Time. Figure 12 and Figure 13 are
the same experiments for the agents that are interested
to select a path with shortest en-route time. Similar
to the previous section, community method has the
closest travel time to the exact path among other ap-
proximate approaches. Approximate path planning
methods in peak hour have larger travel time differ-
ence than non-peak time and in peak time the mean
of community method is 8 percent and its variance is
9 percent away from exact path.
Figure 12: Relative difference of travel time of mean and
variance of paths for exact and approximate approach for
peak and non-peak hours for the agent’s goal of shortest en-
route time.
Figure 13: Ratio of paths with the closest mean-variance to
the exact path for the agent’s goal of shortest en-route time.
4.4 Time and Space Complexity of
Approximate Approaches
As we have seen in the previous experiment, the mean
and variance of approximate approach has the rela-
tive difference of roughly 8 percent to the exact ap-
proach. However, path finding queries are responded
in real time. In query time, source, destination nodes
get connected to their exemplars and a pre-computed
solution is being fetched from distance oracles.
Now, the question is on the amount of space we
need for storing the approximate paths. In this ap-
proach, we reduce the city graphs by grouping the
similar nodes to each other. For example, the city
graph of Salt Lake City with 56753 nodes and it is
reduced to 157 exemplars. Hence, the nodes in one
community are closely connected to each other and
the approximate algorithm is at least 90 percent good
as the exact approach. For each time slot of day/week,
the best path from the 157 nodes are stored in distance
oracles with respect to the two possible goals of the
system. The rest of the nodes are just connecting to
their exemplars. If we consider nodes of the city as N,
and the number of exemplars as M, instead of storing
N ∗N paths we are storing N ∗M +M ∗M paths which
in our case N is 56753 and M is 157.
5 CONCLUSION AND FUTURE
WORK
In this paper, we proposed a scalable algorithm that
is practical in large scale path planning applications
which suits best for the use cases where agents have
goals, and planner aims to satisfies agents’ goals
rather than just providing a path which can move
agents from a source node to a destination node. City
is modelled as a large scale graph and agents have
two types of goals: 1) those who look for the path
with highest probability of reaching destination be-
fore deadline, and 2) the agents who are interested to
have the shortest travel duration while they are flexi-
ble on the time they can leave. Associated with each
path is a defined cost and the goal of the path plan-
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
462

ner is to find a path that satisfies the agents’ goals
with minimum cost. For expediting the path plan-
ning process, the city is partitioned and each part
is represented with an exemplar. The exemplar of
each partition is the node with the highest traffic on
that region. For partitioning the city graph, we used
three approaches: 1) community detection methods,
2) k-means clustering, and 3) grid based partition-
ing. When a path planning request comes, source
and destination nodes are connected to their corre-
sponding exemplars with respect to the path direc-
tion and the path between exemplars is retrieved. The
paths between exemplars are stored in distance ora-
cles based on the preceding year data at the time of
update and the oracles are updated every week to re-
flect the recent changes on the network. Results show
that among all of the graph clustering approaches,
community-based approaches produce closer results
to exact path planning approach. Approximation pro-
vides paths with mean and variance which are not ex-
act but clearly close to that exact paths, while the so-
lution is space and time efficient.
The main contribution of current work is pro-
viding a paradigm to handle large scale path plan-
ning requests utilizing pre-computation and approx-
imation. Graph partitioning reduces the graph size;
pre-computation helps in answering the queries in
real time and approximation helps in reducing the
space needed for storing the paths ahead of the time.
Even though the approximate paths are not as accu-
rate as exact paths, but they have acceptable accuracy
in comparison to the actual paths given the fact that
they saved a lot of time and space in the whole pro-
cess. Possible future work of this research includes:
a) trying other existing graph clustering methods such
as graph separators, b) adding new agents goals to the
domain and c) considering traffic data prediction to
enhance the decision making process which is cur-
rently based on historical data.
REFERENCES
Ahmadi, K. and Allan, V. H. (2017). Stochastic Path Find-
ing under Congestion. In 2017 International Confer-
ence on Computational Science and Computational
Intelligence (CSCI), pages 135–140.
Bast, H., Funke, S., Sanders, P., and Schultes, D. (2007).
Fast Routing in Road Networks with Transit Nodes.
Science, 316(5824):566–566.
Bauer, R., Columbus, T., Rutter, I., and Wagner, D. (2016).
Search-space size in contraction hierarchies. Theoret-
ical Computer Science, 645.
Edler, D., Guedes, T., Zizka, A., Rosvall, M., and Antonelli,
A. (2017). Infomap Bioregions: Interactive Mapping
of Biogeographical Regions from Species Distribu-
tions. Systematic Biology, 66(2):197–204.
Fan, Y. and Nie, Y. (2006). Optimal Routing for Maximiz-
ing the Travel Time Reliability. Networks and Spatial
Economics, 6(3):333–344.
Frederik Lardinois, Jochen Topf, S. C. (2011). Open-
StreetMap. UIT Cambridge.
Garza, S. E. and Schaeffer, S. E. (2019). Community detec-
tion with the Label Propagation Algorithm: A survey.
Physica A: Statistical Mechanics and its Applications,
534:122058.
Geisberger, R., Sanders, P., Schultes, D., and Vetter, C.
(2012). Exact Routing in Large Road Networks Us-
ing Contraction Hierarchies. Transportation Science,
46(3):388–404.
Gutman, R. (2004). Reach-Based Routing: A New Ap-
proach to Shortest Path Algorithms Optimized for
Road Networks. pages 100–111.
Hart, P. E., Nilsson, N. J., and Raphael, B. (1968). A for-
mal basis for the heuristic determination of minimum
cost paths. IEEE Transactions on Systems Science and
Cybernetics, 4(2):100–107.
Macqueen, J. (1967). Some methods for classification and
analysis of multivariate observations. In In 5-th Berke-
ley Symposium on Mathematical Statistics and Prob-
ability, pages 281–297.
Nie, Y. M. and Wu, X. (2009). Shortest path problem con-
sidering on-time arrival probability. Transportation
Research Part B: Methodological, 43(6):597–613.
Niknami, M. and Samaranayake, S. (2016). Tractable
Pathfinding for the Stochastic On-Time Arrival Prob-
lem. In Goldberg, A. V. and Kulikov, A. S., editors,
Experimental Algorithms, Lecture Notes in Computer
Science, pages 231–245. Springer International Pub-
lishing.
Nikolova, E. (2010). Approximation algorithms for reli-
able stochastic combinatorial optimization. In Pro-
ceedings of the 13th International Conference on Ap-
proximation, and 14 the International Conference on
Randomization, and Combinatorial Optimization: Al-
gorithms and Techniques, APPROX/RANDOM’10,
page 338–351, Berlin, Heidelberg. Springer-Verlag.
Ruaridh Clark, M. M. (2018). Eigenvector-based commu-
nity detection for identifying information hubs in neu-
ronal networks | bioRxiv.
Rus, S. L. B. K. G. R. M. (2020). Method and apparatus for
traffic-aware stochastic routing and navigation.
Sabran, G., Samaranayake, S., and Bayen, A. (2014). Pre-
computation techniques for the stochastic on-time ar-
rival problem. In Proceedings of the Meeting on Al-
gorithm Engineering & Expermiments, page 138–146,
USA. Society for Industrial and Applied Mathematics.
Samaranayake, S., Blandin, S., and Bayen, A. M. (2012).
Speedup Techniques for the Stochastic on-time Ar-
rival Problem. In ATMOS.
Utah Traffic, . (2020). UDOT: Utah Department of Trans-
portation.
Yang, Z., Algesheimer, R., and Tessone, C. (2016). A
Comparative Analysis of Community Detection Algo-
rithms on Artificial Networks. Scientific Reports, 6.
Scalable Stochastic Path Planning under Congestion
463
