Dy-COPECA: A Dynamic Version of MC/DC Analyzer for C Program
Sangharatna Godboley
1 a
and Arpita Dutta
2 b
1
Department of CSE, NIT Warangal, Telangana, India
2
Department of CSE, IIT Kharagpur, West Bengal, India
Keywords:
MC/DC, Test Cases, Software Testing, Static MC/DC Analysis, Dynamic MC/DC Analysis.
Abstract:
RTCA/DO-178B&C standards mandate Modified Condition / Decision Coverage (MC/DC) criterion for level-
A category software. In critical safety system applications such as Aircraft or Metro Rail controller systems,
etc., testing engineers have to produce the MC/DC report. There are several MC/DC analyzers, which are
either automated or partially-automated available. Some of the existing analyzers do not consider the depen-
dencies of Predicates/Decisions on each other. These analyzers process each predicate individually based on
MC/DC criterion. They use test cases to identify the total number of atomic conditions present in a decision
which influence the output of whole decision. In this paper, we overcome the limitations of some of the ex-
isting techniques. We propose an approach, which execute the whole program along with unit test cases at
run time to compute MC/DC score. This dynamic mechanism solves the dependency relation between the
variables appearing at different predicates and their branch statements in a single run. We have developed Dy-
namic COverage PErcentage CAlculator (Dy-COPECA) using C and Java language to process C-programs.
We have improved the MC/DC by 42.88% through dynamic MC/DC analysis as compared to static analysis
for the example C-program.
1 INTRODUCTION
Software Testing is an important phase of Software
Development Life Cycle (SDLC). Manual software
testing accounts for 50-80% of total software develop-
ment cost(Myers et al., 2011; Beizer, 2003; Chauhan,
2010; Mall, 2018). Manually created test cases and
computing code coverage are expensive(Gao et al.,
2005), error-prone, and generally not exhaustive (Ma-
jumdar and Sen, 2007). Therefore, automated soft-
ware testing techniques have been discovered (Bird
and Munoz, 1983; Csallner et al., 2008; Gupta et al.,
1998; DeMillo and Offutt, 1993).
White-box testing is one of the types of soft-
ware testing techniques (Ammann et al., 2003).
White-box testing deals with structural testing, where
testers have the knowledge and resources in terms of
source code. There are several code coverage crite-
ria(Grindal et al., 2005; Rajan et al., 2008) are avail-
able. Out of which MC/DC is the second strongest
criterion which requires minimum “n+1” number of
test case and maximum “2n” number of test cases,
where “n” is the total number of atomic conditions
a
https://orcid.org/0000-0002-6169-6334
b
https://orcid.org/0000-0001-7887-3264
present in the predicates of a program.
MC/DC was proposed a few decades
ago(Chilenski and Miller, 1994; Jones and Har-
rold, 2003). Many researchers across the globe are
considering it as an important technique. There are
also several commercialized organizations which
reports MC/DC for critical industrial software ap-
plications. Different researchers have implemented
MC/DC analyzer, but those have several limitations.
The main disadvantage of measuring MC/DC by
the existing techniques is their static mechanism.
As a result, those analyzers are failed to measure
the correct MC/DC for a program. We have also
observed that several existing analysers work with
high manual intervention which means, they are
semi-automated.
In this paper, we report this issue of static mech-
anism to measure MC/DC. The existing analyzer ap-
plies MC/DC mechanism on all the predicates present
in a program individually. These existing works do
not care for the functional effect of variables, atomic
conditions, and predicates which appear one after
other in a program. It means one predicate appears
in a program before another predicate without taking
care of updated values for variables appeared in sec-
Godboley, S. and Dutta, A.
Dy-COPECA: A Dynamic Version of MC/DC Analyzer for C Program.
DOI: 10.5220/0010401501970204
In Proceedings of the 16th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2021), pages 197-204
ISBN: 978-989-758-508-1
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
197

ond predicate. When we compute MC/DC for these
predicates with static mechanism of MC/DC analyzer,
so this will not exercise the actual result / real val-
ues for MC/DC. This is a serious issue to fix, and we
present a solution in this paper. We develop a dynamic
version of MC/DC analyzer which actually takes care
of the updated values of variables present in differ-
ent predicates at different locations according to the
appearance in a program. We will present an exam-
ple for both Static and Dynamic analyses to measure
MC/DC. Also, we compare the differences and handle
those issues appearing in the analyses. We have ob-
served that Dynamic mechanism has a significant ad-
vantage over static mechanism. We can achieve a sig-
nificant improvement in MC/DC percentage, which is
a big advantage of this proposed approach.
The rest of the article is organized as follows: Sec-
tion 2 presents the Background Concepts. Section 3
presents the proposed approach Dy-COPECA. Sec-
tion 4 shows the result analysis using an example.
Section 5 compares our approach with existing work.
Section 6 concludes the paper and suggests some fu-
ture work.
2 BACKGROUND CONCEPTS
MC/DC is a code coverage criterion and was in-
troduced by the RTCA DO-178B standard(Johnson
et al., 1998). Test coverage approaches such as branch
coverage which are popular for traditional programs
are considered as inadequate for safety-critical sys-
tems. Thus, MC/DC was used to overcome this limi-
tation and to achieve a linear growth of test case gen-
eration (Ammann et al., 2003; Bokil et al., 2009).
MC/DC indicates that the outcome of a decision in
the case of a conditional statement must be affected
by the changes made to the individual conditions.
MC/DC must satisfy the following criteria (Hayhurst,
2001):
• Every entry points and exit points of a program
should be invoked at least once.
• Every decisions of a program should be invoked
at least once for both true and false branch values.
• Every atomic conditions present in a decision
should be invoked at least once for both true and
false branches.
• Every possible outcomes of a decision must be af-
fected by the changes made to each condition.
For example, let’s take an example predicate “if(X
&& Y) then ...”. In order to find the MC/DC test
cases for this example, the following steps required
to be performed:
Table 1: Extended truth table.
TC No. X Y result X Y
TC
1
True True True TC
3
TC
2
TC
2
True False False TC
1
TC
3
False True False TC
1
TC
4
False False False
• Create truth table for the predicate.
• Extend the truth table so that it indicates which
test cases can be used to show the independence of
each condition. The extended truth table is shown
in Table 1.
• Show the independence of X by taking test cases
{TC
1
,TC
3
} and the independence of Y by taking
test case {TC
1
, TC
2
}.
• Union of the above test cases are known
as the MC/DC test cases. The resulting
MC/DC test cases are {TC
1
,TC
2
, and TC
3
}, i.e.,
{(True,True)+(True,False)+(False,True)}
Definition 1. Static MC/DC Analysis: “Analyzing a
C program to measure MC/DC using unit test data
without any context consideration before the predi-
cates.”
Definition 2. Dynamic MC/DC Analysis: “Analyz-
ing a C program to measure MC/DC using unit test
data with considering the context before the predi-
cate, which helps to process all the updated values
of variables present in the whole program. ”
Definition 3. Modified Condition / Decision Cover-
age: “MC/DC is code coverage technique, where
Condition is a Leaf level Boolean expression and De-
cision controls the program flow. MC/DC% is de-
fined as the total number of independently affected
conditions (I) out of total conditions (C) present in a
program (Hayhurst, 2001; Hayhurst and Veerhusen,
2001).”
MCDC% =
|I|
|C|
∗100% (1)
We have developed a tool called Dy-COPECA for
measuring MC/DC%. Dy-COPECA stands for Dy-
namic COverage PErcenatge CAlculator that accepts
generated unit test cases along with C program and
produces MC/DC%.
3 PROPOSED APPROACH:
Dy-COPECA
In this section, we discuss the detailed description of
Dy-COPECA using schematic representation.
Fig. 1 explains the schematic representation of
Dy-COPECA. Dy-COPECA produces MC/DC% as
ENASE 2021 - 16th International Conference on Evaluation of Novel Approaches to Software Engineering
198

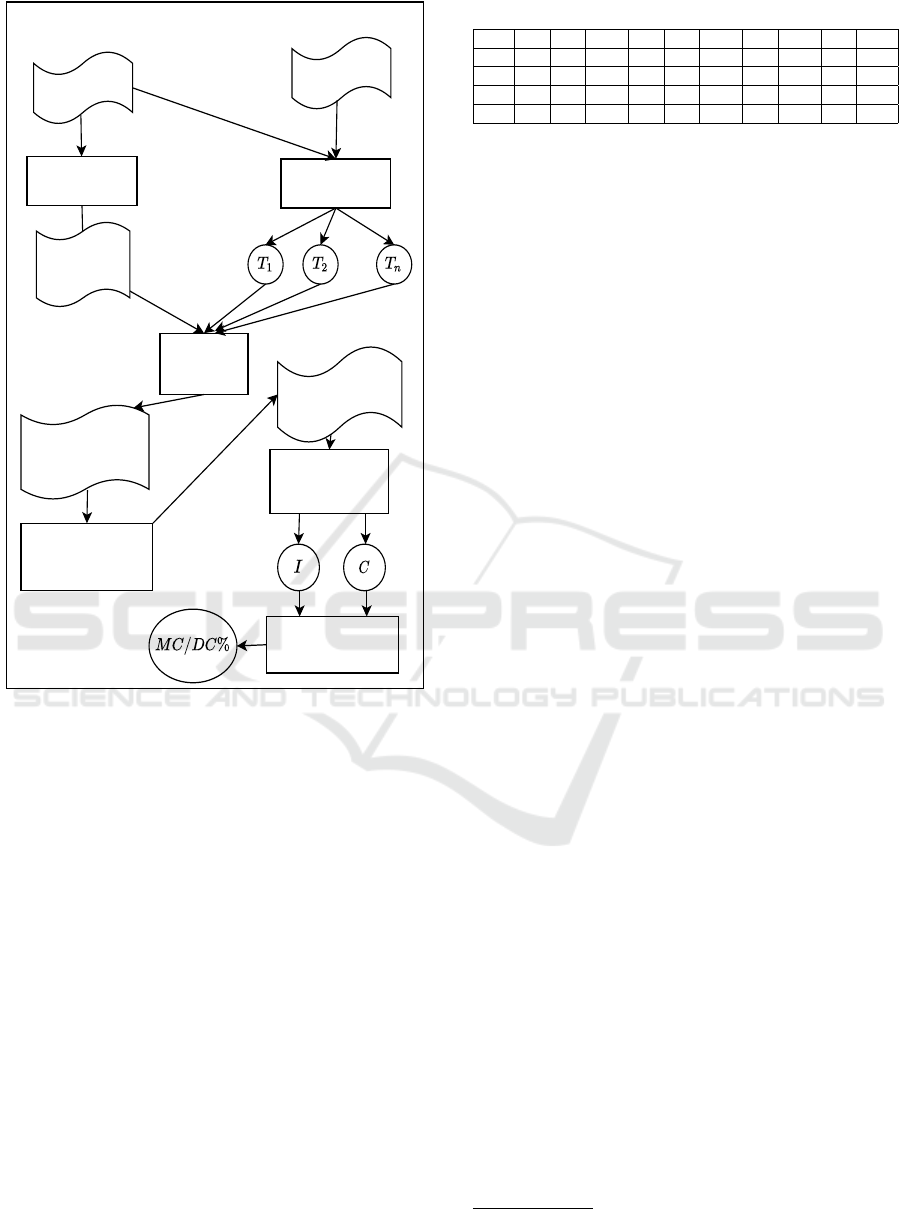
C Program
Pre-processor
C Program
Executable
GCC
Compiler
Unit Test Case
Test Input File
Generator
Test file with Solved
Conditions and
Decisions
MC/DC Extended
Truth Table Generator
ETT with MC/DC
Test Cases
Atomic Conditions
Identifier
Coverage Calculator
Dy-COPECA
Figure 1: Schematic representation of Dy-COPECA.
output after imparting a C-program and unit test data
as inputs. Dy-COPECA consists of six modules.
These are (1) Pre-processor, (2) Test Input File Gener-
ator, (3) GCC Compiler, (4) MC/DC Extended Truth
Table Generator, (5) Atomic Conditions Identifier,
and (6) Coverage Calculator.
Now, let us discuss the functionalities and flow of
execution for these modules. The flow starts with sup-
plying C-program into Pre-processor as input. Pre-
processor creates an annotated C-program and sup-
plied into GCC Compiler to produce an executable
code with functionalities processing test data files
(./a.out). On the other hand, we have unit test data
which generated from any of the test data generator
(Younis et al., 2008) such as symbolic tester or con-
colic tester for C program. The test data generation
is beyond the scope of this paper, so we assumed that
we have already generated unit test data.
In practical, a unit test data file has several fea-
tures for variables such as, variable’s name, variable’s
size, and variable’s input value etc. So, Test Input File
Generator processes C-program along with unit test
Table 2: Assumed test data for example program in Fig. 2.
Var T
1
T
2
T
3
T
4
T
5
T
6
T
7
T
8
T
9
T
10
p 21 21 15 15 80 85 60 70 30 30
q 45 51 45 51 40 35 55 60 55 85
r 0 90 110 90 71 60 25 69 50 80
s 0 0 10 0 50 125 90 119 80 80
data as inputs which separates all test input values in
different files to get executed individually one by one.
Now, the third Module GCC Compiler, which is
the actual reason for dynamic nature of our MC/DC
analyzer. So, from Fig. 1, we can observe that, anno-
tated C program code is imparted along with all test
input files one by one into GCC compiler as inputs
which provides an executable program which pro-
duces a text file with all solved condition and deci-
sions after ran naively. GCC compiler executes C pro-
gram at run time, which allots all concrete input val-
ues corresponding to all variables present in the pro-
gram. It solves all the atomic conditions, decisions,
arithmetic operations, assignments etc. But, our main
focus is to solve atomic conditions and decisions for
MC/DC mechanism.
Next, MC/DC Extended Truth Table Generator
1
module reads a text file as an input and produces ETT
Table with MC/DC Test Cases as an output as shown
in Fig. 1 according to the definition explained in Sec-
tion 2.
Now, Atomic Conditions Identifier module reads
ETT Table with MC/DC Test Cases to identify the set
of Independently affected atomic conditions (I) along
with total number of atomic conditions (C). The last
module Coverage Calculator takes the value of I and
C as inputs, and uses the formula given in Eq. 1 to
measure MC/DC%. Finally Dy-COPECA produces
MC/DC% for the input C-program.
4 EXPERIMENTAL RESULT
ANALYSIS
In this section we discuss about static and dynamic
analyses of MC/DC using an example.
Let us take an example of C program as shown
in Fig. 2. Also, assume that unit test data is avail-
able with us to compute MC/DC as shown in Table
2. First of all, this program has five variables, out
of which four variables are generated automatically
from test case generator and one variable is initialized
in program itself. This program has two predicates,
in which first predicate has three atomic conditions,
second predicate has four atomic conditions.
1
It is to be noted that computation of ETT table does not
follow short-circuiting properties.
Dy-COPECA: A Dynamic Version of MC/DC Analyzer for C Program
199

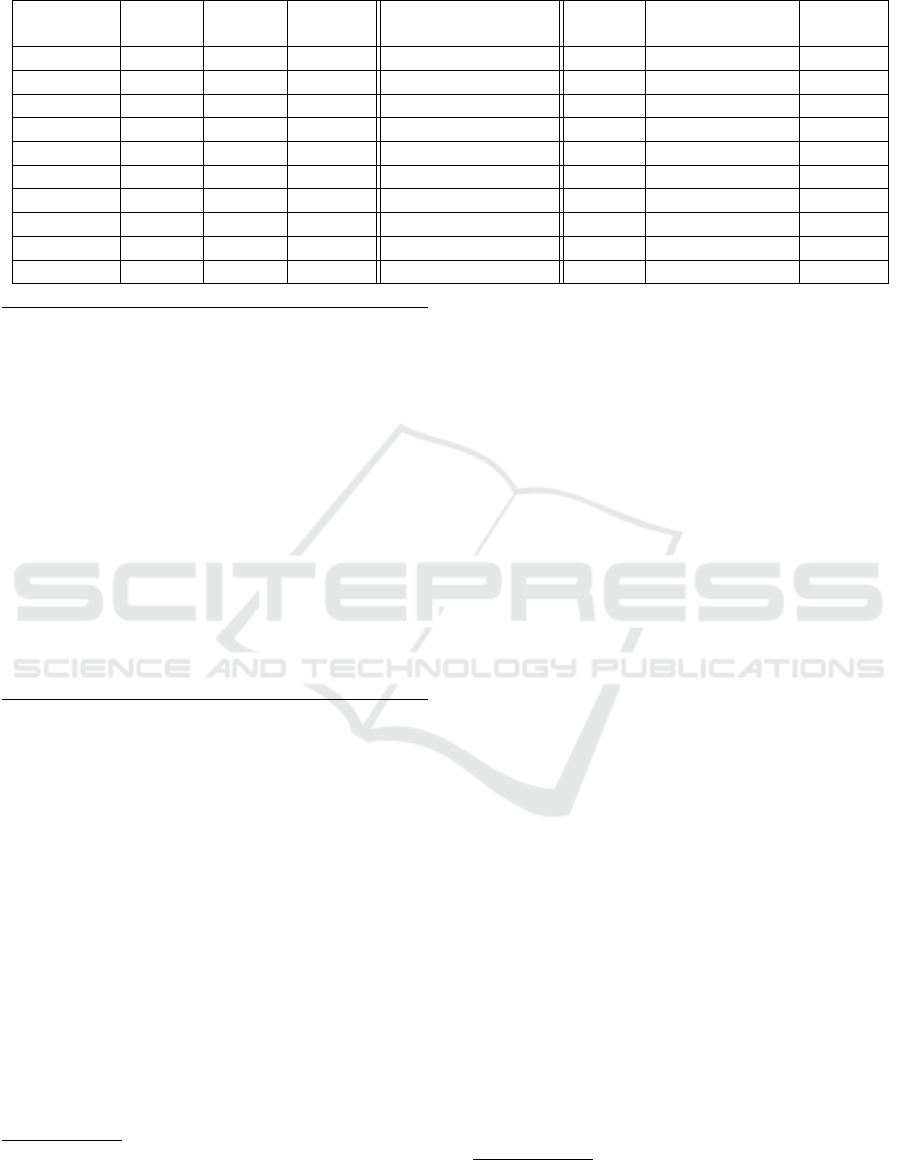
Table 3: Extended Truth Table (ETT) for first predicate of example C program in Fig. 2 using Static and Dynamic Analyses.
Test Cases (p>20) (q<50) (r>100) P
1
=((p>20)&& (p>20) (q<50) (r>100)
((q<50)||(r>100)))
T
1
TRUE TRUE FALSE TRUE T
2
,T
7
,T
8
,T
9
,T
10
T
2
TRUE FALSE FALSE FALSE T
1
, T
5
,T
6
T
3
FALSE TRUE TRUE FALSE
T
4
FALSE FALSE FALSE FALSE
T
5
TRUE TRUE FALSE TRUE T
2
,T
7
,T
8
,T
9
,T
10
T
6
TRUE TRUE FALSE TRUE T
2
,T
7
,T
8
,T
9
,T
10
T
7
TRUE FALSE FALSE FALSE T
1
, T
5
,T
6
T
8
TRUE FALSE FALSE FALSE T
1
, T
5
,T
6
T
9
TRUE FALSE FALSE FALSE T
1
, T
5
,T
6
T
10
TRUE FALSE FALSE FALSE T
1
, T
5
,T
6
1. #include<stdio.h>
2. int main(){
3. int p,q,r,s,x=10;
4. if((p>20)&&((q<50)||(r>100))){
5. x=x+50;
6. printf("This is if-branch of 1st
predicate");}
7. else {
8. x=x+70;
9. printf("This is else-branch of 1st
predicate");}
10. if(((p<=x)&&(q<x))||((r>70)&&(s<120))){
11. printf("This is if-branch of 2nd
predicate");}
12. else{
13. printf("This is else-branch of 2nd
predicate");}
14. return 0;
15. }
Figure 2: An example C program.
4.1 Static MC/DC Analysis
We know that static MC/DC analysis executes test
cases and measures MC/DC% for predicates one by
one. With this fact, let us now create Extended Truth
Table (ETT) for both predicates. We start with pred-
icate “P
1
=((p>20)&&((q<50)||(r>100)))”. Here, we
have three atomic conditions {(p>20), (q<50), and
(r>100)}. Using test data from Table 2, one by one
we create ETT as shown in Table 3
2
. Here, (q<50)
is the only condition which independently affects the
outcome of whole predicate after toggling it value.
The minimum test cases must be “n+1”, where n=1
in this case. There are two MC/DC test cases out of
eight test cases for this first predicate.
Now we create ETT for the second predicate i.e.,
2
Please note that, Table 3 is common for both Static
MC/DC analysis and Dynamic MC/DC Analysis, which
shows the ETT for first predicate. So, we have not drawn
two separate Tables for both analyses.
“P
2
=(((p<=x)&&(q<x))||((r>70)&&(s<120)))”.
Since, this is a static analysis in which, it only able to
process the test input values and available in test data
generated. For P
2
, we have four atomic conditions
{(p<=x), (q<x), (r>70), and (s<120)}. Invoking
this predicate from C-program, we must have test
input values for p,q,r, and s variables, according to
test data generated. We do not have the updated
value of “x” variable, due to which we can not
execute (p<=x) and (q<x). But, now it is possible
to compute the outcome of (r>70) and (s<120)
atomic conditions. It doesn’t mean that we are
able to measure MC/DC%. According to problem,
the run-time value (p<=x) and (q<x) cannot be
computed and these are highly connected to (r>70)
and (s<120) through a Boolean operator “||”. Hence
the whole predicate is not able to compute MC/DC.
Therefore, the MC/DC percentage for C program as
shown in Fig. 2. using static MC/DC analysis can be
computed as follows:
• Total number of atomic conditions present in the
example C-program (C) = 7 {(p>20), (q<50),
(r>100), (p<=x), (q<x), (r>70), and (s<120)}.
• Total number of independently affected atomic
conditions present in predicates of a C program
(I) = 1 {(q<50)}.
• MC/DC test cases = {T
1
= (21,45,0,0) and
T
9
=(30,55,50,80)}. [Minimum number of test
cases]
3
• Using Eq. 1, we achieved 14.28% MC/DC.
4.2 Dynamic MC/DC Analysis
In this section, we discuss dynamic MC/DC analysis
for the C-program shown Fig. 2. We know that
3
We can choose either of the pair from the Table 3 as
MC/DC test cases to show that (q<50) is independently af-
fected atomic condition.
ENASE 2021 - 16th International Conference on Evaluation of Novel Approaches to Software Engineering
200

dynamic MC/DC analyzer executes test cases and
measure MC/DC% for predicates one by one by
taking care of all the values of variables accord-
ing to the procedural control flow of C-program.
For more clarity we can observe the binary ex-
ecution tree and all possible explored paths in
Figures 3 and 4 respectively. We create Extended
Truth Table (ETT) for both the predicates start-
ing with “P
1
=((p>20)&&((q<50)||(r>100)))”.
Here we may observe that the ETT for “P
1
”
is same as static MC/DC analysis which is al-
ready shown in Table 3. So, we are not going
to discuss it again. But, in the second predicate
“P
2
=(((p<=x)&&(q<x))||((r>70)&&(s<120)))”,
which has four atomic conditions {(p<=x), (q<x),
(r>70), and (s<120)}, we can observe that variable
“x” is used in first two atomic conditions. Also,
please observe Figures 2 and 3 where the variable
“x” has different values at different appearance in
the program. According to run-time execution, we
have different values of the variable “x” at different
appearance, and hence (p<=x), and (q<x) able to
show the independently affected atomic conditions.
Additionally, the atomic condition (r>70) is also
shown as independently affected atomic condition.
The Extended Truth Table (ETT) for this predicate
of example C-program using dynamic analysis is
shown in Table 4. Therefore, the MC/DC percentage
for C-program as shown in Fig. 2 using Dynamic
MC/DC analysis can be computed as follows:
• Total number of atomic conditions present in
predicates of the example C-program (C) =
7 {(p>20), (q<50), (r>100), (p<=x), (q<x),
(r>70), and (s<120)}.
• Total number of independently affected atomic
conditions present the program (I) = 4 {(q<50),
(p<=x), (q<x), and (r>70)}.
• MC/DC test cases = {T
1
= (21,45,0,0),
T
4
= (15,51,90,0), T
6
= (85,35,60,125), T
9
=
(30,55,50,80) and T
10
=(30,85,80,80)}. [Min-
imum number of test cases show 4 atomic
conditions (n+1)]
• Using Eq. 1, we computed 57.14% MC/DC.
4.3 Inference of Analysis
We have observed from our first analysis i.e., Static
MC/DC analysis that the obtained MC/DC for C-
program is 14.28% with two MC/DC test cases {T
1
,
and T
9
}. On the other hand, in our second analysis i.e.
Dynamic MC/DC analysis, which processed all pred-
icates and checked for all seven atomic conditions.
Figure 3: Binary Execution Tree in the example program
given in Fig. 2.
1. FALSE-FALSE-FALSE
2. FALSE-FALSE-TRUE-FALSE
3. FALSE-FALSE-TRUE-TRUE
4. FALSE-TRUE-FALSE-FALSE
5. FALSE-TRUE-FALSE-TRUE-FALSE
6. FALSE-TRUE-FALSE-TRUE-TRUE
7. FALSE-TRUE-TRUE
8. TRUE-FALSE-FALSE-FALSE-FALSE
9. TRUE-FALSE-FALSE-FALSE-TRUE-FALSE
10. TRUE-FALSE-FALSE-FALSE-TRUE-TRUE
11. TRUE-FALSE-FALSE-TRUE-FALSE-FALSE
12. TRUE-FALSE-FALSE-TRUE-FALSE-TRUE-FALSE
13. TRUE-FALSE-FALSE-TRUE-FALSE-TRUE-TRUE
14. TRUE-FALSE-FALSE-TRUE-TRUE
15. TRUE-FALSE-TRUE-FALSE-FALSE
16. TRUE-FALSE-TRUE-FALSE-TRUE-FALSE
17. TRUE-FALSE-TRUE-FALSE-TRUE-TRUE
18. TRUE-FALSE-TRUE-TRUE-FALSE-FALSE
19. TRUE-FALSE-TRUE-TRUE-FALSE-TRUE-FALSE
20. TRUE-FALSE-TRUE-TRUE-FALSE-TRUE-TRUE
21. TRUE-FALSE-TRUE-TRUE-TRUE
22. TRUE-TRUE-FALSE-FALSE
23. TRUE-TRUE-FALSE-TRUE-FALSE
24. TRUE-TRUE-FALSE-TRUE-TRUE
25. TRUE-TRUE-TRUE-FALSE-FALSE
26. TRUE-TRUE-TRUE-FALSE-TRUE-FALSE
27. TRUE-TRUE-TRUE-FALSE-TRUE-TRUE
28. TRUE-TRUE-TRUE-TRUE
Figure 4: All possible paths explored in the example pro-
gram given in Fig. 2.
Dy-COPECA: A Dynamic Version of MC/DC Analyzer for C Program
201

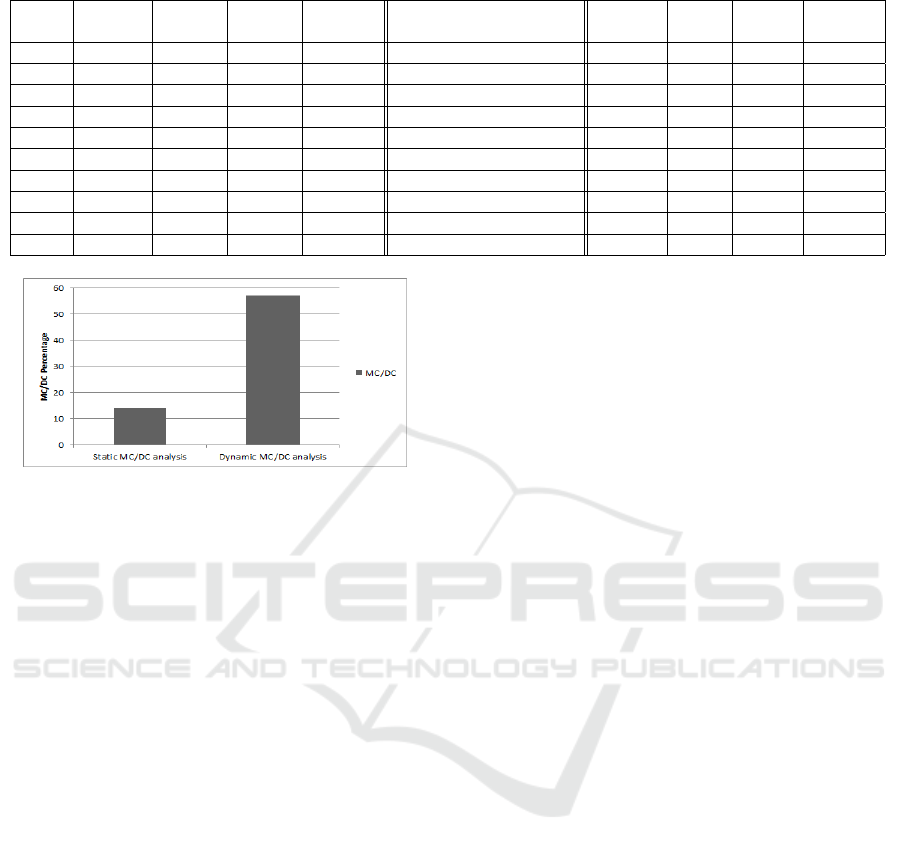
Table 4: Extended Truth Table (ETT) for Second predicate of example C program in Fig. 2 using Dynamic analysis.
Test (p<=x) (q<x) (r>70) (s<120) P
2
=(((p<=x)&&(q<x)) (p<=x) (q<x) (r>70) (s<120)
Cases ((r>70)&&(s>120)))
T
1
TRUE TRUE FALSE TRUE TRUE T
9
T
10
T
2
TRUE TRUE TRUE TRUE TRUE
T
3
TRUE TRUE TRUE TRUE TRUE
T
4
TRUE TRUE TRUE FALSE TRUE T
6
T
5
FALSE TRUE TRUE TRUE TRUE
T
6
FALSE TRUE TRUE FALSE FALSE T
4
T
7
TRUE TRUE FALSE TRUE TRUE
T
8
TRUE TRUE FALSE TRUE TRUE
T
9
TRUE FALSE FALSE TRUE FALSE T
1
T
10
TRUE FALSE TRUE TRUE FALSE T
1
Figure 5: Comparison of analyses.
Dynamic analysis has improved the MC/DC percent-
age and reported 57.14% with four atomic conditions
as Independently affecting conditions. For this, there
are five test cases {T
1
, T
4
, T
6
, T
9
, and T
10
} are re-
quired to compute MC/DC percentage of whole pro-
gram. Due to Dynamic nature of MC/DC analysis,
we achieve 42.88% of MC/DC higher as compared
to static MC/DC analysis. The comparison between
Static MC/DC analysis and Dynamic MC/DC analy-
sis is shown in Fig. 5. We agree that, we have not
achieved 100% MC/DC for C-program due to less
number of test data assumed/available. Once we im-
prove the test data, so we may achieve higher MC/DC.
4.4 Threats to Validity
1. Since, we focused on MC/DC percentage, pro-
grams without predicates are not useful for our
experimental study.
2. In a predicate, there should be at least two condi-
tions, because for MC/DC we require at least one
logical operator.
3. We have not experimented a C-program which
have multiple files to be invoked by main file, so
current version may not handle such type of pro-
grams. We will implement this feature in future
work.
4. Dy-COPECA is unable to solve the issues of re-
dundant test data, in result it computes all the test
cases which are some times not required. Dy-
COPECA required extra features to identify du-
plicate test data.
5 COMPARISON WITH
RELATED WORK
In this section, we discuss some existing related work
on this topic.
Hayhurst et al.(Hayhurst, 2001; Hayhurst and
Veerhusen, 2001) presented a tutorial on MC/DC ap-
proach for aviation software applications that must
comply with regulatory guided for Do-178B/C level
A software. They have provided a five steps process to
determine MC/DC, using that verification analyst rec-
ommend for the certification. From the tutorial avail-
able online, it shows that how to determine MC/DC
for single predicate or decision. Also, this tutorial
do not reflect any automation of the process. Dy-
COPECA is actually fully automated and also able
to execute a complete program which may consists of
any number of predicates.
Chang et al. (Chang and Huang, 2007) pro-
posed and developed a practical regression testing
tool TASTE (Tool fo Automatic Software regression
TEsting). In their paper, they have used an useful
method which focuses on all conditions of Boolean
expression to determine MC/DC. Their proposed ap-
proach used n-cube graph and gray code to imple-
ment the MC/DC criterion. They have differentiated
the necessary and redundant test cases. Also, their
approach is dynamic in nature. Like, Chang et al., we
also proposed Dy-COPECA which measure MC/DC.
Dy-COPECA is dynamic nature to compute MC/DC
at run-time, as like TASTE. Chang et al. have pro-
posed some strategies to generate test cases, whereas
our approach is more generic and can be plugged to
any test cases generator.
Kandl et al.(Kandl and Kirner, 2010) implemented
MC/DC for automotive domain. They have targeted
ENASE 2021 - 16th International Conference on Evaluation of Novel Approaches to Software Engineering
202

to inspect the error-detection rate of a set of test that
attian higher possible MC/DC coverage. They initi-
ated by generation of test cases followed error detec-
tion. Dy-COPECA is not targeted for error detection
according to MC/DC. Also, we assumed for the unit
test cases.
Ghani et al.(Ghani and Clark, 2009) introduce
a search based testing technique to generated test
case and using those test case they have computed
MC/DC automatically. Their tool has advantage to
compute Multiple Condition Coverage (MCC) and
MC/DC. They have used simulated annealing opti-
mization technique. It is not very clear from the paper
that Ghani et al. focuses on dynamic nature or not. In
our proposed approach, we have not used any test case
generator technique, but can be extended in future
work. Also, Dy-COPECA can not determine MCC.
But, it uses dynamic analysis to compute MC/DC.
Like Ghani et al.(Ghani and Clark, 2009),
Awedekian et al.(Awedikian et al., 2009) imple-
mented search based algorithm for MC/DC test cases
generation. Awedekian et al.(Awedikian et al., 2009)
adopted the Hill Climbing(HC) and Genetic Algo-
rithm (GA) to implement their approach. On the other
hand, Dy-COPECA do not uses any test cases gener-
ated technique. Only it follows the definition of stan-
dard Unique cause MC/DC provided by Hayhurst et
al.(Hayhurst, 2001) at NASA. We applied dynamic
behavior on the definition to automate the coverage
tool.
Haque et al.(Haque et al., 2014) have proposed
and developed a tool called MC/DC GEN. They have
considered the issue of “Masking” in MC/DC. Based
on masking MC/DC, they have implemented tool to
generate test cases and determine MC/DC. But, their
tool does not explain the dynamic nature, only they
execute single predicate. In our proposed work, we
are focusing on “Unique cause MC/DC” only. Mask-
ing MC/DC is beyond the scope of this paper. But,
the major advantage of Dy-COPECA is its dynamic
nature over Haque et al.(Haque et al., 2014) work.
Godboley et al.(Godboley et al., 2018b; Godbo-
ley et al., 2018a; Godboley et al., 2017a; Godboley
et al., 2017b; Godboley et al., 2016; Godboley et al.,
2013b; Godboley et al., 2013a; Godboley, 2013) have
proposed several techniques to compute MC/DC us-
ing concolic test case generation technique. Their
MC/DC analyzers were computing MC/DC score
statically i.e. processing one predicate at a time. On
the other hand, Dy-COPECA focused for the dynamic
behavior of the program for MC/DC.
Table 5 shows the comparison with related work.
All the related works considered focused on comput-
ing MC/D criterion. Our main objective of this paper
is to show the dynamic behavior is good to achieve
higher MC/DC. So, we have taken the comparison
factor as the mechanism of computing MC/DC either
static or dynamic. We can observe that only Chang
et al. have worked other than us on dynamic MC/DC
analysis, and other have taken static MC/DC analysis.
Based on our investigation from the paper, we pre-
sented that static is a very serious issue which needed
to be fix. Hence, we have proposed and developed a
tool to overcome the this issue.
Table 5: Comparison with related work.
Author’s Static Dynamic
Name MC/DC MC/DC
Hayhurst et al.(Hayhurst, 2001)
√
X
Chang et al.(Chang and Huang, 2007) X
√
Kandl et al.(Kandl and Kirner, 2010)
√
X
Ghani et al.(Ghani and Clark, 2009)
√
X
Awedekian et al.(Awedikian et al., 2009)
√
X
Haque et al.(Haque et al., 2014)
√
X
Our Proposed work: Dy-COPECA X
√
6 CONCLUSION AND FUTURE
WORK
We have proposed and developed Dy-COEPCA,
which is use to measure MC/DC at run time when
we supply a C-program along with unit test cases. We
have shown the limitations of static nature of cover-
age tool. Due to this issue, MC/DC gets degraded for
a C-program. Also, we have explained the Dynamic
analysis to improve the results. Using an example C-
program the result analyses is explained. We have im-
proved 42.88% of MC/DC through dynamic MC/DC
analysis as compared to static MC/DC analysis.
In future work, we try to plug this Dy-COEPCA
with some test case generator tools such as symbolic
tester, and concolic tester. Also, we plan to implement
a Java version of Dy-COPECA.
REFERENCES
Ammann, P., Offutt, J., and Huang, H. (2003). Cover-
age criteria for logical expressions. In 14th Interna-
tional Symposium on Software Reliability Engineer-
ing, 2003. ISSRE 2003., pages 99–107. IEEE.
Awedikian, Z., Ayari, K., and Antoniol, G. (2009). Mc/dc
automatic test input data generation. In Proceedings
of the 11th Annual conference on Genetic and evolu-
tionary computation, pages 1657–1664.
Beizer, B. (2003). Software testing techniques. Dreamtech
Press.
Bird, D. L. and Munoz, C. U. (1983). Automatic genera-
tion of random self-checking test cases. IBM systems
journal, 22(3):229–245.
Dy-COPECA: A Dynamic Version of MC/DC Analyzer for C Program
203

Bokil, P., Darke, P., Shrotri, U., and Venkatesh, R. (2009).
Automatic test data generation for c programs. In
2009 Third IEEE International Conference on Se-
cure Software Integration and Reliability Improve-
ment, pages 359–368. IEEE.
Chang, J.-R. and Huang, C.-Y. (2007). A study of en-
hanced mc/dc coverage criterion for software test-
ing. In 31st Annual International Computer Software
and Applications Conference (COMPSAC 2007), vol-
ume 1, pages 457–464. IEEE.
Chauhan, N. (2010). Software Testing: Principles and
Practices. Oxford university press.
Chilenski, J. J. and Miller, S. P. (1994). Applicability of
modified condition/decision coverage to software test-
ing. Software Engineering Journal, 9(5):193–200.
Csallner, C., Smaragdakis, Y., and Xie, T. (2008). Dsd-
crasher: A hybrid analysis tool for bug finding. ACM
Transactions on Software Engineering and Methodol-
ogy (TOSEM), 17(2):1–37.
DeMillo, R. A. and Offutt, A. J. (1993). Experimental
results from an automatic test case generator. ACM
Transactions on Software Engineering and Methodol-
ogy (TOSEM), 2(2):109–127.
Gao, J., Espinoza, R., and He, J. (2005). Testing coverage
analysis for software component validation. In 29th
Annual International Computer Software and Appli-
cations Conference (COMPSAC’05), volume 1, pages
463–470. IEEE.
Ghani, K. and Clark, J. A. (2009). Automatic test data
generation for multiple condition and mcdc coverage.
In 2009 Fourth International Conference on Software
Engineering Advances, pages 152–157. IEEE.
Godboley, S. (2013). Improved modified condition/decision
coverage using code transformation techniques. PhD
thesis.
Godboley, S., Dutta, A., Mohapatra, D. P., Das, A., and
Mall, R. (2016). Making a concolic tester achieve in-
creased mc/dc. Innovations in systems and software
engineering, 12(4):319–332.
Godboley, S., Dutta, A., Mohapatra, D. P., and Mall, R.
(2017a). J3 model: a novel framework for improved
modified condition/decision coverage analysis. Com-
puter Standards & Interfaces, 50:1–17.
Godboley, S., Dutta, A., Mohapatra, D. P., and Mall, R.
(2018a). Gecojap: A novel source-code preprocess-
ing technique to improve code coverage. Computer
Standards & Interfaces, 55:27–46.
Godboley, S., Dutta, A., Mohapatra, D. P., and Mall, R.
(2018b). Scaling modified condition/decision cov-
erage using distributed concolic testing for java pro-
grams. Computer Standards & Interfaces, 59:61–86.
Godboley, S., Mohapatra, D. P., Das, A., and Mall, R.
(2017b). An improved distributed concolic test-
ing approach. Software: Practice and Experience,
47(2):311–342.
Godboley, S., Prashanth, G., Mohapatra, D. P., and Ma-
jhi, B. (2013a). Enhanced modified condition/deci-
sion coverage using exclusive-nor code transformer.
In 2013 International Mutli-Conference on Automa-
tion, Computing, Communication, Control and Com-
pressed Sensing (iMac4s), pages 524–531. IEEE.
Godboley, S., Prashanth, G., Mohapatro, D. P., and Majhi,
B. (2013b). Increase in modified condition/decision
coverage using program code transformer. In 2013 3rd
IEEE International Advance Computing Conference
(IACC), pages 1400–1407. IEEE.
Grindal, M., Offutt, J., and Andler, S. F. (2005). Combi-
nation testing strategies: a survey. Software Testing,
Verification and Reliability, 15(3):167–199.
Gupta, N., Mathur, A. P., and Soffa, M. L. (1998). Auto-
mated test data generation using an iterative relaxation
method. ACM SIGSOFT Software Engineering Notes,
23(6):231–244.
Haque, A., Khalil, I., and Zamli, K. Z. (2014). An auto-
mated tool for mc/dc test data generation. In 2014
IEEE Symp. Comput. Informatics, Kota Kinabalu,
Sabah, Malaysia.
Hayhurst, K. J. (2001). A practical tutorial on modified
condition/decision coverage. DIANE Publishing.
Hayhurst, K. J. and Veerhusen, D. S. (2001). A practi-
cal approach to modified condition/decision coverage.
In 20th DASC. 20th Digital Avionics Systems Confer-
ence (Cat. No. 01CH37219), volume 1, pages 1B2–1.
IEEE.
Johnson, L. A. et al. (1998). Do-178b, software considera-
tions in airborne systems and equipment certification.
Crosstalk, October, 199:11–20.
Jones, J. A. and Harrold, M. J. (2003). Test-suite reduc-
tion and prioritization for modified condition/decision
coverage. IEEE Transactions on software Engineer-
ing, 29(3):195–209.
Kandl, S. and Kirner, R. (2010). Error detection rate of
mc/dc for a case study from the automotive domain. In
IFIP International Workshop on Software Technolgies
for Embedded and Ubiquitous Systems, pages 131–
142. Springer.
Majumdar, R. and Sen, K. (2007). Hybrid concolic testing.
In 29th International Conference on Software Engi-
neering (ICSE’07), pages 416–426. IEEE.
Mall, R. (2018). Fundamentals of software engineering.
PHI Learning Pvt. Ltd.
Myers, G. J., Sandler, C., and Badgett, T. (2011). The art of
software testing. John Wiley & Sons.
Rajan, A., Whalen, M. W., and Heimdahl, M. P. (2008). The
effect of program and model structure on mc/dc test
adequacy coverage. In Proceedings of the 30th inter-
national conference on Software engineering, pages
161–170.
Younis, M. I., Zamli, K. Z., and Isa, N. A. M. (2008). Irps–
an efficient test data generation strategy for pairwise
testing. In International Conference on Knowledge-
Based and Intelligent Information and Engineering
Systems, pages 493–500. Springer.
ENASE 2021 - 16th International Conference on Evaluation of Novel Approaches to Software Engineering
204