Health Monitoring of Automotive Suspension System using Machine

Learning

Ahmed Abdelfattah

and Hesham Ibrahim

Mechatronics Department, German University in Cairo, Egypt

Associate Professor, Mechatronics Department, German University in Cairo, Egypt

Keywords:

Suspension Health Monitoring, Machine Learning, Quarter-Car Model.

Abstract:

This paper investigates Knowledge-based condition monitoring of automotive suspension dampers by imple-

menting a quarter car model (QCM). The sprung mass acceleration - frequency power spectral density curves,

for different cases of performance degradation in suspension damping and different operational conditions,

is provided in response to the random road disturbance of different road classes. Training and testing accel-

eration response data are generated by Mtalb/simulink and fed to different classiﬁcation algorithms that are

trained and tested to distinguish between the different damping degradation values, in order to assess their

performance in terms of classiﬁcation accuracy as well as their confusion matrix. In addition, the worthiness

of applying Principal Component Analysis (PCA), as a dimensional reduction technique, to increase all can-

didate classiﬁcation algorithms is explored. Finally, the results of Quadratic Support Vector Machine showed

the best performance in terms of accuracy and confusion matrix, while using dimensional reduction turned to

be inefﬁcient.

1 INTRODUCTION

It is inevitable for suspension system or any other

structure to gradually show signs of damage like re-

duction in performance due to many causes such as

inadequate maintenance, and material aging. Suspen-

sion system needs to be monitored frequently so that

if any damage detected, it could be ﬁxed as soon as

possible in order to avoid unsafe or unreliable service

because of its partial or full failure. Recently, automo-

tive suspension health monitoring has been drawing

more interest as a potential application of the current

promising machine learning techniques (Jayasundara

et al., 2020).

Historically, providers of on-board monitoring

systems, installed on railway vehicles, were conﬁned

to track defects and did not show any concern to the

suspension systems of the vehicle which could lead to

serious failures. On-board health monitoring systems

provide continuous monitoring with real-time detec-

tion of defects and early warning of any defect that

might happen on the future or even if there is a de-

fect now that will indeed help in saving money or

even in saving lives. Sensors, typically including ac-

celerometers, gyros, noise sensors (e.g. microphones)

and (GPS), used to be installed in a railway vehicle

to identify track irregularities, vehicle dynamic be-

haviour, vehicle precise location and velocity. Smart

algorithms like machine learning have been devel-

oped to analyse the data from sensor networks to offer

a precise real-time state estimation and for Fault De-

tection and Isolation (FDI) (Ngigi et al., 2012).

Health monitoring can be classiﬁed into three dif-

ferent categories; model based, signal based, and

knowledge based systems. In model based approach

,the system dynamic behaviour is modelled by mathe-

matical equations which relate the system response to

the input excitation. The main idea behind the model

based approach is to monitor the change in the system

dynamic behavior, using measured real-time system

response, which could be traced back to the degrada-

tion of system properties by the aid of the equations

of motion. (Peng et al., 2010).

Instead, signal based methods use only the mea-

sured output signals, which are further analyzed using

feature extraction methods. Signal-based feature ex-

traction methods are mainly classiﬁed into three dif-

ferent types which are time domain, frequency do-

main and time-frequency domain (Gao et al., 2015).

It does not matter which method is used, the idea is

that different faults in the system gives a totally dif-

ferent combination of values in the extracted features,

Abdelfattah, A. and Ibrahim, H.

Health Monitoring of Automotive Suspension System using Machine Learning.

DOI: 10.5220/0010402503250332

In Proceedings of the 7th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2021), pages 325-332

ISBN: 978-989-758-513-5

325

which enables the classiﬁer to distinguish between

faulty and non-faulty condition,and also between dif-

ferent types of faults(Dai and Gao, 2013). In signal

based methods the relationship between the features

and the system current state, is extracted from the data

set without any human interference. It requires the

identiﬁcation of signal patterns without having prede-

ﬁned examples(Karlsson, 2019).

On the other hand, the core idea of Knowledge

based methods is to create a connection from fea-

ture to system condition autonomously, Which means

that the classiﬁer will be trained by examining a huge

amount of examples and it learns the pattern neces-

sary for fault classiﬁcation on its own. Therefore, this

method requires much more training data compared

to those required in signal based and model based

techniques.Knowledge based method also have dif-

ferent types based on the fault detection and diagnosis

(FDD) method utilized in them.

Hybrid technique is mainly a combination of two

of the above techniques or even all of them which is

the most common Fault Detection Technique (Cecati,

2015)(Gao et al., 2015) and hereinafter, some of the

previous research work of this topic will be cited. In

the process of developing a data-driven health moni-

toring system, two major tasks have to be solved for

improving prediction accuracy and computation ef-

ﬁciency: proper feature extraction from large-scale

sensory data and an accurate data analysis model. The

goal of a good health monitoring of a suspension sys-

tem is high prediction accuracy and low computation

time.

Luo et al.(Luo et al., 2018) proposed a novel

method is proposed to develop a health monitoring

system by integrating a multi- Gaussian ﬁtting fea-

ture extraction method with a long short-term mem-

ory (LSTM) Convolutional Neural Network (CNN)

based damage identiﬁcation method. Firstly, a multi-

Gaussian ﬁtting method is devised to obtain compre-

hensive frequency-domain information of each sub-

sequence of the available vibration signals in order to

represent data of vibration signals and reduce the in-

put data size for data analysis purposes. Then this

data is feed to CNN model in order to obtain a non-

linear relation between the frequency domain features

and real time partial damage level.

In addition, Luo et al(Luo et al., 2019) intro-

duced another method of health monitor by using

Dual-Tree Complex Wavelet enhanced (DTCWT),

to obtain multi scale characteristics information of

measured signals. A deep convolutional neural net-

works (DCNN) model is then employed to automat-

ically extract useful damage features.The proposed

method proved efﬁcient in eliminating noise from the

measured vibration signals.Finally a Contextual long

short-term memory (CLSTM) is built to capture the

nonlinear relationship between the preprocessed vi-

bration signals and corresponding partial damage val-

ues. Chen et al.(Chen et al., 2019) introduced an-

other approach to achieve the same goal by using Ex-

treme Learning Machine (ELM) along side with con-

volutional neural networks. Time series vibration sig-

nals were measured using accelerometers, while good

representative features were obtained using Wavelet

Transform (WT) to convert the one-dimensional time

signals into two-dimensional time-frequency images.

In CNN-ELM, the training samples are ﬁrstly fed into

the CNN architecture to obtain the feature maps, then

all the features are combined together and regarded as

the input of the ELM model which can be efﬁciently

trained by a generalized inverse operation. At the test-

ing phase, the testing samples are fed into the trained

CNN-ELM model to obtain the ﬁnal diagnosis result.

Hong et al.(Hong et al., 2019) presented Multi-

Output Support vector regression (MSVR) method for

health monitoring of trains suspension system. The

main idea was to monitor the stiffness and damp-

ing coefﬁcients the suspension system using vibration

signals measured on trains in real time. First, a simple

suspension system dynamics model is built to gener-

ate a training data set. Furthermore, key features are

extracted from frequency response curves to reﬂect

the impact of spring and damper degradation. Sub-

sequently, a supervised learning model based on the

(MSVR) is built to predict the stiffness and damping

coefﬁcients of suspension systems from features ex-

tracted in the second module Once the model is built,

real time monitoring can be achieved.

KARLSSON (Karlsson, 2019) developed a

model, based on frequency response functions,to sim-

ulate the response of the four corner suspensions and

the goal was to detect which suspension is the faulty

one without quantifying the degradation value itself.

Hong et al. (Hong et al., 2019) provided different

approach based on the bode plot of the vertical ac-

celeration alongside with multi-output support vector

regression. The current paper presents an extension

to the above mentioned work, by introducing accel-

eration frequency response analysis along side with a

classiﬁcation technique, in order to identify and quan-

tify the degradation percentage of the faulty suspen-

sion. A Knowledge-based condition monitoring, of

automotive suspension dampers, is developed by im-

plementing a quarter car model (QCM). The sprung

mass acceleration - frequency power spectral density

curves, for different cases of performance degrada-

tion in suspension damping and different operational

conditions, is provided in response to the random

VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems

326

Figure 1: Machine Learning Classiﬁcation Algorithm.

Figure 2: Quarter Car Model.

road disturbance of different road classes. Training

and testing acceleration response data are generated

by Mtalb/simulink and fed to different classiﬁcation

algorithms that are trained and tested to distinguish

between the different damping degradation values.

Classiﬁcation is utilized, rather than regression, be-

cause classiﬁcation ﬁts more discrete problem while

regression deals with continuous data.

2 MATHEMATICAL MODEL

This section details the mathematical approach, im-

plemented using quarter-car model (QCM), in order

to have a health monitoring of vehicles suspension

systems. A dynamical model is presented ﬁrst which

will be simulated by Matlab/Simulink. Input and out-

put data to and from the simulink model will replace

the real time displacement and acceleration sensors

data which are supposed to be used in training and

testing the machine learning model.

2.1 Quarter Car Modeling

Dynamical model for a quarter-car model with two-

degrees of freedom, namely sprung mass and un-

sprung mass displacements, is implemented in order

to to simulate the car with different speeds, different

masses, different fault factors of the damper coefﬁ-

cient and different road proﬁles or tracks. Tables I

and II list the deﬁnition and numerical values of all

parameters involved in the following two equations

Table 1: List of parameters and their description of QCM.

Parameter Description

Sprung Mass(kg)

Unsprung Mass(kg)

Suspension Stiffness(N/m)

Tire Spring Stiffness(N/m)

Suspension Damper Coefﬁcient(Ns/m)

Tire Damper Coefﬁcient(Ns/m)

Sprung Mass Displacement(m)

Unsprung Mass Displacement(m)

Road Proﬁle(m)

Table 2: Suspension System Parameters values.

Parameter value

42.757 kg

5.6321 kg

10581.2922 N/m

96.0739 Ns/m

98041.2466 N/m

of motion.

¨z

= −k

− z

) − b

( ˙z

− ˙z

) (1)

¨z

= k

− z

) − k

− z

) − b

( ˙z

− ˙z

) (2)

2.2 Road Proﬁle

Road proﬁles differ from each other by the road

roughness which can be described by Power Spectral

Density (PSD) functions.The road roughness can be

seen as a stationary process in the space domain while

the car is moving. Therefore, the following differen-

tial equation 3, which models the road roughness and

velocity of the vehicle, could be very helpful in devel-

oping a training and testing data sets which represent

a wide range of road-vehicle dynamic interaction (He

et al., 2008; Zhang et al., 2007).

˙z

(t) + 2πn

(t) =

)vw(t) (3)

Equation 3 is a ﬁrst order differential equation,

where v is the velocity in (m/s), z

is the road pro-

ﬁle (m), n

is reference spatial frequency of value 0.1

(cycles/m), S

) is the coefﬁcient of road roughness

Table 3: Coefﬁcient of road roughness.

Road Class Roughness (10

−

/(cycle/m))

lower geometric mean upper

A(very good) - 16 32

B(good) 32 64 128

C(average) 128 256 512

D(poor) 512 1024 2048

E(very poor) 2048 4096 -

Health Monitoring of Automotive Suspension System using Machine Learning

327

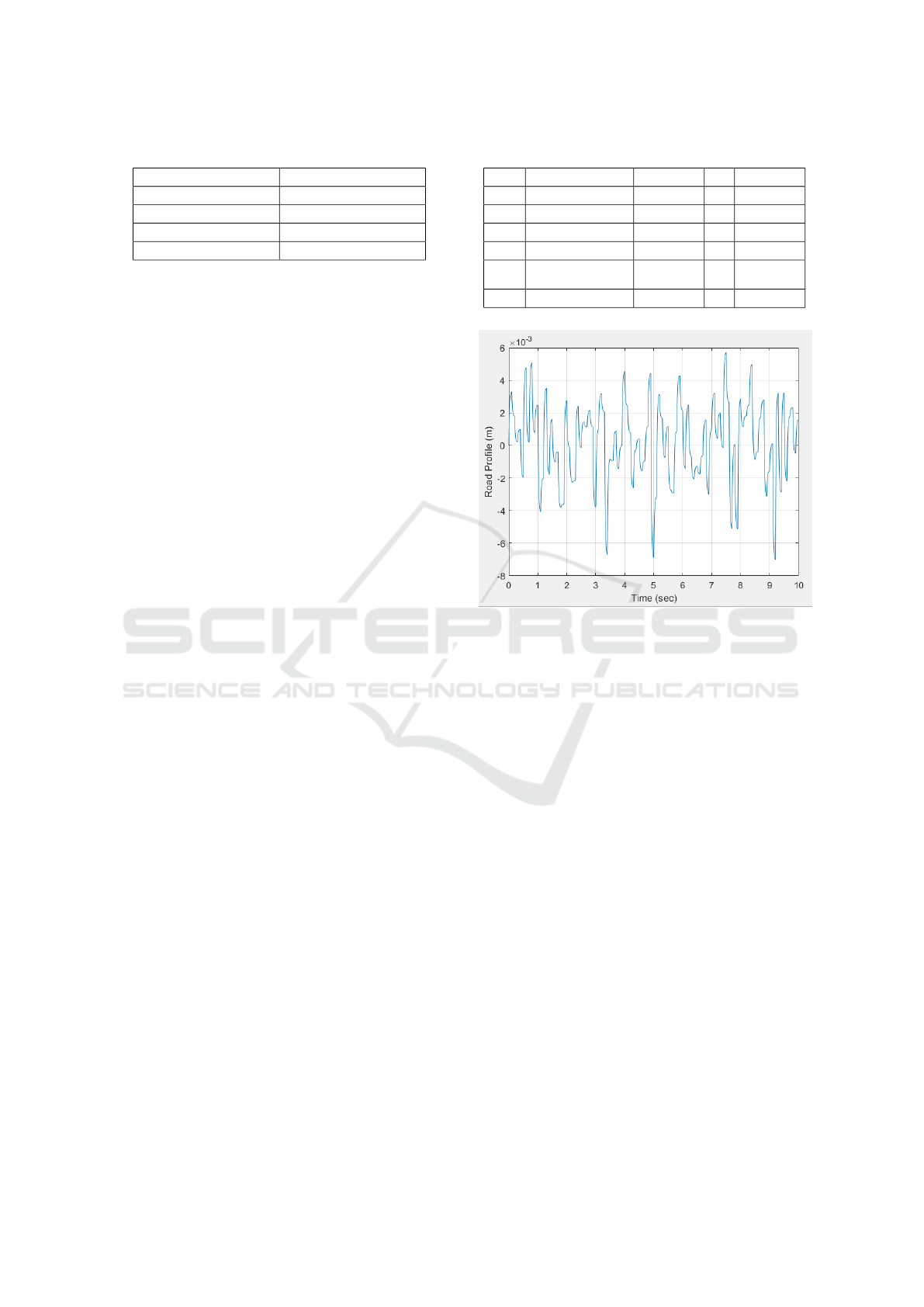
Table 4: Training Simulation variances for the QCM.

Feature Variance

velocity(kmph) 10 30 40 60 100 120

body mass factor 1 1.03 1.04 1.05

damping fault factor 1.0 0.75 0.5 0.25 0.1

road roughness class A B C D E

/(cycle/m) , w(t) is a white noise signal having a

PSD equal to 1. For simplicity S

) is named N and

2πn

is named n.

According to ISO 8608(ISO/TC et al., 1995),

roads are classiﬁed according to their roughness into

5 categories A, B, C, D and E as shown in table 3.

A and B considered to be the highest quality repre-

senting motorways and expressways with more than

60 km/h velocity range, while class C is the average

road type with an average velocity between 30 and 60

km/h. Class D and E therefore are categorized to be

the worst with less than 30 km/h.

2.3 Machine Learning

Classiﬁcation algorithms in machine learning are

trained and tested with different datasets. One im-

portant characteristic that an algorithm should pos-

sess is the ability to generalize, i.e. to be able to

perform well on testing datasets that differ from the

training dataset. For this reason different datasets

with different operational conditions should be incor-

porated in both the training and testing phase to evalu-

ate how well the algorithm can handle varying opera-

tional conditions that it will most certainly be exposed

to in a real-world application of vehicle’s suspension

system health monitoring.

It was decided to simulate the QCM on all ﬁve

different road proﬁle classes by changing their road

roughness coefﬁcient. These changes in the road pro-

ﬁles are accompanied by changes in car body masses

and speed and damping coefﬁcient. Damping coefﬁ-

cients varies with 4 fault factors 0.75 0.5 0.25 0.1 as

well as the reference case (fault factor 1.0). Six differ-

ent speed proﬁles are also simulated 10 20 30 40 60

100 120 kmph as well as 4 different car body masses

with factors of 1 1.03 1.04 1.05 to represent changes

in the number of passengers as table 4.

2.4 Methodology

As explained when making a machine learning algo-

rithm data sets must be provided so that training and

testing is applicable. The common structure of this

data set and will be used in this work is through a de-

sign matrix.

Table 5: Design matrix.

ID Damping fault Feature 1 ... Feature n

1 1.0 xx ... xx

2 0.75 xx ... xx

3 0.5 xx ... xx

4 0.25 xx ... xx

. xx xx ... xx

600 xx xx ... xx

Figure 3: Road surface (class C, velocity 80 kmph).

Each row contains a data point, in table 5 is an ex-

ample of the used design matrix. Each row contains

an ID that identiﬁes that speciﬁc data point, as shown

in the ﬁrst column. The second column contains the

damping value that will be the target in the classiﬁ-

cation algorithm. The rest of the columns contains

the features which will help the algorithm identify to

classify the target. There are total four features like

velocity of the vehicle, the peak of the PSD curve, the

sprung mass of the vehicle and ﬁnally the roughness

of the road the vehicle traveling on.

3 RESULTS AND DISCUSSION

The road proﬁle for a vehicle traveling 80 kmph on a

road class C with a coefﬁcient of road roughness 512

x 10

−6

/(cycle/m) is shown in ﬁg3.

The reason of using PSD in health monitoring is

that it proved a relation between the peak of this PSD

and the damping coefﬁcient. They are inversely pro-

portional so as the damping coefﬁcient increases the

peak of the vertical acceleration PSD extracted from

the accelrometer decreases. This is proved by three

simulations their results shown in ﬁg 4 where all of

the other parameters of the QCM is constant and the

VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems

328

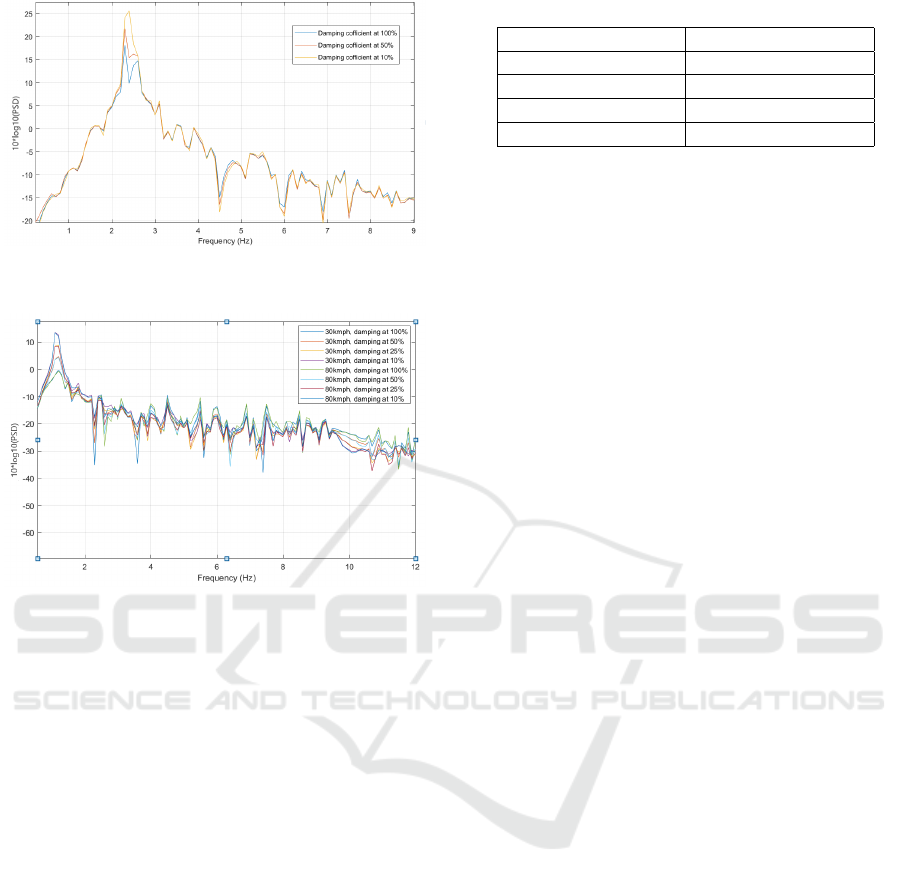
Figure 4: Power spectral densities for sprung mass acceler-

ation of different damping coefﬁcients.

Figure 5: Power spectral densities for sprung mass acceler-

ation of different damping coefﬁcients with different veloc-

ities.

only change is in the damping coefﬁcient in order to

get reliable results to prove this relation.

In Figure 5 the track class (road proﬁle) is kept

constant but the velocity is varied between 30 kmph

and 80 kmph. The variation of velocity with damping

coefﬁcient shown in ﬁgure 5 shows how the velocity

affects the peak of the PSD.

The results will be in terms of the two per-

formance measures for different classiﬁcation

algorithms are presented along with dimensional re-

duction of feature extraction (transformation) which

is called PCA. The ﬁrst performance measure that

will be displayed in this section will be the accuracy

of the classiﬁcation algorithm and also with 5-fold

cross validation. Validation is made to protect the

classiﬁcation algorithms from overﬁttng. The second

performance measure will be the confusion matrix

of each classiﬁcation algorithm also and it will be

explained later in this chapter.

There are total 24 classiﬁcation algorithm trained

with and without PCA made on a dataset containing

6 different velocities, 4 different mass factors, 5

different damping fault factors and 5 different road

roughness classes as in table 4. This result of 600

simulation to create this training dataset and there

Table 6: Testing Simulation variances for QCM.

Feature Variance

velocity(kmph) 20 50 70 80 90 110

body mass factor 1 1.01 1.02 1.06

damping fault factor 1.0 0.75 0.5 0.25 0.1

road roughness class A B C D E

will be another 600 simulations to create another

datasets for more testing as in table 6. This section

will show results for the performance measures on

both the training dataset and according to this result,

the testing data sets will be tested on the algorithms

showed the best performance measures in the training

datasets.

3.1 Results of Training Datasets

The ﬁrst performance measure is the correct clas-

siﬁcation rate (accuracy), deﬁned as the number of

correct classiﬁcations divided by the total number of

classiﬁcations, which is the same as adding the true

positives and true negatives and dividing by the total

number of predictions:

Table 7 shows the output accuracy of each of 24

classiﬁcation algorithm with PCA on and off with 5-

fold cross validation used and it showed a signiﬁcant

drawback of using PCA with our dataset and classiﬁ-

cation algorithms. Both cubic support vector machine

and quadratic support vector machine showed the best

results of the ﬁrst performance measure without PCA.

Also table 8 shows the output accuracy of each of 24

classiﬁcation algorithm with PCA on and off with 10-

fold cross validation and it resulted nearly the same

result when using 5-fold cross validation.

In many applications it is of the best to investigate

what the actual classiﬁcations are. This is often done

by using the confusion matrix. the rows show the true

class, and the columns show the predicted class as in

ﬁg 6. When using holdout, then the confusion ma-

trix is calculated using the predictions on the held-

out observations. The diagonal cells show where the

true class and predicted class match. If these cells are

green, the classiﬁer has performed well and classiﬁed

observations of this true class correctly.

The reason for choosing the confusion matrix as a

performance measure is that it shows the true positive

rates and false negative rates which are extremely im-

portant measure to specify the actual performance of

the classiﬁcation algorithms. The lowest row shows

true class of no fault factor(100% damping coefﬁ-

cient) and the columns shows the predicted classes.In

ﬁg 6 in the lowest row 99% of the simulations with

no fault factors were correctly classiﬁed(predicted)

Health Monitoring of Automotive Suspension System using Machine Learning

329

Table 7: Classiﬁcation algorithms accuracy with 5-fold

cross validation.

Algorithm

Accuracy(%) PCA

OFF ON

Fine Tree 84.7 35.8

Medium Tree 74.5 29.8

Coarse Tree 48.7 21.8

Linear Discriminant 74.0 15.8

Quadratic Discriminant 75.3 14.3

Gaussian Naive Bayes 39.7 14.3

Kernel Naive Bayes 50.8 16.3

Linear SVM 75.0 19.7

Quadratic SVM 96.8 21.2

Cubic SVM 95.5 21.2

Fine Gaussian SVM 72.7 10.5

Medium Gaussian SVM 79.7 14.5

Coarse Gaussian SVM 67.5 15.0

Fine k-nearest neighbors 57.8 33.8

Medium k-nearest neighbors 57.2 47.3

Coarse k-nearest neighbors 44.5 17.0

cosine k-nearest neighbors 53.5 18.5

cubic k-nearest neighbors 57.5 47.3

Weighted k-nearest neighbors 59.0 35.3

Ensemble Boosted Trees 84.0 32.2

Ensemble Bagged Trees 76.5 34.3

Ensemble Subspace D 59.7 15.8

Ensemble Subspace K-N 24.8 33.8

Ensemble RUSBoosted Trees 74.5 28.5

Figure 6: Cubic support vector machine with 5-fold cross

validation confusion matrix.

to have 100% damping coefﬁcient while only 1% of

the simulations were miss-classiﬁed as having 75%

damping coefﬁcient, so 99% is the true positive rate

for correctly classiﬁed points in this class, shown in

the green cell in the True Positive Rate column (right

side). 1% is the false negative rate for incorrectly clas-

siﬁed points in this class, shown in the red cell in the

False Negative Rate column(right side). Figures 7, 8

and 9 shows the confusion matrices of the best algo-

rithms in terms of accuracy.

Table 8: Classiﬁcation algorithms accuracy with 10-fold

cross validation.

Algorithm

Accuracy(%) PCA

OFF ON

Fine Tree 86 38.8

Medium Tree 74.7 27.3

Coarse Tree 49.0 22.8

Linear Discriminant 73.5 15.5

Quadratic Discriminant 74.5 12.0

Gaussian Naive Bayes 39.5 12.0

Kernel Naive Bayes 50.3 15.5

Linear SVM 75.8 18.0

Quadratic SVM 96.3 19.8

Cubic SVM 96.3 22.2

Fine Gaussian SVM 75.7 7.7

Medium Gaussian SVM 83.3 11.7

Coarse Gaussian SVM 67.0 14.2

Fine k-nearest neighbors 58.5 35.3

Medium k-nearest neighbors 61.7 47.7

Coarse k-nearest neighbors 46.7 18.3

cosine k-nearest neighbors 56.2 19.7

cubic k-nearest neighbors 60.3 47.7

Weighted k-nearest neighbors 60.7 36.3

Ensemble Boosted Trees 83.2 29.7

Ensemble Bagged Trees 89.0 35.5

Ensemble Subspace D 59.3 15.5

Ensemble Subspace K-N 26.3 35.3

Ensemble RUSBoosted Trees 74.8 27.3

Figure 7: Quadratic support vector machine with 5-fold

cross validation confusion matrix.

3.2 Results of Testing Datasets of QCM

Figures 10 and 11 shows how our classiﬁcation al-

gorithm (Support vector machine with quadratic ker-

nel function representing it) responded to the testing

datasets which contains 600 different simulations than

the training dataset. It showed extremely promising

results in the previous section in accuracy and con-

fusion matrix that’s why it was chosen to be further

VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems

330

Figure 8: Quadratic support vector machine with 10-fold

cross validation confusion matrix.

Figure 9: Cubic support vector machine with 10-fold cross

validation confusion matrix.

tested and it showed 94% accuracy for the 5-fold val-

idation and 10-fold validation .

4 CONCLUSIONS

The objective of this paper is to propose a health mon-

itoring technique that can work on real time condi-

tions in the future in order to avoid or decrease the hu-

man casualties and the economic loss made because

of suspension systems failure. The vehicle safety and

reliability have become such important ﬁeld as the

number of road vehicles has increased signiﬁcantly

and still increasing. Health monitoring especially

fault detection is now a well known ﬁeld and with the

help of Artiﬁcial Intelligence and various simulations

like for example car models in Matlab.

The general idea of the approach in this work is

to predict the value or the degradation happened in

the suspension system in the damping part (damping

coefﬁcient) using several features like velocity of the

car, the road proﬁle the car traveling on it and the mass

of the sprung mass (mass above the suspension part

excluding the tires) using these features and arrang-

Figure 10: Quadratic support vector machine with 5-fold

cross validation confusion matrix of testing dataset.

Figure 11: Quadratic support vector machine with 10-fold

cross validation confusion matrix of testing datasets.

ing them in the design matrix to introduce them to the

classiﬁcation algorithms for further predictions. All

of this is based on the relation of the peak of the PSD

of the vertical acceleration of the sprung mass and the

damping coefﬁcient. The results of Quadratic Support

vector Machine in QCM is very promising whether in

the training or testing data. Using PCA in both train-

ing and testing data resulted a signiﬁcant decrease in

the performance of the models in terms of both accu-

racy and confusion matrix.

REFERENCES

Cecati, C. (2015). A survey of fault diagnosis and fault-

tolerant techniques—part ii: Fault diagnosis with

knowledge-based and hybrid/active approaches. IEEE

Transactions on Industrial Electronics.

Chen, Z., Gryllias, K., and Li, W. (2019). Mechanical fault

diagnosis using convolutional neural networks and ex-

treme learning machine. Mechanical Systems and Sig-

nal Processing, 133:106272.

Dai, X. and Gao, Z. (2013). From model, signal to knowl-

edge: A data-driven perspective of fault detection and

Health Monitoring of Automotive Suspension System using Machine Learning

331

diagnosis. IEEE Transactions on Industrial Informat-

ics, 9(4):2226–2238.

Gao, Z., Cecati, C., and Ding, S. X. (2015). A survey

of fault diagnosis and fault-tolerant techniques—part

i: Fault diagnosis with model-based and signal-based

approaches. IEEE Transactions on Industrial Elec-

tronics, 62(6):3757–3767.

He, L., Qin, G., Zhang, Y., and Chen, L. (2008). Non-

stationary random vibration analysis of vehicle with

fractional damping. In 2008 international conference

on intelligent computation technology and automation

(ICICTA), volume 2, pages 150–157. IEEE.

Hong, N., Li, L., Yao, W., Zhao, Y., Yi, C., Lin, J., and

Tsui, K. L. (2019). High-speed rail suspension sys-

tem health monitoring using multi-location vibration

data. IEEE Transactions on Intelligent Transportation

Systems.

ISO/TC, T. C., Vibration, M., Measurement, S. S. S., of Me-

chanical Vibration, E., and as Applied to Machines, S.

(1995). Mechanical Vibration–Road Surface Proﬁles–

Reporting of Measured Data. International Organiza-

tion for Standardization.

Jayasundara, N., Thambiratnam, D., Chan, T., and Nguyen,

A. (2020). Damage detection and quantiﬁcation in

deck type arch bridges using vibration based meth-

ods and artiﬁcial neural networks. Engineering Fail-

ure Analysis, 109:104265.

Karlsson, H. (2019). Monitoring vehicle suspension ele-

ments using machine learning techniques.

Luo, H., Huang, M., and Zhou, Z. (2018). Integration

of multi-gaussian ﬁtting and lstm neural networks for

health monitoring of an automotive suspension com-

ponent. Journal of Sound and Vibration, 428:87–103.

Luo, H., Huang, M., and Zhou, Z. (2019). A dual-tree com-

plex wavelet enhanced convolutional lstm neural net-

work for structural health monitoring of automotive

suspension. Measurement, 137:14–27.

Ngigi, R., Pislaru, C., Ball, A., and Gu, F. (2012). Modern

techniques for condition monitoring of railway vehi-

cle dynamics. In Journal of Physics: Conference Se-

ries, volume 364, page 012016. IOP Publishing.

Peng, Y., Dong, M., and Zuo, M. J. (2010). Current status of

machine prognostics in condition-based maintenance:

a review. The International Journal of Advanced Man-

ufacturing Technology, 50(1-4):297–313.

Zhang, Y., Chen, W., Chen, L., and Shangguan, W. (2007).

Non-stationary random vibration analysis of vehicle

with fractional damping. In 13th national conference

on mechanisms and machines.

VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems

332