A Neural Network Modelling and Prediction of Students’ Progression in

Learning: A Hybrid Pedagogic Method

Ethan Lau, Kok Keong Chai, Gokop Longinus Goteng and Vindya Wijeratne

School of Electronic Engineering and Computer Science, Queen Mary University of London,

10 Godward Square, Mile End Rd., Mile End, London E1 4FZ, U.K.

Keywords:

Pedagogic Approach, Blended Learning, Statistical Evaluations, Neural Network.

Abstract:

The COVID-19 pandemic has changed dramatically the way how universities ensure the continuous and sus-

tainable way of educating students. This paper presents the neural network (NN) modelling and predicting

students’ progression in learning through a hybrid pedagogic method. The hybrid pedagogic approach is

based on the revised Bloom’s taxonomy in combination with the ﬂipped classroom, asynchronous and cog-

nitive learning approach. To evaluate the effectiveness of the hybrid pedagogic approach and the students’

progression in learning, educational data is collected that comprises of labs and class test scores, as well as

students’ total engagement and attendance metrics for the programming module considered. Conventional

statistical evaluations are performed to evaluate students’ progression in learning. The NN is further modelled

with six input variables, two layers of hidden neurons, and one output layer. Levenberg-Marquardt algorithm

is employed as the back propagation training rule. The performance of neural network model is evaluated

through the error performance, regression and error histogram. The NN model has achieved a good prediction

accuracy along with limitations. Overall, the NN model presents how the hybrid pedagogic method in this

case has successfully quantiﬁed students’ progression in learning throughout the COVID-19 period.

1 INTRODUCTION

Over the past months, the daily-routine life for na-

tionals have been hugely affected by the coronavirus

COVID-19 crisis. Therefore, the worldwide edu-

cational sectors should focus on the long-term con-

tinuity of education deliveries to guarantee a re-

silient education for equitable and sustainable devel-

opment (United Nations, 2020). Consequently, many

universities around the world are shifted to virtual on-

line teaching, learning and assessments. However,

this requires collective efforts by leveraging the ped-

agogic approach to enhance the online learning plat-

forms while ensuring the vision and strategy of the

universities. Many pedagogic methods have been put

forward but the methodology to assess and predict

students’ progression of learning is extremely limited

at the present pandemic situations. The conventional

questionnaire and feedback surveys from students are

not sufﬁciently enough to evaluate and quantify stu-

dents’ overall learning progression and engagement.

For this reason, this paper presents the neural net-

work (NN) modelling and predicting students’ pro-

gression in learning through the hybrid pedagogic

method. We present how the computer software pro-

gramming module considered in this study have suc-

cessfully implemented the hybrid pedagogic method.

The hybrid pedagogic approach is based on the re-

vised Bloom’s taxonomy in combination with the

ﬂipped classroom, asynchronous and cognitive learn-

ing, while maximising students’ learning experiences.

By effectively evaluating students’ engagement in the

online learning platform this will greatly help to as-

sess the effectiveness of the hybrid pedagogy ap-

proach. This is done by evaluating students learn-

ing behaviour through their level of engagements in

the module. The data information about students’ en-

gagement metrics are obtained through the the lecture

recording software. Apart from that, the assessments

such as the lab and the class test results are adopted

for statistical evaluations and the latter NN develop-

ment. This further presents an exploratory NN mod-

elling and analyses students’ progressing in learning

and serves as a dominant educational quality tool to

mitigate those disparities that hamper the education

quality.

The organisation of the paper is as follows: Sec-

tion 2 presents the reviews of pedagogic methods, the

Lau, E., Chai, K., Goteng, G. and Wijeratne, V.

A Neural Network Modelling and Prediction of Students’ Progression in Learning: A Hybrid Pedagogic Method.

DOI: 10.5220/0010405600840091

In Proceedings of the 13th International Conference on Computer Supported Education (CSEDU 2021) - Volume 1, pages 84-91

ISBN: 978-989-758-502-9

NN and the summary, Section 3 presents the method-

ology of map the hybrid pedagogic approach into NN

modelling, Section 4 presents statistical evaluations,

NN conﬁguration settings and the performance, Sec-

tion 5 concludes the ﬁndings.

2 OVERVIEW OF THE

PEDAGOGIC METHODS

The traditional pedagogic format includes the be-

haviourism, constructivism, social constructivism and

liberationism. Bloom’s taxonomy is one of the

most well-known hierarchical-based pedagogical tool

to complement the strategies of educational objec-

tives (Granello, 2001). Each of the hierarchy con-

tains a domain of intellectual behaviour that stratiﬁes

teaching, learning and assessment activities. It has

been well used in software engineering and computer

science-speciﬁc learning domains (Fuller et al., 2007;

Britto and Usman, 2015; Peter et al., 2016) and also

has helped in improving the assessment methods in

the domain of science, technology, engineering and

mathematics (STEM).

Ever since the pandemic began, the pedagogy in

the educational ﬁeld is changing rapidly, where face-

to-face delivery is no longer the best option to interact

with students. Therefore, there is a need to create a

balance of joint teaching elements in in-class and on-

line while meeting students’ learning outcomes. To-

gether with the evolvement of digital academics, uni-

versities are looking for the approach to ensure the

continuous engagement and active learning among

students. Several recent papers paid a huge empha-

sis on Bloom’s revised taxonomy to ensure adaptive

online-based learning module in responding to the

pandemic (Qadir and al-Furqaha, 2020; Sheth et al.,

2020). Therefore, to accommodate the needs of stu-

dents’ learning needs during and beyond COVID-19,

the revised Bloom’s taxonomy is proposed in this pa-

per that brings together the hybrid learning-based ap-

proach – ﬂipped classroom, asynchronous and cogni-

tive learning.

The revised Bloom’s taxonomy is presented in

Figure 1 where the hybrid pedagogical approach is

implemented. This serves as a strategy to avoid just

having to deliver modules but being able to prepare

students to have conceptual understanding to solve

problems and represent situations (Joffrion, 2005).

The ﬂipped classroom is a type of blended learning

where students at ﬁrst are being introduced the con-

tent at off-campus (pre-classroom activities) and work

together with lecturers to solve the content during the

live lectures (virtual classroom activities). Existing

beneﬁts of using ﬂipped classroom have already been

established, where one of the example of case study

students with ﬂipped classroom (N=24) outperformed

in exams compared with the traditional (N=19) (Pe-

terson, 2016).

Remembering

Understanding

Applying

Analysing

Evaluating

Creating

Flipped classroom

Cognitive &

Asynchronous

learning

Pre-classroom

activities

Virtual classroom

activities

Figure 1: The revised Bloom’s taxonomy.

In addition, the hybrid approach is part of the strat-

egy to activate students’ cognitive-based prior knowl-

edge. Activating prior cognitive knowledge brought

more beneﬁcial effect on knowledge and compre-

hension understanding to enable students to learn

actively (Kostons and Werf, 2015), and thus facil-

itates the conceptual understanding of science and

engineering principles and increases students’ self-

regulated responsibility in participating the lecture.

Furthermore, the ﬂipped classroom implemented with

cognitive-based learning could lead to increased aca-

demic performance (Foldnes, 2016).

Asynchronous learning is an another prevalent

pedagogical strategy where it is used in “Anytime,

Anywhere” basis that includes instructor-led online

face-to-face meetings and chats, recorded lectures,

and tutorials (Wu et al., 2008). Asynchronous learn-

ing method has been well received, where it cre-

ates a great potential for enhancing cognitive learn-

ing progress and the resultant academic performance

among students (Michalsky and Zion, 2007).

In summary, the hybrid pedagogical approach is

applied to improve the existing Bloom’s taxonomy in

responding to students’ learning needs. This is to en-

sure students students have more spaces for them to

elicit the conceptual information when watching the

recorded videos, and to further allow more space for

students’ talk time and understanding on the topic in

the virtual face-to-face meetings. Such mechanism

ensures more learning spaces for students and not

solely depending on the traditional lecturer-centred

rule.

2.1 Neural Network

With the expansion of the education system together

with the restriction in COVID-19, various pedagogy

methods are not being evaluated analytically that can

A Neural Network Modelling and Prediction of Students’ Progression in Learning: A Hybrid Pedagogic Method

actually be combined with machine learning tech-

niques for educational research purposes. Machine

learning techniques leverage the pedagogical methods

that detect at-risks students earlier and to further miti-

gate negative consequences from occurring (Macarini

et al., 2019). Additionally, machine learning tech-

niques improve the accuracy of prediction by collec-

tively classifying the low-engagement students, in-

tervening their learning behaviour and improve their

learning engagements (Hussain et al., 2018).

Therefore, this paper implements a neural net-

work (NN) model that is capable of machine learn-

ing by collecting students’ information and further

predicting students’ progression in learning based on

their learning engagements. NN is formed through a

collection of artiﬁcial neurons that resemble the con-

nection geometry of neurons in human brains in order

to execute a task with improved performance through

learning, training and continuous improvement (Van-

damme et al., 2007; Kardan et al., 2013). The most

common learning rule of NN is back-propagation

(BP), which is a supervised learning approach and can

be used for training the deep neural networks. BP ad-

justs the weights of neurons through the calculated er-

rors and enables the network to learn from the training

process.

Remarkably, NN approach has been receiving

wide attention for educational research purposes in

modelling modelling complex nonlinear functions. It

has been used to not only to accurately predict ﬁ-

nal grades of students, but also to improve the better

understanding of the educational process and evalu-

ation (Kardan et al., 2013; Isljamovic and Suknovic,

2014; Okubo et al., 2017).

Overall, NN has the ability in performing the neu-

ral ﬁtting and prediction, and the ability to classify

any data with arbitrary accuracy theoretically. This is

important to examine the signiﬁcant factors that af-

fect the performance among students. The NN model

would serve as a framework and tool to predict the

future students’ academic performance, and to further

address those issues that hinder the success of student

learning and thus continually improving the pedagog-

ical approaches.

3 METHODOLOGY

This section presents the methodology of implement-

ing the hybrid pedagogic approach in the revised

Bloom’s taxonomy, acquiring educational data, statis-

tical testing for NN modelling, and the methodology

of evaluating the performance of modelled NN.

3.1 Overview of Module

The computer software programming module is con-

sidered in this study. The module aims to intro-

duce different software service platforms and how it

is used to enable heterogeneous systems to work to-

gether within a distributed cloud system. At the end

of this module, students will have acquired the knowl-

edge of the different types of software service plat-

forms available, design and implement client-server

or web-based applications. A total of 181 Year 3

undergraduate students are currently enrolled to the

module. Apart from the delivery of live and recorded

lectures (which will be explained in the next section)

as well as the tutorials, the module’s lab assessment is

based on four sessions of lab exercises (progressive-

based) covered by four lab sessions in 4

, 6

, 8

and 9

of the teaching weeks. Lab task difﬁculties

are increased when students progress themselves un-

til the ﬁnal session of the labs. Students need to sub-

mit all the lab tasks through the online Moodle learn-

ing portal accordingly. After the completion of lab

exercises, students are then needed to take the class

test (Week 12

) that aims to evaluate students’ per-

formance throughout the module learning. All lab as-

sessments and class tests are performed online while

ensuring the important aspect of the UK Quality Code

for Higher Education in achieving the intended learn-

ing outcomes.

3.2 The Hybrid Pedagogic Approach

The revised Bloom’s taxonomy is proposed in this pa-

per which consists the hybrid pedagogical approach –

ﬂipped classroom, asynchronous and cognitive learn-

ing. An example of asynchronous learning based

on anytime, anywhere basis is presented in Table 1,

where students are updated about the asynchronous

lecture time and information on the Moodle. This is to

avoid one way limited communication ﬂow from the

existing Bloom’s taxonomy. It is important to note

that the hybrid strategy proposed in this paper does

not improve the Bloom’s taxonomy but takes students

to a higher cognitive level.

Microsoft Teams is the core lecturing and commu-

nication platform for both lectures and tutorials, apart

from the Moodle portal to enable students to access

the additional resources related. The module team

channel is created in Microsoft Teams to allow stu-

dents studying the computer software programming

module to post any questions related to their learn-

ings.

Flipped classroom, on the other hand, is imple-

mented as part of the blending learning approach that

CSEDU 2021 - 13th International Conference on Computer Supported Education

Table 1: Asynchronous learning timetable.

Session Week 1 Week 2 Week 4 Week 5

Thursday, 08:35 - 09:20 am Live Recorded Live Recorded

Thursday, 09:25 - 10:10 am Live Live Live Recorded

comes with pre-recorded video sessions. The tech-

nique allows pre-classroom activities where students

need to watch the pre-recorded video either on/off

campus, and then continuing the learning by attend-

ing the live lectures to solve the problems. This is

done via virtual face-to-face classroom activities.

To improve students’ learning and comprehen-

sion especially in dealing with the pandemic, all the

tutorials, online quizzes and lab tasks are carefully

constructed based on students’ previous knowledge

in fundamental programming concepts (e.g. Intro-

ductory Java Programming). Such serves as a pre-

requisite for students to undertake the computer soft-

ware programming module. Together with recorded-

video watching, this serves as a pre-cognitive domain

to activate students’ prior knowledge, and to further

apply the cognitive knowledge that facilitates the con-

ceptual understanding of the module during the live

lecture session. This intents to increase students’ self-

regulated responsibility in participating the lecture,

and thereby improving the interactions, engagements

and their resultant learning behaviour in the module.

3.3 Data Collection

No questionnaire or feedback surveys are conducted

in this case. Instead, the evaluations are performed

using the data analytics and are collected from the

lecture recording software, lab assessments ,and the

class test. Additionally, the assessments are per-

formed solely to the Year 3 cohort undertaking the

computer software programming module. In terms of

students’ behaviour and progression in learning, the

dataset information is available and extracted using

the Echo360 lecture recoding software. The Echo360

software provides the course analytics metrics (e.g.

engagement, slide views, video views, polling re-

sponses, attendances) that rolls up the data informa-

tion (Echo360, 2020) for each student enrolled in the

course. In this paper the metrics Total engagement

and Attendance are extracted as the metrics are the

important factors that inﬂuence students’ learning and

progression behaviour, and the resultant performance.

The Total Engagement in this case is the cumulative

total of data points such as Video Views, Q&A En-

tries, Polling Responses (polling questions that were

answered correctly), and Note Events (total number

of distinctive notes student have taken). Attendance

is where students entered the online classroom during

the class time.

3.4 Statistical Testing

Prior to the NN modelling, it is necessary to exam-

ine the relationship between the students’ progres-

sion and learning behaviour that further indicate the

level of engagement in the module, lab assessments

and their class test scores. Statistical testing is per-

formed initially in this study using multiple regres-

sion analysis. Multiple regression analysis is used to

evaluate whether a dependent variable could be pre-

dicted based on independent variables. The signiﬁ-

cant difference is set at α = 0.05. Pearson correla-

tion coefﬁcients are calculated to measure the linear

relationships of four lab assessment scores, the stu-

dents’ engagement metrics (Total engagement and At-

tendance), and the resultant class test score. Those

correlated variables are used further as input neurons

for the NN modelling.

3.5 Neural Network Modelling

The NN in this case is used for neural prediction

of students’ progression in learning and engagement

through input observations of lab assessments, the

metrics of students’ engagement and the class test

scores. Such scheme is performed based on the su-

pervised machine learning. The NN in this paper is

modelled following the earlier research works (Zhang

et al., 2003; Vandamme et al., 2007; Rashid and Ah-

mad, 2016; Lau et al., 2019). This paper does not

to compare the effectiveness of NN performance with

other machine learning techniques.

By conventional deﬁnition, the NN mathematical

model function can simply be formulated as:

Y = f (

W), (1)

where

Y and

X are the output and input vectors.

is a vector of weight parameters representing the con-

nections within the NN.

The input layer gathers data with feature sets and

the input values are fed to the hidden layer. The output

values of jth neuron y

of vector

Y are computed by

means of the weighted sum of input elements x and w,

where w is updated recursively.

= θ

∑

i=1

i j

. (2)

The θ is the activation function (transfer function),

is the total number of ith connection lines to the jth

neuron and x

is the output value from the previous

layer of ith neuron. The hyperbolic tangent function

is used as the activation function (θ) to transfer the

value of weighted sum of inputs to the output layer.

A Neural Network Modelling and Prediction of Students’ Progression in Learning: A Hybrid Pedagogic Method

The resultant activated node for the next input layer is

therefore:

= θ(y

). (3)

For training, the BP-based supervised learning ap-

proach is applied where both inputs and outputs pa-

rameters are supplied to the NN model. BP is used

as the learning rule for the NN model that adjusts the

weights of neurons w

i j

through the errors computed

recursively that further produces desired outputs. The

error function (E) is calculated as the sum of square

difference difference between the target values and

the desired outputs:

E =

∑

−t

)

, (4)

where t

is the target value for neuron i in the output

layer and N

is the total number of output neurons.

The BP-based Levenberg-Marquardt optimisation

algorithm is applied in the NN training. It speeds up

the convergence to an optimal solution by effectively

solving the training algorithms for non-linear prob-

lems (Yu and Wilamowski, 2011; Wilson and Man-

tooth, 2013). The Levenberg-Marquardt is a hybrid-

based training method using the steepest descent (gra-

dient descent) and Gauss-Newton method. The al-

gorithm introduces another approach of approxima-

tion to Hessian Matrix, which is similar to the Gauss-

Netwon method (Yu and Wilamowski, 2011; Math-

Works, 2019):

i j+1

= w

i j

− [J

J + ζI]

−

, (5)

where J denotes the Jacobian matrix, ω

is the error

in the network (MathWorks, 2019), w

i j

is the current

weight and w

i j

is the updated weight, ζ is the damping

factor.

When ζ is small, the Levenberg-Marquardt train-

ing algorithm in Eq. 5 applies the Gauss-Newton

method, and in contrast, becomes gradient descent al-

gorithm when ζ is large. Therefore, ζ is adjusted at

every iteration in order to guide the optimisation pro-

cess and switched between those two algorithms as

the training model.

The number of neuron in the output layer is the

resultant decision prediction of the problem (

Ozc¸elik

and Hardalac¸, 2011). The output layer consists collec-

tions of vector

Y, which is the collection of predicted

class test.

3.6 NN Performance Evaluation

Criteria

In order to evaluate the NN performance, this paper

computes the Mean Square Error (MSE), regression

analysis, and error histogram that mitigates the aris-

ing of over-ﬁtting issues to ensure the appropriateness

of NN performance. A well-trained NN model should

have low MSE value, which means that the predicted

outputs converge closely to the target outputs (t

i j

)

(provided that no over-ﬁtting issues occurred). MSE

is calculated as:

MSE =

∑

j=1

∑

i=1

i j

−t

i j

)

. (6)

As mentioned, over-ﬁtting of the trained network

is possible if obtained MSE value is low. This fur-

ther indicates that NN only works well in the train-

ing stage, but not in validation and testing phase. To

mitigate this a regression is performed along with

computed R-value which demonstrates the goodness

of ﬁtting between the predicted and the desired out-

puts. The plot is useful in examining the ﬁtting perfor-

mance. If poor ﬁtting (low R-value) is obtained, fur-

ther trainings are required with modiﬁcation of hidden

layers and neurons.

Another way of measuring NN performance is to

tabulate the error histogram. The error histogram

demonstrates how the errors are distributed with most

errors are occurred near zero. The error is simply

the difference between the targeted outputs t

i j

and the

predicted outputs y

i j

4 RESULTS

This section presents the ﬁndings, the conﬁguration of

NN, the prediction and the veriﬁcation of NN perfor-

mance for 181 Year-3 undergraduate students. This is

based on the obtained datasets of lab assessments and

class test scores, as well as the information about stu-

dents’ engagement and the attendance metric from the

Echo360 software. In summary the average class test

score is 78.19±10.10 compared with 81.02±11.18

for the previous academic year, which stays fairly

consistent when the teaching model was very differ-

ent.

4.1 Statistical Evaluations

Multiple regression analysis is used to give a bet-

ter indication whether the Class Test (the dependent

variable) could be predicted based on the indepen-

dent variables – Lab scores, students’ Total Engage-

ment and the Attendance metrics. In this paper, we

are focusing on demonstrating the three main outputs

for the multiple regression analysis as such veriﬁes

the need for latter NN model simulation and analysis.

CSEDU 2021 - 13th International Conference on Computer Supported Education

The outputs are the regression summary, Analysis of

Variance (ANOVA) and statistical signiﬁcance analy-

sis of the independent variables.

Table 2 provides the R, R

, adjusted R

and the

standard error of the estimates. The results shows

a marginally good quality of the prediction R value

(the class test) of 0.621. Additionally, the adjusted

value of 0.569 indicates that independent variables

contribute to 56.9% of the variability of the dependent

variable.

Table 2: Regression model summary.

Multiple R 0.621

0.599

Adjusted R

0.569

Standard Error 7.132

The ANOVA tests the goodness of ﬁts for the over-

all multiple regression analysis. The result is shown

in Table 3. As (α < 0.05), the model is a good ﬁt of

the data for the NN model.

Table 3: ANOVA result.

Source Sum of square d.f. Mean square F-cal α

Regression 608.67 6 101.44 1.563 0.002

Residual 11422.4 176 64.90

Total 12030.87 182

The statistical signiﬁcance for each of the inde-

pendent variables is shown Table 4. As α < 0.05, all

the independent variables are statistically signiﬁcant

to the dependent variable (the class test).

Table 4: Statistical signiﬁcance of the independent vari-

ables.

Model Coefﬁcients Standard error t Stat α

(Intercept) 87.83 6.390 13.745 0.001

Lab 1 -0.243 0.075 -3.24 0.000

Lab 2 -0.198 0.052 -3.808 0.000

Lab 3 -0.423 0.032 13.218 0.001

Lab 4 -0.165 0.059 -2.796 0.004

Total Engagement -0.118 0.032 -3.667 0.000

Attendance 13.116 1.344 9.756 0.000

Pearson correlation coefﬁcients are calculated to

examine the degree of closest relationship among the

four Lab scores, the students’ engagement metrics

(Total engagement and Attendance), and the resultant

class test score. The correlation coefﬁcients between

lab scores, total engagement,attendance and the class

test score are shown in Table 5, with ascending order:

Total Engagement, Lab 1, Lab 2, Lab 3, Lab 4 and At-

tendance. These correlated variables are used further

as input neurons for the NN modelling.

For the Person Correlation test, surprisingly, it can

be seen that the correlation coefﬁcient value increases

as students progress themselves from Lab 1 to Lab

4. Apart from that, the attendance metric is with the

highest relationship with the class test score. This

shows that attending the live and recorded lecture, as

well as completing the lab assessments are important

so as to score better in the class test. This is in line

with the explanation where students’ are able to solve

programming questions and perform well with cogni-

tive levels as high as application and analysis in online

learning activities (Othman and Zain, 2015).

4.2 NN Conﬁguration Settings

The NN modelling and evaluations are performed us-

ing MathWorks MATLAB software. The input layer

consists of six variables containing all the four lab as-

sessment scores and the metrics include the total en-

gagement and and the attendance. The modelled NN

has two hidden layers, where each hidden layer con-

sists of 30 neurons as such conﬁguration provides the

best outcome throughout several simulations with dif-

ferent hidden layer and neuron settings. Each hidden

layer with 30 neurons is fed into a single output neu-

ron that carries the decision of the variable, which is

the class test prediction.

The activation function of hyperbolic tangent is

used. Decisions must be taken to divide the dataset

into training, validation and test ratio. Data samples

of 181 students are randomly mixed and 0.7 of the

mixed samples are used for training, 0.15 used for val-

idation and the remaining 0.15 used for the testing.

During the training and learning phase,

Levenberg-Marquardt algorithm in Eq. 5 is used

to determine the optimal weights that are fed to

the next input layer. The damping factor ζ is set

to 0.001. The training epoch is set to 2,000. The

NN training performs continuously and terminates

when the validation error failed to decrease for six

iterations during the validation process. Typically,

the validation protects over-training of NN.

4.3 NN Simulation Results

After the NN training, the NN performance with

MSE ≈ 58.74 or 6.9% (<10%) indicates the sufﬁ-

ciently good performance of NN in completing train-

ing training and validation runs.

Regression plots of NN performance are shown

in Figure 2. For a good data ﬁtting, the data should

have the predicted outputs y

i j

lying closely with tar-

get outputs t

i j

. In this case, the resultant regression

plots achieve marginally good ﬁts with an overall R-

value of 0.595.

The error histogram evaluates the error distribu-

tions based on the resultant NN predictions. The dis-

tribution of errors are shown in Figure 3. Most er-

A Neural Network Modelling and Prediction of Students’ Progression in Learning: A Hybrid Pedagogic Method

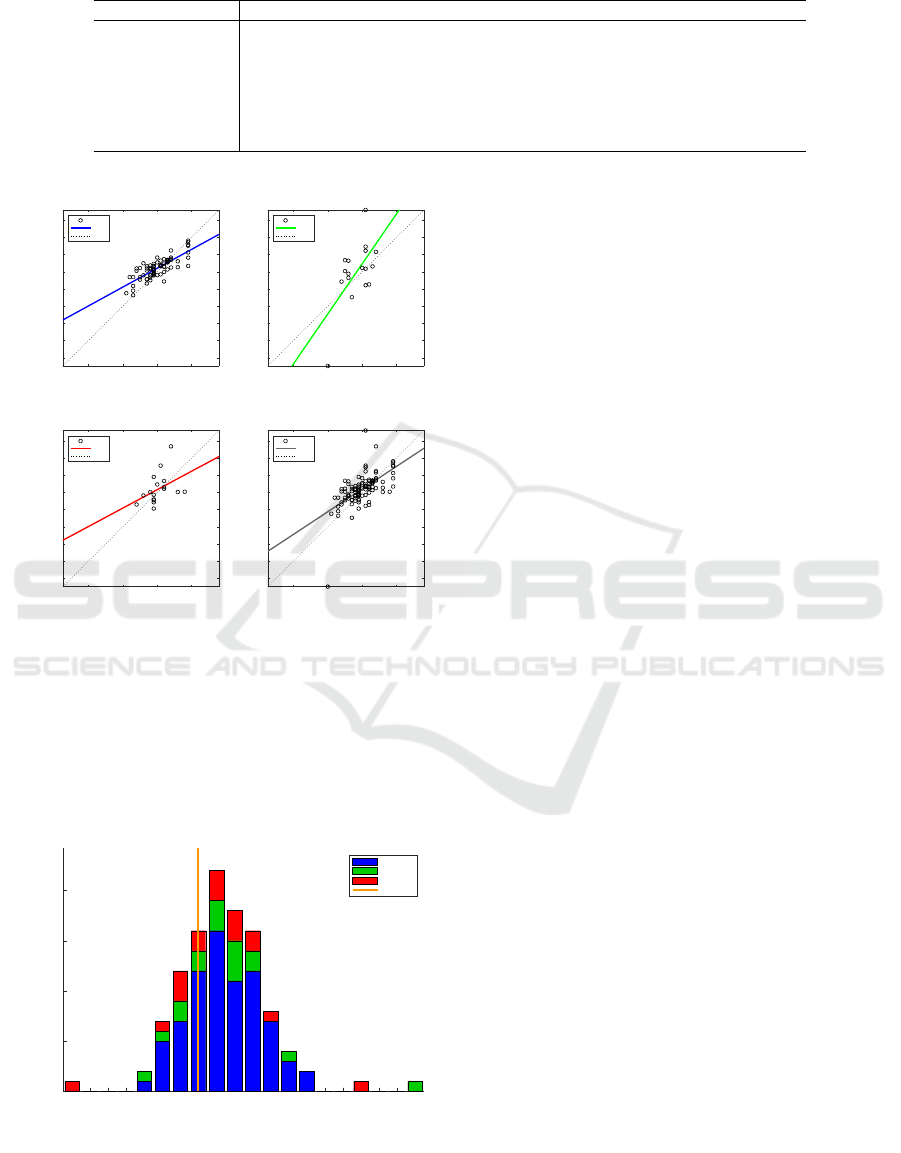
Table 5: Correlation coefﬁcient of four lab assessments, total engagement and attendance, and the class test score.

Lab 1 Lab 2 Lab 3 Lab 4 Total Engagement Attendance Class test

Lab 1 1

Lab 2 0.84 1

Lab 3 0.70 0.70 1

Lab 4 0.85 0.84 0.80 1

Total Engagement 0.31 0.30 0.28 0.31 1

Attendance 0.34 0.31 0.28 0.32 0.92 1

Class Test 0.36 0.37 0.40 0.41 0.36 0.42 1

40 60 80 100

Target

100

110

Output ~= 0.55*Target + 38

Training: R=0.79161

Data

Fit

Y = T

40 60 80 100

Target

100

110

Output ~= 1.5*Target + -32

Validation: R=0.61323

Data

Fit

Y = T

40 60 80 100

Target

100

110

Output ~= 0.54*Target + 39

Test: R=0.41363

Data

Fit

Y = T

40 60 80 100

Target

100

110

Output ~= 0.66*Target + 29

All: R=0.59507

Data

Fit

Y = T

Figure 2: Regression plot for NN model: Top left: Train-

ing data; Bottom left: Test data; Top right: validation data;

Bottom right; resultant regressions.

rors occurred near zeroth point (horizontal axis), and

errors are gradually decreasing when moving away

from zeroth point. This proves that NN performs the

prediction successfully with acceptable error distribu-

tions as shown in Figure 3.

Instances

Error Histogram with 20 Bins

-31.93

-27.35

-22.77

-18.18

-13.6

-9.023

-4.441

0.1397

4.721

9.302

13.88

18.46

23.05

27.63

32.21

36.79

41.37

45.95

50.53

55.11

Errors = Targets - Outputs

Training

Validation

Test

Zero Error

Figure 3: Error histogram plot.

5 CONCLUSIONS

In this paper NN is used to model and predict the

students’ progressing in learning using the available

dataset about their lab assessment scores, class test

and the information about their engagements and at-

tendance metrics using the lecture recording software

analytics. The core purpose is to evaluate the effec-

tiveness of students’ progression in learning through

the revised Bloom’s taxonomy in combination with

the hybrid pedagogic approach – ﬂipped classroom,

asynchronous and cognitive learning throughout the

COVID-19 period.

The multiple regression result showed the statisti-

cally signiﬁcance of all the independent variables to

the dependent variable. Such evaluations veriﬁed the

appropriateness of variables used for the latter NN

modelling. The Person Correlation test also shows

the order of importance on how the progression of

students from Lab 1 to Lab 4 plus attending the live

and recorded video lectures will affect their class test

scores.

Overall, the good NN performance makes NN

such a useful tool for education evaluation purposes.

However, some present limitation of this study are the

low sample size of the dataset obtained. In the light

of the results, it is still strongly believed that educa-

tion modelling settings using NN provides an instru-

mental contribution in evaluating students’ academic

performance. The future NN model may include other

attributes such as the lecturers’ role, some other class-

room activities such as quizzes, course feedbacks and

formative assessments. We strongly believe that the

proposed model is highly generalisable in ﬁtting into

other courses and thus leveraging the ‘Smart’ educa-

tional learning solutions.

REFERENCES

Britto, R. and Usman, M. (2015). Bloom’s taxonomy in

software engineering education: A systematic map-

ping study. In 2015 IEEE Frontiers in Education Con-

ference (FIE), pages 1–8.

CSEDU 2021 - 13th International Conference on Computer Supported Education

Echo360 (2020). Echo360- deﬁnitions of course analytics

metrics. https://learn.echo360.com/hc/en-us/articles/

360035037312. Accessed 25 11 2020.

Foldnes, N. (2016). The ﬂipped classroom and cooperative

learning: Evidence from a randomised experiment.

Active Learning in Higher Education, 17:39–49.

Fuller, U., Johnson, C., Ahoniemi, T., Cukierman, D.,

Hern

an-Losada, I., Jackova, J., Lahtinen, E., Lewis,

T., Thompson, D., Riedesel, C., and Thompson, E.

(2007). Developing a computer science-speciﬁc learn-

ing taxonomy. ACM SIGCSE Bulletin, 39(4):152–170.

Granello, D. (2001). Promoting cognitive complexity in

graduate written work: Using bloom’s taxonomy as a

pedagogical tool to improve literature reviews. Coun-

selor Education and Supervision, 40(4):292–307.

Hussain, M., Zhu, W., Zhang, W., and Abidi, S. (2018). Stu-

dent engagement predictions in an e-learning system

andtheir impact on student course assessment scores.

Computational Intelligence and Neuroscience, 6:1–

21.

Isljamovic, S. and Suknovic, M. (2014). Predicting stu-

dents’ academic performance using artiﬁcial neural

network: a case study from faculty of organizational

sciences. In ICEMST 2014: International Conference

on Education in Mathematics, Science & Technology,

pages 68–72. ISRES Publishing.

Joffrion, H. (2005). Conceptual and procedural understand-

ing of algebra concepts in the middle grades. Master’s

thesis, Ofﬁce of Graduate Studies of Texas A&M Uni-

versity.

Kardan, A. A., H, S., Ghidary, S., and Sani, M. (2013).

Prediction of student course selection in online higher

education institutes using neural network. Computers

& Education, 65:1–11.

Kostons, D. and Werf, G. (2015). The effects of activat-

ing prior topic and metacognitive knowledge on text

comprehension scores. British Journal of Educational

Psychology, 85(3):264–275.

Lau, E., Sun, L., and Yang, Q. (2019). Modelling, pre-

diction and classiﬁcation of student academic perfor-

mance using artiﬁcial neural networks. SN Applied

Sciences, 1(982):1–10.

Macarini, L., Cechinel, C., Machado, M., Ramos, V.,

and Munoz, R. (2019). Predicting students success

in blended learning—evaluating different interactions

inside learning management systems. Applied Sci-

ences, 9:1–23.

MathWorks (2019). trainlm - Levernberg-Marquardt back-

propagation. http://uk.mathworks.com/help/nnet/ref/

trainlm.html. Accessed 17 6 2019.

Michalsky, T. and Zion, M. (2007). Developing students’

metacognitive awareness in asynchronous learning

networks in comparison to face-to-face discussion

groups. Journal of Educational Computing Research,

36(4):395–424.

Okubo, F., Yamashita, T., Shimada, A., and Ogata, H.

(2017). A neural network approach for students’ per-

formance prediction. In LAK17 - The Seventh Interna-

tional Learning Analytics & Knowledge Conference,

pages 598–599. Association for Computing Machin-

ery (ACM).

Othman, M. and Zain, N. (2015). Online collaboration

for programming: Assessing students’ cognitive abil-

ities. Turkish Online Journal of Distance Education-

TOJDE, 16(4):84–97.

Ozc¸elik, S. and Hardalac¸, N. (2011). The statistical mea-

surements and neural network analysis of the effect

of musical education to musical hearing and sensing.

Expert Systems with Applications, 38:9517–9521.

Peter, D., Leth, T., and Bent, T. (2016). Assessing problem-

based learning in a software engineering curriculum

using bloom’s taxonomy and the ieee software engi-

neering body of knowledge. ACM Transactions on

Computing Education, 16(3):1–41.

Peterson, D. (2016). The ﬂipped classroom improves stu-

dent achievement and course satisfaction in a statistics

course: A quasi-experimental study. Teaching of Psy-

chology, 43:10–15.

Qadir, J. and al-Furqaha, A. (2020). A student primer on

how to thrive in engineering education during and be-

yond covid-19. Education Sciences, 10(9):236–258.

Rashid, T. and Ahmad, H. (2016). Using neural network

with particle swarm optimization. Computing Appli-

cation Engineering Education, 24:629–638.

Sheth, S., Ganesh, A., Nagendra, S., Kumar, K., Tejdeepika,

R., Likhitha, C., Murthy, P., and Chand, P. (2020).

Development of a mobile responsive online learn-

ing module on psychosocial and mental health issues

related to covid 19. Asian Journal of Psychiatry,

54:236–258.

United Nations (2020). Policy brief: Education during

covid-19 and beyond - august 2020. Technical report,

United Nations.

Vandamme, J., Meskens, N., and Superby, J. (2007). Pre-

dicting academic performance by data mining meth-

ods. Education economics, 15(4):405–419.

Wilson, P. and Mantooth, H. (2013). Model-based engi-

neering for complex electronic systems. Newnes.

Wu, D., Bieber, M., and Hiltz, S. (2008). Engaging students

with constructivist participatory examinations in asyn-

chronous learning networks. Journal of Information

Systems Education, 19(3):321–330.

Yu, H. and Wilamowski, B. (2011). Levernberg Mar-

quardt training industrial electronic handbook, intel-

ligent systems, volume 5. CRC Press, 2 edition.

Zhang, Q., Kuldip, C., and Devabhaktuni, V. (2003). Ar-

tiﬁcial neural network for rf and microwave design –

from theory to practice. IEEE Transactions on Mi-

crowave Theory and Techniques, 51(4):1339–1350.

A Neural Network Modelling and Prediction of Students’ Progression in Learning: A Hybrid Pedagogic Method