Turning Rate Estimation in Roundabouts: Analysis and Validation of
Different Estimation Methods
M
´
anuel Gressai and Tam
´
as Tettamanti
a
Department of Control for Transportation and Vehicle Systems, Budapest University of Technology and Economics,
Faculty of Transportation Engineering and Vehicle Engineering, 3. Muegyetem rkp., Budapest, Hungary
Keywords:
Traffic Estimation, State Estimation, Roundabout, Turning Rate, Turning Movement, Traffic Count, Kalman
Filter, Constrained Kalman Filter.
Abstract:
The knowledge of turning rates in roundabouts is a crucial element of traffic modeling. Measuring the turning
movements is often carried out by manual traffic counts (noting on paper or using handheld devices), which
is a labor-intensive, therefore expensive process. The aim of this paper is the examination and comparison
of different estimation methods used for turning rates in roundabouts. Traditional iteration based approach as
well as estimators adopted from control theory are discussed, benchmarked, and validated on real-world traffic
data. For the estimation procedures, the traffic flows (measured at each leg of the intersection) are the input. In
this way, the traditional origin-destination traffic count at an intersection can be substituted by automated traffic
detection at the cross-sections together with the adequately implemented estimation process (suggested in the
paper). The calibration of estimation methods is of crucial importance as well. The calibration is demonstrated
based on real-world traffic counts at roundabouts. The different methods have been compared using different
error metrics. As a main finding of the research, it is shown that, given the right tuning, constrained Kalman
Filtering outperforms the unconstrained Kalman Filtering and the traditional iterative procedure.
1 INTRODUCTION
Road traffic infrastructure planning or development
is initiated based on reliable traffic modeling. The
input of the modeling is the knowledge of vehicular
flows on road links and turning rates at intersections.
Traffic volumes at cross-sections can be straightfor-
wardly measured manually or with help of a wide
variety of traffic sensors. At the same time, turning
flows or turning rates can be collected by human re-
sources solely, which is quite costly. Therefore, if
turning flows are collected, typically more than one
person is needed in order to perceive all movements.
The more, observing turnings in roundabouts is ex-
tremely problematic due to the special geometry and
size of this type of junction (Cao and Z
¨
oldy, 2020).
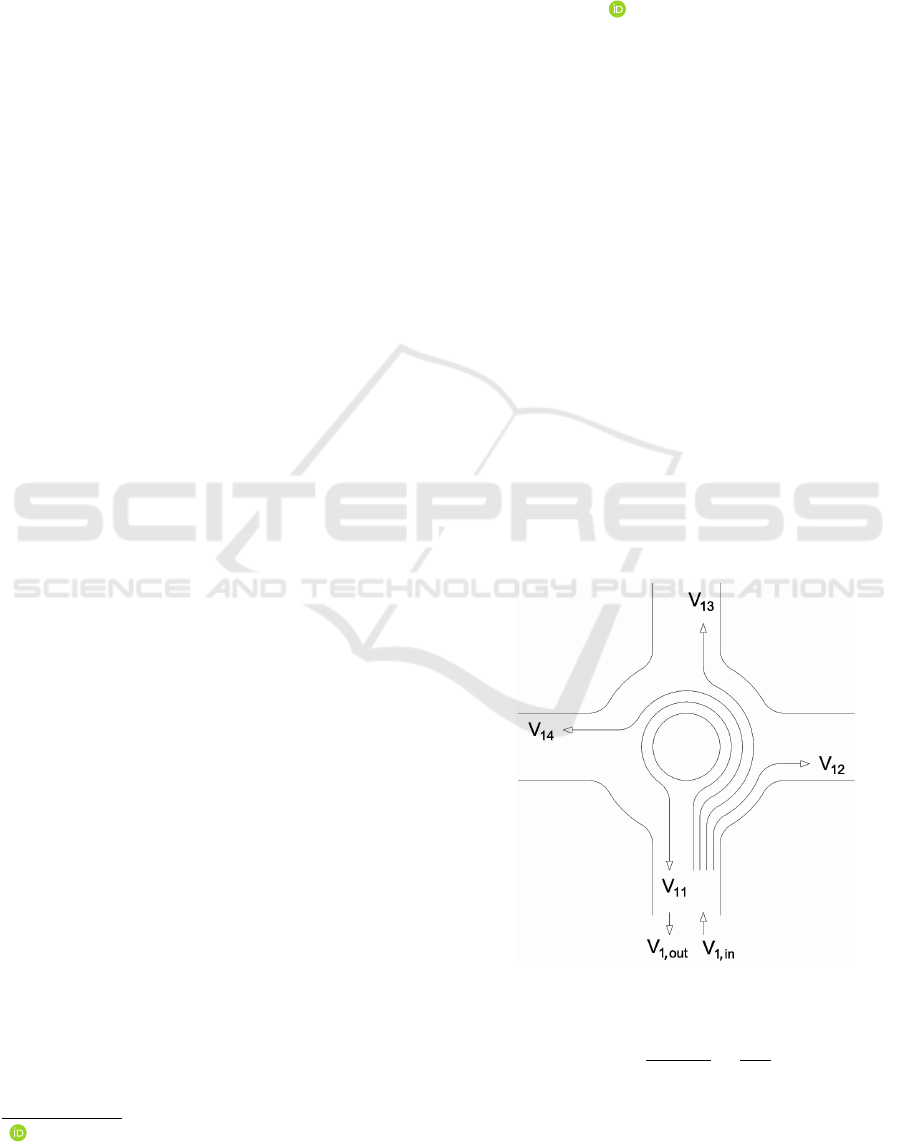
Fig. 1 demonstrates the possible turning move-
ments at a roundabout for vehicles arriving at En-
trance 1. V
1 j
is the turning traffic flow from Entrance
1 to exit j, whereas V
1,in
and V
1,out
are the total traf-
fic volumes entering and exiting at the correspond-
ing junction leg. Using the volumes in Fig. 1, turning
a
https://orcid.org/0000-0002-8934-3653
Figure 1: Turning movements at a roundabout.
rates can be defined as follows:
x
i j
=
V
i j
∑
n
D
j=1
V
i j
=
V
i j
V
i,in
(1)
where n
D
is the number of exits.
There exist, in fact, automated methods for turn-
Gressai, M. and Tettamanti, T.
Turning Rate Estimation in Roundabouts: Analysis and Validation of Different Estimation Methods.
DOI: 10.5220/0010405700650071
In Proceedings of the 7th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2021), pages 65-71
ISBN: 978-989-758-513-5
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
65

ing flow counts. For instance, it can be carried out
by installing cameras on the spot and evaluating the
footage subsequently by using artificial intelligence
(Taylor et al., 2016). However, placing cameras or
shooting aerial videos with drones (Salvo et al., 2014)
can be quite costly as well. Moreover, the legal back-
ground of drones is yet to be simplified for this to be a
real alternative (Budinska, 2019). On the other hand,
in the case of cross-sectional counts, there is a wide
range of solutions for automation (e.g. inductive loop
detectors, cameras, ultrasonic detectors).
Counting traffic on the legs of a roundabout and
adequately estimating turning rates based on the
collected data has the potential to substitute labor-
intensive turning flow counts. This could reduce the
cost of determining turning rates at an intersection
significantly. In this paper, cross-sectional counts are
used as a basis to estimate turning rates at a round-
about. This proposes a possible solution to overcome
the obstacles posed by turning movement observation.
The paper is divided into 5 sections. A detailed
description of the examined estimation methods fol-
lows the introduction. Next, the test sites are intro-
duced, where the traffic counts were carried out for
the research. Then, the testing of different methods
(a traditional iterative procedure and modern Kalman
Filter based methods) and the methodology of deter-
mining the optimal tuning settings are presented. The
methods are then compared using different error met-
rics. Finally, a summary of findings and recommen-
dations for future research is given.
2 ESTIMATION METHODS
This section covers different methods used for turn-
ing rate estimation. Biproportional procedure is dis-
cussed as a traditional iterative algorithm, then the
Kalman Filter and its extension with constraint han-
dling are introduced.
2.1 Biproportional Procedure
The biproportional procedure (BP) is an iterative al-
gorithm (Ben-Akiva et al., 1985), where the varia-
tion of two coefficients (a and b) causes the variation
of turning flows in each iteration. Two sets of input
data are necessary for this procedure. A preliminary
origin-destination matrix (t) and the traffic flows on
each leg of the roundabout (O
i
entering and D
j
exit-
ing counts in case of entrance i and exit j). t
i j
is the
traffic volume from i to j, and there exist n
O
entrances
and n
D
exits. The accuracy of the BP estimation de-
pends largely on the accuracy of prior matrix t (Dixon
and Rilett, 2005).
The BP procedure aims to estimate the elements of
the current OD-matrix T , based on the current flows
on each leg and prior matrix t. Therefore, the result-
ing matrix of the procedure contains traffic volumes,
which then can be converted into turning rates. This
assists the comparison of estimation procedures.
The estimated T has to satisfy the following con-
straints:
O
i
=
n
D
∑
j=1
T
i j
, (2)
D
i
=
n
O
∑
i=1
T
i j
. (3)
To meet the constraints in Eq. (2) and Eq. (3), iter-
ations are executed. Each iteration alters the propor-
tions a and b. These proportions from the previous
iteration are marked as a
∗
and b
∗
. Estimated matrix T
has a minimal difference from prior matrix t, whilst
satisfying the constraints (Dixon et al., 2007).
The initial conditions for the BP procedure are that
a
∗
i
, b
j
, and b
∗
j
are set to 1, while T
i j
is set equal to t
i j
for all turning movements. For a stopping criterion,
a sufficiently small value of ε needs to be reached by
the changes in a
i
and b
j
.
The steps of the algorithm are detailed as follows.
1. Calculation of a
i
:
a
i
=
O
i
∑
n
D
j=1
T
i j
!
a
∗
i
. (4)
2. Calculation of T
i j
:
T
i j
= t
i j
a
i
b
j
. (5)
3. Calculation of b
j
:
b
j
=

D
j
∑
n
O
i=1
T
i j

b
∗
j
. (6)
4. Calculation of T
i j
using Eq. (5).
5. End of iteration. If the changes in a
i
and b
j
are
greater than the previously defined ε, the iteration
starts over from Step 1. If the changes are less
than or equal to ε, the last estimated T
i j
is the re-
sult of the current interval.
The algorithm above depicts only one measure-
ment period. While implementing the BP procedure,
turning flows need to be estimated in each interval.
After the stopping criterion is met, all elements of T
are rounded to the nearest integer. T then becomes
the prior matrix for the next period as the volumes of
O
i
and D
j
are updated as well.
An advantage of the BP procedure is its relatively
low computational requirements. Also, OD-matrices
VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems
66

are estimated based on 8 cross-sectional counts in-
stead of 16 turning movement observations. Another
benefit that derives merely from the characteristics of
the algorithm is that if U-turns are assumed to be zero
in the prior matrix, the estimated matrices also have
zeros in the main diagonal. A disadvantage of the pro-
cedure is its heavy dependence on the accuracy of the
prior matrix.
2.2 Kalman Filter
State space based estimators include a model of the
system and noises. Some procedures are apt to
manage constraints concerning the estimated values
(e.g. for each turning rate to be non-negative). More-
over, these methods estimate the mean and standard
deviation for all states in each interval.
State space based estimators have been applied to
predict turning flows for traditional intersections (Pa-
papanagiotou et al., 2019), (Kulcs
´
ar et al., 2005). At
the same time, by studying the relevant scientific lit-
erature, it can be stated that state space based methods
have not been used to estimate turning rates in round-
abouts so far. Accordingly, in this paper, Kalman Fil-
ter and its constrained extension are implemented for
roundabout traffic flow estimation. First, the algo-
rithms of these approaches are discussed in the sequel.
The basis of Kalman Filtering is the following dis-
crete time-invariant measurement equation (Kalman,
1960):
y(k) = C(k)x(k) + z(k), (7)
where the variables are as follows:
• y(k) - output or measurement vector;
• x(k) - unknown state vector that varies over time;
• C(k) - a weighing matrix called output matrix;
• z(k) - a vector of measurement noise.
Eq. (7) represents that states cannot always be mea-
sured directly and that the measurement is affected by
some level of noise (considered to be white noise).
The objective of Kalman Filtering is to estimate the
state vector as accurately as possible in each interval.
Next, diagonal covariance matrix R is defined con-
taining the variances of measurement noises. State
error covariance matrix P is introduced consisting of
variances concerning the estimated states. G is a gain-
matrix which plays a role in calculating P.
In the case of dynamic systems, defining the
model solely with the measurement equation can
result in rigidity when applying the estimation for
longer time periods. Thus, the system itself and the
noise affecting it need to be modeled as well. The
Kalman Filter is a recursive algorithm containing the
system model and the concerning noises.
Eq. (8) is the state equation describing the system
in discrete linear time varying case:
x(k + 1) = A(k)x(k) + B(k)u(k) + v(k), (8)
where the variables are as follows:
• x(k) - state vector;
• u(k) - input vector or control vector;
• A,B - system matrices;
• v(k) - vector of state noise (the error of the system
model).
Q is a state noise covariance matrix for vector v(k),
just as R is a measurement noise covariance matrix
for vector z(k).
The relation of Q and R matrices play a major role
in the operation of the Kalman Filter. Their values are
to be determined empirically prior to the start of the
algorithm. These can be described as tuning matrices.
If the values of Q are far larger than that of R, the
algorithm relies heavily on the current measurements.
If the values of R exceed that of Q, the Kalman Filter
rather accepts the last interval’s estimation as opposed
to the measurements.
The Kalman Filter algorithm is detailed as follows
(where in time-variant case A, B, and C are varying
matrices, i.e. A(k), B(k), and C(k)).
1. Project state ahead:
ˆx
−
(k) = A ˆx(k − 1) + B(k − 1)u(k − 1). (9)
2. Project the error covariance ahead:
P
−
(k) = A P(k −1)A
T
+ Q. (10)
3. Execute the measurement providing y(k).
4. Compute the Kalman gain:
G(k) = P
−
(k)C
T
(C P
−
(k)C
T
+ R)
−1
. (11)
5. Update estimate with measurement y(k):
ˆx(k) = ˆx
−
(k) + G(k)(y(k) −C ˆx
−
(k)). (12)
6. Update the error covariance:
P(k) = (I − G(k)C) P
−
(k)). (13)
7. Increment k, and go to Step 1 of the algorithm:
k := k + 1.
The estimation algorithm is divided into two parts.
The prediction (Steps 1 and 2) is the projection of
state vector ˆx
−
(k) and error covariance matrix P
−
(k)
based on the previous estimations. The correction
(Steps 3-7) is updating the state estimates and error
covariance matrix knowing the current measurement
values.
Turning Rate Estimation in Roundabouts: Analysis and Validation of Different Estimation Methods
67

In case of estimating turning rates in roundabouts
based on the traffic flow on the legs, the elements of
the state vector in the Kalman Filter are the turning
rates (Tettamanti et al., 2019). A in state equation
(8) is an identity matrix, whereas B can be substituted
with 0 as there is no control vector, i.e. the state vector
to be estimated is as follows:
ˆx(k) =




ˆx
11
ˆx
12
.
.
.
ˆx
n
O
,n
D




, (14)
where ˆx
i j
denotes the estimated turning rate from en-
trance i (i = 1, 2, ..., n
O
) to exit j ( j = 1, 2, ..., n
D
).
C(k) in measurement equation (7) contains the mea-
sured entering traffic flows (marked by q
m
where m
denotes the m
th
leg of the roundabout).
C(k) =
q
1
(k) q
2
(k)
.
.
.
.
.
.
...
q
1
(k) q
2
(k)
!
. (15)
Thus, exiting traffic flows appear in vector y(k) as
measured parameters.
2.3 Kalman Filter with Constraints
Assume that the modeled system satisfies the follow-
ing constraints:
A
eq
x(k) = b
eq
, (16)
A
in
x(k) ≤ b
in
, (17)
where A
eq
and A
in
are known matrices as well as b
eq
and b
in
are known vectors. In this case, estimated
states also need to satisfy these conditions:
A
eq
ˆx(k) = b
eq
, (18)
A
in
ˆx(k) ≤ b
in
. (19)
Compliance with these constraints can be reached by
projecting the state to lie in the constrained space at
each estimation interval (Gupta and Hauser, 2007).
This means that the unconstrained filter runs in a nor-
mal way, but at each iteration the updated state esti-
mate is forced to lie in the constrained space. In this
approach, the analytic solution is no longer available
for filtering. Thus, numerical optimization is needed
to be applied.
The projection is carried out via the follow-
ing constrained optimization problem (Simon, 2010),
(Gupta and Hauser, 2007):
˜x(k) = argmin
x
(x − ˆx(k))
T
W (x − ˆx(k)), (20)
s.t. (16) and (17),
where ˜x is the projected state estimate and W is a
weighing matrix.
W can be chosen as an identity matrix (here-
inafter referred to as cKF-I). The result is then the
least square estimate subject to the constraints, which
means that estimates necessarily get closer to the real
state values. If noises are assumed to be white and W
is set to P(k)
−1
in each interval (hereinafter referred
to as cKF-P), the result is the maximum probability
estimate of the state subject to state constraints (Si-
mon, 2010).
The issue of managing constraints by (20) can be
tackled easily by any standard optimization package.
For this research, MATLAB Optimization Toolbox
was applied.
Initial vector x
0
for the optimization is state vec-
tor ˆx(k) estimated by the Kalman Filter without con-
straints. Adequately defined A
in
and b
in
results in
an inequality constraint enforcing turning rates to be
non-negative. Suitable equality constraint matrix A
eq
and vector b
eq
can set all U-turn rates to zero while
ensuring that the aggregate of turning rates arriving at
the roundabout at a given entrance is 1 at all times.
The procedure of managing constraints is the fol-
lowing. The Kalman Filter algorithm outputs an
ˆx(k) vector in interval k. The optimization subject
to constraints (18) and (19) is then executed on this
estimated state vector using MATLAB optimization
function (quad prog). In interval (k + 1) the Kalman
Filter uses the constrained state vector estimated in
interval k as input data.
3 TEST FIELD
The knowledge of real turning movement volumes
is necessary for the comparison of estimated and
real turning rates. For this research, turning flow
counts were conducted at two different roundabouts
in Kecskem
´
et, Hungary (Fig. 2 and Fig. 3).
Figure 2: Aerial footage of Roundabout 1 at Kecskem
´
et,
Hungary (GPS coordinates: 46.92971298057884,
19.663997128931193).
VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems
68

Figure 3: Aerial footage of Roundabout 2 at Kecskem
´
et,
Hungary (GPS coordinates: 46.88150317109579,
19.707799625939572).
In accordance with the drone’s maximal flight
time, 26-minute aerial video recordings were taken at
the two four-leg intersections. The counts took place
at different times of the day (morning and afternoon).
The 26-minute counts are adequate to be divided into
1, 2, and 5 minute intervals (in the latter case, only 25
minutes are examined). The traffic count was there-
fore conducted for 1-minute intervals, so that 2 and
5-minute intervals could be calculated afterward.
The estimation algorithms introduced in the pa-
per work based on the counted number of vehicles
expressed in passenger car equivalent (PCE, i.e., the
different types of road vehicles expressed as the ratio
of the private car (Lay, 2009)). The traffic counts thus
included the differentiation of vehicle categories.
4 BENCHMARKING THE
ALGORITHMS WITH
REAL-WORLD DATA
In this section, the steps and circumstances of ap-
plying the estimation procedures are detailed; then,
a comparison is made between the different meth-
ods. The real-world traffic counts provide input data
for the estimators as well as a basis for determining
their accuracy, i.e. for validation. The latter is carried
out by comparing state estimates with the real turning
rates, using error metrics. All concerning estimators
are tested for all the collected data with different in-
tervals.
4.1 Error Metrics
Two different error metrics (Chen et al., 2017) have
been applied during the evaluation of estimation pro-
cedures. The first is the mean absolute error (MAE),
for which the formula is as follows:
MAE =
∑
n
k=1
| ˆx
k
− x
k
|
n
(21)
where n is the number of samples (intervals), ˆx
k
is the
state estimation in interval k, and x
k
is the actual state.
The second error metric used to describe the ac-
curacy of the estimators is the root mean square error
(RMSE). The formula for the RMSE is the following:
RMSE =
s
1
n
n
∑
k=1
( ˆx
k
− x
k
)
2
(22)
MAE and RMSE have the same unit of measure as the
examined quantity. In the case of turning rates, this is
a unitless value between 0 and 1. The direction of the
error is neglected in both cases. MAE is an absolute
measure and RMSE contains the squared error, which
always gives a non-negative value. As the expression
under the root symbol is non-negative, RMSE will al-
ways have a real solution.
4.2 Tuning the Kalman Filter
When applying the Kalman Filter, the objective is
to adjust the tuning parameters precisely. The tun-
ing was carried out through the comparison of esti-
mated and real turning rates, searching for the small-
est error measures when varying the tuning parame-
ters. The attributes of the estimation depend on state
noise and measurement noise covariance matrices Q
and R. These set the weighting between the current
measurements and previous estimates. In practice, Q
and R can be defined as diagonal matrices with con-
stant values. Tuning of the Kalman Filter depends on
the ratio of the values of the two matrices. Thus, R
can be defined as an identity matrix, and Q needs to
be altered after each run. In this way, the value of Q is
equal to the Q/R ratio. During the search for the opti-
mal settings, this ratio is set to be 10
20
, and is divided
by 10 after each run, until it reaches 10
−10
. The cor-
responding error measures are calculated for each run
and tabulated. The minimum of errors designates the
optimal tuning parameter ratio. The appropriate Q/R
ratio for the Kalman Filter for the examined traffic
data is 10
−3
.
In the case of the constrained Kalman Filter
(cKF), weighing matrix W is set to be an identity ma-
trix (cKF-I). This leads to 10
−2
as the optimal Q/R
ratio.
Giving W values that are different from an identity
matrix is worth examining to establish if it can im-
prove the accuracy of the estimation. For this purpose,
W is altered subject to a fixed Q/R ratio. This process
has revealed that the errors cannot be decreased sub-
stantially; thus, a fixed W can optimally be chosen to
be an identity matrix.
In order to achieve a more accurate estimation,
weighing matrix W can be defined to vary over time.
Turning Rate Estimation in Roundabouts: Analysis and Validation of Different Estimation Methods
69

A well functioning solution is to set W to the inverse
of the state error covariance matrix P in each interval
(cKF-P) (Simon, 2010). In this case, a local mini-
mum in errors is forming around that of the uncon-
strained Kalman Filter. However, increasing the Q/R
ratio leads to a significant improvement in accuracy.
The optimal ratio is determined to be 10
6
for the cKF-
P.
During the tuning procedure, the optimal parame-
ters were established for the Kalman Filter:
• without constraints (KF) - Q/R = 10
−3
• with constraints, while W = I (cKF-I) - Q/R =
10
−2
• with constraints, while W = P(k) (cKF-P) -
Q/R = 10
6
4.3 Evaluation of the Estimation
Methods
The tendency of error measures are similar in all cases
irrespective of the location or the time of the day.
Therefore, for the sake of transparency and a more
general result, error values are averaged over the dif-
ferent traffic counts. The average values form the ba-
sis for the comparison of different estimation proce-
dures.
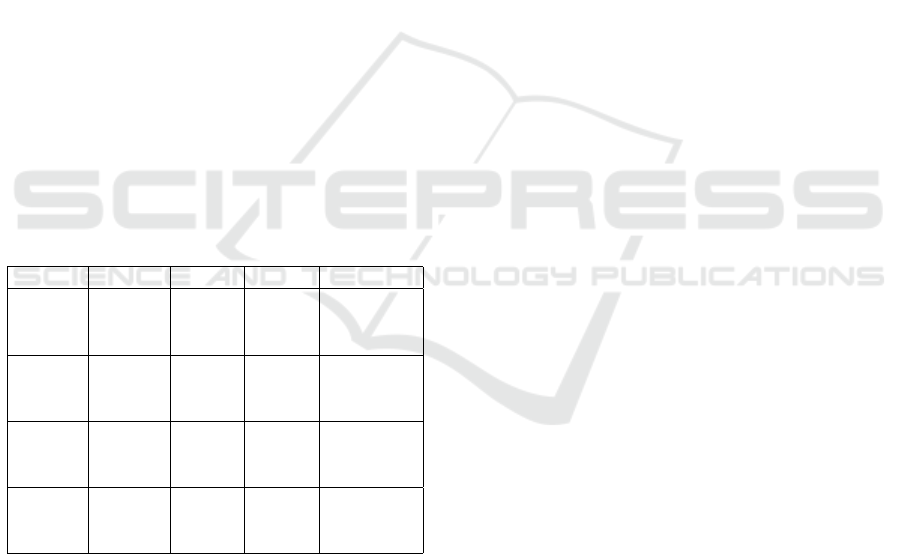
Table 1: Comparison of estimation procedures.
Method Interval MAE RMSE MAE rank
1 min 0.1181 0.1760 9
BP 2 min 0.0822 0.1230 5
5 min 0.0670 0.1050 2
1 min 0.1484 0.2122 12
KF 2 min 0.1036 0.1505 8
5 min 0.0742 0.1118 4
1 min 0.1431 0.2110 11
cKF-I 2 min 0.1026 0.1480 7
5 min 0.0692 0.1048 3
1 min 0.1183 0.1765 10
cKF-P 2 min 0.0843 0.1276 6
5 min 0.0608 0.0945 1
Table 1 lists the average MAE and RMSE values
for all examined estimation methods and all interval
sizes. A ranking in the MAE values is also assigned
to the procedures. Based on the order, it can be stated
that the longer the interval, the more accurate the es-
timation. Whereas shorter intervals result in larger
errors.
The 5-minute interval led to the smallest errors in
the case of every examined method. A possible ex-
planation for this is the following. If the intervals
are short, it is more frequent that a specific turning
movement is not executed during that brief time pe-
riod. This can result in sharp fluctuations in turning
rates, which is harder to track for an estimator.
The order of estimation procedures with 5-minute
intervals based on MAE values is the following:
1. cKF-P (constrained Kalman Filter while W =
P(k))
2. BP - biproportional procedure
3. cKF-I (constrained Kalman Filter while W = I)
4. KF (Kalman Filter)
In the case of 5-minute intervals, the Kalman Fil-
ter with constraints outperforms the BP procedure
(the improvement in error measures is approximately
10%) and the unconstrained Kalman Filter. It is also
observable that the shorter estimation intervals of 1
or 2 minutes provide higher errors in every estimation
procedures. This clearly means that on longer time
intervals, the algorithms can better smooth their esti-
mations.
It is also noted that the performance of the con-
strained Kalman Filter can be improved by tuning the
parameters separately for each junction leg.
5 CONCLUSIONS
Different methods of turning flow counts exist with
different benefits and drawbacks concerning round-
abouts. A traditional iterative algorithm (bipropor-
tional procedure) and Kalman Filter based methods
(never used before for roundabout turning rate esti-
mation) have been benchmarked. The exact method-
ology to apply these procedures was also introduced
in detail.
The main contribution of the paper is the validated
comparison of different methods on real-world data
sensed by drone and then counted manually. Ana-
lyzing the results, the following conclusions can be
drawn:
• in general, longer intervals result in more accurate
estimations;
• managing constraints improves the accuracy of
the state space based estimators significantly;
• the adequately tuned constrained Kalman Filter
outperforms the unconstrained Kalman Filter and
the traditional iterative procedure.
The continuation of this research is twofold. On the
one hand, another state space based estimator, the
Moving Horizon Estimation (MHE) will be imple-
mented for the same estimation problem, by which
the current state can be estimated based on more than
VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems
70

one previous step. On the other hand, the evaluation
of the estimation procedures will be extended with the
help of microscopic road traffic simulation. After the
validation of simulation models using real-world traf-
fic data, different traffic situations can be tested easily.
Thereafter, changes in the accuracy and tuning of es-
timators can be further examined.
ACKNOWLEDGEMENTS
The research was supported by the Hungarian Gov-
ernment and co-financed by the European Social
Fund through the project ”Talent management in
autonomous vehicle control technologies” (EFOP-
3.6.3-VEKOP-16-2017-00001).
REFERENCES
Ben-Akiva, M., Macke, P. P., and Hsu, P. (1985). Alter-
native methods to estimate route-level trip tables and
expand on-board surveys. Transportation Research
Record.
Budinska, I. (2019). On ethical and legal issues of us-
ing drones. In Aspragathos, N. A., Koustoumpardis,
P. N., and Moulianitis, V. C., editors, Advances in Ser-
vice and Industrial Robotics, pages 710–717, Cham.
Springer International Publishing.
Cao, H. and Z
¨
oldy, M. (2020). An investigation of au-
tonomous vehicle roundabout situation. Periodica
Polytechnica Transportation Engineering, 48(3):236–
241.
Chen, C., Twycross, J., and Garibaldi, J. M. (2017). A new
accuracy measure based on bounded relative error for
time series forecasting. PloS one, 12(3):e0174202.
Dixon, M. P., Abdel-Rahim, A., Kyte, M., Rust, P., Coo-
ley, H., and Rodegerdts, L. (2007). Field evaluation of
roundabout turning movement estimation procedures.
Journal of Transportation engineering, 133(2):138–
146.
Dixon, M. P. and Rilett, L. (2005). Population origin–
destination estimation using automatic vehicle iden-
tification and volume data. Journal of Transportation
Engineering, 131(2):75–82.
Gupta, N. and Hauser, R. (2007). Kalman filtering
with equality and inequality state constraints. arXiv
preprint arXiv:0709.2791.
Kalman, R. (1960). A new approach to linear filtering and
prediction. Journal of Basic Engineering (ASME),
82(D):35–45.
Kulcs
´
ar, B., B
´
ecsi, T., and Varga, I. (2005). Estimation of
dynamic origin destination matrix of traffic systems.
Periodica Polytechnica ser. Transp. Eng, 33(1-2):3–
14.
Lay, M. (2009). Handbook of Road Technology. Spon Press,
Abingdon, UK.
Papapanagiotou, E., Kaths, J., and Busch, F. (2019).
Kalman filter for turning rate estimation at signalized
intersections, based on floating car data. Transporta-
tion Research Procedia, 41:398 – 402. Urban Mobil-
ity – Shaping the Future Together mobil.TUM 2018
– International Scientific Conference on Mobility and
Transport Conference Proceedings.
Salvo, G., Caruso, L., and Scordo, A. (2014). Urban traffic
analysis through an uav. Procedia - Social and Be-
havioral Sciences, 111:1083 – 1091. Transportation:
Can we do more with less resources? – 16th Meeting
of the Euro Working Group on Transportation – Porto
2013.
Simon, D. (2010). Kalman filtering with state constraints: a
survey of linear and nonlinear algorithms. IET Control
Theory & Applications, 4(8):1303–1318.
Taylor, C., Kennedy, R., Yang, Y., Commission, D. V. R. P.,
et al. (2016). Automated video-based traffic count
analysis. Technical report, University of Pennsylva-
nia.
Tettamanti, T., Luspay, T., and Varga, I. (2019). Road
Traffic Modeling and Simulation. Akad
´
emiai
Kiad
´
o. https://mersz.hu/tettamanti-luspay-varga-
road-traffic-modeling-and-simulation.
Turning Rate Estimation in Roundabouts: Analysis and Validation of Different Estimation Methods
71