
Real-time Periodic Advertisement Recommendation Optimization
under Delivery Constraint using Quantum-inspired Computer
Fan Mo
1
, Huida Jiao
1
, Shun Morisawa
1
,
Makoto Nakamura
2
, Koichi Kimura
2
, Hisanori Fujisawa
2
,
Masafumi Ohtsuka
3
and Hayato Yamana
4a
1
Dept. of Computer Science and Communications Engineering, Waseda University, Tokyo, Japan
2
Fujitsu Laboratories Ltd., Kanagawa, Japan
3
Geniee, Inc., Tokyo, Japan
4
School of Science and Engineering, Waseda University, Tokyo, Japan
m.ohtsuka@geniee.co.jp
Keywords: Computational Advertisement, Advertisement Recommendation, Digital Annealer, Real-time Bidding.
Abstract: For commercial companies, tuning advertisement delivery to achieve a high conversion rate (CVR) is crucial
for improving advertising effectiveness. Because advertisers use demand-side platforms (DSP) to deliver a
certain number of ads within a fixed period, it is challenging for DSP to maximize CVR while satisfying
delivery constraints such as the number of delivered ads in each category. Although previous research aimed
to optimize the combinational problem under various constraints, its periodic updates remained an open
question because of its time complexity. Our work is the first attempt to adopt digital annealers (DAs), which
are quantum-inspired computers manufactured by Fujitsu Ltd., to achieve real-time periodic ad optimization.
With periodic optimization in a short time, we have much chance to increase ad recommendation precision.
First, we exploit each user’s behavior according to his visited web pages and then predict his CVR for each
ad category. Second, we transform the optimization problem into a quadratic unconstrained binary
optimization model applying to the DA. The experimental evaluations on real log data show that our proposed
method improves accuracy score from 0.237 to 0.322 while shortening the periodic advertisement
recommendation from 526s to 108s (4.9 times speed-up) in comparison with traditional algorithms.
1 INTRODUCTION
The market size of online advertising increases every
year, and real-time bidding (RTB) has become a
typical delivery mechanism of online advertisements
(hereafter, ads). In RTB, the advertisers publish their
ads with the help of a demand-side platform (DSP).
The DSP enables RTB and tracks the delivery of ads.
Ad delivery aims to increase the number of
conversions: the cases when a customer completes a
specific action with the advertiser’s product, such as
buying or subscribing. Whether a user converts or not
reflects the performance of the ad delivery. Thus, a
DSP needs to choose ads with a high conversion rate
(CVR) according to each user’s behavior.
A common task of DSP is to meet the needs of
advertisers to obtain as much user engagement as
possible. Previous studies(Abrams et al., 2007; Wu et
a
https://orcid.org/0000-0001-7542-4826
al., 2018) aimed to optimize ads from advertisers’
perspective with budget constraints. Yang et al.
(2019) focused on maximizing the DSP’s profit while
helping advertisers obtain valuable impressions under
a given bidding budget. However, related studies
neglected another critical requirement of DSP
delivery constraints. DSP may want to deliver a
specific number of ads in each category from many
advertisers during a specific period because some
categories have higher benefits for DSP than the
others. Besides, because maximizing the CVR while
satisfying delivery constraints is a combinatorial
optimization problem, it is challenging and time-
consuming to train and periodically update the ad
optimization models under the delivery constraints
with a general-purpose computer.
This paper proposes a new method that satisfies
the delivery constraints using an Ising computer —
Mo, F., Jiao, H., Morisawa, S., Nakamura, M., Kimura, K., Fujisawa, H., Ohtsuka, M. and Yamana, H.
Real-time Periodic Advertisement Recommendation Optimization under Delivery Constraint using Quantum-inspired Computer.
DOI: 10.5220/0010414704310441
In Proceedings of the 23rd International Conference on Enterprise Information Systems (ICEIS 2021) - Volume 1, pages 431-441
ISBN: 978-989-758-509-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
431

Fujitsu digital annealer (DA), a quantum-inspired
annealing machine (Aramon et al., 2019). This article
is the extended version of our poster paper (Mo et al.,
2020).We aim to improve the CVR by periodic ad
optimization. Periodic updates of the user model
improve CVR because we can use the users’ latest
behaviors to tune the model.
We model the periodic ad recommendation
optimization problem as follows: in a short fixed
period (e.g., 20 min), DSP needs to update the user
model while satisfying the constraints, such as
delivering a specific number of ads in each category
to users (for example, 1,000 ads for category A and
5,000 ads for category B). Due to the massive number
of ads and users, it is challenging for the DSP to train
the model quickly and accurately decide the ad
category with the highest probability of conversion
for the target user. We first predict the conversion
probability of each ad category for each user by
adopting two prediction models. Then we transform
the optimization task into a quadratic unconstrained
binary optimization (QUBO) model (Aramon et al.,
2019) to solve the optimization problem. The
contributions of our work are as follows.
We propose a new real-time periodic
recommendation model to speed up ad
recommendations while satisfying the ad
delivery constraints. With offline experiments
on a real dataset, we show that the ad
recommendation accuracy can be improved
while satisfying the constraints.
Our model is the first attempt to combine ad
recommendation with a quantum-inspired
computer DA, which can solve the
combinatorial optimization problem quickly
and accurately. We propose how to use a DA
computer to achieve ad recommendations
under the constraints, including transforming
the problem to the QUBO model.
The remainder of this paper is organized as
follows. Related work is introduced in Section 2. Our
proposed method is presented in Section 3. Section 4
presents the experimental evaluation, followed by the
conclusion in Section 5.
2 RELATED WORK
We review the previous studies and techniques on
computational advertisement in this section,
including click-through rate (CTR) and conversion
rate (CVR) prediction, ad recommendation, and
constrained bidding optimization related to our work.
2.1 CTR and CVR Prediction
CTR and CVR predictions (Shan et al., 2018; Su et
al., 2017), which play an essential role in the online
advertising industry, are modeled as classification
problems. Logistic regression (Agarwal et al., 2009;
Shan et al., 2018) and generalized linear models are
the most popular ways to model a prediction task for
achieving a high area under the curve (AUC). Shan et
al. Shan et al. (2018) proposed a triplet-wise learning
model, adopting regression to rank the impressions in
the following order: conversions (most valuable
impressions), click-only impressions, and non-click
impressions (least valuable ones). Recently,
factorization machines (FMs) (Juan et al., 2017; Pan
et al., 2018) have also been adopted for this purpose.
FMs can work on large sparse data to resolve cold-
start problems. Pan et al. (2018) presented a field-
weighted FM for improved capturing of feature
interactions between different fields. To further
improve the prediction accuracy, several deep
learning-based models (Wang et al., 2017; Yang et
al., 2019) have been proposed for learning nonlinear
features and historical information. Huang et al.
(2017) proposed a hybrid model using deep neural
networks as a deep layer to capture nonlinear
relationships in advertisement data while utilizing
FM as a shallow layer to finish the prediction task.
Their model successfully overcame the obstacle
where a shallow-layer model could not use high-order
features and reduced computational complexity.
Ad recommendation resembles CTR or CVR
prediction. Kang et al. (2020) proposed a real-time ad
recommendation system that preprocesses a user’s
history data with a tree structure to obtain accurate
recommendation results.
2.2 Constrained Bidding Optimization
Although our work is similar to an ad
recommendation, the difference is that we need to
satisfy constraints, which makes our problem
challenging. Maximizing the conversion ratio under
constraints is a combinatorial optimization problem.
In computational advertising, most of the
constraints, such as budgets, are set from the
advertiser’s perspective. In particular, the advertisers
want to maximize their benefits under budget
constraints through a DSP. Abrams et al. (2007) were
among the first to consider bidder’s budgets to
optimize ad delivery while predicting bid prices. Wu
et al. (2018) combined the Markov decision process
with a model-free reinforcement learning framework
to
address the complexity of optimizing the bidding
ICEIS 2021 - 23rd International Conference on Enterprise Information Systems
432

Figure 1: Prediction model.
strategy under budget constraints. Yang et al. (2019)
considered two types of constraints: bidder budgets
and cost-per-click (CPC). They chose CPC as a
crucial performance indicator constraint. After
defining two constraints, they proposed an optimal
bidding strategy to maximize CVR based on a linear
programming problem. The study most similar to
ours is that of Grigas et al. (2017). They optimized
ads from the DSP’s perspective: under the budget
constraints, DSP aims to maximize its profit while
helping advertisers to obtain valuable impressions. To
achieve this goal, they used Lagrangian relaxation to
develop their model and then transformed the
problem into an optimization problem.
The research above aimed to optimize ads under
various constraints, including budgets and CPC;
however, periodic updates of the optimization problem
remained an open question because of its time
complexity. Even if we optimize the problem once, the
optimized result cannot be applied to the real system
for a long time because the preconditions for the
optimization vary over time, which results in
decreasing the effectiveness of the optimization result.
Thus, periodic updates of the optimization
problem are necessary to improve performance. Once
we can realize periodic updates, we may increase the
accuracy of estimating the users’ behavior and
improve the optimization.
3 PROPOSED METHOD
To meet the needs of DSP for the ad delivery
constraints and to reflect users’ behavior changes, we
2
IAB Tech Lab - Taxonomy,
https://www.iab.com/guidelines/taxonomy/
propose a DA-based method to optimize ads
periodically. Our goal is to achieve a higher CVR by
updating the optimization periodically in a short time.
In each period, we execute a prediction algorithm,
such as Logistic regression model or XGBoost, to
capture the probabilities of each user’s candidate ad
category, after which we solve the optimization
problem by using DA, a quantum-inspired computer.
3.1 Problem Formulation
Our goal is to optimize the delivered categories of ads
for each user—with a high possibility of user
conversions—while satisfying the number of ad
deliveries for each category in a fixed period with
periodic updates. We analyze each user’s web page
visit history to predict what ad category will be
converted. For this, we adopt 26 categories (shown as
) of ads defined by the IAB taxonomy
2
.
We formulate our problem as follows. Figure 1
shows our prediction model consisting of the training
and testing phases. In the training phase, we create a
feature vector for each user ∈
who
converted during period
using his/her visit
history during period
. By using the feature
vector, we train a classification model to predict the
category of ads converted by each user. In the testing
phase, we predict and optimize ads to be delivered to
every user, shown as
, who visited web pages
during
just before the prediction starting time
,
. After the prediction and the optimization,
the results are adopted during the next period
for the users in
. This is different from the usual
machine learning methods. We precalculate the ad
Real-time Periodic Advertisement Recommendation Optimization under Delivery Constraint using Quantum-inspired Computer
433

delivery category for each user
regardless of
his/her future appearance in
because we do
not have enough time to decide the ad category to
deliver after knowing that he/she appears. We ignore
predicting the ad category for the users not included
in
, that is, a different strategy is adopted to
deliver ads. Based on the know-how that users will
appear in the log data continuously in a short period,
updating both the prediction and the optimization
frequently is necessary to achieve high accuracy.
Besides, to satisfy the constraints, frequent updates of
the optimization problem are indispensable.
We assume that each ad in 26 categories has
constraints, where
is the delivery ratio of category
c against the entire category satisfying
∑
∈
1.
The actual constraint is the number of deliveries
defined for each ad. We calculate
based on the
given number of ads in each ad category during
. Subsequently, for each ad category ∈,
we estimate the conversion probability for each user
in
, shown as
,
, based on the pre-trained
classification model and his/her access log during
,
to
,
. Because the ratio
of delivered ad categories for test users set
must
satisfy the number of delivery constraints ∀∈
,
|
|
, we optimize to choose the
category for each user in
with as high
,
as
possible under the delivery constraints. Although
some users appear in
multiple times, we
assume that each user appears only once during
for simplicity, which is acceptable if we can
shorten
by adopting our proposed method.
3.2 Overview
Our framework consists of two steps: 1) a
preprocessing step on standard CPUs, 2) an
optimization step on DA. In the preprocessing step, for
each user, our method predicts the CVR of each
candidate category by using a pre-trained prediction
algorithm. In the optimization step, we combine the
predicted CVR with the delivery constraints and
generate the final category for each user using DA. We
use DA for optimizing the delivery categories under
the constraints. Note that the prediction algorithm and
the optimization method are independent, which makes
our method highly portable.
3.3 Conversion Probabilities of Ad
Categories for Each User
In this subsection, we describe a method to calculate
the probability of the ad category that a user will
convert. Training data is collected to extract each
user’s visited web pages’ categories and his/her
converted ads’ categories. Each user ∈
has a
feature vector
,
,…,
,
|
|
, where
,
represents the ratio of the web page category ∈
user visited during
weighted by time, as
shown in (1). Here, the weighting is linear from 0 to
1, where the recent history has a larger weight.
,
,
∑
,
∈
(1)
where
,
∑
1
,
∈
,
|uservisitedawebpage
ofadcategory∈
attimein
,
,
whentraining
,
whenpredicting
(2)
We use a prediction algorithm to calculate the
conversion probabilities of each ad category. To train
the prediction algorithm,
is used as the input
vector, and the converted category
is used as the
output label for each user ∈
who converted
during
. At
,
, we input the feature
vector of each user ∈
and calculate the
conversion probability
,
for each candidate ad
category ∈.
3.4 Optimizing Category Predictions
3.4.1 DA and QUBO Model
DA by Fujitsu Ltd. (Aramon et al., 2019) aims to
solve a combinatorial optimization problem at high
speed with digital circuits inspired by quantum
computing. DA can search for the minimum value of
the energy function of a QUBO model. As a quantum
computer, DA can only adopt the input of the QUBO
model, as shown in (3):
1
2
,
,
(3)
where ,,and con are the inputs of DA, and ∈
0,1 is a bit. Weight matrix reflects the quadratic
coefficients of the model, while vectors and
represent linear coefficients and a constant,
respectively. The value of con, the elements in W, and
the elements of b must be integers. DA calculates the
ICEIS 2021 - 23rd International Conference on Enterprise Information Systems
434

global minimum value of
and outputs the value
of all bits x when
reaches a minimum.
3.4.2 DA-based Category Prediction
Even after the conversion probabilities
,
for each
user are calculated in Section 3.3, we cannot simply
choose the category with the highest probability as
the prediction result because the number of ads in
each category must satisfy the number of delivery
constraints. Maximizing accuracy while satisfying
the constraints is a combinatorial optimization
problem, which is time-consuming and challenging to
solve using a conventional computer. Instead, we use
DA to accelerate the optimization.
Our research goal is to maximize the prediction
accuracy under the constraints of delivery
distribution. The outputs of the DA must satisfy two
constraints: 1) each user should be assigned only one
category (constraint 1); 2) the number of ads to be
delivered in each category must meet the delivery
constraint (constraint 2).
We combine the probabilities with the constraints
and apply them to the QUBO model. Based on the
research goal, we define an objective function with
three terms in (4):
,
,
|
|
|
|
,
|
|
1
|
|
,
|
|
|
|
,
where
,
is the probability from 0 to 100 (in
percent) that user will convert to category , which
is calculated from the prediction algorithm in Section
3.3;
,
∈
0,1
shows that ads of category are
assigned to user when
,
1 and are not
assigned to user when
,
0. We adopt one-hot
encoding to represent each user’s assigned ad
category with
|
|
bits.
|
|
and
|
|
are the numbers
of users and categories, respectively. Moreover
|
|
is the delivery constraint of category that
we must satisfy, where
is the delivery ratio of
category c. Furthermore, , , and are three
parameters. We assign category as a predicted
result for user if and only if
,
1.
The constraints in (4) are soft, which causes
several users to violate the constraint. Thus, we apply
the following post-process. If he/she has multiple
assigned categories, the category with the highest
probability is assigned from the multiple assigned
categories that do not have full assignments, i.e., from
remaining categories among the multiple assigned
categories. Besides, if he/she has no categories, the
category with the highest probability among the
remained categories is assigned.
3.5 Transforming Objective Function
to the QUBO Model
To utilize DA, we have to transform our defined
objective function into a QUBO model and to derive
three necessary inputs: weight matrix , vector, ,
and constant of DA in (3). For convenience, we
denote each bit
as
,
∙
|
|
. As in the
QUBO model, our objective function also has
quadratic, linear, and constant terms. In our objective
function, we mix quadratic, linear, and constant terms
in the function's three terms. However, in a QUBO
model, the input of the quadratic coefficient is a
weight matrix , the input of the linear coefficient is
vector , and the input constant is . Thus, we
must expand the objective function to extract
coefficients of each term and reorganize them into ,
, and of the QUBO model. Subsequently, we
feed them to DA as inputs. Because the function has
three parts, for convenience and clarity, we introduce
those three parts in the order below.
The first part
∑∑
,
,
|
|
|
|
in (4) is to
maximize the accuracy because this term can reach a
lower value linearly when a category with higher
probability is selected for the user. We extract the
linear coefficient into
, as in (5).
,
, ∗
|
|
The second part
∑
∑
,
|
|
1
|
|
ensures the
existence and uniqueness of the assigned category for
each user. If and only if there exists one assigned
category recommended to one user, both
∑
,
|
|
1
term and its square are 0. If there are no or multiple
solutions,
∑
,
|
|
1
becomes larger than 0,
producing a penalty value. This part generates
quadratic terms, linear terms, and constants of the
QUBO model shown in (3). We sort quadratic
coefficients, linear coefficients, and constants into
,
, and
, as shown in (6)(7)(8).
,
2,
|
|
|
|
Real-time Periodic Advertisement Recommendation Optimization under Delivery Constraint using Quantum-inspired Computer
435

2
|
|
The third part
∑
∑
,
|
|
|
|
ensures that the
number of ads for each category satisfies the delivery
constraints. For each category, the closer the number
of the predicted category to the upper bound, the
smaller
∑
,
|
|
will be obtained. This part also
generates a quadratic term, a linear term, and a
constant of the QUBO model. Again, we sort
quadratic coefficients, linear coefficients, and
constant into
,
and
in (9), (10), and
(11).
,
2,
wheremod
|
|
mod
|
|
2
,where
mod
|
|
We combine quadratic, linear, and constant terms
in three parts to form the final weight matrix W,
vector b, and constant con of the QUBO model and
feed them to DA as inputs, where
;
;
. The process of transforming into the QUBO
model is shown in Algorithm 1.
3.6 Utilization of DA
After we feed the weight matrix , vector , and
constant con to DA as input, DA provides two
annealing modes to be selected: normal mode and
replica-exchange mode (Aramon et al., 2019).
Because the normal mode requires us to train
annealing parameters, for convenience, we choose the
exchange mode, which performs “parallel tempering”
and can set the temperature automatically. When the
energy is stable, the DA returns the status of all bits.
For each user, we check the status of the
corresponding bits and judge whether both
constraints are satisfied. We adopt the result only
when the following two constraints are satisfied: a
user is assigned to only one category c (constraint 1),
and the total number of users to receive ads of
category c does not violate the maximum number DC
(constraint 2). Otherwise, the post-process described
in Section 3.4.2 is adopted. The process of utilizing
DA is shown in Algorithm 2.
Algorithm 1: Transforming an objective function to the
QUBO model.
Input: : conversion probability of all users
,,:parameters of trade-off
: delivery constraint of all ad categories
|
|
: number of ad categories
|
|
: number of users
Output: ,,: coefficients of the QUBO
model
1
←
|
|
∙
|
|
2
Initialize ,
,
as zero
matrices
3
Initialize ,
,
,
as 1
zero vectors
4
for ←1 to n do
5
←2
6
←2
7
end for
8
for ←1 to
|
|
do
9 enumerate each pair of categories
10
for ,
in combinations(
|
|
,2) do
11
∙
|
|
∙
|
|
←2
12
∙
|
|
∙
|
|
←2
13
end for
14
end for
15
←0
16
for ←1 to
|
|
do
17 enumerate each pair of users
18
for ,
in combinations(
|
|
,2) do
19
∙
|
|
∙
|
|
←2
20
∙
|
|
∙
|
|
←2
21
end for
22
←
23
end for
24
←
|
|
25
for ←1 to
|
|
do
26
for
←1 to
|
|
do
27
1∙
|
|
←
,
28
end for
29
end for
30
←∙
∙
31
←∙
∙
∙
32
←∙
∙
33
return ,,
ICEIS 2021 - 23rd International Conference on Enterprise Information Systems
436
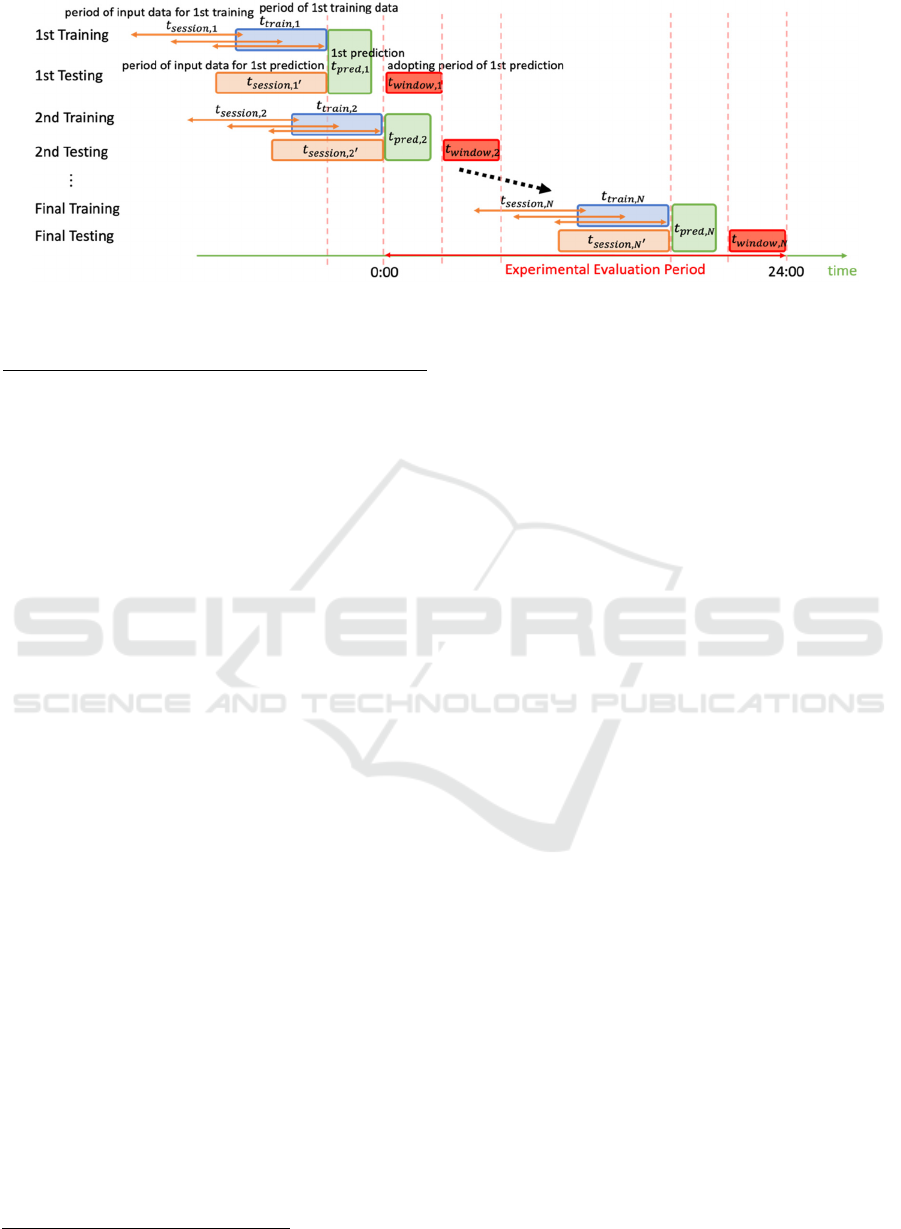
Figure 2: Overview of periodic recommendation.
Algorithm 2: Utilizing DA.
Input: : conversion probability of all users
,,:parameters of trade-off
: delivery constraints of all ad categories
|
|
: number of ad categories
|
|
: number of users
Output: result: predicted ad category for all users
1
,,←Transform
,
,,,,
2
←DigitalAnnealing,,
3
←∅
4
for ←1 to
|
|
do
5
←
∑
||
6
if =1 then only 1 result bit with value 1
7
for
←1 to
|
|
do
8
if
,
=1 then
9
←
10
←
1
11
end if
12
end for
13
else
14
←
∪user needs a post-process
15
end if
16
end for
17
18
apply post-process to ∀ in
described in Section 3.4.2
19
return
4 EXPERIMENT EVALUATION
4.1 Dataset
We used real log data for the experimental evaluation.
The log data consists of an auction log and a
conversion log accumulated by Geniee DSP
3
. The
auction log is generated when a user visits a web page
3
Geniee, Inc. https://en.geniee.co.jp/
with an advertisement tag, and RTB is performed.
The conversion log is generated when a user who
views an advertisement performs a conversion.
In this experiment, the identification (id) assigned
to each unique browser is assumed to be the user’s
unique id. The visit history of web page categories
used as input features can be aggregated from the
auction log using the user’s unique id and time stamp.
We use the ratio of each advertisement category in the
auction log in each
as the delivery constraint.
We used raw data collected from November 6th,
2019 to November 8th, 2019. The 24-hour data on
November 7th was used to tune time-parameters, i.e.,
,
, and
. As for
, it must
satisfy less than
so that we will confirm it in
the experiment. The 24-hour data on November 8th
was used for the experimental evaluation. We split the
evaluation data by
to simulate the proposed
method. For example, 24-hour evaluation data are
split into 72 windows when
= 20 min.
As shown in Figure 2,
slides over time,
and we use the data during
period as training
data. Importantly, when tuning time parameters with
data on November 7th, in several
(such as
00:00 to 00:20), we need to use data on November 6th
to generate
and
. The number of
converted users was 9,823 on November 6th, 9,328
on November 7th, and 9,874 on November 8th. The
number of users in the training and test datasets,
and
, depends on the time parameters.
Notably, some of the converted users in
did
not visit the web pages during
, so they were
not included in
. The number of converted users
included in
was 4,706 out of 9,823 on
November 8th.
Real-time Periodic Advertisement Recommendation Optimization under Delivery Constraint using Quantum-inspired Computer
437

4.2 Evaluation Metrics
The novelty of our proposed method is solving the
combinatorial optimization problem periodically
around a short time, maximizing the CVR while
satisfying the number of delivery constraints. To
confirm that our proposed method predicts an ad
category for each user with high accuracy while
satisfying the delivery constraints in an appropriate
duration, we use three metrics:
,
and execution time. Here, we assume
that the ground truth is the category in which each
user was converted in
. We do not use the
AUC metric (which is common in CVR prediction)
because our task is different: to predict the conversion
category under the delivery constraints. We need to
verify whether our prediction is correct. Thus, we
adopted accuracy instead of AUC.
is the average ratio of correctly
predicted users to all converted users in
.
∩
|
|
,
where
∩
is the set of converted users with
the same predicted category as the category in the
ground truth;
is the set of all converted users
in
.
shown in (13) is the ratio of
correctly predicted users to all converted users in the
test dataset. We introduce
as a fair
comparison between the different time parameters
because when we change
, it affects the set of
converted users.
∑
∩
|
|
,
where
is the set of total converted users in the test
dataset.
Finally, the execution time measures the time (in
seconds) spent to generate the recommendation.
All the experiments were executed on a server
with the following configuration: two Intel Xeon
Gold 6148 CPUs, 2.40 GHz (20 cores, 40 threads),
with 192 GB of memory, running on CentOS 7.6. The
optimization process (finding the minimum value and
bits of the QUBO function) was run on DA (Aramon
et al., 2019).
4.3 Prediction Algorithm
In order to generate the conversion probabilities of ad
categories for each user described in section 3.3, we
need to adopt a base algorithm to receive the input
feature vector
and output the conversion
probability
,
for each candidate ad category ∈.
In our experiment, we chose Logistic regression and
XGBoost (Chen et al., 2016) as prediction algorithms
for their effectiveness and high speed.
4.4 Baseline Methods
We compared our proposed DA method with two
baselines: “Random” and the genetic algorithm
(shown as GA).
The “Random” method omits the optimization
step and adopts a random selection of ad categories
but adopts the post-process shown in Section 3.4.2 to
satisfy the delivery constraints. By comparing our
method with Random, we can confirm the
effectiveness of solving delivery constraints.
The genetic algorithm (GA) (Goldberg, 1989)
was also chosen to solve the combinational problem
as a popular and efficient method to confirm the
effectiveness of DA in solving delivery constraints
more strictly. GA runs on common CPUs and does
not require binary bits. Instead of one-hot encoding,
we can use one variable to represent all the candidate
results of each user so that the objective function is
simplified as in (14).
,
|
|
,
|
|
|
|
,
where
,
is the probability that user will convert
to category
;
is the delivery number of category
that we must satisfy;
,
∈0,1 is a binary
variable where
,
equals 1 when the converted
category
equals category , as shown in
(15);
∑
,
|
|
is used as a count for each category,
that is, how many ads are delivered; and are two
parameters.
,
1,
0,
Compared with (4), (14) omits the constraint that
ensures that each user has only one prediction result.
As in DA, GA does not guarantee satisfying the given
constraint. Therefore, we also adopt the post-process
described in Section 3.4.2.
ICEIS 2021 - 23rd International Conference on Enterprise Information Systems
438

Figure 3: Result of
without constraints when changing the time parameters: (a) Fixed at
= 4 h,
= 6 h, and varying
; (b) Fixed at
= 20 min,
= 6 h, and varying
; (c) Fixed at
=
20 min,
= 4 h, and varying
.
Table 1: Experiment Results (
t
train
= 4 h and
t
session
= 6 h).
Method
Prediction
algorithm
Optimization Technique
Violation
rate
Execution time
(s) (
)
Baseline
Logistic
regression
Random(
=20 min)
0.180 0.219 0.595
GA(
=20 min)
0.202 0.239 0.030 525
Proposed
DA(
=20 min)
0.229* 0.278*
0.020 108
DA((
=5 min)
0.324*
0.020 108
Baseline
XGBoost
Random(
=20 min)
0.180 0.216 0.595
GA(
=20 min)
0.198 0.237 0.029 526
Proposed
DA(
=20 min)
0.229* 0.277*
0.013
109
DA(
=5 min)
0.322*
0.013 108
* Statistically significant at p < 0.01 when comparing with our proposed method, DA, with Random and GA
4.5 Time Parameters Tuning
In this section, we tune the parameters t
window
, t
train
,
and t
session
to achieve the best average
by evaluating the classification
using the prediction algorithm without considering
the delivery constraints. We used the 24-hour data on
November 7th to tune the parameters.
Figure 3 shows the results of
when parameters
,
, and
are
varied. As shown in Figure 3(a), the accuracy
increases with a decrease in the model update interval
because the latest action of the user can be
reflected by a decrease
. In Figure 3(b), the
accuracy peaks when the training data period
is
four hours because if
is small, the number of
data points in
becomes small, resulting in poor
learning outcomes. However, if
is extremely
large, the accuracy decreases due to training on old
data. In Figure 3(c), a larger
increases the
accuracy because more visit history of the user is
reflected by increasing
.
Finally, we set the parameters as
= 20
min,
= 4 h, and
= 6 h for the rest of the
experiments. Further tuning such as decreasing
and increasing
will be available as
long as
holds.
4.6 Experimental Results under the
Delivery Constraints
We used the 24-hour data on November 8th for the
evaluation which was split into 72 time slots because
of
= 20. Parameters ,,and in our
objective function in (4) and parameters and in
the GA’s objective function in (14) were tuned on the
first 10 time slots of the data. In contrast, the
remaining 62 time slots data were used for evaluation.
By adopting a grid search, we chose 1,
5,10, 1, and 10.
Table 1 shows the results. Because the constraints
in (4) and (14) are soft, we show the percentage of
users who violated the constraints, shown as violation
rate in Table 1. During the post-process for violated
users described in Section 3.4.2, we chose each user’s
ad category from among his/her top six ad categories.
Recall that
shows the averaged
accuracy per window. Thus, we can compare with
only when the same parameters
(
,
, and
) are used among the
methods. On the contrary, if the different parameters
are used, we cannot use
for fair
comparison because the converted users in each
window will be different. In such a case, we must use
which shows the correctly predicted
users against all converted users in the whole test
Real-time Periodic Advertisement Recommendation Optimization under Delivery Constraint using Quantum-inspired Computer
439

dataset. Compare with the result in Mo et al., 2020,
the
of GA-based method improves
because of fine-tuned batch size.
We conducted a paired t-test for accuracies
between each baseline and our proposed method. As
a result, we confirmed that our proposed method
outperforms the baselines, which is statistically
significant at p < 0.01. In addition, we confirmed that
our proposed method achieved the shortest execution
time. Notably, we do not compare the execution time
with the Random method because the method is not a
combinational optimization algorithm and has the
lowest recommendation accuracy.
We also experimented with different
to
confirm the effectiveness of shorting window size.
Because the DA completed the execution within 5
min, we set
to 5 min with the other time
parameters as in the previous setting (
= 6 h
and
= 4 h). As shown in Table 1, we confirmed
increased drastically as
was
shortened, which means that if the optimization
algorithm runs faster, the number of users that we
correctly predict their ad categories increase. Hence,
shortening the periodic optimization on DA is
important.
To summarize the experimental results, with
Logistic regression, we successfully shortened the
periodic advertisement recommendation from 525s to
108s and increased the accuracy from 0.239 to 0.324
compared to GA. With XGBoost, we also shortened
the execution time from 526s to 108s while
improving accuracy from 0.237 to 0.322.
5 CONCLUSION
In this paper, we proposed a new method, namely the
DA method, to optimize ads periodically in a short
period by using DA to solve the optimization
problem: maximizing CVR while satisfying the
delivery constraints, that is, the number of ads
delivered for each category. Our method consists of
two steps: 1) prediction to generate ad candidates for
each user, and 2) optimization of candidates to meet
the number of ad delivery constraints, which is
difficult to solve within an acceptable period on a
general-purpose computer. Experiments on a real
dataset showed that our proposed method
successfully improved the accuracy by shortening the
periodic advertisement recommendation: 0.239 to
0.324 with prediction algorithm Logistic regression
while shortening the execution time from 525s to
108s; and 0.237 to 0.322 with XGBoost while
shortening the execution time from 526s to 108s.
Our future plan includes conducting online tests
to verify the performance of our proposed model.
REFERENCES
Abrams, Z., Mendelevitch, O., and Tomlin, J., 2007.
Optimal delivery of sponsored search advertisements
subject to budget constraints. In Proceedings of the 8th
ACM conference on Electronic commerce, pp. 272-278.
Agarwal, D., Chen, B., and Elango, P., 2009. Spatio-
temporal models for estimating click-through rate. In
Proceedings of the 18th international conference on
World wide web, pp. 21-30.
Aramon, M., Rosenberg, G., Valiante, E., Miyazawa, T.,
Tamura, H., and Katzgrabeer, H., 2019. Physics-
inspired optimization for quadratic unconstrained
problems using a digital annealer. Frontiers in
Physics, 7(48), pp.1-14.
Chen, T., and Guestrin, C., 2016. XGBoost: A scalable tree
boosting system. In Proceedings of the 22nd ACM
SIGKDD International Conference on Knowledge
Discovery & Data Mining, pp. 785-794.
Goldberg, D. E., 1989. Genetic Algorithms in Search,
Optimization and Machine Learning. Addison-Wesley
Longman Publishing Company.
Grigas, P., Lobos, A., Wen, Z., and Lee, K., 2017. Profit
Maximization for Online Advertising Demand-Side
Platforms. in Proceedings of the ADKDD'17, pp. 1-7.
Huang, Z., Pan, Z., Liu, Q., Long, B., Ma, H., and Chen, E.,
2017. An Ad CTR Prediction Method Based on Feature
Learning of Deep and Shallow Layers. In Proceedings
of the 2017 ACM on Conference on Information and
Knowledge Management, pp. 2119-2122.
Juan, Y., Lefortier, D., and Chapelle, O., 2017. Field-aware
factorization machines in a real-world online
advertising system. In Proceedings of the 26th
International Conference on World Wide Web
Conference, pp. 680-688.
Kang, S., Jeong, C., and Chung, K., 2020. Advertisement
Recommendation System Based on User Preference in
Online Broadcasting. In Proceedings of 2020
International Conference on Information Networking,
pp. 702-706.
Mo, F., Jiao, H., Morisawa, S., Nakamura, M., Kimura, K.,
Fujisawa, H., Ohtsuka, M., and Yamana, H., 2020.
Real-Time Periodic Advertisement Recommendation
Optimization using Ising Machine. In Proceedings of
2020 IEEE International Conference on Big Data
(IEEE BigData 2020), 3pages (accepted as poster
presentation).
Pan, J., Xu, J., Ruiz, A., Zhao, W., Pan, S., Sun, Y., and Lu,
Q., 2018. Field-weighted factorization machines for
click-through rate prediction in display advertising. In
Proceedings of the 2018 World Wide Web Conference,
pp. 1349-1357.
Shan, L., Lin, L., and Sun, C., 2018. Combined Regression
and Tripletwise Learning for Conversion Rate
Prediction in Real-Time Bidding Advertising. in
ICEIS 2021 - 23rd International Conference on Enterprise Information Systems
440

Proceedings of the 41st International ACM SIGIR
Conference on Research & Development in
Information Retrieval, pp. 115-123.
Su, Y., Jin, Z., Chen, Y., Sun, X., Yang, Y., Qiao, F., and
Xu, W., 2017. Improving click-through rate prediction
accuracy in online advertising by transfer learning. In
Proceedings of the International Conference on Web
Intelligence, pp. 1018-1025.
Wang, R., Fu, B., Fu, G., and Wang, M., 2017. Deep &
cross network for ad click predictions. In Proceedings
of the ADKDD'17, pp. 1-7.
Wu, D., Chen, X., Yang, X., Wang, H., Tan, Q., Zhang, X.,
and Gai, K., 2018. Budget constrained bidding by
model-free reinforcement learning in display
advertising. In Proceedings of the 27th ACM
International Conference on Information and
Knowledge Management, pp. 1443-1451.
Yang, X., Deng, T., Tan, W., Tao, X., Zhang, J., Qin, S.,
and Ding, Z., 2019. Learning Compositional, Visual
and Relational Representations for CTR Prediction in
Sponsored Search. In Proceedings of the 28th ACM
International Conference on Information and
Knowledge Management, pp. 2851-2859.
Yang, X., Li, Y., Wang, H., Wu, D., Tan, Q., Xu, J., and
Gai, K., 2019. Bid optimization by multivariable
control in display advertising. In Proceedings of the
25th ACM SIGKDD International Conference on
Knowledge Discovery & Data Mining, pp. 1966-1974.
Real-time Periodic Advertisement Recommendation Optimization under Delivery Constraint using Quantum-inspired Computer
441
