Online State Estimation for Microscopic Traffic Simulations using

Multiple Data Sources*

Kevin Malena

1 a

, Christopher Link

, Sven Mertin

, Sandra Gausemeier

and Ansgar Trächtler

1,2

Heinz Nixdorf Institute, Paderborn University, Fürstenallee 11, Paderborn, Germany

Fraunhofer Institute for Mechatronic Systems Design IEM, Zunkunftsmeile1, Paderborn, Germany

Keywords: Microscopic Traffic Simulation, Online State Estimation, Mixed Road Users, Sensor Fusion, Integer

Programming, Route Choice, Vehicle2Infrastructure.

Abstract: The online fitting of a microscopic traffic simulation model to reconstruct the current state of a real traffic

area can be challenging depending on the provided data. This paper presents a novel method based on limited

data from sensors positioned at specific locations and guarantees a general accordance of reality and

simulation in terms of multimodal road traffic counts and vehicle speeds. In these considerations, the actual

purpose of research is of particular importance. Here, the research aims at improving the traffic flow by

controlling the Traffic Light Systems (TLS) of the examined area which is why the current traffic state and

the route choices of individual road users are the matter of interest. An integer optimization problem is derived

to fit the current simulation to the latest field measurements. The concept can be transferred to any road traffic

network and results in an observation of the current multimodal traffic state matching at the given sensor

position. First case studies show promosing results in terms of deviations between reality and simulation.

1 INTRODUCTION

In recent years, the evolution of Intelligent

Transportation Systems (ITS) has been rapid due to

constantly improving modelling software for traffic

systems as well as the related sensor and computing

technology. Depending on the different purposes of

research and the wide range of data acquisition

technologies there are several methods on how to

reconstruct, analyze and improve the traffic state. The

motives range from the strategic change of the traffic

infrastructure or the recommendation of a certain

route (e.g. navigation systems) to the improvement of

the safety of road users. Another challenging aim is

to control the traffic through its Traffic Light Systems

(TLS). The stabilization of inner-city traffic with

intelligent traffic controls offers a practicable and

pleasant way of counteracting the problems of slow

traffic and congestions at intersections. Therefore it is

necessary to observe and approximate the current

traffic situation in the surroundings of the TLS the

https://orcid.org/0000-0003-1183-4679

*Research supported by the Ministry of Economy, Innova-

tion, Digitalization and Energy of North Rhine-Westphalia,

Germany.

best possible way. Based on these requirements to

develop a fast reacting solution for the control of

TLS, this paper formulates a novel approach on how

to online-estimate the current traffic state by

combining a microscopic traffic simulation model

with real-time field measurements. The methodology

is developed for a real road traffic system in Schloß

Neuhaus (Paderborn, Germany), but also transferable

to any comparable road traffic system. On top of

conventional induction loops and telegrams for public

transport (PT), i.e. vehicle-to-infrastructure (V2I)

communication, the road network is equipped with

further detectors. Their online measurements consist

of the arrival time and the speed of each individual

crossing road user. Working on basis of radar

technology, these detectors immediately classify

vehicle types compliant with data policies. This

classification plays a central role in this approach

because the extra information provides new

possibilities for traffic estimation and forecasting

since there cannot be a direct detection of individual

386

Malena, K., Link, C., Mertin, S., Gausemeier, S. and Trächtler, A.

Online State Estimation for Microscopic Trafﬁc Simulations using Multiple Data Sources.

DOI: 10.5220/0010414903860395

In Proceedings of the 7th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2021), pages 386-395

ISBN: 978-989-758-513-5

vehicle routes by e.g. license plates (due to

governmental restrictions in Germany). Thus, it is not

possible to obtain complete and continuous

information about the state of the complex traffic

system. The simulation-based Dynamic Traffic

Assignment (DTA) technique presented here

estimates and predicts individual route choices for all

road users in order to model the current traffic state.

To overcome the difficulty of mutual interactions

between road users and the traffic infrastructure such

as TLS, a microscopic traffic simulation is used. This

incorporation of a simulation offers a major

advantage over a purely algorithmic information

processing of the measured data. The concept

attempts to solve the problem resulting from

discontinuous, event-based and only locally recorded

data by using route predictions to link past, current

and future field measurements. All available data

resources like the specially equipped radar detectors

and the less informative induction loops can be

combined in this versatile approach. In order to

finally control the TLS optimally, the traffic has to be

assigned dynamically using the online measured data.

This requires a sufficient accordance of the real

measured data with the data generated in the

microscopic simulation. The resolution and accuracy

of the simulation as well as the algorithmic efficiency

are of particular importance. The microscopic level

allows to distinguish between different vehicle types

and enables the required online responsiveness of

future TLS to individual road users. The needed fast

responsiveness also implies short time intervals for

the DTA algorithm. In order to remain efficient, the

replicated simulation network itself has to be limited.

It should only contain the main parts of the test area,

i.e. solely the high traffic roads close to TLS and

sensor locations. The traffic state reconstruction itself

is formulated as an assignment problem. Based on the

measurements of the mixed traffic of road users, the

state description is mathematically translated into an

integer linear programming problem for a predefined

short time interval.

2 LITERATURE REVIEW

There are different purposes to estimate the traffic

state within areas and therefore different ways to

achieve the needed estimation. For example if cities

want to improve their transport infrastructure, it is

important to know which areas are usually loaded or

free at what specific time. It is usually for such

requirements that macroscopic statements on Origin-

Destination (OD) flows, which have been determined

offline solely on the basis of historical data, are

sufficient to make the necessary conclusions (Osorio,

2019a; Osorio, 2019b).

In contrast to these applications, which do not need

an online data processing, there are others which

require the estimation of the traffic state almost

immediately. Examples are navigation systems for

route suggestions or TLS to cope with the current

situation in the best possible way. The intention in

this research is to deliberately influence the traffic

flow through the area’s TLS rather than the routes of

the road users themselves. The more precise the road

traffic model is, the more efficient the control strategy

for the TLS can become. That justifies why this paper

formulates an approach to maintain a well

approximated traffic state that allows sophisticated

signaling for the TLS optimization. In order to reach

this aim, the simulation model needs to be adjusted

with and to the data provided by the field

measurements. There is already relevant literature

like (Chen, Osorio, & Santos, 2019) which uses

efficient Simulation-based Optimization (SO)

algorithms to reduce travel times with signal control.

However the control itself is mostly limited to a fixed-

time strategy or there are no complex phases used, i.e.

there is no lane specific release within the phases or

the very important phase transitions are unattended

(Kamal, Imura, Hayakawa, Ohata, & Aihara, 2015;

Zheng et al., 2019). In addition, it is usually not

shown how the traffic state was identified to

determine the control. Therefore it is to be assumed

that a perfect knowledge of the current traffic state is

presupposed or this important step was not

considered. On the contrary, (Wang, Wang, Xu, &

Wongpiromsarn, 2013) are a positive example who

disclose or at least name their data collection. The

difficulty and novelty within this project is that not

only green times or phase lengths for TLS are

variable, but that the phase sequence itself with its

complex phases should also be determined. This

phase selection is based on the current traffic situation

and thus in particular on the individual vehicles and

their types considered in this estimation. Because of

that, the traffic and especially the demand modelling

is crucial. According to the guidelines for traffic

simulation (Antoniou et al., 2014), the aim of the

necessary calibration for microscopic simulation

models is to close the gap between reality and

simulation. The demand calibration is mentioned as

basis for further steps such as car-following or lane-

changing models. Most other research deals with

driver behavior settings as calibration parameters

(Paz, Molano, Martinez, Gaviria, and Arteaga, 2015).

Their focus lies on the vehicle distribution at local

Online State Estimation for Microscopic Trafﬁc Simulations using Multiple Data Sources

387

detection positions and not on the route choice of

individual vehicles to achieve those detections. This

is a major difference to the research presented here.

Their data bases mostly consist of complete pre-

defined OD connections or the test area is as simple

as a highway with off- and on-ramps, e.g., in the

Kalman Filter based application in (Antoniou, Ben-

Akiva, & Koutsopoulos, 2010). In a highway scenario

there is no need for a complex route prediction since

all detectors just have one predecessor and successor.

The DTA concept presented in this paper is designed

for a more complex urban network allowing vehicles

to take routes to different subsequent detectors after a

local detection. Therefore the selection of the

individual routes can be considered as calibration

parameters. In contrast to fully detected vehicle

routes, field measurements just as the previous

mentioned enhanced traffic counts (radar detections

with vehicle type specification) are combined to

estimate the most likely individual vehicle route. The

combination of this data quality and the purpose to

control an urban traffic network through its TLS is

unique since also the online reaction time to estimate

the traffic state has to be very short. For example in

(Bierlaire & Crittin, 2004), the synthetic data have

several minutes as time interval, which is not

sufficient for this application. The desired choice of

TLS phase sequences requires the reaction time of

only a few seconds to adapt best to the current traffic.

3 PROBLEM FORMULATION

3.1 General Conditions & Idea

The concept of this DTA algorithm is to feed a

microscopic simulation model with real-time sensor

measurements to act as an (almost continuous) event-

based observer for the current traffic state. Many

operations can be performed offline in advance, but

others like the processing of the measured data have

to be done online whilst simulating the microscopic

traffic scenario. The keyword real-time is crucial

here, as there has to be sufficient computing time

remaining for the prospective TLS control. In order

to reconstruct the traffic situation between the local

detector positions, predictive route choices have to

link past and future measurements. The structure of

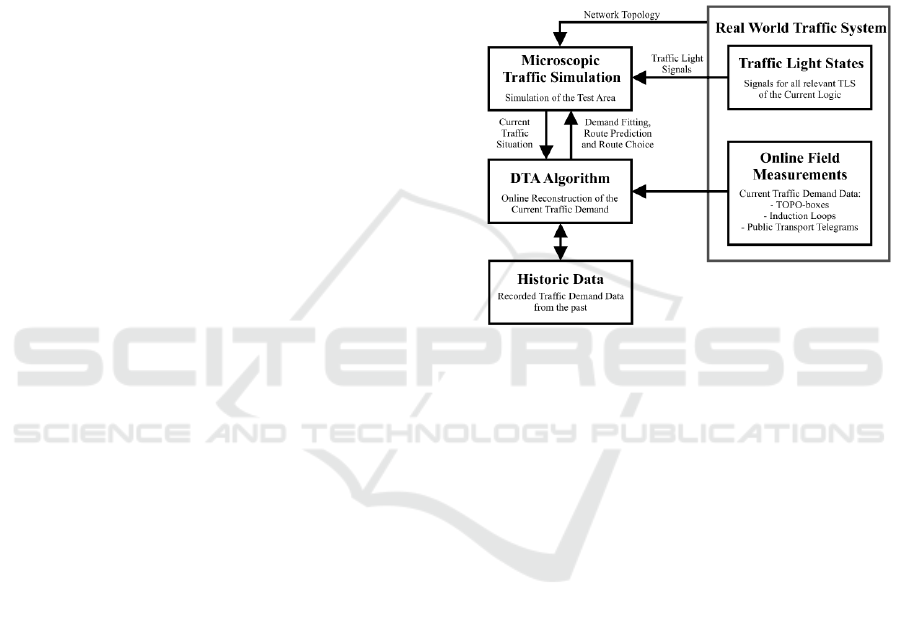
the presented simulation-based method is sketched in

Figure 1. The block diagram shows how the real

world scenario interacts with the simulation and what

kind of data is used for which purpose. As mentioned

before, an essential aspect is the differentiation

between the online and offline processing and

calculations. There are several calculations which can

be performed prior to the actual simulation as a kind

of initialization process where for example average

travel times for each vehicle type combined with the

different traffic light states are computed. The

intervals of other state estimators are relatively large

(often minutes). The idea of adjusting a running

simulation and the outsourcing of calculations are

among others the reasons why very small update

intervals (a few seconds) can be used for this online

state estimation.

Figure 1: Block diagram of the presented DTA concept.

The main online field measurements in this

research consist of superior traffic counts, i.e. not

only a time stamp for crossing the detector, but also

the vehicle type and the current speed are detected via

radar technology. These detectors are so-called

TOPO-Boxes and this kind of detection is necessary,

because the future TLS control should contain a

vehicle specific prioritization. Nevertheless, the

concept is able to be enhanced by incorporating less

detailed measurements of induction loops and/or

PT telegrams (V2I communication type of specific

PT buses and the TLS). These additional sensor

information are inferior to those of the TOPO-Boxes

and therefore result in different interdependent levels

in the decision making process of individual vehicle

routing. The vehicle types within this whole approach

are generally classified according to the 8+1 class

defined by the German Federal Road Research

Institute (BASt) in (Bundesministerium für Verkehr,

Bau und Stadtentwicklung, 2012). Thus passenger

vehicles along with motorcycles, trucks, trailer etc.

are taken into account. Additionally bicycles are

detected so that the detection and the simulation are

extended to the so-called ‘8+1+F’ classification (RTB

GmbH & Co. KG, 2019).

VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems

388

Subject to the variety of available data sources, the

algorithm has multiple routing levels. The most

important source allows the differentiation between

the above defined vehicle types. This is the reason

why the next subsection describes the highest routing

level in more detail (TOPO-Box Routing) and the last

subsection is dedicated to the interaction of all

considered and already mentioned levels.

3.2 TOPO-Box Routing

Since the TOPO-Boxes are mandatory due to their

type differentiation and their positioning between

successive TLS, this part of the paper dives deeper

into the mathematical description of the respective

dynamic problem. Some aspects of graph theory are

used to illustrate and explain the methodology of this

traffic estimation problem. Inspired by relevant

literature like (Bierlaire & Crittin, 2004), the traffic

network under research is modelled by a directed

graph to process the simulated data. The graph

 







is represented byits set of nodes  and

its set of links  . These nodes  can either be

junctions or geometric points which meet the given

traffic infrastructure. The geometric points are the

discretization tool to model curves etc. which directly

influence the simulation, e.g. in terms of possible

speeds and accelerations. Streets of the complex

traffic system are therefore modelled through the

links  . Special attention has to be paid to the

TLS-nodes



 , as they play a central role in

controlling the system. In contrast to (Bierlaire

& Crittin, 2004), the sensors monitoring the system

are not directly represented by a subset of the links,

but as geometric points 



 . The graph  does

only depend on the given infrastructure and not on the

time and is therefore used to describe the empty

traffic network. For all links   the respective

travel time to reach each detector   



calculated. For the presented approach it is important

that these travel times are stored prior to the actual

online simulation to determine the traffic state. Due

to different traffic light states and system loads, the

travel times will be modified over time. Any vehicle

state at any time can be accurately transmitted to the

data processing of the algorithm by the occupancy

vector 







It contains the vehicle type, the current

speed and the current position on a specified edge of

each single vehicle such that















ℎ



















vehicle type







ℎ



















vehicle speed









ℎ



















vehicle position







ℎ



















vehicle's link





(1)

The time dependent traffic state can be represented

through this occupancy with 

ℎ







being the

current number of vehicles in the system and each

vehicle type is associated with a different integer

(first entry of each row of







The aim of this theoretical construction is to help

assigning individual vehicles within the simulation to

specific sensors when there is a new measurement in

reality. The basic idea for the decision whether or not

a vehicle should be routed to a nearby sensor is to

check if the vehicle ‘fits’ to the corresponding sensor

measurement. The most important criteria to fit are

the accordance of measured and simulated vehicle

type and the needed travel time to reach the sensor.

Since the simulation has to run in real-time, the

simulation must be regularly adapted to the

measurements so that the traffic state can be well

estimated. Other criteria like the speed are less

appropriate, as they can be very discontinuous due to

curves, for example, and thus make the assignment

process more difficult. But since the speed is

measured, this information is used in a different way

to predict the future vehicle situation the best way

(explained later). It is a key aspect of the approach

that each of the mentioned vehicle types is handled

separately resulting in several subproblems.

Obviously there are several situations in complex

traffic systems where the route of vehicles has to be

assigned in different ways. In this DTA concept each

vehicle can be in any of the following positions to get

routed, which can be determined depending on the

current occupancy 







and the current

measurements. The first case is that the respective

vehicles are not in reach of any sensor; i.e. the travel

time to arrive at any of the specified sensors lies

beyond a user-defined threshold of the algorithm.

This means that those vehicle cannot fulfill any of the

measurements. The second case is that vehicles are

close to just one sensor. Here it is determined that if

there exists a detection in the reality, the vehicle is

routed towards this sensor to satisfy the measurement

(i.e. ‘deterministic routes or vehicles’). The last

scenario is that vehicles are able to reach multiple

detectors due to their calculated travel time.

Depending on the measurements of these sensors it is

possible to construct an optimization problem which

minimizes the travel time and maximizes the

assignment of currently available vehicles

simultaneously (so-called ‘flexible routes or

vehicles’). The derivation of this binary optimization

problem follows.

The time discretization of the problem is

determined by the step size  . Of particular

importance for the construction of the online

Online State Estimation for Microscopic Trafﬁc Simulations using Multiple Data Sources

389

optimization problem is the difference between

deterministic and flexible routed vehicles. The

previous designation indicates that vehicles with just

one reachable detector can be directly assigned to the

respective detector, whereas the routes for vehicles in

a ‘flexible assignment area’ are not predefined. The

assignment of these vehicles to sensors that have

current demand is subject of optimization. The

complexity of this optimization problem depends on

the number of vehicles  which are able to reach

multiple detectors as well as on the number of

reachable sensors 



for each of these vehicles

  . Because not all vehicles are even within

range of a single sensor it applies

  









. A flexible vehicle with its   





 reachable detectors results in 



 binary

optimization variables 









which determine

whether or not a vehicle will be routed towards the

respective sensor. The total number of optimization

variables at the 

step is

  











(2)

Because each of the vehicles can only be routed

once, the sum of all optimization variables for each of

the  vehicles needs to be less than or equal to





. This leads to the first  inequality conditions of the

optimization problem for the 

time step













 













 













 









 

 







   





(3)

where



 assigns the optimization variable





to the vehicle  . In order to route

the exact number of detected vehicles in the

corresponding time interval to the respective sensors,

additional constraints are added to the problem

formulation. These constraints are based on the

number of sensors   



 and ensure that already

assigned deterministic vehicles are considered. This

second part of the restrictions yields to





 













 









 

















 







   





(4)

with

 



 assigning the optimization variable





to the sensor  









 









 



being the total number of

measurements for sensor  









 









 



being the number of already (in

this time interval) deterministically routed

vehicles to sensor  









 









 



representing the measurements

still to be fulfilled for sensor  









If there are more vehicles that can be

deterministically routed than measurements

(









 









), the adjusted field measurements

are set to zero, i.e. 









  and just the nearest











vehicles are routed.

Through this inequality constraints the

optimization problem can be formulated as

























subject to 

















 























(5)

Just as already introduced, the objective 









can be chosen to minimize the travel times of the

vehicles to satisfy the detections and simultaneously

maximize the number of assigned vehicles in the

simulation. In this case the objective would be



















 



  











(6)

where

 







 



are the travel times for each vehicle

to the respective sensors,

 







  describe weighting factors for travel

time and assignment

If the current demand of a specific sensor cannot

be satisfied through the assignment of available

vehicles, new vehicles have to be inserted into the

simulation to fulfill the measurement, i.e. the

inequality constraints in (4) are not met with equality.

Notice that these insertions or spawns lead to a

general consistency in terms of traffic counts and

their equivalents in reality are incoming vehicles from

unobserved side streets. Once a vehicle is assigned to

a detector in the simulation, it cannot be reassigned

until it reaches the desired detector. A follow-up

destination is set for each vehicle assignment, i.e. a

route prediction based on probabilities derived from

historical data is performed. The details of this

stochastic process will not be further discussed here.

It closes the gap between the matching of a field

measurement and the intrusion of a vehicle into an

area for successive routing. Without the follow-up

VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems

390

routes there would be no routable vehicles for the

TOPO-Box Routing and all vehicles would have to be

spawned or generated. The data processing of the

historical ‘offline’ route prediction is done prior to the

main simulation and updated frequently during the

simulation. In doing so, a daytime-specific route can

be assigned to the vehicles online. This route can be

considered as less prioritized than the online route

choice determined by the optimization. The routable

vehicles for each vehicle type within the simulation

can be derived from the current occupancy 







with an additional query whether the previous

destination has already been reached. In the end of

every simulation step there has to be a check if still

routable vehicles are about to cross a detector. Since

these vehicles were not assigned through the routing,

a crossing is not justified and the vehicles need to be

removed from the simulation to ensure the

measurements of reality. In reality, these vehicles

have entered unobserved roads or parking lots.

3.3 Interaction of Different Routings

The previous section points out the concept of the top

level routing, but there are two more implemented

levels which optionally help the traffic state

estimation to be more accurate. It is clear that the

more information and data the algorithm is capable of

processing, the more precise the traffic estimation can

become and the better the TLS-control can adapt to

the current traffic. The second routing level affecting

all types of vehicles is based on the induction loop

data. As they are widely used nowadays, this

information can complement the TOPO-Box

measurements without the need to buy additional

measuring equipment. For the purpose of controlling

TLS they are extremely worthy since the radar

technology is quite vulnerable in congested areas.

Therefore, the TOPO-Boxes are not set up in the

direct vicinity of an intersection. On the contrary, the

induction loops are usually only to be found in these

areas which is why the combination of data sources

can be particularly profitable. The third and last data

source uses V2I-technology, but exclusively for

regularly driving PT buses. Those buses transmit

their PT line number at specified locations within the

system when approaching and leaving TLS. Right

now it is already used to prioritize the PT, but in a

way that has a strong negative impact on the other

traffic and thus additionally leads to unnecessary

congestion.

Because of that, the TOPO-Box Routing is

extended in this approach with the so-called

Induction-Loop Routing and the PT-

Telegram Routing. The TOPO-Boxes are the most

detailed and reliable data source in terms of detecting

vehicles, but due to the relatively poor network

coverage and the network complexity it is still hard to

estimate the traffic state between measuring points.

The induction loops are lane based, so better capable

of detecting turning ratios at intersections and the

PT telegrams directly offer the future route of the

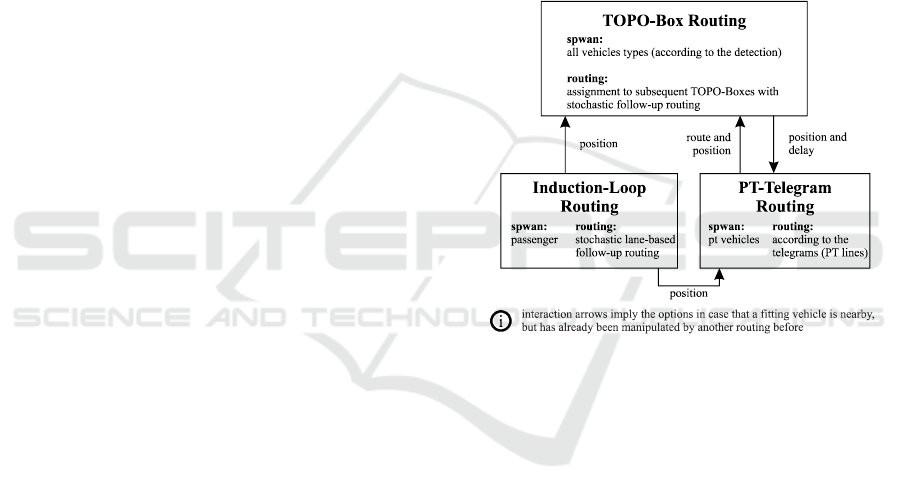
concerning bus since it is static. Figure 2 illustrates

the algorithm’s answer to the question how those

advantages can be combined. It shows the mutual

interaction (if allowed) of the different routing

concepts according to the drawn arrows. All routing

concepts have their own general spawn and routing

strategies, which change based on the vehicles’

previous assignments of other concepts.

Figure 2: Methods and interaction of the different routing

concepts.

To understand these interactions, it is important to

recall the principle of the TOPO-Box Routing. Here,

the vehicles (of all different types) get fixed routes

until passing the detector. Afterwards they are

equipped with flexible follow-up routes based on

stochastic turning ratios, historical data, etc. This

means that after crossing the aim detector an

‘educated guess’ is made how the vehicle will behave

until a successive measurement that fits the vehicle

comes up. As a consequence the routes of the non-

assigned vehicles (not assigned to a consecutive

TOPO-Box) can be manipulated to fit all different

data sources e.g. those of the induction loops. In

Figure 2 the boxes are divided into ‘spawn’ and

‘routing’. This addresses exactly whether a

corresponding vehicle in the vicinity of the sensor is

available for this routing or not. The routing level

interactions describe the vehicle handling depending

on the previously used routing. An arrow from the

Online State Estimation for Microscopic Trafﬁc Simulations using Multiple Data Sources

391

Induction-Loop Routing to the TOPO-Box Routing

therefore implies the influence of the Induction-Loop

Routing on vehicles which have already been

assigned by the TOPO-Box Routing. As an example,

if a truck is detected by a TOPO-Box with no truck in

the vicinity of this sensor, a new one is spawned,

routed to this sensor and provided with a stochastic

follow-up route. Continuing this example, the truck

enters an intersection after crossing the TOPO-Box

with the desire to drive straight (derived from the

stochastic follow-up route). Suppose an induction

loop on the left turning lane is activated, then, as

indicated in Figure 2, the position of the truck is

changed and shifted to the left lane. Also, the route is

manipulated in such a way that the vehicle turns left

and approaches a destination in that direction.

Otherwise, if the target TOPO-Box location is behind

crossing the intersection straight, then the truck could

not be used for the Induction-Loop Routing. This is

because the left lane is not on the truck’s route, so the

change of position towards the induction loop

indicated by the arrow cannot be applied. Depending

on the absence of other vehicles a new one (passenger

type) would have to be spawned to match the

measurement. The usage of the PT telegrams is rather

simple and therefore kept short, since for buses the

educated guess can be swapped with the determined

fixed routes known due to the PT lines information.

After overwriting, the routes are fixed and the PT

buses can only be delayed or repositioned.

4 ALGORITHMIC PROCEDURE

For the traceability of the algorithm a step-by-step

guideline is presented in order to outline the

interaction of the microscopic traffic simulation

performed in SUMO (Lopez et al., 2018) and the

algorithmic data processing in MATLAB. First the

required traffic network for the simulation and the

correct representation of the traffic infrastructure has

to be built accurately in SUMO. This is a time-

consuming process, but clear due to the

unambiguousness of the infrastructure. The necessary

communication of microscopic traffic simulation and

data processing is realized with the interface

TraCI4Matlab (Acosta, Espinosa, & Espinosa,

2015).A brief summary of the concept to reproduce

the dynamics of the traffic system is as follows:

Step 0. Pre-Simulation calculation of all necessary travel

times. Loading and processing of historical data to

assign prediction routes (follow-up routes).

Initialization of the SUMO simulation.

Step 1. Change of the traffic lights according to the

recorded data and adaptation of the travel times.

Step 2. Check of the current vehicle situation in the traffic

system to decide their availability for the different

routing concepts.

Step 3. TOPO-Box Routing.

For each vehicle type: Solution of the integer linear

optimization problem.

a. Generation of the inequality constraints using the

current measurements and the simulation’s vehicle

states. Vehicles in areas with just one reachable

sensor within the travel time threshold are assigned

and given follow-up routes.

b. Performing of the integer linear optimization.

c. Assignment of the flexible vehicles resulting from

the optimization with determination of consecutive

destinations.

d. If there is still unsatisfied demand (leftover

detections), new vehicles of the respective type are

created and added to the simulation at the required

location with subsequent post-destination routes.

Step 4. Induction-Loop Routing.

Step 5. PT-Telegram Routing.

Step 6. Removal of vehicles that would cross the TOPO-

Boxes unwanted (no detection recorded at this time)

in the considered time interval.

If the desired simulation period is covered, stop,

otherwise return to step 1 for the next simulation step.

After this short overview some aspects will be

described in more detail. Prior to the initialization

step 0 the traffic network must be provided. Since

SUMO is used as simulation tool, its own network

editor NETEDIT (Lopez et al., 2018) is employed to

prepare the test area usually using OSM-data like in

(Feldkamp & Strassburger, 2014), but with the

SUMO-internal program OSMWebWizard. Also the

local sensors can be positioned here. To initialize the

simulation, the net information is employed to create

look-up tables including the travel times via

TraCI4Matlab. These tables store the travel times

depending on traffic light signals and vehicle types.

Since the road permissions for vehicles within the

network vary with their types and the simulation also

uses different general driving parameters, this

calculation procedure has to be done for each of the

vehicle types. A not further discussed offline-

algorithm determines the probabilities for the

follow-up routesup routes after reaching a destination

in the third step and also for step 4 beginning from the

induction loop lane. This algorithm tries to link traffic

counts of different detectors based on measurements

of the past creating routing probabilities. Even if no

historical data is available, random follow-up routes

can be assigned.

VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems

392

Figure 3: Transformation of the real test area in a) to the OSM-imported SUMO network in b) and its reduction to the

‘observable’ main roads equipped with the positions of TOPO-boxes and TLS in c).

After this preparation, the SUMO simulation can be

started. SUMO is used to handle the driver specific

behavior and mutual interaction between all vehicles

of all types. Each simulation step begins with the

setting of the current TLS signals and the query of the

current vehicle state. Based on an implemented

trigger, the routable vehicles with no fixed route are

filtered (follow-up routes from previous steps). The

filtering is followed by the different routing concepts

ordered according to their priority and ability to

interact with steps 3 to 5. Step 3 guarantees the

satisfaction of the detected vehicle demand through

whether deterministic, optimization based or

necessary leftover routing. These routing types are

superior to the follow-up routing after crossing a

detector. The superiority itself is realized by

overwriting the previous route. Since the TOPO-Box

measurements also include the vehicles’ speeds, the

velocity parameters of the routed vehicles are

adjusted through a simple not further explained

algorithm. For the removal of vehicles that do not

correspond to a field measurement, the routing trigger

and the distance to the upcoming detector is checked.

If a certain distance is underrun, the vehicle is

removed (step 6). As mentioned before, this

corresponds to unobservable events such as stopping

at parking lots or turning into unobserved roads or a

false route prediction. The procedure for the

reconstruction of the traffic state is highly sequential

which is why certain modifications can have positive

impacts in terms of efficiency. The removal of

vehicles has to be performed every simulation step for

each vehicle type whereas the vehicle assignment

based on the real-time data can be split for the types

and distributed on several seconds to increase the

efficiency without losing the consistency with field

measurements.

5 CASE STUDY

5.1 Test Area Setup

The chosen test area of the pilot project in Schloß

Neuhaus (Paderborn, Germany) covers a total area of

approximately  



with multiple entries and exits.

In the following Figure 3 a bird's eye view of the real

road network in a) (Land NRW, 2019) is transferred

via the import of OSM data (OpenStreetMap

contributors, 2019) into a SUMO traffic simulation

network in b). Besides some necessary manual

adjustments, especially to replicate the real TLS and

the multimodality of the road permissions, the import

has been reduced by the unobservable roads (see c)).

The final network consists of a total of 441 nodes

(junctions and geometrical points) and 622 edges or

links including six TLS which will be object of future

optimization. These key numbers of the respective

graph are a result of a post-import discretization to

determine the travel times depending on the edges

more correctly because their length is limited to a

maximum of   This way, a more time-

consuming online calculation can be avoided. The

real test area is equipped with around

20 TOPO-Boxes, which are also shown in Figure

3 c). Those detectors are capable of measuring the

current traffic for both directions of the road on which

they are installed. For this reason, twice the number

of sensors are inserted in the simulation at the

corresponding positions. Concerning the other data

sources, there are nearly 70 induction loops

surrounding the six TLS controlled intersections and

60 notification marks of the pt telegrams. The TLS

junctions are also illustrated in Figure 3 c). This

system architecture enables the application of the

routing without further adjustments.

TOPO-boxes

TLS

b) c)a)

Online State Estimation for Microscopic Trafﬁc Simulations using Multiple Data Sources

393

5.2 Simulation Results

The approach was tested using several data sets from

different days in the near past, i.e. selected days in

October and November 2020 building various

scenarios with different vehicle loads. For the

following average data shown in Table 1, each of the

scenarios included a 30-minute time slot.

Table 1: Average deviation between real-life and

simulation measurements.

Total TOPO-Box Crossings



Total Induction Loop Crossings



Vehicle Speeds



The exceeding of the induction loop counts is based

on the lower priority of those measurements. The

TOPO-Boxes are the most important and reliable data

sources and therefore the Induction-Loop Routing is

not able to change already assigned vehicle routes.

Since Induction-Loop Routing itself tries to meet its

unfulfilled measurements, the number of crossings is

increased by  because the rights to manipulate

the vehicle routes are intentionally missing (see

Figure 2). The vehicle speeds vary minimally

dependent on the higher local occupancy of the

system. Some intentional safety mechanisms in

SUMO prevent the exact mapping of the set speeds to

make the overall simulation more realistic. With this

system setup, the average speed deviation of 

corresponds to a difference of less than  



. If the

induction loop measurements prove to be more

reliable in the future, the occurring deviations can

even be reduced by allowing more interactions

towards the top level routing (see Figure 2 again).

Generally it can be said that due to the design of the

approach the TOPO-Box measurements are almost

perfectly approximated. But in order to get a better

temporal breakdown of the results as well as some

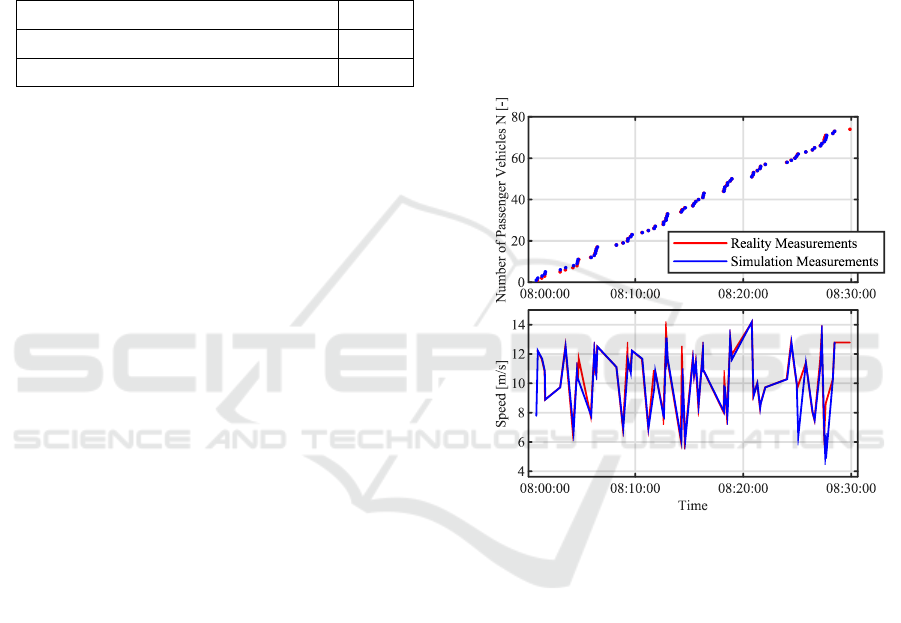
explicit vehicle counts a specific example is given

below in Figure 4. It illustrates exemplary

measurements of the above mentioned time slots,

where each slot and each sensor provides comparable

results for each vehicle type. In the upper part of

Figure 4, the crossings of the passenger vehicles are

shown. The accordance of simulation and reality is

easy to notice as well as the absence of settling

processes. This is due to the fact that the time interval

used for all test results shown in this paper is only .

Additionally, the speeds for the corresponding

vehicles are pictured in the lower part of the figure.

The real average speed for this time slot is  



and the simulated average is 



The distribution of the induction loop crossings or

counts is not shown separately here, as it is

comparable to Figure 4 (with more deviation), but

does not include the same information because no

speeds are measured in reality. Due to the

PT-Telegram Routing there is nearly no deviation of

TOPO-Box crossings for buses (  ) since the

routes are fixed and the area coverage of the

telegrams together with the TOPO-Boxes allows

steady adjustments.

As a conclusion for the results, the estimation at

the local detection points (TOPO-Boxes and

induction loops) works very good and in combination

with SUMO also the speeds can be simulated

accurately.

Figure 4: Comparison of the reality and simulation

measurements for a single TOPO-Box regarding passenger

vehicles.

6 CURRENT & FUTURE WORK

The individual routes are not directly necessary for

the actual control of the traffic system. Since these

traffic records are also very expensive and difficult to

enforce in Germany, a simulated validation option is

preferred. This is why currently an extensive

validation study is performed using ground truth

models and surrogate data as suggested in (Antoniou

et al., 2014). First examples with some vehicle

convoys show good results, as the system states can

be estimated reliably, but the study still has to be

extended to a completely realistic traffic.

In the future, the presented method will have to be

improved while maintaining its generic character.

VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems

394

Within possible enhancements it is important to take

note of an efficient implementation because of the

real-time capability. Also, topics like the robustness

to corrupted measurements have to be discussed more

detailed. At the moment incorrect detections are

compensated at the next sensor. In terms of sensor

coverage, at least the main roads of the network have

to be covered. Pedestrians are another aspect which

will be added to the simulation based on their

identification by pressing the corresponding push

buttons at the intersection. This information will be

taken directly from the TLS control unit.

In parallel, various TLS control concepts are

currently under development, which have to be

coupled with the presented traffic state estimator.

This coupling will become very interesting,

especially under the aspect of state estimations with

deviations from reality.

The last future issue addressed here is that to reach

the overall goal of controlling TLS in the field based

on such a state estimation, some additional interfaces

and latencies should be kept in mind. Especially their

common standards, i.e. in this project the OCIT

standard (OCIT Developer Group (ODG), 2019),

have to be considered.

ACKNOWLEDGEMENTS

The authors would like to thank all participants of the

Pilot Project Schlosskreuzung (PPS) for the provided

data. This paper is part of the PPS and funded by the

Ministry of Economy, Innovation, Digitalization and

Energy of North Rhine-Westphalia.

REFERENCE

Acosta, A. F., Espinosa, J. E., & Espinosa, J. (2015).

TraCI4Matlab: Enabling the Integration of the SUMO

Road Traffic Simulator and Matlab® Through a

Software Re-engineering Process. In M. Behrisch & M.

Weber (Eds.), Lecture Notes in Mobility. Modeling

Mobility with Open Data. 2nd SUMO Conference 2014

(pp. 155–170). Springer-Verlag.

Antoniou, C., Barcelo, J., Brackstone, M., Celikoglu, H. B.,

Ciuffo, B., Punzo, V., et al. (2014). Traffic simulation:

Case for guidelines. Luxembourg: Publications Office

of the European Union.

Antoniou, C., Ben-Akiva, M., & Koutsopoulos, H. N.

(2010). Kalman Filter Applications for Traffic

Management. In V. Kordic (Ed.), Kalman Filter. InTech.

Bierlaire, M., & Crittin, F. (2004). An Efficient Algorithm

for Real-Time Estimation and Prediction of Dynamic

OD Tables. Operations Research, 52(1), 116–127.

Bundesministerium für Verkehr, Bau und Stadtentwicklung

(2012). Technische Lieferbedingungen für Strecken-

stationen.

Chen, X., Osorio, C., & Santos, B. F. (2019). Simulation-

Based Travel Time Reliable Signal Control.

Transportation Science, 53(2), 523–544.

Feldkamp, N., & Strassburger, S. (2014). Automatic

generation of route networks for microscopic traffic

simulations. In A. Tolk (Ed.), 2014 Winter Simulation

Conf. (WSC 2014), 2848–2859, Piscataway, NJ: IEEE.

Kamal, M. A. S., Imura, J., Hayakawa, T., Ohata, A., &

Aihara, K. (2015). Traffic Signal Control of a Road

Network Using MILP in the MPC Framework.

International Journal of Intelligent Transportation

Systems Research, 13(2), 107–118.

Land NRW (2019). Karte Schloß Neuhaus. Datenlizenz

Deutschland -Namensnennung -Version 2.0 (www.gov

data.de/dl-de/by-2-0).

Lopez, P. A., Wiessner, E., Behrisch, M., Bieker-Walz, L.,

Erdmann, J., Flotterod, Y.-P., et al. (2018). Microscopic

Traffic Simulation using SUMO. In 2018 IEEE

Intelligent Transportation Systems Conference, 2575–

2582, Piscataway, NJ: IEEE.

OCIT Developer Group (ODG) (2019). Online Portal

Arbeitsgemeinschaft zur Standardisierung von

Schnittstellen in der Straßenverkehrstechnik.

OpenStreetMap contributors (2019). Schloß Neuhaus Map,

from https://www.openstreetmap.org.

Osorio, C. (2019a). Dynamic origin-destination matrix

calibration for large-scale network simulators.

Transportation Research Part C: Emerging

Technologies, 98, 186–206.

Osorio, C. (2019b). High-dimensional offline origin-

destination (OD) demand calibration for stochastic

traffic simulators of large-scale road networks.

Transportation Research Part B: Methodological, 124,

18–43.

Paz, A., Molano, V., Martinez, E., Gaviria, C., & Arteaga,

C. (2015). Calibration of traffic flow models using a

memetic algorithm. Transportation Research Part C:

Emerging Technologies, 55, 432–443.

RTB GmbH & Co. KG (Ed.) (2019). Produktprospekt

TOPO: Fahrzeug-klassifizierungssysteme. Deutsch-

land, Bad Lippspringe.

Wang, Y., Wang, D., Xu, B., & Wongpiromsarn, T. (2013).

Junction-based Model Predictive Control for urban

traffic light control. In 2013 International Conf. on

Connected Vehicles and Expo (ICCVE) (pp. 54–59).

IEEE.

Zheng, G., Zang, X., Xu, N., Wei, H., Yu, Z., Gayah, V., et

al. (2019). Diagnosing Reinforcement Learning for

Traffic Signal Control.

Online State Estimation for Microscopic Trafﬁc Simulations using Multiple Data Sources

395