
Motivating Upper Secondary Students to Learn Mathematics with
Working Life Exercises
Päivi Porras
1
and Johanna Naukkarinen
2
1
Technology, LAB UAS, Skinnarilankatu 36, Lappeenranta, Finland
2
School of Energy Systems, LUT University, Lappeenranta, Finland
Keywords: Mathematics, STACK, Moodle, GeoGebra, Virtual Reality.
Abstract: This paper describes a massive open online course (MOOC) that targets upper secondary school students.
During the years that we have been working in LUMA Centre Saimaa (an organization to inspire and motivate
children and youth in mathematics, science and technology), we have noticed that upper secondary school
students often fail to see the connection between mathematics studied at that level and their future career plans.
This work-in-progress paper describes a construction and first user experiences of project TyöMAA, which
aims at strengthening the high school students’ perceptions of the applicability of mathematics in the working
life. This is done by giving upper secondary school mathematics teachers real working life examples
connected to topics in their courses and developing a MOOC for students in which they can solve work-
related mathematical problems.
1 INTRODUCTION
A decreasing interest in mathematics is not only a
problem in technology and other STEM fields but
also in fields like physiotherapy, nursing, tourism,
and hospitality. Contextual framing of mathematics
problems has often been suggested as means to
motivate and engage students, but the related
empirical evidence is still somewhat scarce (Beswick
2011). Appropriate contextual framing naturally
depends on the topics and level of mathematics
taught, but also on the age and interests of the
learners. Kärkkäinen and Luojus (2019) discovered
that more than 75% of Finnish high school students
were indecisive of their occupational interests and
had related concerns and worries. Hence, it can be
deduced that the future working life is a meaningful
context for many high school students and could
provide a fruitful starting point also for
contextualizing mathematics problems.
Mathematics-oriented teachers are usually more
familiar with technology and STEM fields and, for
that reason, may unintentionally neglect the
application of mathematics in other fields. However,
mathematics is needed everywhere. Expecting
teachers to be able to provide a wide array of working
life related mathematics examples is unrealistic and
the teachers need to be supported in this by other
professionals (Nieminen 2015). In our project, we
create examples of mathematical problems related to
all fields covered at our campus: technology, nursing
and health care, business, tourism and hospitality and
the arts. This helps teachers to motivate students, as
they can illustrate where mathematics is needed in
those areas.
Prior experiment of using engineering problems in
high school mathematics teaching indicates that these
exemplars can increase the student perception of
practicality and usefulness of mathematics even if the
examples are not taken from students’ everyday life or
situations that they can directly and personally relate
to. In this case the practical value of mathematics was
enhanced through meaningful connection of
mathematics to the scientific problems and working
life. (Nieminen 2015). Earlier studies show also that
the perception of usefulness of mathematics for real
life and future career increase the student motivation
towards the subject (Summala 2020). Although the
utility value of mathematics can be argued to increase
specifically the extrinsic motivation of the students, it
has been noted not to decrease the intrinsic motivation
to learn (Porras, 2015).
Little and Jones (2010) point out possible
dilemmas in the use of real-world contextual framing.
First dilemma relates with the perceived utility of
mathematics, where “[o]n the one hand, by making a
connection between the abstract world of
mathematics and everyday, or scientific contexts, we
208
Porras, P. and Naukkarinen, J.
Motivating Upper Secondar y Students to Learn Mathematics with Working Life Exercises.
DOI: 10.5220/0010429102080215
In Proceedings of the 13th International Conference on Computer Supported Education (CSEDU 2021) - Volume 2, pages 208-215
ISBN: 978-989-758-502-9
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

are reinforcing the utility of mathematics as a
language for explaining the patterns and symmetries
of the ‘real’ world. On the other hand, if we
manipulate and ‘sanitise’ real-world experiences to
enable them to be modelled by a pre-ordained set of
mathematical techniques, then the result can appear
to be artificial and contrived.” ( Little & Jones, 2010,
p. 137) Another dilemma concerns the effect of
framing the questions in real-life contexts. On one hand
this has been argued to help to solve the mathematical
task by providing mental scaffolding, on the other hand
it can complicate the task by making assumptions of
certain context knowledge outside mathematics. (Ibid.)
We aim to address both these dilemmas by searching
and offering as genuine working-life problems as
possible without extensive “sanitation”, but with
prerequisite context knowledge.
We believe that the high school students’
motivation towards mathematics can be enhanced by
presenting them mathematical tasks contextually
framed in working-life problems from different
occupations. In addition to enhancing the interest in
mathematics, this is also hoped to provide students
support in the development of their professional
identities. The following sections provide an
overview of the work we have conducted so far, and
we finish with some ideas of how to investigate the
outcomes and effectiveness of our solutions.
2 THE FRAMEWORK OF THE
MOOC
One important aspect of planning the massive open
online course (MOOC) was that it should not be
confined to time or place. Upper secondary school
mathematics is mainly studied over three years, so it
is not reasonable to assume that students will use this
MOOC in a short period of time. Repetition is also an
important factor in deep learning (Roedinger & Pyc,
2012).
A second aspect was that the MOOC should
appeal to both female and male students, regardless
of whether they were planning futures in STEM fields
or other areas. All students seeing the importance of
mathematics would be a victory for us, especially if
they initially considered mathematics as difficult and
not needed after school.
Due to the first aspect, the use of the MOOC
should be as automated as possible. The teacher(s) of
this MOOC cannot be available whenever the
students want to access it. In addition, if help is not
available when needed, it may decrease motivation.
Thus, a third aspect was to create the course in a form
in which it provides hints and advises students during
their learning without the presence of teachers. This
kind of support is sometimes called instructional
scaffolding (Reid et al., 2015).
2.1 Technical Setup of the MOOC
This section describes the technical elements of the
course. Technical resources have a major effect on
what and how the material can be produced. They
may also influence a student’s motivation and self-
regulation levels. Unfortunately, online material does
not always take advantage of many of the possibilities
offered by the Internet (Kainulainen, 2006).
Moodle (www.moodle.org) is a free and open-
based learning management platform that is
commonly used in Finnish universities. As it enables
automatic grading and has good analytic tools for
analysing learning, it suited this course well. Moodle
is easy to use, even if learners like the upper
secondary school students have had no prior
experience using it.
STACK is a computer-aided assessment package
for mathematic questions on the Moodle platform
(https://moodle.org/plugins/qtype_stack). It enables
the randomizing of variables, as well as providing
feedback based on a student’s answer. Various
question types can be formed, for example, algebraic,
numerical, multiple choice (radio button or checkbox)
and equivalence reasoning. When combining
different kinds of question types, understanding can
be reviewed in addition to calculation skills. STACK
supports JSXGraph (http://jsxgraph.uni-bayreuth.de/
wiki/) and GeoGebra for graphing. JSXGraph is more
convenient if a graph is based on provided functions
(either by a teacher or by a student as an answer), but
GeoGebra enables curve-sketching problems and has
3D-graphing for better illustrations.
GeoGebra is an open-source dynamic
mathematics software application (www.geogebra.
org), in which geometry (2D and 3D), algebra,
spreadsheets, graphing, statistics and calculus are
presented in an illustrative way. For example, 3D
geometric objects can be easily rotated with the
software. It can have a major effect on understanding,
especially if a student’s spatial conceptualization is
not strong. GeoGebra also allows teachers to write
interactive lecture books with GeoGebra applets,
create videos, etc.
Although the examples and exercises follow the
curriculum of upper secondary level mathematics, in
the real working life examples, there may be concepts
that are not familiar to the students. As GeoGebra is
Motivating Upper Secondary Students to Learn Mathematics with Working Life Exercises
209

commonly used in Finnish upper secondary schools,
it was also selected by us as a main source for
additional material for students. As mentioned earlier,
GeoGebra can also be used in STACK questions.
Virtual reality (VR) makes it possible to study
things in a simulated environment (Poitras, 2020). In
some cases, studying in a simulated environment may
even be safer than studying in the real world, such as
with cliff blasting or handling dangerous chemicals
by a beginner. Virtual reality is becoming more
common, but it is still not an everyday activity for
most of us. Because we are not able to take students
to different kinds of workplaces during this project,
we will make the most of virtual reality to give them
simulated working life experiences as best as we can.
2.2 Learning Outline
This course was planned in close cooperation with
local upper secondary school teachers. The teachers
gave us insights and tips about difficult topics and
pointed out the ones in which students do not see the
connection to their future careers.
In upper secondary school in Finland, students can
select either a long or short syllabus in mathematics.
Even when selecting the long syllabus in
mathematics, they can still skip physics and
chemistry except for one compulsory course. Those
students who select the short syllabus usually select
only compulsory physics and chemistry. Hence,
mathematical applications in even physics and
chemistry remain out of reach for many students. For
instance, vectors are mainly connected with forces,
and forces are usually applied to technology in
mathematics. Forces are rarely connected with bodily
movements in examples, although they have a big
role in areas like physiotherapy. In addition, vectors
are studied only in the long syllabus, but students
interested in physiotherapy studies mainly select the
short syllabus and therefore make no connection
between mathematics and their career interests.
Figure 1 presents one interactive graph in
GeoGebra with a background photo selected. This
example is in the teaching material to demonstrate
how a kettlebell of 20 kg causes a force of 3.8 kN at
point D if the lifting is done with the back, not the
legs. Standing straight upright, this force on your
spine would be equivalent to the force of supporting
an object of 386 kg on the top of your head.
This is only one example in which a broader
understanding of mathematics (and physics) would
improve comprehension of a professional field,
although there may not be a need to perform the actual
calculations until later in one’s education.
Figure 1: Vectors in physiotherapy.
2.2.1 Course Structure
The starting point in planning this MOOC was
motivation. A person modifies his or her motivation
from external settings and, little by little, intrinsic
motivation may be aroused (Legault, 2016).
Although most upper secondary level students may
come to this MOOC for an external reward (to get a
course mark for their curriculum), success in the
exercises and real-life cases is hoped to also increase
their intrinsic motivation.
The course is divided into separate exercises for
the short and long syllabuses. The local teachers also
discussed that the first-year mathematics could be on
its own and the last two years presented together. The
main reason for this was that the third year is more
about preparing for the matriculation exam than
studying new topics. Students can work on the course
until they graduate from upper secondary school.
Although the course was divided into short and
long syllabus content, the students were permitted to
select any of the exercises. Some students in the short
syllabus may have good calculation skills and may
want to challenge themselves with exercises from the
long syllabus. Also, those struggling in the long
syllabus may want to try exercises from the short
syllabus to improve their self-esteem.
One part of using extrinsic motivation to cultivate
intrinsic motivation is to reward, not punish. Thus,
students do not need to solve all the exercises of the
package to get acceptable scores. The scores were
weighted by their difficulty level to motivate students
to select more challenging exercises. Applied
problems were weighted twice as much as mechanical
exercises, and exercises of the long syllabus were
worth more points than corresponding exercises in the
short syllabus.
This course was planned to be studied in close
connection with upper secondary mathematics
courses. Thus, extra lecture material was provided
only in some special cases. There was an interactive
GeoGebra book available in cases like that of the
CSEDU 2021 - 13th International Conference on Computer Supported Education
210
vectors mentioned earlier. Some topics were handled
in videos (MP4 and H5P). These videos also provided
guidance on correct answering techniques for the
STACK questions. H5P is an interactive video format
in which it is possible to add clarifying questions. In
a question type called “Crossroads”, a student can be
made to start a video again from a preselected time if
he or she answers incorrectly.
Students do not need to do all the exercises from
the selected package at once. The idea behind this is
that it is better to do one than not to do anything.
Secondly, the packages can contain question topics
that have not yet been handled by their teacher, so
they may not even have the knowledge to solve them.
Thirdly, a student may notice the need to review
earlier topics before continuing in exercises.
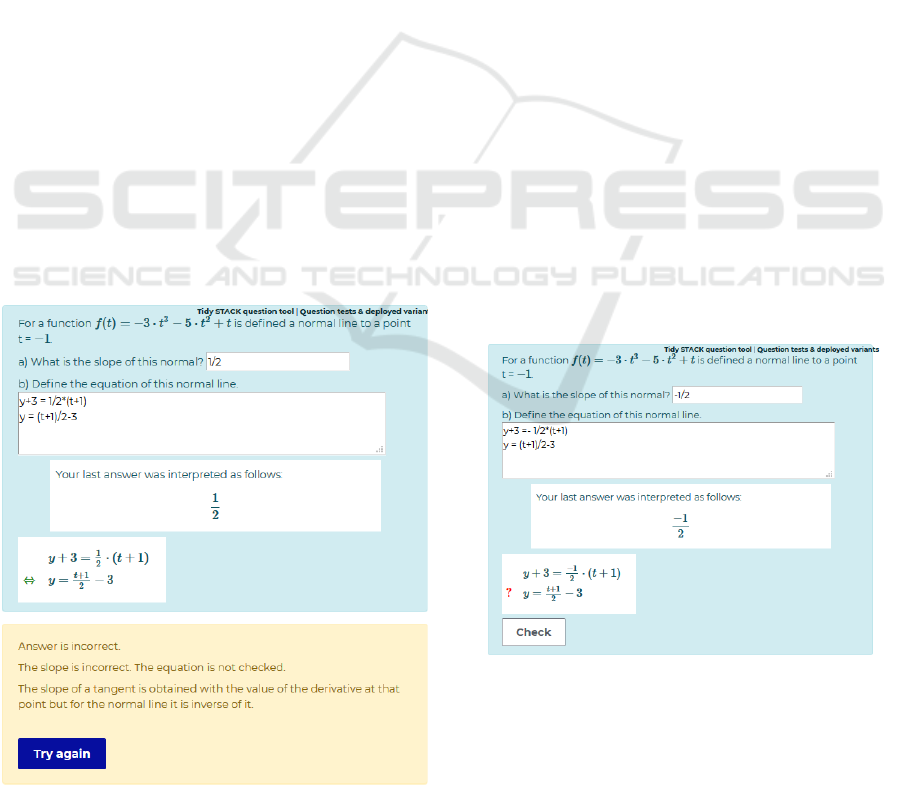
2.3 STACK Exercises
The Moodle activity called “Quiz” has different
behavioural modes. The mode “Interactive with
Multiple Tries” was used for all the exercises in this
MOOC. In STACK questions, the feedback on a
selected answer can be given both in a potential
feedback tree and in an option with hints. In Figure 2,
there is an example of solving a normal line equation.
In the potential response tree, sub-question a is first
checked, and it is indicated as incorrect. The second
comment in the yellow box tells the student that the
value of the slope is incorrect and that the equation
was not checked. The third comment was given by the
Figure 2: Feedback in STACK.
first hint. Hints make it possible for a student to
attempt the same exercise several times to correct his
or her mistakes. If the second attempted answer was
incorrect, then the second hint would be given. Hints
are general and cannot be customized based on a
student’s answer. A small deduction on a student’s
score is made whenever the answer is incorrect. With
two used hints, the maximum score for the exercises
would be 0.80 instead of one.
2.3.1 Equivalence Reasoning
In Figure 2, there is also an example of “Equivalence”
reasoning in STACK. The last two white boxes are
the validation boxes for the student’s answer: what
the student entered and how STACK interpreted the
given answer. In this case, all the given intermediate
steps were logical, so no errors were found. This
illustrates how entering answers or other mistakes are
noted before any reference as to whether the answer is
mathematically correct or not is made. As noted, the
slope was incorrect, so this answer cannot be correct.
In Figure 3, the student has corrected the slope and
uses it in the first row of question b. As a student has
not yet corrected it in the second line, the red question
mark can be seen at the beginning of the line. Thus,
the student will need to change his or her answer
before asking for it to be checked. This may help in
motivation, as answers are not judged to be incorrect
for keying or minor calculation mistakes. If a student
solves the exercises on paper first (as instructed), a
keyed solution is quite easy to review for further
unnoticed mistakes.
Figure 3: Error in an intermediate step.
2.3.2 Radio Buttons and Dropdown Menus
Mathematics is not only solving exercises with
methods provided by a teacher but also understanding
why they are used. Languaging (Joutsenlahti & Kulju,
Motivating Upper Secondary Students to Learn Mathematics with Working Life Exercises
211

2017) is an excellent way for a student to explain his
or her thinking when solving an exercise. However,
this kind of method is not suitable for a MOOC, in
which the feedback is obtained instantaneously. One
way for a student to express his or her thinking in a
system with automatic feedback is with radio buttons
and dropdown menus. Although the choices are pre-
scripted, the process does force students to think
through their solutions.
Figure 4: Example with radio buttons and a dropdown
menu.
Figure 4 shows an exercise for solving a quadratic
polynomial inequality. The main method of solving
for zeros from the standard form has been omitted
here. The main aspect is interpreting the solved zeros
with the original inequality to form the solution.
2.3.3 Graphs for Feedback
One way of providing feedback for a student without
showing the correct answer is with graphs. The
equation of a line shown in Figure 5 is incorrect.
Although the validation box on the right shows that
the equivalence reasoning is correct, the student has
given values of y in the wrong order. The line in the
student’s solution is shown together with the given
points (rather than just having the system judge the
solution to be incorrect). This hopefully helps
students to figure out their mistakes and/or
misunderstandings. This graph is not shown if there
are errors in the equivalence reasoning for defining an
equation (indicated by the red question mark at the
beginning of a line).
Figure 5: The equation of a line is defined incorrectly.
2.3.4 Applied Exercises
The applied exercises are verbal information, and
only a final answer is required. There are different
kinds of paths for solving applied exercises, and we
did not want to restrict the solution to only one correct
method. However, the final solution should be the
same despite the method selected.
An exercise shown in Figure 6, is part of exercises
in short syllabus. In this exercise, currency, amount,
and the transaction fee are all randomized. Although
the final answer is given, it will give hints for some
most typical mistakes.
Figure 6: Applied problem in economics.
CSEDU 2021 - 13th International Conference on Computer Supported Education
212

Students with their plans in social and health care
as, for example, nurses or paramedics do not always
see mathematics very important part of their work. In
Figure 7, is one example of math needed in
paramedics. If the amount oxygen is too low, it may
be life-threatening. If there too much over the
minimum requirement, there may not be enough
space in an ambulance.
Figure 7: Paramedics also need mathematics.
In Figure 8, there is an example of exercise in
geometry, which could be easily faced in civil or
mechanical engineering. At the first sight, the
exercise may look easy. The closer look reveals that
actual radius is not given (but chord is) and must be
solved. Solving this exercise requires knowledge in
circles, cylinders, and density.
Figure 8: Geometry is important in technology.
2.4 Applying Mathematics in Virtual
Reality
The upper secondary students who actively take part
in this course will be asked to visit campus as a final
activity (if COVID-19 restrictions allow it at the time).
Part of this project was to produce a virtual reality
experience in which students can solve applied
problems related to working life. All the activities in
the virtual reality will be connected to the exercises
solved in the MOOC, but they will be extended
versions of them.
We were able to liaise with Pulsan Asema
(https://www.pulsanasema.fi/en/), which is a very
popular resort in Lappeenranta, Finland. An
inventory model of the resort was digitalized some
years ago by Saimaa UAS, Finland, and our project
can use that digital information in the VR model. The
VR model is so accurate that even the location of the
plumbing can be checked. This allows us to add
actual working life exercises from civil engineering
through hospitality in the same VR model. Figure 9
shows an exercise concerning hospitality. An order
made by a customer is given on the screen to the right,
a recipe is to the left of the window, and a cake tin
needs to be found to see measurements. The volume
of this “old” cake tin is not known, so the student must
calculate it to know how much pastry is needed.
Figure 9: Exercise about an order made to Cafe.
3 NEXT STEPS
The project started in 2019. At that time, co-operation
with upper secondary teachers in science, mostly in
mathematics, occurred to find an appropriate level for
the exercises. The teachers also provided ideas and
identified topics that were neglected or were difficult
for the students (and therefore required attention). For
example, the concept of percentage is experienced as
quite difficult by students in the short syllabus,
although it is one of the most important topics in
many postgraduate studies, like economics, tourism
and hospitality.
The first students were enrolled in this course in
June 2020. A total of 25 students were accepted to the
course; 12 of them joined the Moodle platform, and
one student from the short syllabus passed Part A
(Part B will be available in spring 2021). This student
was very active and asked for help several times. She
Motivating Upper Secondary Students to Learn Mathematics with Working Life Exercises
213

did not lose her motivation, although there were
several coding mistakes. Thanks to her, we were also
able to code some different kinds of solution methods,
which had not been anticipated by the teachers in
engineering. As mentioned previously, there is
usually not just one correct method to solve a problem
in mathematics.
There are several possible reasons for a low
commitment to the course. In general, the completion
rate of MOOCs has been known to be weak (Alraimi
et al., 2015); self-paced MOOCs especially appear to
have low retention rates (Ihantola et al., 2020). In our
MOOC, over half of the enrolled students did not
even start the course. Of the 12 students that joined
the MOOC platform, only a few, in fact, solved
anything, and we suspect that most of them just joined
the course to get access to material. However, the
COVID-19 pandemic might have affected behaviour
in the course in many ways. Because of the pandemic,
the upper secondary school students thought that they
could not get any summer jobs in 2020 and enrolled
in this course to at least promote their studies. The
situation was surprisingly better than assumed, and
jobs became available, although later than normally.
Another pandemic-related explanation is that because
the students were studying online several months
during spring 2020, they had become restless with
online study and wanted a break from it. In any case,
we need to study this situation more.
To better understand the situation and student
experiences with the MOOC and to develop the
exercises and materials further, we are currently
collecting feedback with a form linked to the MOOC.
The feedback is provided anonymously, and it can be
targeted either to specific exercises or the course in
general. In the future, we are hoping to be able to
translate the course into English and Russian, as there
are two special upper secondary schools in our area.
The correct feedback is important part of a good
online exercise (Mäkelä et al, 2016), and especially if
feedback is automated. If a student feels positive and
encouraged after feedback, it may affect positively in
motivation and in engaging their studies (Kennette &
Chapman, 2021). Therefore, we collect students’
observations of cases where the feedback should be
improved to encourage instead of discouragement.
4 CONCLUSION
The worry of low interest in mathematics seems to be
worldwide (Yeh & al., 2019, Azmidar & al., 2017). If
the connection to one’s own life cannot be captured,
the interest is unlikely to arise. Like Legault (2016)
mentions, the inner interest arise motivation and will
to progress. The mathematics teacher of 2020 in
Finland Piia Haapsaari, who was selected by
mathematics teachers’ union MAOL, mentions that
she thought as a teenager not to be good enough in
mathematics. A good teacher and appropriate
teaching methods opened the lock: the success in
given tasks increased the inner interest
(https://esaimaa.fi/uutiset/kotimaa/33d7a047-b57a-
4bec-af99-f4495a0bb901).
Based on the feedback we have received at the
project steering group meetings and teacher webinars,
local upper secondary teachers are excited about this
course and material, want to learn more about it and
want to offer it to students. Of course, the demand for
upper secondary schools to cooperate with higher
education from fall 2021 forward helps us as well.
When this cooperation really starts, we will be able to
better see how much students are able to utilise the
course. One definite challenge is the already packed
upper secondary school curriculum and the resulting
heavy timetable of students, which may result in
reluctance to engage in any non-compulsory activities.
As both, contextual framing and use of modern
technology in the teaching of mathematics are
complex issues with positive and negative aspects,
the evaluation of the effect of MOOC on student
motivation must be carefully planned and executed.
We have started this work by establishing feedback
channels to the students and teachers, but more and
more versatile data is needed for proper data
triangulation and analysis. This is an essential part of
future work in the project.
ACKNOWLEDGEMENTS
We thank European Social Fund for funding this
project (S21637).
REFERENCES
Alraimi, K., Zo, H., & Ciganek, A. (2015). Understanding
the MOOCs continuance: The role of openness and
reputation. Computers & Education 80, 28-38.
Azmidar, A., Darhim, D., & Dahlan, J. (2017). Enhancing
Students' Interest through Mathematics Learning.
International Conference on Mathematics and Science
Education .
Beswick, K. (2011). Putting Context in Context: An
Examination of the Evidence for the Benefits of
'Contextualised' Tasks. International Journal of
Science and Math Education 9, 367-390.
CSEDU 2021 - 13th International Conference on Computer Supported Education
214

Ihantola, P., Fronza, I., Mikkonen, T., Noponen, M., &
Hellas, A. (2020, December 4). Deadlines and MOOCs:
How Do Students Behave. Frontiers in Education:
Education for a Sustainable Future. Uppsala, Sweden.
Joutsenlahti, J., & Kulju , P. (2017). Multimodal
Languaging as a Pedagogical Model - A Case Study of
the Concept of Division in Mathematics. Education
Sciences.
Kainulainen, S. (2006). Oppimista tukeva verkko-
oppimateriaali – lähtökohtia verkko-oppimateriaalin
tuottamiseen [Material Supporting Online Learning].
Retrieved from Theseus: https://www.theseus.fi/
bitstream/handle/10024/19582/TMP.objres.30.pdf?seq
uence=1&isAllowed=y
Kennette, L., & Chapman, M. (2021). Providing positive
student feedback in an online environment. Retrieved
from Academia Letters: https://doi.org/10.20935/
AL203
Kärkkäinen, J., & Luojus, L. (2019). Ammatillinen
identiteetti ja koulumotivaation toisen asteen
opiskelijoilla [Professional identity and study
motivation at upper secondary school]. Jyväskylän
yliopisto.
Legault, L. (2016). Instrinsic and Extrinsic Motivation. In
V. Zeigler-Hill, & T. K. Shackelford, Encyclopedia of
Personality and Individual Differences. Springer
International Publishing.
Little, C., & Jones, K. (2010). The effect of using real world
contexts in post-16 mathematics questions. In M.
Jourbert, & P. Andrews, Proceedings of the British
Congress for Mathematics Education.
Mäkelä, A.-M., Ali-Löytty, S., Humaloja, J.-P.,
Joutsenlahti, J., Kauhanen, J., & Kaarakka, T. (2016).
STACK assingments in university mathematics
education. 44th SEFI Conference. Tampere.
Nieminen, I. (2015). Practical Mathematics in High
School. Tampere University.
Poitras, E. (2020). Foreword. In G. Akcayir, & C.
Demmans Epp, Designing, Deploying, and Evaluating
Virtual and Augmented Reality in Education (p. xiv).
IGI Global Reference Book.
Porras, P. (2015). Utilising student profiles in mathematics
course arrangements. Lappeenranta: Yliopistopaino.
Reid, D. R., Bowen, A. S., & Koretsky, M. D. (2015).
Development of interactive virtual laboratories to help
students learn difficult concepts in thermodynamics.
Chem. Eng.Educ 49 (4), 229-238.
Roedinger, H., & Pyc, M. (2012). Inexpensive techniques
to improve education: Applying cognitive psychology
echance eduational practise. Journal of Applied
Research in Memory and Cognition 1, 242-248.
Summala, T. (2020). Ensimmäisen ja toisen vuoden lukio-
opiskelijoiden motivaatio matematiikassa [The first and
the second year upper secondary school students'
motivation in mathematics]. Itä-Suomen yliopisto.
Yeh, C., Cheng, H., Chen, Z.-H., Liao, C., & Chan, T.-W.
(2019). Enhancing achievement and interest in
mathematics learning through Math-Island. Research
and Practice in Technology Enhanced Learning (14).
Motivating Upper Secondary Students to Learn Mathematics with Working Life Exercises
215
