
CC-separation Measure Applied in Business Group Decision Making
Jonata C. Wieczynski
1 a
, Giancarlo Lucca
2,3 b
, Eduardo N. Borges
2 c
, Grac¸aliz P. Dimuro
2,5 d
,
Rodolfo Lourenzutti
4 e
and Humberto Bustince
5 f
1
Programa de P
´
os-Graduac¸
˜
ao em Computac¸
˜
ao, Universidade Federal do Rio Grande, Av. It
´
alia Km 8, Rio Grande, Brazil
2
Programa de P
´
os-Graduac¸
˜
ao em Modelagem Computacional, Universidade Federal do Rio Grande, Rio Grande, Brazil
3
Centro de Ci
ˆ
encias Computacionais, Universidade Federal do Rio Grande, Rio Grande, Brazil
4
Department of Statistics, University of British Columbia, Vancouver, Canada
5
Departamento de Estad
´
ıstica, Inform
´
atica y Matem
´
aticas, Universidad Publica de Navarra, Pamplona, Spain
Keywords:
Decision Making, TOPSIS, GMC-RTOPSIS, Generalized Choquet Integral, CC-integrals.
Abstract:
In business, one of the most important management functions is decision making. The Group Modular Cho-
quet Random TOPSIS (GMC-RTOPSIS) is a Multi-Criteria Decision Making (MCDM) method that can work
with multiple heterogeneous data types. This method uses the Choquet integral to deal with the interaction be-
tween different criteria. The Choquet integral has been generalized and applied in various fields of study, such
as imaging processing, brain-computer interface, and classification problems. By generalizing the so-called
extended Choquet integral by copulas, the concept of CC-integrals has been introduced, presenting satisfactory
results when used to aggregate the information in Fuzzy Rule-Based Classification Systems. Taking this into
consideration, in this paper, we applied 11 different CC-integrals in the GMC-RTOPSIS. The results demon-
strated that this approach has the advantage of allowing more flexibility and certainty in the choosing process
by giving a higher separation between the first and second-ranked alternatives.
1 INTRODUCTION
Business managers rely on the right decisions to keep
their business competitive. Many times a decision
has to be made by multiple analysts and considering
various criteria. This is a time consuming and ex-
pensive task. Although, most of the time, it can be
solved by an algorithm or mathematical model, like
route, supplier chain, and location problems (Deveci
et al., 2017; Alazzawi and
˙
Zak, 2020; Shyur and Shih,
2006), releasing the pressure of the decision from the
managers, and allow them to work on other processes
of the company/industry.
The Technique for Order of Preference by Simi-
larity to Ideal Solution (TOPSIS) (Huang and Yoon,
1981) is one of the multi-criteria decision making
(MCDM) methods that ranks the best possible solu-
a
https://orcid.org/0000-0002-8293-0126
b
https://orcid.org/0000-0002-3776-0260
c
https://orcid.org/0000-0003-1595-7676
d
https://orcid.org/0000-0001-6986-9888
e
https://orcid.org/0000-0003-2434-4302
f
https://orcid.org/0000-0002-1279-6195
tion among a set of alternatives. This approach is
based on pre-defined criteria, using the alternative’s
distance to the best and worst possible solutions for
the problems, Positive and Negative Ideal Solutions
(PIS and NIS), respectively.
In 2017, the Group Modular Choquet Random
TOPSIS (GMC-RTOPSIS) (Lourenzutti et al., 2017)
was introduced. The method generalized the orig-
inal TOPSIS allowing it to deal with multiple and
heterogeneous data types. The approach models the
interaction among the criteria by using the discrete
Choquet integral (Choquet, 1954). The Choquet inte-
gral allows a function to be integrated by using non-
additive fuzzy measures (Choquet, 1954; Candeloro
et al., 2019), which means that it can consider the in-
teraction among the elements that are being integrated
(Murofushi and Sugeno, 1989; Dimuro et al., 2020).
The GMC-RTOPSIS learns the fuzzy measure associ-
ated with the criteria with a Particle Swarm Optimiza-
tion (PSO) algorithm (Wang et al., 2011) .
The C
T
-integrals (Lucca et al., 2016) is a general-
ization of the Choquet integral that replaces the prod-
uct operation by triangular norm (t-norm) functions
(Klement et al., 2011). The C
T
-integrals are a family
452
Wieczynski, J., Lucca, G., Borges, E., Dimuro, G., Lourenzutti, R. and Bustince, H.
CC-separation Measure Applied in Business Group Decision Making.
DOI: 10.5220/0010439304520462
In Proceedings of the 23rd International Conference on Enterprise Information Systems (ICEIS 2021) - Volume 1, pages 452-462
ISBN: 978-989-758-509-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

of integrals that are pre-aggregation functions (Lucca
et al., 2016). Additionally, C
T
-integrals are averaging
functions, i.e., the result is always between the mini-
mum and maximum of the input.
The T-separation measure (Wieczynski et al.,
2020) was introduced and applied in the GMC-
RTOPSIS instead of the Choquet integral. In
this study, the authors considered five different T-
separation measures to tackle Case Study 2 from
(Lourenzutti et al., 2017). The problem consists of
choosing a new supplier for a company by asking var-
ious decision-makers to give their opinions with dif-
ferent criteria. The problem is posed with a variety
of data types, such as probability distributions, fuzzy
numbers, and interval numbers. The paper also pro-
posed to use the t-norm that better discriminates the
first ranked alternative to the second one by calcu-
lating the difference of the rankings. The approach
presented good results when using the Łukasiewicz
t-norm (T
Ł
), giving a better separation between the
ranked alternatives than the standard Choquet inte-
gral.
After introducing the C
T
-integrals, Lucca et al.
have proposed the CC-integrals (Lucca et al., 2017a).
CC-integrals are a generalization of the Choquet in-
tegral in its expanded form, satisfying some proper-
ties, such as averaging, idempotency, and aggregation
(Grabisch et al., 2009). The authors applied the CC-
integral in classification problems, showing that the
function based on the minimum is the one that pro-
duced the highest performance of the classifier. The
CC-integrals have been studied in the literature by
Dimuro et al., where the properties of CMin integrals
(Lucca et al., 2017b; Dimuro et al., 2018; Mesiar and
Stup
ˇ
nanov
´
a, 2019) were analyzed.
In this paper, we define the CC-separation mea-
sure and use it in the GMC-RTOPSIS instead of the
Choquet integral. We also apply our approach in an
application as an example, the same used in (Louren-
zutti et al., 2017; Wieczynski et al., 2020). Finally, we
analyze its results and compare them to other works.
The paper is organized as follows: Section 2 in-
troduces the basic concepts about the fuzzy set the-
ory and TOPSIS decision making. In Section 3 we
define the CC-separation measure. In Section 4 we
show our methodology, the problem used to test the
CC-separation measure, and the results achieved by
using it. Lastly, the conclusion is in Section 5.
2 PRELIMINARY CONCEPTS
In this section, we recall the preliminary concepts
necessary to develop the paper.
2.1 Fuzzy Set Theory
A Fuzzy Set (Zadeh, 1965) is defined on a universe X
by a membership function µ
a
: X → [0,1], denoted by
a =
{h
x, µ
a
(x)
i
| x ∈ X
}
.
We call a trapezoidal fuzzy number (TFN) the fuzzy
set denoted by a = (a
1
,a
2
,a
3
,a
4
), where a
1
≤ a
2
≤
a
3
≤ a
4
, if the membership function µ
a
is defined on
R as:
µ
a
(x) =
x−a
1
a
2
−a
1
, if a
1
≤ x < a
2
1, if a
2
≤ x ≤a
3
a
4
−x
a
4
−a
3
, if a
3
< x ≤a
4
0, otherwise.
A measure of the distance between two TFNs a =
(a
1
, a
2
, a
3
, a
4
) and b = (b
1
, b
2
, b
3
, b
4
) is defined
as:
d(a,b) =
s
1
4
4
∑
i=1
(a
i
−b
i
)
2
.
The defuzzified value of a TFN a = (a
1
,a
2
,a
3
,a
4
) is
given by:
m(a) =
a
1
+ a
2
+ a
3
+ a
4
4
.
An intuitionistic fuzzy set (IFS) A is defined on a uni-
verse X by a membership function µ
A
: X →[0, 1] and
a non-membership function ν
A
: X → [0,1] such that
µ
A
(x) + ν
A
(x) ≤ 1, for all x ∈X , that is:
A =
{h
x,µ
A
(x),ν
A
(x)
i
| x ∈ X
}
.
Let ˜µ
A
and
˜
ν
A
be the maximum membership degree
and the minimum non-membership degree, respec-
tively, of an IFS A.
An IFS A is an intuitionistic trapezoidal fuzzy
number (ITFN), denoted by
A =
h
(a
1
,a
2
,a
3
,a
4
), ˜µ
A
,
˜
ν
A
i
where a
1
≤ a
2
≤ a
3
≤ a
4
, if µ
A
and v
A
are given, for
all x ∈R, by
µ
A
(x) =
x−a
1
a
2
−a
1
˜µ
A
, if a
1
≤ x < a
2
˜µ
A
, if a
2
≤ x ≤a
3
a
4
−x
a
4
−a
3
˜µ
A
, if a
3
< x ≤a
4
0, otherwise
and
ν
A
(x) =
1−
˜
ν
A
a
1
−a
2
(x −a
1
) + 1, if a
1
≤ x < a
2
˜
ν
A
, if a
2
≤ x ≤a
3
1−
˜
ν
A
a
4
−a
3
(x −a
4
) + 1, if a
3
< x ≤a
4
1, otherwise.
CC-separation Measure Applied in Business Group Decision Making
453

The distance between two ITFNs A =
h
(a
1
, a
2
, a
3
, a
4
), ˜µ
A
,
˜
ν
A
i
and B =
h
(b
1
, b
2
, b
3
, b
4
), ˜µ
B
,
˜
ν
B
i
is:
d(A,B) =
1
2
[d
˜µ
(A,B) + d
˜
ν
(A,B)]
where
d
κ
(A,B) =
1
4
(a
1
−b
1
)
2
+ (1 + (κ
A
−κ
B
)
2
)
(1 + (a
2
−b
2
)
2
+ (a
3
−b
3
)
2
)
−1 + (a
4
−b
4
)
2
1/2
for κ
A
= ˜µ
A
and κ
B
= ˜µ
B
when κ = µ; and for κ
A
=
˜
ν
A
and κ
B
=
˜
ν
B
when κ = ν.
Aggregation functions (AF) (Grabisch et al.,
2009) are used to unify inputs into a single value rep-
resenting them all and are defined as a function that
maps n > 1 arguments onto the unit interval, that is,
a function f : [0, 1]
n
→ [0,1] such that the bound-
aries, f (0
0
0) = 0 and f (1
1
1) = 1, with 0
0
0,1
1
1 ∈ [0,1]
n
,
and the monotonicity properties, x
x
x ≤ y
y
y =⇒ f (x
x
x) ≤
f (y
y
y), ∀x
x
x,y
y
y ∈ [0,1]
n
, hold.
A triangular norm (t-norm) is an aggregation func-
tion T : [0,1]
2
→ [0,1] that satisfies, for any x,y,z ∈
[0,1]: the commutative and associative properties and
the boundary condition.
An overlap function (Bustince et al., 2010) O :
[0,1]
2
→[0,1] is a function that satisfies the following
conditions:
• O is commutative;
• O(x,y) = 0 ⇐⇒ xy = 0;
• O(x,y) = 1 ⇐⇒ xy = 1;
• O is increasing;
• O is continuous.
A bivariate function Co : [0,1]
2
→ [0, 1] is called a
copula (Nelsen, 2007) if, for all x,x
0
,y,y
0
∈ [0,1] with
x ≤x
0
and y ≤ y
0
, the following conditions hold:
• Co(x,y) +Co(x
0
,y
0
) ≥Co(x, y
0
) +Co(x
0
,y);
• Co(x,0) = Co(0,x) = 0;
• Co(x,1) = Co(1,x) = x.
The Choquet integral is defined based on a fuzzy mea-
sure (Sugeno, 1974), that is, a function m from the
power set of N to the unit interval, m : 2
N
→ [0,1],
that for all X,Y ⊂ N holds the conditions:
(1) m(
/
0) = 0 and m(N) = 1;
(2) if X ⊂Y , then m(X) ≤ m(Y ).
From this, Choquet defined the integral as: Let m
be a fuzzy measure. The Choquet integral (Choquet,
1954) of x
x
x ∈[0,1]
n
with respect to m is defined as:
C
m
: [0,1]
n
→ [0,1]
x
x
x →
n
∑
i=1
x
(i)
−x
(i−1)
m(A
(i)
)
where (i) is a permutation on 2
N
such that x
(i−1)
≤
x
(i)
for all i = 1,. .. ,n, with x
(0)
= 0 and A
(i)
=
{(1),.. ., (i)}.
Notice that one can use the distributive law to ex-
pand the Choquet integral into:
C
m
=
n
∑
i=1
x
(i)
m(A
(i)
) −x
(i−1)
m(A
(i)
)
(1)
Recently, the Choquet integral was generalized by
copula functions. By substituting the product oper-
ator by copulas in the expanded form of the Choquet
integral (Eq. 1), CC-Integrals (Lucca et al., 2017a)
were introduced.
Let m be a fuzzy measure and Co be a bivari-
ate copula. The Choquet-like integral based on cop-
ula with respect to m is defined as a function C
Co
m
:
[0,1]
n
→ [0,1], for all x
x
x ∈[0,1]
n
, by
C
Co
m
=
n
∑
i=1
Co
x
(i)
, m(A
(i)
)
−Co
x
(i−1)
, m(A
(i)
)
(2)
where (i), x
(i)
and A
(i)
is defined as the Choquet inte-
gral.
It is important to note that the Choquet integral,
the C
T
-integrals, and the CC-integrals are averag-
ing functions, i.e., the results from them are always
bounded by the minimum and maximum of their in-
put.
2.2 Decision Making
The GMC-RTOPSIS (Lourenzutti et al., 2017) is a
decision making algorithm that improved the classic
TOPSIS (Huang and Yoon, 1981) by allowing groups
of decision-makers, modularity in the input, multiple
input types and, by using the Choquet integral, the
ability to measure the interaction among different cri-
teria.
Figure 1 shows an overview of the decision mak-
ing process with the Choquet integral. Here three
different decision-makers give their ratings for three
products based on three criteria. These ratings are
then processed and inserted in the Choquet integral,
where the interaction between the criteria is calcu-
lated. After, the results are ranked according to their
highest classiness coefficient value.
ICEIS 2021 - 23rd International Conference on Enterprise Information Systems
454

Figure 1: Image description of the decision making process
using the Choquet integral. Source: the authors.
To describe the GMC-RTOPSIS method let q rep-
resent the q-th decision maker in a collection of
Q ∈ N = {1,2, 3,...} ones. Let A
A
A = {A
1
,..., A
m
}
be the set of alternatives for the problem and C
C
C
q
=
{C
1
,...,C
n
q
} represent the criteria set for decision
maker q. With C
C
C = {C
C
C
1
,...,C
C
C
Q
} = {C
1
,...,C
n
},
where n =
∑
Q
q=1
n
q
, representing the criteria set of all
the decision makers. From these notations we can
represent each of the q-th decision maker by the ma-
trix below (Eq. (3)), called decision matrix DM:
DM
q
=
C
1
C
2
··· C
n
q
A
1
s
q
11
(Y
Y
Y
q
) s
q
12
(Y
Y
Y
q
) ··· s
q
1n
q
(Y
Y
Y
q
)
A
2
s
q
21
(Y
Y
Y
q
) s
q
22
(Y
Y
Y
q
) ··· s
q
2n
q
(Y
Y
Y
q
)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
A
m
s
q
m1
(Y
Y
Y
q
) s
q
m2
(Y
Y
Y
q
) ··· s
q
mn
q
(Y
Y
Y
q
)
(3)
Each matrix cell s
q
i j
(Y
Y
Y
q
), with 1 ≤ i ≤m, 1 ≤ j ≤ n
q
,
is called the rating of the criterion j for alternative
i. Also, notice that the rating is a function of Y
Y
Y =
(Y
Y
Y
rand
, Y
Y
Y
det
), which are factors that model random
and deterministic events. Random events are modeled
by stochastic processes, and deterministic are events
which are not random, like time, location or a param-
eter of a random event. A fixed value x of the deter-
ministic vector is called a state, and the set of all states
is represented by X .
In possession of all decision matrices from all
decision-makers Q, the algorithm can be applied. The
process is quite similar to the original TOPSIS, pre-
sented in 1981. It uses the same definition of Posi-
tive Ideal Solution (PIS) and Negative Ideal Solution
(NIS) that are, respectively, the one that is closer to
the best possible solution and the one that is distant
from the best possible solution, see Eq. (4). The
most significant difference is that each criterion may
use a different distance measure since each may have
its own type. So, the distances of each criterion are
calculated separately and aggregated afterward in the
separation measure step of the algorithm (see Figure
2).
In order to ease the comprehension of our ap-
proach, we present in Figure 2 the steps of the GMC-
RTOPSIS, where:
Step 0. Select a state x ∈ X not yet processed;
Step 1. Normalize all matrices;
Step 2. Select the PIS, denoted by s
+
j
(Y
Y
Y ), and
the NIS, denoted by s
−
j
(Y
Y
Y ), considering, for each
j ∈ {1,. ..,n}, respectively:
s
+
j
(Y
Y
Y ) =
max
1≤i≤m
s
i j
, if it is a benefit criterion,
min
1≤i≤m
,s
i j
if it is a cost/loss criterion,
(4)
s
−
j
(Y
Y
Y ) =
min
1≤i≤m
s
i j
, if it is a benefit criterion,
max
1≤i≤m
s
i j
, if it is a cost/loss criterion;
Step 3. Calculate the distance measure for each
criterion C
j
, with j ∈ {1,..., n}, to the PIS and
NIS solutions, that is,
d
+
i j
= d(s
+
j
(Y
Y
Y ), s
i j
(Y
Y
Y )),
d
−
i j
= d(s
−
j
(Y
Y
Y ), s
i j
(Y
Y
Y )),
where i ∈ {1,. .. ,m} and d is a distance measure
associated with the criteria data type;
Step 4. Calculate the separation measure, for each
i ∈ {1,. .. ,m}, using the Choquet integral as fol-
lows:
S
+
i
(Y
Y
Y ) =
s
n
∑
j=1
d
+
i( j)
2
−
d
+
i( j−1)
2
m
Y
Y
Y
(C
C
C
+
( j)
)
S
−
i
(Y
Y
Y ) =
s
n
∑
j=1
d
−
i( j)
2
−
d
−
i( j−1)
2
m
Y
Y
Y
(C
C
C
−
( j)
)
where d
+
i(1)
≤ . .. ≤ d
+
i(n)
, d
−
i(1)
≤ . .. ≤ d
−
i(n)
, for
each j ∈ {1,... ,n}, C
+
( j)
is the criterion cor-
respondent to d
+
i( j)
, C
−
( j)
is the criterion corre-
spondent to d
−
i( j)
, C
C
C
+
( j)
= {C
+
( j)
,C
+
( j+1)
,...,C
+
(n)
},
C
C
C
−
( j)
= {C
−
( j)
,C
−
( j+1)
,...,C
−
(n)
}, C
C
C
+
(n+1)
= C
C
C
−
(n+1)
=
/
0, d
+
i(0)
= d
−
i(0)
= 0 and m
Y
is the learned fuzzy
measure by a particle swarm optimization algo-
rithm (Wang et al., 2011).
Here, the separation measure is the square root of
the Choquet integral of squared distances, and this
means that it is the square root of a d-Choquet in-
tegral (Bustince et al., 2020). Also, for each state,
we may have a different fuzzy measure, which
means that the fuzzy measure is dependent on Y
Y
Y
det
CC-separation Measure Applied in Business Group Decision Making
455
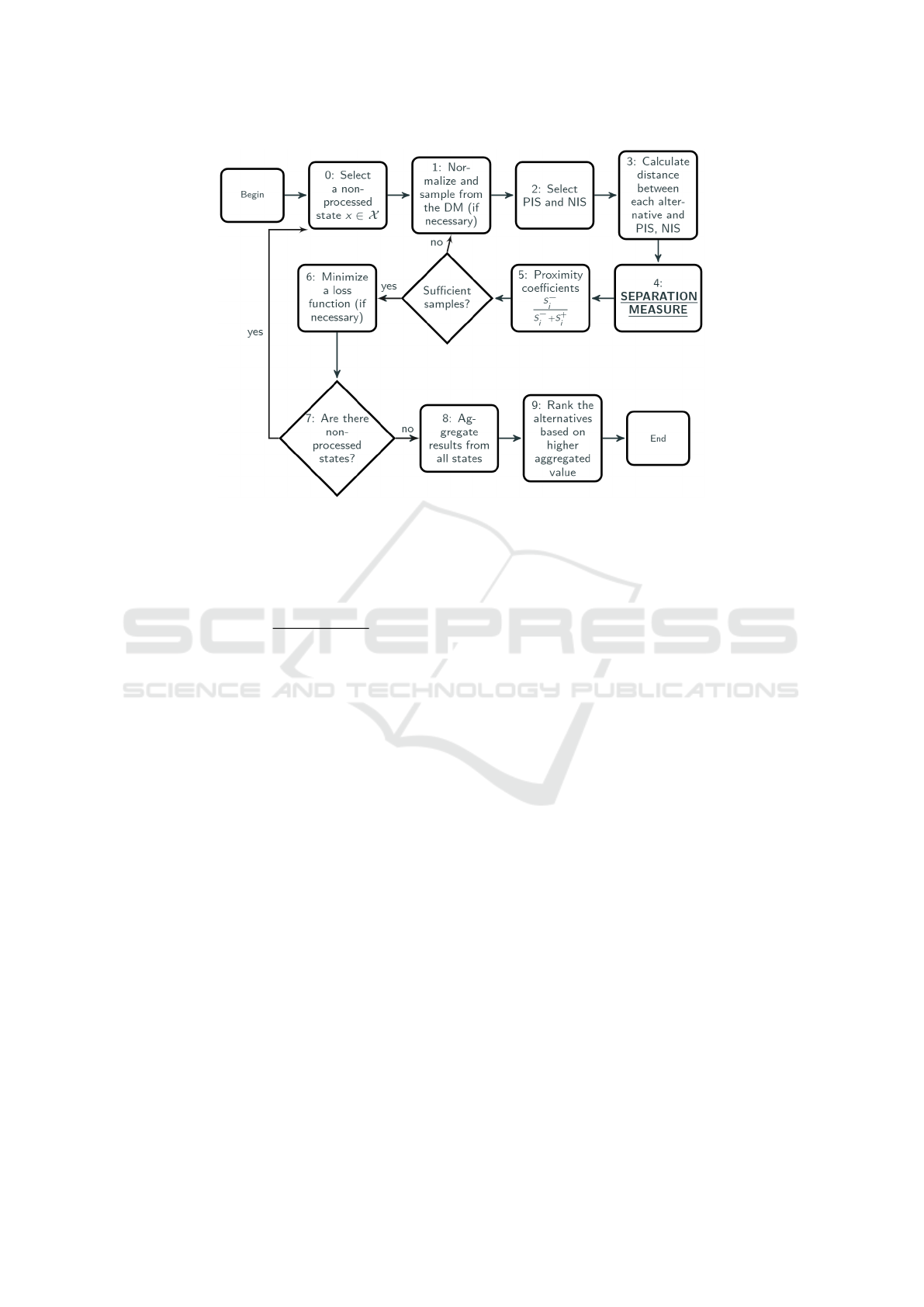
Figure 2: Diagram of the GMC-RTOPSIS process. The separation measure step is where the CC-separation measure is used.
Source: The authors.
Step 5. For each i ∈ {1,..., m}, calculate the
relative closeness coefficient to the ideal solution
with:
CC
i
(Y
Y
Y ) =
S
−
i
(Y
Y
Y )
S
−
i
(Y
Y
Y ) + S
+
i
(Y
Y
Y )
;
Step 6. By using probability distributions in the
DM, it is introduced a bootstrapped probability
distribution in the CC
i
values, so as a point repre-
sentation for this distribution we minimize a pre-
defined risk function:
cc
i
= argmin
c
R(c)
= argmin
c
Z
R
L(c, CC
i
(Y
Y
Y )) dF(CC
i
(Y
Y
Y )); (5)
Step 7. If there is at least one non-processed state
x, return to Step 0;
Step 8. Aggregate the cc
i
values from all the
states with
c
cc
i
= f
x∈X
(cc
i
(x)), where f is an ag-
gregation function.
Step 9. Finally, rank the alternatives from the
highest to the lowest
c
cc
i
values.
3 GENERALIZATION OF THE
GMC-RTOPSIS BY USING
CC-INTEGRALS
Using the Choquet integral in the separation mea-
sure, the GMC-RTOPSIS method allows for interac-
tion among different criteria. This is the step where
this study incorporates the CC-integrals in place of
the Choquet integral.
We introduce the CC-separation measure by:
Definition 3.1 (CC-separation measure). Let Co be
a bivariate copula and m a fuzzy measure. A CC-
separation measure S
∗
: [0,1]
2
→ [0,1] is defined, for
all i ∈ {1,. .. ,m}, by the functions:
S
+
i
(Y
Y
Y ) =
"
n
∑
j=1
Co
d
+
i( j)
2
, m
Y
Y
Y
C
C
C
+
( j)
−Co
d
+
i( j−1)
2
, m
Y
Y
Y
C
C
C
+
( j)
#
1/2
S
−
i
(Y
Y
Y ) =
"
n
∑
j=1
Co
d
−
i( j)
2
, m
Y
Y
Y
C
C
C
−
( j)
−Co
d
−
i( j−1)
2
, m
Y
Y
Y
C
C
C
−
( j)
#
1/2
where d
+
i( j)
, d
−
i( j)
, C
C
C
+
( j)
, C
C
C
−
( j)
and m
Y
Y
Y
are defined as in
Step 4 of the GMC-RTOPSIS algorithm. Note that
the separation measure is the squared root of the CC-
integral, which is an aggregation function as shown
in (Lucca et al., 2017a).
ICEIS 2021 - 23rd International Conference on Enterprise Information Systems
456

4 EXPERIMENTAL
FRAMEWORK
In this section, we present the application of the CC-
separations in the GMC-RTOPSIS. To do so, we start
describing the methodology adopted in the study; af-
ter that, the example in which we apply our approach
is described, and lastly, the obtained results are pre-
sented and discussed.
4.1 Methodology
In this study, we will apply the proposed CC-
separation measure to the Case Study 2 introduced
in (Lourenzutti et al., 2017) and used in (Wieczyn-
ski et al., 2020) to ease the comparison between the
different CC-integrals.
To perform the simulation, we used 10,000 sam-
ples from the DM. We also applied a particle swarm
optimization to learn the fuzzy measure using 30 par-
ticles and 100 interactions. The PSO is used since the
original method had good outcomes with the method.
In this study we used the copula functions from
Table 1. We highlight that we used 2 different values
for the α parameter, which are α = 0.1, selected from
the literature (Lucca et al., 2017a), and α = 0.6, which
was the best fit for the problem presented in this paper
based on the difference between the first and second
ranked alternatives, when compared to other α values.
For the risk function, given in Eq. (5), it was used
the squared loss:
L(cc, CC
i
) = (cc −CC
i
)
2
.
This result in the mean function being the point esti-
mator for the process.
Also, we use the aggregation function bellow in
the Step 8 of the algorithm:
WAM
i
= w(S
1
) ·cc
i
(S
1
) + w(S
2
) ·cc
i
(S
2
).
For the analysis of the results from the different cop-
ula functions, we use the difference between the alter-
native ranked first to the second ranked with:
∆
R1,R2
= max ( ˆc
1
) −max ( ˆc
2
)
where ˆc
1
= {cc
i
| i ∈ {1,.. ., m}} and ˆc
2
= ˆc
1
−
{max( ˆc
1
)}.
Lastly, since we are altering only the Choquet
function, the algorithm maintains its original com-
plexity.
4.2 The Considered Problem
A company needs a new supplier for a provision and
is evaluating four different suppliers, namely A
1
, A
2
,
A
3
and A
4
. The company called three of its managers
to analyze the suppliers and give their ratings based
on their criteria.
The first manager is a budget manager. He con-
sidered the price per batch (in thousands) as C
(1)
1
,
warranty (in days) as C
(1)
2
and payment conditions
(in days) as C
(1)
3
. Also, it was considered that the
demand for the product is higher in December. He
modeled it by using a binary variable τ, that is τ = 0
when the month is between January and November,
and τ = 1 when it is December. Finally, he assigned a
weight for each of his criterion with a weighting vec-
tor: w
w
w
(1)
= (0.5, 0.25, 0.25).
The second manager, a product manager, consid-
ered the price as C
(2)
1
, delivery time (in hours) as C
(2)
2
,
production capacity C
(2)
3
, product quality C
(2)
4
and the
time to respond to a support request (in hours) as
C
(2)
5
. Additionally, to account for the reliability in the
production process and what a failure in the process
could cause to the supplier’s production capacity, he
let P
i
be a random variable such that P
i
= 0 occurs
when there are no failures in the production process
of the supplier A
i
, and P
i
= 1 when there are fail-
ures. Also, in December, the production is acceler-
ated, so the chance of failure is higher, so he modeled
a stochastic process with the help of the function:
f
i
(x,y) = x
1 + y(P
i
+ τ)
2
.
Lastly, the production capacity was modeled by using
ITFNs:
s
2
13
=
(0.8
1+P
1
,0.9
1+P
1
,1.0
1+P
1
,1.0
1+P
1
), 1.0, 0.0
s
2
23
=
(0.8
1+4P
2
,0.9
1+4P
2
,1.0
1+4P
2
,1.0
1+4P
2
), 0.7, 0.1
s
2
33
=
(0.6
1+2P
3
,0.7
1+2P
3
,0.8
1+2P
3
,1.0
1+2P
3
), 0.8, 0.0
s
2
43
=
(0.5
1+3P
4
,0.6
1+3P
4
,0.8
1+3P
4
,0.9
1+3P
4
), 0.8, 0.1
.
This manager selected the same weight for all criteria,
i.e w
w
w
(2)
= (0.2, 0.2, 0.2, 0.2, 0.2).
The commercial manager was the third. He con-
sidered the product lifespan (in years) as C
(3)
1
, social
and environmental responsibility as C
(3)
2
, the quan-
tity of quality certifications as C
(3)
3
and the price as
C
(3)
4
. The weighting vector provided by this manager
is w
w
w
(3)
= (0.25, 0.12, 0.23, 0.4).
The P
i
distribution was determined by historical
data of each supplier and it is given as follows:
• For τ = 0:
p(P
1
= 0|S
1
) = 0.98,
p(P
2
= 0|S
1
) = 0.96,
p(P
3
= 0|S
1
) = 0.97,
p(P
4
= 0|S
1
) = 0.95.
CC-separation Measure Applied in Business Group Decision Making
457

Table 1: Examples of Copulas.
(I) T-norms
Definition Name/Description
T
M
(x,y) = min{x,y} Minimum
T
P
(x,y) = xy Algebraic Product
T
L
(x,y) = max{0,x + y −1} Łukasiewicz
T
NM
(x,y) =
(
min{x, y} if x + y > 1
0 otherwise
Nilpotent Minimum
T
HP
(x,y) =
(
0 if x = y = 0
xy
x+y−xy
otherwise
Hamacher Product
(II) Non-associative overlap functions
Definition Reference/Description
O
B
(x,y) = min{x
√
y,y
√
x} Cuadras-Aug
´
e family of copulas (Nelsen, 2007)
O
mM
(x,y) = min{x,y}max{x
2
,y
2
} (Dimuro and Bedregal, 2014; Pereira Dimuro et al., 2016)
O
α
(x,y) = xy(1 + α(1 −x)(1 −y)),
where α ∈ [−1,0[ ∪ ]0,1]
(Alsina et al., 2006; Lucca et al., 2015)
(III) Non-associative copulas, which are neither t-norms nor overlap functions
Definition Reference/Description
C
F
(x,y) = xy + x
2
y(1 −x)(1 −y) (Klement et al., 2011)
C
L
(x,y) = max{min{x,
y
2
},x + y −1} (Alsina et al., 2006)
C
Div
(x,y) =
xy+min{x,y}
2
(Alsina et al., 2006)
• For τ = 1:
p(P
1
= 0|S
2
) = 0.96,
p(P
2
= 0|S
2
) = 0.92,
p(P
3
= 0|S
2
) = 0.96,
p(P
4
= 0|S
2
) = 0.90.
Considering all the DMs, we have the following
underlying factors: a random component Y
Y
Y
rand
=
(P
1
,P
2
,P
3
,P
4
) and a deterministic component Y
det
= τ
that has two states: S
1
when τ = 0 and S
2
when
τ = 1. The underlying factors can be represented by
Y
Y
Y = (Y
Y
Y
rand
, Y
Y
Y
det
). The managers agreed that the state
S
2
was more important, since the production is higher,
so they gave it a higher weight for it in the aggregation
step (Step 8 of the method) by setting w(S
1
) = 0.4 and
w(S
2
) = 0.6.
The DMs of all managers are presented in Table
2, where the linguistic variables (W, P, I, G and E) are
defined as in Table 3.
The company, considering the opinion of manager 2
more important, assigned a weighting vector for the
managers represented by w
w
w = (0.3, 0.4, 0.3). Fur-
thermore, they wanted to include some interaction be-
tween the criteria, so a variation of 30% was allowed
for each fuzzy measure in relation to the coefficient
in the additive fuzzy measure. This measure is calcu-
lated computationally by means of the PSO algorithm
(Wang et al., 2011; Lourenzutti et al., 2017).
4.3 Obtained Results
The aggregated ranked results are presented in Table 4
(for all the results see APPENDIX Table 5). The table
shows for each copula function Co, the rank of alter-
natives from columns 2 to 5, with its aggregated val-
ues inside parenthesis. The last column shows the dif-
ference between alternatives ranked first and ranked
second.
We can see that for the t-norms the values are pro-
ICEIS 2021 - 23rd International Conference on Enterprise Information Systems
458

Table 2: Decision matrices for the managers.
(a) Budget manager
Alternatives C
(1)
1
C
(1)
2
C
(1)
3
τ = 0 τ = 1
A
1
260.00(1 + 0.15τ) 90 G G
A
2
250.00(1 + 0.25τ) 90 P W
A
3
350.00(1 + 0.20τ) 180 G I
A
4
550.00(1 + 0.10τ) 365 I W
(b) Production manager
Alternatives C
(2)
1
C
(2)
2
C
(2)
3
C
(2)
4
C
(2)
5
A
1
260.00 U( f
1
(48, 0.10), f
1
(96, 0.10)) s
2
13
I [24, 48]
A
2
250.00 U( f
2
(72, 0.20), f
2
(120, 0.20)) s
2
23
P [24, 48]
A
3
350.00 U( f
3
(36, 0.15), f
3
(72, 0.15)) s
2
33
G [12, 36]
A
4
550.00 U( f
4
(48, 0.25), f
4
(96, 0.25)) s
2
34
E [0, 24]
(c) Commercial manager
Alternatives C
(3)
1
C
(3)
2
C
(3)
3
C
(3)
4
A
1
Exp(3.5) W 1 260.00
A
2
Exp(3.0) W 0 250.00
A
3
Exp(4.5) P 3 350.00
A
4
Exp(5.0) I 5 550.00
Table 3: Linguistic variables and their respective trape-
zoidal fuzzy numbers.
Linguistic variables Trapezoidal fuzzy numbers
Worst (W) (0, 0, 0.2, 0.3)
Poor (P) (0.2, 0.3, 0.4, 0.5)
Intermediate (I) (0.4, 0.5, 0.6, 0.7)
Good (G) (0.6, 0.7, 0.8, 1)
Excellent (E) (0.8, 0.9, 1, 1)
portional to the ones presented in the study that used
C
T
-integral instead of the Choquet integral (Wieczyn-
ski et al., 2020). As in that paper, here the T
Ł
t-norm
has the greatest difference, with ∆
R1, R2
= 0.0700. Al-
though, only the T
MN
t-norm performs well compared
with other copulas such as O
α
and C
F
.
The copula O
α
with α = 0.6 achieved the sec-
ond greatest difference among the tested ones, with
∆
R1, R2
= 0.0502. The next of this family tested was
the one with α = 0.1, as it is the main value used in the
literature, it resulted in a quite lower difference value,
with only ∆
R1, R2
= 0.0294. Among the copulas from
the α family, we have C
F
, with ∆
R1, R2
= 0.0466 and
T
MN
with ∆
R1,R2
= 0.0454.
Notice that when using C
div
, C
L
and T
M
copulas the
alternatives A
3
and A
4
change position. This is from
the influence of the state 2 result, where these func-
tions may have weighted higher criteria for alternative
A
4
. Furthermore, the relative small difference ∆
R1,R2
make the top of the rank prone to invert positions.
Our last analysis considered the CC-separations
that presented the lowest ranks. Precisely, it is
observable in the obtained results that the copulas
T
HP
,T
P
,O
B
and T
M
obtained a similar performance
and the lowest separation.
5 CONCLUSIONS
The GMC-RTOPSIS is a decision method that
chooses the alternative that is closer to an ideal solu-
tion. It is capable of dealing with multiple data types
as inputs and, also, through the Choquet integral, con-
siders the interaction among different criteria.
In this paper, we presented the CC-separation
measure. A new measure to be used in the GMC-
RTOPSIS method that utilizes the CC-integrals in-
stead of the Choquet integral. The CC-integrals is a
generalization of the Choquet integral that presented
CC-separation Measure Applied in Business Group Decision Making
459

Table 4: Rank of the alternatives with each of the C functions, ordered by difference between the value of the alternative
ranked first and second.
Co function Ranked 1st Ranked 2nd Ranked 3rd Ranked 4th ∆
R1,R2
T
Ł
A
3
(0.6462) A
4
(0.5762) A
1
(0.4616) A
2
(0.3782) 0.0700
O
α=0.6
A
3
(0.5897) A
4
(0.5395) A
1
(0.4716) A
2
(0.4282) 0.0502
C
F
A
3
(0.5991) A
4
(0.5525) A
1
(0.4453) A
2
(0.4194) 0.0466
T
NM
A
3
(0.5919) A
4
(0.5493) A
1
(0.4713) A
2
(0.3910) 0.0425
O
α=0.1
A
3
(0.5953) A
4
(0.5659) A
1
(0.4453) A
2
(0.3962) 0.0294
O
mM
A
3
(0.5995) A
4
(0.5715) A
1
(0.4454) A
2
(0.3927) 0.0280
C
Div
A
4
(0.5234) A
3
(0.5016) A
1
(0.4868) A
2
(0.4250) 0.0218
C
L
A
4
(0.5273) A
3
(0.5097) A
1
(0.4914) A
2
(0.4361) 0.0176
T
HP
A
3
(0.5351) A
4
(0.5221) A
1
(0.5049) A
2
(0.4308) 0.0131
T
P
A
3
(0.5821) A
4
(0.5701) A
1
(0.4346) A
2
(0.3977) 0.0120
O
B
A
3
(0.5511) A
4
(0.5395) A
1
(0.4713) A
2
(0.4133) 0.0116
T
M
A
4
(0.5229) A
3
(0.5118) A
1
(0.4737) A
2
(0.4386) 0.0110
good results when applied in classification problems.
By using an example from the literature, we tested
the method with 11 different copula functions, with
one of them using two distinct parameters. The re-
sults indicate that the Łukasiewicz t-norm is the best
copula function to use in this example problem since
it gives the greatest separation between the alterna-
tives ranked first and second. Additionally, the Over-
lap alpha family, with α = 0.6, the C
F
and the T
NM
also presented good separations.
By being able to verify the separation between the
ranks, we can choose more confidently the alternative
that better suits the problem. Therefore, by using mul-
tiple functions in the CC-separation measure, we can
see how the problem behaves in different situations.
Finally, future work will consider learning the α
parameter of the overlap alpha family, using distinct
optimization methods.
ACKNOWLEDGMENTS
We would like to thank Dr. Helida S. San-
tos for reviewing the text. This study was sup-
ported by PNPD/CAPES (464880/2019-00) and
CAPES Financial Code 001, CNPq (301618/2019-4),
FAPERGS (19/2551-0001279-9, 19/ 2551-0001660)
and, the Spanish Ministry of Science and Tech-
nology (PC093-094TFIPDL, TIN2016-81731-REDT,
TIN2016-77356-P (AEI/FEDER, UE)).
REFERENCES
Alazzawi, A. and
˙
Zak, J. (2020). Mcdm/a based design
of sustainable logistics corridors combined with sup-
pliers selection. the case study of freight movement
to iraq. Transportation Research Procedia, 47:577 –
584. 22nd EURO Working Group on Transportation
Meeting, EWGT 2019, 18th – 20th September 2019,
Barcelona, Spain.
Alsina, C., Frank, M. J., and Schweizer, B. (2006). As-
sociative Functions: Triangular Norms and Copulas.
WORLD SCIENTIFIC.
Bustince, H., Fernandez, J., Mesiar, R., Montero, J., and Or-
duna, R. (2010). Overlap functions. Nonlinear Anal-
ysis, 72:1488–1499.
Bustince, H., Mesiar, R., Fernandez, J., Galar, M., Pater-
nain, D., Altalhi, A., Dimuro, G., Bedregal, B., and
Takac, Z. (2020). d-choquet integrals: Choquet inte-
grals based on dissimilarities. Fuzzy Sets and Systems.
(submitted).
Candeloro, D., Mesiar, R., and Sambucini, A. R. (2019). A
special class of fuzzy measures: Choquet integral and
applications. Fuzzy Sets and Systems, 355:83 – 99.
Theme: Generalized Integrals.
Choquet, G. (1953–1954). Theory of capacities. Annales
de l’Institut Fourier, 5:131–295.
Deveci, M., C¸ etin Demirel, N., and Ahmeto
˘
glu, E. (2017).
Airline new route selection based on interval type-
2 fuzzy mcdm: A case study of new route between
turkey- north american region destinations. Journal of
Air Transport Management, 59:83 – 99.
Dimuro, G. P. and Bedregal, B. (2014). Archimedean over-
lap functions: The ordinal sum and the cancellation,
idempotency and limiting properties. Fuzzy Sets and
Systems, 252:39 – 54. Theme: Aggregation Functions.
ICEIS 2021 - 23rd International Conference on Enterprise Information Systems
460

Dimuro, G. P., Fern
´
andez, J., Bedregal, B., Mesiar, R.,
Sanz, J. A., Lucca, G., and Bustince, H. (2020). The
state-of-art of the generalizations of the choquet in-
tegral: From aggregation and pre-aggregation to or-
dered directionally monotone functions. Information
Fusion, 57:27 – 43.
Dimuro, G. P., Lucca, G., Sanz, J. A., Bustince, H., and
Bedregal, B. (2018). Cmin-integral: A choquet-like
aggregation function based on the minimum t-norm
for applications to fuzzy rule-based classification sys-
tems. In Torra, V., Mesiar, R., and Baets, B. D., ed-
itors, Aggregation Functions in Theory and in Prac-
tice, pages 83–95, Cham. Springer International Pub-
lishing.
Grabisch, M., Marichal, J.-L., Mesiar, R., and Pap, E.
(2009). Aggregation Functions. page 480.
Huang, C. and Yoon, K. (1981). Multiple Attribute Deci-
sion Making: Methods and Applications. A State-of-
the-Art Survey. Number 186 in Lecture Notes in Eco-
nomics and Mathematical Systems. Springer, Berlin,
Heidelberg.
Klement, E. P., Mesiar, R., and Pap, E. (2011). Triangu-
lar Norms. Springer, Dordrecht; London. OCLC:
945924583.
Lourenzutti, R., Krohling, R. A., and Reformat, M. Z.
(2017). Choquet based TOPSIS and TODIM for dy-
namic and heterogeneous decision making with crite-
ria interaction. Information Sciences, 408:41–69.
Lucca, G., Dimuro, G. P., Mattos, V., Bedregal, B.,
Bustince, H., and Sanz, J. A. (2015). A family of
Choquet-based non-associative aggregation functions
for application in fuzzy rule-based classification sys-
tems. In 2015 IEEE International Conference on
Fuzzy Systems (FUZZ-IEEE), pages 1–8, Los Alami-
tos. IEEE.
Lucca, G., Sanz, J. A., Dimuro, G. P., Bedregal, B., Asi-
ain, M. J., Elkano, M., and Bustince, H. (2017a).
CC-integrals: Choquet-like Copula-based aggrega-
tion functions and its application in fuzzy rule-based
classification systems. Knowledge-Based Systems,
119:32–43.
Lucca, G., Sanz, J. A., Dimuro, G. P., Bedregal, B.,
Fern
´
andez, J., and Bustince, H. (2017b). Analyzing
the behavior of a CC-integral in a fuzzy rule-based
classification system. In 2017 IEEE International
Conference on Fuzzy Systems (FUZZ-IEEE), pages 1–
6, Los Alamitos. IEEE.
Lucca, G., Sanz, J. A., Dimuro, G. P., Bedregal, B.,
Mesiar, R., Kolesarova, A., and Bustince, H. (2016).
Preaggregation Functions: Construction and an Ap-
plication. IEEE Transactions on Fuzzy Systems,
24(2):260–272.
Mesiar, R. and Stup
ˇ
nanov
´
a, A. (2019). A note on cc-
integral. Fuzzy Sets and Systems, 355:106 – 109.
Theme: Generalized Integrals.
Murofushi, T. and Sugeno, M. (1989). An interpretation
of fuzzy measures and the choquet integral as an inte-
gral with respect to a fuzzy measure. Fuzzy Sets and
Systems, 29(2):201 – 227.
Nelsen, R. B. (2007). An introduction to copulas. Springer
Science & Business Media.
Pereira Dimuro, G., Bedregal, B., Bustince, H., Asi
´
ain,
M. J., and Mesiar, R. (2016). On additive generators
of overlap functions. Fuzzy Sets and Systems, 287:76
– 96. Theme: Aggregation Operations.
Shyur, H.-J. and Shih, H.-S. (2006). A hybrid mcdm
model for strategic vendor selection. Mathematical
and Computer Modelling, 44(7):749 – 761.
Sugeno, M. (1974). Theory of Fuzzy Integrals and its Ap-
plications. PhD thesis, Tokyo Institute of Technology,
Tokyo.
Wang, X.-Z., He, Y.-L., Dong, L.-C., and Zhao, H.-Y.
(2011). Particle swarm optimization for determin-
ing fuzzy measures from data. Information Sciences,
181(19):4230–4252.
Wieczynski, J. C., Dimuro, G. P., Borges, E. N., Santos,
H. S., Lucca, G., Lourenzutti, R., and Bustince, H.
(2020). Generalizing the GMC-RTOPSIS method us-
ing CT-integral pre-aggregation functions. In 2020
IEEE International Conference on Fuzzy Systems
(FUZZ-IEEE), pages 1–8, Glasgow.
Zadeh, L. A. (1965). Fuzzy sets. Information and Control,
8(3):338–353.
CC-separation Measure Applied in Business Group Decision Making
461

APPENDIX
Table 5: Mean and standard deviation of the alternatives for
State 1 and State 2. The highest mean for each function and
state is in boldface and the highest for the criterion has an
asterisk*.
State 1 (S
1
, τ = 0) State 2 (S
2
, τ = 1)
Alternatives A
1
A
2
A
3
A
4
A
1
A
2
A
3
A
4
Function mean std.dev mean std.dev mean std.dev mean std.dev mean std.dev mean std.dev mean std.dev mean std.dev
T
Ł
0.4702 0.0482 0.4360 0.0116 0.6438* 0.0367 0.5588 0.0119 0.4558 0.0506 0.3397 0.0334 0.6478* 0.0477 0.5878* 0.0250
O
α=0.6
0.4852 0.0134 0.4791* 0.0232 0.5742 0.0731 0.5078 0.0108 0.4625 0.0266 0.3943 0.0165 0.6001 0.0593 0.5607 0.0214
C
F
0.4774 0.0181 0.4604 0.0173 0.6074 0.0858 0.5270 0.0135 0.4239 0.0194 0.3921 0.0208 0.5935 0.0710 0.5695 0.0174
T
NM
0.4643 0.0269 0.4276 0.0178 0.5939 0.0469 0.5654 0.0186 0.4759 0.0399 0.3666 0.0362 0.5905 0.0379 0.5386 0.0368
O
α=0.1
0.4568 0.0127 0.4282 0.0117 0.6013 0.0791 0.5656 0.0098 0.4377 0.0275 0.3749 0.0223 0.5913 0.0611 0.5661 0.0232
O
mM
0.4519 0.0134 0.4218 0.0171 0.6119 0.0772 0.5668 0.0156 0.4411 0.0308 0.3733 0.0150 0.5912 0.0789 0.5746 0.0271
C
Div
0.5100 0.0101 0.4654 0.0187 0.5139 0.0202 0.5221 0.0191 0.4713 0.0293 0.3980 0.0088 0.4934 0.0242 0.5242 0.0307
C
L
0.5251* 0.0082 0.4670 0.0144 0.5335 0.0058 0.5242 0.0126 0.4690 0.0427 0.4155 0.0165 0.4938 0.0186 0.5293 0.0314
T
HP
0.4976 0.0083 0.4648 0.0141 0.5328 0.0169 0.5253 0.0125 0.5097* 0.0198 0.4081 0.0114 0.5367 0.0207 0.5199 0.0157
T
P
0.4567 0.0120 0.4270 0.0093 0.5976 0.0655 0.5674* 0.0098 0.4198 0.0396 0.3782 0.0190 0.5718 0.0605 0.5719 0.0360
O
B
0.4843 0.0148 0.4443 0.0138 0.5584 0.0422 0.5487 0.0101 0.4626 0.0360 0.3926 0.0156 0.5462 0.0388 0.5334 0.0306
T
M
0.4701 0.0478 0.4615 0.0217 0.5326 0.0018 0.5279 0.0231 0.4761 0.0270 0.4234* 0.0232 0.4980 0.0087 0.5195 0.0269
ICEIS 2021 - 23rd International Conference on Enterprise Information Systems
462
