An Integrated Task and Personnel Scheduling Problem to Optimize

Distributed Services in Hospitals

ıcolas P. Campana

1 a

, Giorgio Zucchi

2,3 b

, Manuel Iori

4 c

, Carlo Alberto Magni

5 d

and Anand Subramanian

6 e

Departamento de Ci

encia da Computac¸

ao, Universidade Federal de Lavras, Av. Central, Campus Universit

ario,

37200-000, Lavras (MG), Brazil

FMB, Marco Biagi Foundation, University of Modena and Reggio Emilia, Largo Marco Biagi 10, 41121 Modena, Italy

R&D Department, Coopservice S.coop.p.a, Via Rochdale 5, 42122 Reggio Emilia, Italy

DISMI, Department of Sciences and Methods for Engineering, University of Modena and Reggio Emilia,

42122 Reggio Emilia, Italy

Department of Economics “Marco Biagi”, University of Modena and Reggio Emilia, 41121 Modena, Italy

Departamento de Sistemas de Computac¸

ao, Centro de Inform

atica, Universidade Federal da Para

ıba, Rua dos Escoteiros,

Mangabeira, 58055-000, Jo

ao Pessoa-PB, Brazil

Keywords:

Personnel Scheduling, Distributed Services, Mathematical Model, Metaheuristic.

Abstract:

This paper addresses a real-life task and personnel scheduling problem arising in a large Italian company that

needs to provide cleaning services inside a hospital. In this case study, the challenge is to determine a schedule

of the employees to clean the whole hospital aiming to minimize the total labor cost, taking into account the

fact that the building is a complex structure with multiple levels and each room has different peculiarity. To

solve the problem, we propose a three-step approach using mathematical models and metaheuristic algorithms.

The solution obtained indicates that the schedule attained by our method is better than the one generated by

the company. In addition, to test and validate our approach more thoroughly, a set of artiﬁcial instances have

been created. The results indicate that our method can help organizations to quickly generate and test a large

variety of solutions. Our ﬁndings can be of general interest for other personnel scheduling problems involving

distributed services.

1 INTRODUCTION

One of the key operational processes in hospitals is

the organization of the cleaning tasks that need to be

performed by employees regularly, to maintain the

necessary level of cleanliness and sanitary security.

Scheduling cleaning tasks is a complex problem (Bar-

tolini et al., 2017) that belongs to the general ﬁeld of

personnel scheduling (Van den Bergh et al., 2013);

it is a very crucial activity for hospitals, especially

in this moment, in which we are facing the Covid-

19 pandemic, which calls for an additional level of

saniﬁcation. Our interest originates from the activity

https://orcid.org/0000-0001-5499-6876

https://orcid.org/0000-0002-5459-7290

https://orcid.org/0000-0003-2097-6572

https://orcid.org/0000-0003-3066-8426

https://orcid.org/0000-0002-9244-9969

of Coopservice, a large third-party service provider

that is responsible for the cleanliness and sanitary se-

curity of a large number of hospitals in Italy. How-

ever, the problem can be generalized to a large variety

of services that should be carried out in a distributed

manner across large facilities. To provide their ser-

vices, third-party companies must take part in tender

processes for cleaning services. To achieve success,

they have to submit cost-efﬁcient offers. In a hospital,

there are often many costs that cannot be inﬂuenced

substantially by the company. This means that per-

sonnel costs and personnel management become the

critical factor. Therefore, an efﬁcient and automated

planning of personnel schedules enables one to create

a competitive advantage in tender processes.

To solve the problem, we need to create clean-

ing schedules for a speciﬁc planning period (e.g., a

month), and then allocate the available employees to

Campana, N., Zucchi, G., Iori, M., Magni, C. and Subramanian, A.

An Integrated Task and Personnel Scheduling Problem to Optimize Distributed Services in Hospitals.

DOI: 10.5220/0010441804630472

In Proceedings of the 23rd International Conference on Enterprise Information Systems (ICEIS 2021) - Volume 1, pages 463-472

ISBN: 978-989-758-509-8

463

the schedules by minimizing the total labor cost while

satisfying given services requirements. In view of

this, we propose a hybrid three-step approach based

on the combined use of heuristics and mathematical

models.

As inputs, we are given a set of employees, as

well as a set of locations, each with an associated set

of cleaning tasks with some physical characteristics,

such as the level of sanitary risk, location size and

time windows. The ﬁrst step focuses on a standard

one-week period of work. In this period, we ﬁrst al-

locate the cleaning tasks to the days so as to balance

the workloads. This is achieved by solving a mixed-

integer linear programming (MILP) model. Secondly,

for each day in the period, we create a set of clean-

ing routes by solving a vehicle scheduling problem

with time windows (VSPTW). The cleaning routes

are sequences of visits to locations within the given

time windows. Due to its NP-Hardness, we solve the

VSPTW by means of an adapted variable neighbor-

hood descent approach, using some well-known lo-

cal search procedures (Br

aysy and Gendreau, 2005a;

aysy and Gendreau, 2005b). At the third step, we

solve a personnel scheduling problem (PSP). Con-

sidering a larger one-month period and incorporating

further operational constraints to solve the problem,

we develop constructive and local search heuristics

aimed at assigning the cleaning schedules to the em-

ployees and minimizing the total labor cost.

An overview of the three-step approach is pre-

sented in Figure 1.

Optimal allocation of cleaning tasks to days

Step 1

Creation of cleaning routes minimizing travel distance

Step 2

Personnel scheduling minimizing total labor cost

Step 3

Figure 1: Three-step approach.

Our three-step approach was used to solve a real

instance derived from a real-world Italian hospital

operated by Coopservice, and the results obtained

were positively conﬁrmed by the company’s man-

agers. Moreover, to test and validate our approach

a set of artiﬁcial instances have been created. For

all instances, we attained full coverage of the clean-

liness requirements of the hospital, thus satisfying the

needed sanitary level.

The main contribution of this paper is to propose a

decomposition method to solve a case-study that can

help companies to quickly generate and test a large

variety of solutions for integrated task and person-

nel scheduling for distributed services, ensuring the

minimization of the costs, in terms of working hours,

for the company. In addition, it could enable com-

panies to reorganize cleaning activities, as entire de-

partments and locations can change their risk level be-

cause of the COVID-19 emergency. Moreover, it can

be used to quickly reorganize the scheduling of em-

ployees in case some workers are subjected to quar-

antine periods due to the infection.

The remainder of this paper is organized as fol-

lows. Section 2 gives a formal problem deﬁnition.

Section 3 provides a brief literature review. Section

4 describes our three-step approach. Section 5 re-

ports the results of our algorithm and, ﬁnally, Section

6 presents the concluding remarks.

2 PROBLEM DEFINITION

In a hospital complex, we have a set of buildings B,

and every building b ∈ B also has an internal ﬂoor di-

vision L

. For each ﬂoor l ∈ L

, there is a set U

locations to be cleaned. Each location v ∈ U

on a

ﬂoor l of a building b has an associated type (e.g., el-

evator, ofﬁce, toilet, etc.) and risk level, which can

be classiﬁed as low, medium, or high. These two at-

tributes have an impact on both the weekly cleaning

frequency and effort. For example, a toilet has to be

cleaned more often than a simple ofﬁce.

Let D = {1, ...,7} be the set of days. The weekly

frequency f

for cleanness of each location v is pro-

vided by the hospital, in other words, f

gives the

number of days in the week in which v has to be

cleaned. The company generates a set P

of feasi-

ble patterns, which are the possible combinations for

the weekly assignment at location v. When a pat-

tern p is assigned to the location v, all the clean-

ing tasks of v must be executed in each of the days

in the pattern. For example, assuming that f

3, we could have the following pattern set: P

{{1,3,5},{2,4, 6},{3, 5,7}}. In this case, if the com-

pany selects the ﬁrst pattern, then the cleaning tasks

at location v are scheduled to be performed on days 1,

3 and 5.

The problem is rather complex; thus, we describe

it by using three steps, which also correspond to the

ICEIS 2021 - 23rd International Conference on Enterprise Information Systems

464

main steps of our solution algorithm described later

in Section 4.

Step 1. For each location v, we deﬁne a set of clean-

ing tasks T

; each task k ∈ T

has a total duration of

minutes. In practice, the duration varies accord-

ing to the type of task, which can be either a complete

cleaning or a fast cleaning, and with the size of the lo-

cation (expressed in m

) and its type. Moreover, each

task k ∈ T

also has a time window [a

, u

], which

determines the earliest and latest times to execute task

k. The company wishes to decrease the total amount

of cleaning time during weekends (e.g., on days d =

6 and d = 7) by a factor β

, due to contractual con-

straints with the employees, and also because the ac-

tivities of the physicians are usually reduced.

Step 2. For each building b ∈ B, we are given a graph

= (N

), where the set of nodes N

is com-

posed of its starting and ending node where all per-

sonnel starts and ends the routes, here deﬁned as ρ

and the corresponding cleaning locations of b. More

precisely, N

= {ρ

} ∪ {v : v ∈ U

,l ∈ L

}. Each ρ

of a corresponding block b ∈ B has an associated time

window [a

], where a

and u

are the earliest

and latest departure and arrival times in the day, re-

spectively. The maximum schedule duration was de-

ﬁned, along with the company, as a target duration τ.

Moreover, we assume that all locations on the

same ﬂoor l ∈ L

are interconnected, meaning that

there is an arc connecting each pair of nodes located at

l. The ﬂoors are connected through elevators, which

are also cleaning locations. Thus, we deﬁne a subset

⊂ N

composed of all locations that are elevators

in the building b. We can then deﬁne the arc set as

= {(i, j) : i, j ∈ U

,i 6= j,l ∈ L

} ∪ {(i, j) : i, j ∈

,i 6= j}. Furthermore, each arc (i, j) ∈ A

has an

associated traveling distance d

i j

and time t

i j

Step 3. Regarding the personnel scheduling, the com-

pany provides a set of heterogeneous employees E.

Each employee e ∈ E has a contract type C

, de-

termining the maximum number of days he/she can

work in a week (as in our case, where it is set to a

month). There are two types of work patterns: (i)

“5+2”, which means ﬁve days of work and two days

of rest; and (ii) “6+1”, which consists of six days of

work and the Sunday of rest. Note that in the ﬁrst

pattern the days can be arranged in any permutation,

whereas in the second one there is only one possible

option.

The company also speciﬁes a maximum amount

of days C

that any employee can work consecutively

without a rest day. This value is useful when the ros-

tering period is longer than a week. In addition, each

employee has a maximum amount of working hours

per week, deﬁned by M

. Furthermore, let M

be the

maximum working hours in a day, deﬁned by the Ital-

ian law, and W T

be the maximum waiting time be-

tween two sequences of cleaning routes. Also, let δ

be the number of days associated with the scheduling

period.

The objective of the ﬁrm is to minimize the total

labor cost. Taking the average historic unit cost h (as

provided by the hospital) as a proxy for the unit cost

of all workers, the objective function is:

min Z = h · z (1)

where z is the total working time. Let λ

be the

total working time of an employee e ∈ E. Then, mini-

mization of (1) boils down to minimization of (2) be-

low:

min z =

∑

e∈E

(2)

The Integrated Task and Personnel Scheduling

Problem (ITPSP) aims at optimize (2) while meeting

the operational constraints deﬁned at steps 1, 2 and 3.

3 LITERATURE REVIEW

The literature on complex OR problems arising in the

ﬁelds of logistics and scheduling is vast and it is not

our goal here to provide a comprehensive review. In-

stead, we turn our attention to decomposition-based

methods closely related to our work.

Considering that we face an integrated task and

personnel scheduling problem, we focus our re-

view on approaches that integrate these two aspects.

(Smet et al., 2016) introduced a problem called Task

Scheduling and Personal Rostering Problem (TSRP),

which they solved by means of a very Large Neigh-

borhood Search and a column generation algorithm.

The TSRP considers non-preemptive tasks, ﬁxed

tasks, ﬁxed shifts and qualiﬁcations, and aims at min-

imizing the weighted sum of constraint violations. In-

deed, in the TSRP it is often impossible to obey to all

the contractual constraints, as they are often imposed

by authorities with conﬂicting priorities. The TSRP

differs from the ITPSP that we face for two reasons:

(i) the TSRP has ﬁve shifts rather than a task demand

shift (see (Ernst et al., 2004), for the problem termi-

nology); (ii) in the TSRP only one task can be as-

signed to a shift. In (Lap

egue et al., 2013), the authors

introduced a very similar problem, the Personnel Task

Scheduling Problem (PTSP), and a variant known as

Shift Minimization Personnel Task Scheduling prob-

lem (SMPTSP) in which the shifts are not ﬁxed and

are deduced from the task assignment. The PTSP

is a problem in which a set of tasks with ﬁxed start

An Integrated Task and Personnel Scheduling Problem to Optimize Distributed Services in Hospitals

465

and ending times have to be allocated to a heteroge-

neous workforce. In (Guyon et al., 2010), the au-

thors proposed a decomposition method to solve an

integration of the employee timetabling and produc-

tion scheduling problems. At the ﬁrst level, they

solved a traditional timetabling problem. At the sec-

ond level, they aimed at supplying feasible schedules

for a set of uninterruptible tasks. In (Maenhout and

Vanhoucke, 2018), the authors proposed a perturba-

tion meta-heuristic for the integrated personnel shift

and task re-scheduling problem. In that context, some

schedule disruptions can arise as a result of some

operational variability, creating the necessity of re-

scheduling the already planned roster. More recently,

(Kletzander and Musliu, 2020) proposed a framework

to solve a General Employee Scheduling Problem

(GESP), in which a wide range of different constraints

needs to be considered to allow the speciﬁcation of

different requirements without the need to introduce a

new problem formulation for each variant of the prob-

lem. They used an XML format to specify the formu-

lation in a human and machine readable way. The

GESP deals with the scheduling of shifts as well as

optional tasks and breaks for a set of employees over

a certain period of days. (Elahipanah et al., 2013) in-

troduced the Flexible Activity and Task Assignment

Problem (FATAP), which takes place in a ﬂexible en-

vironment where the detailed activity and task de-

mands are uncertain, allowing the decision maker to

use additional temporary employees, scheduling over-

time for regular employees and moving meals break.

The authors used a two-phase approach, ﬁrstly solv-

ing an approximate MILP model and a column gen-

eration heuristic embedded into a rolling horizon pro-

cedure. In (Doi et al., 2018), the authors proposed

a decomposition-based meta-heuristic algorithm for

practical airline crew rostering problems with fair

working time. Another interesting paper is the one by

(Salazar-Gonz

alez, 2014), in which the author devel-

oped an arc-ﬂow variable formulation to solve an inte-

grated ﬂeet-assignment, aircraft-routing, crew-pairing

problem, and a MILP formulation to solve a crew ros-

tering problem of a Spanish air carrier company.

The ITPSP that we face differs from the problems

analyzed in the previous literature because it con-

tains a very general combination of constraints de-

rived from the real-world application at hand. The

tasks have an interval time to be executed, but no ﬁxed

start time. The shifts are not ﬁxed, and the tasks are

non-preemptive. In addition, in the third step, we con-

sider employees with no qualiﬁcation differences and

use the historic average unit cost as a proxy for the

unit cost of each worker, so that minimization of total

personnel cost is equivalent to minimization of total

working time. Lastly, we need to solve this problem

for a planning horizon of one month using a standard

weekly plan for the tasks to execute.

4 PROPOSED ALGORITHM

Decomposing the problem into multiple steps can be

considered a very useful alternative for huge and com-

plex problems (Vance et al., 1997; Juette and Thone-

mann, 2012; Hoffmann et al., 2017). Therefore, we

propose a three-step approach to solve the TPSP, as

described in the following.

In the ﬁrst step, we solve a MILP model that seeks

to minimize the maximum number of daily working

hours (see Section 4.1) to determine a weekly pattern

p for each location v. In this phase, one deﬁnes all lo-

cations that must be cleaned on each day. For conve-

nience, we denote this problem as location scheduling

(LS).

Next, for each day, we solve the VSPTW using a

local search procedure based on Randomized Variable

Neighborhood Descent (RVND), as described in Sec-

tion 4.2. More precisely, the second step aims at min-

imizing the total travel distance, while respecting the

time windows of each location, generating a cleaning

schedule for all days.

In the last step, we solve a personnel scheduling

problem (PSP), explained in detail in Section 4.3. The

objective is to organize the available personnel to ex-

ecute the cleaning schedule generated in the previ-

ous step, for a given scheduling period (usually one

month), minimizing the total working time of the em-

ployees according to (2) (and, therefore, minimizing

the total cost).

Algorithm 1 provides an overview of the proposed

approach.

Algorithm 1: Iterative three-step algorithm.

1: procedure 3-S T E P (U,E,ε,η, φ)

2: s

∗

← ∅  Final solution

3: H ← ∅  Set of weekly patterns

4: while time limit ε not reached do

5: m ← buildNewMILPModel(H,U)

6: WeeklyPattern ← LS(m);

7: C Schedule ← VSPTW(WeeklyPattern,η,φ)

8: P Schedule ← PSP(C Schedule,E)

9: if f (P Schedule) ≤ f (s

∗

) then

10: s

∗

← P Schedule

11: end if

12: H ← H ∪WeeklyPattern

13: end while

14: return s

∗

15: end procedure

ICEIS 2021 - 23rd International Conference on Enterprise Information Systems

466

Our algorithm iteratively executes the three steps

mentioned above until a time limit ε is achieved. At

each iteration, the method builds a new assignment

problem using the information of all previous assign-

ments (line 6). The idea is to generate diversiﬁed-

yet-efﬁcient weekly patterns, as described in Section

4.1. The solution found in the ﬁrst step is then pro-

vided to the second step, where one aims at determin-

ing the cleaning schedule by solving a VSPTW (line

7). The third step is responsible for obtaining a per-

sonnel schedule using the VSPTW solution as in input

(line 8), thus generating a ﬁnal solution for the TPSP.

In case of improvement, the best TPSP solution found

is updated (lines 9–11). Finally, the set of weekly pat-

terns is updated before the next iteration (line 12).

4.1 First Step: Generating a Weekly

Pattern

In periodic routing problems, choosing a visiting pat-

tern for the customers can be a very useful strategy

(Cordeau et al., 1997). In our case, we are interested

in selecting a weekly pattern from P

for each loca-

tion v, assigning locations to days. The objective is to

minimize the maximum working time across all days.

Let Q

be equal to 1 if the pattern p contains

day d, 0 otherwise. Since some days may have less

amounts of work (e.g., at the weekends) we denote as

as the balance factor for each day d ∈ D. Let θ

the time to execute all the tasks of location v in the day

d, given by θ

= β

∑

k∈T

,∀v ∈ U, ∀d ∈ D. Note

that this value does not inform if the day d is present

in the patterns of v. Let x

be the binary variable as-

suming value 1 if pattern p is assigned to location v, 0

otherwise. In addition, let variable z

denote the max-

imum daily working time. The MILP formulation can

be written as follows:

min z

(3)

∑

p∈P

= 1 ∀v ∈ U (4)

∑

v∈U

≤ z

∀d ∈ D (5)

∈ {0,1} ∀v ∈ U,∀p ∈ P

(6)

≥ 0. (7)

The objective function (3) aims at ﬁnding a bal-

anced solution by minimizing the maximum working

time across all days. Constraints (4) impose that ex-

actly one pattern must be selected for each location

v. Constraints (5) compute the maximum daily work-

ing time. Finally, constraints (6) and (7) deﬁne the

domain of the variables.

At each iteration τ of Algorithm 1, the MILP

model is modiﬁed by inserting a hamming-distance

constraint (8), which is based on the optimal cuts for

two-stage stochastic linear programs with recourse

(Laporte and Louveaux, 1993). We deﬁne ξ as a per-

centage of how many variables must change with re-

spect to the previous solutions generated. In order

to obtain different solutions at every execution of the

algorithm, we add the following constraint to model

(3)-(7)

∑

(v,p)∈s

(1 − x

) +

∑

(v,p) /∈s

≥ ξ s

∈ T (8)

where s

denotes the solution obtained at iteration τ

and T denotes the set of solutions generated during

all iterations.

4.2 Second Step: Generating the

Cleaning Schedule

In this step, one has to determine the daily sequence

and start time of the visits to locations that the em-

ployees have to perform, here called cleaning sched-

ule. In our case, this is achieved by solving a VSPTW

for each day, where the customers are the locations

and the depot is the starting and ending point ρ

, each

of them with an associated time window (see Section

2).

To solve the VSPTW, we have designed a heuris-

tic procedure whose pseudocode is described in Algo-

rithm 2. Let N

be the subset of locations that should

be visited on day d, and let N =

d∈D

. In addition,

let T be the set containing the VSPTW solutions ob-

tained on each day. Parameters η and φ are related to

the local procedure, and are described further in this

section. For each day, the algorithm generates an ini-

tial solution using a greedy approach (line 4), which

is possibly improved by a local search procedure (line

5) based on RVND (Subramanian et al., 2010). The

solution found after the local search step is then ap-

pended to T (line 6).

Algorithm 2: VSPTW.

1: procedure VSPTW(N, η, φ)

2: T ← ∅

3: for d ∈ D do

4: s ← GreedyAlgorithm(N

)

5: s ← RV ND(s, η, φ)

6: T ← T ∪s

7: end for

8: return T

9: end procedure

The constructive procedure generates an initial so-

lution starting from the lowest to the highest ﬂoor,

An Integrated Task and Personnel Scheduling Problem to Optimize Distributed Services in Hospitals

467

with a view of minimizing the displacement of em-

ployees inside the building. At each ﬂoor, the task

with minimum latest time window is inserted at the

last position of the sequence. In case of tie, the al-

gorithm selects the task whose location is the near-

est with respect to the last task inserted. If there are

no more tasks on the given ﬂoor, then one contin-

ues the insertion from the next ﬂoor. When it is no

longer possible to add a task without violating the

constraints, a sequence (or a cleaning route) is created

and the procedure is repeated until no more tasks are

left to be inserted. Note that a daily cleaning sched-

ule is composed of all cleaning routes associated with

that day.

The local search engine consists of an adaptation

of the RVND procedure. Three classical inter-route

neighborhood structures were considered, in particu-

lar, cross-exchange, relocate and swap. Whenever an

improving move is found, an intra-route local search

is applied, also in a RVND-like fashion, using 2-

opt and swap neighborhoods. The ﬁrst improvement

strategy is adopted, and the algorithm performs the

search in φ percent of neighborhood size. The lo-

cal procedure is iteratively called for up to η times.

Furthermore, since a local search move between two

ﬂoors that are considered far enough is not likely

to yield an improving move (e.g., a swap between

tasks of the ﬁrst and ninth ﬂoors), we have deﬁned

a ﬂoor vicinity rule, which only allows moves involv-

ing ﬂoors l − 1, l and l + 1.

Finally, in order to build the cleaning schedule,

one should deﬁne the optimal start times of the vis-

its by minimizing the total duration of each cleaning

route. The timing problem considered here was in-

troduced and solved using the so-called forward slack

time procedure by (Savelsbergh, 1992). Let k ∈ σ be a

task, where σ is a cleaning route composed of n tasks.

We are given the following for each task k: (i) q

the service time; (ii) ST

is the earliest feasible start

time; (iii) W T

is the cumulative idle time; and (iv)

is the partial forward slack time. We begin with

the following values: ST

= a

, W T

= 0, and FD

− a

. Next, we compute the remaining values:

= max(ST

k−1

+ q

k−1

) k ∈ σ (9)

W T

= W T

k−1

+ (ST

− ST

k−1

− q

k−1

) k ∈ σ (10)

= min(FD

k−1

− ST

+W T

) k ∈ σ. (11)

Finally, the start time of the cleaning route is given

by st

∗

= a

+ min(FD

,W T

(The reader is referred to (Vidal et al., 2012), for

a comprehensive review on timing problems.)

4.3 Third Step: Personnel Scheduling

In the personnel scheduling phase, the objective is to

minimize the total working time (and, therefore, the

total cost) by assigning employees to duties, which is

in turn derived from the cleaning routes generated in

the second step. Algorithm 3 describes the procedure

developed to the referred subproblem.

Algorithm 3: Overall Heuristic.

1: procedure PSP(T ,E)

2: C ← CreateDailyDuties(T )

3: E

← AssignEmployeesToDuties(E,C

)

4: E

∗

← LocalSearch(E

)

5: return E

∗

6: end procedure

Firstly, one determines the duties associated with

a day of work, which is composed of a set of one or

more cleaning routes (line 2). In particular, the al-

gorithm employs the best ﬁt strategy by maximizing

the number of tasks in the duty, always satisfying the

constraints of the problem, and avoiding intersections

between the times speciﬁed in the cleaning schedule.

Note that a duty may comprise more than one clean-

ing route, and the process of putting them together can

be seen as a packing problem (Krishnamoorthy et al.,

2012). The total time of a duty is given by the sum

of the execution times of all cleaning routes plus the

possible waiting times between them.

Secondly, the algorithm assigns the employees to

the duties (line 3). More precisely, the available em-

ployees are sorted in non-ascending order according

to the their contractual working time. A ﬁrst-ﬁt pol-

icy is then applied for each day, assigning employ-

ees to the duties, followed by a local search (line 4).

The procedure ﬁrst tries to interchange the weekly du-

ties between two different employees (as long as they

have different M

). If this change fails to yield a fea-

sible improvement, the algorithm attempts to perform

another move involving same pair of employees. In

this case, a day is chosen at random, and the respec-

tive duties from that day are interchanged between the

employees. The procedure terminates when no im-

proving move is obtained.

In Figure 2, we present a graphical representation

of the proposed algorithm in order to help the reader

understand the presented methodology.

ICEIS 2021 - 23rd International Conference on Enterprise Information Systems

468

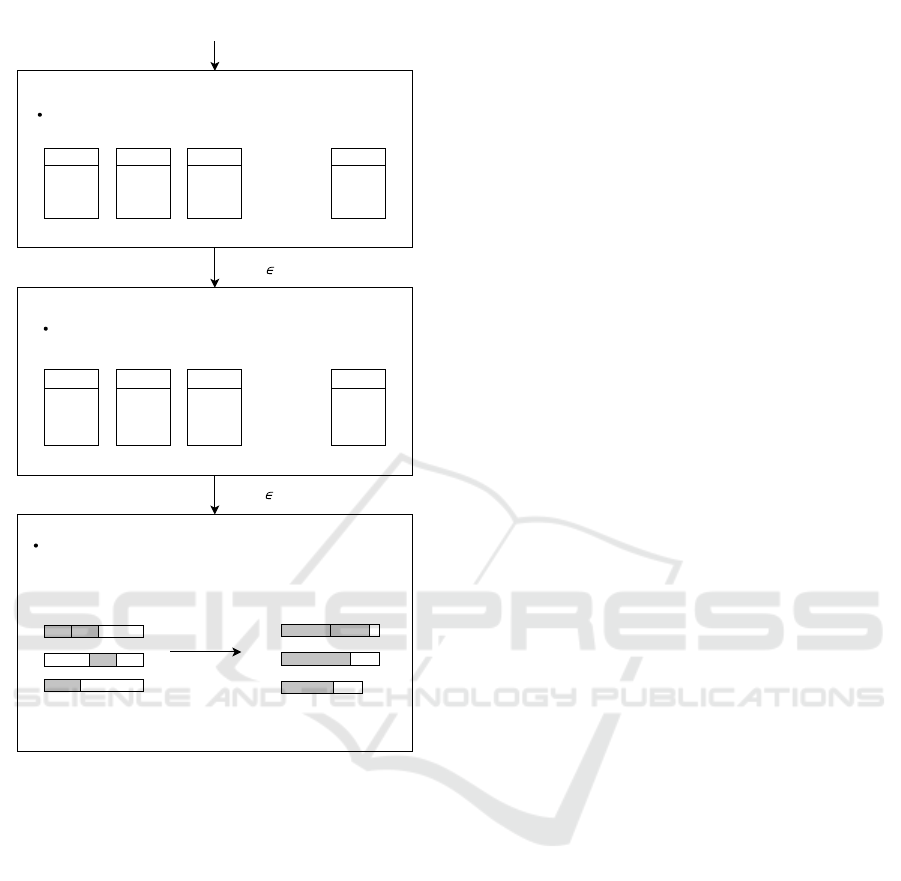
Step I: allocation of cleaning tasks to days

Let N

be the set of locations that should be visited on day d

Set of

locations v

Set of

locations v

Set of

locations v

...

Set of

locations v

Step II: creation of cleaning routes for all days

Let T

be the subset of cleaning routes on day d

Set of

cleaning

routes

Set of

cleaning

routes

Set of

cleaning

routes

...

Set of

cleaning

routes

N = ∪

d D

Step III: personnel scheduling

Let E be the set of heterogeneous employees

1. Creation of the daily

duties with the routes

2. Assign employees to

duties

Day 1

...

Let D={1,...,7} be the set of days. For each location v we have a

set of cleaning task T

and a set P

of feasible patterns

T = ∪

d D

Figure 2: An overview of the proposed algorithm.

5 COMPUTATIONAL

EXPERIMENTS

To validate the proposed algorithm, we solved a real-

life instance of the company, and to evaluate the ro-

bustness of the method, we created 20 random in-

stances based on real data. The algorithm was coded

in Python 3.7.3 and executed on an Intel(R) Xeon(R)

CPU E3-1245 v5 3.50GHz with 32GB of memory,

running Linux Ubuntu 18.04 LTS 64-bits.

The CBC (https://github.com/coin-or/Cbc) solver

from COIN-OR was used to solve the MILP model

presented in Section 4.1 (Lougee-Heimer, 2003). A

limit of 10 seconds was imposed for the solver. Re-

garding the overall procedure, a time limit of 1,800

seconds was imposed. To improve performance, we

have parallelized the implementation of Algorithm

2 using 4 cores, beneﬁting from the fact that the

VSPTW can be addressed independently for each day.

5.1 Parameters

For all experiments, we used the following parameter

values, as deﬁned by the company:

• β: 50%;

• µ: 50 meters per minute;

• τ: 480 minutes;

• W T

: 20 minutes;

• C

: 6 days;

• δ: 14 days.

Moreover, we adopted ε = 1,800 seconds, and

φ = 10% after conducting preliminary experiments.

In addition, the values of the two remaining param-

eters, η and ξ, were chosen after comparing the re-

sults obtained by different combinations with the one

provided by the company on the real-life instance, as

described in Section 5.3.

5.2 Instances

The real-life instance was created using BIM (Build-

ing Information Modeling), which is a data model

that stores different types of information and con-

sists of parametric objects representing building com-

ponents. Objects may have non-geometric attributes

with functional, semantic or topological information

(Volk et al., 2014). In the hospital associated with

the real-life instance (see Figure 3), there is a build-

ing containing 15 ﬂoors with a total of 2,422 loca-

tions, not uniformly distributed, and divided into 47

types. The instance has 227 locations referred to as

elevators. Each location has a coordinate (x,y) in a

normalized Cartesian plane.

In addition, we generated 20 artiﬁcial instances by

simply combining the ﬂoors of the real-life instance.

More precisely, we randomly chose a subset of ﬂoors,

always keeping the original information regarding the

existing locations on the respective ﬂoor, and built a

new instance by sorting such selected ﬂoors in an ar-

bitrary fashion.

In vehicle routing and scheduling problems, the

distance between two locations is often computed us-

ing the Euclidean distance. In our problem, we have

a three-dimensional building, so we compute the dis-

tance between two locations by considering ﬂoors and

elevators as follows. If the two locations i and j are on

the same ﬂoor, their distance d

i j

is computed by the

shortest path. Otherwise, we calculate the distance

matching the closest elevators on both ﬂoors that min-

imizes the total distance of traveling from i to j. This

An Integrated Task and Personnel Scheduling Problem to Optimize Distributed Services in Hospitals

469

Figure 3: An overview of the hospital.

is done by taking the distance from i to the closest el-

evator plus the distance from that elevator to j. Let L

be the function that returns the location v of the ﬂoor

and κ denote an elevator. Function SP in (12) calcu-

lates the shortest path from i to j:

SP(i, j) = min

,κ

∈

L(i)

iκ

+ d

L( j)

. (12)

The cost c

i j

is therefore given by:

i j

(

SP(i, j) if L (i) 6= L( j)

i j

otherwise

(13)

Let µ be the standard walking speed which was

empirically observed by the company. The travel time

from i to j is given by t

i j

= c

i j

/µ.

5.3 Results for the Real-life Instance

The two parameters in which we experimented with

different values were η and ξ (η indicates the num-

ber of times in which the local procedure is iteratively

called and ξ deﬁnes a percentage of how many vari-

ables must change with respect to the previous so-

lutions generated). We conducted tests for all com-

binations of the following values: η ∈ {20,30,40}

and ξ ∈ {1, 20%,50%}. The main objective in test-

ing these combinations is to deﬁne the standard pa-

rameters for the company to run the algorithm. Ta-

ble 1 shows the results achieved on the real-life in-

stance. For each tested combination of η and ξ, we

report the best solution found z computed as in (2)

and the percentage gain over the solution provided by

the company, whose value is z

= 135780. It can be

observed that the setting η = 40 and ξ = 1 yields the

best improvement of 5.83%. The percentage gain is

computed as 100(z

− z)/z

5.4 Results for the Artiﬁcial Instances

We also carried out a similar experiment for the ar-

tiﬁcial instances. For each instance, we considered

Table 1: Results obtained for the real-life instance.

η ξ z %gain

20 1 128,323 5.81

20 20 128,330 5.81

20 50 128,324 5.81

30 1 128,309 5.82

30 20 128,328 5.81

30 50 128,327 5.81

40 1 128,302 5.83

40 20 128,320 5.81

40 50 128,335 5.80

the same values of η and ξ speciﬁed in the previous

section. Table 2 reports the information of each in-

stances, namely, the number of ﬂoors and locations,

together with the combination of η and ξ that yielded

the best result. In the last two columns, we provide

the value of the objective function and the CPU time

required to ﬁnd the best solution. The results show

that, on average, 1186 seconds are necessary for the

method to obtain the best solution. By observing

the results obtained, and computing the frequency of

the parameter setting for which the best solution was

found, we found that the best conﬁguration of η and

ξ are 20 and 50, respectively.

Table 2: Best results found on the artiﬁcial instances.

Instance Floor Locations η

best

z t

∗

1 4 534 30 50 46,336 568.73

2 11 1,678 30 20 126,520 634.37

3 6 857 30 50 66,136 1,646.40

4 3 483 40 50 38,936 1,355.59

5 14 2,020 20 20 164,512 1,705.86

6 5 743 40 1 51,098 209.24

7 10 1,451 20 50 106,348 844.65

8 3 494 30 20 40,442 1,671.83

9 3 439 20 1 31,626 997.60

10 11 1,613 20 50 132,850 1,487.25

11 11 1,643 30 1 128,154 662.20

12 3 399 30 1 43,918 1,577.16

13 9 1,226 40 20 106,160 176.98

14 5 777 20 20 81,944 1,716.20

15 15 2,191 20 20 180,794 969.58

16 2 223 40 50 23,728 1,483.14

17 11 1,645 30 20 126,366 1,594.48

18 6 897 20 50 70,277 1,298.90

19 13 1,915 40 1 165,114 1,457.60

20 13 1,875 20 50 150,448 1,662.42

Figure 4 depicts an example of the behavior of the

proposed algorithm on instance 18, when consider-

ing the best conﬁguration of parameters found, i.e.,

best

= 20 and ξ

best

= 50. The plot shows the impor-

tance and effectiveness of using an iterative approach,

as illustrated by the results obtained in the last step of

each iteration. In this case, it can be observed that the

best result is achieved at iteration 21.

ICEIS 2021 - 23rd International Conference on Enterprise Information Systems

470

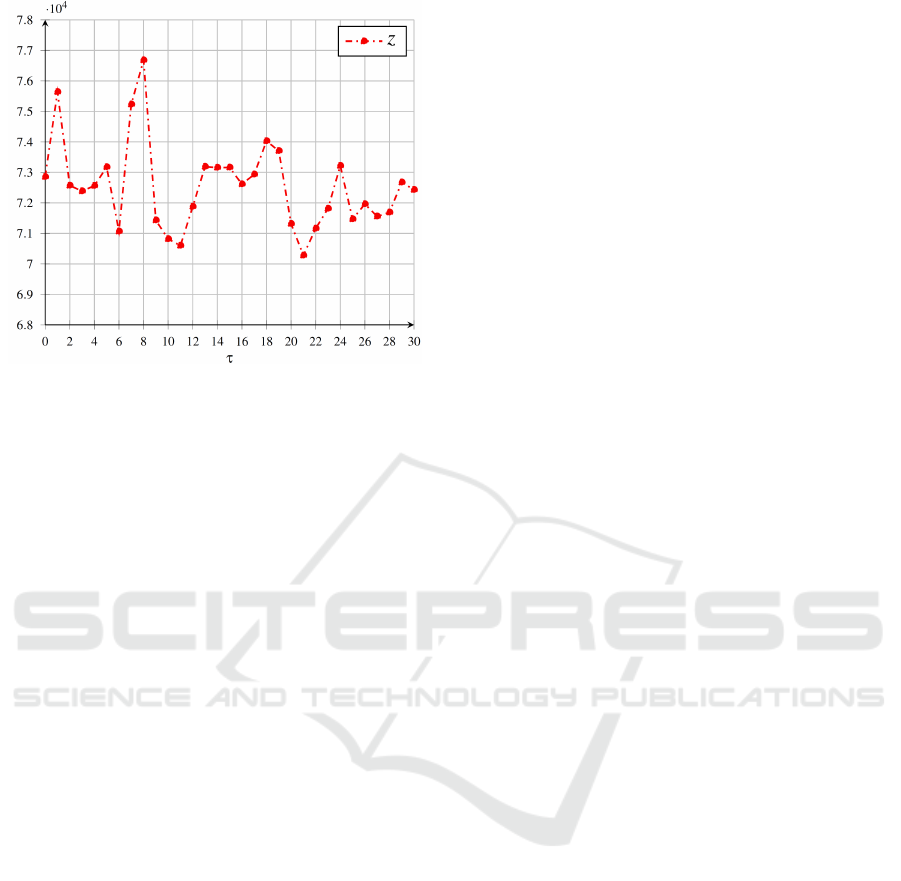
Figure 4: Variation of z for each iteration τ in the instance

number 18.

6 CONCLUSIONS

In this paper, we proposed an iterative three-step pro-

cedure to solve a real-life problem of integrated task

and personnel scheduling aiming to minimize the to-

tal labor cost. By implementing this approach, the

solution obtained by our formulation was capable of

improving the schedule adopted by the company in an

acceptable CPU time for this very complex problem.

Tests were also performed on larger and randomly

generated instances to measure the scalability of the

proposed method and to ﬁnd a combination of η and

ξ that can produce the best results based on the dimen-

sion of the building. The results are preliminary and

yet they are very positive from the company perspec-

tive, which is now able to generate and simulate many

different scenarios. Because Coopservice spends a

large part of its revenues on human resources (more

than 20,000 employees), it is crucial to have a strategy

to properly manage the personnel, especially during

emergency situations such as epidemic crises (Zucchi

et al., 2020). Future research might include: (i) the

insertion of more complex cost functions in (1) that

could take account of different employees’ levels; (ii)

a sensitivity analysis for the many parameters used in

models and algorithms; (iii) a deeper evaluation of the

importance of each key parameter making use of the

Finite Change Sensitivity Index (FCSI) (Borgonovo,

2010a; Borgonovo, 2010b); (iv) a more profound eco-

nomic cost analysis related to the labor cost assum-

ing it differs across workers and changes over time,

meaning that one should take into account a possi-

ble evolution of h, and consider the total proﬁt (or the

total value) as the objective function for a given (suf-

ﬁciently large) span of time. Moreover, to improve

performance in terms of solution quality, one could

incorporate metaheuristic strategies, such as pertur-

bation schemes in Algorithms 2 and 3, with a view of

obtaining better local optimal solutions.

ACKNOWLEDGMENTS

We acknowledge ﬁnancial support by Coopservice

and by University of Modena and Reggio Emilia

(grant FAR 2018). This research was also par-

tially supported by CNPq, grants 428549/2016-0 and

307843/2018-1.

REFERENCES

Bartolini, E., Dell’Amico, M., and Iori, M. (2017). Schedul-

ing cleaning activities on trains by minimizing idle

times. Journal of Scheduling, 20(5):493–506.

Borgonovo, E. (2010a). A methodology for determining

interactions in probabilistic safety assessment models

by varying one parameter at a time. Risk Analysis: An

International Journal, 30(3):385–399.

Borgonovo, E. (2010b). Sensitivity analysis with ﬁnite

changes: An application to modiﬁed eoq models. Eu-

ropean Journal of Operational Research, 200(1):127–

138.

aysy, O. and Gendreau, M. (2005a). Vehicle routing prob-

lem with time windows, part I: Route construction

and local search algorithms. Transportation Science,

39(1):104–118.

aysy, O. and Gendreau, M. (2005b). Vehicle routing

problem with time windows, part II: Metaheuristics.

Transportation Science, 39(1):119–139.

Cordeau, J.-F., Gendreau, M., and Laporte, G. (1997). A

tabu search heuristic for periodic and multi-depot ve-

hicle routing problems. Networks: An International

Journal, 30(2):105–119.

Doi, T., Nishi, T., and Voß, S. (2018). Two-level

decomposition-based matheuristic for airline crew

rostering problems with fair working time. European

Journal of Operational Research, 267(2):428–438.

Elahipanah, M., Desaulniers, G., and Lacasse-Guay, E.

(2013). A two-phase mathematical-programming

heuristic for ﬂexible assignment of activities and tasks

to work shifts. Journal of Scheduling, 16:443–460.

Ernst, A. T., Jiang, H., Krishnamoorthy, M., and Sier, D.

(2004). Staff scheduling and rostering: A review of

applications, methods and models. European Journal

of Operational Research, 153(1):3–27.

Guyon, O., Lemaire, P., Pinson,

E., and Rivreau, D. (2010).

Cut generation for an integrated employee timetabling

and production scheduling problem. European Jour-

nal of Operational Research, 201(2):557 – 567.

An Integrated Task and Personnel Scheduling Problem to Optimize Distributed Services in Hospitals

471

Hoffmann, K., Buscher, U., Neufeld, J. S., and Tamke, F.

(2017). Solving practical railway crew scheduling

problems with attendance rates. Business & Informa-

tion Systems Engineering, 59(3):147–159.

Juette, S. and Thonemann, U. W. (2012). Divide-and-price:

A decomposition algorithm for solving large railway

crew scheduling problems. European Journal of Op-

erational Research, 219(2):214–223.

Kletzander, L. and Musliu, N. (2020). Solving the general

employee scheduling problem. Computers & Opera-

tions Research, 113:104794.

Krishnamoorthy, M., Ernst, A., and Baatar, D. (2012). Al-

gorithms for large scale shift minimisation personnel

task scheduling problems. European Journal of Oper-

ational Research, 219(1):34 – 48.

Lap

egue, T., Bellenguez-Morineau, O., and Prot, D. (2013).

A constraint-based approach for the shift design per-

sonnel task scheduling problem with equity. Comput-

ers & Operations Research, 40(10):2450–2465.

Laporte, G. and Louveaux, F. V. (1993). The integer L-

shaped method for stochastic integer programs with

complete recourse. Operations Research Letters,

13(3):133–142.

Lougee-Heimer, R. (2003). The common optimization

interface for operations research: Promoting open-

source software in the operations research community.

IBM Journal of Research and Development, 47(1):57–

66.

Maenhout, B. and Vanhoucke, M. (2018). A perturbation

matheuristic for the integrated personnel shift and task

re-scheduling problem. European Journal of Opera-

tional Research, 269(3):806–823.

Salazar-Gonz

alez, J.-J. (2014). Approaches to solve the

ﬂeet-assignment, aircraft-routing, crew-pairing and

crew-rostering problems of a regional carrier. Omega,

43:71–82.

Savelsbergh, M. W. (1992). The vehicle routing prob-

lem with time windows: Minimizing route duration.

ORSA Journal on Computing, 4(2):146–154.

Smet, P., Ernst, A. T., and Berghe, G. V. (2016). Heuris-

tic decomposition approaches for an integrated task

scheduling and personnel rostering problem. Comput-

ers & Operations Research, 76:60–72.

Subramanian, A., Drummond, L. M. d. A., Bentes, C.,

Ochi, L. S., and Farias, R. (2010). A parallel heuris-

tic for the vehicle routing problem with simultaneous

pickup and delivery. Computers & Operations Re-

search, 37(11):1899–1911.

Van den Bergh, J., Beli

en, J., De Bruecker, P., Demeule-

meester, E., and De Boeck, L. (2013). Personnel

scheduling: A literature review. European Journal of

Operational Research, 226(3):367–385.

Vance, P. H., Barnhart, C., Johnson, E. L., and Nemhauser,

G. L. (1997). Airline crew scheduling: A new for-

mulation and decomposition algorithm. Operations

Research, 45(2):188–200.

Vidal, T., Crainic, T., Gendreau, M., and Prins, C. (2012).

A unifying view on timing problems and algorithms.

Tech. Rep. 43, CIRRELT.

Volk, R., Stengel, J., and Schultmann, F. (2014). Build-

ing information modeling (bim) for existing build-

ings—literature review and future needs. Automation

in construction, 38:109–127.

Zucchi, G., Iori, M., and Subramanian, A. (2020). Person-

nel scheduling during covid-19 pandemic. Optimiza-

tion Letters, pages 1–12 (forthcoming).

ICEIS 2021 - 23rd International Conference on Enterprise Information Systems

472