
A Full-Featured, Enhanced Cost Function to Mitigate Motion
Sickness in Semi- and Fully-autonomous Vehicles
Isa Moazen and Paolo Burgio
HiPeRT Lab., University of Modena and Reggio Emilia, Italy
Keywords: Motion Sickness, Autonomous Driving, Comfort, Model-Predictive Control, Cost-function, Embedded
Control Systems.
Abstract: Current full- and semi- Autonomous car prototypes increasingly feature complex algorithms for lateral and
longitudinal control of the vehicle. Unfortunately, in some cases, they might cause fussy and unwanted effects
on the human body, such as motion sickness, ultimately harnessing passengers' comfort, and driving
experience. Motion sickness is due to conflict between visual and vestibular inputs, and in the worst case
might causes loss of control over one’s movements, and reduced ability to anticipate the direction of
movement. In this paper, we focus on the five main physical characteristics that affect motion sickness,
including them in the function cost, to provide quality passengers' experience to vehicle passengers. We
implemented our approach in a state-of-the-art Model Predictive Controller, to be used in a real Autonomous
Vehicle. Preliminary tests using the Unreal Engine simulator have already shown that our approach is viable
and effective, and we implemented and evaluated using Motion Sickness Dose Value and Illness Rating and
then tested it in an embedded platform. We implemented it on our embedded platform, NVIDIA Jetson AGX
Xavier that is representative of the next-generation AV Domain Controller.
1 INTRODUCTION
In semi- and full AVs, vehicle control shall consider
passengers’ stress, and not decrease their level of
comfort (Elsner, 2018). It was proven that a tight
relationship exists between comfort and trust, as well
as the acceptance of automated vehicles (Bellem et
al., 2018).
The mostly known comfort issues for the
passengers is probably Motion Sickness. Its common
symptoms are: headache, pallor, sweating, nausea,
vomiting, and disorientation, and they can be
measured by Physiological signals, Vestibule Ocular
Reflex (VOR) parameters, and Posture stability.
There are several ways to mitigate this, such as
instance visual cues, Posture and vehicle
controllability, and Immersive Experience (Iskander
et al., 2019).
Motion is primarily sensed by the organs of
balance located in the inner ear and our eyes, which
are mainly or uniquely sensitive to accelerations. The
vestibular section of the inner ear is partly comprised
of three semi-circular canals that detect head angular
acceleration. The main issue stems from the fact that
our bodies are not used to low-frequency oscillating
motion, and our “biological IMUs” are highly
sensitive to this. In carsickness, the lateral
accelerations (sway) in the low-frequency bands (0.1-
0.5 Hz) are most relevant and their effects increase in
higher accelerations. In general, researchers proved
(Diels, 2014) that it might happen when the frequency
is below 1 Hz.
The potential sources of AV motion sickness are
variation in horizontal and vertical acceleration,
posture instability, loss of controllability and loss of
anticipation of motion direction, Head downward
inclination, and lack of synchronization between
virtual motion and the vehicle motion profile
(Iskander et al., 2019). Although motion sickness is
most frequently caused by a conflict between visual
and vestibular inputs, loss of control over one’s
movements and reduced ability to anticipate the
direction of movement are also important in the
etiology of motion sickness (Sivak and Schoettle,
2015). All three factors, to varying degrees, are more
frequently experienced by vehicle passengers than by
drivers, who rarely experience motion sickness
(Sivak and Schoettle, 2015). Possible counter
measures can be categorized into two groups:
prevention solutions and mitigation solutions.
Moazen, I. and Burgio, P.
A Full-Featured, Enhanced Cost Function to Mitigate Motion Sickness in Semi- and Fully-autonomous Vehicles.
DOI: 10.5220/0010446604970504
In Proceedings of the 7th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2021), pages 497-504
ISBN: 978-989-758-513-5
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
497

Roughly speaking, the degree of motion sickness may
be predicted by an acceleration frequency weighting
that is independent of frequency from 0.0315 to 0.25
Hz and reduces at 12 dB per octave (i.e., proportional
to displacement) in the range 0.25 to 0.8 Hz (Iskander
et al.., 2019).
We contribute to research with the original design
of a control software component for AVs that
minimizes the most important costs. In this paper, we
used an Adaptive Model Predictive Control (AMPC)
that can estimate and update the model in real-time
along with five constraints to build our cost function
to minimize.
We have chosen the constraints that are relevant
to Motion Sickness and comfort, either direct or
indirect. Acceleration frequency is one of the
constraints that directly affects the Motion Sickness
and the range of Frequency in which Motion Sickness
occurs is in 0.0315<F<0.8 Hz (Donohew & Griffin,
2004). Speed limitation is not directly related to
Motion Sickness level. However, as the speed goes
up, Acceleration Frequency for the speed regulation
will arise. Therefore, we consider a speed limitation
based on our Acceleration Frequency. The European
New Car Assessment Program (Euro NCAP)
performed standardizing tests on different
autonomous vehicles with a constant speed of 20 – 60
km/h (Standard, 1987). We also consider a threshold
of acceleration because it affects both Motion
Sickness and Comfort driving (Standard, 1987). It is
also one of the factors that increase Motion Sickness
Dose Value (MSDV). Therefore, having the
limitation with an appropriate planner can lower the
MSDV and raise comfort. We also consider the
distance from the next vehicle to brake with a
minimum acceleration, as we discussed before. In
particular, with higher distance from the next vehicle,
we require a lower braking acceleration. Finally,
since the lateral acceleration is the other important
source in MSDV (Donohew & Griffin, 2004), we
need a lane keeper to reduce our lateral accelerations
to a minimum quantity.
The system is tested on MATLAB/Simulink
(MATLAB, 2020) and then implemented on an
NVIDIA Xavier AGX. We evaluate our work based
on ISO 2631-1 (Standard, 1987) which a measure of
the probability of nausea that is called motion
sickness dose value (MSDV) and a simple linear
approximation between MSDV and mean passenger
named illness rating (IR) are considered as the
evaluation methods.
In the following sections, we first review the state-
of-the-art in motion sickness and MPC controller.
Then we describe the details of our controller.
Finally, we show our implementation, and discuss
experimental results with respect to the reference
metrics of motion sickness.
2 MOTION SICKNESS IN AV
LITERATURE
Several works are done for the motion sickness
mitigation and minimization in the recent years. In
(Elsner, 2018) a library of cost functions, consisting
of progress, comfort, and safety costs, is used to
evaluate the strategies generated by the three modules
distance keeper, lane selector, and merge planner. In
(Sivak & Schoettle, 2015), two strategies for reducing
the visual-vestibular conflict while watching videos
are investigated. One approach imposes visual stimuli
on or around the video screen to mimic the perceived
motion and forces of the moving vehicle. The other
method involves controlling the position of displayed
images in synchronization with vehicle motions and
passenger's head motions produced by vehicle
acceleration/deceleration, thus providing a video that
appears to be stabilized in relation to the movement
of the vehicle. In (Lambert et al., 2019), a method is
proposed for generating optimal Path Planning with
Clothoid Curves for passenger comfort, and their cost
is based on the squared distance along the curve,
made up of the first clothoid length, the second
clothoid length, and the straight line to the goal at the
end. An application of Motion Planning is presented
in (Htike et al., 2020) in order to minimize MSDV in
self-driving vehicles. Most of the works are
considering some parameters but not all to minimize.
However, since the Motion Sickness occurs based on
different sources, to minimize it, we need to consider
all of the Motion Sickness sources. In this manner, we
require to distinguish the actual direct and indirect
sources and try to minimize or remove them.
Furthermore, it is essential to consider comfort
driving while minimizing the Motions Sickness rate.
To overcome these important factors, as opposite to
the other works, our work considers the direct and
indirect sources of Motion Sickness and tries to
minimize them all in a single cost function to enhance
passengers’ comfort.
Considering recent AMPC implementations in
autonomous driving, concentrating on their cost
functions, there are several efforts. In (Easa &
Diachuk, 2020), an adaptive model predictive control
with three constraints, Lane Change-Related
Constraint, Location in Opposite Lane Constraint,
and Maneuver Completion, is applied for tracking the
VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems
498
references being generated for the Autonomous
Vehicles on Two-Lane Highways. In (Shi et al.,
2020), they constructed an adaptive model predictive
control trajectory tracking system with the four
constraints. In (Wu et al., 2020), an adaptive model
predictive control (AMPC) scheme is developed to
improve the yaw stability for four-wheel-
independently actuated electric vehicles by
minimizing the total longitudinal forces of all wheels.
In (Luan et al., 2020), the side slip angle of the centre
of mass and the side slip angle of the tire as hard
constraints and the lateral acceleration as a soft
constraint are considered to propose an Adaptive
Model Predictive Control for Uncertain model
(UMAMPC) algorithm to predict control variables
for the next sampling time and alleviate the target
angle discontinuity. In (Geng and Liu, 2020), they
develop a fault tolerant path tracking control
algorithm through combining the adaptive model
predictive control algorithm for lateral path tracking
control and Kalman filtering approach with two states
chi-square detector and residual chi-square detector
for detection and identification of sensor fault in
autonomous vehicles by using the incremental
constraint of tire and the incremental constraint of
lateral acceleration.
In all of the above works, that are proposed for
controlling the autonomous vehicles by AMPC,
below than five constraints are used. In this work, we
use five constraints in an AMPC that minimize the
MSDV with consideration of comfort.
3 CONTROL SYSTEM
To design the controller, we defined a Vehicle Model
and used the tire forces to specify our state space.
Then, we entered our state space in AMPC and
defined our constraints in it.
3.1 Vehicle Model
For an MPC control design, we require to define our
Vehicle Model. It was found that the vehicle side slip
angle is less than 1◦ in the highway autonomous or
manoeuvre driving under clothoid constraints (Kang
et al., 2014). Thus, it is considered that the tire slip
angle is also negligible under highway driving
conditions, including cases employing an advanced
driver assistant system (ADAS). It makes it possible
to use a standard dynamic “bicycle model”
(Rajamani, 2011) to describe the Vehicle Dynamics.
Such as a recent work (Antonelli et al., 2019) that uses
the higher speed until 35 m/s (126 km/h) with a
bicycle dynamic model, we use a bicycle dynamic
model for our tests between the speed of 0 km/h to 80
km/h and we use them in our first scenario. In the
bicycle model, the two left and right wheels are
represented by one single wheel. The model is
derived assuming both front and rear wheels can be
steered by δf and δr angles and the distances of front
and rear wheels are a and b. The model neglects roll
and pitch motions. The Motion of the vehicle is
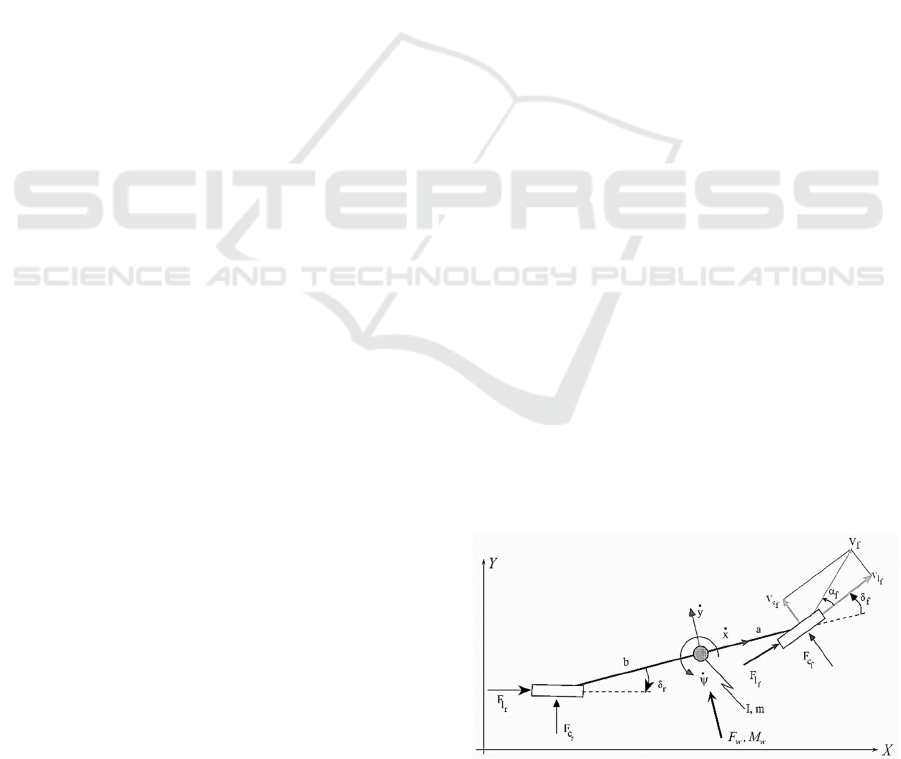
represented by X, Y and ψ. Figure 1 depicts a diagram
of the vehicle model, which has the following
longitudinal, lateral, and turning or yaw equations:
𝑚𝑥 𝑚𝑟𝑦 𝐹𝑥
𝐹𝑥
(1)
𝑚𝑦 𝑚𝑟𝑥𝜓
𝐹𝑦
𝐹𝑦
(2)
𝐼
𝜓
𝑎𝐹
𝑏𝐹
(3)
The vehicle’s equations of motion in an absolute
inertial frame are
𝑌
𝑥sin𝜓 𝑦cos𝜓 (4)
𝑋
𝑥cos𝜓 𝑦sin𝜓 (5)
Longitudinal and lateral tire forces lead to the
following forces acting on the centre of gravity:
Fy = Fl sin δ + Fc cos δ, (6)
Fx = Fl cos δ − Fc sin δ. (7)
Tire forces for each tire are
Fl = fl(α, s, μ, Fz), (8)
Fc = fc(α, s, μ, Fz), (9)
where α is the slip angle of the tire and s is the slip
ratio. The tire model is considered as indicated in
(Filip, 2018) velocities, respectively, are expressed as
vl = vy sin δ + vx cos δ, (10)
vc = vy cos δ − vx sin δ, (11)
and
v
yf
= ẏ + aψ
v
yr
= ẏ − bψ
, (12)
v
xf
= ẋ v
xr
= ẋ. (13)
Figure 1: Bicycle Model of the Vehicle.
A Full-Featured, Enhanced Cost Function to Mitigate Motion Sickness in Semi- and Fully-autonomous Vehicles
499

If we consider δr =0, then:
𝑥 𝑟y
(14)
ÿ𝑟y
(15)
𝑟͘
(16)
Using the equations (1)-(16), the nonlinear
vehicle dynamics will have the states of
𝑋
𝑌
ψ
𝑣𝑥𝑣𝑦𝑟
.
3.2 Adaptive Model Predictive Control
System
MPC (Muske & Rawling, 1993) is a method for
process control that actively uses the dynamic model
of the system. If the nonlinearity is high, however,
MPC performance could deteriorate. In this case, one
can use an AMPC that constantly predicts the new
operating conditions. (Önkol and Kasnakoğlu, 2018).
An adaptive MPC algorithm is designed by using
the recursively-identified state-space models with
dynamic adjustments of MPC constraints and
objective function weights (Hajizadeh et al., 2020).
Adaptive MPC controllers adjust their prediction
model at run time to compensate for nonlinear or
time-varying plant characteristics. Furthermore,
Adaptive control for constrained systems has mainly
focused on improving performance with the adapted
models, while the constraints are satisfied robustly for
all possible model realizations and the worst
disturbance bounds (Aswani et al., 2013). In this
paper, we used an Adaptive MPC to update our state-
space online and get the linear part of our nonlinear
system. This approach is implemented with the most
important costs that we wanted to control.
In AMPC, the controller uses the time-varying
Kalman filter (TVKF) instead of the static one to
provide consistent estimation with the updated plant
dynamics. The TVKF approach can be expressed as
follows
𝐿
𝐴
𝑃
|
𝐶
,
𝑁𝐶
,
𝑃
|
𝐶
,
𝑅
𝑀
𝑃
|
𝐶
,
𝐶
,
𝑃
|
𝐶
,
𝑅
(17)
𝑃
|
𝐴
𝑃
|
𝐴
𝐴
𝑃
|
𝐶
,
𝑁𝐿
𝑄
In equation (17), Q, R, and N matrices are
constant covariance matrices, and Ak and Cm, k are
matrices depicting the state-space description of the
system. The Pk|k−1 is the state estimate error
covariance matrix at k constructed from the
information from time k−1. TVKF is constructed to
update regularly the L and M matrices with the
updated plant dynamics.
3.2.1 Constraints
The Model Predictive Control can directly include
constraints in the computation of the control moves
which leads to linear program (LP) or quadratic
program (QP) to be solved at each sampling instance,
with the constraints written directly as constraints in
the LP/QP.
The MPC algorithm solves a quadratic
optimization problem at each time interval. The
solution of the problem determines the so-called
manipulated variables (MV), which are essentially
the input variables adjusted dynamically to keep the
controlled variables (CV) at their set-points. The
AMPC approach follows the same cost optimization
algorithm as MPC with the cost function
𝐽
𝑧
∑∑
,
𝑟
𝑘𝑖
|
𝑘
𝑦
𝑘 𝑖|𝑘
(18)
where k represents the current control interval, p
is the prediction horizon (interval number), 𝑛
is the
number of plant output variables, 𝑧
is the quadratic
problem (QP) selection which is depicted as the
formula 𝑧
𝑢
𝑘|𝑘
𝑢
𝑘1|𝑘
…𝑢
𝑘𝑝
1|𝑘
𝑘, 𝑦
𝑘𝑖
|
𝑘
is the jth CV at the ith
prediction horizon step, 𝑟
𝑘𝑖
|
𝑘
is the ith
references variable at the ith prediction horizon step,
𝑠
is the scale factor for the jth plant output variable,
and 𝑤
,
is the tuning weight coefficient reflecting the
relative importance of the plant output variable.
Among these variables 𝑛
, 𝑠
, p, and 𝑤
,
, are
determined during the controller design and stay
constant.
Acceleration Frequency. The range of Frequency in
which Motion Sickness is tested in 0.0315<F<0.8 Hz.
However, the maximum Motion sickness occurs at
0.2 Hz (Donohew & Griffin, 2004). So we fixed
frequency at 0.2 Hz which means T= 5 s. In particular,
that we prevent inserting acceleration every 5
seconds.
Speed Limit. As discussed, the test speed is in the
range of 20 – 60 km/h (Standard, 1987). Since we
need to consider having acceleration and braking in
our work, we raised this limitation to 0 - 80 km/h and
in our tests, we consider these values.
Acceleration Limit. Acceleration limitation is an
important source for comfort and the different level
of comfort is measured based on it (Standard, 1987).
VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems
500
Based on ISO 2631 (Standard, 1987) for
determination of acceleration, the best range of the
acceleration is <0.315 m/s2 that is named not
uncomfortable. In this standard, the best range of
acceleration is <1 m/s2 that is fairly uncomfortable
and it is the border of the uncomfortable range of
measurements. So we maintain this range.
Distance to the Front Vehicle. With a higher
distance from the next vehicle, we decrease the
braking acceleration. It means that we will have more
time to plan smooth braking, with the consideration
of our acceleration limit, and it lowers the MSDV.
There is a Two-Second Distance rule from the next
vehicle (Road Safety Authority, 2011). The mean
deceleration is 2.5 m/s2 (Yimer et al., 2020) and our
deceleration should not exceed 1 m/s2. Therefore, we
raised the distance to Five-Seconds Distance to fulfil
these requirements.
Lane Keeper. As discussed, we have high
importance in lateral acceleration to minimize the
MSDV. Therefore, our system maintains the
boundaries and controls the Y as the centre of the road
lines. It is obtained by having a reference Y of the
road and try to follow it. In the results, we show that
our controller follows it properly.
3.3 Motion Sickness Evaluation
The total MSDV resulted from lateral and
longitudinal motion is given as (Standard, 1987):
MSDV=
𝑎
,
𝑡
+
𝑎
,
𝑡
(19)
where ax,w(t) and ay,w(t) are the frequency weight
acceleration in the longitudinal and lateral direction.
ax,w (t) = ax (t) × Wf (20)
ay,w (t) = ay (t) × Wf (21)
where ax(t) and ay(t) are the longitudinal and lateral
acceleration. Wf is the weighting factor defined in
British Standard 6841 (Standard, 1987) for evaluating
low frequency motion with respect to motion
sickness. From the standards (Standard, 1987),
(Anon, 1997), a simple linear approximation between
MSDV and mean passenger illness rating is given as:
IR = K × MSDV (22)
where IR is predicted illness rating and K is an
empirically derived constant. The illness rating value
is divided into four levels; 0 indicates feeling fine, 1
indicates slightly unwell, 2 indicates quite ill, and 3
indicates absolutely dreadful (Standard, 1987),
(Anon, 1997).
4 IMPLEMENTATION
The system was tested in MATLAB/Simulink
(MATLAB, 2020) and then implemented by an
NVIDIA Xavier AGX. This platform is
representative of next-generation AV Domain
Controller where AD software components, such as
our controller, will execute.
To verify the validity of the proposed AMPC
controller. CarSim (Mechanical Simulation
Corporation, 2020) is used to provide a vehicle
dynamics model and MATLAB/Simulink is mainly
for providing control function.
Two different scenarios, straight and turn, were
tested. The scenarios were designed in
drivingScenarioDesigner and tested by using Unreal
Engine (Epic Games, 2019) for the visualization of
the output.
4.1 Scenarios
Since the MSDV is mainly a result of the lateral and
longitude accelerations, we require to define the
scenarios based on the existence of longitudinal
acceleration, braking, and lateral acceleration.
Therefore, we define a straight scenario that has the
longitudinal acceleration and braking, and a turn
scenario that has longitudinal and lateral
accelerations.
4.1.1 Straight Road
In the straight scenario, we made a velocity profile.
As it has shown in Figure 2, there were two vehicles
in the scenario that the front vehicle (the truck) had
60 km/h speed and our vehicle model was 200 meters
back of this vehicle with 80 km/h.
Figure 2: Our scenario in the drivingScenarioDesigner
schematic in MATLAB.
4.1.2 Turn
We designed the other scenario for a comparison
between our method and the other works. This
scenario consists of different turns as shown in Figure
3. The speed limit of this scenario is between 0 to 40
A Full-Featured, Enhanced Cost Function to Mitigate Motion Sickness in Semi- and Fully-autonomous Vehicles
501

km/h and at the first, the vehicle reaches the 40 km/h
with our acceleration limitation that we discussed in
constraints.
Figure 3: The Scenario visualization in Unreal Engine.
4.2 Adaptive Model Predictive
Controller Design
We designed our AMPC using mpcDesigner
(MATLAB, 2020) and Simulink. For each time step,
our controller updated to make new states for the next
prediction horizon. In Simulink, as shown in Figure
4, we used the Adaptive MPC block for this
implementation which in it, the constraints and the
MPC parameters are attached to it by mpcDesigner
tool. The different blocks are to build the
requirements of the Adaptive MPC block. We also
brought our reference scenarios as discussed before.
The prediction horizon considered as 10 seconds and
the control horizon was 5 seconds with the sample
time of 0.1 seconds. The tuning of weights was done
by mpcDesigner tuning tool for closed-Loop
Performance and State Estimation along with
Figure 4: The Simulink implementation of Adaptive MPC.
considering the system stability. The constraints, as
discussed before, were defined in our controller using
the mpcDesigner tuning tool.
4.3 Simulator
The system is tested with the Unreal Engine simulator
(Epic Games, 2019) which connects to the Simulink.
Our simulator considered the scenario data made by
drivingScenarioDesigner, and added the output of the
system to visualize and evaluate our system.
4.4 Embedded Platform
The target embedded platform, NVIDIA Jetson AGX
Xavier is representative of the next-generation AV
Domain Controller. This platform with a GPGPU of
512-core Volta with Tensor Core and a CPU of ARM
8-core v8.2 64-bit is an appropriate choice for the AD
systems.
To have a realistic implementation, we can’t rely
on the Matlab/Simulink implementatn, and we
utilized embedded coder of MATLAB/Simulink to
convert our algorithm into C++ source code, which is
then compiled for the target platform.
5 RESULTS AND DISCUSSION
Firstly, we calculated our results regarding of the first
scenario, Straight scenario. Then, we investigated the
results of the second scenario which is Turn. Finally,
we tried to understand our timing results in the
embedded platform to be able to use it along with
other infrastructures.
We evaluated the scenarios by MSDV and IR then
we compared our work with the latest works in this
area. Our results shown different advantages
compared to the previous approaches.
5.1 Results of the Scenarios
5.1.1 Straight Road
The straight scenario included two vehicles and a
velocity profile. Our vehicle was behind a truck that
was slightly far. It started from 0 and reached 80 km/h
(22.22 m/s) and as soon as founded the distance of 5
seconds, it started slowing down to maintain the 5
seconds of the distance. Afterwards, it followed the
truck by the truck’s velocity. As shown in Figure 5,
Figure 6, and Figure 7, the output of our controller
follows the base-line with a small error.
Figure 5: The scenario (blue) and our (orange) Y.
Figure 6: The scenario (blue) and our (orange) Yaw angle.
VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems
502

Figure 7: The scenario (orange) and our (blue) Velocity.
5.1.2 Turn
In the turn scenario, we maintained the acceleration
limitation based on AMPC algorithm designed by
Simulink and mpcDesigner. Figure 8, Figure 9, and
Figure 10 show the results.
Figure 8: The scenario (orange) and our (blue) Velocity.
Figure 9: The scenario (blue) and our (orange) Y.
Figure 10: The scenario (blue) and our (orange) Yaw angle.
5.2 MSDV and IR Analysis
Our evaluation is based on MSDV and IR. IR
generally increases overtime during a motion
sickening stimulus (Reason & Graybiel, 1969). In
(Standard, 1987), IR is considered as 0 when the
passenger feels fine, 1 with a feeling of slightly
unwell, 2 as quite ill, and 3 when the passenger is
absolutely dreadful. As shown in Table 1, the output
of the system more than having a small amount of IR
which almost is zero, it has a comparison between the
minimum IR of the previous work.
Table 1: The results of the IR evaluation.
Scenario
Time
(s)
IR (min)
Straight 50 0.07
Turn 32 0.0017
Turn in (Htike et al., 2020) 29.73 0.044
Table 1 shows that the IR of the Turn scenario is
much lower than the straight one. It is exactly what
we expected considering the accelerations used in
both scenarios since the Turn scenario has a much
lower time of accelerating.
The results show that our performance is better
since we try to use the acceleration as small as we can
and we try to make it limited to 1 m/s2. Furthermore,
our planner can make an IR near to zero. Therefore, it
has a fine feeling according to (Standard, 1987).
5.3 Embedded Platform Performance
When running on the production-like embedded
domain controller, our controller achieves 8.7 FPS,
making it suitable to interact with the other AV
components.
6 CONCLUSIONS
In this paper, we showed that by having a complex
cost function with an emphasis on Motion Sickness
Mitigation and consideration of comfort, we can
achieve a smooth controller that does not make
people sick. This work showed that the AV can have
an algorithm for Motion Sickness mitigation along
with the other tasks and make the AV more reliable
than before.
For the next works, we can add other necessary
features of AV such as LiDAR to detect and import
the data for the Motion Sickness Mitigation
Algorithm. It can finally be an algorithm which is
used with the other infrastructures.
We also plan to adopt more complex vehicle models,
such as the kinematic and dynamic model, to validate
our approach at highest speeds (i.e., > 150km/h), and
to possibly include other classes of vehicles, such as
busses and coaches, which potentially issue Motion
Sickness much more than cars.
ACKNOWLEDGEMENTS
This work was supported by the Prystine Project,
funded by Electronic Components and Systems for
European Leadership Joint Undertaking (ECSEL JU)
A Full-Featured, Enhanced Cost Function to Mitigate Motion Sickness in Semi- and Fully-autonomous Vehicles
503

in collaboration with the European Union’s H2020
Framework Programme and National Authorities,
under grant agreement n° 783190.
REFERENCES
Anon, B. (1997). Mechanical vibration and shock-
evaluation of human exposure to whole-body vibration.
Intl. Organization for Standardization, ISO, 2631.
Antonelli, D., Nesi, L., Pepe, G., & Carcaterra, A. (2019,
June). A novel approach in Optimal trajectory
identification for Autonomous driving in racetrack.
In 2019 18
th
European Control Conf. (ECC) (pp. 3267-
3272). IEEE.
Aswani, A., Gonzalez, H., Sastry, S. S., & Tomlin, C.
(2013). Provably safe and robust learning-based model
predictive control. Automatica, 49(5), 1216-1226.
Bellem, H., Thiel, B., Schrauf, M., & Krems, J. F. (2018).
Comfort in automated driving: An analysis of
preferences for different automated driving styles and
their dependence on personality traits. Transportation
research part F: traffic psychology and behaviour, 55,
90-100.
Diels, C. (2014). Will autonomous vehicles make us
sick? Contemporary ergonomics and human factors.
Taylor & Francis, 301-307.
Donohew, B. E., & Griffin, M. J. (2004). Motion sickness:
effect of the frequency of lateral oscillation. Aviation,
Space, and Environmental Medicine, 75(8), 649-656.
Easa, S. M., & Diachuk, M. (2020). Optimal Speed Plan for
the Overtaking of Autonomous Vehicles on Two-Lane
Highways. Infrastructures, 5(5), 44.
Elsner, J. (2018). Optimizing Passenger Comfort in Cost
Functions for Trajectory Planning. arXiv preprint
arXiv:1811.06895.
Epic Games. (2019). Unreal Engine. Retrieved from
https://www.unrealengine.com.
Filip, J. (2018). Trajectory Tracking for Autonomous
Vehicles.
Geng, K., & Liu, S. (2020). Robust Path Tracking Control
for Autonomous Vehicle Based on a Novel Fault
Tolerant Adaptive Model Predictive Control
Algorithm. Applied Sciences, 10(18), 6249.
Hajizadeh, I., Hobbs, N., Sevil, M., Rashid, M., Askari, M.
R., Brandt, R., & Cinar, A. (2020, May). Performance
Monitoring, Assessment and Modification of an
Adaptive MPC: Automated Insulin Delivery in
Diabetes. In 2020 European Control Conference
(ECC) (pp. 283-288). IEEE.
Htike, Z., Papaioannou, G., Velenis, E., & Longo, S. (2020,
May). Motion Planning of Self-driving Vehicles for
Motion Sickness Minimisation. In 2020 European
Control Conference (ECC) (pp. 1719-1724). IEEE.
Iskander, J., Attia, M., Saleh, K., Nahavandi, D., Abobakr,
A., Mohamed, S., . & Hossny, M. (2019). From car
sickness to autonomous car sickness: A review.
Transportation research part F: traffic psychology and
behaviour, 62, 716-726.
Kang, C. M., Lee, S. H., & Chung, C. C. (2014, October).
Lane estimation using a vehicle kinematic lateral
motion model under clothoidal road constraints. In 17th
International IEEE Conference on Intelligent
Transportation Systems (ITSC) (pp. 1066-1071). IEEE.
Lambert, E., Romano, R., & Watling, D. (2019, May).
Optimal path planning with clothoid curves for
passenger comfort. In Proceedings of the 5th Intl. Conf.
on Vehicle Technology and Intelligent Transport Systems
(VEHITS 2019),Vol.1, pp.609-615. SciTePress.
Luan, Z., Zhang, J., Zhao, W., & Wang, C. (2020).
Trajectory Tracking Control of Autonomous Vehicle
with Random Network Delay. IEEE Transactions on
Vehicular Technology.
MATLAB. (2020). version (R2020a). Natick,
Massachusetts: The MathWorks Inc.
Mechanical Simulation Corporation. (2020). Introduction
to CarSim.
Muske, K. R., & Rawlings, J. B. (1993). Model predictive
control with linear models. AIChE Journal, 39(2), 262-
287.
Önkol, M., & Kasnakoğlu, C. (2018). Adaptive model
predictive control of a two-wheeled robot manipulator
with varying mass. Measurement and Control, 51(1-2),
38-56.
Rajamani, R. (2011). Vehicle dynamics and control.
Springer Science & Business Media.
Reason, J. T., & Graybiel, A. (1969). Changes in subjective
estimates of well-being during the onset and remission
of motion sickness symptomatology in the slow rotation
room (Vol. 1083). US Naval Aerospace Medical
Institute, Naval Aerospace Medical Center.
Road Safety Authority, (2011). The two-second rule,
Government of Ireland.
Sivak, M., & Schoettle, B. (2015). Motion sickness in self-
driving vehicles. University of Michigan, Ann Arbor,
Transportation Research Institute.
Shi, J., Sun, D., Qin, D., Hu, M., Kan, Y., Ma, K., & Chen,
R. (2020). Planning the trajectory of an autonomous
wheel loader and tracking its trajectory via adaptive
model predictive control. Robotics and Autonomous
Systems, 103570.
Standard, B. S. I. (1987). 6841, Guide to Measurement and
Evaluation of Human Exposure to Whole-Body
Mechanical Vibration and Repeated Shock. London,
UK: BSI.
Wu, J., Wang, Z., & Zhang, L. (2020). Unbiased-
estimation-based and computation-efficient adaptive
MPC for four-wheel-independently-actuated electric
vehicles. Mechanism and Machine Theory, 154,
104100.
Yimer, T. H., Wen, C., Yu, X., & Jiang, C. (2020). A Study
of the Minimum Safe Distance between Human Driven
and Driverless Cars Using Safe Distance Model. arXiv
preprint arXiv:2006.07022.
VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems
504
