A Conceptual Framework for Extending Domain Model of

AI-enabled Adaptive Learning with Sub-skills Modelling

Ioana Ghergulescu

, Conor Flynn

, Conor O’Sullivan

, Ivo van Heck

and Martijn Slob

Adaptemy, Dublin, Ireland

AlgebraKIT, Eindhoven, The Netherlands

Keywords: AI-enabled Adaptive Learning System, User Modelling, Scaffolding.

Abstract: This paper proposes a conceptual framework of an AI-ALS that extends the Domain Model with sub-skill

modelling, to empower teachers with insights, create student awareness of sub-skills mastery level and

provide better learning recommendations. The paper also presents the BuildUp Algebra Tutor, an online maths

platform for secondary schools based on the proposed framework, that provides step-by-step scaffolding.

Results from a pilot study with 5

grade students showed that the scaffolding improved the student success

rate by 27.43%, and that the learner model achieves high sub-skill prediction performance with an AUC of

up to 0.944. Moreover, survey results show an increase in student self-reported metrics such as confidence.

1 INTRODUCTION

The demand for online and personalized learning is

stronger than ever (Docebo, 2020). While the past

decade has seen a multitude of online courses, the

scale of online learning reached a massive and

unprecedented scale in 2020 with over 1.2 billion

students impacted by the COVID-19 pandemic and

many schools and universities moving their classes

online (Li & Lalani, 2020). In this context it has

become more important than ever to enable effective

teaching and learning in online environments.

While personalised and adaptive learning has

been a research topic for a few decades, it only started

to be the focus of industry over the past decade

(Alamri et al., 2020). Previous research showed that

students enjoy the benefits of personalization, the

freedom of inquiry-based learning, but they also

require structure and guidance (Wanner & Palmer,

2015). Personalised and adaptive learning has several

benefits for students (e.g., increase learning

efficiency, increase students’ motivation, engage

students in active learning, promote higher level of

learner confidence, etc.), as well as for educators

(e.g., help educators to obtain insights on learners’

needs and preferences, help educators to manage and

track student progress via learning analytics, etc.)

https://orcid.org/0000-0003-3099-4221

(Alamri et al., 2020; Ghergulescu et al., 2016;

Kurilovas et al., 2015; Wanner & Palmer, 2015).

Adaptive and personalised learning solutions are

increasingly integrating artificial intelligence (AI)

algorithms to orchestrate greater interaction with

learners, to deliver personalized resources and

learning activities, to gather learner data to help

identify skills gaps, and to provide tailored learning

(Docebo, 2020).

AI-enabled Adaptive Learning Systems (AI-ALS)

have the potential to empower teachers as well as to

support students in achieving their potential. AI has

been adopted extensively in education, helping

educators to improve their efficiency with repetitive

tasks such as assessment, and to improve the quality

of their teaching. Moreover, AI-ALS foster student

uptake and retention, improve the learner experience

and overall quality of learning (Chen et al., 2020).

The classical architecture of an AI-ALS is based

on Domain Model (DM), Learner Model (LM) and

Adaptation Engine (Ghergulescu et al., 2019). The

DM represents the foundation of an overlay approach

to knowledge modelling and includes a representation

of the knowledge domain and content metadata.The

Learner Model maintains information about the

learners such as knowledge level, preferences, etc.

The AI Engine is responsible for updating the models

and for performing the adaptation.

116

Ghergulescu, I., Flynn, C., O’Sullivan, C., van Heck, I. and Slob, M.

A Conceptual Framework for Extending Domain Model of AI-enabled Adaptive Learning with Sub-skills Modelling.

DOI: 10.5220/0010451201160123

In Proceedings of the 13th International Conference on Computer Supported Education (CSEDU 2021) - Volume 1, pages 116-123

ISBN: 978-989-758-502-9

Mathematics is one subject where personalised

learning could be improved through sub-skill

modelling. Solving a maths problem is a multi-step

process that requires learners to have good conceptual

knowledge, as well as good procedural skills or the

ability to correctly apply procedures and strategies to

solve problems (Liljedahl et al., 2016). A number of

publications have showed that maths learners hold

many misconceptions and gaps related to conceptual

knowledge which can lead to errors during problem-

solving (Booth et al., 2017; Feldman et al., 2018;

Hansen et al., 2020; Muzangwa & Chifamba, 2012).

This paper proposes a conceptual framework of an

AI-ALS that extends the Domain Model with sub-

skill modelling. Modelling sub-skills will enable a

system to empower a teacher with insights into the

student’s (lack of) mathematical sub-skills, to create

student awareness of sub-skills’ mastery level and to

provide better recommendations what to do next. The

paper also presents and evaluates the BuildUp

Algebra Tutor, an online maths platform for

secondary schools based on the proposed framework.

The rest of this paper is organized as follows.

Section 2 presents the proposed conceptual

framework. Section 3 presents the BuildUp Algebra

Tutor AI-ALS that was developed based on the

proposed framework. Section 4 presents the

evaluation case study methodology and results, while

section 5 concludes the paper.

2 CONCEPTUAL FRAMEWORK

2.1 Framework Overview

Figure 1 presents the proposed conceptual framework

of an AI-enabled Adaptive Learning System (AI-

ALS), whose main components are: Domain Model

(DM), Learner Model (LM) and AI Engine. The DM

represents the foundation of an overlay approach to

knowledge modelling. DM makes a separation

between the curriculum model and the content model.

The curriculum model is a representation of the

“knowledge domain”. It includes knowledge items

(concepts) and the relationships between them. The

curriculum prerequisite network (also called the

curriculum map) defines the prerequisite

relationships between the knowledge items. For

example, ‘multiplication and division of integers’ is

prerequisite for the knowledge item ‘order of

operations’. Furthermore, concepts may have other

metadata that affects to whom they are relevant (e.g.,

exam level). Some previous theoretical frameworks

for domain modeling divide the abilities to be taught

Figure 1: Conceptual AI-ALS framework.

into concepts (knowledge) and skills (know−how)

(Kraiger et al., 1993; Schmidt & Kunzmann, 2006).

Previous research works have used ontologies to

model relations between concepts (Capuano et al.,

2009, 2011).

The content model is defined by all the metadata

about the content. Content objects are individual

pieces of content, activities, quizzes, questions, etc.

Content objects can have metadata that reflects how

they are used (e.g., type of activity such as exercise,

quiz, etc.) or skill used (e.g., listening, writing, etc.).

Content objects are linked to curriculum concepts to

build a course.

The sub-skill model is a representation of sub-

skills. Sub-skills are micro-evidence within a content

object like steps in a question. The sub-skills are

defined in a taxonomy and typically derived from

response analysis of learner interactions. DM enables

to create and update a complex learner model and to

enable multiple layers of personalisation and

adaptation.

The learner model maintains information about

the learners such as: knowledge level (i.e., what they

know, at what mastery level they know a concept,

and what they don’t know), preferences, other

pedagogy-relevant traits (e.g., self-direction, self-

efficacy, motivation, etc.).

The AI engine is responsible for updating the

models and for performing the adaptivity across

various layers such as content difficulty adjustment,

learning loops, and learning path recommendations.

Furthermore, the AI engine uses student interactions

data and machine learning to infer the sub-skills

A Conceptual Framework for Extending Domain Model of AI-enabled Adaptive Learning with Sub-skills Modelling

117

structure and associations between sub-skills and

concepts and between sub-skills and questions, as

well as to continuously update the models.

2.2 Enhancing the Domain Model

The proposed conceptual framework enhances the

traditional domain model of AI-ALS with a sub-skill

model that is a representation of sub-skills. Sub-skills

are the formal procedures that a student needs to

master to be able to solve non-trivial problems.

Examples of maths sub-skills are the arithmetic

procedures learned in primary education, as are the

procedures to simplify algebraic expressions,

expanding brackets, factoring, solving quadratic

equations, integration, etc.

The sub-skill model enables to gather deeper

evidence from each question at fine-level data below

a concept level, data that would be especially

powerful for error analysis. Initially the sub-skill

model contains a taxonomy of sub-skills organised in

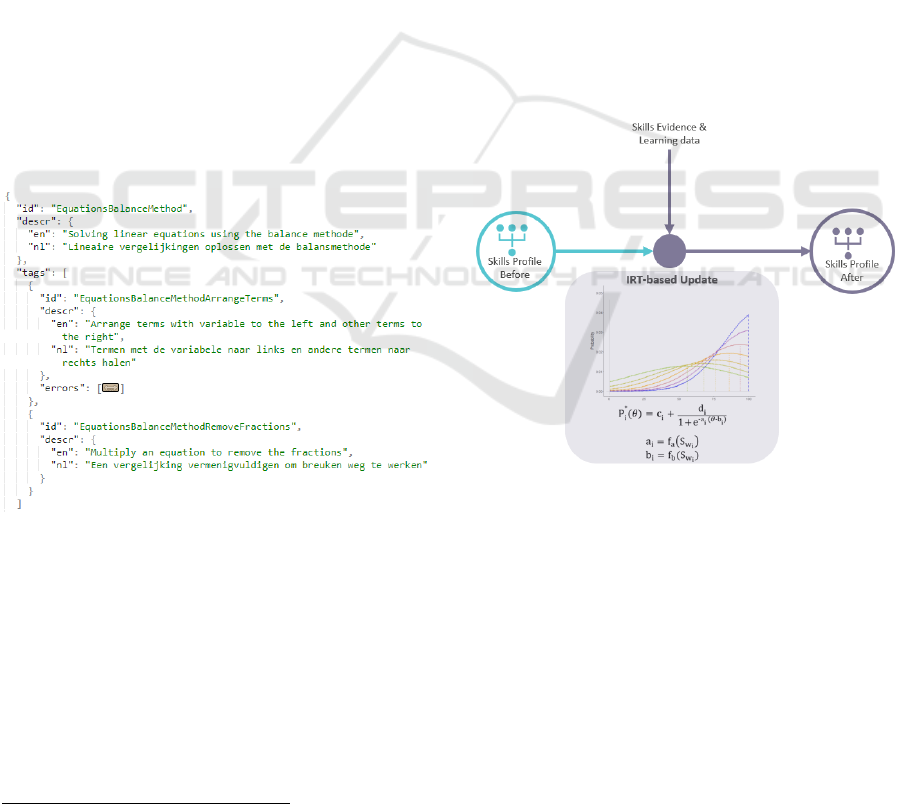
a hierarchical view. For example, “Arrage terms with

variable to the left and other terms to the right” and

“Multiply an equation to remove the fractions” are

sub-skill tags in “Solving linear equations using the

balance method” tags collection (see Figure 2).

Figure 2: Example of sub-skills tags (AlgebraKiT, 2020).

Other possible structures between sub-skills are

learned by the AI engine based on response analysis

of learner’s interactions with the system on both

positive and negative evidence of the student's

mastery of sub-skills. Positive evidence of mastery is

generated when a student solves a maths problem,

while negative evidence of mastery is generated when

a student makes a mistake or fails to solve a problem.

Adaptemy – www.adaptemy.com

2.3 Enhancing the Learner Model

Sub-skill tags are generated as the student interacts

with the system and solves questions. Evidence on

tags can be positive or negative and weighted.

There are three 'sources' for tags:

 finish tags corresponding to successfully

applying the sub-skill to solve the problem;

 hint tags corresponding to hints requested on

applying a sub-skill;

 error feedback tags corresponding to errors.

The learner’s strength on each sub-skill can be

estimated similarly to the rest of the learner model.

Sub-skills can be modelled through a probability

distribution vector and estimated using a customised

Item Response Theory (IRT) (see Figure 3). For

example, for each student the engine will maintain a

profile for all the sub-skills in the sub-skills model.

As a student interacts with a question and there is

evidence of a sub-skill, the sub-skill profile,

characterised through a probability distribution, is

updated given the evidence type (positive or negative)

and using a customized IRT (Franzen, 2017).

Figure 3: Sub-skills Modelling through Item Response

Theory (IRT)-based Update.

3 BuildUp ALGEBRA TUTOR

BuildUp is an online maths platform used by

secondary schools throughout Ireland. BuildUp is

developed and operated by Adaptemy

. BuildUp

Algebra Tutor follows on from the BuildUp Junior

Certificate course and is developed based on the

proposed conceptual framework. It integrates two AI

engines: the Adaptemy AI Engine for learner

CSEDU 2021 - 13th International Conference on Computer Supported Education

118

modelling, adaptation and personalisation, and the

AlgebraKiT Engine for sub-skill detection and step-

by-step scaffolding.

The AlgebraKiT player was integrated into the

Adaptemy question player. The AlgebraKiT Engine

was integrated with the Adaptemy Content

Management System (CMS) and the Adaptemy AI

Engine. The two engines communicate using API

calls through Adaptemy’s CMS. The Learning Data

(including sub-skill evidence) is streamed to the

Adaptemy AI Engine that updates the Learner Model

(including the sub-skills profile).

3.1 AlgebraKiT Engine

AlgebraKiT provides a solution that evaluates each

step a student does when solving a maths problem,

recognizes and explains errors automatically, and

offers immediate hints to the student. The engine was

extended to generate sub-skill tags that describe what

maths sub-skills are required to solve a problem and

to detect what sub-skills are related to mistakes. The

sub-skills are defined in the sub-skill taxonomy,

which exists separately from AlgebraKiT’s

evaluation maths engine.

The sub-skill tags are references to the sub-skills

in the taxonomy, that are generated by AlgebraKiT’s

maths engine. So, the maths engine does not use or

know the contents of the sub-skill taxonomy. Instead,

the engine is built around a large collection of maths

rules that are applied in sequence by the engine to

solve a problem. This collection of rules represents

the procedures a student (should) be able to use.

Maths rules and sub-skills are therefore closely

related, although multiple rules can be associated

with the same sub-skill.

The maths engine applies a maths rule on a

mathematical expression to generate a new

expression. So, expressions are the result of some

maths rule. This is also true for the mathematical

expressions that are inputted by a student; these

expressions are the result of a mathematical

procedure the student performed mentally.

Figure 4 shows how tags are generated when

AlgebraKiT generates the worked solution for a

problem. The assumption is that the related sub-skills

also describe the procedures that the student will

apply. This is not completely certain as a student is

free to choose his own solution path, but this

uncertainty can be handled by the statistical analysis

of multiple exercises.

In case a student inputs an incorrect expression,

the engine looks to find the mental procedure that the

Figure 4: Tags generation workflow.

student applied, to which sub-skill this is related to,

and what the mistake is. This information must be

bootstrapped from the previous expression and the

incorrect expression. When an explanation for the

error is found with sufficient certainty, the procedure

generates a human-readable description of the

mistake and the tags that indicate the related sub-skill.

3.2 Adaptemy AI Engine

Adaptemy’s AI Engine is developed based on

existing research in the areas of Intelligent Tutoring

Systems and Adaptive E-Learning. It makes use of a

curriculum model, a content model and a learner

model. The rich information from the three models

enables the AI engine to personalize the learning and

to accurately update the models. For each student, the

Adaptemy AI Engine maintains an ability profile on

all the concepts in the curriculum. The ability on the

concept that has been worked on is updated based on

direct evidence using Item Response Theory (IRT).

The profile of the other concepts is also updated based

on the question outcome as indirect evidence through

Bayesian Networks updates. As there is empirical

evidence that knowledge depreciation (forgetting)

occurs, the engine models forgetting (what was

forgotten after it is initially learned for each concept)

and updates the student profile overnight. The

Adaptemy AI Engine contains several layers of

adaptation and personalization. Through this, a

system that integrates the Adaptemy AI Engine can

provide immediate personalized feedback to the

student, engaging content sequencing that adapts to

the student’s performance, adaptive assessment and

scoring, learning paths recommendations and student

motivation detection and learning loops.

The Adaptemy AI Engine was evaluated in

several previous studies (Dang & Ghergulescu, 2018;

Ghergulescu et al., 2015, 2016). The effectiveness of

the learning recommendations provided by the

Adaptemy AI Engine was evaluated based on data

from over 80k lessons (Dang & Ghergulescu, 2018).

The results showed that when students followed the

recommendations, they had both a higher success rate

and a higher average ability improvement as

compared to when the recommendations were not

A Conceptual Framework for Extending Domain Model of AI-enabled Adaptive Learning with Sub-skills Modelling

119

followed. The feasibility of integrating adaptive

learning powered by the Adaptemy system in the

classroom was analysed with 62 schools and 2691

students (Ghergulescu et al., 2015). The results

showed that 97% of teachers believe that students

enjoy using the Adaptemy system and want to use it

at least once per week. A further study with over

10,000 students using the system for more than 6

months in over 1,700 K12 math classroom sessions

was carried out to analyse the Adaptemy system’s

learning effectiveness (Ghergulescu et al., 2016). The

students’ math ability improved by 8.3% on average

per concept for an average of 5 minutes and there was

a statistical significant improvement across various

ability ranges. Moreover, a 25% problem solving

speed increase was observed for the first revision, and

38% increase for the second revision.

The Adaptemy AI Engine was extended as per the

proposed conceptual model to work with a sub-skills

model. Furthermore, the learner model was extended

with a profile per students for all the sub-skills in the

taxonomy. When the student finishes the questions,

multiple sub-skills are updated based on the sub-skills

evidence using a customised IRT for sub-skills. The

score of the question, question discriminant and

difficulty are computed as functions of the weight of

the tag and question metrics.

3.3 Student Learning Journey in

BuildUp Algebra Tutor

In the BuildUp Algebra Tutor, students can navigate

to different topics and concepts within topics. When

selecting a concept, the student can take a self-

directed approach and select which concept to

practise or they can follow the recommendations

provided by the system. Furthermore, teachers can

assign concepts as homework and direct students to

what concepts to practice.

Encouragements and guidance are presented to

students before they start working on questions on

concept. Figure 5 shows an example of a question. As

it can be seen from the figure, each step is evaluated

and feedback is provided to the student.

In the background, the learner profile is updated

as students are working through the question. Figure

6 shows the sub-skills dashboard that was developed

to illustrate changes in sub-kills in terms of mastery

level and accuracy given the sub-skills evidence.

Furthermore, recommendations are provided to

students.

At the end of each concept, students are presented

with a summary of their results and encouragement.

Figure 5: Example of question.

Figure 6: Sub-skills Dashboard.

4 CASE STUDY

4.1 Methodology

A preliminary pilot was conducted to investigate the

effectiveness of the BuildUp Algebra Tutor platform.

Three classes of 5th grade students (16-17 years old)

from one Irish secondary school have participated in

the pilot. As part of the pilot the students have

practised with Algebra concepts. 26 students worked

through a total of 288 questions and previewed

another 27 questions.

4.2 Success Rate

Without step-by-step scaffolding students will

experience success if they answer a question correctly

CSEDU 2021 - 13th International Conference on Computer Supported Education

120

and fail when making a mistake and entering the

wrong answer. With step-by-step scaffolding students

receive at each step progressive hints when requested

and/or guidance when they make a mistake. Students

experience success when they finish the question

correctly.

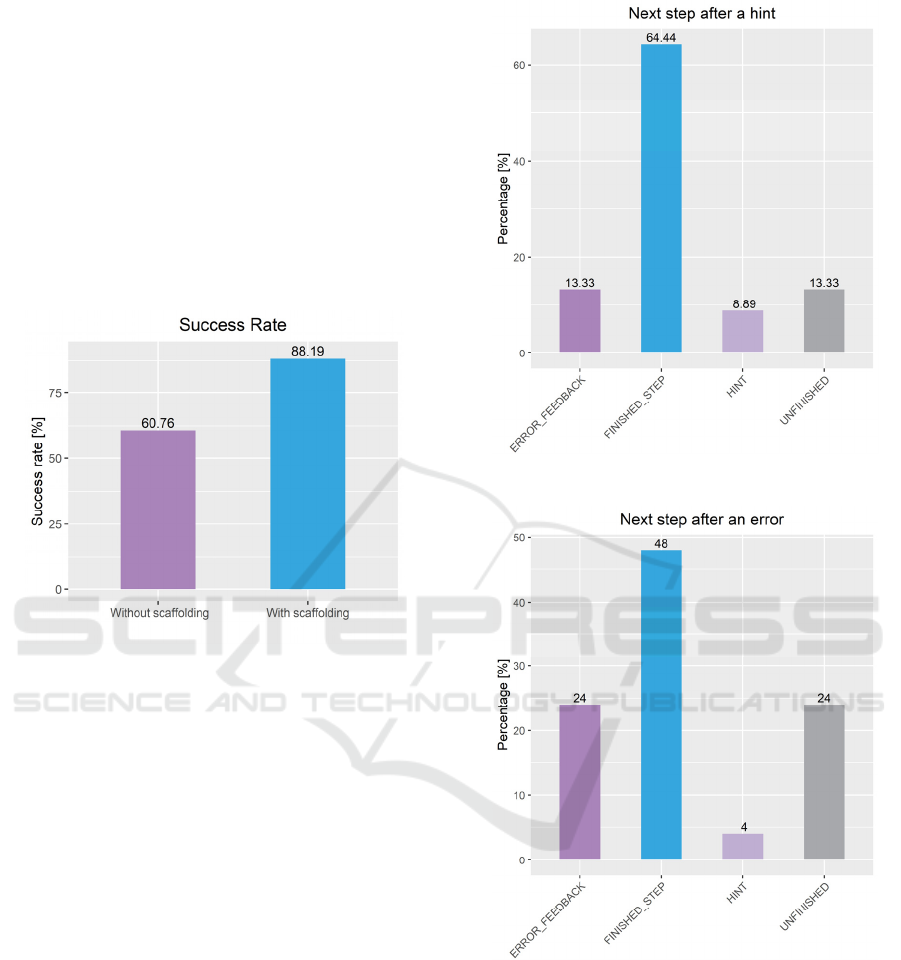
The results analysis showed that for 60.76% of

question workings students have provided the correct

answer without receiving any scaffolding. For

27.43% of question workings students have received

step-by-step scaffolding which helped them to

successfully complete the questions, thus increasing

the success rate to 88.19% (see Figure 7).

Figure 7: Success Rate Results.

4.3 Scaffolding Effectiveness

When using step-by-step scaffolding students can

request hints at any time while answering a question.

Scaffolding can be considered successful when the

students overcome the challenge and apply the sub-

skill to successfully complete the question. As

explained in sub-section 3.2, three types of sub-skill

tags are generated as the student interacts with the

system, namely: finish, hint and error tags.

An analysis was conducted to investigate how

students progressed after they requested hints or made

errors, respectively. Figure 8 shows that after students

requested a hint they have successfully completed the

question in 64.44% of cases, requested another hint in

8.89% of cases, did an error in 13.33% of cases, and

did not complete the question in 13.33% of cases (i.e.,

during the pilot duration). The number of hint

requests are considered when computing the question

score. However, in the pilot, students received only

completion status per question and not score details.

Figure 8: Progress after a hint.

Figure 9: Progress after an error.

Figure 9 shows that after students made an error

they have successfully completed the question in 48%

of cases, requested a hint in 4% of cases, did another

error in 24% of cases, and did not complete the

question in 24% of cases.

The results showed that identifying sub-skills and

offering related scaffolds was effective as the students

successfully completed the questions in most cases

after receiving hints or feedback on errors.

A Conceptual Framework for Extending Domain Model of AI-enabled Adaptive Learning with Sub-skills Modelling

121

4.4 Learner Model Sub-skill Prediction

The learner model estimates the students’ strength on

each sub-skill using Item Response Theory. AUC (or

Area Under the Receiver Operating Characteristic

Curve) was used to evaluate the performance of the

learner model sub-skill prediction. AUC is commonly

used for classification problems in machine learning,

where the predicted variable is binary. It is a more

stable performance metric than accuracy.

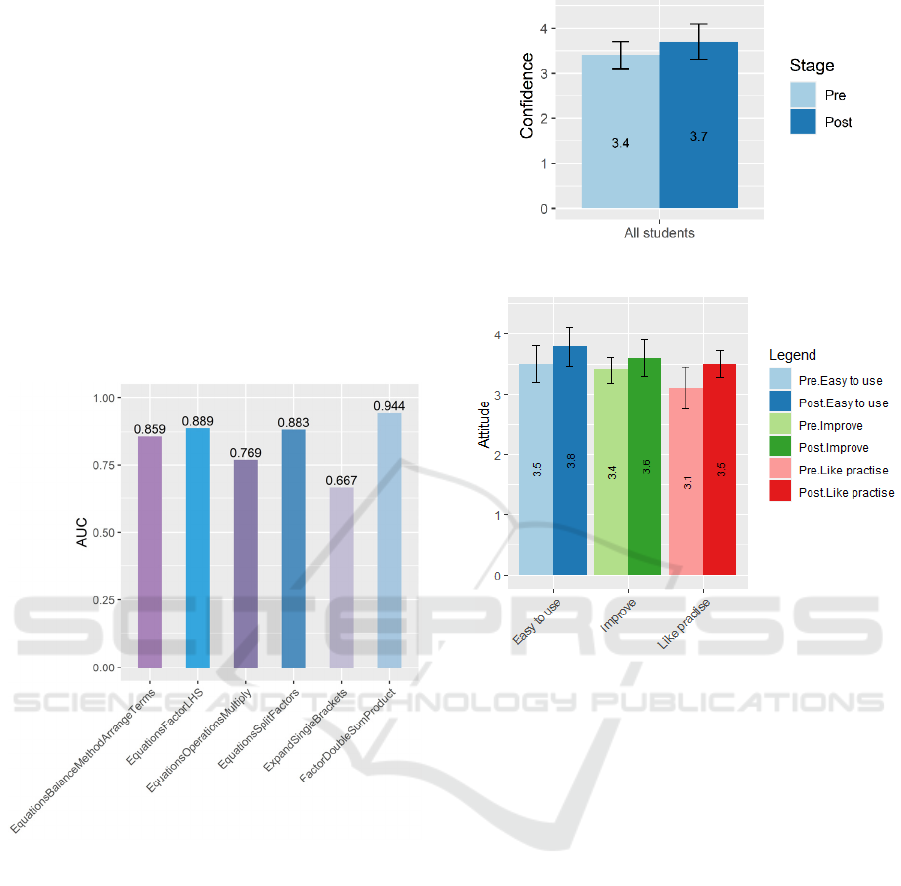
As it can be seen from Figure 10, the sub-skill

prediction performance of the learner model is high

with an AUC of up to 0.944. Having an accurate

learner model prediction is very beneficial as it would

make for more effective recommendations to students

and teachers.

Figure 10: Sub-skill prediction performance.

4.5 Learner Subjective Feedback

Students received a pre-survey and a post-survey to

investigate subjective aspects of the learning

experience. The students were asked to rate their

confidence that they can solve the Maths problems

before and after practising with BuildUp Algebra

Tutor. A 5-point Likert scale (i.e., 1 – ‘not at all

confident’ to 5 – ‘extremely confident’) was used.

Figure 11 shows that the mean confidence of the

students was higher for the post-survey, but the

difference was not statistically significant.

Students were also asked to rate if they liked to

practice maths using traditional methods (pre-survey)

and the BuildUp platform (post-survey), how easy to

Figure 11: Student confidence results.

Figure 12: Students attitude results.

use they find them, and if they think they can improve

their maths using traditional methods / BuildUp. A 5-

point Likert scale (i.e., 1 – ‘strongly disagree’ to 5 –

‘strongly agree’) was used. Figure 12 shows that the

mean ratings are higher for BuildUp Algebra Tutor

than traditional methods.

5 CONCLUSIONS

AI-enabled Adaptive Learning Systems are

increasingly adopted due to their potential to

empower the teacher through smart dashboards that

provide insights into the students’ knowledge and

progress, as well as to improve the efficiency and

quality of teaching. AI-ALS also have the potential to

improve the learning efficiency through personalised

learning experiences tailored to students’ needs,

preferences and skillset.

This paper proposes a conceptual framework of an

AI-ALS that extends the Domain Model with sub-

skill modelling. Modelling sub-skills is very useful

for subjects such as Mathematics where learners are

CSEDU 2021 - 13th International Conference on Computer Supported Education

122

required to have good conceptual knowledge and

skills in applying problem-solving procedures, but

often learners have misconceptions and make errors.

The paper also presented the BuildUp Algebra

Tutor, an online maths platform for secondary

schools, that incorporates the proposed framework

and integrates two AI engines: the Adaptemy AI

Engine for learner modelling, adaptation and

personalisation, and the AlgebraKiT Engine for sub-

skill detection and step-by-step feedback.

A pilot study with 5

year students was conducted

to evaluate the benefits of BuildUp Algebra Tutor.

The results have showed that the step-by-step

scaffolding improved the student success rate by

27.43%. The sub-skill prediction performance of the

learner model is high with an AUC of up to 0.944.

However, the AUC varied across the different sub-

skills which will require further investigation.

Moreover, survey results showed an increase in

student’s self-reported metrics such as confidence.

Future work will investigate how sub-skill

modelling can improve the accuracy of the learner

model in terms of student’s ability on concepts and

further improve the adaptive learning solution.

REFERENCES

Alamri, H. A., Watson, S., & Watson, W. (2020). Learning

Technology Models that Support Personalization

within Blended Learning Environments in Higher

Education. TechTrends, 1–17.

AlgebraKiT. (2020). Skill detection—AlgebraKiT

Documentation. https://docs.algebrakit-learning.com/

concepts/skill-tags/

Booth, J. L., McGinn, K. M., Barbieri, C., & Young, L. K.

(2017). Misconceptions and Learning Algebra. In S.

Stewart (Ed.), And the Rest is Just Algebra (pp. 63–78).

Springer International Publishing. https://doi.org/

10.1007/978-3-319-45053-7_4

Capuano, N., Dell’Angelo, L., Orciuoli, F., Miranda, S., &

Zurolo, F. (2009). Ontology extraction from existing

educational content to improve personalized e-Learning

experiences. 2009 IEEE International Conference on

Semantic Computing, 577–582.

Capuano, N., Gaeta, M., Salerno, S., & Mangione, G. R.

(2011). An ontology-based approach for context-aware

e-learning. 2011 Third International Conference on

Intelligent Networking and Collaborative Systems,

789–794.

Chen, L., Chen, P., & Lin, Z. (2020). Artificial Intelligence

in Education: A Review. IEEE Access, 8, 75264–

75278.

https://doi.org/10.1109/ACCESS.2020.2988510

Dang, X., & Ghergulescu, I. (2018). Effective Learning

Recommendations Powered by AI Engine. Proceeding

International Workshop on Personalization

Approaches in Learning Environments (PALE), 6.

Docebo. (2020). ELearning Trends 2020 | Enterprise

Learning Strategy | Docebo Report. https://www.doce

bo.com/resource/elearning-trends-2020-docebo-report/

Feldman, M. Q., Cho, J. Y., Ong, M., Gulwani, S., Popović,

Z., & Andersen, E. (2018). Automatic Diagnosis of

Students’ Misconceptions in K-8 Mathematics.

Proceedings of the 2018 CHI Conference on Human

Factors in Computing Systems, 1–12.

Franzen, M. (2017). Item Response Theory. Encyclopedia

of Clinical Neuropsychology, 1–1.

Ghergulescu, I., Flynn, C., & O’Sullivan, C. (2015).

Adaptemy – Building the Next Generation Classroom.

86–95.https://www.learntechlib.org/primary/p/151335/

Ghergulescu, I., Flynn, C., & O’Sullivan, C. (2016).

Learning Effectiveness of Adaptive Learning in Real

World Context. 1391–1396. https://www.learntech

lib.org/primary/p/173137/

Ghergulescu, I., Moldovan, A.-N., Muntean, C., &

Muntean, G.-M. (2019). Atomic Structure Interactive

Personalised Virtual Lab: Results from an Evaluation

Study in Secondary Schools. 605–615. https://www.

scitepress.org/Link.aspx?doi=10.5220/0007767806050

615

Hansen, A., Drews, D., Dudgeon, J., Lawton, F., & Surtees,

L. (2020). Children′s Errors in Mathematics. SAGE.

Kraiger, K., Ford, J. K., & Salas, E. (1993). Application of

cognitive, skill-based, and affective theories of learning

outcomes to new methods of training evaluation.

Journal of Applied Psychology,

78(2), 311–328.

Kurilovas, E., Zilinskiene, I., & Dagiene, V. (2015).

Recommending suitable learning paths according to

learners’ preferences: Experimental research results.

Computers in Human Behavior, 51, 945–951.

Li, C., & Lalani, F. (2020). The rise of online learning

during the COVID-19 pandemic. World Economic

Forum.

https://www.weforum.org/agenda/2020/04/coronaviru

s-education-global-covid19-online-digital-learning/

Liljedahl, P., Santos-Trigo, M., Malaspina, U., & Bruder,

R. (2016). Problem Solving in Mathematics Education.

Springer International Publishing.

Muzangwa, J., & Chifamba, P. (2012). Analysis of Errors

and Misconceptions in the Learning of Calculus by

Undergraduate Students. Acta Didactica Napocensia,

5(2), 1–10.

Schmidt, A., & Kunzmann, C. (2006). Towards a human

resource development ontology for combining

competence management and technology-enhanced

workplace learning. 1st Workshop on Ontology Content

and Evaluation in Enterprise (OntoContent 2006),

4278, 1078–1087.

Wanner, T., & Palmer, E. (2015). Personalising learning:

Exploring student and teacher perceptions about

flexible learning and assessment in a flipped university

course. Computers & Education, 88, 354–369.

A Conceptual Framework for Extending Domain Model of AI-enabled Adaptive Learning with Sub-skills Modelling

123