A Comparison of Lateral Intention Models for Interaction-aware Motion

Prediction at Highways

Vinicius Trentin

, Antonio Artu˜nedo

, Jorge Godoy

and Jorge Villagra

Centre for Automation and Robotics, Spanish National Research Council, Madrid, Spain

Keywords:

Interaction-aware, Motion Prediction, Lane Change.

Abstract:

To safely navigate in complex scenarios is crucial to know the predictions of the vehicles involved in the

scene. The future behavior of the trafﬁc participants is dependent on their intentions, the road layout and the

interaction between them. In this work, a framework is presented to compute the motion predictions of the

surrounding vehicles considering all possible routes obtained from a given map. At each time step, with a

Dynamic Bayesian Network, the probability of being on a speciﬁc route and the intention to change lanes are

computed. Our framework, based on Markov chains, is generic and can handle various road layouts and any

number of vehicles. We apply the framework in a two-lane highway and evaluate the inﬂuence of different

lane-changing methods on the predictions of the vehicles present at the scene.

1 INTRODUCTION

Autonomous vehicles promise to bring many beneﬁts

to society, such as low accident rates, safety, fuel sav-

ing, better life quality, reduce stress, among others. In

order to assure the safety aspect, the algorithms im-

plemented need to deal with a large number of pos-

sible scenarios, with a varying degree of complexity,

and be able to predict the movement of the other ve-

hicles present in the scene considering their mutual

interactions.

The behavior of trafﬁc participants is full of uncer-

tainties in the real world. In order to improvethe driv-

ing quality, autonomous vehicles should evaluate the

threats, should take seriously the ones with high prob-

ability to happen and should not overreact to the ones

with low probability. Probabilistic intention and mo-

tion predictions are unavoidable to accomplish safe

and high-quality decision-making and motion plan-

ning for autonomous vehicles (Zhan et al., 2018).

In this paper, we propose an approach to com-

pute the motion prediction of the surrounding vehi-

cles in all their possible routes in a short-term hori-

zon. In comparison with a previous work for mo-

tion prediction of the same authors sketched in (Med-

https://orcid.org/0000-0001-5732-3263

https://orcid.org/0000-0003-2161-9876

https://orcid.org/0000-0002-3132-5348

https://orcid.org/0000-0002-3963-7952

ina Lee et al., 2019) and with other works found in

the literature, more accurate results are producedhere,

since this newapproach can accommodaterestrictions

caused by the interaction between vehicles. Since we

focus on the lateral interaction, three models for the

lateral intention are compared. For the motion pre-

diction, the approach used is compared with two base-

lines: a set-based motion prediction and a probabilis-

tic prediction considering constant velocity.

This paper is divided as follows: Section 2

presents a short review of some works similar to the

one presented in this article. Section 3 described the

proposed approach with the lateral models evaluated

being presented in Section 4. Section 5 shows some

experimental results and Section 6 concludes.

2 RELATED WORK

Since our work is composed of two main building

blocks, some of the related work to each part and on

the combination of both are presented below.

2.1 Interaction Awareness

Considering that the intention of the other driverscan-

not be measured directly, it is necessary to estimate it.

Klingelschmitt et al. (2016), present a framework

for assessing trafﬁc scenes with interaction between

180

Trentin, V., Artuñedo, A., Godoy, J. and Villagra, J.

A Comparison of Lateral Intention Models for Interaction-aware Motion Prediction at Highways.

DOI: 10.5220/0010460701800191

In Proceedings of the 7th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2021), pages 180-191

ISBN: 978-989-758-513-5

trafﬁc participants. They transform the possible be-

havior patterns of the vehicles involved into hypothe-

ses and compute the joint probability of each hy-

pothesis by reconstructing the individual probability

of each behavior. As a result, they obtain the fully

interaction-aware joint probability distribution over

all the hypotheses. Their approach grows exponen-

tially as the situation complexity and the number of

vehicles involved increase.

Lefevre et al. (2013) implement a Dynamic

Bayesian Network to reason about the situations and

the risks at intersections on a semantic level. The

risk is assessed based on the comparison of the in-

tentions with what is expected from the drivers at a

given scenario. They model the expected vehicle’s

motions based on the road network (stop signs, give

away lines), distance to the intersections and previous

pose and velocity. The intention to stop is computed

based on the previous intention and current expecta-

tion. With the intention and the maneuver, the fu-

ture pose and velocity can be estimated. An evolution

of this approach considering also lateral expectations

has been recently presented (Villagra et al., 2020).

Although these methods take into account the

interdependence between vehicles to ﬁnd the most

probable route combination or if the situation offers

risk, they do not include the motion prediction of the

trafﬁc participants, as all areas they can reach, which

is crucial when planning the ego vehicle trajectory.

2.2 Motion Prediction

Althoff and Magdici (2016) propose the use of set-

based predictions with reachability analysis to ﬁnd all

possible reachable sets based on a given map and the

positions and velocities of the trafﬁc participants. Al-

though this approach ensures a safe planning for the

ego vehicle, given that all vehicles follow the trafﬁc

rules, it is too conservative and given a complex sce-

nario with many vehicles, the ego vehicle might have

to come to a full stop since all paths are occupied.

In another work, Althoff (2010) abstracted the

motion model into Markov chains using reachability

analysis. He considers the vehicle’s dynamics, their

mutual interactions (only based on the road geome-

try and trafﬁc rules) and also the limitation of driving

maneuvers due to road geometry, resulting in crash

probabilities for the possible paths of the ego vehicle.

In Zechel et al. (2019), the authors present an ap-

proach to compute the motion predictions of the ve-

hicles, without prior knowledge of the scene, con-

sidering separately the lateral and longitudinal move-

ment. The longitudinal over-approximation is based

on intervals obtained from real data. The lateral over-

approximationis computedwith the use of acceptance

distributions where it evaluates all considered lateral

accelerations for one speciﬁc driver inﬂuence, such

a static or dynamic obstacle. They compare their ap-

proach with the occupancypredictions computed with

SPOT and the comparison showed that the occupancy

area size could be reduced up to 70% for a prediction

horizon up to 1.3 s without errors.

Although these methods can predict the motion of

the surrounding vehicles, they can have low accuracy

in complex situations involving many vehicles, such

as an intersection, due to their interdependent inten-

tions and resulting actions.

2.3 Motion Prediction with Interaction

Awareness

As already mentioned, in order to have a better esti-

mation of the future positions of the vehicles involved

in the scene, the motion prediction and the interaction

awareness should be jointly considered.

Schulz et al. (2018) use a Dynamic Bayesian Net-

work with a particle ﬁlter to evaluate the interaction

between vehicles and estimate their route and maneu-

ver intentions. From these intentions, an action, rep-

resented by an acceleration and yaw rate values, is

obtained and the motion prediction is computed. This

method considers only the most probable action for

the whole time horizon of the prediction, which, in

complex scenarios, may negatively inﬂuence the mo-

tion planning search space.

In Koschi and Althoff (2017a), the authors ex-

pand their work from Althoff and Magdici (2016) to

include the interaction between drivers in their set-

based predictions. They do it by comparing vehicles

driving on the same lane and removing the unreach-

able areas of the following vehicles. As a result, the

drivable area of the ego vehicle increases, since some

previews occupied areas are removed. This approach,

however, considers neither intentions nor trafﬁc rules

in the predictions.

3 FRAMEWORK FOR

INTERACTION-AWARE

MOTION PREDICTION

In Figure 1 the ﬂowchart of the work is presented.

Each of the building blocks appearing in the ﬁgure

will be brieﬂy described in the following sections.

A Comparison of Lateral Intention Models for Interaction-aware Motion Prediction at Highways

181

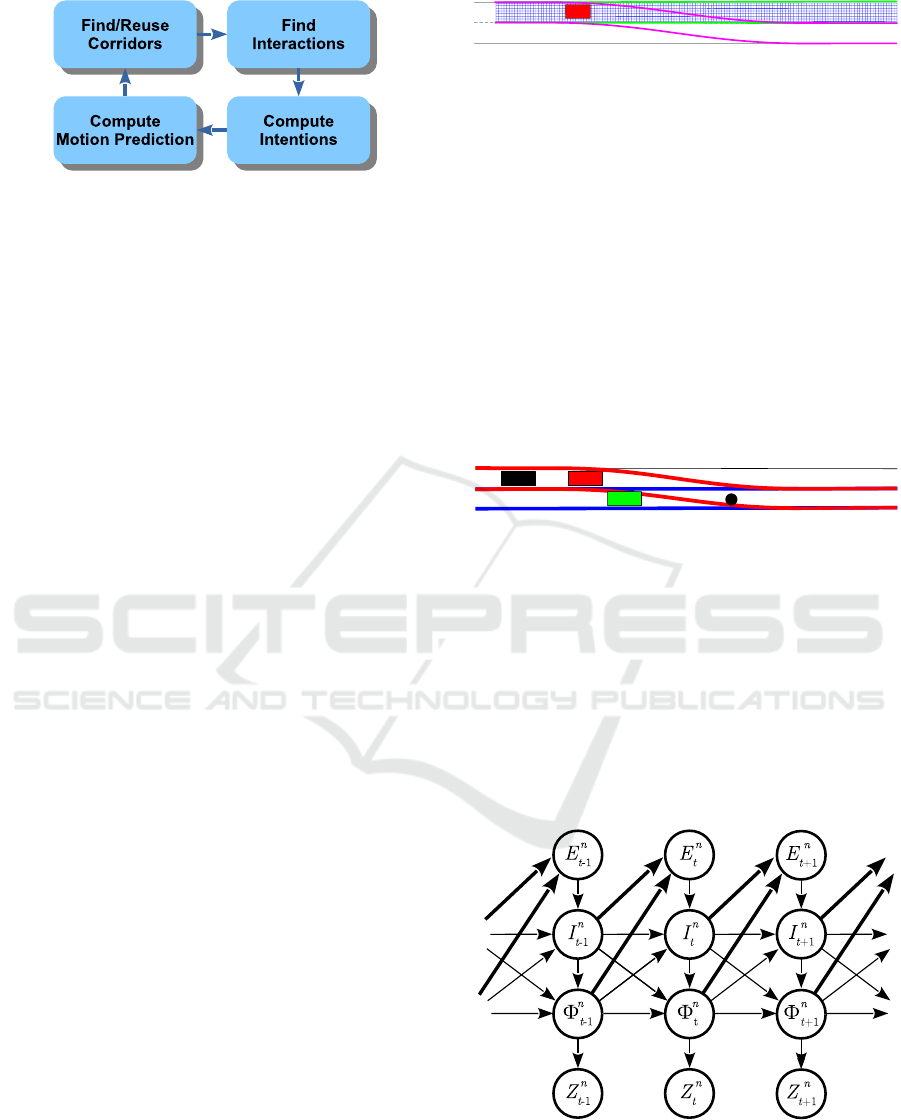
Figure 1: Flowchart.

3.1 Find/Reuse Corridors

Given a map formed by lanelets (Bender et al., 2014),

their relational and physical layers are used in order

to obtain all the navigable corridors for the vehicles in

the scene. The length of these corridors has, at min-

imum, the distance that the car can reach in a time

interval with its current speed, assuming a constant

maximum acceleration.

First, we obtain the current lanelet(s) where the

vehicle is located, comparing the position and the ori-

entation in the physical layer. Next, a graph search is

performed for surrounding lanelets starting from the

vehicle lanelet(s) to create a lanelet-sequence for each

corridor.

In the next iterations, the corridors found can be

either expended or removed, if necessary. The ex-

pansion occurs if its predicted occupancy probabili-

ties fall in cells that are farther then a percentage of

the grid length (85% in our case). The removal occurs

if the current measured orientation of the vehicle has

a difference bigger than a threshold when compared

with the center line of the corridor.

At each iteration, the lanelet in which the center

of the vehicle is located is found. Based on this in-

formation, each corridor is deﬁned as being left, cen-

ter, right or not reachable with respect to the position

of the vehicle. To reach the corridors at right/left, a

B´ezier curve is created that concatenates the two road

segments (the one in the current lane with the one in

the adjacent lane) with a length of max(4v, 10)m, be-

ing v the current vehicle’s velocity and 4 is the con-

sidered duration of a lane change (in seconds). These

values were deﬁned after analyzing the patterns of a

lane change.

The detection of a lane change is based on the po-

sition of the vehicle and occurs in one iteration: at

instant t the vehicle is in lanelet x and at instant t + 1

the vehicle is in lanelet y.

With the exception of the ego vehicle, for each

corridor of the other vehicles, a grid is created based

on the shape of the road. For the ego vehicle, a route is

assumed. An example of the corridors of a vehicle is

shown in the Figure 2, where for one of the corridors

the grid is drawn.

Figure 2: Example of corridors and grid.

3.2 Find Interactions

A search of surrounding vehicles is performed for all

the vehicles in the scene, generating a table that con-

tains the distances and velocities.

In order to restrict the motion probabilities in cor-

ridors that have another vehicle or that can collide

with the corridors of other vehicles, the collision point

between these corridors is obtained as can be seen in

Figure 3. They result from the intersection between

the corridors’ center lines, where the chosen point is

the ﬁrst where the distance is less than a given thresh-

old. So far, these types of collisions are not being con-

sidered when both vehicles are changing lanes, being

this a future work.

Figure 3: Example of collision between corridors.

3.3 Compute Intentions

In order to compute the intention of the trafﬁc partic-

ipants, the Dynamic Bayesian Network (DBN) pro-

posed by Villagra et al. (2020) is inferred using a par-

ticle ﬁlter. For each of the vehicles present in the

scene, with the exception of the ego vehicle, the net-

work represented in Figure 4 is instantiated, where

bold arrows represent the inﬂuences of the other vehi-

cles on vehicle n.

Figure 4: Bayesian network.

The relations among variables appearing in Figure

4 allows to model the driving scene as the following

generalized distribution (Lefevre et al., 2013):

VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems

182

P(E

0:T

,Φ

0:T

) = P(E

,Φ

)×

∏

t=1

∏

n=1

[P(E

t−1

) ×P(I

|Φ

t−1

)×

P(Φ

|Φ

t−1

) ×P(Z

|Φ

)]

(1)

where the variables are described below:

• Expected maneuver E

: represents the expected

lateral behavior of the vehicle n at instant t ac-

cording to trafﬁc rules. It models the probability

that the vehicle can make a lane change without

hindering trafﬁc. It can assume two values: stay

and change.

• Intended maneuver I

: represents the intention of

the vehicle and includes the route the vehicle in-

tends to follow.

• Physical vehicle state Φ

: represents the pose and

speed of the vehicle. They are calculated at each

instant based on the intentions.

• Measurements Z

: represents the real measure-

ments of the physical state of the vehicle, ex-

tracted directly from exteroceptive sensors of the

ego-vehicle or via V2X communications.

3.3.1 Lateral Expectation

The decision to change lanes should be based on the

desire to quit the current lane, the selection of the

target lane and the feasibility of the change.

Lane changes are usually classiﬁed as mandatory

or discretionary, depending on the drivers motivation.

A Mandatory Lane Change (MLC) is performed

when the driver is trying to move his/her vehicle from

its current lane into the target lane in anticipation

to a left or right exit or a lane closure immediately

downstream. A Discretionary Lane Change (DLC)

is conducted to improve driving conditions when

the driver desires a faster speed, greater following

distance, etc. in the target lane Vechione et al. (2018);

Toledo et al. (2003).

When implementing the aforementioned particle

ﬁlter, for every vehicle in every particle the vehicles

followers and leaders in all possible lanes are deter-

mined and the distances bumper-to-bumper and the

velocity differences are found. This information is

used to compute the expected lateral motion of the

vehicles present at the scene, for which three models

were selected, implemented and compared (see

Section 4 for more details). Two of these models use

only DLC and the third one uses a hybrid approach

between MLC and DLC.

3.3.2 Lateral Intention

The lateral intention is computed based on the previ-

ous intentions (I

t−1

) and the current expectation(E

The intention will be considered equal to 1 (change

lane) if a random value is smaller then the probability

generated by Table 1.

Table 1: Lateral Intention.

t−1

Probability

0 0 0.1

1 0.5

1 0 0.5

1 0.9

In this step it is also deﬁned the new corridor of

each vehicle in each particle. If the intention is to

change, one of the corridors in the target lane deﬁned

in the previous step is selected.

3.4 Compute Predictions

To compute the probabilistic predictions of the vehi-

cles present at the scenarios, the library CORA (Al-

thoff, 2015) has been used following the strategy pro-

posed in Althoff (2010). The predictions are com-

puted by abstractions of the system dynamics into

Markov chains, where the state space X and input

space U are discretized into intervals. The former

representing the longitudinal position s and velocity

v, each interval with size 0.5 m x 1 m/s, respectively,

and the latter representing the acceleration a normal-

ized into [-1, 1].

The longitudinal vehicle’s dynamics are expressed

using the following differential equation:

˙s = v

˙v =











max

u, 0 < v < v

∪u ≤0

max

u, v > v

∩u > 0

0, v ≤ 0

(2)

where a

max

is the maximum acceleration allowed, v

is a switching velocity that changes the acceleration

dynamics, and u is the input ranging from −1 to 1.

For the lateral dynamics, it is assumed that the ve-

hicle can occupy the entire lane width with a constant

standard deviation.

The transition probability matrices of the Markov

chains for a time step Φ(τ), and for a time interval

Φ([0,τ]), where τ is the time increment, are computed

ofﬂine with reachability analysis that aims to compute

an over-approximation of the set of states a system

can reach given its initial states, inputs and parame-

ters. For each state of the state space and for each

A Comparison of Lateral Intention Models for Interaction-aware Motion Prediction at Highways

183

input of the input space, the motion model is applied

for a time interval τ resulting in a set covering one

or more cells from the state space. The probability

of reaching the cell j, starting from cell i under the

inﬂuence of input β is computed as follows:

(τ) =

V(R

(τ) ∩X

)

V(R

(τ))

(3)

where the operatorV returns the volume of the set and

(τ) is the reachable set starting from cell i applying

input β. The transition probabilities between the input

states are represented by the input transition matrix

Γ(t

). This matrix is composed by two parts: a tran-

sition matrix Ψ, which models the intrinsic behavior

of the vehicle when there are no priorities for certain

input values, and a priority vector λ, representing the

restrictions caused by the road layout, the interaction

with other vehicles or a combination of both. A de-

tailed explanation of these variables can be found in

Althoff (2010). These parts are joined as follows

βδ

= norm(

βδ

)

βδ

= λ

βδ

,∀i :

∑

= 1,0 ≤λ

≤ 1 (4)

to form the transition matrix where i is the index of

a state space and β and δ are indices of two possible

input states. The reason this matrix is not joined into

the transition matrix Φ(τ), is that the priority vector λ

can change at each step.

The probabilities distribution for future time steps

p(t

k+1

) and time intervals p(t

k+1

) are computed as

follows:

p(t

k+1

) = Γ(t

)Φ(τ)p(t

)

p(t

k+1

) = Φ([0,τ])p(t

)

(5)

For each corridor from each vehicle a Markov

chain is instantiated and the predictions are computed

for a time interval. These predictions are multiplied

with the sum of the weights of the particles that con-

tains the corridors and they are later joined into a sin-

gle grid based on the ego-vehicle position, whose size

is based on the ego-vehicle’svelocity and the situation

context.

4 LATERAL MODELS

The models implemented and compared are presented

below. These models were selected based on their

simplicity and low computational cost.

4.1 Model 1

The ﬁrst model implemented is based on Mathew

(2019). The desire to change lane is computed by

the deceleration a provoked by the leading vehicles

(when they exist) traveling in front of each vehicle in

the current and adjacent lanes:

a =

ρv

∆v

∆x

(6)

where v is the velocity of the vehicle, ∆v is the dif-

ference between the velocities of the vehicle and the

one of the leading vehicle, ∆x is the distance between

vehicles and ρ, m and l are parameter models. With

the acceleration values a

in each of possible lanes,

the utility U

of each lane i is deﬁned as:

∑

j=1

(7)

where a

is the acceleration with respect to the leading

vehicle of lane i and N is number of possible target

lanes.

If the leading vehicle in the current lane is making

the target vehicle brake, the lane with the highest util-

ity is selected, otherwise, a random lane, among the

possible lanes, is selected.

Once the lane is selected, it is necessary to ver-

ify that the deceleration imposed to the new follower,

computed with (6), is below a given threshold b, such

that a > −b.

If the safety criteria is met, the probability to ac-

cept the gap is computed as:

P(lead) = 1 −e

−λ(t

lead

−τ)

P(lag) = 1−e

−λ(t

lag

−τ)

(8)

where t

lead

and t

lag

are the time gaps with respect to

the leading and following vehicle in the target lane.

The probability to change lane is the result of

the multiplication of P(lead) and P(lag) and the ex-

pected lateral movement will be 1 if this probability

is bigger than a random value.

4.2 Model 2

The second model implemented is the Minimizing

Overall Braking Induced by Lane Changes (MOBIL)

(Kesting et al., 2007), used in combination with the

Intelligent Driver Model (IDM) (Treiber et al., 2000).

As in the previous model, this one also includes

a safety criteria: the deceleration of the new follower

in the target lane, after the lane change, cannot

exceed a given safety limit b

saf e

> −b

saf e

(9)

VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems

184

The authors of MOBIL propose two types of in-

centive criterion for lane changing: one considering

symmetric passing rules and an asymmetric one. The

one adopted in this work is the asymmetric model,

where the right most lane is the default lane and the

lanes on the left should only be used for overtaking

purposes.

The incentive criterion for a lane change to a left

(L) lane and to a right (R) lane are:

L = ˜a

−a

+ p( ˜a

−a

) > ∆a

+ ∆a

bias

R = ˜a

−a

+ p( ˜a

−a

) > ∆a

−∆a

bias

(10)

where ˜a

, a

, ˜a

, a

, ˜a

and a

are the accelerations

of the target vehicle, old follower and new follower

after and before the lane change, p is the politeness

factor, ∆a

and ∆a

bias

are the acceleration threshold

and bias, respectively. It can be noticed that the lane

change to a right lane considers only the advantages

to the old follower. A lane change to a left lane, on the

other hand, takes into account the effects caused to the

new follower. The politeness factor p determines how

much the others vehicles inﬂuence the lane-changing

decision of the target vehicle.

The IDM acceleration of each vehicle α depends

on the distance s

and on the velocity difference ∆v

to the leading vehicle. It is composed of two parts:

the acceleration a[1−(v

)

] on a free road and the

braking −a(s

∗

)

caused by a leading vehicle.

˙v

= a

1−





−

∗

,∆v

)

∗

(v,∆v) = s

+ vT +

v∆v

√

(11)

where a is the maximum acceleration, b is the desired

comfortable deceleration, s

is the minimum distance,

is the desired velocity and T is the safe time gap.

4.3 Model 3

The third model implemented is based on Toledo et al.

(2005). The authors argue that the classiﬁcation of the

lane changes into MLC or DLC does not allow the

capture of trade-offs between the two types. For this

reason, they created a method that includes both types

in a single model.

This model penalizes the most right lane, since it

considers this lane as being of low speed, caused by

the entrances and exits.

At the highest level of the model, the driver

chooses a target lane. It is the lane, among all the

possible lanes, the driver recognizes as the best lane

to be in after considering a wide range of factors and

goals. The utilities of the various lanes are given by:

int

= β

−0.011D

int

+ 0.119S

int

+ 0.022∆X

front

int

ad j

int

+0.115∆S

front

int

−2.783δ

taigate

int

+δ

int

−2.633∆CL

int

+ β

path

exit

]

−0.371

−0.980δ

next exit

∆Exit

−α

(12)

where U

int

is the utility of lane i as a target lane to the

driver n at time t, βi is the lane i constant, D

int

and S

int

are the lane-speciﬁc densities and speeds, ∆X

front

int

and

∆S

front

int

are the spacing and relative speed of the front

vehicle in lane i. δ

ad j

int

, δ

int

and δ

tailgate

are indicators

with value 1 if i is the current or an adjacent lane,

if i is the current lane, if vehicle n is being tailgated

at time t, respectively, lane, 0 otherwise. ∆CL

int

the number of lane changes required to get to lane i

from the current lane. β

path

is the path plan impact

coefﬁcient for lane i, δ

next exit

is the distance to the

exit driver n intends to use. δ

next exit

indicates with 1

if the driverintends to take the next exit, ∆Exit

are the

number of lane changes required to get to the exit lane

from lane i. α

is the parameter of the driver speciﬁc

random term ν

The target lane is chosen as the lane with the high-

est utility. The probabilities are given by a multino-

mial logit model:

P(TL

= i|ν

) =

exp(V

int

)|ν

)

∑

j=TL

exp(V

jnt

|ν

)

(13)

Once the utilities are computed one has to eval-

uate the lead and lag gaps, which are deﬁned by the

bumper-to-bumperdistance between the lead and sub-

ject vehicle and the bumper-to-bumper distance be-

tween the lag distance and the subject vehicle.

The gap is acceptable if it is bigger than the critical

gap:

P(G

> G

gd,cr

,ν

) = Φ

ln(G

) −G

gd,cr

(14)

where Φ[] denotes the cumulative standard normal

distribution, G

and G

gd,cr

are the gap and the criti-

cal gap for vehicle n at time t, referring superscript d

to the direction of change (current, left or right) and g

to the type of gap (lead or lag).

The critical lead and lag gaps are given by:

lead d,cr

= exp(1.553 −6.389max(0,∆S

lead d

)

−0.14min(0,∆S

lead d

−0.008ν

)

lag d,cr

= exp(1.429 + 0.471max(0,∆S

lagd

)

−0.234ν

)

(15)

A Comparison of Lateral Intention Models for Interaction-aware Motion Prediction at Highways

185

∆S

lead d

and ∆S

lead d

are the relative speeds of the lead

and lag vehicles in the direction of change d.

The probability to accept the gap is the result of

the multiplication of the acceptance of the lead and

lag gap and the expected lateral movement will be

to change if this probability is bigger than a random

value.

5 EXPERIMENTAL RESULTS

5.1 Scenario

We evaluate the framework proposed in the previous

section in a scenario simulated with SCANeR Stu-

dio simulator (AVSimulation, 2019). It is a two-lane

highway with the ego vehicle (black) and 4 other ve-

hicles (magenta, red, green and yellow), where 4 lane

changes are executed. The information about the sur-

rounding vehicles is received by the ego vehicle as a

vector of high-levelobjects containing their estimated

pose, velocity, and size. Figure 5 shows the initial po-

sition and the path followed by each vehicle and Fig-

ure 6 shows the velocities of each vehicle throughout

the simulation.

5.2 Execution of the Lateral Models

The simulation is executed three times, one for each

lateral model. Figure 7 shows the graphs of expecta-

tion and intention for each vehicle with the three mod-

els in the simulated scenario, where it can be noticed

the speciﬁcities of each model. In the expectation of

the green vehicle (Figure 7b), once it overtakes the

yellow vehicle, the expectation to change lanes from

Model 1 stays around 0.5, since no deceleration is

caused, meaning both lanes are possible and feasible.

For Model 2, the right most lane has always the prior-

ity, which can be seen as the expectation stays around

1 when the vehicle is on the left lane and the right lane

is available. For Model 3, in the same situation, the

expectation is to stay on the current (left) lane, since

it penalizes the right most lane and also penalizes lane

changes. The penalization to change lanes can be seen

in the expectation of the yellow vehicle (Figure 7c)

that stays the whole simulation on the right lane and

the expectation stays around 0. Since this vehicle is

already on the right lane, the expectation for Model 2

stays around 0 and for Model 1 stays around 0.5 when

both lanes are feasible.

Figure 8 shows the evolution of the probabilities

for each vehicle and each model. These probabilities

are computed as 1 − p

right

, where p

right

is the prob-

ability of being on the right most corridor. As men-

tioned before, the probability of each corridor is the

sum of the weights of the particles that contains this

corridor. Each line, marked with the color of the ve-

hicle on the top right corner, represents the evolution

of this vehicle. The x axis is the time and the y axis

is the probability of being on each lane, being 0 the

right (bottom) lane and 1 the left (top) lane. The line

in black is the ground truth, the lane in which the ve-

hicle is at, at each instant. The three models are repre-

sented by the lines in red, green and blue, respectively.

The magenta dashed line is the orientation of the vehi-

cle withe respect to the orientation of the lane and the

numbers mark the lane changes whose leading times

for each model are presented in Table 2. The dashed

line in blue is the threshold for the detection of a lane

change.

Table 2: Leading time.

Lane

Change

Model

1 2 3

1 1.0 s 0.9 s 0.7 s

2 0.8 s 0.8 s 0.9 s

0.8 s 0.9 s 0.8 s

4 0.7 s 0.8 s 0.9 s

0.9 s 0.7 s 0.6 s

6 1.2 s 1.0 s 1.0 s

5.3 Predictions and Evaluation

Figure 9 shows an example of the predictions com-

puted with the model from Section 3.4 in the last time

interval (2.9 - 3.0 s) for all three models. The time

when these predictions were made was chosen at 4.6

s, to show an instant where interactions become more

intense.

The differences of the models in these ﬁgures are

more visible in the lane change of the red vehicle. In

this particular frame, the intention from the red vehi-

cle to change lanes is more visible in Model 1 than in

Model 3, which conﬁrms the differences in the lead-

ing time for this lane change (1) in Table 2.

The advantages of the proposed DBN are high-

lighted when compared with the baselines predictions

computed with constant velocity and with the avail-

able version of the library SPOT (Koschi and Althoff,

2017b), which produces set-based reachable sets. For

the model with constant velocity, the prediction mean

and variance used are obtained as follows:

p(k) = N (µ

, σ

)

= x

+ v∗k∗dt

= k∗dt

(16)

VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems

186

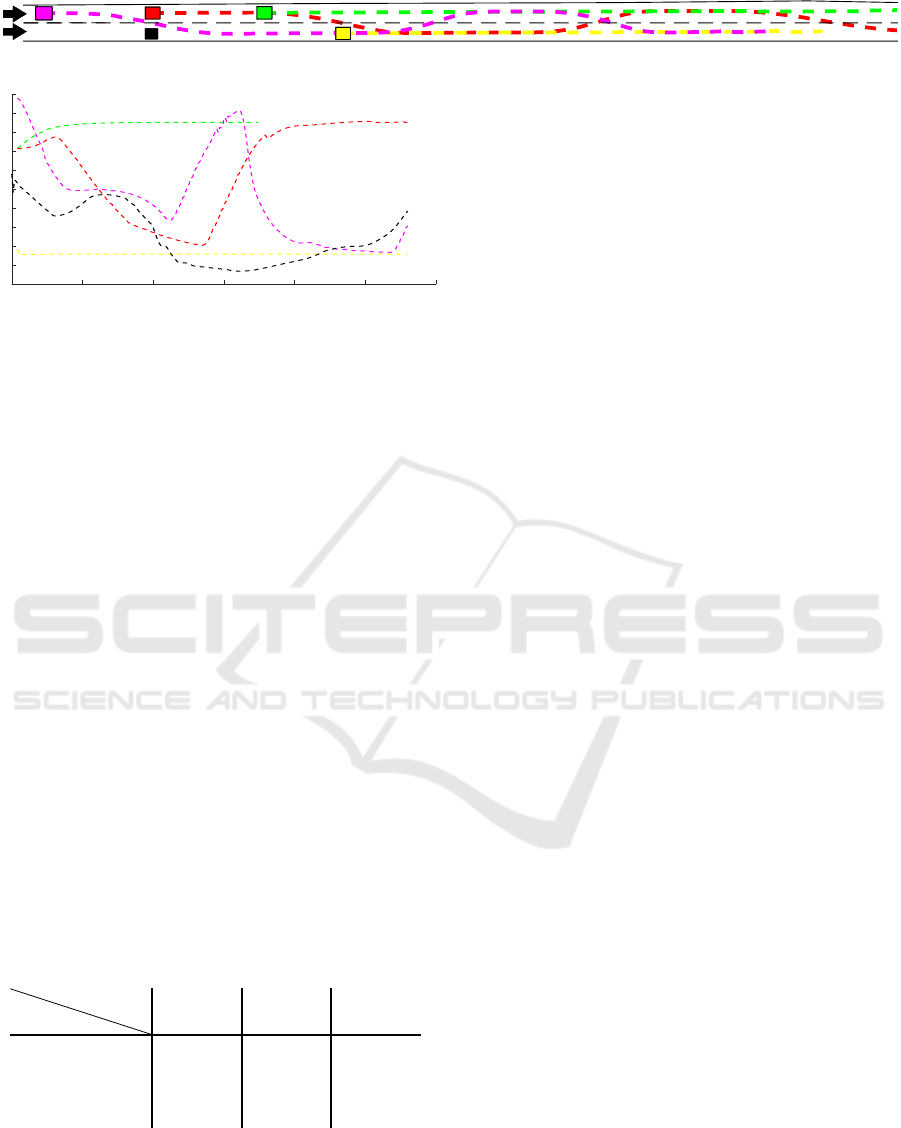
Figure 5: Paths evolution of each vehicle in the simulated scenario.

0 5 10 15 20 25 30

Time (s)

Velocity (m/s)

Figure 6: Velocities throughout the execution of the simu-

lation.

The predictions in the time interval 2.9 - 3.0 s

for the same time in the simulation for both baseline

methods are shown in Figure 10. In the method with

constant velocity, both corridors are equally probable

and the acceleration history and lane shape are irrel-

evant: the size of the distribution is the same for all

vehicles at every step. The results from SPOT, on the

other hand, do include the acceleration’s limits and

take into account the shape of the road (for the cor-

ridors changing lane), but they are too conservative,

leaving almost no free space for the motion planning

of the ego vehicle.

Figure 11 shows the correlation of the prediction

and the actual vehicle pose at the time interval (1.4 -

1.5 s) for all three models. It also includes a numeri-

cal evaluation of the prediction at the considered time.

The metric used consists in getting the likelihood of

the cell the center of the vehicle is located at from a

prediction made 1.5 s before. It is one of the criteria

used to assess the lateral models behaviour that are

compared. Since the red vehicles is the one with the

most different values among the models, its evalua-

tion is shown in a zoomed in box on the right of each

ﬁgure. Table 3 presents the sum of the evaluations for

each vehicle for each model for the whole simulation.

Table 3: Evaluation of the predictions per model.

Vehicle

Model

1 2 3

Red 0.34718 0.34871 0.34644

Green

0.22011 0.22223 0.22637

Yellow 0.51265 0.52836 0.52215

Magenta

0.33666 0.34174 0.34041

The vehicles with the more accurate predictions

are vehicles that do not change lanes, the green and

the yellow (the green vehicle leaves the simulation

10.5 seconds before its end). Besides the early detec-

tion of the lane change, it is also due to the fact that

the lane changing corridors do not perfectly match the

movement executed by the vehicles. Other factor that

inﬂuences the precision of the prediction is the lateral

position of the vehicle within the lane. So far, the lat-

eral distribution is the same for every vehicle, being

the mean the center of the lane. The use of an adap-

tive distribution, considering the lateral displacement

of the vehicle is part of a future work.

5.4 Evaluation Metrics

To evaluate the quality of the results, three metrics

were deﬁned: the lead time of the detection l, the

probability p of being on the current position based

on the predictions of a previous time, and the false

lane change detection f.

• The lead time l is deﬁned as the time where the

corridor that is changing lanes has the biggest pri-

ority and maintains the dominance until the lane

change is detected.

• The probability p is sum of the evaluation’s prob-

abilities for the whole simulation.

• The false detection f is the sum of intervals where

the probability is bigger on a corridor that is not

the correct one or a noise in the lane change. The

intervals between the lead time and the detection

of a lane change are not included. One example

of a false detection is marked in Figure 8.

Each metric is computed as follows:

∑

v=1

∑

c=1

, p

∑

i=1

∑

v=1

, f

∑

i=1

∑

v=1

where l

is the leading time of the lane change c of

the vehicle v for the model k, p

is the accuracy of

a previous prediction at time interval i for the vehicle

v for the model k, f

is the false detection for the

vehicle v at the time interval i for the model k, N is the

number of vehicles, Nc

is the number of lane changes

for the vehicle v and M is the number of simulated

intervals.

Table 4 presents the values of each metric for the

three models. For this scenario, model 1 yield better

leading times, although the predictions from model 2

and 3 are slightly more accurate. The reason for this is

mostly due to the fact that the lane changing corridors

do not perfectly match the movement executed by the

vehicles. The number of false detection are the same

A Comparison of Lateral Intention Models for Interaction-aware Motion Prediction at Highways

187

0 5 10 15 20 25

0.2

0.4

0.6

0.8

Probability

Expectation

MODEL 1

MODEL 2

MODEL 3

0 5 10 15 20 25

0.2

0.4

0.6

0.8

Probability

Intention

MODEL 1

MODEL 2

MODEL 3

(a) Red Vehicle

0 5 10 15 20 25

0.2

0.4

0.6

0.8

Probability

Expectation

MODEL 1

MODEL 2

MODEL 3

0 5 10 15 20 25

0.2

0.4

0.6

0.8

Probability

Intention

MODEL 1

MODEL 2

MODEL 3

(b) Green Vehicle

0 5 10 15 20 25

0.2

0.4

0.6

0.8

Probability

Expectation

MODEL 1

MODEL 2

MODEL 3

0 5 10 15 20 25

0.2

0.4

0.6

0.8

Probability

Intention

MODEL 1

MODEL 2

MODEL 3

0 5 10 15 20 25

0.2

0.4

0.6

0.8

Probability

Expectation

MODEL 1

MODEL 2

MODEL 3

0 5 10 15 20 25

0.2

0.4

0.6

0.8

Probability

Intention

MODEL 1

MODEL 2

MODEL 3

(d) Magenta Vehicle

Figure 7: Expectation and intention for each vehicle.

VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems

188

0.5

0 5 10 15 20 25

0.5

Time (s)

Probability

False detection

Figure 8: Evolution of each vehicle in the simulation: the line in black is the ground truth; the lines in red, green and blue

represent the evolution of the Model 1, 2, and 3, respectively; the blue line is the threshold to identify the lane change; the

line in magenta is the orientation of the vehicle with respect to the center line of the lane.

(a) Model 1

(b) Model 2

Figure 9: Predictions at the interval 2.9 - 3.0 s for each of the models.

(a) Constant velocity

(b) SPOT

Figure 10: Baseline predictions at the interval 2.9 - 3.0 s.

Table 4: Metrics of each model.

Parameter

Model

1 2 3

l 5.4 s 5.1 s 4.9 s

1.41660 1.44103 1.43536

f 1 1 1

for the three models.

A video with the evolution of the three simulations

is available in https://youtu.be/HxXE8bc8-5Y.

We evaluate the three models in another scenario

with 3 lanes and 5 vehicles where a higher number of

false detection is present. The paths followed by each

vehicle and their velocities are shown in Figures 12

and 13, respectively. Due to a lack of space, only the

A Comparison of Lateral Intention Models for Interaction-aware Motion Prediction at Highways

189

(a) Model 1 - Red : 0.000328 Green : 0.001216 Yellow : 0.001815 Magenta : 0.001189

(b) Model 2 - Red : 0.000260 Green : 0.001227 Yellow : 0.001848 Magenta : 0.001207

Figure 11: Evaluation of the predictions.

Figure 12: Paths evolution of each vehicle in the second simulated scenario.

result table (Table 5) will be presented.

0 5 10 15 20 25 30

Time (s)

Figure 13: Velocities throughout the execution of the sec-

ond simulation.

Table 5: Metrics of each model for the second scenario.

Parameter

Model

1 2 3

l 7.6 s 7.1 s 7.8 s

p 0.9488 0.96688 0.95825

71 87 52

In this case, model 3 yield better leading time and

the lowest number of false detection. The predictions

from model 2 are better but its number of false detec-

tion is the highest among the three models.

To combine both experiments, the values of l is

normalized by the number of lane changes and the

values of p and f are normalized by the number of

simulated intervals each vehicle is present and the

number of vehicles. Table 6 presents the sum of

the normalized results of both simulations for each

model.

Table 6: Normalized sum of the results.

Parameter

Model

1 2 3

norm

1.9857 1.8643 1.9309

norm

0.002150 0.002187 0.0021789

norm

0.0609 0.0732 0.0448

Based on the results from Table 6, for the sce-

narios evaluated, model 3 produced, in general, better

results:

• its normalized false detection is the best among

the all models; and

• its normalized predictions are more accurate than

the ones from model 1, that has the best normal-

ized leading time; and

• its normalized leading time is better than the one

from model 2, that has the best normalized pre-

dictions;

6 CONCLUSION AND FUTURE

WORK

In this work we present the framework currently be-

ing used by the AUTOPIA Group for the motion pre-

diction and interaction-aware of vehicles at highways.

Three models for the lane change were implemented

and compared. With the metrics used in this work, the

model from Toledo et al. (2005) yield better results.

A comparison of the motion prediction with two

baseline models was presented. The results from

VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems

190

SPOT, although more accurate, are too conservative,

leaving the ego vehicle, in some cases with no or al-

most no space for the motion planning. The impor-

tance of interactions modeled with a DBN is high-

lighted when compared with the simple model with

constant velocity, where all the possible corridors

have the same probability and the acceleration input

has no inﬂuence in the predictions.

As future work, we intend to use the framework

presented in more complex scenarios, such as high-

ways with entrances and exits, and use public avail-

able datasets.

ACKNOWLEDGEMENTS

This work has been partially funded by the Span-

ish Ministry of Science and Innovation, the Commu-

nity of Madrid through SEGVAUTO 4.0-CM (S2018-

EMT-4362) Programme, and by the European Com-

mission and ECSEL Joint Undertaking through the

Projects NEWCONTROL (826653) and SECREDAS

(783119).

REFERENCES

Althoff, M. (2010). Reachability analysis and its appli-

cation to the safety assessment of autonomous cars.

PhD thesis, Technische Universit¨at M¨unchen, Mu-

nich, Germany.

Althoff, M. (2015). An introduction to cora 2015.

Althoff, M. and Magdici, S. (2016). Set-based prediction of

trafﬁc participants on arbitrary road networks. IEEE

Transactions on Intelligent Vehicles, PP:1–1.

AVSimulation (2019). Scaner studio user manual.

Bender, P., Ziegler, J., and Stiller, C. (2014). Lanelets: Ef-

ﬁcient map representation for autonomous driving. In

2014 IEEE Intelligent Vehicles Symposium Proceed-

ings, pages 420–425.

Kesting, A., Treiber, M., and Helbing, D. (2007). General

lane-changing model MOBIL for car-following mod-

els. Transportation Research Record, (1999):86–94.

Klingelschmitt, S., Damerow, F., Willert, V., and Eggert, J.

(2016). Probabilistic situation assessment framework

for multiple, interacting trafﬁc participants in generic

trafﬁc scenes. In 2016 IEEE Intelligent Vehicles Sym-

posium (IV), pages 1141–1148.

Koschi, M. and Althoff, M. (2017a). Interaction-aware oc-

cupancy prediction of road vehicles. In 2017 IEEE

20th International Conference on Intelligent Trans-

portation Systems (ITSC), pages 1–8.

Koschi, M. and Althoff, M. (2017b). Spot: A tool

for set-based prediction of trafﬁc participants. In

2017 IEEE Intelligent Vehicles Symposium (IV), pages

1686–1693.

Lefevre, S., Laugier, C., and Ibanez-Guzman, J. (2013).

Intention-aware risk estimation for general trafﬁc sit-

uations, and application to intersection safety. Inria

research report, RR-8379.

Mathew, T. V. (2019). Lane changing mod-

els. https://www.civil.iitb.ac.in/tvm/nptel/534\

LaneChange/web/web.html. (Accessed on

11/19/2020).

Medina Lee, J. F., Trentin, V., and Villagra, J. (2019).

Framework for motion prediction of vehicles in a sim-

ulation environment. pages 520–527.

Schulz, J., Hubmann, C., L¨ochner, J., and Burschka,

D. (2018). Interaction-aware probabilistic behav-

ior prediction in urban environments. CoRR,

abs/1804.10467.

Toledo, T., Choudhury, C., and Ben-Akiva, M. (2005).

Lane-changing model with explicit target lane choice.

Transportation Research Record, 1934.

Toledo, T., Koutsopoulos, H., and Ben-Akiva, M. (2003).

Modeling integrated lane-changing behavior. Trans-

portation Research Record, 1857.

Treiber, M., Hennecke, A., and Helbing, D. (2000).

Congested trafﬁc states in empirical observations

and microscopic simulations. Physical Review E,

62(2):1805–1824.

Vechione, M., Balal, E., and Cheu, R. L. (2018). Compar-

isons of mandatory and discretionary lane changing

behavior on freeways. International Journal of Trans-

portation Science and Technology, 7(2):124 – 136.

Villagra, J., Artu˜nedo, A., Trentin, V., and Godoy, J. (2020).

Interaction-aware risk assessment: focus on the lateral

intention. In IEEE 3rd Connected and Automated Ve-

hicles Symposium.

Zechel, P., Streiter, R., Bogenberger, K., and G¨ohner, U.

(2019). Over-approximation of the driver behavior

as occupancy prediction. In 2019 IEEE 14th Interna-

tional Conference on Intelligent Systems and Knowl-

edge Engineering (ISKE), pages 735–742.

Zhan, W., de La Fortelle, A., Chen, Y., Chan, C., and

Tomizuka, M. (2018). Probabilistic prediction from

planning perspective: Problem formulation, repre-

sentation simpliﬁcation and evaluation metric. In

2018 IEEE Intelligent Vehicles Symposium (IV), pages

1150–1156.

A Comparison of Lateral Intention Models for Interaction-aware Motion Prediction at Highways

191