Approximate Query Processing for Lambda Architecture

Aleksey Burdakov

, Uriy Grigorev

, Andrey Ploutenko

and Oleg Ermakov

Bauman Moscow State Technical University, Moscow, Russia

Amur State University, Blagoveschensk, Russia

Keywords: Lambda Architecture, Stream Processing, Approximate Query Processing, Sapprox.

Abstract: The lambda architecture is widely used to implement streaming data processing systems. These systems create

batch views (subsets of data) at the Serving Layer to speed up queries. This operation takes significant time.

The article proposes a novel approach to lambda architecture implementation. A new method for Approximate

Query Processing in a system with Lambda Architecture (LA-AQP) significantly reduces aggregate (sum,

count, avg) calculation error. This is achieved by using a new way of calculating the reading segments

probabilities. The developed method is compared with the modern Sapprox method for processing large

distributed data. Experiments demonstrate that LA-AQP almost equals Sapprox in terms of volume and time

characteristics. The introduced accuracy measures (δ-accuracy and ε-accuracy) are up to two times better

than Sapprox for total aggregate calculation. Aggregate values can vary greatly from segment to segment. It

is shown that in this case the LA-AQP method gives a small error in the total aggregate calculation in contrast

to Sapprox.

1 INTRODUCTION

Real-time large data volume processing is an

important requirement for modern high-load systems.

Streaming data processing serves this task. Data

stream processing applies to various fields: search

engines, social networks, fraud detection systems,

trade and financial systems, equipment monitoring

systems, military and intelligence systems

(Kleppmann, 2017).

Lambda architecture enables implementation of

streaming data processing (Marz et al., 2015).

Sources (Kiran et al., 2015; Gribaudo et al., 2018)

provide lambda architecture implementation for data

processing backend in Amazon EC2. It provides high

bandwidth with low network maintenance costs. The

lambda architecture enables streaming processing

implementation in many other areas: heatmap

tracking (Perrot et al., 2017), query processing (Yang

et al., 2017), medical surgery predictions

(Spangenberg et al. 2017), etc.

https://orcid.org/0000-0001-6128-9897

https://orcid.org/0000-0001-6421-3353

https://orcid.org/0000-0002-4080-8683

https://orcid.org/0000-0002-7157-4541

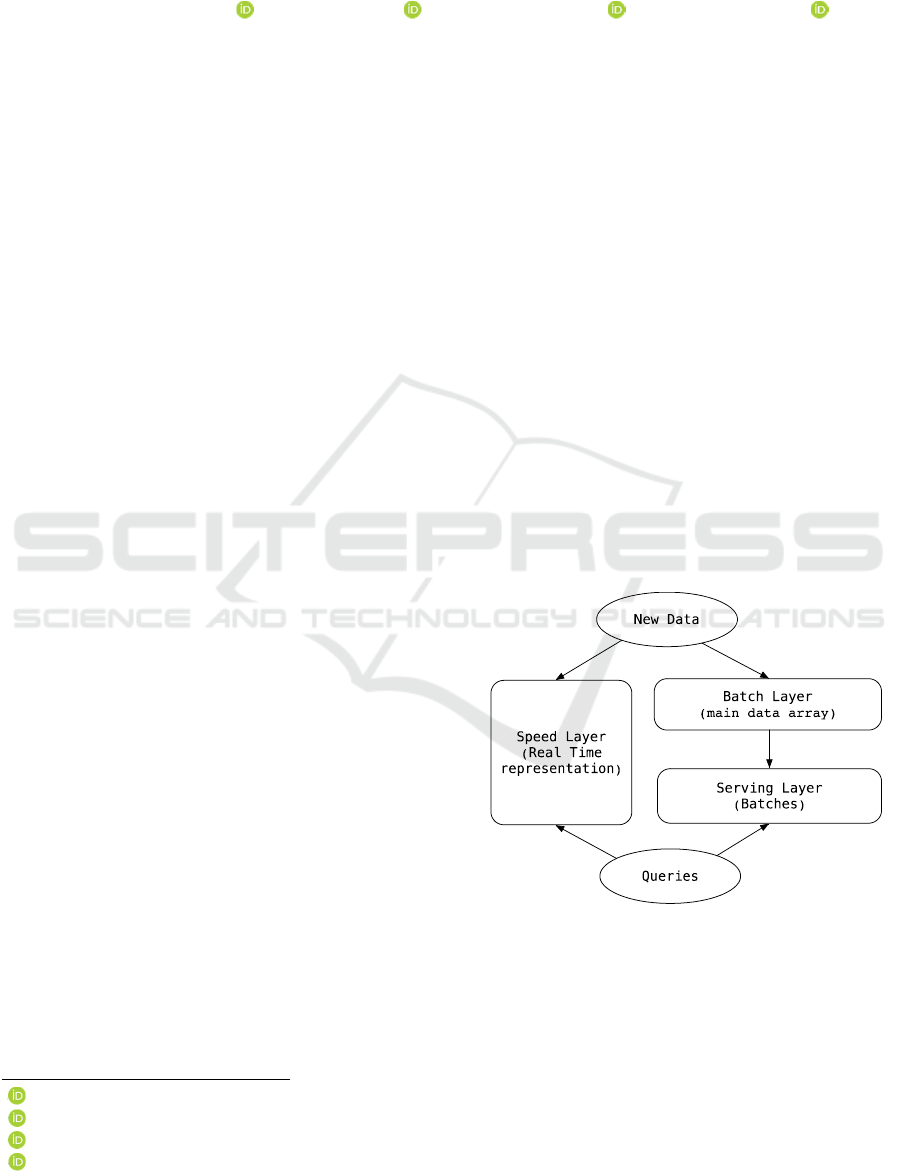
The lambda architecture (see Fig. 1 (Marz et al.,

2015)) has Batch, Speed and Serving Layers.

Figure 1: Lambda Architecture.

Apache Hadoop-based Data Lake typically

represent a Batch Processing Layer. This layer stores

a dataset master copy. The Serving Layer generates

batch representations from the data. Each batch is a

Burdakov, A., Grigorev, U., Ploutenko, A. and Ermakov, O.

Approximate Query Processing for Lambda Architecture.

DOI: 10.5220/0010465802530261

In Proceedings of the 6th International Conference on Internet of Things, Big Data and Security (IoTBDS 2021), pages 253-261

ISBN: 978-989-758-504-3

253

data chunk prepared for fast query processing. The

Speed Layer provides real-time data processing, since

data cannot quickly reach the Serving Layer.

The described lambda architecture

implementation has a number of significant

drawbacks:

1. Effective implementation of different levels

may require different databases. This in turn requires

different development, support and data access

software tools. Source (Marz et al., 2015) provides an

example of the Batch Layer implementation based on

the Hadoop Distributed File System (HDFS), while

the Serving Layer is based on ElephantDB, and Speed

Layer uses Cassandra database.

2. A new request may require a new batch

representation (data subset). This will lead to

searching the large Batch Layer database.

3. The new data appears at the Serving Layer with

a delay. This leads to introduction of a cumbersome

Speed Layer in order to provide prompt access to such

data (Psaltis, 2017).

The article proposes a novel approach to building

systems with lambda architecture. It allows the

Serving Layer implementation in a form of metadata

describing data segments of the Batch Layer. The new

approach provides an approximate query processing

based on this metadata.

2 LAMBDA ARCHITECTURE

WITH SERVING LAYER IN

METADATA FORM

The proposed new Lambda Architecture is shown on

Fig. 2.

Figure 2: New Lambda Architecture.

First, new data blocks come from a source (e.g.

Kafka/ Storm) to the changelog. The entries in each

block are sorted by timestamp, but they are not sorted

throughout different blocks.

After a certain period of time, e.g. one second, the

background process is started. It sorts the incoming

block records by timestamp (merge sort). This

process then adds the sorted record segments to the

main dataset (Batch Layer).

The background process analyzes each record

segment. It extracts the attributes, calculates the

aggregated values, and stores them as metadata

(Serving Layer). One line of metadata corresponds to

one segment of the Batch Layer. The processed

blocks are removed from the change log (the log is

compacted), and the background process goes into a

waiting state. The new blocks received during the

execution of the background process will be

processed in the next period of this process activation.

Batch level segment records are stored as <key>

<value>, where "key" is a timestamp and "value" is a

JSON document. All records of the main data set are

sorted by key (by analogy with LSM trees based on

SS tables (Kleppmann, 2017; O’Neil, 1996)).

Metadata is used to approximate the aggregated

values (sum, avg, count) of some JSON document

attributes. As noted, one metadata record corresponds

to one segment of the Batch Layer. Metadata records

are stored as <key><value>, where “key” is the

number of the corresponding segment, “value” is a

JSON field.

The search attributes for which the search is

performed will be denoted as SA. The attributes by

which the aggregation is performed will be

designated as AA. The information for each search

attribute SA

is stored in the metadata record as JSON

field elements. This item has the following structure:

<k is the SA

value number> <number of

records in the g segment with the kth SA

value> {<aggregate value by the AA

attribute for the kth SA

value in the g

segment>}

= <Z

><M

>{<A

igm

(1)

The values of each SA

search attribute are stored

in a dictionary, which is common for all segments.

The dictionary is a hash table located in RAM. The

hash table elements have the following form: <SA

value> <k - number of SA

value> = < C

> <Z

The dictionary is populated as new values of the

search attribute appear in the data stream when

parsing data segments. The length of a numeric field

<k - the number of the SA

value> is often much

shorter than the length of the character field <SA

IoTBDS 2021 - 6th International Conference on Internet of Things, Big Data and Security

254

value>. Therefore, the size of the metadata record

will be smaller.

The following data is additionally stored in the

metadata record:

<g-th segment timestamp> <g-th segment

number of records> <g segment number of

search attributes> {<aggregate value by

attribute AA

for this segment g>}

><S

><Q

>{<A

(2)

The A

igm

and A

aggregate values in (1) and (2)

accumulate as records are retrieved from the data

stream.

The considered lambda architecture organization

has the following advantages over the classical

scheme (see Fig. 1):

1. One database can be used to implement the

Package and Serving Layer.

2. There is no need to build batch views at the

Serving Layer. The Approximate Query Processing is

fast, and it only requires changing the view which

means only changing the SELECT query. Moreover,

aggregate values computation is usually performed at

some time interval. Having a timestamp index at the

Serving Layer allows quick reading of the required

segments from the main data set.

3. The Speed Layer is optional. For example, let

us assume that a background compaction process is

invoked every second. If the minimum statistics

collection interval is one minute, then the Speed

Layer is not needed. This Layer would be required if

statistics was collected every second.

3 RELATED WORK

Modern clusters provide enormous processing power.

But querying large-scale datasets remains

challenging. To solve this problem, approximate

calculations are used in big data analytics

environments (Laptev et al., 2012; Agarwal et al.,

2013; Pansare et al., 2011; Goiri et al., 2015; Kandula

et al., 2016).

There are various ways of dataset approximate

query processing (Cormode et al., 2011): data

sampling, histograms, wavelets.

Histogram and wavelet application presents the

following issues: 1) it is difficult to distribute data

across several nodes and process them in parallel, 2)

it is very difficult to perform the table join operation.

Therefore, the most acceptable way of

Approximate Query Processing is selecting data from

the general population. Let us consider some

methods in this area.

BlinkDB (Agarwal et al., 2013) generates patterns

on the most commonly used column sets (QCS) in

WHERE, GROUP BY, and HAVING clauses. If the

query does not match the pattern, then the aggregate

calculation error can be large. But the important thing

is that it is not possible to generate separate samples

for all data subsets.

The data sampling system ApproxHadoop (Goiri

et al., 2015) works on the assumption that the

requested datasets are evenly distributed across the

entire dataset. Unfortunately, in many real cases,

dataset subsets are actually spread unevenly across

the entire dataset partitions. The system suffers from

inefficient sampling and large variance in the

computed aggregate value.

Source (Zhang et al., 2016) proposed a more

effective method for processing large distributed data

(Sapprox method) and presented comparison results

of Approximate Query Processing in Sapprox,

ApproxHadoop and BlinkDB. The Sapprox method

was the most effective. Let us consider it in more

detail.

The Sapprox method uses the following metadata

storage structures:

1. List of attributes of the dataset table:

{<name of the search attribute of the SA

of the dataset table> <pointer to the hash

table with the values of the search attribute

of the SA

2. Hash table with the search attribute SA

values:

{<k-th value of SA

> <pointer to the table

of occurrences of the k-th value of SA

3.Table of occurrences of the k-th SA

value:

<k-th value of SA

> {<g - segment

number> <number of records in the g-th

segment with k-th value of SA

>{<g><M

4. Table of segment offsets in the HDFS

file system: {<segment number>

<segment offset in HDFS (bytes)>}

(3)

Sapprox allows approximate aggregate value

calculation (agg - sum, count) in the following

queries:

SELECT {agg(AA

) as A

}

FROM table

WHERE SA

and SA

and ...

and SA

(4)

Approximate Query Processing for Lambda Architecture

255

The algorithm is provided below:

1. For all i=1..h, g=1 ... N, calculate the

probability that the record of the g-th segment

satisfies the condition for the i-th search attribute (SA

= C

): P

= M

/S, where M

is the number of

records in the g-th segment with the k

-th value of the

(see (3)), S is the number of records in the

segment (it is the same for all g), N is the total number

of segments in the HDFS data array.

2. For each g=1...N calculate the probability that

the record of the g-th segment satisfies the condition

specified after the WHERE keyword (see (4)):

∏

3. For each g = 1 ... N calculate the probability



4. Get a sample of 'n' segment numbers using the

probability distribution function {π

5. Read these 'n' segments. Find records in each

segment that satisfy the WHERE clause. Calculate

the aggregated value τ

(j=1..n) for each AA

attribute

of the found records (see (4)).

6. Estimate each desired aggregate A

value with

the formula:

() ( )



(5)

Estimate (5) is unbiased. For a sufficiently large

‘n’ value (5) has normal distribution (Zukerman,

2020) (Lyapunov theorem). It was shown in (Liese et

al., 2008) that the random variable

t= 1 ( ( ) ) / ( )nn Dn

ττ

−⋅ −

has Student’s

distribution with n-1 degrees of freedom, where τ is

the mathematical expectation τ(n), i.e. the true value

of A

() ( ( ()))/

Dn n n

τπ τ

=−



is an

estimate of the sample variance. We derive the

following formula:

|()| ( ())

(1)

nt n

ττ τ

−

−<= −

−



(6)

where α is the degree of confidence of inequality

(6). For n>121 the coefficient t

n-1,

practically does

not depend on ‘n’, and for α=0.9; 0.95; 0.99 it is equal

to 1.645, respectively; 1,960; 2.576.

The Sapprox method has several serious

disadvantages:

1. The probability distribution {π

} depends only

on the probabilities {P

} that the segment records

satisfy the WHERE condition. This can lead to a

large estimation error if the aggregated values of τ

differ significantly for different segments (see the

Discussion section).

2. It is possible to calculate the aggregated

attribute values of only one table (table joins are not

supported). The search term includes elementary

terms with the logical operation 'and'. The query does

not explicitly support the GROUP BY clause.

3. When executing a query, it is necessary to read

and analyze metadata for all N segments that are

stored in the main data set (indexing by timestamps is

not supported).

4. It is necessary to read both metadata and data

segments even when a search condition is specified

for only one attribute.

5. Only HDFS file system is used, which makes it

difficult to move to other systems for storing the main

data and metadata.

6. The record number in different segments must

be the same (S). This can result in reading the same

segment from different nodes.

7. When adding a new value of the search

attribute or a new segment it is necessary to modify

the metadata created earlier (see (3)).

4 NEW APPROXIMATE QUERY

PROCESSING METHOD

Structures (1) and (2) describe metadata of the system

with the proposed lambda architecture (see Fig. 2).

These include the aggregated values calculated for

each search attribute value in the segment (A

igm

) and

for the segment as a whole (A

). They can be

obtained by processing streaming data entering the

system.

A method of Approximate Query Processing in a

system with Lambda Architecture (LA-AQP) was

developed. It allows approximately calculation of the

aggregated values (agg - sum, count, avg) when

executing queries of the following form:

SELECT SA

,{agg(AA

) as A

}

FROM array JSON-documents

WHERE TSR and [Predicate(SA

,SA

, ...,

)] GROUP BY SA

(7)

TSR defines timestamp search condition (time

slot, multiple time slots),

Predicate (SA

, SA

, ..., SA

) includes elementary

conditions for search attributes {SA

}, logical

operations AND, OR, NOT, and parentheses.

The low level A

igm

and A

values are known

(see (1) and (2)). But the problem is how to use them

IoTBDS 2021 - 6th International Conference on Internet of Things, Big Data and Security

256

to quickly estimate the total aggregate A

accordance with query (7). So the A

igm

or A

metadata values cannot be simple added because only

a part of the segment records match the WHERE

search condition. The challenge is calculating the

aggregate value that is linked to this part of the

records. The problem of estimating the number of

record parts that satisfy the search condition is also

not trivial. A probabilistic approach is used to solve

it.

The algorithms for query (7) execution are

provided below:

Algorithm 1. No predicate.

1. Read metadata records for TSR using a

timestamp index.

2. Check all found metadata records. Accumulate

the values A

+= A

rgm

for each k-th value of the

search attribute SA

and each aggregated attribute

(see (1)). SA

is an attribute by which grouping

is performed (see (7)).

Algorithm 2. Predicate is present.

1. For TSR, read metadata records using a

timestamp index.

2. For each metadata record found, calculate the

probability P

that the segment record satisfies the

condition specified in the Predicate. This requires the

following steps:

- calculate the probability that the segment record

satisfies the elementary condition for the i-th search

attribute (SA

= C

{ki}

): P

= M

{ki}

, where C

{ki}

one or several values {k

} from the search dictionary

the SA

attribute, M

{ki}

is the number of records in

the g-th segment with the values {k

} of the SA

search attribute, S

is the number of records in the g

segment (see (1), (2));

- calculate the probability P

that the record of the

g-th segment satisfies the condition specified in the

Predicate. For this one should use recursive functions

for calculating probabilities (Table 1).

Table 1: Probabilities for elementary conditions.

Condition Probability

<condition>AND<condition > ·

<condition>OR<condition > +-·

NOT<condition> 1-

probabilities for elementary conditions

initially act as .

3. Calculate the probability π

for each g

segment and each aggregated attribute AA

- calculate d

=(A

)·(P

·S

) - this is an

estimare of an aggregate value in the segment; indeed,

the expression in the first parentheses is an estimate

of the aggregate value per segment record (see (2));

and the expression in the second parentheses is an

estimate of the number of segment records that satisfy

the condition specified in the Predicate;

- calculate the probability

gm gm gm

{g}

π=d/ d



where {g} is the set of segment numbers obtained

from the read metadata.

Perform the following steps of the algorithm for

each AA

4. Get a sample of ‘n’ segment numbers {g} using

the probability distribution function {π

}

. Sampling

should be done with repetition. Otherwise, estimate

(5) will be biased and the confidence interval

calculated using formula (6) will be erroneous.

Samples of segment numbers for different AA

may

have a non-empty intersection.

5. Read these 'n' segments from the main dataset.

Find JSON documents in each segment that satisfy

the condition specified in the Predicate. Calculate the

aggregated value τ

(j = 1..n) for them for the AA

attribute (ie select the AA

values from JSON

documents). For each k-th value of the SA

attribute, accumulate the values A

+= AA

jrk

6. Estimate the aggregated A

value (without

grouping) using the formula (5). Calculate the

confidence interval using formula (6). The confidence

interval for the group aggregate A

(see clause 5)

does not exceed this value. This is derived from the

fact that the variance D(n) for A

is equal to the sum

of the variances calculated for A

The LA-AQP method has the following

advantages:

1. The confidence interval, calculated using the

formula (6), decreases. The quantity d

/π

(see item

3 of Algorithm 2) is some approximation of the

quantity τ

/π

in D (n) (see (6)). Since

jm jm gm

{g}

d/π= d



these relationships are the

same for different j. Therefore, the variance D (n) can

be expected to be smaller.

2. It is not necessary to read segments from the

main data set of the Batch Layer to obtain the result

in some important cases (see Algorithm 1).

3. An arbitrary Predicate for search attributes of

JSON documents and use the GROUP BY clause (see

(7)) can be specified in a query.

4. There is a timestamp index that allows reducing

the number of analyzed metadata records and,

thereby, reducing the sample size.

5. The number of S

JSON documents in the

segments can be different (see (2)).

6. The old metadata records are not changed when

new records are added during the data stream

processing.

Approximate Query Processing for Lambda Architecture

257

7. Different distributed file systems (not

necessarily HDFS) can be used to implement the

method. The required segments of the main dataset

are read at offset.

8. There is no need to develop a method for

related tables approximate query processing.

Suppose it is necessary to approximately process the

following query:

SELECT sum(Cost) FROM Customer T1,

Purchases T2 WHERE T1.id1=T2.id1 AND Name=

“José”.

If linked tables are used (Figure 3, left), then the

tables "Customer" and "Purchases" need to be split

into segments. Let their number be N1 and N2

respectively. In further processing, it is necessary to

consider pairs of segments in order to take into

account the relationship of segments by the common

attribute id1. The number of such pairs (new

segments) equals N1×N2.

The JSON document stores all information

related to the client (see Figure 3, right). So that the

tables were already joined by the id1 attribute in these

documents. In this case, the number of segments is

reduced to N1.

Figure 3: Related tables and the corresponding structure of

the JSON document.

5 COMPARISON OF SAPPROX

AND LA-AQP APPROXIMATE

QUERY PROCESSING

METHODS

The comparison was carried out on a computer with

a four-core processor and 16 GB RAM. Testing of

Sapprox and LA-AQP methods was done on synthetic

dataset. The system received a stream of financial

transactions in JSON format. Each document

included the following fields:

- sum is the payment amount (random value from

0 to 10,000),

- city is the client's city (one of 1000 random

cities),

- user_id is the id of a specific client (one of

1,000,000 random user IDs),

- factor is deposit / withdrawal (one of 2 values),

- a variable number of additional fields.

Outlying peak values were generated to simulate

the trend of increasing payments in different cities.

They did not coincide with the distribution function

of payment amounts at the previous points in time.

The developed system prototype consists of three

main components: balancer, database, and

multithreaded daemon for segment processing.

The balancer splits the incoming JSON

documents into segments and writes them to the

database (Data table).

The database is implemented with PostgreSQL

DBMS. Each segment is an inheritor of the base table.

Each new segment is a separate table where JSON

documents are stored. Segment reading performs

read operation of the blocks associated with the table.

Metadata is stored in a separate table. This table key

is the segment index, and the value is a JSON field.

The value is saved in the metadata instead of the

search attribute value number for the LA-AQP

method. The dictionary was not implemented in the

developed prototype. It also stores aggregated values

for search attributes and for the segment as a whole

(see (1), (2)).

The multithreaded daemon scans for new

database segments. It starts the process of building

metadata for these segments (generates metadata

records). The balancer and daemon were written in

the Golang (Go) language, which was chosen due to

the ease of writing asynchronous code (Donovan et

al., 2015; Cox-Buday et al., 2017).

68 million records (JSON documents) were

generated for the test, the segment size was set to

S=10,000 records. The following query was tested

(no timestamp constraints):

SELECT sum(Data.sum)

FROM Data

WHERE city = ‘City_1’ and factor =

‘Expense’;

(8)

The experiments were repeated 3 times for each

method and each sample size (10% and 30%).

Table 2 shows the averaged volume-time

characteristics of SQL (exact execution of the query

(8)), as well as the Sapprox and LA-AQP methods.

According to these data, the Sapprox and LA-AQP

methods performed on par.

IoTBDS 2021 - 6th International Conference on Internet of Things, Big Data and Security

258

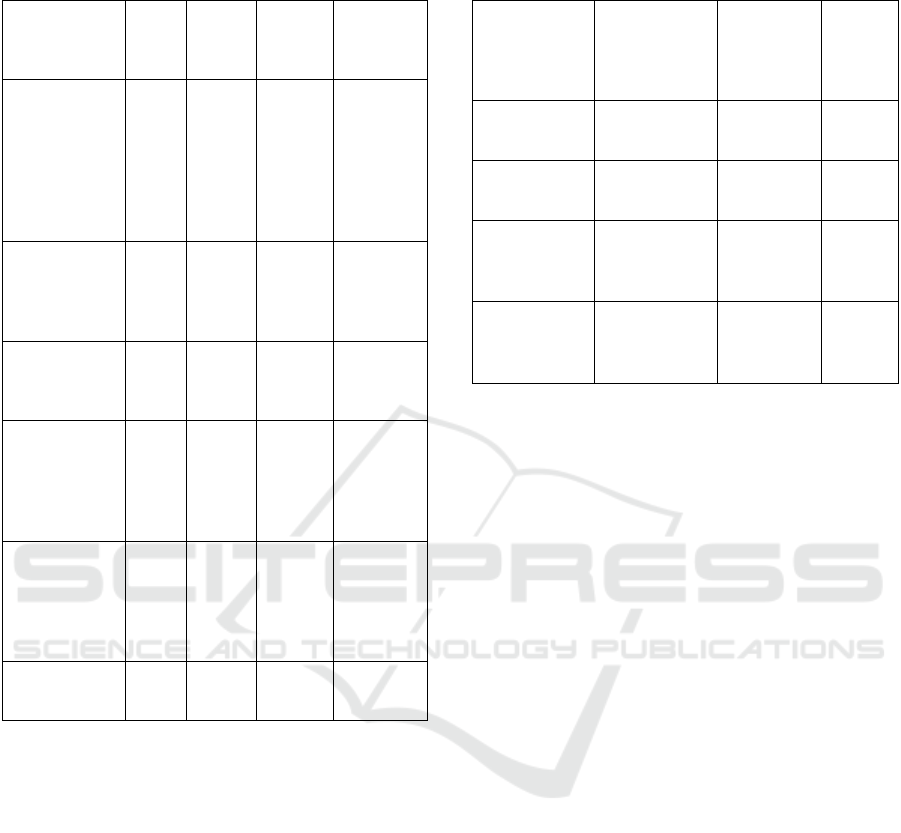
Table 2: The averaged volume-time characteristics of SQL

for Sapprox and LA-AQP methods.

Characteristic SQL Sapprox LA-AQP

LA-AQP/

Sapprox

Difference

Time to

include one

segment

(10,000

records) into

the database

(ms)

242 373 384 +3%

Time to build

metadata for

one segment

(ms)

31 31 0%

Request

execution

time (ms)

33,372

Request

execution

time (ms),

sample size

10%

1,132 1,143 +1%

Request

execution

time (ms),

sample size

30%

2,833 2,847 +0,5%

Total database

size (GB)

12 12 12 0%

Table 3 shows the characteristics of the sum

aggregate calculation accuracy. The accuracy was

evaluated in two ways:

1. δ=max (1-L/E, U/E-1),

where L is the lower limit of the calculated

aggregate; E is the aggregate exact value; U is the

upper bound of the calculated aggregate.

2. ε is the value of the confidence interval (this is

the doubled value of the right-hand side of inequality

(6)) divided by 5,000. The exact value of the

aggregate sum divided by 5,000 is 63,014,300/5,000

= 12,603.

Table 3 demonstrates that the developed LA-AQP

method is almost two times better in δ-accuracy than

the Sapprox method. Moreover, the LA-AQP method

with a 10% sample is better in δ-accuracy than the

Sapprox method with a 30% sample. In terms of ε-

accuracy, the LA-AQP method is almost 1.8≈2 times

better than Sapprox.

Table 3: The characteristics of the sum aggregate

calculation accuracy.

Characteristic Sapprox LA-AQP

LA-AQP

difference

from

Sapprox

δ, 10% sample

volume

0.12 0.07 -42%

δ, 30% sample

volume

0.09 0.04 -56%

ε, 10% sample

volume,

α=0,9/0,95/0,99

1209/1440/1896 704/838/1106 -42%

ε, 30% sample

volume,

α=0,9/0,95/0,99

1050/1253/1647 544/648/847 -48%

6 DISCUSSION

In the developed LA-AQP method, when calculating

the probabilities π

, the values of the aggregates in

the segment are taken into account. This is the

fundamental difference between LA-AQP and

Sapprox as well as other methods. As shown in

Section 4, this allows reducing the confidence

interval (6) when estimating τ.

The aggregated values of τ

can differ

significantly for different segments. The Sapprox

method in this case can lead to a large estimation error

τ. Let us give a small example.

Let the number of segments be N=2000 and the

sample size n=100. Suppose that P

=0.1, g = 1 ... N,

i.e. 10% of the records in each segment satisfy the

WHERE search condition. Let the aggregated values

of any attribute of these records be distributed over

segments significantly unevenly: τ

= 10000, τ

=1, j=2

... 2000.

Then for Sapprox π

= P

/(N⋅ P

)=0.0005, g = 1 ...

N (see item 3 of the algorithm in Section 3). The

probability that in n = 100 trials the 1st segment will

not be selected equals (1-π

)

=0,95. From formula

(5), we obtain an aggregate estimate:

1st option - 1st segment is not selected:

τ(n)=(1/n)⋅n⋅((τ

=1)/(π

=0.0005)=2,000;

2nd option - 1st segment will be selected with

probability 1-0.95 = 0.05:

τ(n)=(1/n)⋅( (τ

=10,000)/π

+(n-1)⋅(τ

=1)/π

201,980.

Approximate Query Processing for Lambda Architecture

259

In fact τ=(τ

=10,000)+(N-1)⋅(τ

=1)=11,999. The

estimation error τ is large in options 1 and 2.

Let us show that with the same initial data, the

LA-AQP method allows estimating τ with a much

smaller error. In this case, we obtain (see item 3 of the

algorithm 2 in Section 4):

=((τ

=10,000)⋅P

((τ

=10,000)⋅P

+ (N-1)⋅(τ

=1)⋅P

)= 0.83;

=((τ

=1)⋅P

((τ

=10,000)⋅P

+(N-1)⋅(τ

=1)⋅P

)=8.33E-5, j=2...N.

The probability that for n=100 trials the 1st

segment will not be selected is (1-π

)

=1.1E-77 (i.e.

it is practically 0). We derive an aggregate value

estimate from formula (5):

Option 1 - the 1st segment will be selected only

one time out of n = 100:

τ(n)=(1/n)⋅((τ

=10,000)/

+(n-1)⋅(τ

=1)/π

)=12,005;

Option 2 - the 1st segment will be selected 100

times out of n=100:

τ(n)=(1/n)⋅(n⋅(τ

=10,000)/π

)= 12,048.

Option 3 - the 1st segment is not selected (this is

an almost impossible event):

τ(n)=(1/n)⋅(n⋅(τ

=1)/π

)= 12,004.

Therefore the error in calculating the aggregate is

small (exact value τ=11,999) in options 1, 2 and 3 for

LA-AQP. The sample size 'n' is not important in this

example, and it can be equal to one. It also does not

matter which segment numbers are selected for

processing. The calculation error using the LA-AQP

method will be small in any case.

To achieve the same level of error in Sapprox,

it is necessary to significantly increase the sample

size n. It should be comparable to N.

The LA-AQP method allows specifying a more

complex search condition and a GROUP BY clause

in a query (see (7)). Sapprox allows only AND (see

(4)) connection of elementary conditions.

7 CONCLUSIONS

The existing systems with lambda-architecture

requires constantly repeat package updates for new

analytical queries execution acceleration. This

consumes large time since it searches in a large

database. The developed approach allows avoiding

creation of package representations due to the

introduction of metadata level. The queries are

executed promptly but with a certain error. The

developed LA-AQP method reduces this error.

Expression (5) gives an unbiased estimate of the

τ aggregate for any probability distribution function

{π

}, π

>0. The issue is in the sample size. The

developed method for calculating {π

} makes it

possible to obtain a good aggregate estimation

accuracy for small n values. This is achieved due to

the fact that when calculating {π

}, estimates of the

values of the aggregates in the segment are used. As

a result, the values τ

/π

in (5) become approximately

the same. This allows minimizing the sample

variance D(n) (see (6)).

The LA-AQP method allows executing queries

with a general search condition and with a grouping

(see (7)). For calculations, aggregate values are used

at the level of individual attributes and segments. The

overhead costs of obtaining such aggregates are low:

they accumulate as data arrives in the stream. The

accuracy of the general aggregates increases

approximately twofold as compared with the Sapprox

method.

The future work includes development a method

for processing queries at the Speed Layer in a Lambda

Architecture system.

REFERENCES

Agarwal, S., Mozafari, B., Panda, A., Milner, H., Madden,

S., and Stoica, I. (2013). Blinkdb: Queries with

bounded errors and bounded response times on very

large data. In Proceedings of the 8th ACM European

Conference on Computer Systems, EuroSys ’13, pages

29–42, New York, NY, USA, 2013. ACM.

Cormode, G. et al. (2011). Synopses for massive data:

Samples, histograms, wavelets, sketches // Foundations

and Trends® in Databases. – 2011. – Vol. 4. – №. 1–3.

– P. 1-294.

Cox-Buday, K. (2017). Concurrency in Go: Tools and

Techniques for Developers. "O'Reilly Media, Inc.",

2017.

Donovan, Alan AA, and Kernighan B. W. (2015). The Go

programming language. Addison-Wesley Professional,

2015.

Gribaudo, M., Iacono, M., Kiran M. A. (2018).

Performance modeling framework for lambda

architecture based applications // Future Generation

Computer Systems. – 2018. – Vol. 86. – pp. 1032-1041.

Goiri, R., Bianchini, S., Nagarakatte and Nguyen, T. D.

(2015). Approxhadoop: Bringing approximations to

mapreduce frameworks. In Proceedings of the

Twentieth International Conference on Architectural

Support for Programming Languages and Operating

IoTBDS 2021 - 6th International Conference on Internet of Things, Big Data and Security

260

Systems, ASPLOS ’15, pages 383–397, New York, NY,

USA, 2015. ACM.

Kandula, S., Shanbhag, A., Vitorovic, A., Olma, M.,

Grandl, R., Chaudhuri, S. and Ding, B. (2016). Quickr:

Lazily approximating complex adhoc queries in bigdata

clusters. In Proceedings of the 2016 ACM SIGMOD

International Conference on Management of Data,

SIGMOD ’16, New York, NY, USA, 2016. ACM.

Kiran, M. et al. (2015). Lambda architecture for cost-

effective batch and speed big data processing // 2015

IEEE International Conference on Big Data (Big

Data). – IEEE, 2015. – pp. 2785-2792.

Kleppmann, M. (2017). Designing data-intensive

applications: The big ideas behind reliable, scalable,

and maintainable systems. "O'Reilly Media, Inc.",

2017.

Laptev, N., Zeng, K. and Zaniolo, C. (2012). Early accurate

results for advanced analytics on mapreduce. Proc.

VLDB Endow., 5(10):1028–1039, June 2012.

Liese, F., Miescke, K.J. (2008). Statistical Decision Theory

Estimation, Testing, and Selection. Springer Series in

Statistics, 2008.

Marz, N., and James W. (2015). Big Data: Principles and

best practices of scalable real-time data systems. New

York; Manning Publications Co., 2015.

O’Neil, P. et al. (1996). "The log-structured merge-tree

(LSM-tree)." Acta Informatica 33.4 (1996): 351-385.

Pansare, N., Borkar, V. R., Jermaine, C., and Condie, T.

(2011). Online aggregation for large mapreduce jobs.

Proc. VLDB Endow, 4(11):1135–1145, 2011.

Perrot, A. et al. (2017). HeatPipe: High Throughput, Low

Latency Big Data Heatmap with Spark Streaming //

2017 21st International Conference Information

Visualisation (IV). – IEEE, 2017. – pp. 66-71.

Psaltis, A. G. (2017). Streaming Data: Understanding the

Real-Time Pipeline. Manning Publications, 2017.

Spangenberg, N., Wilke M., Franczyk B., 2017. A Big Data

architecture for intra-surgical remaining time

predictions // Procedia computer science. – 2017. –

Vol. 113. – pp. 310-317.

Yang, F. et al. (2017). The RADStack: Open source lambda

architecture for interactive analytics // Proceedings of

the 50th Hawaii International Conference on System

Sciences. – 2017. - pp. 1703-1712.

Zhang, X., Wang, J., Yin, J. (2016). Sapprox: enabling

efficient and accurate approximations on sub-datasets

with distribution-aware online sampling // Proceedings

of the VLDB Endowment. – 2016. – V. 10. – №. 3. – pp.

109-120.

Zukerman, M. (2020). Introduction to Queueing Theory

and Stochastic Teletrac Models. [Online]. Available:

http://www.ee.cityu.edu.hk/~zukerman/classnotes.pdf.

[Accessed: Sept. 22, 2020]

Approximate Query Processing for Lambda Architecture

261