Similarity-inclusive Link Prediction with Quaternions
Zuhal Kurt
1a
, Ömer Nezih Gerek
2b
, Alper Bilge
3c
and Kemal Özkan
4d
1
Department of Computer Engineering, Atılım University, Ankara, Turkey
2
Department of Electrical & Electronics Engineering, Eskişehir Technical University, Eskişehir, Turkey
3
Department of Computer Engineering, Akdeniz University, Antalya, Turkey
4
Department of Computer Engineering, Eskişehir Osmangazi University, Eskişehir, Turkey
Keywords: Graphs, Link Prediction, Recommender System, Quaternions.
Abstract: This paper proposes a Quaternion-based link prediction method, a novel representation learning method for
recommendation purposes. The proposed algorithm depends on and computation with Quaternion algebra,
benefiting from the expressiveness and rich representation learning capability of the Hamilton products. The
proposed method depends on a link prediction approach and reveals the significant potential for performance
improvement in top-N recommendation tasks. The experimental results indicate the superior performance of
the approach using two quality measurements – hits rate, and coverage - on the Movielens and Hetrec datasets.
Additionally, extensive experiments are conducted on three subsets of the Amazon dataset to understand the
flexibility of this algorithm to incorporate different information sources and demonstrate the effectiveness of
Quaternion algebra in graph-based recommendation algorithms. The proposed algorithms obtain
comparatively higher performance, they are improved with similarity factors. The results show that the
proposed quaternion-based algorithm can effectively deal with the deficiencies in graph-based recommender
system, making it a preferable alternative among the other available methods.
1 INTRODUCTION
Recommender systems provide recommendations
about various products and services to their users by
applying other users’ data. Their success is important
for both users and e-commerce sites utilizing such
systems. Providing accurate and dependable
recommendations increases user satisfaction, in turn
boosting the sales of products and services.
Conversely, inaccurate, and unreliable product
recommendations force users towards searching
alternative sites for shopping. These systems are a
challenging research field with many unresolved
problems and many different hybrid recommendation
algorithms proposed to overcome these problems.
Graph-based hybrid models that use different
information sources (text, images, ratings, etc.) for
recommendation have been gaining more attention in
a
https://orcid.org/0000-0003-1740-6982
b
https://orcid.org/0000-0001-8183-1356
c
https://orcid.org/0000-0003-3467-9915
d
https://orcid.org/0000-0003-2252-2128
recent years, (Yuan, 2012, Zhang, 2017, and Kurt,
2020).
Also, another key observation is that most studies
in the recommendation algorithms have been mainly
based on real-valued representations R, neglecting the
rich potential of other spaces such as complex C and
hypercomplex spaces H, (Zhang, 2019). This study
investigates the concept of complex algebra and
quaternion algebra, that are effectively established in
the area of mathematics. Complex and hypercomplex
representation learning methods are not only
expanding the vector space also composing multiple
spaces together. However, these spaces have tight
links with associative retrieval, asymmetry, and
learning latent inter-dependencies between
components by multiplication of complex numbers or
Hamilton products. The associative nature of
complex representations going beyond multi-view
representations is effectively developed in these
studies (Danihelka, 2016, and Hayashi, 2017).
842
Kurt, Z., Gerek, Ö., Bilge, A. and Özkan, K.
Similarity-inclusive Link Prediction with Quaternions.
DOI: 10.5220/0010469808420854
In Proceedings of the 23rd International Conference on Enterprise Information Systems (ICEIS 2021) - Volume 1, pages 842-854
ISBN: 978-989-758-509-8
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Furthermore, the asymmetry of simple inner products
in hypercomplex space (Trouillon, 2016, and Tay,
2018) yields a strong inductive bias to solving the
asymmetrical problem of user-item matching. Since,
the user and item embeddings are mainly belonged to
a different class of entities.
Quaternion representations are based on
hypercomplex numbers with three imaginary
numbers. These representations are recently getting
more attention and showing promise in real-world
applications such as speech recognition (Trabelsi,
2017), image and signal processing (Witten, 2006,
and Parcollet 2019). This is the same case with multi-
view representations, however the latent components
are connected by a complex-number system.
Furthermore, the Hamilton product gives the
interactions between imaginary and real numbers,
enables an expressive blend of numbers that forms the
final representation. Accordingly, the interaction
function is also important to the recommendation
system research area, it is evident that the Hamilton
products are the proper option for user-item
representation learning.
In (Zhang, 2019), novel recommendation
algorithms in non-real spaces are proposed based on
leveraging rich and expressive complex number
multiplication or Hamilton products to compose user-
item pairs. These proposed algorithms are called
Complex collaborative filtering and Quaternion
collaborative filtering (QCF), and they open up a new
different way to apply collaborative filtering-based
neural recommendation algorithm in non-real spaces.
All in all, these approaches demonstrate the
effectiveness of Quaternion algebra in recommender
systems. The deep learning research area has seen
significant improvement in the last decade;
nevertheless, much of these works have been
implemented in real-valued numbers. Recent studies
show that a deep learning-based system utilizing
complex numbers can be deeper for a fixed parameter
budget regarding its real-valued counterpart. In
(Gaudet, 2018), the benefits of generalizing one step
further into the hyper-complex numbers, quaternions
especially, are examined and yielded the framework
of the deep quaternion networks. Moreover, the
theoretical basis by reviewing quaternion
convolutions, generating a new quaternion weight
initialization design, and developing some algorithms
for quaternion batch-normalization are introduced in
(Gaudet, 2018).
Quaternion-based multi-valued architecture is
introduced in some research fields, demonstrating
that it has the potential with numerical examples of
multi-channel prediction and classification
(Greenblatt, 2018, and Saoud, 2017). A variety of
real-valued learning frameworks have been presented
in prior literature, hence multi-valued architecture is
utilized in order to compensate for their drawbacks.
However, a better way to represent multidimensional
data is utilizing quaternions (Greenblatt, 2018). The
motivation behind this representation is that a four-
dimensional associative normed division algebra over
the real numbers enables the multiplication and
division of points in three-dimensional space
(Greenblatt, 2018).
Furthermore, an adaptive method for a tag-rating
based recommender system is introduced in (Yuan,
2012). A term-association matrix is represented to
describe the relationship between the tags’ and items’
properties in this approach. Quaternions are used for
the definition of the term-association matrix, and the
components of this matrix are users, items, tags, and
ratings, each a part of a quaternion number. A
privileged matrix factorization method for CF by
utilizing the quaternions is introduced in (Du, 2017).
This method is utilized by review texts that are in
companion with rating values to assist the learning of
user and item factors/representation. This
recommendation algorithm is also considered as a
rating prediction problem based on the quaternions.
Again, a user representation, an item representation,
a rating, and a review are denoted as parts of a
quaternion number in this algorithm (Du, 2017).
A novel graph-based recommendation algorithm
depending on social networks is proposed by (Wang,
2010). This social network is developed between
users and items, considering the information of
ratings and tags. The users’ co-tagging behaviours
and the similarity relationship among these users are
utilized by the graph to enhance the performance.
This algorithm is also based on the Random Walk
with Restarts method and yields a more natural and
efficient way to represent social networks. Utilizing
the similarity relationships and the tags make the
adjacency matrix denser and improve the
recommendation accuracy rate.
Rating conversion is implemented to generate an
adjacency matrix based on the representation of
complex numbers with real and imaginary parts in the
Similarity Inclusive Link Prediction (SIMLP) and
Complex Representation-based Link Prediction
(CORLP) algorithms (Xie, 2015, Kurt, 2019 and
2020). In these algorithms, similar or dissimilar links
were weighted by real numbers, whereas the like or
dislike links were weighted by complex numbers
(Xie, 2015, Kurt, 2019). The problem of
recommendation generation is considered as a link
prediction problem since the complex numbers yield
Similarity-inclusive Link Prediction with Quaternions
843

a natural algebraic link among real and imaginary
parts. Moreover, the available link prediction
algorithms may be applied with the proposed SIMLP
method and without any modifications.
In this paper, the proposed SIMLP algorithm is
reformulated based on the representation of
quaternion numbers with a scalar and imaginary
vector part in the quaternion form. The similar valued
links are denoted as a scalar part, and the dissimilar,
like, and dislike valued links are denoted as the
imaginary vector part of the quaternion. As a
quaternion number provides a link between real and
imaginary vector parts in the bipartite graph model,
the problem of recommendation generation can still
be considered as a link prediction problem. Besides
that, the available link prediction algorithms can
operate with the proposed quaternion-based
recommendation method as in the SIMLP method.
With this goal in perspective, this paper presents a
new quaternion-based graph framework for
recommendation generation. Initially, we give a
simple overview of the quaternions and a quaternion-
based triangle closing model, and then utilize this
model to generate a quaternion-based similarity-
inclusive link prediction method in a graph structure.
The remainder of the paper is organized as follows:
The detailed representation of the proposed
recommendation algorithms appears in Section 2. The
evaluation measurements that are used in this study
are given in Section 3. The application of the
experiments in three real-world datasets and the
discussion of the experimental results are included in
Section 4. Finally, the results and future research
directions are summarized.
1.1 Quaternions
The quaternions were first introduced by William
Rowan Hamilton, and they are members of a
noncommutative division algebra (Mishchenko,
2000). The formula of quaternion algebra can be
mathematically stated as:
222
1ijkijk====−
,
(1)
The quaternions are just one example of a more
general class of hyper-complex numbers proposed by
Hamilton, and the set of quaternions is represented as
,H Η
or Q
8
.
Quaternions can be considered as an extension of
complex numbers and operate in a four-dimensional
space. It comprises of a real number and three
imaginary numbers. By analogy with the complex
form, complex numbers can be represented as a sum
of real and imaginary parts,
aib+⋅
, hence a
quaternion number can also be denoted as a linear
combination of real and imaginary parts;
abicjdkΗ= + ⋅ + ⋅ + ⋅
(2)
The Hamilton product of two Quaternions can
be written as the products of the bases elements and
the distributive law. Assume that two quaternions are
given as
111 1 1
abicjdkΗ= +⋅+⋅+⋅
and
222 2 2
abicjdkΗ= +⋅+⋅+ ⋅
, then the Hamilton
product of them can be represented as follows:
1212121212
12 12 12 12 12 12 12 12
1 2 12 12 1 2
()
()()
()
aa bb cc dd
ab ba cd dc i ac bd ca db j
ad bc cb da k
Η⊗Η = − − − +
++− ⋅+ −++ ⋅
++−+ ⋅
It can be inferred that the multiplication of
quaternions is both distributive and associative, but it
is not commutative.
Moreover,
H
can be represented as:
(,)wv w x i y j z kΗ= = + ⋅ + ⋅ + ⋅
, when
w
is real
(scalar), and
v
is an imaginary (vector) part.
w
x
wscalarpart
vector part
yv
z




Η= =





(3)
1.2 Quaternion-based Triangle Closing
Model
In this paper, a quaternion-based triangle closing
model is proposed depending on the graph models,
which are introduced in (Harary, 1955 and 1967,
Kunegis, 2012). Moreover, the new design of the
model based on the social graph models is presented
by (Kunegis, 2012). The extended version of this
model is recommended based on the usage of other
number systems to identify each edge/link, such as
the quaternions or the complex number systems. The
only possible relationship in a social graph depends
on the friendship (Kunegis, 2012). Then, the social
recommendation problem can be considered as
recommending new friends depending on existing
friendships. The fundamental model utilized for this
purpose can be considered as the major law of the
triangle closing model: people who have (possibly
many) common friends can be all friends. Figure 1.
(a) illustrates this principle of triangle closing model.
Two adjacent friend links let us predict a new friend
link; hence, “
The friend of my friend is my friend” as
a rule is given in Figure 1 (a). Another triangle closing
principle in a social graph with friend and foe
ICEIS 2021 - 23rd International Conference on Enterprise Information Systems
844

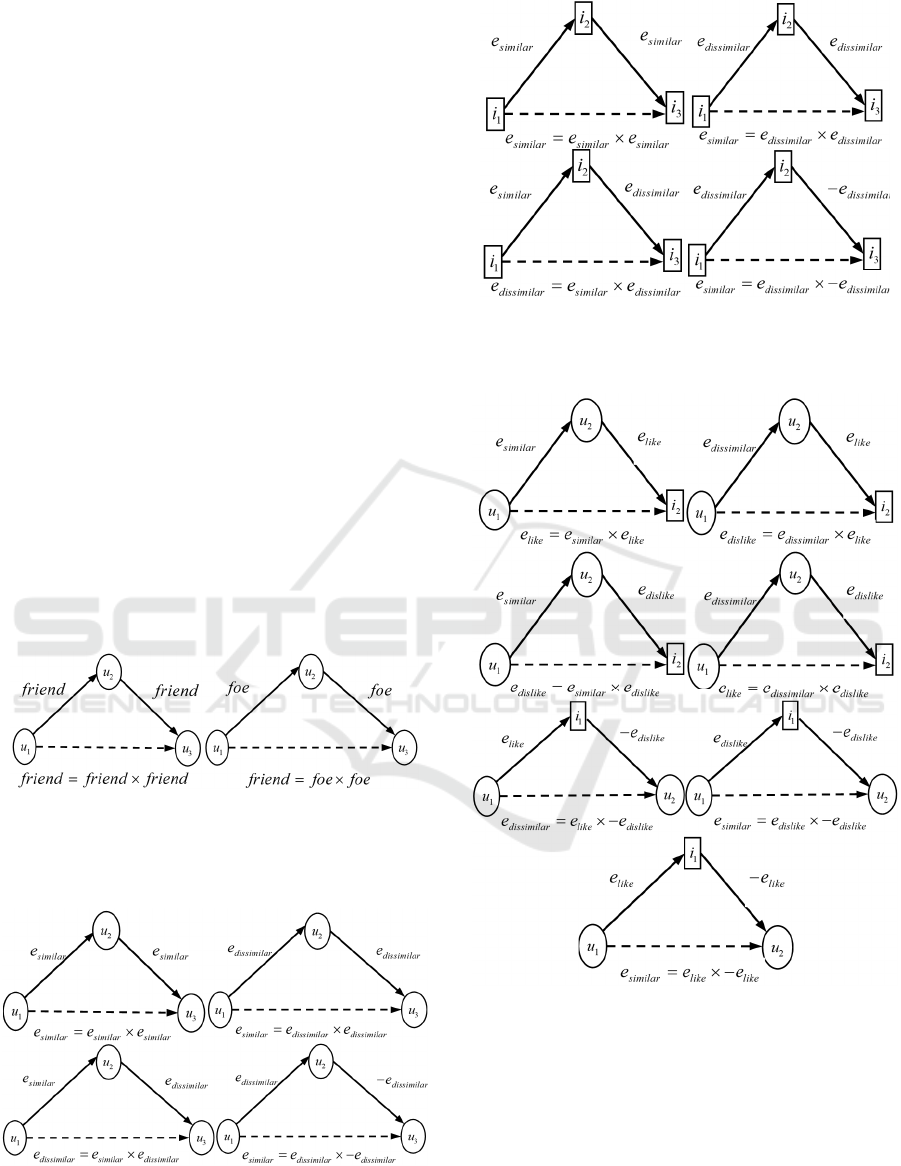
relationships is illustrated in Figure 1 (b). In such a
social graph, new links can be inferred using the
principle that can be stated as “The enemy of my
enemy is my friend”, (Kunegis, 2012). Moreover,
these two principles can be converted for the user-
item interaction graph by utilizing the user-user and
item-item similar and dissimilar relationships. Hence,
two adjacent similar links let us predict a new similar
link. Furthermore, two adjacent dissimilar links let us
predict a new similar link, illustrated in Figures 2 and
3.
The triangle closing model can be generated with
four different combinations. First of all, the vertices
of the triangle model may only be constructed with
users’ nodes, which means that the triangle model is
generated with three user nodes. This triangle model
has two types of relationships. For the user-user links,
there is a similarity factor,
similar
e
or
dissimilar
e
between
two individuals. This triangle model is illustrated in
Figure 2. Similarly, the vertices of the triangle model
may be generated with only item nodes, which means
that the triangle model is generated with three-item
nodes. In a similar manner, this triangle model has
two different relationships. There is a similarity factor
similar
e
or
dissimilar
e
in this triangle model for the item-
item links. This triangle model is illustrated in Figure
3.
(a) (b)
Figure 1: (a) Triangle closing model with only the friend
relationship, (b) triangle closing model with friend and foe
relationship.
Figure 2: The triangle closing principle illustrated as the
multiplication rule between similar/dissimilar relationships
for only three user nodes.
Figure 3: The triangle closing principle illustrated as the
multiplication rule between similar/dissimilar relationships
for only three item nodes.
Figure 4: The triangle closing principle illustrated as the
multiplication rule between similar/dissimilar and
like/dislike relationships for two users’ and an item’ nodes.
Secondly, the vertices of the triangle model may
be generated with two users nodes and an item node.
For the user-item links, there is a similarity factor,
like
e
or
dislike
e
, between a user and item nodes. As a
result of the necessity of recognizing the asymmetry
between the item and the user, the triangle model
includes item-user links. Then, there is a similarity
Similarity-inclusive Link Prediction with Quaternions
845

factor,
like
e−
or
dislike
e−
, between the item and user
nodes. Subsequently, in the case of a link from user
u
to item
i
with the weight
like
e
or
dislike
e
, there is
always a reverse link from item
i
to user
u
with a
weight of
like
e−
or
dislike
e−
. Moreover, there is a
similarity factor,
similar
e
or
dissimilar
e
, between two
user nodes for the user-user links. This triangle model
is illustrated in Figure 4.
Lastly, the vertices of the triangle model may be
generated with a user node and two item nodes.
Similarly, there is a similarity factor,
like
e
or
dislike
e
,
for the user-item links and
like
e−
or
dislike
e−
for the
item-user links between user nodes and item nodes.
Furthermore, there is a similarity factor,
similar
e
or
dissimilar
e
, between two item nodes for the item-item
links. This triangle model is illustrated in Figure 5
.
Figure 5: The triangle closing principle illustrated as the
multiplication rule between similar/dissimilar and
like/dislike relationships for two items and a user node.
In the quaternion-based triangle model,
,
like dislike
ee
and
,
similar dissimilar
ee
are normalized values just for the
weights. This rule has four parts based on the triangle
model comprising: three user nodes and their
relations (see Figure 2), three-item nodes and their
relations (see Figure 3), two users and an item node
and their relations (see Figure 4), and finally a user
node and two item nodes and their relations (see
Figure 5). These are the major ideas of collaborative
filtering from a different aspect, (Xie, 2015, Kurt,
2019). Since these multiplication principles of this
model can be mathematically represented as follows:
22 2
,
similar like di dissimilslike ar
eeee−==−=−
,
similar dlike like d eissim iila l kris
eeee e=⋅= ⋅
,
dislike li sdi mssi lmilar dislke i i ar ike
eeeee=⋅=⋅
dislike dislikedissimilar like like
eeeee=⋅− =−⋅
(4)
Therefore, to solve this system of equations (Eq.
4), four different and nonzero constants need to be
evaluated:
,
similar dissimilar
ee
, and
,
like
e
dislike
e
.
Quaternion numbers provide an easy way to solve
this system of equations when we set
,,
like dislike dissimilar
eie je k== =
and
1
similar
e =
, where
i, j, k
are the imaginary unit vector. The
requirements can be formalized as follows:
222
1ijkijk====−
and
2
11.=
(5)
From this symbolization, a link has endpoints of
the same type, and two items or two users may be
weighted with a real number if there is a similarity
factor
similar
e
. It means that the more similar the
endpoints have the higher such value. A link has
endpoints of the same type, among two users or two
items, might be weighted with an imaginary weight
k
if there is a dissimilarity factor
dissimilar
e
. It means
that the more dissimilar the endpoints are, the
higher their value is. Besides that, a link with an
imaginary weight can be a user-item or item-user
link depending on the sign and interest. Such as, if a
user
u
dislikes an item
i
, then the link is weighted
with
j
from
u
to
i
, and the reversed link is
weighted with
j−
from
i
to
u
. Equivalently, if
the user
u
likes the item
i
, then the link is
weighted with
i
from
u
to
i
, and the reversed link
is weighted with
i−
from
i
to
u
. As opposed to
similar links, we may categorize
,
like dislike
ee
and
like
e−
,
dislike
e−
only when the sign of the link’s
weight and the direction of the link are known at the
same time. Since the sign of a similar link’s weight
is independent from the direction of the link, it can
ICEIS 2021 - 23rd International Conference on Enterprise Information Systems
846

be concluded that the similar links provide the
following rule:
,
.
similar similar
dissimilar dissimilar
ee
ee
=−
=−
(6)
1.3 Quaternion-based Adjacency
Matrix
The adjacency matrix
A
is expanded as a quaternion
matrix, and it can be mathematically formulated as:
similar like dislike dissimilar
ij k=+⋅+⋅+ ⋅AA A A A
,
(7)
where the combination of item-item similarity
I
I
A
and user-user similarity matrices
UU
A
is denoted as
s
imilar
A
, the combination item-item dissimilarity
1
nn II×
− A
and user-user dissimilarity matrices
1
mm UU×
− A
are denoted as
dissimilar
A
, and the user-
item preference matrix is denoted as
UI
A
using both
like
A
,
dislike
A
relationships. Moreover, the conjugate
transpose of
UI
A
can be described in the same way as
in (Kurt, 2019),
T
I
UUI
=−AA
. The preference
matrices
like
A
dislike
A
and the dissimilarity matrix
dissimilar
A
are complex matrices, while the similarity
matrix
s
imilar
A
is a real matrix.
The proposed Q-SIMLP algorithm differs slightly
from the SIMLP-based recommendation method in
the modeling of the adjacency matrix, and while
calculating the powers of the adjacency matrix and
providing the final recommendation in the same way.
The user-user and item-item similarity and
dissimilarity matrices of the user-item preference
matrix are computed by utilizing cosine similarity
measurement. After that, these similarity and
dissimilarity factors are passed through from a
threshold at 0.5. Then, the dissimilar links are
multiplied by
k
, and these links are indicated as
k
in the imaginary part of the quaternions as stated in
Eq. (7). Moreover, a user-item-like relational matrix
is generated based on whether the rating is greater
than 3, as stated in Eq. (7), while the user-item-dislike
relational matrix is generated based on whether the
rating is less than 3, as stated in Eq. (7). Following the
summation of these matrices, the main adjacency
matrix can be represented as in Eq. (7).
The components of quaternion-based adjacency
matrix are mathematically stated as:
11 1 11 1
11
11 1 11 1
1 1
11
.
00 00
00 00
,
00 00
00 0
0
0
00
..
0
nn
mmn m mm
nn
mmn nn
il ke similar
dislik
n
e
rr u u
rr uu
rr tt
rr tt
rr




==

−−




−−

=
 
      
 
 
 
  



AA
A
1
1
11 1
1
11 1
1
11 1
1
1
.
,
00
00
1100
1100
001
01
1
.
0
n
mmn
n
mmn
n
mmn
dissimi
n
n
lar
nn
rr
rr
rr
uu
uu
tt
tt





−−




−−

−−




−−
=

−−




−−










   

A (8)
(8)
where
ij
u
denotes the similarity relationship
between the
th
i
and
th
j
users,
ij
t
denotes the
similarity relationship among the
th
i
and
th
j
items,
ij
r
expresses the like or dislike relationship among
the
th
i
user and
th
j
item, and
ij
r−
expresses the
conjugate transpose of the like or dislike relationship
between the
th
i
user and
th
j
item in Eq. (8). When
ij
r
expresses the like relationship between the
th
i
user and
th
j
item,
ij
r
is multiplied by i, which is an
imaginary part of quaternions. Equivalently, if
ij
r
represents the dislike relationship between the
th
i
user and
th
j
item,
ij
r
is multiplied by
j
, again an
imaginary part of quaternions. Moreover,
ij
1u−
expresses the dissimilarity relationship between the
th
i
user and
th
j
users, and
ij
1t−
expresses the
dissimilarity relationship between the
th
i
item and
th
j
item as in Eq. (8). Equivalently,
ij
1u−
and
ij
1t−
are multiplied by
k
as an imaginary part of
quaternions.
Similarity-inclusive Link Prediction with Quaternions
847

After the summation of these matrices, the main
adjacency matrix
A
is built as in Eq. (9).
....
11 1n 11 1n
m1 mm m1 mn
11 1n 11 1n
n1 nn m1 mn
11 1n
m1
uu0000rr
uu0000rr
i
00t t r r00
00t t r r00
00r r
00r
 
 
 
 
 
=+ ⋅+
 
−−
 
 
 
 
 
−−
 
  
  
  
 
      
 

   

A
...
11 1n
mn m1 mn
11 1n 11 1n
m1 mn n1 nn
1u 1u0 0
r1u1u00
jk
r r0 0 0 0 1t 1t
r r0 0 0 0 1t 1t
−−
 
 
 
 
 
−−
⋅+ ⋅
 
−− − −
 
 
 
 
 
−− − −
 



  
    
  
(9)
Furthermore, this adjacency matrix is square, and
eigenvalue decomposition can be applied to this
matrix in Eq. (9). In the proposed quaternion-based
method with another approach, the link prediction
function can be multiplied by a parameter
α
; then,
the predictions applied to
A
can be represented as:
() () () ()
357
123
· · · · . . .P α =λ α +λ α +λ α +λ α +AA A A A
(10)
2 QUATERNION-BASED
SIMILARITY-INCLUSIVE LINK
PREDICTION METHOD
Rating conversion is necessary to generate the
quaternion-based adjacency matrix in the proposed Q-
SIMLP method, where the ratings/values in the user-
item rating matrix are changed by imaginary numbers
i
or
j
based on whether the rating is greater than or
equal to 3. In this sense, if the rating is less than 3, it is
replaced with
j
, which means that the user expresses
‘dislike’ for the item; equivalently, imaginary value
i
is given to defining ‘like’, while the rating is greater
than or equal to 3. Moreover, when the user-item pair
(,)ui
is not appeared in the training set, the
corresponding component of the adjacency matrix is
equal to zero. Following that, the user-user similarity
and item-item similarity matrices of the preference
matrix are generated by utilizing a cosine similarity
measure to calculate the similarity values. On the other
hand, we find the user-user dissimilarity and item-item
dissimilarity matrices by utilizing the user-user
similarity and item-item similarity matrices of the
preference matrix, respectively, as stated in Eq. 6.8.
Then, the components of the similarity and the
dissimilarity matrices of the preference matrix are
passed through a threshold at 0.5. These matrices
include only binary values, with the similarity matrices
represented as a scalar part of the quaternion-based
adjacency matrix, as formulated in Eq. 8. The user-user
dissimilarity and item-item dissimilarity matrices are
multiplied by
k
, and these matrices are taken as one of
the imaginary parts of the adjacency matrix. After
generating the summation of the like relationships and
dislike relationships matrices and the dissimilarity
matrices, the entire imaginary part of the quaternion-
based adjacency matrix is developed.
The evaluation of the powers of the quaternion-
based adjacency matrix and providing the final
recommendation follow the same procedure as the
SIMLP algorithm for the proposed Q-SIMLP
algorithm. The hyperbolic sine function is considered
as a link prediction function for the proposed Q-SIMLP
algorithm. Hence, the closest values among the nodes
are evaluated by the power sum of the adjacency
matrix, and the summation of each entry of the top-
right and top-left components represents the degree of
whichever item is relevant to a specific user. Following
the summation of the odd powers of the adjacency
matrix, the prediction scores that denote item
recommendation to a particular user are obtained.
These scores are denoted as the summation of a
scalar/real part and the imaginary part
i
of the entire
score. Since only the like relationships are taken into
consideration for recommendation generation, the
prediction scores are sorted in a descending order since
the user will like the item if the score is positive, or will
dislike the item when the score is negative. When the
scores are positive and higher in value, such items will
be recommended to a selected user as new and never-
seen-before alternatives. Furthermore, top-N
recommendation lists are produced for every user by
these ranked prediction scores (Bedi, 2017).
2.1 Quaternion-based Hybrid
Recommender System
The proposed quaternion-based hybrid recommendat-
ion algorithm differs slightly from the Q-SIMLP
method in the modeling of the adjacency matrix. For
the present system, the user-item ratings and visual
images of the entire items in the datasets are known.
Hence, the method benefits from such visualization by
means of the AlexNet features, as mentioned in
(amazon website). On the other hand, each users’
visual feature vector is generated in accordance to their
preferences. In the beginning, all items noticed, rated,
ICEIS 2021 - 23rd International Conference on Enterprise Information Systems
848

or purchased by a user identified. Then, the AlexNet
feature vectors of these items are extracted and
summed up. Lastly, the summation mean is calculated
using the number of items that users’ either noticed,
rated, or purchased before. Since each user can be
represented as a 4096-dimensional visual feature
vector, a user visual-feature matrix can be generated
for each dataset. Following the generation of the user
visual-feature and item visual-feature matrices, we can
find the user-user and item-item similarity matrices by
utilizing these feature matrices.
The quaternion-based adjacency matrix generation
for the hybrid recommendation algorithm is modified
in the same manner as the proposed Q-SIMLP
algorithm. Also, the rating conversion part of the
adjacency matrix follows the same procedures to
generate the adjacency matrix. Following that, the
user-user similarity matrix is generated from the user
visual-feature matrix by applying cosine similarity
measures to evaluate similarity values. Besides that,
the item-item similarity matrix is generated from the
item visual-feature matrix by applying the cosine
similarity measures to compute the similarity values.
In other aspects, the user-user and item-item
dissimilarity matrices are generated by applying the
user-user similarity and item-item similarity matrices,
respectively. Then, the components of the similarity
and dissimilarity matrices of the system are passed
through a threshold at 0.5 since these matrices only
consist of binary values. Similar to Q-SIMLP
algorithm, we take the similarity matrices as a scalar
part of the adjacency matrix, as formulated in Eq.
(11). Also, the user-user and item-item dissimilarity
matrices are multiplied by
k
and taken as one of the
imaginary parts of the adjacency matrix. Following
the summation of these matrices, the main adjacency
matrix can be formed as in Eq. (11).
visual - similar like dislike visual -dissimilar
=+×i+×j+ ×kAA A A A
(11)
This quaternion-based adjacency matrix is a
square matrix. Therefore, the same link prediction
(hyperbolic) function can be used on this adjacency
matrix in Eq. (11) to evaluate the power sum of this
matrix. In this way, the recommendation
methodology adopted here is the same as in the Q-
SIMLP recommendation algorithm.
An example of a user-item signed graph generation
process for a quaternion-based hybrid recommender
system is illustrated in Figure 6 and Figure 7. The
user-item rating matrix and bipartite signed graph
model of this rating matrix are drawn in Figure 6 (a).
The green links represent ‘like’ edges denoted as
i
,
and the red links represent ‘dislike’ edges denoted as
j
in the bipartite signed graph as in Figure 6 (a). The
user-feature matrix and user-user relationship graph
are drawn in Figure 6 (b). The green links represent
user-user ‘similar’ relationships, while the red links
represent user-user ‘dissimilar’ relationships in
Figure 6 (b). The item-feature matrix and item-item
relationship graphs are drawn in Figure 6 (c). Finally,
the generated user-item signed graph for the
quaternion-based hybrid recommender system is
drawn in Figure 7.
(a)
(b)
(c)
Figure 6: (a) User-item rating matrix and bipartite signed
graph, (b) user-feature matrix and user-user relationship
graph, (c) item-feature matrix and item - item relationship
graph.
Figure 7: The generated user-item signed graph.
3 EXPERIMENTAL
EVALUATION
The proposed Q-SIMLP algorithm, along with other
methods, is applied on two real-world datasets for
Similarity-inclusive Link Prediction with Quaternions
849

comparison: MovieLens (grouplens, website) and
MovieLens Hetrec, (hetrec2011, website). First of all,
rating conversion is applied to the user-item rating
matrix in these datasets, they are converted into two
imaginary parts,
i
and
j
, of the quaternions. Then,
the cosine similarity measure is applied to the user-
item rating matrices of these datasets to find the
similarity values. Finally, the user-user and item-item
similarity matrices of user-item rating matrices for
these datasets are obtained after the cosine similarity
values are passed through a threshold at 0.5 and 0.7
for Movielens and Hetrec datasets, respectively.
Likewise, the user-user and item-item dissimilarity
matrices of the user-item rating matrices for these
datasets are obtained after the dissimilarity values are
passed through a threshold at 0.5 and 0.3 for
Movielens and Hetrec datasets, respectively. Also,
the threshold of dissimilarity values is represented for
these datasets. The threshold of similarity values for
the Hetrec dataset is indicated as 0.7, since this
dataset is sparser than the Movielens dataset.
Following the combination of all these matrices, the
major quaternion-based adjacency matrices are built
as a square matrix for these two datasets as in Eq. (8).
Hence, we can apply the hyperbolic sine function on
the adjacency matrix as a link prediction function, as
in (Xie, 2015, Kurt, 2019). Moreover, we multiply the
link prediction function with a parameter
α
, since
the predictions applied to
A
can be represented as:
() ( ) ( )sinh sinh⋅=⋅=⋅⋅
T
AAUΛ U ααα
(12)
When the adjacency matrix is a square
n
by
n
matrix, the sum of the
n
eigenvalues of
A
is the
same as/equivalent to the trace of
A
;
1
()trace
=
λ=

A
n
i
i
(13)
The theory and proof of Eq. (13) are given in the
Appendix as theorem 2 in (Kurt, 2019, phd thesis).
Furthermore, we assumed that the trace of the
adjacency matrix is equal to the length of the
adjacency matrix since all the components of
adjacency matrix values (similar, dissimilar, like, and
dislike values) are evaluated as binary values before
the rating conversion as quaternion numbers. Then,
the scaling parameter
α
is chosen as
1/ ( )length=A α
,
(14)
since the largest eigenvalue cannot be bigger than the
trace of the adjacency matrix. Hence, to normalize the
eigenvalues of
A
, we set
α
as in Eq. (14). Moreover,
to evaluate the results of CORLP and SIMLP
approaches,
α
is set as same as in the Q-SIMLP
method.
(a)
(b)
Figure 8: Comparison of the Q-SIMLP, CORLP, and
SIMLP methods by coverage and hits rate for the top-N
recommendation on MovieLens (a) and Hetrec (b) datasets.
The testing methodology adopted in the proposed
rating-based recommendation algorithm is the same
as in these two former studies (Xie, 2015, Kurt,
2019). The ratings are divided by two subsets, for
training and testing, for each dataset as in (Kurt,
2019). Also, the rating conversion threshold value is
set as 2.5 for the Hetrec dataset, hence this dataset
includes decimal rating numbers. The performance of
ICEIS 2021 - 23rd International Conference on Enterprise Information Systems
850

the proposed Q-SIMLP recommendation method is
measured by using the metrics, hits rate, and
coverage. Figure 8 illustrates the comparison of the
proposed Q-SIMLP, SIMLP, and CORLP
recommendation algorithm with path length 3 for the
top-N recommendation on the Movielens (a) and
Hetrec (b) dataset. Figure 8 shows that the hits rate of
the Q-SIMLP method is higher than the SIMLP and
CORLP method. However, the coverage of the Q-
SIMLP method is relatively less than the SIMLP
method, and still more than the CORLP method on
these two datasets. It can be seen in Figure 8 that the
Q-SIMLP method can give better results for the top-
10 recommendation task when compared to the
results of the SIMLP and CORLP for the top-100
recommendation task. Also, the hits rate of the Q-
SIMLP method for the top-100 recommendation task
is higher than the hits rates of the SIMLP and CORLP
methods for the same purpose. Hence the quaternion-
based recommendation algorithm can reach more
accurate results in a faster and easier way compared
to the other approaches. It is concluded that the Q-
SIMLP method provides accurate recommendations
by consuming less time.
Another question to be addressed is whether the
proposed Q-SIMLP approach that utilizes cosine
similarities performs better than CORLP and SIMLP
approaches for the top-N recommendation tasks. The
hits rate and coverage are utilized as the evaluation
metrics to measure the performance of the proposed
Q-SIMLP recommendation algorithm. One-way
Anova test is applied to further evaluate performance
differences between Q-SIMLP and SIMLP and
CORLP approaches, respectively. Thus, these special
hypotheses examined in this paper are:
• H1: The Q-SIMLP-based recommendation
approach obtains a higher hits rate than the
SIMLP and CORLP approaches do.
• H2: The Q-SIMLP-based recommendation
approach obtains higher coverage than the
SIMLP and CORLP approaches do.
Table 1: The p-values of the comparison of the Q-SIMLP
between CORLP and SIMLP methods regarding hits rate
on MovieLens and Hetrec datasets.
Methods
Dataset
CORLP SIMLP
Movielens 0.0005 0.0479
Hetrec 0.0137 0.0538
Table 1 has only one p-value that reflects no
significant differences between the Q-SIMLP and
SIMLP methods concerning hits rate on the Hetrec
dataset. Since this p-value is very close to 0.05
Table 2: The p-values of the comparison of the Q-SIMLP
between CORLP and SIMLP methods regarding coverage
on MovieLens and Hetrec datasets.
Methods
Dataset
CORLP SIMLP
Movielens 0.0087 0.00006
Hetrec 0.0249 5×10
-11
(0.0538≅ 0.05), it can be concluded that there are
statistically significant differences between CORLP,
SIMLP, and Q-SIMLP methods concerning hits rate
for the experiments on Movielens and Hetrec
datasets. Table 2 indicates that there are statistically
significant differences among CORLP, SIMLP, and
Q-SIMLP methods concerning coverage for the
experiments on Movielens and Hetrec datasets, hence
all the p-values are smaller than 0.05. The hypotheses
H1 and H2 are supported for each evaluation metric
utilized in this paper.
The proposed quaternion-based hybrid
recommendation algorithm is implemented on three
real-world Amazon datasets (amazon website): Cell
phone, Beauty, and Clothing. These datasets are
introduced in (Zhang, 2017). As the same process in
the Q-SIMLP algorithm, quaternion-based rating
conversion is applied to the user-item rating matrices
in these datasets. Then, the cosine similarity measure
is applied to user visual-feature and item visual-
feature matrices of these datasets. Thus, the user-user
and item-item similarity matrices of user-item rating
matrices for these datasets are obtained after the
cosine similarity values are passed through a
threshold at 0.6, 0.7, and 0.6 for Cell phone, Beauty,
and Clothing datasets, respectively. Similarly, the
user-user and item-item dissimilarity matrices of
user-item rating matrices for these datasets are
reached after the dissimilarity values are passed
through a threshold at 0.4, 0.3, and 0.4 for Cell phone,
Beauty, and Clothing datasets, respectively. At the
same time, the threshold of dissimilarity values
depends on these values as observed in these datasets.
Accordingly, the one for the Beauty dataset is the
highest since this dataset is sparser than the others.
Following the combination of all these matrices,
the main quaternion-based adjacency matrices are
generated as a square matrix for these three datasets
as in Eq. (11) since the hyperbolic sine function can
be applied to the adjacency matrix as a link prediction
function, as in (Kurt, 2019). Next, we multiply the
hyperbolic sine function by a scaling parameter α, as
introduced in the Q-SIMLP algorithm.
The testing methodology adopted in the
quaternion-based hybrid recommendation algorithm
slightly alternates from the other hybrid-SIMLP
recommendation method that is introduced in (Kurt,
Similarity-inclusive Link Prediction with Quaternions
851

2020). Three product categories of different sizes and
density levels are adopted, along with the standard
10-core datasets generated from each 5-core dataset,
for the experiments. The density level of a dataset is
calculated as in (Zhang, 2017);
#
,1
#
y
zero elements
s
parsity density sparsit
total elements
==−
(15)
in which
# zero el ements is denoted as the number of
zero values in the user-item rating matrix of a dataset,
and the total number of elements in this matrix is
denoted as
#total e lements
.
Table 3: Statistics of the 10-core datasets.
D
atasets #Users #Items #Interactions Density
Clothing 5197 4248 37515 0.3%
Cell Phones 3214 2743 34083 0.39%
B
eauty 5123 4774 74497 0.17%
Table 4: The performance comparison of Q-Hybrid and
Hybrid-SIMLP methods for the top-10 recommendation.
Datasets Measures
Methods
Recall
(%)
Hit Ratio
(%)
Precision
(%)
Beauty Hybrid-SIMLP 29,21 61,73 2,92
Q-Hybrid
32,15 75,80 3,22
Clothing Hybrid-SIMLP 22,25 42,30 2,23
Q-Hybrid
36,84 65,18 3,68
Beauty Hybrid-SIMLP 29,75 57,59 2,98
Q-Hybrid
30,78 66,58 3,08
Firstly, the user-item rating matrix of the 5-core
data is filtered out for each user that has at least 10
ratings to generate a temporary 10-core dataset.
Secondly, the temporary 10-core dataset is further
filtered out for each item that has at least 5 ratings. The
remaining items in the temporary 10-core data, which
do not have 5 ratings, are omitted from the temporary
dataset set for the generation of the final 10-core
dataset. Since, the 10-core data is a subset of the 5-core
data (Zhang, 2017), in which all users have at least 10
ratings and the items have at least 5 ratings. The
statistics of the 10-core datasets are shown in Table 3.
The ratings are divided by two subsets as in the
former experimental methodology. The test set
includes only 5-star ratings and only items that are
relevant to the corresponding users. The detailed
procedure applied to produce the test and the training
sets is the same as mentioned in (Zhang, 2017). Also,
the performance of the quaternion-based hybrid
recommendation algorithm is measured by using
the metrics, hit-ratio, precision, and recall in the
same way as in (Zhang, 2017). The results of the
proposed quaternion-based hybrid recommendation
(Q-Hybrid) method utilizing with top-10
recommendation tasks are demonstrated in Table 4.
The results demonstrate that the Q-Hybrid
recommendation algorithm obtains a higher hit-ratio,
precision, and recall than other Hybrid-SIMLP
recommendation algorithms on the Beauty, Cell
Phone and, Clothing datasets. It is concluded that
quaternion-based representations yield improvements
for the performance of hybrid recommendation
algorithms.
Moreover, the comparison results of the proposed
Q-Hybrid approach with the Hybrid-SIMLP are
discussed in terms of significance. In detail, whether
the proposed Q-Hybrid approach performs better than
the Hybrid-SIMLP approach for the top-N
recommendation task. The range of N is taken from
10 to 100 for experiments on Cell Phone, Clothing,
and Beauty datasets. The hit-ratio, recall, and
precision are used as the evaluation metrics to
measure the performance of the proposed Q-Hybrid
and Hybrid-SIMLP recommendation algorithms.
After that, the two-factor Anova test is employed to
evaluate the performance differences between the two
methods (Huang, 2002). Thus, the specific
hypotheses analyzed in this paper are:
• H1: The Q-Hybrid recommendation approach
obtains a higher hit-ratio than the Hybrid-
SIMLP recommendation approach does.
• H2: The Q-Hybrid recommendation approach
obtains higher recall than the Hybrid-SIMLP
recommendation approach does.
• H3: The Q-Hybrid recommendation approach
obtains higher precision than the Hybrid-
SIMLP recommendation approach does.
Table 5: The p-values of the comparison among Q-SIMLP
and Hybrid-SIMLP methods regarding to hit-ratio, recall,
and precision on Cellphone, Beauty, and Clothing datasets.
Measures
Datasets
Hit-Ratio Recall Precision
Cellphone 0.0002 0.5543 0.8507
Beauty 0.00001 0.0160 0.9126
Clothing 0.0008 0.0011 0.0588
Table 5 indicates that there are statistically
significant differences between Q-Hybrid and
Hybrid-SIMLP methods concerning hit-ratio for the
experiments on Cell Phone, Beauty, and Clothing
datasets. H1 is supported by the experimental results
on each dataset defined in this paper. It can be seen in
Table 5 that there are statistically significant
differences between Q-Hybrid and Hybrid-SIMLP
methods concerning recall for the experiments on
ICEIS 2021 - 23rd International Conference on Enterprise Information Systems
852

Beauty and Clothing datasets, not for the tests on the
Cell Phone dataset. Moreover, H2 is supported only
for the experiments on Beauty and Clothing datasets.
Besides that, it can be concluded that there are no
statistically significant differences between Q-Hybrid
and Hybrid-SIMLP methods concerning precision for
the experiments on each dataset. Finally, H3 is not
supported by the experimental results on each dataset.
(a)
(b)
Figure 9: Cell Phone: (a) recall(N) and (b) precision-versus-
recall on all items.
(a)
(b)
Figure 10: Beauty: (a) recall(N) and (b) precision-versus-
recall on all items.
The recall(N) and precision(N) results of the
proposed Q-Hybrid recommendation algorithm on
Cell Phone, Beauty, and Clothing datasets are
obtained and drawn respectively in Figure 9 (a),
Figure 10 (a) and Figure 11 (a). Furthermore, the
precision-versus-recall comparison of the results for
each dataset are drawn in Figure 9 (b), Figure 10 (b),
and Figure 11 (b). It can be seen from these figures
that the precision and recall results of the Q-Hybrid
method improve, compared to those of the Hybrid-
SIMLP method, with increasing N for the top-N
recommendation task.
Quaternion toolbox in Matlab (toolbox website),
also known as ‘qtfm_2.6’, is used for the experiments
to generate the quaternion-based adjacency matrix
and to evaluate the hyperbolic sine of this matrix.
(a)
(b)
Figure 11: Clothing: (a) recall(N) and (b) precision-versus-
recall on all items.
4 CONCLUSIONS
Quaternion-based recommendation algorithms are
promising methods to overcome the sparsity problem
of recommender systems. The proposed method, Q-
SIMLP, relies on such a link prediction approach with
the weights in the graph represented by quaternion
numbers that precisely separates the “like” and
“dislike” between a user and an item node, and
distinguish “similarity” and “dissimilarity” between
two users (or two items) nodes. The experimental
results show that the Q-SIMLP method performs
better than the remaining complex number-based
algorithms, such as SIMLP and CORLP, regarding
coverage and hits rate on the MovieLens and
MovieLens Hetrec datasets. The obtained
improvements of Q-SIMLP are attributed to the
inclusion of similarity and dissimilarity factors
between users and items, as well as like and dislike
relationships between users and items. The Anova
results indicate that the proposed Q-SIMLP algorithm
Similarity-inclusive Link Prediction with Quaternions
853

is significantly better than CORLP and SIMLP
methods in graph-based recommendation algorithms.
In addition, the Q-Hybrid recommendation
method performs better than the proposed Hybrid-
SIMLP algorithm in (Kurt, 2020), regarding hit-ratio,
recall, and precision on the real-world Amazon sub-
datasets. The improvements of our proposed method
are attributed to the inclusion of similarity and
dissimilarity factors between users’ feature and
items’ feature vectors. The experimental results show
that our approach demonstrates superior performance
on real-world datasets compared to other algorithms.
Furthermore, the proposed algorithm is adaptable by
incorporating different information sources. In
conclusion, Q-Hybrid can effectively deal with the
deficiencies in other hybrid algorithms thanks to its
improved design.
REFERENCES
Bedi, P., Gautam, A., Bansal, S., Bhatia, D. 2017. Weighted
Bipartite Graph Model for Recommender System Using
Entropy Based Similarity Measure. In ISTA’17, 2
nd
International Symposium on Intelligent Systems
Technologies and Applications, Springer, Cham, pp.
163-173.
Danihelka, I., Wayne, G., Uria, B., Kalchbrenner, N., Graves,
A., 2016. Associative long short-term memory. arXiv
preprint, arXiv:1602.03032.
Du, Y., Xu, C., Tao, D., 2017. Privileged matrix factorization
for collaborative filtering. In IJCAI’17, 26
th
International
Joint Conference on Artificial Intelligence, pp. 1610-
1616.
Gaudet, C. J., Maida, A. S., 2018. Deep quaternion networks.
In IJCNN’18, International Joint Conference on Neural
Networks, pp. 1-8, IEEE.
Greenblatt, A. B., Agaian, S. S., 2018. Introducing
quaternion multi-valued neural networks with numerical
examples. Information Sciences, 423, 326-342.
Harary, F., 1955. On the notion of balance of a signed graph,
Michigan Mathematical Journal, 2, 143–146.
Harary, F., Palmer, E.M., 1967. On the number of balanced
signed graphs. Bulletin of Mathematical Biophysics,
29(4), 759-765.
Hayashi K., Shimbo M., 2017. On the equivalence of
holographic and complex embeddings for link
prediction. arXiv preprint, arXiv:1702.05563.
Huang, Z., Chung, W., Ong, T. H., Chen, H., 2002. A graph-
based recommender system for digital library. In
JCDL’02, 2nd ACM/IEEE-CS joint Conference on
Digital libraries, ACM., Oregon, USA, pp. 65-73.
Kunegis, J., Gröner, G., Gottron, T. 2012. Online dating
recommender systems: The split-complex number
approach. In RSWeb’12, 4
th
ACM Recsys Workshop on
Recommender Systems and the Social Web, ACM., pp.
37-44.
Kurt, Z., Ozkan, K., Bilge, A., Gerek, O. N. 2019. A
similarity-inclusive link prediction based recommender
system approach. Elektronika IR Elektrotechnika, 25(6),
62-69.
Kurt, Z., 2019. Graph-Based Hybrid Recommender Systems.
(PhD thesis), Anadolu University, Eskişehir, Turkey.
Kurt Z, Gerek O.N., Bilge A., Özkan K., 2020. A Multi
Source Graph-Based Hybrid Recommendation
Algorithm, will be published in the Springer Series:
Lecture Notes on Data Engineering and Communicat-
ions Technologies (Trends in Data Engineering Methods
for Intelligent Systems), Springer, Berlin, Heidelberg.
Mishchenko, A., Solovyov, Y., 2000. Quaternions. Quantum
11, 4-7 and 18.
Parcollet, T., Morchid, M., & Linarès, G., 2019. Quaternion
convolutional neural networks for heterogeneous image
processing. In ICASSP’19, International Conference on
Acoustics, Speech and Signal Processing, pp. 8514-8518,
IEEE.
Saoud, L. S., Ghorbani, R., Rahmoune, F., 2017. Cognitive
quaternion valued neural network and some
applications. Neurocomputing, 221, 85-93.
Tay, Y., Luu, A. T., Hui, S. C., 2018. Hermitian Co-Attention
Networks for Text Matching in Asymmetrical Domains.
In IJCAI’18, 27
th
International Joint Conference on
Artificial Intelligence, pp. 4425-4431.
Trouillon, T., Welbl, J., Riedel, S., Gaussier, É., & Bouchard,
G., 2016. Complex embeddings for simple link
prediction. In ICML’16, International Conference on
Machine Learning.
Trabelsi, C., Bilaniuk, O., Zhang, Y., Serdyuk, D.,
Subramanian, S., Santos, J. F., Pal, C. J. 2017. Deep
complex networks. arXiv preprint, arXiv: 170509792.
Wang, Z., Tan, Y., Zhang, M., 2010. Graph-based
recommendation on social networks. In 12th Internation-
al Asia-Pacific Web Conference, pp. 116-122, IEEE.
Witten, B., Shragge, J., 2006. Quaternion-based signal
processing. In SEG Technical Program Expanded
Abstracts 2006, pp. 2862-2866, Society of Exploration
Geophysicists.
Xie, F., Chen, Z., Shang, J., Feng, X., Li, J. 2015. A link
prediction approach for item recommendation with
complex number. Knowledge-Based Systems, 81, 148-
158.
Yuan, X., Huang, J. J., 2012. An adaptive method for the tag-
rating-based recommender system. In AMT’12,
International Conference on Active Media Technology,
Springer, Berlin, Heidelberg, pp. 206-214.
Zhang, Y., Ai, Q., Chen, X., Croft, W. B., 2017. Joint
representation learning for top-n recommendation with
heterogeneous information sources. In CIKM’17, 26
th
Conference on Information and Knowledge
Management, ACM., pp. 1449-1458
Zhang, S., Yao, L., Tran, L. V., Zhang, A., Tay, Y., 2019.
Quaternion collaborative filtering for recommendation.
arXiv preprint, arXiv:1906.02594.
Amazon website: http://jmcauley.ucsd.edu/data/amazon/.
Grouplens website: http://grouplens.org/datasets/ movielens/
100k/.
Hetrec 2011 website: http://ir.ii.uam.es/hetrec2011/
datasets.html.
Toolbox website: Quaternion toolbox for Matlab,
http://qtfm.sourceforge.net/.
ICEIS 2021 - 23rd International Conference on Enterprise Information Systems
854