Design of a Very Low Frequency Test Device for Faults Diagnosis

in Underground Cable

Anis Ammous

, Mohamed Ali Zdiri

, Ammar Assaidi

Abdulrahman Alahdal

and Kaiçar Ammous

Department of Electrical Engineering, College of Engineering and Islamic Architecture, Umm Al-Qura University, K.S.A.

Department of Electrical Engineering, National School of Engineers of Sfax, University of Sfax, Tunisia

Keywords: VLF Generator, Cables Faults, Neural Network, Fault Location, Spline, Identification.

Abstract: In this paper, we present the design of a Very low frequency (VLF) generator made of power electronics

converter coupled to a mechanical system. This device is used to detect and locate faults in cables. This

VLF test is an AC type test at 0.1 Hz of a cosine-rectangular waveform performed on an underground cable.

Simulations were carried out for the following cable faults: open-circuit, short-circuit, resistance fault and

spark gap. For each fault type, simulations are performed for different locations in order to collect databases

in a neural network relating the distance and the corresponding voltage from the fault location. This allows

to register the range of voltages variation in each fault, which is useful for its identification. In addition,

these databases are used to determine the fault location using the Spline interpolation method. The tests

were performed on a 20 km cable length. The obtained results show the high performance and efficiency of

the investigated methods in terms of cable fault identification precision and localization.

1 INTRODUCTION

Overhead lines and underground cables provide

energy transport from power generation plants.

Distribution underground networks and especially

transmission networks are undergoing rapid

development imposed by the growth of urban areas

on the one hand and on the other hand for a better

quality of service and environment required by the

citizen consumer of electricity. The structure of the

cables directly influences the number of

measurements to be carried out to characterize the

types of faults (H. KUZYK, 2006).

Compared to overhead lines, the structure of

underground cables is complicated by the presence

of metal shielding near the central conductor.

Therefore, the inductive and capacitive effects are of

extreme importance, which requires special attention

when calculating the physical parameters of

underground cables such as resistances, chokes and

mutual inductances as well as capacitances (M.

Pays, 1994). In addition, underground electricity

cables have many advantages compared to overhead

lines. Indeed, they require virtually no maintenance

and above all are not affected by hard weather

conditions. On the other hand, and from an

operational point of view, repairing time of a faulty

cable is relatively long due to time-differed steps

necessary for fault location and troubleshooting

procedure.

The electricity transmission network, especially,

using underground cables is never immune to

electrical incidents due to internal and external

origins, causing blackouts. These faults are mostly

from external origin due to earthmoving works (H.

KUZYK, 2006). When an incident occurs, the direct

consequence is the power outage. It is therefore

appropriate for the power company to ensure the

restoration of electrical energy as soon as possible,

hence the need to identify the types and locations of

faults. The faults types are classified mainly into

four families which are open-circuit, short-circuit,

resistance and spark gap faults.

In order to ensure the continuity of electrical

power supply, electricity companies seek to identify

and locate the faulty cable segment with a good

precision in a short time in order to reduce

downtime. This can only be achieved by

implementing simple, fast and precise pre-location

techniques based on an exact determination of the

physical parameters of the cable in order to reduce

repairing time and cost. The different operating

196

Ammous, A., Zdiri, M., Assaidi, A., Alahdal, A. and Ammous, K.

Design of a Very Low Frequency Test Device for Faults Diagnosis in Underground Cable.

DOI: 10.5220/0010472001960203

In Proceedings of the 10th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS 2021), pages 196-203

ISBN: 978-989-758-512-8

disturbances observed in the electrical networks

lead, in most cases, power cuts and a important

number of incidents, which are due to external

injuries or internal breakdowns of cables or their

accessories.

Currently, diagnostic methods are developed and

used in a several sectors such as cable faults and

power converters faults (M.A. Zdiri et al., 2019;

M.A. Zdiri et al., 2019; M.A. Zdiri et al., 2020). The

main goal of diagnostic techniques is to prevent

downtime during maintenance on electric network,

independently to its voltage level. It will allow the

operator to determine accurately the cable state

(effects of aging, degree of humidity, or even water

trees) and to warn operator about the deterioration

on the insulation of medium and high voltage cables

by using the dielectric diagnostics (TAN) and the

partial discharge (DP) (H. KUZYK, 2006). The

nature of a fault can easily be determined by simple

methods of measuring insulation resistance and

conductor continuity. The cable tests goal consist to

explore new installations (commissioning, checking

junction and ending boxes) during repair works. The

tests can be carried out with direct current or (VLF)

alternative current (M. Baur, 2008). The VLF

method, recently developed for cables in synthetic

material, has also proved its effectiveness for cables

insulated with impregnated paper. In addition, it

allows a much more interesting and precise

diagnosis, which made its success and incorporation

into European standards (Norme, DIN VDE, 1995).

In (H. Oetjen, 2004), the authors compare different

VLF techniques related to the correlation between

the data of test field and test parameters.

Furthermore, a new design and realization of a VLF

technique based on 0.1 Hz sinusoidal waveform is

presented in (S. Seesanga et al., 2008). In order to

detect and identify cables faults in medium voltage,

the authors in (B.V. Wong et al., 2016) investigate

the VLF test combined with Tan Delta and Partial

Discharge. In addition, the authors in (C. Xie et al.,

2018) highlighted the capacity of the main VLF

testing methods for the cables XLPE (

Cross-linked

polyethylene)

of newly installed 10 kV in approval

tests. Meanwhile, the failures of insulation of XLPE

cables have become a hard security hazard. The

authors in (X. Tan et al., 2019) propose a new type

of 0.1 Hz VLF sinusoidal waveform generator that is

characterized by a novel control and simple

structure.

Despite the existence of different methods in

literature, there is still a lot to be done in order to

develop new methods to improve the reliability of

underground cables. In this paper, we have proposed

a cosine-rectangular waveform VLF device at 0.1

Hz, based on power switches, to detect and identify

the faults of an underground cable with 20 km

length. Using this VLF generator, we tested four

types of faults, which are open-circuit fault, short -

circuit fault, resistance fault and spark gap fault.

These different tests are stored in the neural

network, which make it possible to identify the type

of fault. In addition, the Spline interpolation method

was used for each voltage range corresponding to a

specific fault type. Therefore, the detection,

identification and localization of the cable fault,

these done based on the neural network and the

Spline method.

In conclusion, the simulation results prove to

verify the high performances of these methods in

terms of detection and identification precision of

cables faults.

2 DESIGN OF A 0.1 Hz VLF

GENERATOR FOR TESTING

CABLE FAULTS

As seen previously, we have listed the different

types of HVA underground cable for fault location

tests. Subsequently, we will focus our study on a

very precise and revolutionary test, which is the

VLF test. Therefore, we will study the operation of

the VLF test device and we will try to design a new

device and improving it by mean of simulation for

verification. A very low frequency dielectric test

will check the dielectric state of a polymer cable. In

this section, we will give the operation principle of a

cosine-rectangular VLF device and propose another

device allowing to obtain the same desired

waveform at the output.

2.1 Constitution

The VLF test is featured in several applications with

slow detection time for weak spots on synthetic

cables (PE/XLPE) and paper cables (PILC) and also

excess stress in (BAUR) cables. The cosine-

rectangular VLF waveform is patented and approved

by the CEI and IEEE organizations. A VLF device

generally consists of an HVA DC test unit generator,

a storage coil, an electronic switch (rotary rectifier),

a voltmeter, a discharger switch and a support

capacitor.

Design of a Very Low Frequency Test Device for Faults Diagnosis in Underground Cable

197

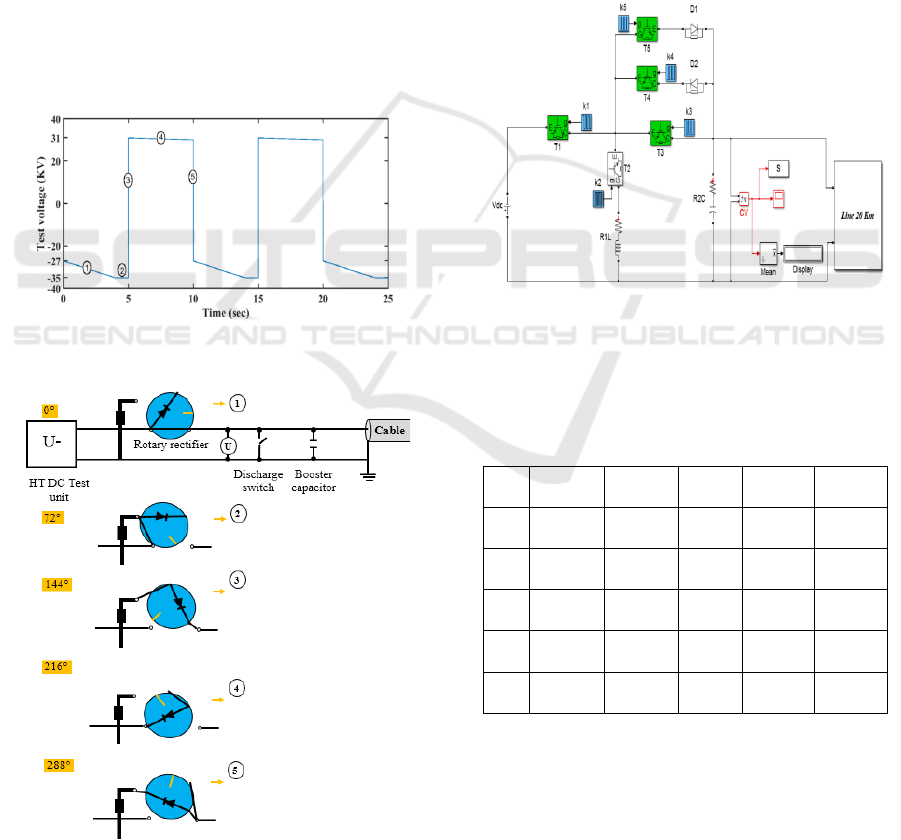
2.2 Operation

The VLF test does not damage the cable structure,

however, it does cause rapid growth of electrical

treeing if they exist. Compared with other test

devices, VLF devices have lower weight and lower

power consumption along with higher test reliability.

The figure 1 illustrates the voltage curve

characterizing a device of the 0.1 Hz VLF test.

The principle of operation is based on the

position of the rotary diode based rectifier and the

charging and discharging of a capacitor. We can

remark that at an operation state corresponding to an

angle multiple of 72° and a well-defined time. After

a complete turn of the device (passage of the five

stages), we can observe the waveform at the exit of

the capacitor (charge and discharge). Based on the

operating sequences, an equivalent circuit is

modelled and the operating equations are sorted for

each step sequence.

Figure 1: Voltage curve characterizing a 0.1 Hz VLF test

device.

Figure 2: Different rotating rectifier position sequences of

a VLF device.

Different rotary rectifier positions associated to

the VLF generator are shown in figure 2.

2.3 Design of a New Cable Fault Test

VLF Generator

After showing the operation principle of the classical

VLF device, we will propose another type of VLF

device made up of totally controlled components as

shown in figure 3. In this paper, we have focused

our study only on the VLF generator at 0.1 Hz. It is

to be noted that this new VLF generator is based on

IGBT's and diodes. In order to design this device, we

have chosen the following values: Vdc = 40 kV; L =

0.1 H; R1 = 0.001 Ω; C = 0.001 F; R2 = 0.1 Ω.

Figure 3: Model of the new proposed 0.1Hz VLF device.

The table 1 gives the different switching intervals

of each power device for a switching frequency

equal to 0.1 Hz.

Table 1: Power switches Control at 0.1 Hz.

time

(

)

[0-2] [2-5] [5-6] [6-8] [8-10]

k1 On-state On-state Off-stat

Off-state Off-state

k2 Off-state On-state On-state Off-state On-state

k3 On-state Off-state Off-stat

Off-state Off-state

k4 Off-state Off-state Off-stat

Off-state On-state

k5 Off-state Off-state On-state Off-state Off-state

In order to apply the proposed VLF generator to a

cable, we will choose a 20 km unipolar one

decomposed into 10 portions of 2 km with own

linear characteristics impedance. This VLF

generator is used in order to see the behaviour of the

output signal during tests on a healthy and faulty

SMARTGREENS 2021 - 10th International Conference on Smart Cities and Green ICT Systems

198

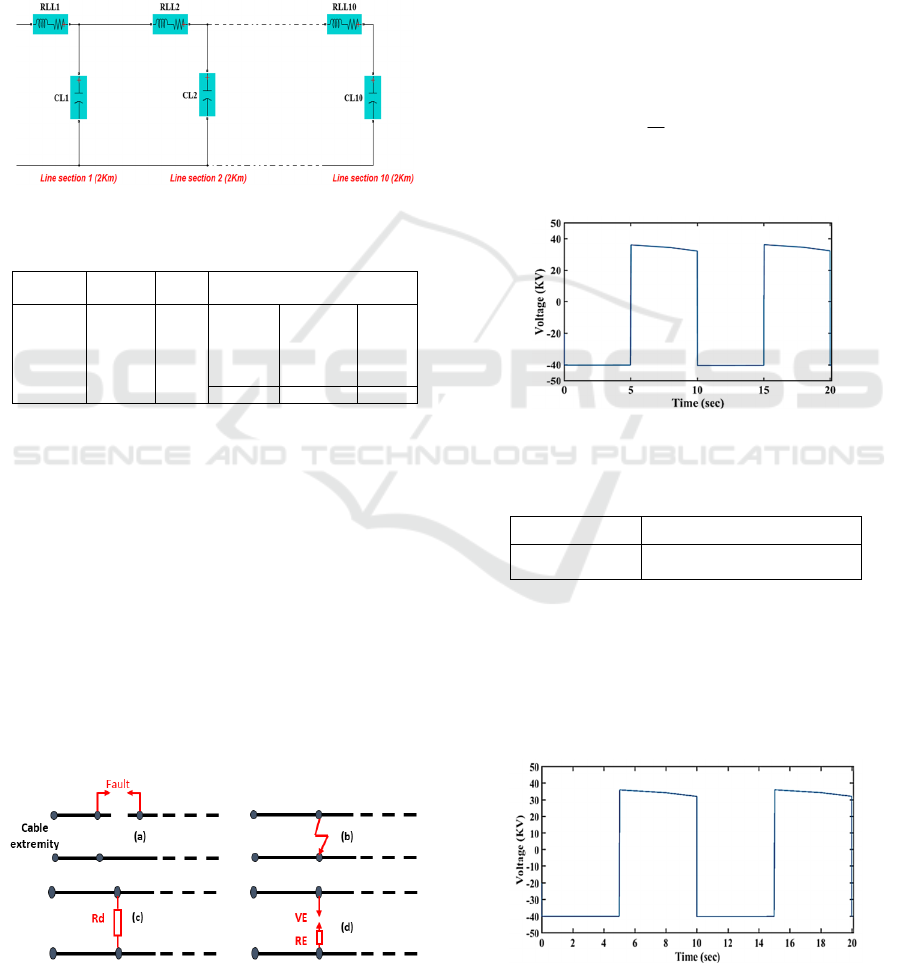
cable. The figure 4 represents the equivalent model

of a 20 km underground cable subdivided into 10

blocks of 2 km length each.

Table 2 illustrates the actual characteristics of an

underground cable from the manufacturer PIRELLI

which can withstand a voltage of 40 kV with an

aluminium conductive core with PR insulator, direct

current resistance R = 0.125 Ω/km at 20 °C, self-

induction L = 0.38 mH/km and capacitance C =

0.212 𝜇𝐹/km.

Figure 4: Model of a 20 km electric cable.

Table 2: Characteristics of an ALU-PR cable.

Builder

Voltage

(kV)

Type Impedance

PIRELLI 18/30 (36) 1*240

ALU-

resistance

(Ω/km)

(at 20 ° C)

Self-

induction

for external

cable

(

mH/km

)

Capacity

(μF/km)

0.125 0.38 0.212

3 SIMULATION RESULTS

As mentioned before, the most common faults

affecting underground cables are open-circuit, short-

circuit, resistance and spark gap faults as presented

in figure 5. To locate the fault of an underground

cable, we carried out tests on a cable of length 20

km. We registered the fault results for different cable

distances. Indeed, we determine for each distance

the mean voltage corresponding to it. We built a

database consisting of the different values of the

average voltages that the cable can withstand for

well-defined lengths.

Figure 5: (a) Open-circuit fault. (b) Short-circuit fault. (c)

Resistance fault and (d) Spark gap fault.

Moreover, we then applied the cubic spline

interpolation method (Schumaker, 2007) according

to the values of the obtained faults. The investigation

phase of the interpolation method consists in being

able to determine the exact location of the failure on

the cable by measuring the voltage value at its input.

This procedure will be applied in the different

simulations of the cable faults.

In the healthy case of the cable, we applied the

signal from the VLF at 0.1 Hz generator to a healthy

cable of 20 km long. Figure 6 shows the waveform

of the voltage at the input of the cable.

The average value of the voltage in the healthy or

faulty case is determined by the following

expression:

()

moy

VVtdt





(1)

Furthermore, table 3 illustrates the voltage

average value of a cable with 20 km long.

Figure 6: Waveform of the voltage terminals across a

healthy cable at 0.1 Hz.

Table 3: Simulation results on a healthy cable.

Cable length Voltage average value (V)

20 km -2947.86 V

3.1 Open-circuit Fault

In simulation, we are going to use a breaker in order

to apply the cable open-circuit fault. For a fault

located at a distance equal to 2 km, we obtain the

voltage signal shown in figure 7.

Figure 7: Voltage signal due to the opening of a 2 km line

portion.

Design of a Very Low Frequency Test Device for Faults Diagnosis in Underground Cable

199

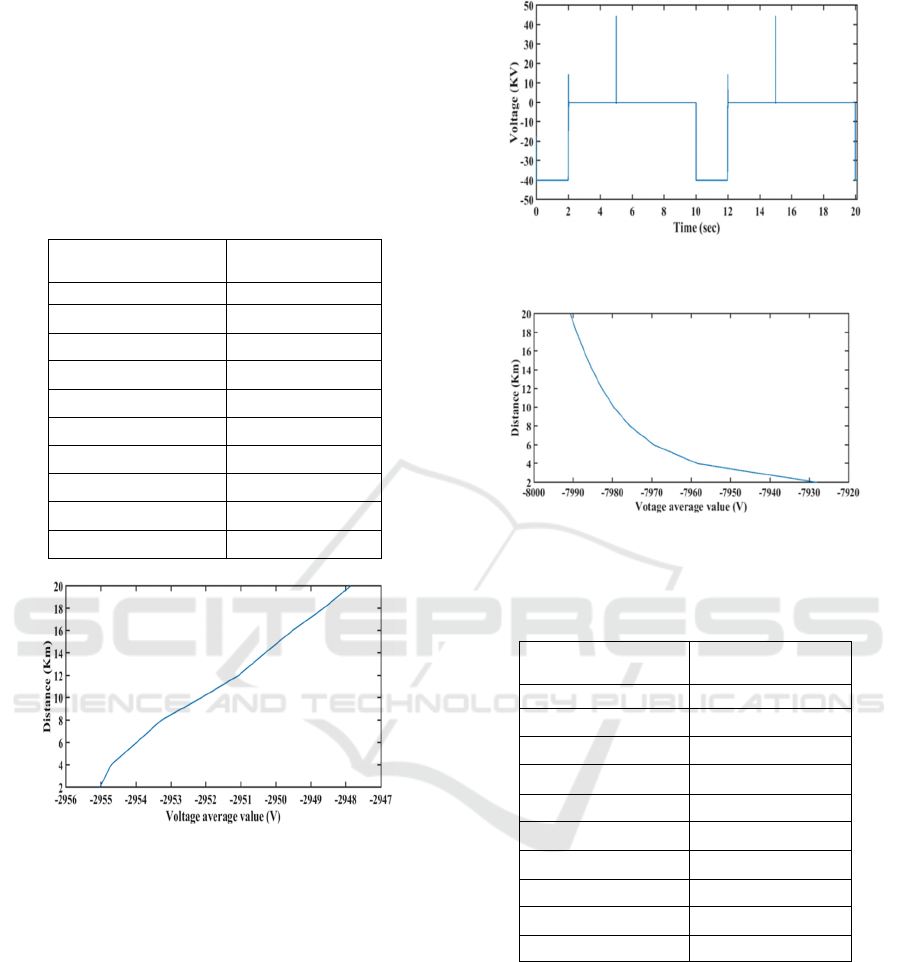
The table 4 shows the different average values of

each cable section with an open-circuit fault.

In order to determine the intermediate points, we

applied the Spline method. Thus, we brought out the

interpolation of the voltage curve corresponding to

the open-circuit of a cable portion, as shown in

figure 8.

Table 4: Simulation results due to an open-circuit fault in a

cable portion.

Cable portion Cutout

location (km)

Voltage average

value (V)

2 -2955.02

4 -2954.71

6 -2953.98

8 -2953.27

10 -2952.13

12 -2951.06

14 -2950.31

16 -2949.52

18 -2948.64

20 -2947.86

Figure 8: Interpolation curve of the opening fault of a 20

km cable.

3.2 Short-circuit Fault

The short circuit fault is achieved by applying a

signal equal to ‘1’ to the breaker, which is connected

in parallel with the rest of the cable. For a fault in 20

km cable length, the voltage signal is obtained as

shown in the figure 9.

Table 5 shows the different voltage average

values for each cable portion with a short-circuit

fault. In order to determine the intermediate points

of this fault type, we applied the Spline method.

Thus, we brought out the interpolation curve of the

short-circuit fault of cable, as shown in the figure 10.

Figure 9: Voltage signal for a short-circuit fault appearing

at the end of 20 km cable length.

Figure 10: Interpolation curve of the short-circuit fault of a

20 km cable.

Table 5: Simulation results of voltage signal with a short-

circuit fault in a cable portion.

Cable short circuit

location (km)

Voltage average

value (V)

2 -7927.95

4 -7958.36

6 -7969.45

8 -7975.53

10 -7979.60

12 -7982.65

14 -7985.1159

16 -7987.2172

18 -7989.0752

20 -7990.7630

3.3 Resistance Fault

The resistance fault in a cable is ensured by using a

priming resistance Rd = 100 Ω. For a fault located at

a distance of 2 km, the output voltage signal is

obtained as shown in the figure 11.

SMARTGREENS 2021 - 10th International Conference on Smart Cities and Green ICT Systems

200

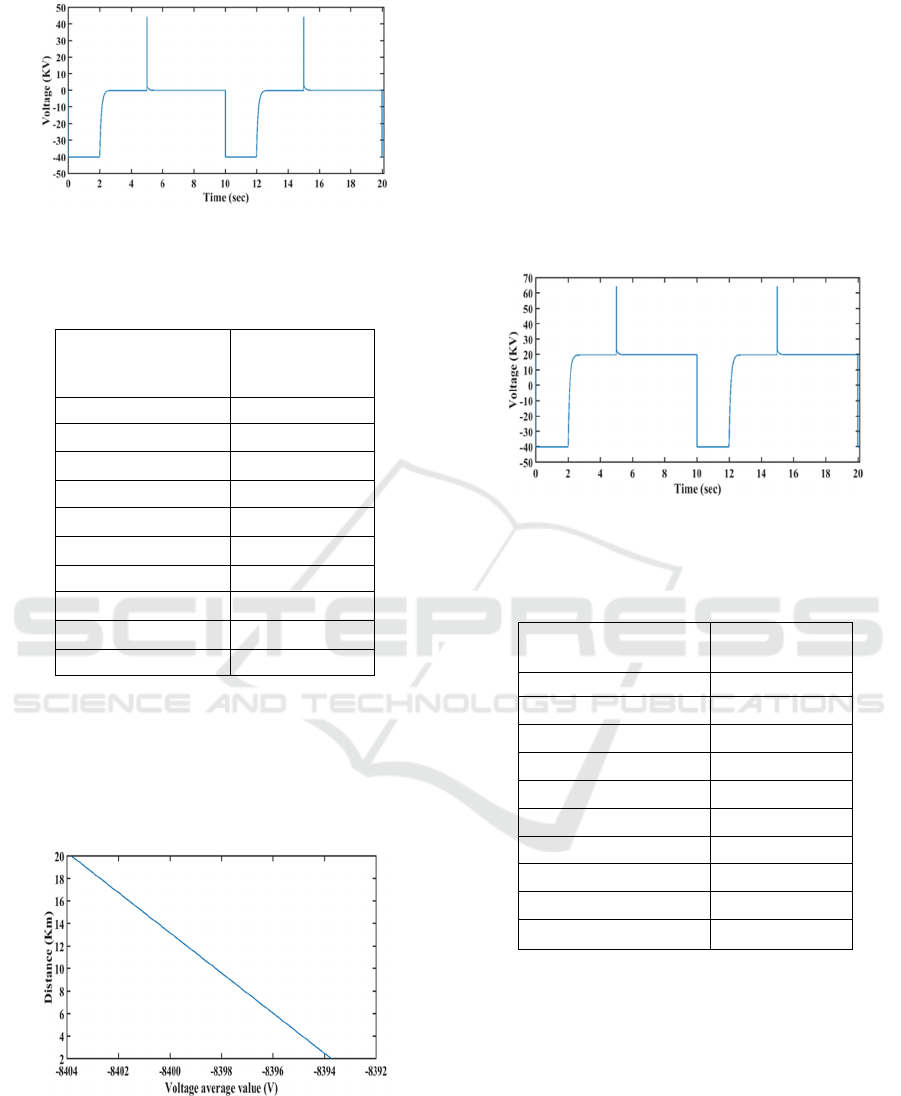
Figure 11: Voltage Signal due to a resistance fault

between portion 1 and 2 of a 20 km cable.

Table 6: Simulation results on a cable with resistance fault

of a section.

Cable Portion

Resistance fault

location (km)

Voltage average

value (V)

2 -8393.72

4 -8394.84

6 -8395.96

8 -8397.08

10 -8398.20

12 -8399.32

14 -8400.45

16 -8401.57

18 -8402.69

20 -8403.81

The table 6 shows the different average values for

each section with a resistance fault.

In order to determine the intermediate points, we

applied the Spline method. Thus, we brought out the

interpolation curve of the resistance fault of a cable

section, as shown in the figure 12.

Figure 12: Interpolation curve due to a resistance fault of a

20 km section.

3.4 Spark Gap Fault

We will apply a voltage signal for the cable spark

gap fault at the distance 20 km with a priming

resistance RE = 100 Ω and a priming voltage VE =

20 kV. For a spark gap fault located at a distance of

20 km, the output voltage signal is obtained as

shown in figure 13.

Table 7 shows the voltage average values of each

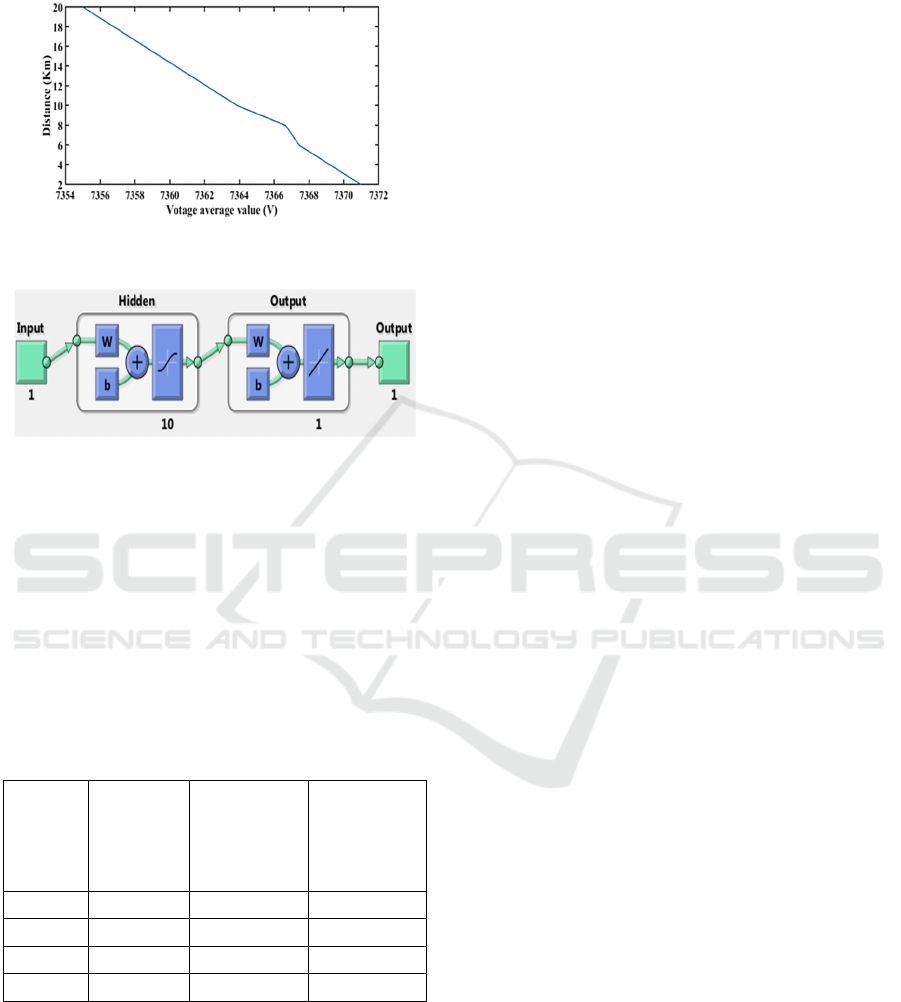
section with spark gap fault. Then, in order to locate

the fault more precisely, we applied the Spline

method. Thus, we brought out the interpolation

voltage curve corresponding to the spark gap fault of

a cable portion as shown in figure 14.

Figure 13: Signal of a spark gap fault at the end of 20 km

cable.

Table 7: Simulation results on a spark gap fault of a cable

section.

Cable Portion spark

gap fault position (km)

Voltage average

value (V)

2 7370.98

4 7369.20

6 7367.43

8 7366.66

10 7363.88

12 7362.11

14 7360.33

16 7358.56

18 7356.79

20 7355.01

3.5 Identification and Localization of

Fault

In order to identify and locate the different faults, we

will pursue the following steps:

 Build databases for the different fault types;

 Applies the Artificial Neural Network ANN (A.

Maheshwari et al., 2018) to determine the type of

fault. This is done by determining for each fault the

range of variation of the average voltage. In the

ANN technique, the output indices 1, 2, 3 and 4 can

be assigned for open-circuit fault, short-circuit fault,

Design of a Very Low Frequency Test Device for Faults Diagnosis in Underground Cable

201

resistance fault and spark gap fault. The ANN model

is shown in the figure 15.

Figure 14: Interpolation curve of the spark gap fault at the

end of 20 Km cable.

Figure 15: ANN model.

To test the performance and effectiveness of these

used methods, a test was performed for a four

random values of average voltage. The identification

technique gives the results shown in table 8. From

the identified defaults locations this table shows the

exact values of the voltages from the direct tests on

the cable and by using the used VLF generator. The

comparison between these voltages values proves

the high performance and efficiency of the proposed

method.

Table 8: Identification and localization of studied faults.

Voltage

average

value (V)

Fault

identification

Default

Localization

(km)

(from Neural

Network and

Spline)

Exact average

voltage (V)

corresponding

to the

identified

localization

-2950

Open-circuit 14.8293 -2950.6853

-7970

Short-circuit 6.1458 -7970.0029

-8400

Resistance 13.1980 -8400.1066

7365

Spark gap 9.6556 +7365.5748

4 CONCLUSION

An energy transmission network, even underground,

is exposed to electrical incidents causing the

shutdown of the electricity supply. Improving the

quality of service is essentially depending on the

speed and precision with which a fault is located. To

do this, we studied the VLF device to detect and

identify High Voltage of type A underground cable

faults. In this paper, the VLF method is investigated

since it has a wider detection range and less

aggressive for underground cables.

Subsequently, we gave a new electronic version

of the VLF device based on the operating steps of

power switches. Thus, we have modelled an

underground cable with real parameters, in order to

simulate the different types of faults most frequently

observed. A database by performing faults for

different distances and for each type of fault is

performed using the neural network. In order to

detect precisely these different types of faults, we

have proposed the Spline interpolation method.

Simulations were done using

MATLAB/Simulink. As conclusion, the results

obtained are very interesting and promising in terms

of detection, identification and localization of

distinct fault type in underground cables.

ACKNOWLEDGEMENTS

The authors extend their appreciation to the

Deputyship for Research & Innovation, Ministry of

Education in Saudi Arabia for funding this research

work through the project number 1212.

REFERENCES

A. Maheshwari, V. Agarwal, and S. K. Sharma.

"Transmission line fault classification using artificial

neural network based fault classifier," Int. J. Electr.

Eng. Technol.(IJEET), vol. 9, pp. 170-181, 2018.

B.V. Wong, Y. Tian, and T. Neier. “Practical experience

using VLF Tan Delta and partial discharge

measurement in medium voltage cable,” In 2016

China International Conference on Electricity

Distribution (CICED), pp. 1-5. IEEE, 2016.

C. Xie, Y. Wang, X. Shao, and Y. Jin. “The Application

Research of Very Low Frequency Diagnostic Methods

in Acceptance Tests on New Cable Systems of

Medium Voltage,” In 2018 China International

Conference on Electricity Distribution (CICED), pp.

47-53. IEEE, 2018.

H. KUZYK, “Défauts dans les câbles de transmission

d’énergie,” Technique de l’ingénieur, Reference :

D4541 V2, 2006.

H. KUZYK, “Diagnostic de câble,” Technique de

l’ingénieur, Reference : D4541 V2, 2006.

H. KUZYK, “Les types de câbles souterrains,” Technique

de l’ingénieur, Reference: D4541 V2, 2006.

SMARTGREENS 2021 - 10th International Conference on Smart Cities and Green ICT Systems

202

H. Oetjen, “Principals and field experience with the 0.1 Hz

VLF method regarding the test of medium voltage

distribution cables”, Conference Record of the 2004

IEEE International Symposium on Electrical

Insulation, pp. 376-379. IEEE, 2004.

L. Schumaker, “Spline functions: basic theory,”

Cambridge University Press, 2007.

M. A. Zdiri, B. Bouzidi and H. Hadj Abdallah,

“Performance investigation of an improved diagnostic

method for open IGBT faults in VSI fed IM drives,” In

Diagnosis, Fault Detection & Tolerant Control,

Springer, Singapore, pp. 155-171, 2020.

M. Baur, “Test des câbles, Nouvelles méthodes dans la

maintenance des câbles à hautes tension avec mesure

et diagnostic,” Baur Prif-Und Mess Technik GmbHA

6832 Sulz/Austria, 2008.

M. Pays, “Câbles de transport d’énergie - Technologies.

Caractéristiques,” Reference: D4520, 1994.

M.A. Zdiri, B. Bouzidi, and H. Hadj Abdallah,

“Performance investigation of an advanced diagnostic

method for SSTPI-fed IM drives under single and

multiple open IGBT faults,” COMPEL International

Journal of Computations and Mathematics in

Electrical and electronic engineering, vol. 38, no. 2,

pp. 616-641, 2019.

M.A. Zdiri, B. Bouzidi, and H. Hadj Abdallah, “Synthesis

of an improved diagnosis method for open IGBT

faults dedicated to FSTPI fed IM drives,” Journal of

Electrical Systems, vol. 15, no. 2, pp. 314-330, 2019.

Norme, DIN VDE 0276-1001, 1995.

S. Seesanga, W. Kongnun, A. Sangswang, and S. Chotigo.

“A new type of the VLF high voltage generator,”

In 2008 5th International Conf. on Electrical

Engineering/Electronics, Computer, Telecommunica-

tions and Information Technology, vol. 2, pp. 929-932.

IEEE, 2008.

X. Tan, J. Chen, C. Li, L. Hu, J. Cao, and X. Zeng. “A

New Type of VLF Sinusoidal Waveform Generator

Used for AC Withstand Voltage Testing of Power

Cables,” In 2019 IEEE Asia Power and Energy

Engineering Conference (APEEC), pp. 10-13. IEEE,

2019.

Design of a Very Low Frequency Test Device for Faults Diagnosis in Underground Cable

203