Can Formative Assessment Practices Appear Spontaneously during

Long Distance Learning?

Giorgio Bolondi

, Agnese Del Zozzo

, Federica Ferretti

, Marzia Garzetti

and George Santi

Faculty of Education, Libera Università di Bolzano, Viale Ratisbona, 16, Bolzano, Italy

Department of Mathematics, Università degli studi di Trento, Via Sommarive, 14, Trento, Italy

Department of Mathematics, Università di Ferrara, Via Macchiavelli, 30, Ferrara, Italy

GeorgeRichardPaul.Santi@unibz.it

Keywords: Formative Assessment, Long-Distance Learning, Mathematics Education, Eye of the Theoretician.

Abstract: Within the context of Long-Distance Learning (LDL) during the first Italian lockdown due to Covid-19

pandemic, our eye as researchers in mathematics education looks at the modification of student-teacher

interactions regarding the exchange of feedback. We claim that digital-technology based environment fostered

the spontaneous emergence of teaching and learning practices that can be associated with formative

assessment. Through the analysis of answers to a questionnaire and the observation of a class during LDL we

outline the relation between the theoretical construct of formative assessment and observed practices. This

analysis allows to highlight what factors of digital-technology based environment shape class interaction and

what directions can be taken to exploit the potential of digital technologies in teaching and learning context,

in particular within mathematics education field.

1 INTRODUCTION

Starting from February 2020 Italy has been

overwhelmed by the Covid-19 pandemic. This

resulted in a strong national lockdown that lasted until

June 2020. To maintain the educational relationship

teachers and students have adapted their practices to

long-distance learning (LDL): this adaptation process

was not neutral nor painless and has brought to a deep

change in teachers-students interaction modalities.

LDL allowed the emergence of many relevant

spontaneous phenomena. Within this context, our eye

as researchers in mathematics education look at the

modification of student-teacher interactions

regarding the exchange of feedback: on the one hand,

feedback from the teacher on student's work, on the

other hand, feedback for the teacher on what the

student has understood, or on the acquired skills. We

focus on the modification of these exchanges and

their reason, which we identify as the use of certain

digital technologies to mediate student/teacher

communication. We can conceive this change as an

emerging phenomenon characterized by an enormous

density of didactical information. In this position

paper, we claim that such emerging phenomenon,

often perceived by teachers as overwhelming, can be

shaped using the theoretical construct of Formative

Assessment (FA). We also believe that the FA

construct can not only be a lens but also a tool for

managing such a phenomenon. In order to support our

claim, we propose to think about it as an example of

an eye of a theoretician in Radford’s (2010, p.4) sense:

Mathematicians’ eyes have been culturally

educated to organize the perception of things in

particular rational ways [...] The domestication of the

eye is a lengthy process in the course of which we

come to see and recognize things according to

“efficient” cultural means. It is the process that

converts the eye (and other human senses) into a

sophisticated intellectual organ – a “theoretician”.

According to his perspective, in this work, the

observer, or the eye, is the researcher in mathematics

education who knows the FA construct, the observed

phenomenon (thus, the perceived thing) is the

spontaneous didactical practice during pandemic

induced LDL, and the theoretical lens that

domesticates the eye is FA. Not all the involved

teachers were aware of the construct of FA, anyway,

as we are going to show, some widespread

spontaneous practices in managing the huge amount

of “didactical data” during LDL can be linked to some

theoretical features of FA.

Bolondi, G., Zozzo, A., Ferretti, F., Garzetti, M. and Santi, G.

Can Formative Assessment Practices Appear Spontaneously during Long Distance Learning?.

DOI: 10.5220/0010475506250632

In Proceedings of the 13th International Conference on Computer Supported Education (CSEDU 2021) - Volume 1, pages 625-632

ISBN: 978-989-758-502-9

625

The paper is organised as follows: in Section 2 we

introduce the construct of FA and we specify how we

use it in our analysis, then in Section 3 we specify our

claim in the light of the theoretical framework. In

Section 4 we present some data, in Section 5 we

clarify our approach to these data then in Section 6

we analyse them in order to support our claim. In the

last Section 7 we outline how and why this work can

be valuable both for teachers and researchers to

analyse and exploit the experience of LDL.

2 THEORETICAL FRAMEWORK

Our reflections embrace the idea of promoting the use

of FA as a tool for improving the mathematics

teaching-learning process. To frame our observation,

we refer to the theoretical framework of LLP-

Comenius Project FAMT&L – Formative

Assessment for Mathematics Teaching and Learning

(Bolondiet al., 2016). One of the main objectives of

the FAMT&L project was to improve the skills of

mathematics teachers in the use of FA as a tool for

methodological quality in mathematics teaching

(Ferretti, Michael-Chrysanthou, & Vannini, 2018;

Gagatsis et al., 2019) and one of the outcomes of the

project was the following definition of FA in

mathematics (Ferretti et al., 2018, p.33):

The FA is connected with a concept of learning

according to which all students are able to

acquire, at an adequate level, the basic skills of a

discipline. The learning passes through the use of

teaching methodologies which can respond

effectively to different learning time for each

student, their different learning styles, their zones

of proximal development.

The FA is an assessment FOR teaching and

learning.

In line with the FAMT&L framework (Ferretti et al.,

2018), we embrace the idea that the FA: i) is part of

the teaching-learning process and regulates it; ii)

identifies, in an analytical way, the strengths and

weaknesses of student’s learning, in order to allow

teachers to reflect on and may modify their own

practices; iii) allows in a form of formative feedback

to establish a dialogue between teacher and student

and to design educational interventions aimed to the

recovery; iv) promote and foster the learning of all

students through differentiated teaching that ensures

each student different rhythms and different teaching

and learning strategies; v) involves the student in the

https://docs.google.com/document/d/1gjlm-hSpV7t10iN

RX1FsyApzZaB6376qSy_ywt3jktU/edit?usp=sharing

analysis of own errors/weaknesses and own ability to

promote self- and peer-assessment and active

participation in the teaching-learning process. In

particular, our approach of FA is in line with the

definition given by Leahy, Lyon, Thompson, &

Wiliam (2005) and Black & Wiliam (2009), where

FA criteria and strategies are also highlighted:

S1. Clarifying and sharing learning intentions and

criteria for success.

S2. Engineering effective classroom discussions and

other learning tasks that elicit evidence of student

understanding.

S3. Providing feedback that moves learners forward.

S4. Activating students as instructional resources for

one another.

S5. Activating students as the owners of their own

learning.

In the following, we simply refer to these as five

FA strategies or as S1, S2, S3, S4, S5. Starting from

these strategies, within the FAMT&L project, the

structured FAMT&L Grid, a specific video analysis

tool was designed, built and used.

The FAMT&L Grid was developed starting from

the international debate on FA, and it is composed of

several indicators. For our work, we considered a

subset of 72 indicators, chosen in agreement with two

of the authors of the grid as the more suitable, to

detect FA within the LDL context. Moreover, we

decided to categorize these indicators according to S1,

S2, S3, S4, S5. The result of this work is a table,

which we make available in an external online

document

. The table has taken the role of a

theoretical tool of analysis, and it enabled us to

highlight what aspects of the lesson could be linked

to specific features of the construct of FA, and to

better understand how some phenomenon, typical of

the digital environment, could be related to strategies

of FA.

3 CLAIM

In line with the eye of a theoretician perspective

(Radford, 2010), the theoretical framework allows us

to redefine the initial claim as it follows: a researcher

in mathematics education, observing some

spontaneous practices in LDL, if carried out with

appropriate platforms, can recognise features that

create a fertile ground for FA. Especially, we argue

that teaching and learning practices conducted in

some digital-technology based environment have

CSEDU 2021 - 13th International Conference on Computer Supported Education

626

characteristics that can be associated with at least

three out of five FA strategies, in particular:

1. Immediacy and automaticity of storage and

collection of documentation, which allows

monitoring over time of the students' path, related

to S1 and S2.

2. Individualisation of didactics: the increased

documentation about the student’s work allows

the teacher to give more individualised feedback

and to enhance more individualised strategies,

related to S3.

4 DATA

The data we consider for this work are part of a

research on LDL teaching and learning practices in

Italian schools of different order and grade during the

lockdown. In this context, our focus is on some

questions of a questionnaire administered to teachers

and on ethnographic observation of teaching-learning

practices in a grade 12 class, both conducted during

the first Italian lockdown. We highlight that this is not

a data collection specifically designed to support our

hypothesis but, rather, it is the sharing of some of the

evidence in favour of the thesis that we wish to

introduce here.

4.1 Questionnaire

The questionnaire has been administered during the

month of April 2020 in order to gain information on

a fluid process started a month earlier and that was

settling itself day by day. The questionnaire contains

32 questions, both open-ended and multiple-choice

ones, organized in five sections according to the aim.

For a detailed description of the entire questionnaire,

we refer the reader to Del Zozzo, Garzetti, & Santi

(2020).

We selected a convenience sample: the need to

reach teachers during a fixed period has guided the

selection, we spread the questionnaire through

mailing lists of teachers that collaborate with us in

other projects, asking, when possible, to share it with

others. Overall, from secondary school teachers, we

obtained 99 answers. In this study we consider only

the following three questions in order to give a

broader picture in relation to the phenomenon we are

discussing.

https://edu.google.com/products/gsuite-for-education/ G

SE is now called Google Workspace for Education.

https://support.google.com/meet/?hl=en#topic=7306097

• One item of a question where teachers are asked

to express their agreement/disagreement with

different items: I can give feedback to each

student for every task she sends me, and it seems

to me that some students are improving.

• Two subsequent questions where teachers are

asked to rank the differences in feedback

restitution between LDL and physical classroom

and to explain the reason of the difference.

These data allowed us both to notice that practices

that could be related to FA were emerging among

teachers, and to shape the classroom observation. We

found consistency between teachers’ word in the

questionnaire and observed teachers’ practices.

4.2 Classroom Observation

From 11

of May until the end of classes (between 5

and 10

of June), we had the opportunity to conduct

ethnographic observation in several classes of

different school grades during LDL.

In this paper, we refer to one of the observed

classes: a grade 12 class of a Technical Institute

enrolled in the G Suite for Education

(GSE). It

appears important to highlight how the analysed

didactical practices did not consist in a controlled and

planned intervention organised by the researchers,

and thus the involved teachers were not aware of FA

construct. Here, we do not go into the methodological

details of this observation, for which we refer to

Ferretti, Del Zozzo & Santi (2020). Nevertheless, it is

important to remark that, as far as classroom practice

in the context of LDL is concerned, each virtual

classroom is dichotomous, and it has two components:

one synchronous and one asynchronous. When our

observation began, we were provided with a link to

access the synchronous component - implemented

with Google Meet

(GM) - and access to the

asynchronous component - implemented with Google

Classroom

(GC). In particular, regarding GC, two of

us were added to the class in the platform with the

role of additional teachers. This choice allowed us to

access the entire archive of materials and all the

message exchanges (both public, with the whole class,

and private between the teacher and each student) that

had taken place since the beginning of the creation of

this class in GC, the 27

of February. Thus, our

observation was conducted as follows. Regarding

classroom dynamics in the synchronous component,

it was indirect (since we only know what is reported

https://support.google.com/edu/classroom/?hl=en#topic=

10298088

Can Formative Assessment Practices Appear Spontaneously during Long Distance Learning?

627

or described in GC) for what happened between 27

of February and 9

of May, direct from 11

of May

until the end of the school year, on 5

of June.

Regarding the classroom dynamics in the

asynchronous component, we had the opportunity to

analyse the entire teaching flow from the first day of

class creation in GC (27

of February) to the last day

of interaction between teachers and students in the

platform (12

of July).

For clarity, in GC there are different areas of work

and interaction with different functionalities and

permissions for action and access among teacher and

students; the main areas we considered are the Stream

page, the Classwork page, and the Assignment space.

In the following, using "episode" we mean what

happens in the virtual classroom, in both its

synchronous and asynchronous components, in a

fixed time starting with a teacher's assignment on a

certain set of exercises or tasks, and ending with the

assignment of a new task on a different set of

exercises. With respect to the aim of the present work,

we focus on the following three episodes, that we

consider as paradigmatic of the teaching and learning

practices we observed: episode 1 between 17

and

of March, episode 2 between 24

and 30

March, and episode 3 on the 18

of May.

Episode 1: First Assignments on GC. During

episode 1, only asynchronous exchanges on the GC

platform are considered. On 17

of March, a task is

assigned to be completed by March the 20

, and in

this time frame, we consider the interactions between

T and students that occurred in the various spaces of

the platform. In the following, the unfolding of

episode 1 is presented, with the aim of showing how

the different spaces interact with each other during

the different activities. In the descriptions of the

remaining episodes, we do not repeat this pattern and

only highlight the changes in the structuring of the

activities involved. T indicates the mathematics

teacher, and the class was composed of 29 students.

of March. In GM: 2-hour synchronous lesson.

In GC: on the instruction page a homework

assignment (exercises from the textbook) is published

with deadline 20

of March; in the Stream, it appears

the notification of the assignment with the link to

access it.

and 19

of March. In GC: one student

communicates in her workspace that she has not the

textbook. Consequently, in the instruction page T

modifies the assignment by adding the scanning of

the pages of the book in which the exercises are

presented. Also, public exchanges between students

and T appear in this space. Contextually, in other

students’ workspaces, we see private exchanges

between students and T about the assignment and we

also see that 24 out of 29 turn in their homework by

sending photos of their notebooks.

of March. In the Stream of GC, a reminder of

the meeting on GM is posted with the related topic:

homework correction. Then, in GM: 1-hour

synchronous lesson is conducted in which the

exercises are corrected. After the lesson, in GC, in

students’ workspaces, there are requests for feedback

on the correction carried out synchronously during

the meeting. In particular, one student sent her own,

report of correctly completed exercises and of errors,

and uploaded photos of her corrected work with

corrections marked in red. We see that this practice

becomes a routine for the whole classroom from

episode 2.

Episode 2: The Institutionalisation of Self-

correction. Episode 2 opened with an assignment on

GC, like episode 1. The difference with episode 1 is

the institutionalisation of a process of correction of

the assignment which will be maintained until mid-

May: the teacher asked for the assignment to be

handed in on 27

of March and on that date, she

published videos with the correction of the exercises.

She then assigned as a task on GC the correction of

the exercises already done, asking the students to do

it on the text of the exercises already done in a

different colour than the one used previously.

Throughout the process, there are synchronous

lessons and many asynchronous exchanges between

T and individual students.

Episode 3: Peer Assessment on GM. Episode 3

occurred in GM: for the entire duration of the episode,

the teacher shared the screen. It is a planned assessment

session involving four students. The session consisted

of three phases. In the first phase, the teacher asked

them to carry out a function study in a document shared

with and editable by the whole class: each of the 4

involved students carried out a part of the exercise and

corrected the work of the previous students. In the

second phase, the teacher asked the whole class to draw

the graph of a function given certain characteristics,

and then she shared and analysed the answers of the

four involved students. In the third phase, it took place

the correction of one of the exercises assigned to the

whole class and conceived as preparation for the

assessment period. The correction discussion involved

all four students and was triggered by the solved

exercise of one of them.

So far, we described the data, without making

explicit our intentionality as researchers in

mathematics education. Now we try to systematize

our process in support of our claim referring to

Radford’s work.

CSEDU 2021 - 13th International Conference on Computer Supported Education

628

5 OUR APPROACH

Using the metaphor of the eye of the theoretician

(Radford, 2010), quoted in Section 1, we recall the

structure of our work as it has been conducted and

will be presented in the first analysis. We emphasize

that a crucial point is the objectification process

(Radford, 2008) in which the students encounter the

object of knowledge. In our case the object is FA, the

theoretical eye is our eyes as researchers, and the

students are the teachers involved in the project.

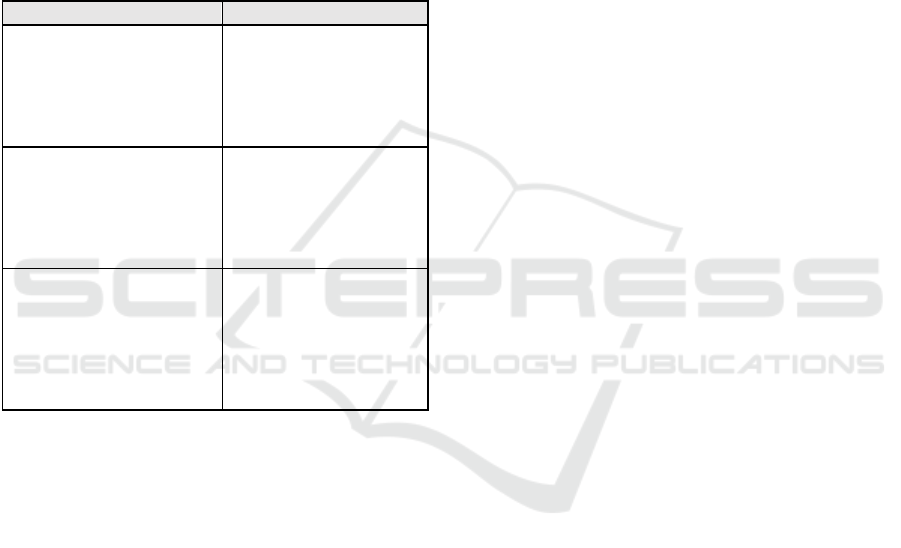
Table 1: Parallelism with Radford’s quote (p.4), continuing

from section 1.

Radford’s quote In our context

[...] The domestication of the

eye is a lengthy process in the

course of which we come to

see and recognize things

according to “efficient”

cultural means. [...]

In the observed practices,

the researchers recognized

features that are consistent

with the FA construct.

I am not saying that the

students did not see two rows.

They surely did. But they did

not deem it important to

recognize the figures as being

divide

into two rows.

The teachers who do not

intentionally perform FA,

but the researcher links

teachers’ practices to a

construct she is aware of,

the construc

of FA.

the capacity to intuit and

attend to them in certain

manners rather than others,

belongs to those sensibilities

that students develop as they

engage in processes of

objectification.”

Teachers can develop their

sensibility as they engage in

a process of objectification

of FA.

Section 4 outlines the data collected, now we need

to start the process of justification described in the last

two rows of Table 1: in this respect we introduce the

analysis of the data and the first results obtained both

from the questionnaire and from the observation.

6 ANALYSIS

6.1 Analysis of the Questionnaire

Working Methodology. Our starting point has been

the answers to the questions in which teachers

highlighted how their way of giving feedback to

students was changed. Looking at the answers we

could find a relation between the tools used for LDL

and the changes, but we could also find some

examples of the changes. More precisely, we selected

the ones where we found coherence between the

content of the answer and at least one of the five

strategies of FA.

Analysis Outcome. Most teachers declared changes

in the way they were giving feedback (79%) to

students, and almost 60% of the involved teachers

agreed with the claim I can give feedback to each

student for every task she sends me, and it seems to

me that some students are improving.

This phenomenon found a first explanation in the

open answers to question Q24: How did it change [in

the way you give feedback]? In the answers, 41 out of

99 of the teachers referred to individualization of

feedbacks and to an increased possibility to check on

students’ work giving personalized corrections. The

results show a strong presence of the strategies S2 and

S3. Indeed, globally, watching at the 41 selected

answers we see that at least one between S2 or S3 is

present. As some of the teachers affirm, this can be a

direct consequence of the technological environment

involved in LDL, which structurally leads to the

dematerialization of didactical materials, including

students' work. Indeed, there are at least two

important common features of such technological

environment: one is the automatic storage of the huge

amount of data exchanged by participants and the

other is the ease of access to these data. We see in this

sense a parallelism with Goody’s observation (1977,

p. 37) regarding the invention of writing and printing:

It changed the nature of communication beyond

face-to-face contact as well as the system for the

storage of information. […] No longer did the

problem of memory storage dominate man's

intellectual life; the human mind was freed to

study static "text" (rather than be limited by

participation in the dynamic "utterance").

The questionnaire provides an overview of an

emerging phenomenon, that we, as researchers in

mathematics education, associate with FA: this does

not mean that it is FA, but that it shares some

characteristics of FA, related to S2 and S3.

6.2 Analysis of Classroom Observation

Working Methodology. Starting from our

theoretical framework we tried to define an

observation tool grounded in the definition of FA

given by the literature that could detect the specific

practices observed during LDL. In order to do so, we

first needed to redefine some of the usual classroom

practices in the new environment. The definitions we

present here clarify the effect of some of the structural

features of the classroom in a virtual environment

during the lockdown, that is, the structure given by

the mediation of digital technologies that allows

Can Formative Assessment Practices Appear Spontaneously during Long Distance Learning?

629

maintaining the educational relationship between

students and teachers in that context.

The result of our work is in the following: we

indicate the aim of an action in the classroom, then

we show the instantiation of that action in LDL

classroom with GSE tools in comparison to the class-

room in the school building.

Action: Positioning in the classroom.

School Building: Desk/teacher desk, objects used,

body/physical presence, etc.

Virtual Classroom: It is multiple: on one side the

physical workstation with objects used (pen,

notebook, hardware...), on the other the software used,

and the different accounts, etc.

Action: Communicative interaction in the

classroom.

School Building: written and oral communication,

deictic language, gestures, etc. Oral interactions are

mostly public, and the exchanges can have different

objectives (explanation, evaluation, feedback,

affective-relational), etc.

Virtual Classroom: written and oral

communication, via mail, private messages, public

messages, videoconferencing; content exchange in

class subgroups or pairs. In the case of the

asynchronous component in GC, any activity

assignment that the teacher makes to the whole class

(or to a group of students) also implies that this

activity is sent to each student in the class (or

belonging to the group). The need to mediate

communicative intentions and deictic language by

using "additional" devices (e.g., indicating becomes

moving the mouse in a screen that is situation visible

to the other), etc.

Action: observing student’s work.

School Building: rotating between desks; calling

to the teacher’s desk, etc.

Virtual Classroom: flexible mode depending on

the software used: grid view on GM, scrolling

through delivered tasks on GC, use of collaborative

documents and/or applications that allow you to see

the work being done, asking for screen sharing, etc.

Action: to collect/send materials.

School Building: delivery on paper, writing on the

blackboard (or teacher's PC screen projection), use of

textbook and other resources, use of electronic

Virtual Classroom: sending photos of paper

materials, using shared collaborative documents,

sharing web resources via links (i.e., text string

https://docs.google.com/document/d/1l2Yu5Lth6QAmB

MHdJxxmU1XyOfGJ1BeXlQp0nSmU6MA/edit?usp=s

haring

sharing, indeed, each web resource associated with a

link), etc.

As a second step, we analysed the three episodes

using the chosen FAMT&L indicators categorised

according to the five FA strategies, as we describe in

the theoretical framework (Section 2). It is worth

mentioning that the FAMT&L table was created for

the analysis of video recordings of lessons in the

physical classroom. Nevertheless, we assume that it

is legitimate to use it to analyse the unfolding of a

possible lesson on LDL in a non-experimental

environment for which we have documentation. Each

of the three selected episodes in the classroom was

analysed individually by two researchers: the aim was

to find out which practices were implemented

according to the ones in the table. After the individual

selection the inter-rater reliability was calculated

through Cohen’s K (Landis & Koch, 1977) obtaining

good concordance for all the three episodes

(respectively 0,69, 0,63 and 0,69 for episode 1,2 and

3). The union of the indicators selected by each

researcher has been chosen as the final option after a

discussion about the indicators on which the

researchers initially disagreed. We provide the reader

with the three coding tables of episode 1,2 and 3 in an

external online document

; the analysis which follows

refers to such tables. In the external document also

examples taken from each episode are given.

Analysis Outcome. We observe that out of 72

considered indicators, 38 are detected in episode 1,

taking place mid-March, 49 are detected in episode 2,

taking place at the end of March, and 53 in episode 3,

which takes place the 18th of May. Moreover, we also

see a distribution of the detected indicators along the

five FA strategies. This makes our assumption well-

founded: we can affirm that FA can be used as a lens

to look at some of the emerging phenomena in LDL,

when implemented with the described tools. In

particular, looking at the 30 indicators present in all

the three episodes, we find that 9 of them can be

considered a consequence of the use of a specific

LDL environment, in this case some tools of the GSE.

We comment on them briefly.

1.T fixes with the students the date for the

assessment.

13.T distributes the text of the test/task.

When considering the platform GC, together with

any assignment, not only the assignment is sent to the

students, but also notifications and reminder related

to the task. Moreover, once an action is done in the

CSEDU 2021 - 13th International Conference on Computer Supported Education

630

platform, every person that is part of that GC class

and has the right to see that action can immediately

access to and interact with it.

26. T asks questions to the whole class.

27. T asks questions to a single student.

These two indicators can be stackable on some

occasion on GC: for example, when an assignment is

sent to the whole class, each student receives it

individually and has at his disposal a private space of

interaction with the teacher.

36. T uses a structured tool of observation.

37. T takes some record of the behaviour of

one/all student/s.

38. T takes some record about how much the

students have achieved to handle the content of the

test/task.

39. T takes records from her/his desk.

40. T takes records passing among the students.

These five are related to the structure of the

technological environment which leads to the

dematerialization of didactical materials, including

students 'work, and their automatic archiving for its

own design, as affirmed also by some of the teachers

involved in the questionnaire.

We affirm that these 9 indicators, which we have

seen as being structural to some tools used for LDL,

are sufficient to create a fruitful ground for FA

practices. Actual practices of FA then obviously

depend on the teacher's intentions.

Considering the observed teacher T, she managed

all the information granted by the environment she

was in, in specific ways during LDL, and especially

along the three analysed episodes. Observing her

actions with our theoretical tool, we noticed that

among the other indicators that were presented in all

the three episodes, 11 could be related to the 9

previously listed: they effectively represented her

specific way to manage the information she was

getting from students through the media used. Thus,

the spontaneous emerging of FA practices can be

related to this managing of the structural

characteristics of the considered LDL environment:

we can say that at least the following 11 indicators

make the teacher’s practices in LDL readable as

effective FA practices:

4. T asks some questions to the students to verify

if the students understood the aims of the assessment.

8. T asks some questions to the students to verify

that the students understood the test/task instructions.

20. T provides advices or suggestion during the

test/task.

22. T gives enough time so that every student can

work through the test/task (without anxiety).

30. T asks a new question based on a wrong

answer to the previous one.

31. T asks a new question based on the previous

one.

42.T illustrates the results of the test/task to the

whole class.

45.T gives back the results in a short time.

46.T describes the mistakes as an occasion to

learn.

68. T analyses the data she/he collected in the

classroom.

70. T writes the profiles with respect to knowledge.

We care to mention one last practice that was

implemented by T during episode three. In two

different moments T, who has at her disposal the

solution of the same task as made by the student,

decides to communicate with one student upon her

answer using the answers of other students producing

a sort of dialogue between answers. This dialogue

involves T, the students, and their written productions:

it elicits evidence of student understanding (S2) and

it activates students as instructional resources for one

another (S4), and for this reason can be considered a

practice of FA. However, it cannot be easily tracked

by FAMT&L’s indicators because, as far as we

noticed, it is strictly linked to the structure of a digital

technology-based environment and especially storage

and ease access we mentioned in Section 6.1.

Recalling our claim, we argue that teaching and

learning practices conducted in digital-technology

based environment have characteristics that can be

associated with at least three out of five FA strategies

and can therefore be a starting point to enhance

practices of FA. Thanks to classroom observation we

were able to better understand the emergent

phenomenon, dividing what is structural to the used

tools, and what is specific to the teacher’s actions and

choices. More precisely, we structured our perception

of observed classroom dynamics during the lockdown

with the lenses of FA, and with the five FA strategies

and the selection of indicators we described in the

theoretical framework (Section 2).

Summarising, we noticed that there are 9 out of 72

FAMT&L indicators of FA whose existence is a

consequence of the digital tool used for the teaching

environment (e.g., GC). These 9 indicators are

associated with the strategies S1 and S2 regarding the

possibility to elicit evidence of student understanding

and the clarification of learning intentions and criteria

for success. Observing T’s agency and its unfolding

under the lens of FA and our theoretical tool, we were

able to see that a specific managing of the effect of

the 9 indicators leads to practices readable as

effective FA practices according to our construct.

Can Formative Assessment Practices Appear Spontaneously during Long Distance Learning?

631

7 CONCLUSIONS

Digital technologies have allowed the realization of

LDL during the first Italian lockdown, resulting in a

massive use of such technologies for almost the entire

school population over three months. On the one hand,

the possibility of collecting and sharing information

in an efficient way is a known effect of digital

technologies. On the other hand, during the first

lockdown in our country, the widespread use of

digital technologies has become constitutive of any

didactical practices, generating a huge amount of data

at the disposal of students and teachers. Despite the

undeniable difficulties encountered, this period will

result in a wealth of experience on which teachers and

students can decide to work, making the most of it.

Within this work, we tried to shape this wealth of

experience using the construct of FA, that guides our

eye as researcher in mathematics education and limits

the multiple phenomena we observed during LDL.

More precisely, we structured a theoretical tool based

on FA theoretical framework in order to link FA

indicators to spontaneous teachers’ and students’

actions and behaviours we observed. We found that

the listed above 9 out of 72 indicators can be ensured

simply by being in a digital-technology based

environment and they are responsible for the huge

amount of didactical data that can be managed.

Nevertheless, not every teacher takes advantage of

this possibility in the same way, some of them feel

overwhelmed by all the received information. One

way to manage the increased workload could be the

intentional use of FA construct in its entirety, and FA

practices. For example, the use of S4 and S5 would

allow the teacher to redistribute workload between

her and the students. We could say that is the

management of the effect of the 9 indicators that led

to the emerging of practices that could be associated

with the FA construct. We have evidence of at least

one teacher whose spontaneous didactical agency can

be described using more than half of the FA indicators,

widespread along with the five FA strategies and we

believe that other teachers can take advantage from

this work. Indeed, every teacher that implemented

asynchronous practices, or that recorded her

synchronous lessons during LDL, has at her disposal

a huge amount of data of the same kind we analysed

about her didactical practices, and can eventually

analyse them herself. Moreover, professional

development on FA from now on could work not only

on shared experiences and individual practices, but

also in the direction of a decreasing of the workload

thanks to intentional use of FA from the teachers’ side.

As we show in the analysis of classroom observation,

some peculiarities of such environment impact the

deepest feature of human interaction, for instance, we

can refer to the storage and access to data introduced

in section 6. Thus, another direction seems to be of

high relevance within the context of digital-

technology based environment: the study of the

specific instantiations of known theoretical constructs

of mathematics education.

REFERENCES

Black, P., & Wiliam, D. (2009). Developing the theory of

formative assessment. Educational Assessment,

Evaluation and Accountability, 21(1), 5–31.

Bolondi, G., Ferretti, F., Gimigliano, A., Lovece, S., &

Vannini, I. (2016). The Use of Videos in the Training

of Math Teachers: Formative Assessment in Math.

Integrating Video into Pre-Service and In-Service

Teacher Training, 128.

Del Zozzo, A., Garzetti, M., Santi, G. (2020). Shaping

digital deconstruction: teaching and learning of

Mathematics during the lockdown. Magister, 32(1),

Sección Extraordinaria, pp. 78-86. ISSN: 2340-4728

https://doi.org/10.17811/msg.32.1.2020

Ferretti, F., Michael-Chrysanthou, P., & Vannini, I. (2018).

Formative assessment for mathematics teaching and

learning: Teacher professional development research

by videoanalysis methodologies. FrancoAngeli: Rome.

Ferretti, F., Del Zozzo, A., & Santi, G. (2020). La didattica

della matematica a distanza ai tempi del Covid-19 e la

sua interazione con l’identità docente. Annali online

della Didattica e della Formazione Docente, 12(20),

84-108.

Gagatsis, A., Michael-Chrysanthou, P., Christodoulou, T.,

Iliada, E., Bolondi, G., Vannini, I., Ferretti, F., Sbaragli,

S. (2019). Formative assessment in the teaching and

learning of mathematics: Teachers’ and students’

beliefs about mathematical error. Scientia Paedagogica

Experimentalis, 56(2), pp. 145–180.

Goody, J. (1977). The domestication of the savage mind.

Cambridge: Cambridge University Press

Landis, J. R., & Koch, G. G. (1977). The measurement of

observer agreement for categorical data. Biometrics, 33,

159-174.

Leahy, S., Lyon, C., Thompson, M., & Wiliam, D. (2005).

Classroom assessment: Minute-by minute and day-by-

day. Educational Leadership, 63(3), 18-24.

Radford, L. (2010). The eye as a theoretician: Seeing

structures in generalizing activities, For the Learning of

Mathematics, 30(2), 2-7.

Radford, L. (2008). The ethics of being and knowing:

Towards a cultural theory of learning. In L. Radford, G.

Schubring & F. Seeger (Eds.), Semiotics in

mathematics education: epistemology, history,

classroom, and culture (pp. 215-234). Rotterdam:

Sense Publishers.

CSEDU 2021 - 13th International Conference on Computer Supported Education

632