MMR: Multiple Majority Rule Model with Bias

Sancho Rodriguez Corrales, Edwin Armas, Martin King, Joshua Moorehead,

Omar Abou Nassif Mourad and Salem Othman

Wentworth Institute of Technology, 550 Huntington Ave, Boston, MA, U.S.A.

othmans1@wit.edu

Keywords: Bias, Majority Rule Model, Opinion, Opinion Dynamics.

Abstract: The Galam Majority Rule model describes how an opinion can spread in a network of nodes with no pre-

existing edges. The model is used to describe opposing opinions that are represented in two states (Susceptible

or Infected). This paper introduces a Multiple Majority Rule model (MMR) that improves the cons

surrounding the Galam Majority Rule model by allowing opinion bias and adding a third state (undecided).

The paper presents a comparative study between both models’ behavior and performance. Lastly, the paper

analyzes the impact of the bias in the consensus of a majority.

1 INTRODUCTION

In the last few decades, opinion dynamics models

have been developed to model the spread of opinion

in a population. People’s opinion can change based

on those they interact with. The Galam Majority Rule

model does not consider social constructs that make

people biased to what they believe (Rossetti, 2017).

Furthermore, it represents a two-state system where

every node in the population has an initial state:

Susceptible and Infected. This model gives a clear

advantage to the infected state skewing results

towards an infected majority.

Our Multiple Majority Rule model (MMR) can be

used as a two-state system: Adopter and Rejector, and

as a three-state system: Adopter, Rejector, and

Undecided which classifies a population that has not

formed an opinion yet. Unlike the Galam Majority

Rule model, the MMR model includes a modifiable

opinion bias which considers the impact of social

constructs on opinion dynamics. While a population

may have two equal majorities, the bias can be

adjusted so that one population has a higher

probability of becoming prominent.

An experimental analysis has been carried out

with the MMR model, to understand the effect of the

bias. We analyze how changing the bias parameter

will impact reaching a consensus and its effectiveness

in comparison to the inherent bias used in the Galam

Majority Rule model.

The paper is organized as follows: In Section 2,

we go through the Galam Majority Rule model, how

it works, and the cons that come with the model. In

Section 3, we go through the MMR model, how it

works, and its cons. Section 4 analyzes the differences

between the Galam and MMR model. Section 5

covers the results of how the bias influences the

outcome of the MMR model. Section 6 discusses

related work. Finally, in Section 7 we conclude the

paper, underlying the advantages of the MMR model,

and further work that can be done.

2 THE GALAM MAJORITY

RULE MODEL

Model States: The Galam model is composed of

nodes existing in one of two states, susceptible and

infected. Each state represents a definitive opinion

with one in support of the opinion and the other

against it.

Model Parameters: This model has three key

parameters which are Fraction Infected, Q-group, and

Iterations.

Fraction Infected: This parameter represents the

percentage of nodes that start as infected. Its value is

between zero and one, where zero means the whole

population is susceptible and one means the entire

population is infected.

Q-group: It represents a group of people of size Q,

which is a value from one to the maximum number of

Corrales, S., Armas, E., King, M., Moorehead, J., Mourad, O. and Othman, S.

MMR: Multiple Majority Rule Model with Bias.

DOI: 10.5220/0010475802070214

In Proceedings of the 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2021), pages 207-214

ISBN: 978-989-758-528-9

207

nodes, where one means there is one person in the Q-

group and the maximum number of nodes means the

Q-group is equal to the total population. Regardless

of size, all nodes in the Q-group are fully connected.

After each iteration, the model adds up the total

number of susceptible and infected nodes within the

Q-group. Whichever state holds the most nodes

becomes the majority, updating the Q-group state to

the majority. If there is a tie in the Q-group, then the

Q-group defaults to infected.

Iterations: It determines the number of times a Q-

group is selected.

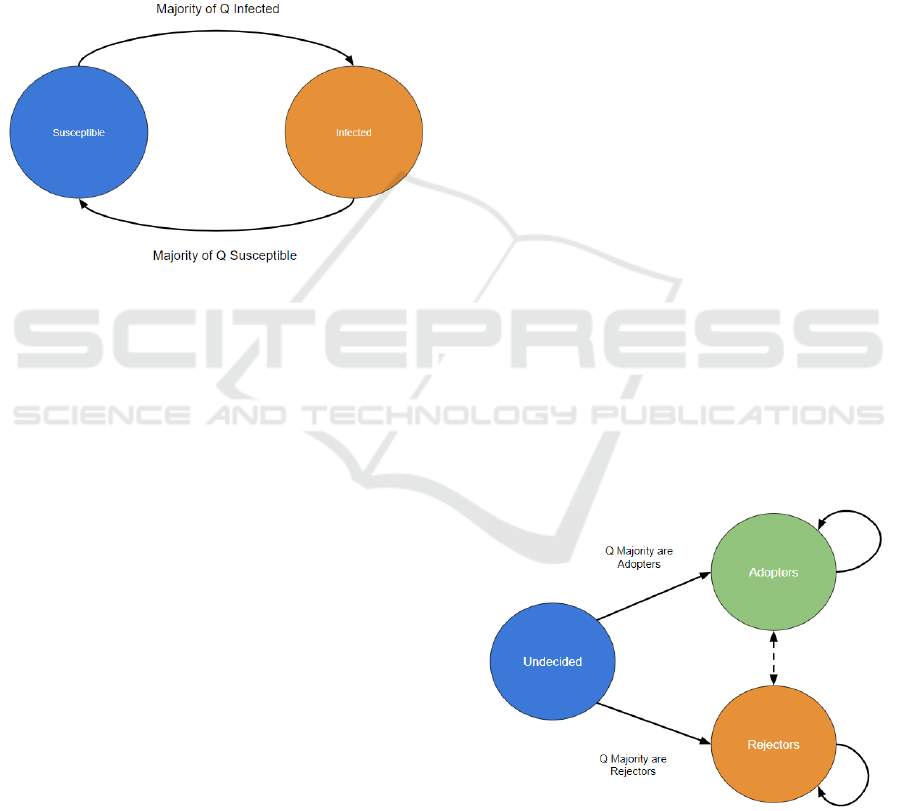
Figure 1: Diagram of the possible states and their

relationship for the Galam Majority Rule model. Nodes can

change from susceptible to infected and from infected back

to susceptible. The status of the nodes depends on the

majority status of the selected nodes for the Q-group.

2.1 Drawbacks with the Galam

Majority Rule Model

The Galam Majority Rule model is meant to model

the change in people’s opinions by using two states.

They found that the consensus for the nodes generally

tends towards whichever state had the majority in the

beginning (Krapivsky, 1). In real life, opinions that

start as a minority initially can become the majority

in the end. This model does not take into

consideration social biases that might influence the

decision making of the population. The algorithm

used by NDLib to compute the majority is biased

towards the infected status in every instance where

there is a tie, which results in a skewed experiment

when the size of the Q-group is even (Rossetti, 2017).

3 MULTIPLE MAJORITY RULE

MODEL (MMR)

Model States: Depending on the configuration, the

model can have up to three states. Undecided, people

who have yet to develop an opinion. Adopters and

Rejectors, which are those states that reflect the

people who have a predetermined opinion on a given

topic.

Model Parameters: This model has five key

parameters which are Fraction Adopter, Fraction

Rejector, Q-group, Iterations, and Bias.

Fraction Adopter: This parameter represents the

percentage of nodes that start as adopters. Its value is

between zero and one.

Fraction Rejector: This parameter represents the

percentage of nodes that start as rejectors. Its value is

between zero and one.

Q-group: Same functionality as in the Galam

Majority Rule Model but If there is a tie in the Q-

group, then the Q-group uses the bias parameter to

determine the majority.

Iterations: It determines the number of times a Q-

group is selected.

Bias: Given the case where a Q-group contains two

equal majorities, the bias value represents the

probability that the Q-group will change their opinion

to the adopter state. This value should only be set

inclusively between zero and one. When the bias

value is zero, the probability that the adopters are

selected as the majority in the Q-group is 0%. If the

bias value is one, the probability that the rejectors are

selected as the majority is 0%.

If the sum of Fraction Adopter and Fraction

Rejector is one, the MMR model behaves as a two-

state system. However, if the sum of these two

parameters does not sum to 1, the difference between

the sum and one represents the undecided population,

which models a three-state system.

Figure 2: Diagram of the possible states and their

relationship for the MMR model. If a node is undecided, it

can only go to the adopter or rejector state. If a node is either

an adopter or a rejector, it can be swayed to the opposite

state or stay at its current state depending on the Q-group

majority.

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

208

4 ANALYZING DIFFERENCE

BETWEEN GALAM AND MMR

MODEL

In this section, we tested the behavior of both models

using different cases to compare the reliability of their

results. The first subsection (A) discusses how each

model behaves when a tie occurs. In subsection (B),

we test the MMR model as a two-state system against

the Galam Majority Rule model. Lastly, in subsection

(C), we analyze the behavior of the MMR model as a

three-state system.

4.1 The Case of a Tie

The Galam Majority Rule model produces a skewed

result when the Q-group size is even. For Q-groups

that have an even number, there is the possibility of a

draw between both populations. A tie can only occur

if the Q-group is even. In the event of a tie, the Galam

Majority Rule model defaults the infected state to the

majority. This clearly shows that the model design is

skewed against the susceptible state. Table 1 &

Figure 3 below show the probability of the susceptible

state becoming the majority using different even

numbers for the size of the Q-group initializing both

populations at 50%.

Given a two-state system, like the Galam Majority

Rule model, using a Q-group size of 2, there are 3

possible outcomes in the Q-group. Two susceptible

nodes, one susceptible and one infected, or two

infected nodes. From this information, we can deduce

that the probability of the susceptible becoming the

majority in an iteration is one-third. The results in

Table 1 show the probability of the susceptible

population becoming the majority in a total of 400

iterations. The number of iterations selected was the

average number of iterations needed to reach a clear

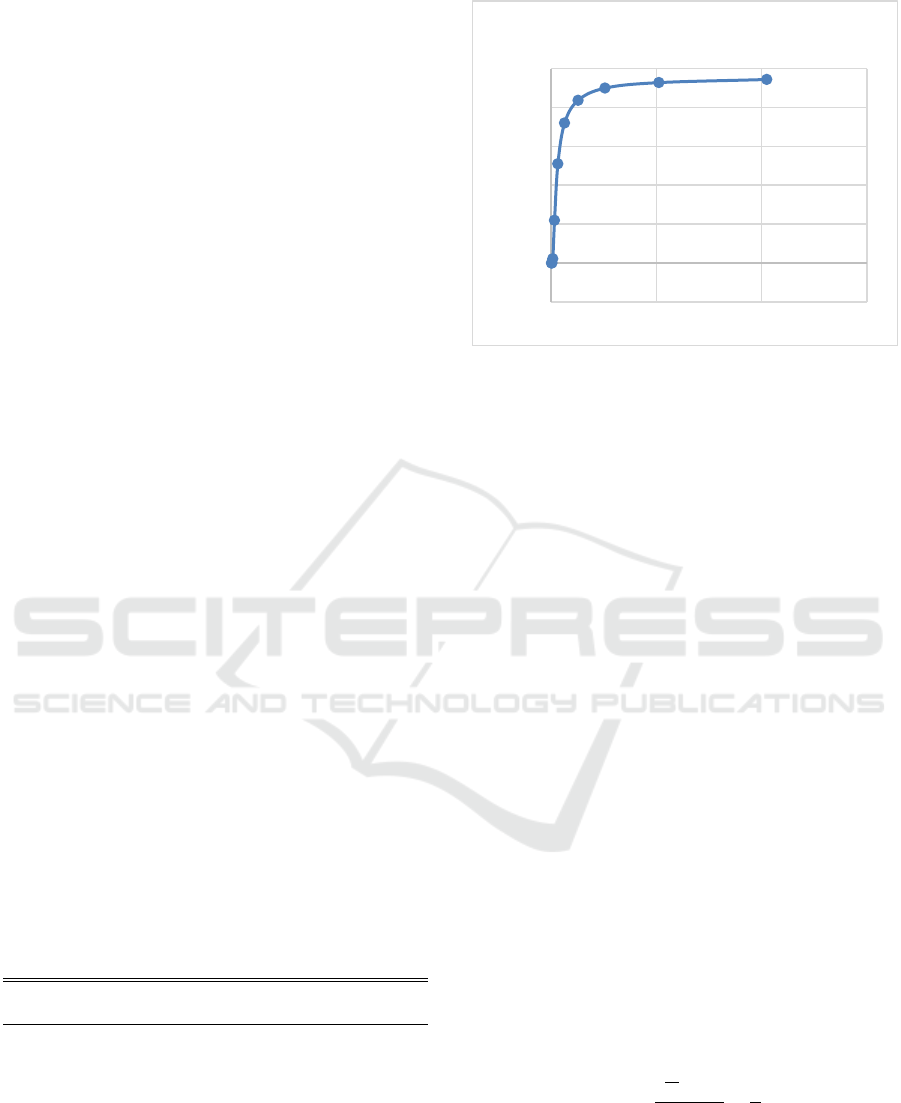
Table 1: Probability of a Susceptible Majority with an even

q-Group.

Q-group size

Probability of Susceptible

orit

2 < 0.00001

4 0.00002123787

8 0.011234105

16 0.109768941

32 0.25510399

64 0.36009636

128 0.418360442

256 0.449851167

512 0.4641378

1024 0.472096004

Figure 3: Plot showing how changing the size of the Q-

group using even terms affects the probability that the

susceptible state will become the majority.

majority. Hence, this is the reason we used 400

iterations to calculate the probability of a susceptible

majority.

Table 1 shows that when the size of the Q-group is

an even number such as 2, the susceptible population

has a significantly less than 1% chance of becoming

the majority. Given an even number, the plot shows

that, as the size of the Q-group approaches infinity,

the probability of the susceptible state winning

approaches 50%. This means that the Galam

Majority Rule model results in a very skewed

experiment when the Q-group consists of a small even

number of nodes. However, the experiment becomes

less skewed as you increase the size of the Q-group.

For example, when the size of the Q-group is 1024 the

susceptible population has a 47% chance of becoming

the prevalent majority.

Although the experiment becomes more balanced

as the Q-group increases in size, the simulation also

becomes unrealistic. It is assumed that every person

in a Q-group interacts with everyone else in the same

Q-group simultaneously. Using a large Q-group size

such as 500 would mean each node is connected to

the other 499 nodes in the Q-group. To assume that

every node share 499 common connections is

unrealistic.

lim

→

1−



𝑄



𝑄+1

(1)

Q is the value assigned to the size of the Q-group.

Equation (1) is used to calculate the probability of the

susceptible state becoming the majority in a single

iteration. Using limits, as the size of the Q-group

reaches infinity, this probability of susceptible

-0,1

0,1

0,2

0,3

0,4

0,5

0 500 1000 1500

Probability of Susceptible Majority

Q-group Size

Galam Majority Rule

MMR: Multiple Majority Rule Model with Bias

209

majority approaches one-half.

We used (1) to calculate the probability of the

susceptible state becoming the majority in a single

iteration. To compute the probability of the

susceptible state becoming the majority after the total

number of iterations, we calculated the cumulative

binomial probability, where the probability of success

in a single iteration was the value coming from (1).

Now let us measure the probability of the

susceptible state becoming the majority after the total

number of iterations instead of a single iteration.



400

𝑘







0.4



0.6



(2)

k is the number of successful iterations for susceptible

majority. To find out the probability of the susceptible

state becoming the majority after the total number of

iterations, we used the cumulative binomial

probability function (2). The probability of success on

a single trial is 0.40. The number of trials equals the

number of iterations, which we set to 400.

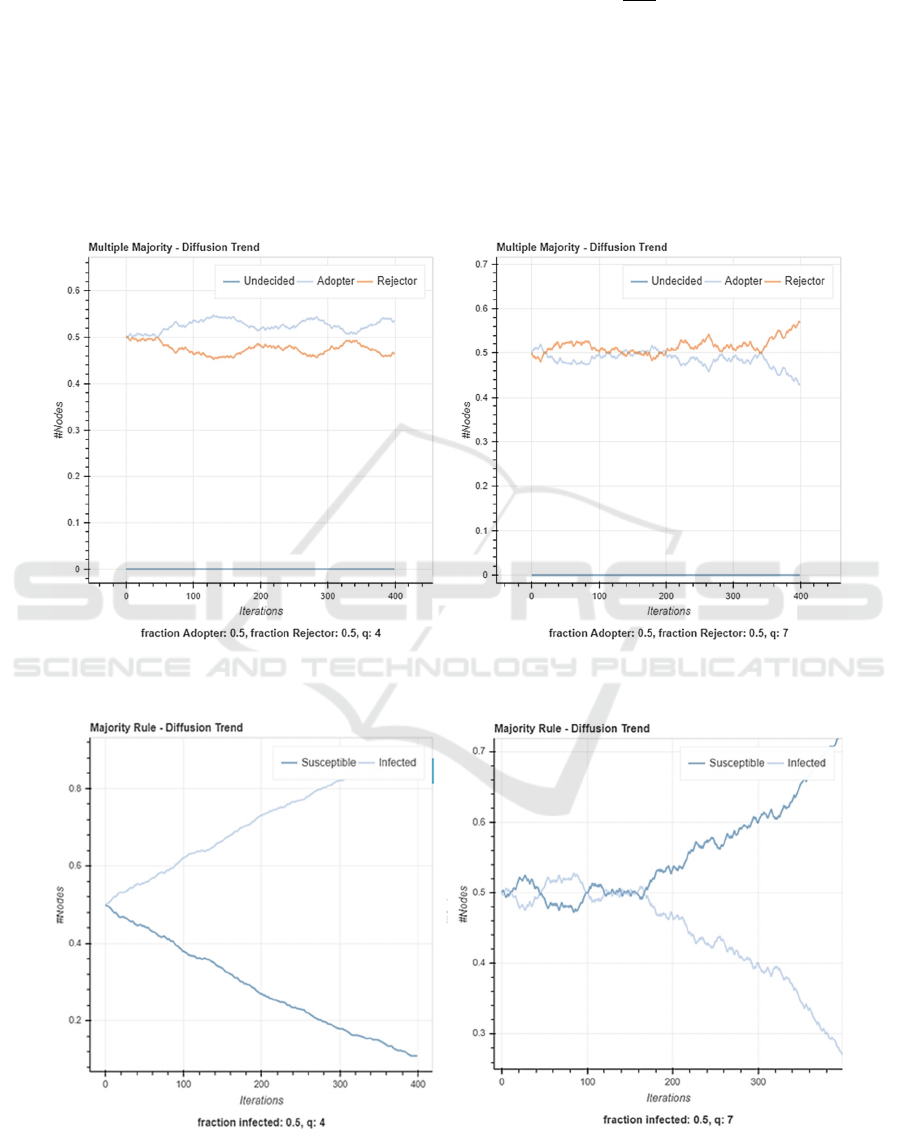
Figure 4: MMR model with a two-state system where both populations are set to 50%. 1000 nodes were selected for this

experiment along with 400 iterations, a neutral bias, and a Q-group size of 4 and 7 from left to right.

Figure 5: Galam Majority Rule model configured with the same initial parameters as shown in Figure 4 without the bias

parameter.

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

210

Finally, the last field is the number of successes,

which is the minimum number of successful iterations

for a population to take over the majority, which in

this case is 201. After you input all the values in their

respective fields you will find the probability of

success on a single trial. The sum of all the equations

with the different values of k will give you the

probability of the susceptible population becoming

the majority after 400 iterations. This probability

could be expressed by P(400 ≤ X ≥ 201) where X is

the number of iterations required to be the final

majority.

In the case of the MMR model if a tie occurs,

regardless if Q is even or odd, the outcome of the

majority is chosen depending on what the bias value

is. The user can choose to have a biased or unbiased

experiment favoring either adopters or rejectors, or

neither. If the user chooses to make a balanced

simulation, the bias value must be set to 0.5, which

will result in the majority being chosen stochastically

whenever a tie occurs (

Chaouiya, 2013)

𝑄2

⁄

𝑄

(3)

Equation 3 is used to calculate the probability of

the adopter or rejector population becoming the

majority using a two-state MMR model. The formula

assumes the model uses a neutral bias and both

populations start at 50%.

Since (3) can be simplified to one-half, we can

conclude that, given a neutral bias, both populations

have exactly a 50% chance of becoming the majority

in a two-state system. It must be noted that you can

use a Q-group of any size, even or odd and the

probability will not change.

4.2 The Case of Two States

The following charts showcase the MMR model

functioning as a two-state system in comparison with

the Galam Majority model in its respective order.

Figure 4 illustrates that when using the MMR model,

changing the size of the Q-group from an even or odd

number does not dictate that a specific population will

become the majority.

The left plot in Figure 5 demonstrates that when

you use an even number as the size of the Q-group,

the results are skewed towards the infected state. The

plot on the right shows that once the Q-group size has

been modified to an odd number, the Galam Majority

Rule model produces a balanced simulation where

neither population is advantaged.

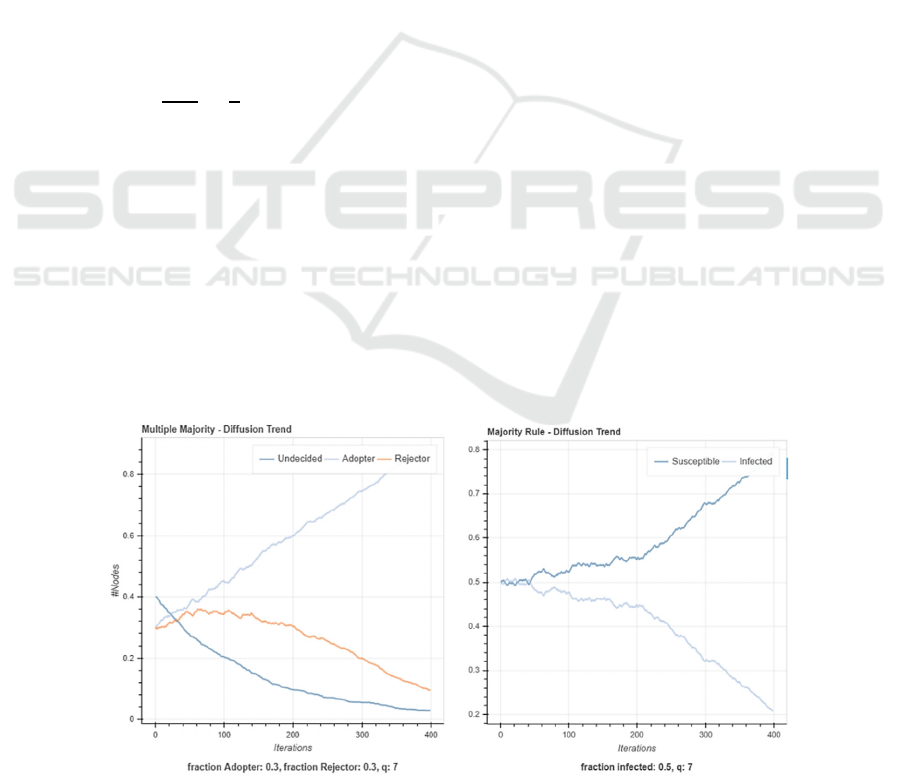
4.3 The Case of Three States

The Galam Majority Rule model cannot simulate a

three-state system. The MMR model introduces the

undecided state which represents a group of nodes

without a defined stance. It was found that the

addition of the undecided nodes increases the rate at

which nodes become opinionated. This does not

necessarily mean that a majority will be computed

sooner. The higher the population of undecided, the

more variance there is in the results. This means that

ignoring those nodes which are undecided might

make a big difference when computing a majority

with regards to time. In most cases, if you conduct an

experiment where the population is divided into 50%

of adopters and 50% of rejectors, the rate at which a

majority is computed is slower than that of an

experiment conducted with 30% of adopters, 30% of

rejectors and 40% of undecided.

Figure 6: Plots showing the impact of using the MMR model as a three-state system on the left in respect to a two-state system

Galam Majority Rule model simulation on the right. These plots also use a population of 1000 nodes.

MMR: Multiple Majority Rule Model with Bias

211

Figure 7: Plots showing a 0% bias for adopters and 100% bias for rejectors.

As shown in Figure 6, after 200 iterations using the

MMR model, 30% of the population changed their

initial stance. While using the Galam Majority Rule

model resulted in ~10% of the population changing

their initial status on the same mark. As expected,

using the three-state system MMR model results in a

faster simulation even though the two-state system

reaches a consensus sooner because of the lead start

in population.

5 THE IMPACT OF BIAS IN THE

MMR MODEL

In this section, we discuss how various values for the

bias can affect the outcome of a given simulation and

how the size of the Q-group has an effect on the bias

and its effectiveness.

5.1 Analyzing Bias Results

The results below show as expected, the two lines that

represent both states display polarizing results at 0%

and 100% bias. These lines get closer as they reach

the neutral bias value which is 0.5. From this point,

shifting the bias to one side or the other will be the

reason a state will have an advantage over the other.

With the ability to be able to set a bias before

running the model, we can visualize how the value of

the bias affects the outcome of the simulation. For the

data collected, we looked at different breakpoints of

bias values to visually see the impact it had. For

Figures 7-9, all the charts were initially configured to

have 7500 nodes, 2500 iterations, adopter, and

rejector populations at 40% each and undecided

population at the remaining 20%. Except for Figure

10.2, every left plot has a Q-group size of 4 and the

right plot has a Q-group size of 7. At the extreme ends

where the bias for either rejector or adopter is 0% or

100%, the charts show clearly that the majority

opinion with the favorable bias will end up with an

overwhelming majority. As the bias gets to the

25/75% split, this gap between the majority and

minority opinions begins to close. When there is a

neutral bias, the majority opinion only slightly hovers

above the 50% mark and not straying far from it.

As seen from these results, the dispersion between

the two states as we modify the values of the bias from

0 to 1. The closer it approaches either 0 or 1 the more

disparate the lines become. As we can see 0.5 is the

midpoint between the minimum and the maximum

bias and it is the point where neither state has an

advantage over the other. As we can see from this

diagram, both sides of the plot are symmetric,

meaning that setting a bias of 0.25 or a bias of 0.75

will make both simulations behave the same, just

changing which state is in the majority.

6 RELATED WORK

The Galam Majority Rule model has been studied and

researched extensively. It has been shown that the

Galam Majority Rule model generally results in the

final opinion being equal to the initial majority

(Krapivsky, 2003). This paper explores the spread of

opinion using the Galam Majority Rule model. It

found that for most systems the final opinion always

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

212

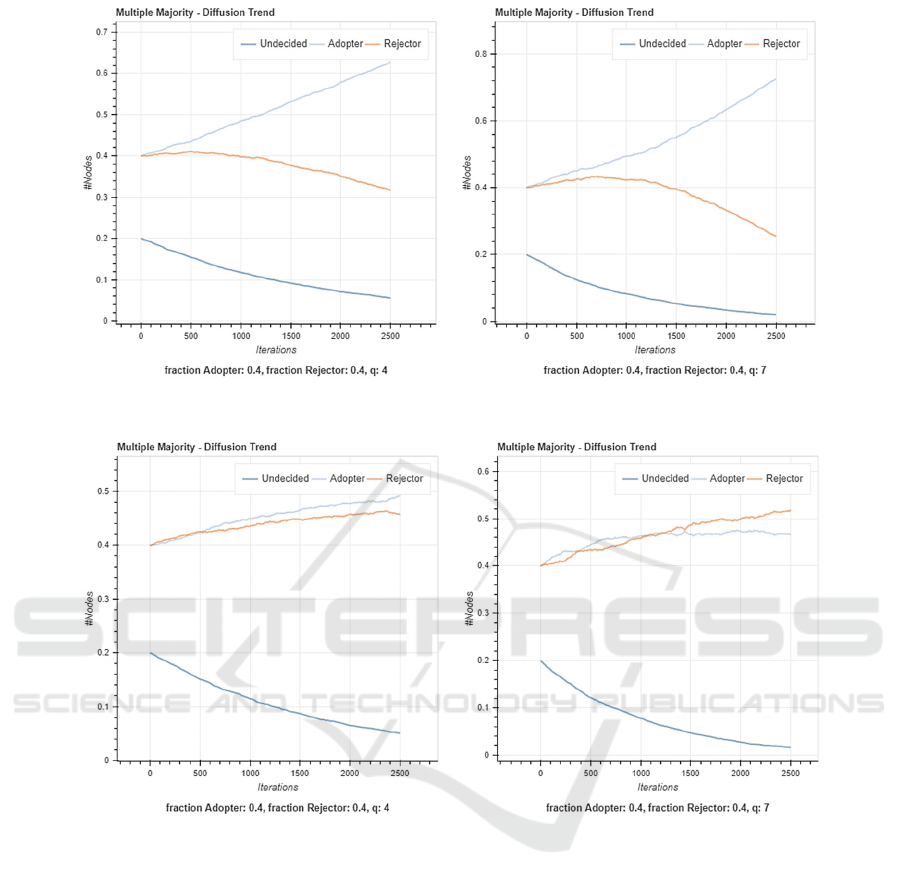
Figure 8: Plots showing a 25% bias for adopters and 75% bias for rejectors.

Figure 9: Plots showing a neutral bias (50%) for adopter and rejector.

equals that of the initial majority except when the

dimension of the model is one. The Galam Majority

Rule model when stubborn nodes are introduced into

the network (Mukhopadhyay, 2020). It shows that

when nodes are biased towards a preferred opinion,

the bias can affect the consensus of the preferred

opinion and can be achieved with a high probability.

It also shows that when stubborn agents with fixed

opinions are present, the resulting network will have

metastability, fluctuating between each of the

different states of the configuration. Our MMR model

behaves similarly to the gene regulatory networks

when they update their next gene when a tie occurs

(Chaouiya, 2013).

7 CONCLUSION AND FUTURE

WORK

The Galam Majority Rule model is a simple model

that shows the spread of opinions throughout a

population. However, it has an unmodifiable bias,

which results in creating skewed results. This model

does not allow for nodes without a definitive opinion.

It was found that counting for undecided agents in a

network makes the model more accurate with respect

to time as well as giving the model more variance in

the results. The bias has proved that it can be the

determining factor of a population reaching a

majority even if they started in the minority.

MMR: Multiple Majority Rule Model with Bias

213

The Galam Majority Rule model has proven not to

be consistent, as using an even number for the size of

the Q-group results in a skewed experiment against

the susceptible population. Alternatively, the MMR

model has proven that while using a neutral bias

neither population has an advantage. Furthermore, the

MMR model can be used as a two-state system to

replace the Galam Majority Rule model. Our model

can also be used to include undecided agents and add

a bias to account for how strong each of the opposing

populations’ opinions is.

For future work, the network graph the model uses

on the back end consists of nodes and edges which are

only formed between the nodes in the Q-group. We

believe that our MMR model could be further

improved if the nodes in the Q-group were not picked

at random and there was an underlying network layer

that simulated pre-existing connections like how

people interact in real-life. Then Q-groups could be

selected from nodes who are neighbors. This would

more accurately represent the way information

spreads in society. Further research could be

conducted by considering the eccentricity and

betweenness when selecting nodes to form Q-groups

from the network graph.

Lastly, use of statistical analysis may be considered

to find the average outcome of multiple model

simulations, and machine learning, to find the value

of the bias for different topics.

REFERENCES

Krapivsky, P. L., & Redner, S. (2003). Dynamics of

majority rule in two-state interacting spin systems.

Physical Review Letters, 90(23), 238701.

Mukhopadhyay, A., Mazumdar, R. R., & Roy, R. (2020).

Voter and Majority Dynamics with Biased and

Stubborn Agents. arXiv preprint arXiv:2003.02885.

Rossetti, G., Milli, L., Rinzivillo, S., Sîrbu, A., Pedreschi,

D., & Giannotti, F. (2018). NDlib: a python library to

model and analyze diffusion processes over complex

networks. International Journal of Data Science and

Analytics, 5(1), 61-79.

Rossetti, G., Milli, L., Rinzivillo, S., Sirbu, A., Pedreschi,

D., & Giannotti, F. (2017, October). Ndlib: Studying

network diffusion dynamics. In 2017 IEEE

International Conference on Data Science and

Advanced Analytics (DSAA) (pp. 155-164). IEEE.

Chaouiya C, Ourrad O, Lima R (2013) Majority Rules with

Random Tie-Breaking in Boolean Gene Regulatory

Networks. PLoS ONE 8(7): e69626.

https://doi.org/10.1371/journal.pone.0069626.

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

214