Manipulatives for Teaching Introductory Programming to Struggling

Students: A Case of Nested-decisions

Tlou Ramabu

, Ian Sanders

and Marthie Schoeman

Department of Computer Science, Tshwane University of Technology, Pretoria, South Africa

Department of Computer Science, University of South Africa, Pretoria, South Africa

Keywords: Programming, Nested-decision, Manipulatives, Struggling Students, Comprehension.

Abstract: Programming is one of the major subjects within the field of computing. In the higher education sector, some

introductory programming students succeed while others find it difficult to progress or learn the material.

Methods of teaching to program do not accommodate struggling students. Among introductory programming

issues, the nested-decision statement is one of the misconceived concepts. In the literature, there is evidence

that some programming educators make use of physical manipulatives to teach introductory programming.

However, there is no framework or validation methods used to identify and use the manipulatives. In this

study, we designed a manipulative called Nested-decider to assist struggling introductory programming

students to develop an appropriate conceptual knowledge about nested-decisions. The details of the design

and its functionalities are presented in this paper. We believe that teaching and learning nested-decisions with

the proposed Nested-decider manipulative could be a useful pedagogical intervention towards enhancing

struggling students’ comprehension. This is ongoing research where we identify and test various

manipulatives for struggling introductory programming students. The results will also help us to develop a

manipulatives – oriented pedagogical framework, which can be used to inform identification and use of

manipulatives.

1 INTRODUCTION

Programming is a major subject in the field of CS, but

is found to be difficult to learn by many Introductory

Programming Students (IPS) (Kelleher and Pausch,

2005; Jenkins, 2007). More specifically, certain

introductory programming concepts can be too

difficult or challenging for IPS to learn (Tuparov,

Tuparova and Tsarnakova, 2012). Qian and Lehman

(2017) say the source of some of students’ challenges

in programming are linked to incorrect prior

programming knowledge. In an attempt to help

students, some academic departments make use of

extra resources like tutors, mentors and assistants

(Forbes et al., 2017) as a supplement to formal

teaching in order to help Struggling Introductory

Programming Students (SIPS).

Teaching programming to IPS is a major

challenge (McDonald, 2018). Each topic may require

a special and relevant pedagogical approach. In the

literature we found few assistive methods that target

https://orcid.org/0000-0001-9081-8145

a specific topic or concept within introductory

programming education. Our overall study focusses

on developing an alternative pedagogical approach

for teaching and learning certain introductory

programming concepts. The approach we adopt is to

develop a manipulatives-oriented pedagogy suitable

for SIPS. Manipulatives are physical objects used in

the classroom with the aim of improving teaching,

learning and comprehension.

This paper reports on the manipulative called

Nested-decider for teaching and learning nested-

decisions. The purpose of the manipulative is to help

SIPS acquire conceptual knowledge and comprehend

nested-decisions better. In order to describe the

proposed manipulative adequately, Section 2 outlines

issues of learning programming decisions, followed

by the design details of the Nested-decider in Section

3. The conclusion is addressed in Section 4.

Ramabu, T., Sanders, I. and Schoeman, M.

Manipulatives for Teaching Introductory Programming to Str uggling Students: A Case of Nested-decisions.

DOI: 10.5220/0010477505050510

In Proceedings of the 13th International Conference on Computer Supported Education (CSEDU 2021) - Volume 1, pages 505-510

ISBN: 978-989-758-502-9

505

2 ISSUES OF LEARNING

PROGRAMMING DECISIONS

The struggle of learning to program often results in a

low retention rate, increasing dropout and academic

exclusion in the computing courses (Lister et al., 2004;

Gomes and Mendes, 2007; Rubio et al., 2014). Certain

programming concepts can be too difficult or

challenging to learn (Tuparov, Tuparova and

Tsarnakova, 2012). Some of the challenges include

misconceptions about assignments, tracing, decisions,

recursion, parameters, initialization and references

(Bayman and Mayer, 1983; Kahne, 1983; Samurça,

1989; Pea, 1986; Eckerdal and Thuné, 2005; Sajaniemi

and Kuittinen, 2008; Schoeman, Gelderblom and

Muller, 2013; Brown and Altadmri, 2017).

The misconceptions about decision-statement

issues date as far back as the 80’s where Pea (1986)

referred to them as a “conceptual” bug. Pea (1986)

says these kind of issues are caused by lack of

conceptual understanding of programming concepts

which can occur to all primary to college (HEIs)

students. Decisions and nested-decisions can be

challenging to comprehend (Sirkiä and Sorva, 2012).

In a study conducted by Sleeman et al. (1988) about

errors in introductory Pascal programming, the

authors found that students thought that the contents

of both the if-then and else clauses can be executed at

the same time. A similar study by Sirkiä and Sorva

(2012) also found that some students thought that if-

then can execute regardless of whether it evaluates to

true or false. A comprehensive study by Altadmri and

Brown (2015) investigated common programming

errors. The authors studied Java compilations of

250 000 novice programs across the world. Part of the

findings include misconceptions about operators in a

decision statement such as comparison operators (= =),

assignment (=) operators, short-circuits operators (&&

and ||) and conventional operators (& and |). A lack of

conceptual knowledge about decisions contributes to a

lot of mistakes during programming (Qian and

Lehman, 2017). The following section gives the design

and functionality of the proposed manipulative.

3 NESTED-DECIDER

MANIPULATIVES

3.1 The Scope

The main purpose of the Nested-decider manipulative

is to:

- Demonstrate how the short-circuit (&&)

operator works.

- Demonstrate how the short-circuit (||) operator

works.

- Demonstrate how the else clause works and

when to use it.

- Make SIPS understand that a nested decision

stops evaluating the rest of the conditions if

one condition evaluates to true.

- Make SIPS understand when to construct a

nested decision instead of an array of

separated or non-nested decisions.

- Enhance SIPS conceptual understanding about

how the nested-decision statement works.

In order to make SIPS understand gradually, we

start modelling a simple non-nested if (x) then {p}

statement with components of the manipulatives and

without short-circuit operators. Thereafter, short-

circuit operators are incorporated in the nested-

decision statement and modelled accordingly. The

manipulative does not consider or model the contents

within a decision statement.

3.2 Background on the Nested-decider

Manipulative

The components for assembling the manipulative are

modelled and named for the sake of referencing

purposes. Fig. 1 below shows the components used to

build the manipulative.

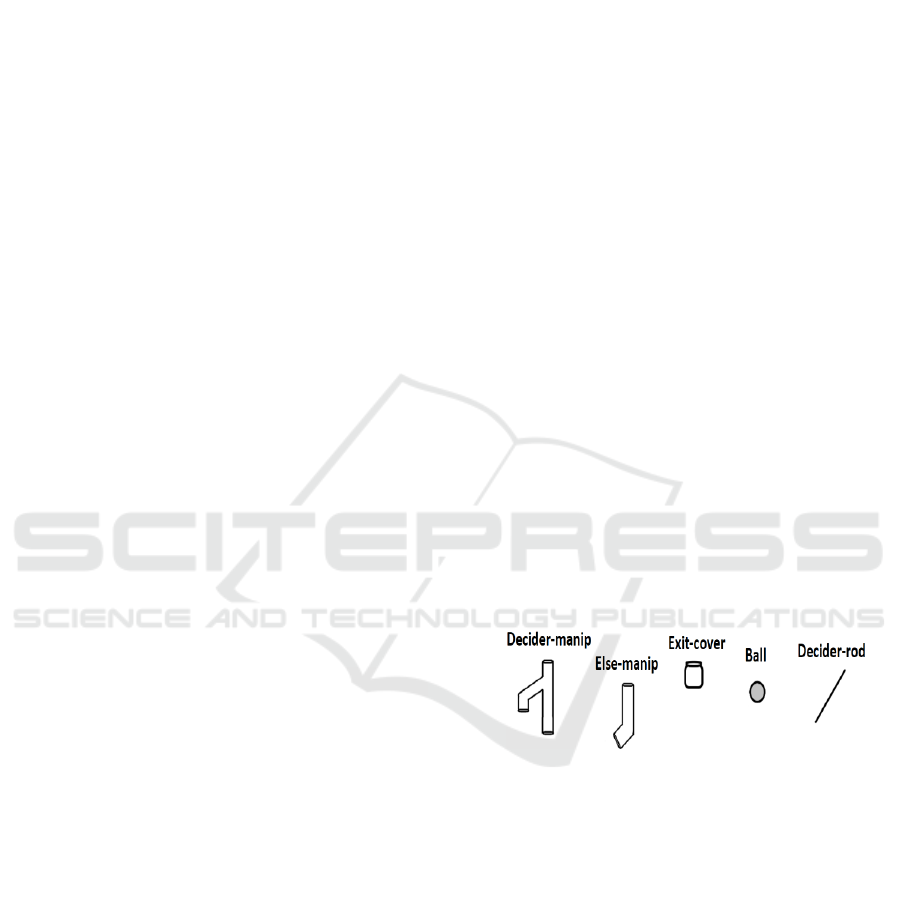
Figure 1: Components of the manipulative.

In Fig. 1, Decider-manip is a main component that

allows a ball to take a true or false route based on an

appropriate condition of a decision statement. It is a

transparent tube which should help SIPS to easily see

and comprehend the movements of the ball within it.

Else-manip represents an else clause and must be

connected to a Decider-manip if necessary. An Exit-

cover is used to connect at the bottom of the Decider-

manip and Else-manip. The Exit-cover allows a user

to remove the ball and restart the process repeatedly.

The top end of each component is bit thinner in order

to allow a smooth assembly of another component. A

ball represents the flow within a decision statement.

Decider-rod is used to block the ball at the

intersection within a Decider-manip. The small holes

CSEDU 2021 - 13th International Conference on Computer Supported Education

506

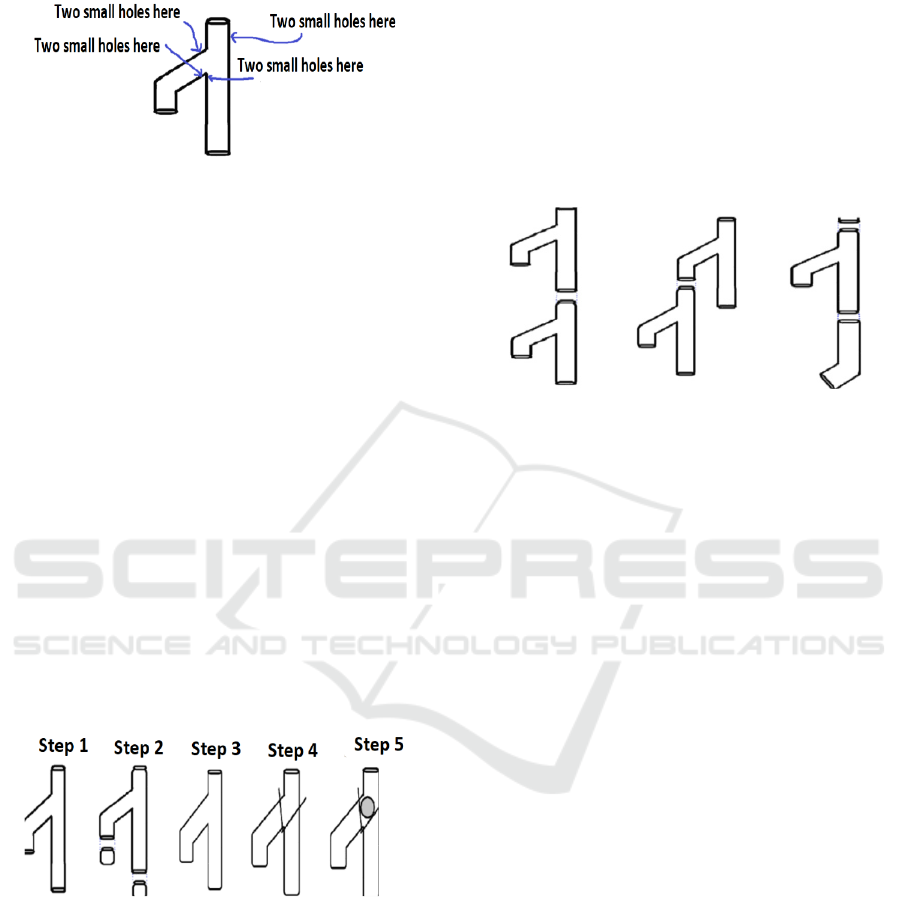
where Decider-rods are to be inserted are pointed out

in Fig. 2 below.

Figure 2: Nested-decider holes’ positions.

Basically, a Nested-decider consists of assembled

components based on the nature of a given decision

statement. The Nested-decider is assembled by a

lecturer and can later be assembled by SIPS. When

the manipulative is fully assembled, a lecturer should

demonstrate how a certain decision statement works.

In addition, SIPS can later do a demonstration under

the supervision of a lecturer. Practically, a user places

a ball in the transparent tube then makes use of

Decider-rods to navigate the ball along necessary

routes. The ball is always blocked by the Decider-

rods on the intersection of the Decider-manip. The

user is expected to make informed decisions based on

a given programming code (decision statement) by

removing the correct number of Decider-rods from

the correct side of the Decider-manip. For better

understanding of how a ball and Decider-rods work,

a manipulative for a simple decision statement is

given in the following section. Given a decision

statement like if (x) then {p}, the user is expected to

develop an appropriate manipulative by following the

steps in Fig. 3 below.

Figure 3: Simple decision-manipulative.

In Step 1 you take a Decider-manip, Step 2 you

connect the Exit-covers at both bottom ends of the

Decider-manip. Step 3 displays a complete set-up after

step 2 is completed. In Step 4, you insert the Decider-

rods through the small holes that cross the center of the

Decider-manip. In step 5, a ball is inserted and is in a

complete mode. On the intersection, the left side (the

side where Decider-manip is curved) represents a true

evaluation from an if condition. Alternatively, the right

side (non-curved straight exit) represents a false

evaluation. If the condition of a simple decision

statement evaluates to true, the user is expected to

remove the Decider-rod on the left side then the ball

will take a left curved direction and drop at the bottom

inside the Exit-cover. At the end, the user is expected

to understand that one side of the path has opened and

has made an informed decision by removing the correct

Decider-rod. In the case of a complex (Nested)

decision statement when the use of manipulative

becomes more useful, the components can be

assembled as depicted in Fig .4 below.

Figure 4: A nested manipulative build-up.

The first depiction of the design in Fig. 4 attempts

to assemble an if (x) then {y} elseif (p) then {r}

statement and can be nested as long as necessary by

connecting another Decider-manip at the end of the

last Decider-manip. The first depiction in Fig.4

doesn’t necessarily need to face the same direction, it

can be turned clock- or anti-clock-wise if necessary.

The second depiction in Fig. 4 represents a compound

decision statement like if (x) then {y} if (p) then {r}.

The nesting within a compound decision statement

can also be as long as necessary by connecting other

Decider-manips. The last depiction in Fig. 4 shows an

Else-manip with a possible connection to Decider-

manip. The connection represents a …if (x) then {y}

else {q} kind of statement. An Exit-cover can be fitted

anytime during the assembling phase to indicate the

end of the decision statement. For more information,

the following section explains a complete Nested-

decider with short-circuit operators included.

3.3 Nested-decider with Short-circuit

Operators

In this section, we demonstrate how short-circuit

operators can be taught using the manipulative. We do

that by building a complete Nested-decider

manipulative with an else clause included. The Nested-

decider is intended to be used primarily by the lecturer

to teach nested-decisions to SIPS. If necessary, SIPS

can play around with the manipulative for more

understanding. The manipulative should be used in an

appropriate scenario and nested-decision program. In

Manipulatives for Teaching Introductory Programming to Struggling Students: A Case of Nested-decisions

507

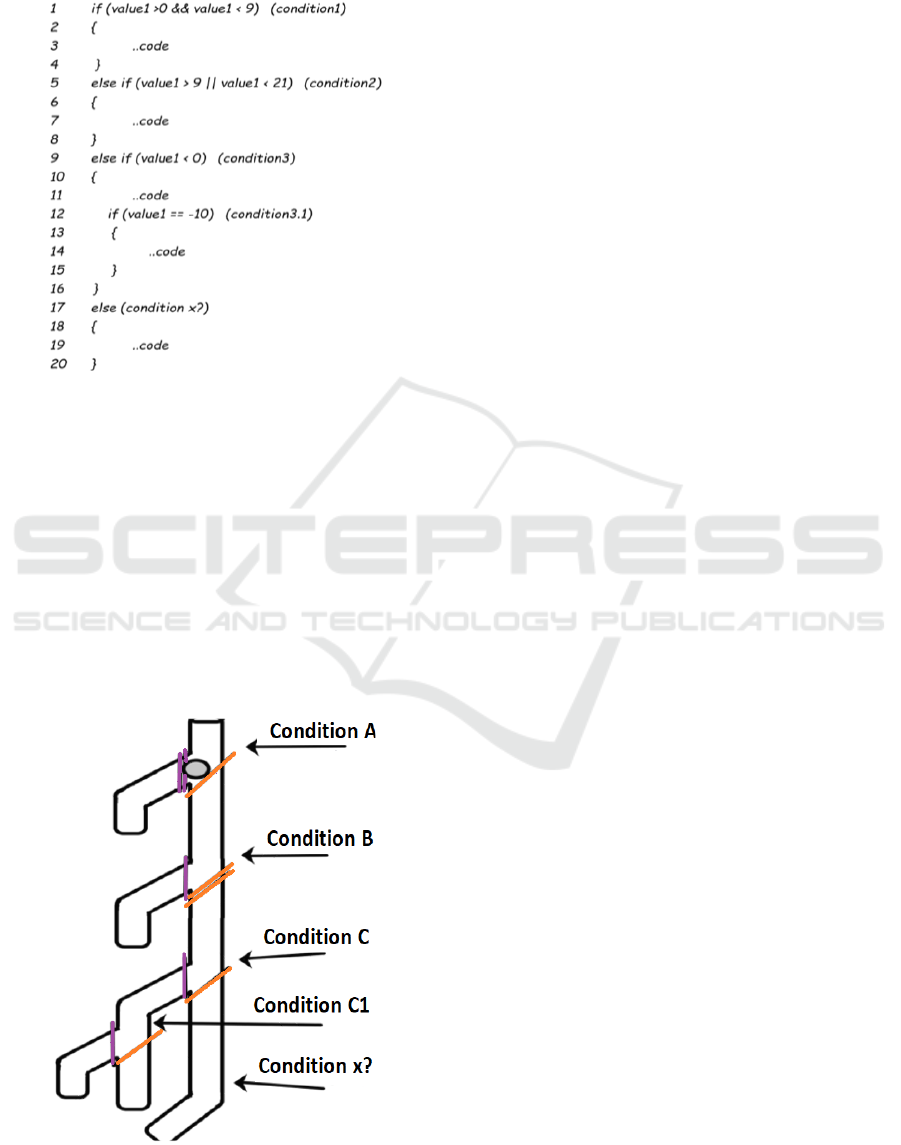
order to understand the overall manipulative

functionality, a Java/C++ decision statement depicted

in Fig. 5 is considered.

Figure 5: Nested-decision statements.

Now the teacher has assembled the Nested-

decider manipulative in Fig. 6 based on the code

depicted in Fig. 5. The process of assembling the

components can yield some enhancement in

comprehension, therefore SIPS should later attempt

to build the manipulative based on a given code.

Another important process is for a lecturer to unblock

the paths by removing Decider-rods based on the

conditions. Note that the purple Decider-rods are for

true conditions and the orange Decider-rods are for

false conditions. The same unblocking exercise can

be practiced later by SIPS.

Figure 6: The intersections of the manipulative.

On the first part of the manipulative in Fig. 6

(condition A), you can see that there are 2 Decider-

rods that blocked the tube on the left side and 1

Decider-rod that blocked the tube on the right side.

All the Decider-rods have blocked the tube on the

intersection within a Decider-manip. When the

correct pattern of removing the Decider-rods is

applied, the ball will automatically take the

unblocked path.

A condition 1 in Fig. 5 represents condition A in

Fig. 6, because 2 conditions are expected to evaluate

to true for the content of an if-statement to execute.

Hence, true && true = true. If value1 = 5, then

value1 > 0? is true, and the lecturer/student is

expected to remove one of the 2 purple Decider-rods

from the left side. The ball will still be trapped on the

intersection because of the remaining Decider-rods

on both sides. On the very same first line in Fig. 5, the

right side condition says value1 < 9? This evaluates

to true, therefore the user should remove the second

purple Decider-rod, then the ball will instantly take a

path of the left side. Now the lecturer is expected to

be able to explain condition 1 better with actions

taken on the intersection of the manipulative. SIPS

are expected to see and understand that the && short-

circuit operator requires both conditions to be true for

the contents of the decision statement to execute.

Hence 2 purple Decider rods that represent true

condition on the left side are removed when each

condition becomes true. SIPS should be able to see

that it is now impossible for the ball to reverse in

order to get into other tubes. Therefore, the same

scenario must be explained in relation to the real

programming code. Furthermore, it should be clear

that the ball can’t move into the next intersection if

the Decider-rod on the right side (orange Decider-rod

for false condition) is not removed. A lecturer must

also emphasize that a compound decision statement

such as (if (value1 >9) if (value2 > 20)) can also be

used to represent condition 1, and it will not affect

how the user interacts with the manipulative. This

will help SIPS to play around decision statements and

manipulatives for further improvements and

understanding.

If value1 = 12, the left-hand side of condition 1

(Fig. 5) will be true and one of the right side Decider-

rod will be removed. On the right-hand side of

condition 1, value1 is not less than 9, therefore the

user is expected to remove the only Decider-rod, and

then the ball will automatically roll into the next

intersection (condition 2 in Fig. 5 and condition A in

Fig. 6). Therefore, SIPS will see that true && false =

false. They will also understand that it did not matter

whether one of the Decider-rod was removed or not,

CSEDU 2021 - 13th International Conference on Computer Supported Education

508

one false condition will cause a ball to roll into the

next intersection. This is because short-circuit

operators do not evaluate all its operands when

necessary. This promotes unnecessary evaluations

and promotes efficient memory saving when coding.

The other possibilities that can be demonstrated and

understood through ball movements are false && true

= false and false && false = false. The kind of ball

movements will also help SIPS with comprehending

how short-circuit (&& and ||) operators work.

If the ball is in the second intersection (condition

B) in Fig. 6, note that there are 2 Decider-rods on the

right side and one Decider-rod on the left side. The

Decider-rods are put in such way that they represent

condition 2 in Fig. 5. The reason behind a single

Decider-rod on the left side is because true || true =

true, true || false = true and false || true = true, hence

in the || evaluation true is required to be the common

denominator for a true evaluation. The only way a

ball can move to the next intersection is through false

|| false = false. Just like a short-circuit evaluation in

the && works, the || applies the same logic because

whenever a true evaluation is detected first, the right

side evaluation is automatically ignored because it is

unnecessary. The evaluation of short-circuit operators

starts from left to right. Therefore, in the case of if

(true || whatever.) and if (false && whatever.), the

“whatever” word indicates that whether it is true or

false, it doesn’t matter and is not even evaluated.

If the intersection is blocked with a single

Decider-rod on the right side and a left side as well, it

means a condition is not compound nor tied by a

logical operator. See condition 3 and condition 3.1 in

Fig. 5 which should be represented by a condition C

and condition C1 in Fig. 6.

Another important aspect in the Nested-decider

manipulative is the else clause. On the else clause of

the decision statement, the question mark is put there

to indicate that the condition is not necessary even

though it can be placed as value1 > 20 (line number

17 in Fig. 5). If one decides to put elseif value1 > 20

in line 17 instead of an else clause only, the program

will still work fine. However, with the Nested-decider

now SIPS can see and understand that the process of

removing pins will unnecessarily delay the

completion time of a nested-decision and will waste

computer memory during real code execution. In Fig.

6, the Else-manip at the end of the manipulative is

important because it indicates the else clause, and the

ball can be blocked with a Decider-rod just to

demonstrate an unnecessary delay during the

demonstration.

We believe that when we apply the proposed

Nested-decider to real SIPS, the overall manipulative

will give them more insight and conceptual

understanding about nested-decisions, short-circuit

operators and the else clause. Furthermore, the

manipulative can be adjusted in any way required by

the lecturer/student to fit the applicable scenarios of

nested decisions.

4 CONCLUSION

The main objective of this paper was to share a

designed manipulative which is meant to help

struggling introductory programming students with

conceptual knowledge and comprehending nested-

decisions better. We demonstrated the design details

of the manipulative (called Nested-decider) and its

functionalities. We demonstrated the Nested-

decider’s ability to show the critical aspects of nested-

decisions. We believe that the manipulative will serve

as an assistive tool for struggling students to learn

nested-decisions and ease their cognitive load. The

proposed manipulative has not yet been implemented

to teach struggling introductory programming

students. This will be done by following an

appropriate pedagogical framework (not reported in

this paper) in the form of action research with SIPS at

a higher education institution. During the action

cycles, both the lecturer and SIPS are expected to use

the manipulative. As part of future work, we will

share the implementation results in our next

publication.

REFERENCES

Altadmri, A., & Brown, N. C. (2015, February). 37 million

compilations: Investigating novice programming

mistakes in large-scale student data. In Proceedings of

the 46th ACM Technical Symposium on Computer

Science Education, 522-527. ACM.

Forbes, J., Malan, D. J., Pon-Barry, H., Reges, S., &

Sahami, M. (2017, March). Scaling Introductory

Courses Using Undergraduate Teaching Assistants. In

Proceedings of the 2017 ACM SIGCSE Technical

Symposium on Computer Science Education, 657-658.

ACM.

Jenkins, T. (2007). On the Difficulty of Learning to

Program. Proceedings of the 3rd Annual Conference of

the LTSN Centre for Information and Computer

Sciences, 53–58.

Kelleher, C., & Pausch, R. (2005). Lowering the barriers to

programming: A taxonomy of programming

environments and languages for novice programmers.

ACM Computing Surveys (CSUR), 37(2), 83-137.

Manipulatives for Teaching Introductory Programming to Struggling Students: A Case of Nested-decisions

509

McDonald, C. (2018). Why Is Teaching Programming

Difficult?. In Higher Education Computer Science, 75-

93. Springer, Cham.

Pea, R. D. (1986). Language-independent conceptual

“bugs” in novice programming. Journal of Educational

Computing Research, 2(1), 25-36.

Qian, Y., & Lehman, J. (2017). Students’ misconceptions

and other difficulties in introductory programming: a

literature review. ACM Transactions on Computing

Education (TOCE), 18(1).

Sirkiä, T., & Sorva, J. (2012). Recognizing Programming

Misconceptions: An Analysis of the Data Collected

from the UUhistle Program Simulation Tool. Master's

thesis, Department of Computer Science and

Engineering, Aalto University.

Sleeman, D., Putnam, R. T., Baxter, J., & Kuspa, L. (1988).

An introductory Pascal class: A case study of students'

errors. Teaching and Learning Computer

Programming: Multiple Research Perspectives. RE

Mayer. Hillsdale, NJ, Lawrence Erlbaum Asociates,

237-257.

Tuparov, G., Tuparova, D., & Tsarnakova, A. (2012).

Using interactive simulation-based learning objects in

introductory course of programming. Procedia-Social

and Behavioral Sciences, 46, 2276-2280.

Lister, R., Adams, E. S., Fitzgerald, S., Fone, W., Hamer,

J., Lindholm, M., ... & Simon, B. (2004, June). A multi-

national study of reading and tracing skills in novice

programmers. In ACM SIGCSE Bulletin, 36(4), 119-

150.

Gomes, A., & Mendes, A. J. (2007, September). Learning

to program-difficulties and solutions. In International

Conference on Engineering Education–ICEE.

Rubio, M. A., Romero-Zaliz, R., Mañoso, C., & Angel, P.

(2014, October). Enhancing an introductory

programming course with physical computing modules.

In Frontiers in Education Conference (FIE), 1-8. IEEE.

Bayman, P., & Mayer, R. E. (1983). A diagnosis of

beginning programmers' misconceptions of BASIC

programming statements. Communications of the ACM,

26(9), 677-679

Kahney, H. (1983, December). What do novice

programmers know about recursion. In Proceedings of

the SIGCHI conference on Human Factors in

Computing Systems, 235-239. ACM.

Samurçay, R. E. N. A. N. (1989). The concept of variable

in programming: Its meaning and use in problem-

solving by novice programmers. Studying the novice

programmer, 9, 161-178.

Brown, N. C., & Altadmri, A. (2017). Novice Java

programming mistakes: large-scale data vs. educator

beliefs. ACM Transactions on Computing Education

(TOCE), 17(2), 7.

Schoeman, M., Gelderblom, H., & Muller, H. (2013).

Investigating the effect of program visualization on

introductory programming in a distance learning

environment. African Journal of Research in

Mathematics, Science and Technology Education,

17(1-2), 139-151.

Sajaniemi, J., & Kuittinen, M. (2008). From procedures to

objects: A research agenda for the psychology of

object-oriented programming education. Human

Technology: An Interdisciplinary Journal on Humans

in ICT Environments.

Eckerdal, A., & Thuné, M. (2005, June). Novice Java

programmers' conceptions of object and class, and

variation theory. In ACM SIGCSE Bulletin,37(3), 89-

93. ACM.

CSEDU 2021 - 13th International Conference on Computer Supported Education

510